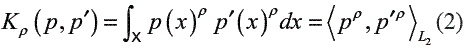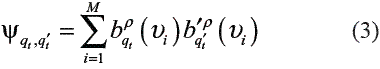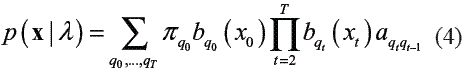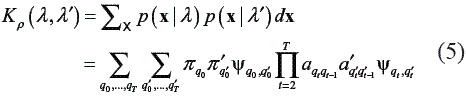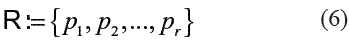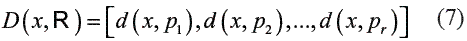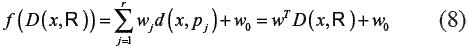Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230On-line version ISSN 2422-2844
Rev.fac.ing.univ. Antioquia no.50 Medellín Oct./Dec. 2009
Dissimilarity-based classification for stochastic models of embedding spaces applied to voice pathology detection
Clasificación basada en disimilaridades para modelos estocásticos de espacios de embebimiento aplicada a detección de patologías de voz
Julián Arias Londoño1,2*, Juan Godino Llorente2, Jorge Jaramillo Garzón1, Germán Castellanos Domínguez1
1Universidad Nacional de Colombia, Sede Manizales, GC&PDS, Campus La Nubia, Km. 9 Vía Al Aeropuerto La Nubia, Caldas, Colombia
2Universidad Politécnica de Madrid, Dept. ICS, EUIT Telecomunicación, Ctra. Valencia, km. 7, 28031, Madrid, España
Abstract
This paper investigates a new way for modelling the nonlinear behavior present in athological voice signals. The main idea is modelling the timedelay reconstructed attractors, taking into account the spatial and temporal information of the trajectories by means of a discrete Hidden Markov model (HMM). When the attractors are modeled with HMM it is possible to compute a probabilistic kernel-based distance among models to construct a dissimilarity space. This approach enables the possibility of comparing attractor families by their profiles, rather than evaluating individual nonlinear features of each subject. Classification of dissimilarity space is carried out by using a naive 1-nearest neighbors rule and it is compared with another classification scheme that employs two conventional nonlinear statistics: largest Lyapunov exponent and correlation dimension. Results show that the maximum accuracy with the proposed scheme is a 18.71% greater than the maximum accuracy obtained from the classification based on the conventional nonlinear statistics.
Keywords: Nonlinear analysis of pathological voices, embedding spaces, hidden Markov models, dissimilarity space classification
Resumen
En este trabajo se investiga una forma alternativa de modelar el comportamiento no lineal presente en las señales de voz patológicas. El método consiste en modelar atractores reconstruidos mediante la técnica de retardo de tiempo, teniendo en cuenta la información espacial y temporal de las trayectorias en el atractor a partir de modelos ocultos de Markov (HMM) discretos. A partir de modelos HMM entrenados para los espacios embebidos es posible calcular una medida de distancia basada en un kernel probabilístico, que posibilita la construcción de un espacio de disimilitud. Esta aproximación permite la comparación de familias de atractores a partir de la comparación de prototipos en lugar de evaluar características no lineales individuales de cada sujeto. La clasificación del espacio de disimilitud se lleva a cabo usando un clasificador por vecino más cercano y se compara con otro esquema de clasificación que emplea dos características convencionalmente empleadas en análisis no lineal: máximo exponente de Lyapunov y dimensión de correlación. Los resultados muestran que la máxima eficiencia alcanzada con el esquema propuesto es un 18,71% más alta que la máxima exactitud obtenida a partir de clasificación basada en estadísticas no lineales convencionales.
Palabras clave: Análisis no lineal de voces patológicas, espacios de embebimiento, modelos ocultos de Markov, clasificación de espacios de disimilitud
Introduction
In the analysis of physiological signals there exist several approaches that attempt to characterize the non-linear behavior of the underlying system. Different investigations have shown that changes in nonlinear dynamic measures may indicate states of pathophysiological dysfunction [1]. This fact suggests that chaos theory and nonlinear dynamic methods might potentially be applied to diagnose physiological disorders and to evaluate the effects of clinical treatments [1]. For the particular case of automatic detection of voice disorders, it has been shown that there exist several factors that lead to nonlinear behavior in the speech signal [2, 3]. Much of the work done in this area is based on the use of acoustic parameters, noise measurements and cepstral coefficients [4,5]. However, several researchers have shown that there is a physical phenomenon involved in the voice production process that can not be characterized by the above measures, termed Nonlinear Behavior. Such a behavior in speech is produced by some mechanics as: nonlinear pressure-flow relation in the glottis, nonlinear stress-strain curves of vocal fold tissues, and nonlinearities associated with vocal fold collision [1]. In reference [6], the authors introduced a classification for sustained vowel speech sounds, taking into account nonlinear dynamic concepts. Type I sounds are those that are nearly periodic. Type II sounds are those that are aperiodic or does not have dominant period. Type III sounds are those that appear to have no periodic pattern at all. From this classification, the problem is that normal voices can usually be classified as Type I and sometimes Type II, whereas voice disorders commonly lead to all three types of sounds [7]. Additionally, conventional parameters as Shimmer and Jitter are defined only for voice signals nearly periodic and thus their usefulness may break down for Type II and Type III signals [1].
On the other hand, the conventional method used to perform an analysis over a time series based on nonlinear techniques, employs the Takens’ theorem to construct the embedding attractor of the signal [8]. From this attractor some nonlinear statistics as the correlation dimension and maximum Lyapunov exponent are estimated [8] in order to perform the automatic classification. However, nonlinear statistics require the dynamics of speech to be purely deterministic (nonlinear statistics rely on a state space reconstruction and are likely to vary when the distribution of points in this state space changes), and this assumption is inadequate since randomness due to turbulence is an inherent part of speech production [7;9]. There are also numerical, theoretical and algorithmic problems associated with the calculation of nonlinear measures for real speech signals, casting doubt over the reliability of such tools [7]. In the last few years, a new measure called Approximate Entropy (ApEn) has been widely used. This measure can theoretically characterize the complexity of a large variety of systems [10]. ApEn is a measure of the rate of generation of new information, which can be applied to the typically short and noisy time series of clinical data. Nevertheless, in practice it has been shown that ApEn is heavily dependent on the record length and is uniformly lower than expected for short records [10]. Additionally, its calculation is expensive because it requires the evaluation of several trajectories for different embedding dimensions. In this work, a new way to characterize attractor trajectories is proposed. The main idea is modelling the embedding spaces taking into account the spatial and temporal information of the trajectories using a discrete Hidden Markov Model (HMM). A HMM is a stochastic model that models the variability of a time series allowing the comparison between sequences of different lengths with no obvious alignment principle across temporal observations [11]. By using this class of models it is possible to represent the dynamic behavior of the state space without any assumption about the nature of the underlying system (deterministic or stochastic). This approach enables the possibility of comparing attractor families by their profiles, rather than evaluating individual nonlinear features of each subject. In order to establish the discriminant capacities of the proposed approach in the problem of automatic detection of pathological voices, we carried out some experiments using conventional nonlinear statistics (correlation dimension and maximum Lyapunov exponent) as baseline in the framework of nonlinear analysis. The paper is organized as follow: section 2 describes the mathematical models and technique used to construct the patter recognition system. The section 3 presents the database, experiments and results. In the section 4 conclusions and discussions are pointed out and finally, some acknowledgments are presented.
Methodology
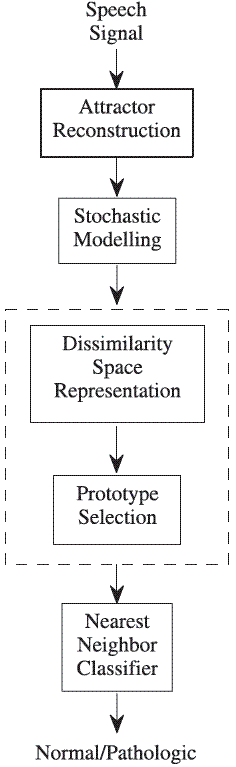
Figure 1 shows a sequential scheme for the particular patter recognition system proposed in this work. Each of the stages in the scheme will be explained in the follow.
Figure 1 Pattern recognition system for classifying nonlinear components of the normal/pathologic speech signals. The dashed box is equivalent to the extraction and selection stages in a conventional patter recognition system
Attractor reconstruction
The state space reconstruction is based on the Time-Delay Embedding Theorem [8], which can be written as follows: Given a dynamic system with a m-dimensional solution space and an evolving solution h(t), let x be some observation x(h(t)). Let us also define the lag vector (with dimension m and common time lag τ) x(t) = (xt , xt-τ, xt-2 τ, xt-(m-1)τ). Then, under very general conditions, the space of vectors x(t) generated by the dynamics contains all the information of the space of solution vectors h(t). The mapping between them is smooth and invertible. This property is referred to as diffeomorphism and this kind of mapping is referred to as an embedding. Thus, the study of the time series x(t) is also the study of the solutions of the underlying dynamical system h(t) via a particular coordinate system given by the observable x.
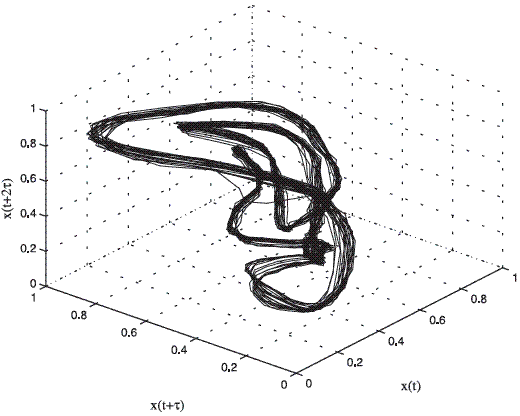
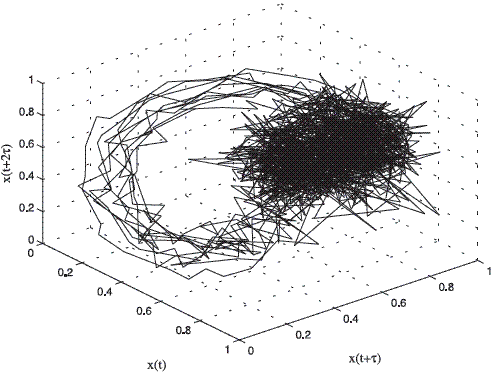
The embedding theorem establishes that, when there is only a single sampled quantity from a dynamical system, it is possible to reconstruct a state space that is equivalent to the original (but unknown) state space composed of all the dynamical variables [8]. In this work the embedding dimension m was chosen by using the false neighbors method and time-delay τ by using the first minimum of the auto mutual information function [8]. For the case of pathological voices, it is known that if the laryngeal vibrations are stable, the energy in the system is constant and the orbits in the attractor are tightly wound. If laryngeal vibrations are unstable, the energy in the system can not be maintained at a constant level and trajectories will tend to deviate [12]. Figures 2 and 3 show the attractors for a normal and a pathologic signal respectively extracted of the database [13].
Stochastic modelling
The technique used at this stage was chosen on the basis of the modelling capabilities that it presents. The HMMs are stochastic models that allow the representation of time series. The use of hidden states makes the model generic enough to handle a variety of complex realworld time series, while the relatively simple prior dependence structure still allows the use of efficient computational procedures [14]. A HMM is a Markov chain whose outputs are random variables generated from probability functions associated to each state. Let x = {x0,…, xT} be an ordered multivariate sequence of length T and q = {qo,…, qT} a particular state sequence. A firstorder discrete HMM can be denoted by:
where A = {aij} is the matrix of state transition probabilities in which aij = p (qt = j| qt-1 = i).
B = { …j(.)}, j (t) = (t | t = ) is the emission matrix. The xt takes values of a finite set of symbols v = {v1,…, vM} called codebook, where M is the number of symbols. The models with this output structure are referred as discrete HMMs.π is the column vector of initial state probabilities. The number of states of the model is denoted by nq.
The parameters of the model were estimated in a standard procedure employing the maximum likelihood criterion by means of a Baum-Welch algorithm.
Figure 2 Three-dimensional phase portrait of the normal register AXH1NAL.wav of the database [13]
Figure 3 Three-dimensional phase portrait of the pathological register LB18AN.wav of the database [13]
Kernel between HMMs
The similarity measure based on probability product kernel (PPK) used in this work was proposed in [11]. The Kernel function computes a generalized inner product between two probability distributions and allows integrating generative models as HMMs within a discriminative learning paradigm. The PPK between distributions p and p’ is defined as
where normally ρ 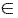 {1/ 2, 2,3,…}. For HMMs, the PPK is considered as the statistical average of similarities of all possible co-state sequences drawn from the two HMMs [15]. Based on eq. (2), the PPK of two different emission matrices is given by [11]:
{1/ 2, 2,3,…}. For HMMs, the PPK is considered as the statistical average of similarities of all possible co-state sequences drawn from the two HMMs [15]. Based on eq. (2), the PPK of two different emission matrices is given by [11]:
For HMM with discrete emissions, given the observations sequence x and the model λ, the likelihood is [14]:
When ρ = 1, the PPK of two HMMs with discrete emissions is given by
In this work the forward procedure described in [15] was used for the calculation of PPK, but the computing time for the induction step in such algorithm was decreased by using a Hadamard product into a matricial scheme (see algorithm 1).
Algorithm 1: Probability product kernel for HMM
Require: λ1, λ2 and T {T is the profile observation sequence}
Initialization
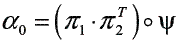
Induction
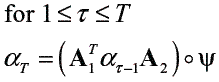
Termination
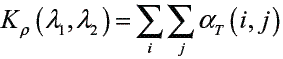
Ensure: Kρ value.
Dissimilarity-based classification
In this step, suppose a set of prototype objects:
Called the representation set, and suppose a dissimilarity measure d (., .) , computed or derived from the objects. Such a dissimilarity measure must be nonnegative and obey the reflexivity condition, d (x, x) = 0 , but it might be non-metric.
An object x is represented as a vector of the dissimilarities computed between x and the prototypes from R :
Then, for a training set T of n objects, a classifiercan be built on the n X r dissimilarity matrix D(T ,R) relating all training objects to allprototypes [16].
Prototype selection
There exists a number of ways to select the representation set R. One method that has achieved good results is Linear Programming (LP) [17]. In this method, the selection of prototypes is done automatically by training a properly formulated separating hyperplane:
In a dissimilarity space D (T ,R) . In this approach, a sparse solution w is obtained, which means that many weights wj become zero. The objects from the initial set R (R = T, for instance), corresponding to nonzero weights are the selected prototypes, so the representation set RLP.
Classifier
In the classification stage a naive 1-nearest neighbor classifier was used [18]. The classifier was designed to compute the ratio between the distances to the closest samples of each class. This measure is called score. The scores given by the detector stage for normal and pathological voices are used to plot the true and false score curves. The decision about presence or absence of pathology is taken by establishing a decision boundary that ensures the minimum classification error. In this work, it is used the threshold that corresponds to the minimum average error rate: the Minimum Cost Point (MCP) [18]. According to the Bayes decision theory, this point could be calculated by taking into account that the risk of the two possible errors (false acceptance or false positive, and false rejection or false negative) is different [18]. However, throughout this paper, it is considered that the risk corresponding to both errors is equal. When a threshold H is chosen, the samples with scores greater or equal to H, are labeled as class 1 (by convention the pathological class) whereas the samples with scores lower than H are labeled as class 2 (normal).
Experiments and results
Corpus of speakers database
The used database was developed by The Massachusetts Eye and Ear Infirmary Voice Laboratory (MEEIVL) [13]. Due to the different sampling rates of the recordings stored in this database, a downsampling with a previous half band filtering was carried out, when needed, in order to adjust every utterance to a 25 kHz sampling rate. 16 bits of resolution were used for all the recordings. The registers contain the sustained phonation of the /ah/ vowel from patients with a variety of voice pathologies: organic, neurological, and traumatic disorders. The registers were previously edited to remove the beginning and ending of each utterance, removing the onset and offset effects in these parts of each utterance. A subset of 173 registers of pathological and 53 normal speakers was selected according to those enumerated in [19]. The larger number of recordings belonging to the pathological set allows a better modeling of a class that has a larger inherent variability. This fact does not imply a slant of the system towards the pathological class, because typically, the dispersion in the feature space of the pathological voices is greater than in the normal class.
Experimental setup
To assess the performance of the proposed approach, we performed tests in which we compare the behavior of the system changing the number of the states in the model in the grid {10,15, 20}, the size of the codebook in the grid {32,64,128, 256}. Additionally, due to the fact that embedding dimension (ED) changes in each voice signal, the size of the space to be modeled changes too. Due to this, there were established several criteria for choosing an ED for all signals that henceforth will be called overall embedding dimension (OED). In a first try, was estimated OED as the average of the ED’s for all voices, but in this case, the information used to reconstruct the attractor of the some registers is not enough. In the second scheme, the OED was established as the maximum ED present in the database, for insuring that in all embedding spaces the minimum dimension necessary is used. In the third scheme the OED was established as 30% bigger than the maximum ED in order to have a high tolerance interval for new registers with more complex dynamics. For training the HMMs, the points of the attractor on the embedding space were grouped by means of the k-means clustering algorithm into a set of 200 points. Next, the HMMs obtained from the attractors are used as prototypes to construct a dissimilarity space using a probability product kernel as similarity measure between two HMMs. The construction of dissimilarity spaces from HMM was proposed in [20], and it showed better classification results than conventional method using maximum a posteriori rule.
In order to design the dissimilarity based classifier, an initial representation set R of 158 signals (121 pathologic and 37 normal, corresponding to 70% of the samples of each class) was extracted from the database. Then, the distances among all objects in the representation set were calculated by constructing the 158X158 dissimilarity matrix D (R,R). The linear programming method described in section 2.4.1 was then applied over the dissimilarity space, obtaining a final representation set RLP of r prototypes. The remaining objects in each case were returned to the training set T for the classification stage. Using the dissimilarity matrices D (T, RLP), a naive 1-nearest neighbors classifier was trained and validated using the leave one out schema. In order to compare the performance of the proposed approach, a classification procedure employing conventional non linear statistics was realized. From each signal the Largest Lyapunov exponent (LLE) and the correlation dimension (CD) were estimated [8], and a algorithm for computing LLE was based on [12] and the algorithm for computing the CD was based on [21]. The results are presented by means of confusion matrices [5], giving the following rates: true positive rate (tp) (also called sensitivity, is the ratio between pathological files correctly classified and the total number of pathological voices); false negative rate (fn) (ratio between pathological files wrongly classified and the total number of pathological files); true negative rate (tn) (also called specificity, is the ratio between normal files correctly classified and the total number of normal files); false positive rate (fp), (is the ratio between normal files wrongly classified and the total number of normal files). Thus tp + fn =100%, and tn + fp = 100%. The final accuracy of the system is the ratio between all the hits obtained by the system and the total number of files.
As a figure of merit the Receiver Operating Characteristic (ROC) curve may be plotted using the scores given by each classifier to show the performance of the proposed architecture. The ROC is a popular tool in medical decision-making [5]. It reveals diagnostic accuracy expressed in terms of sensitivity and 1-specificity or fp. In additions, in this work the Area Under the ROC Curve (AUC) was considered. The AUC is a single scalar representing an estimation of the expected performance of the system.
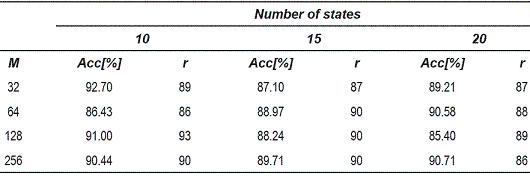
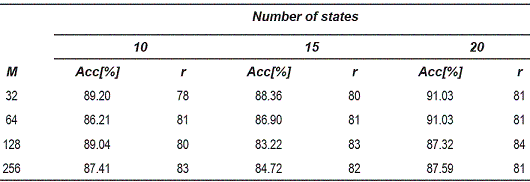
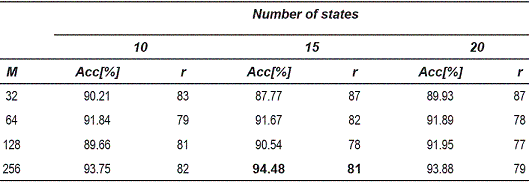
The tables 1, 2 and 3, show the accuracy obtained for the 1-nearest neighbors rule in the dissimilarity space. Each table corresponds to different OEDs used for the reconstruction of the attractors.
Table 1 Accuracy for the 1-nearest neighbor classifier for 5-dimensional attractors
Table 2 Accuracy for the 1-nearest neighbor classifier for 7-dimensional attractors
Table 3 Accuracy for the 1-nearest neighbor classifier for 10-dimensional attractors
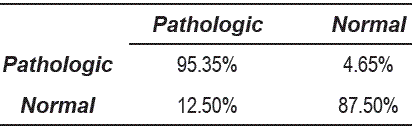
From the tables 1, 2 and 3, can be observed that the best performance is obtained for OED = 10, which shows that the representation of voice signals was better in the embedding space of high dimension. Table 4 shows the matrix confusion for the best result obtained form the dissimilarity space.
Table 4 Confusion matrix for the best result by using 1-nearest neighbor classifier of dissimilarity space
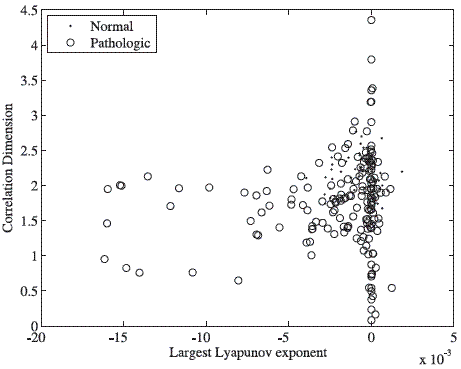
On the other hand, the number of selected prototypes was almost constant through the different experiments. However, it is important to notice that in all cases, the strategy used for prototype selection, did not exclude any normal sample. Figure 4 shows the feature space obtained from two nonlinear statistics over the database [13].
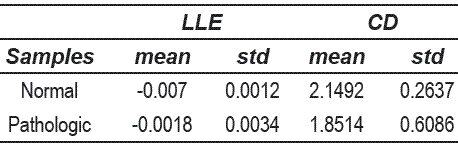
It can be observed that the pathological voices are more sparse distributed than the normal voices in the feature space. Also, it is clear that features used are not discriminant because both classes are overlapped. From the point of view of the nonlinear analysis, since many voice signals have a positive LLE, this fact implies that the trajectories in the embedding space diverge exponentially fast (i.e. there is presence of chaos) and many other are close of this behavior. Table 5 shows some statistical moments for the nonlinear features of the figure 4.
Figure 4 Feature space obtained from two nonlinear statistics: Largest Lyapunov exponent and Correlation dimension for the database [13]. The distributions of both classes in the feature space are highly overlapped
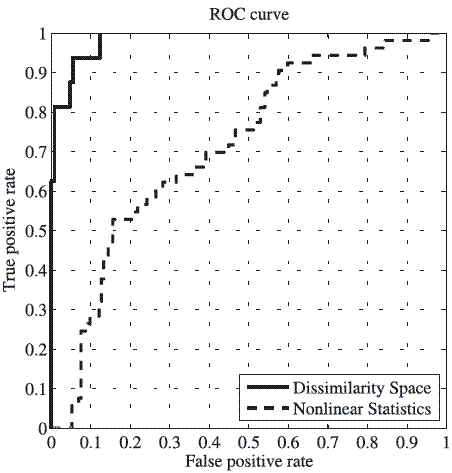
Figure 5 shows ROC curves for the best accuracy for the two different schemes and their AUCs. It is clear that the performance of the system by using dissimilarities is much better than using conventional nonlinear statistics. However, the proposed approach attempts to improve the nonlinear behavior characterization of the speech signals and this one can be combined with schemes that employ acoustical and noise features (systems using these measures have been employed with success [4;5]) in order to obtain better results.
Table 6 shows the confusion matrix obtained for the classification performed. It can be observed that the maximum accuracy with this method is 18.71% lower than the maximum accuracy obtained from the dissimilarity based classification.
Table 5 Attributes of the nonlinear statistics
Table 6 Confusion matrix for 1-nearest neighbor classifier by using nonlinear features
Figure 5 ROC curve for the best accuracy obtained by using dissimilarity space and nonlinear features. The AUC for the dissimilarity space is 0.9845 and for the nonlinear statistics is 0.7150. The difference between both schemes is clear
Conclusions
The proposed scheme for nonlinear analysis does not depend on the signal length, because for all samples the same number of points was taken into account for training the attractor model. The study shows that the time analysis of the nonlinear component from the signal, allows extracting more discriminant information to carry out an accurate detection of the presence of voice pathology. Although the HMMs used in this work are of first order, the methodology followed has shown its capability of modelling the representations of the voices in the embedding space. Increasing the order of the HMMs could improve the attractor modelling capabilities, but also increase the computational complexity, so it is necessary to explore the feasibility and limitations of using higher order models. The methodology presented in this work does not attempt to replace the more classical acoustic parameters-based analysis, but proportionate a different alternative for the nonlinear analysis of voice signals, that can be used in conjunction with traditional methods. Additionally, the dissimilarity based classification scheme allows the comparison among different pathological voices with respect to some prototypes. This fact, opens the possibility of building dissimilarity spaces that could help identify grades of pathology (levels of voice quality), by using the distance between a sample to the normal prototypes as rate of disease.
Acknowledgements
This work was supported by: Convocatoria de apoyo a doctorados nacionales del Instituto Colombiano para el Desarrollo de la Ciencia y la Tecnología Francisco José de Caldas, Colciencias 2007, and TEC2006-12887-C02 by the Ministry of Science and Technology of Spain.
References
1. J. J. Jiang, Y. Zhang, C. McGilligan. Chaos in voice, from modeling to measurement, Journal of Voice. Vol. 20. 2006. pp. 2-17. [ Links ]
2. Y. Zhang, J. Jiang, L. Biazzo, M. Jorgensen. Perturbation and nonlinear dynamic analysis of voices from patients with laryngeal paralysis, Journal of Voice. Vol. 19. 2004. pp. 519-528. [ Links ]
3. Y. Zhang, C. McGilligan, L. Zhou, M. Vig, J. Jiang. Nonlinear dynamic analysis of voices before and after surgical excision of vocal polyps. Journal of the Acoustical Society of America. Vol. 115. 2008. pp. 2270-2277. [ Links ]
4. J. I. Godino-Llorente, P. Gómez-Vilda, M. Blanco- Velasco. Dimensionality Reduction of a Pathological Voice Quality Assessment System Based on Gaussian Mixture Models and Short-Term Cepstral Parameters. IEEE Transactions on Biomedical Engineering. Vol. 53. 2006. pp. 1943-1953. [ Links ]
5. N. Sáenz-Lechón, J. I.Godino-Llorente, V. Osma- Ruiz, P. Gómez-Vilda. Methodological issues in the development of automatic systems for voice pathology detection. Biomedical Signal Processing and Control. Vol.1. 2006. pp. 120-128. [ Links ]
6. I. R. Titze, R. Baken, H. Herzel. Evidence of chaos in vocal fold vibration. Vocal Fold Physiology: New Frontiers in Basic Science. Singular Publishing Group. San Diego. CA. 1993. pp 143-188. [ Links ]
7. M. A. Little. P. E. McSharry. S. J. Roberts, D. A. Costello, I. M. Moroz. Exploiting nonlinear recurrence and fractal scaling properties for voice disorder detection. Biomedical Engineering Online. Vol. 6. 2007. pp. 1-35. [ Links ]
8. H. Kantz, T.Schreiber. Nonlinear time series analysis, 2a ed., Cambridge University Press. Cambridge. UK. 2003. [ Links ]
9. M. C. Scharry, Detection of dynamical transitions in biomedical signals using nonlinear methods, Proceedings of 8th International Conference KES, Lecture Notes in Computer Science. Ed. Springer. Wellington. New Zeland. Vol. 3215. 2004. pp. 483- 490. [ Links ]
10. J. S. Richman, J. R. Moorman. Physiological timeseries analysis using approximate entropy and sample entropy. Am J Physiol HeartCirc Physiol. Vol. 278. 2000. pp. H2039-H2049. [ Links ]
11. T. Jebara, R. Kondor, A. Howard. Probabilistic product kernels. Journal of Machine Learning Research. Vol. 5. 2004. pp. 819-844. [ Links ]
12. A. Giovanni, M. Ouaknine, J. M. Triglia. Determination of largest lyapunov exponents of vocal signal: Application to unilateral laryngeal paralysis. Journal of Voice. Vol. 13. 1999. pp. 341-454. [ Links ]
13. Massachusetts Eye and Ear Infirmary. Voice disorders database. version 1.03. [CD-ROM]. 1994. Lincoln Park. N.J. Kay Elemetrics Corp. [ Links ]
14. O. Cappé, E. Moulines, T. Rydén. Inference in Hidden Markov Models. Ed. Springer. New York. 2005. pp. 1-654. [ Links ]
15. L. Chen, H. Man. Fast schemes for computing similarities between Gaussian HMMs and their applications in texture image classification, EURASIP Journal on Applied Signal Processing. Vol. 13. 2005. pp. 1984-1993. [ Links ]
16. E. Pekalska, R. Duin. Dissimilarity representations allow for building good classifiers, Pattern Recognition Letters. Vol. 23. 2002. pp 943-956. [ Links ]
17. E. Pekalska, R. Duin, P. Placík. Prototype selection for dissimilarity-based classifiers Pattern Recognition. Vol. 39. 2006. pp. 189-208. [ Links ]
18. R.O. Duda, P. E.Hart, D. G. Stork. Pattern Classification. Ed. Jhon Wiley & Sons.. New York. 2001. pp. 305-307 [ Links ]
19. V. Parsa, D.Jamieson. Identification of pathological voices using glottal noise measures. Journal of Speech, Language and Hearing Research. Vol. 43. 2000. pp. 469-485. [ Links ]
20. M. Bicego, V. Murino, M. Figueiredo, Similaritybased classification of sequences using Hidden Markov Models. Pattern Recognition. Vol 37. 2004. pp 2281-2291. [ Links ]
21. M. Small, Applied Nonlinear Time Series Analysis: Applications in Physics, Physiology and Finance. Ed. World Scientific. Singapore. 2005. pp. 1-245. [ Links ]
(Recibido el 27 de noviembre de 2008. Aceptado el 9 de mayo de 2009)
*Autor de correspondencia: teléfono: + 57 + 6 + 887 94 00 ext 55793, fax: + 57 + 6 + 887 94 00 ext. 55713, correo electrónico: jdariasl@unal.edu.co (J. Arias)