Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista Facultad de Ingeniería Universidad de Antioquia
versão impressa ISSN 0120-6230versão On-line ISSN 2422-2844
Rev.fac.ing.univ. Antioquia n.62 Medellín jan./mar. 2012
ARTÍCULO ORIGINAL
Modeling and control of grid connected photovoltaic systems
Modelado y control de sistemas fotovoltaicos conectados a la red eléctrica
Daniel González1, Carlos Andrés Ramos Paja1, Andrés Julián Saavedra Montes1*, Eliana Isabel Arango Zuluaga1, Carlos Eduardo Carrejo2
1Universidad Nacional de Colombia. Carrera 80 No 65-223. Medellín, Colombia.
2Laboratoire d’Analyse et d'Architecture des Systèmes LAAS-CNRS. Total Gaz et Energies Nouvelles, 7. Avenue du Colonel Roche 31077. Toulouse Cedex 4, France.
*Autor de correspondencia: teléfono: + 57 + 4 + 425 52 97, fax: + 57 + 4 + 234 10 02, correo electrónico: ajsaaved@unal.edu.co (A. Saavedra)
(Recibido el 28 de enero de 2011. Aceptado el 10 de febrero de 2012)
Abstract
In grid-connected Photovoltaic (PV) applications, DC-links based on large electrolytic capacitors, which introduce reliability problems, are used to attenuate voltage oscillations caused by the sinusoidal power injection into the grid. This paper proposes the unified modeling of the complete PV system in grid-connected operation to design control strategies that mitigate the DC-link voltage oscillations as well as irradiance disturbances caused by environmental perturbations, it making feasible the use of non-electrolytic capacitors. The developed control strategies have been associated with a maximum power point tracking technique to maximize the power produced by the PV panel. Finally, the proposed solution has been validated by means of analytical expressions, simulations, and experimental results.
Keywords: Photovoltaic systems, grid connected, state space model, control systems
Resumen
En los sistemas fotovoltaicos con conexión a la red eléctrica se utilizan enlaces de DC basados en condensadores electrolíticos, los cuales introducen problemas de confiabilidad, para atenuar las oscilaciones de voltaje causadas por la inyección de potencia sinusoidal a la red. Este artículo propone un modelado unificado del sistema fotovoltaico con conexión a la red, para el diseño de estrategias de control que mitiguen las oscilaciones de voltaje en el enlace DC y los disturbios en la irradiación solar causados por cambios ambientales, haciendo factible el uso de condensadores no electrolíticos. Las estrategias de control desarrolladas se asocian a una técnica de seguimiento del punto de máxima potencia para maximizar la potencia producida. Finalmente, las solución propuesta se validó usando expresiones analíticas, simulaciones, y resultados experimentales.
Palabras clave: Sistemas fotovoltaicos, conexión a la red, espacio de estados, control
Introduction
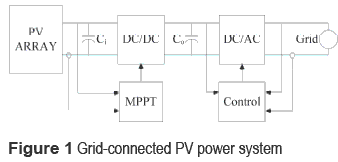
In the few past years, the reduction of fossil fuel reserves and climate change have impulse the use of renewable power supplies to decrease global warming, and one candidate to replace pollutant generators is the Photovoltaic panel (PV), which is becoming more important for both standalone and grid-connected systems [1]. A typical structure for grid-connected PV systems is described in figure 1 [2], where the PV panel is interfaced by means of a DC/DC converter and a DC/AC inverter to the grid. The connection between the DC/DC converter and the inverter is performed by a DC-link, which commonly consists in a bulk capacitor CO.
In such a system, the first objective is to impose a desired voltage to the PV panel that guarantee the maximum power production, named Maximum Power Point (MPP) voltage [3]. Therefore, the controller that defines the PV voltage is named Maximum Power Point Tracking (MPPT) controller. From the electrical scheme it is observed that the PV voltage is defined by the DC/ DC converter input capacitor Ci, therefore the PV panel and DC/DC converter can be considered as a single system that must be controlled to reject disturbances, i.e. irradiance, and load or inverter.
Since grid connected inverters regulate the bulk capacitor energy, there are two typical cases in single-phase applications: the first possibility deals with non-controlled inverters that perform deficient bulk voltage regulation, where the inverter consumes sinusoidal current at the maximum power available. Therefore, the DC/DC converter output voltage exhibits disturbances at multiple frequencies, which may also be transferred to the input port causing a mismatch in the MPP calculation [4], producing low power conditions. Therefore, an appropriate control strategy must be applied to mitigate such an oscillation [5]. Moreover, it is important to note that the main frequency of the bulk voltage oscillation is twice the grid frequency [4].
The second, and most common, case deals with a properly controlled inverter that accurately regulates the bulk capacitor DC voltage, where the DC/DC converter output voltage is affected by a sinusoidal voltage waveform at twice the grid frequency [5] around a DC level defined by the inverter. The magnitude of such a sinusoidal oscillation inversely depends on the bulk capacitance, requiring high capacitive DC-link to reduce its amplitude. Therefore, non-reliable electrolytic capacitors are currently used to reduce costs in the design of the DC-link [3], but more reliable non-electrolytic capacitors are desirable to improve the system robustness and reliability. For that matter, it is important to mitigate the bulk voltage oscillations by means of control approaches to avoid large electrolytic bulk capacitances. Furthermore, such a voltage disturbance may also be transferred to the DC/DC converter input port as in the first case, reducing the system power production and efficiency.
This paper proposes the unified modeling of the PV panel and DC/DC converter, in both inverter typical operation conditions, to design control strategies that mitigate the bulk voltage oscillation and allow the use of non-electrolytic capacitors. The controllers have been design taking into account the dynamics of the DC/DC converter and the inverter, and an experimentally validated model represents the PV panel. Furthermore, the control strategies interact with a Perturb and Observe (P&O) MPPT algorithm to optimize the PV power [4]. The remains of the paper are organized as follows: the next section describes the modeling and control strategies to regulate the PV voltage considering a non-controlled grid-connected inverter. Then, the same objective is addressed but considering a wellregulated grid-connected inverter, which in addition is validated by means of experimental results. Finally, some conclusions of the work are given.
Pv system with a non-controlled grid-connected inverter
In this operation condition the inverter is modeled by its nominal input impedance in parallel with a current perturbation, which represents the current requested by the inverter to inject sinusoidal power to the grid. Thus, the power conversion chain can be modeled as a single system composed by the PV panel, the DC/DC converter, and the inverter as a full system.
Modeling of the PV system
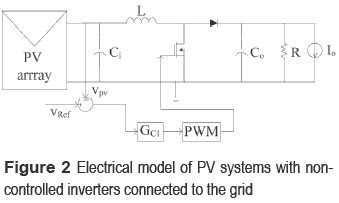
Figure 2 shows the electrical scheme proposed to model the PV system, where the PV panel, its associated DC/DC converter in closed loop, and the non-controlled grid-connected inverter are observed. The boost DC/DC converter has been adopted since typical grid-connected inverters require DC-link voltages higher than common PV voltages [6]. Moreover, the inductor current control must be adopted instead of voltage control since boost converters are non-minimum phase systems in voltage mode [7].
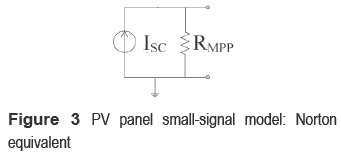
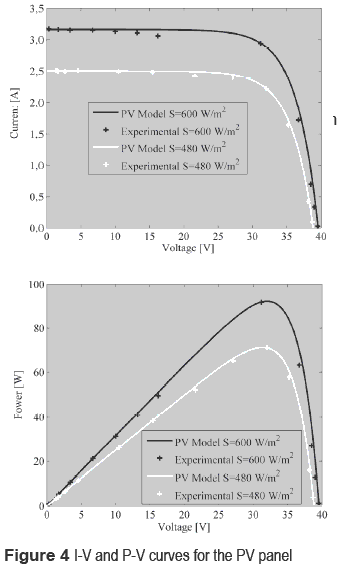
In such a system, the inductor current iL, and input and output capacitors voltages vCi and vCo, have been chosen as state variables. Moreover, the manipulated variable is the converter duty-cycle d, 0 ≤ d ≤ 1, and the perturbation sources are the PV panel short-circuit current ISC that models the irradiance variations, and the load current perturbation IO. Figure 3 describes the PV panel small-signal model used to analyze the system, which represents the PV panel operating at its nominal MPP by means of a Norton equivalent [6]. Figure 4 presents the polarization and power curves of the PV module used in the analysis: a series array of two BP585 PV panels.
The PV model used for the system simulations considers the non-linear behavior of the PV panel [8], and its parameters were calculated to accurately reproduce the experimental measurements taken from the real device. In particular, for an irradiance S1 = 600 W/m2, the PV panel exhibits an ISC = 3.15 A, an open circuit voltage VOC = 33.15 V, and a maximum power produced PMPP = 92 W. Similarly, for S2 = 480 W/m2, the PMPP = 70 W. Figure 4 shows the satisfactory agreement between the model and the experimental measurements.
From the electrical models of figures 2 and 3, and the operating point given by the MPP of figure 4, the semi-period where the MOSFET is turned ON defines the following relations:
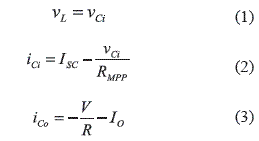
where vL and vCi correspond to the inductor and input capacitor voltages, iCo represents the output capacitor current, V represents the DC- link nominal voltage, R and IO models the grid-connected inverter, and ISC and RMPP correspond to the Norton equivalent of the PV panel around its MPP. Similarly, in the semi-period where the MOSFET is turned off:
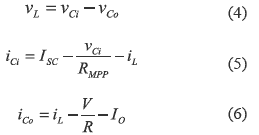
where iL and iCo represent the inductor and input capacitor currents.
The state-space model of the proposed system can be described as:
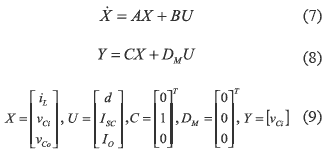
Moreover, matrix C defines the input capacitor voltage as the system output Y. Also, from equations (10) and (12) it is concluded that matrix DM is null. Applying the average modeling technique [5, 7], the differential equations of the system are obtained:
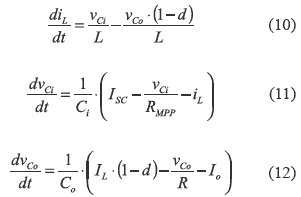
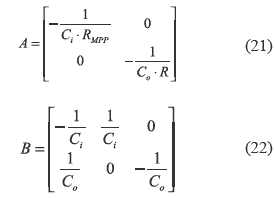
From (7), (10), (11) and (12), matrixes A and B are:
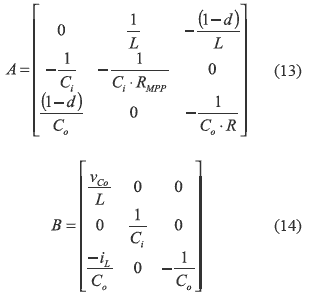
The system described by (7-14) is non linear, therefore it is linearized around the MPP to design simple PI or PID controllers [9]. From (10-12), the system equilibrium point is:
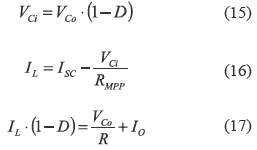
where the steady-state duty-cycle D in the MPP is given by:
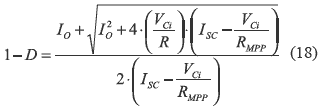
Since 0 ≤ D ≤ 1, ISC limits the maximum steady state PV current IPV = VCi/RMPP to

PV system control design
The parameters adopted to design the system controller correspond to a real prototype used for experimental validation: L = 56 µH, Ci = 44 µF, CO = 44 µF, DC-link nominal voltage VDC-link = 70 V, ISC = 4.7 A, and in the MPP the PV parameters are RMPP = 77 Ω and VMPP = 33.15 V. Finally, the inverter nominal input impedance is R = 100 Ω and the DC/DC converter switching frequency is FSW = 100 kHz.
The system non-linear model was linearized around the MPP, and the system stability was analyzed by means of the root-locus technique, where a PI current controller was designed to ensure a null steady state error in the inductor current control. The controller design specifications also concern a 0.707 damping ratio that provides a tradeoff between rising time and settling time, and a 20 kHz closed loop bandwidth, which ensures a closed-loop gain lower than 0 dB at the switching frequency [5][10] limiting the system response to the frequencies where the average linearized model is valid [5]. The designed GC1 controller is given by:
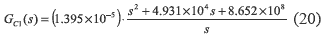
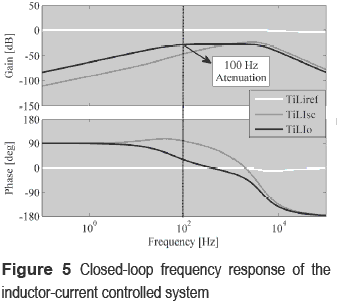
Some closed-loop transfer functions are defined to analyze the system behavior: the reference- to-inductor current transfer function TiLiref, the short-circuit current-to-inductor current transfer function TiLIsc, and the load current- to-inductor current transfer function TiLIo. The frequency responses for those transfer functions are represented in figure 5, where TiLiref exhibits a satisfactory tracking of the reference in the desired range; i.e. up to 20 kHz. Furthermore, it is observed the mitigation of the short-circuit current and load disturbances. This feature is important to reject the 100 Hz load disturbances injected by the inverter connected to a 50 Hz grid, where TiLIo reports a 28.35 dB attenuation of the perturbation on IO. Finally, TiLIsc exhibits a satisfactory rejection of the irradiance perturbations, which are normally up to 50 W/(s m2) [6] or 1 Hz, therefore the controller mitigates its impact on the inductor current by 61 dB.
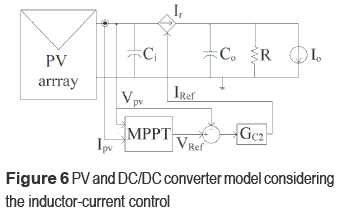
The next step is to design a new linear model taking into account the inductor-current control, which can be modeled by a controlled current source Ir, where the control objective is to regulate the input capacitor voltage, i.e. PV voltage. This new model is illustrated in figure 6.
Following the same analysis performed for the inductor current control, the set of equations that describe the system behavior are expressed in state space as:
where the input and output capacitors voltages vCi and vCo are the state variables. The system inputs are the inductor current reference Iref, ISC, and IO. Since a current controlled boost converter is a minimum-phase system [7], a PI controller GC2 (24) has been designed to regulate the PV voltage, i.e. vCi voltage. The design requirements were a 0.707 damping ratio, null steady-state error, and a 4 kHz closed-loop bandwidth to limit the system response to the frequency range where the model is valid and the current control is stable [5, 10].
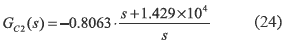
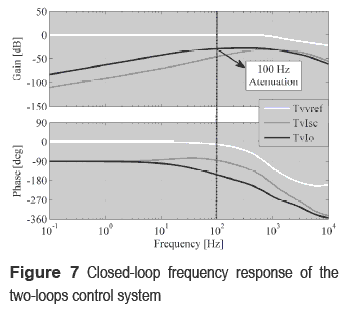
The final system has two control loops, an inner inductor-current control (20) and an external voltage loop (24). Again, some closed-loop transfer functions were used to analyze the system behavior: the reference-to-input capacitor voltage transfer function Tvvref, the short- circuit current-to-input capacitor voltage transfer function TvIsc, and the load current-to-input capacitor voltage transfer function Tvlo. Figure 7 depicts the frequency response of the closed loop system, where Tvvref makes evident the accurate tracking of the reference up to 4 kHz. Such a reference is provided by the MPPT controller, figure 6, to set the PV voltage at the MPP [4], optimizing the power produced by the panel. Furthermore, disturbances on the short-circuit current and load current are mitigated, i.e. -30 dB at 100 Hz in IO and -100 dB at 1 Hz in ISC.
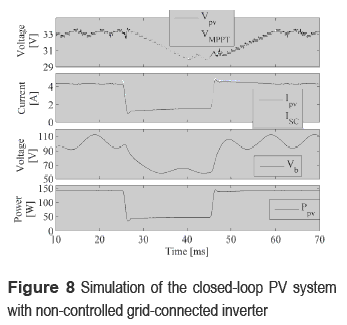
Such analytical results make evident the satisfactory behavior of the proposed solution. To illustrate the control system behavior, a simulation considering the nonlinear PV model [8] has been performed with the following irradiance profile: S1 = 960 W/m2, changing to S2 = 560 W/m2 at 25 ms, and returning to S1 at 45 ms. Moreover, the example considers a non- electrolytic bulk capacitor of 44 µF that generates a minimum voltage oscillation of 30 % of the desired DC voltage at 100 Hz. Additionally, a MPPT controller was introduced following the schemed given in figure 6, which uses the perturb and observer technique [4]. Figure 8 shows the simulation of the system considering the cascade control of GC1 and GC2, where a satisfactory tracking of the reference VMPPT by the PV voltage VPV is observed. Also, perturbations in the bulk capacitor voltage Vb and short circuit current are successfully rejected by the system. Finally, figure 8 shows the power produced by the PV panel, which is stable despite the bulk voltage oscillations.
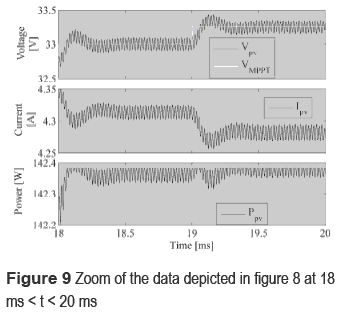
Figure 9 shows a zoom of the data depicted in figure 8 in 18 ms < t < 20 ms, where the tracking speed of the reference provided by the MPPT controller is observed, achieving a stabilization time of 350 µs. Such a figure also depicts the small 50 mW oscillation in the power generated by the converter operation, which corresponds to a power loss of 0.12 % of the power produced.
PV system with a voltage regulated grid-connected inverter
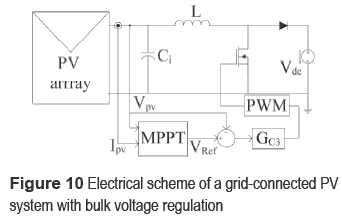
This case is the most common operating condition in grid-connected PV systems [6], where the grid-connected inverter has an additional control loop to regulate the bulk voltage, i.e. DC-link voltage. Therefore, in this case the inverter can be modeled by a voltage source exhibiting a 100 Hz sinusoidal oscillation around the regulated DC voltage, it by considering a 50 Hz grid [6]. Figure 10 shows the electrical scheme for this operation condition, where the MPPT controller interacts with an input voltage controller for the converter [7].
Following the analysis presented in the previous section, the equations that describe the system dynamics in the semi-period when the MOSFET is turned on are:
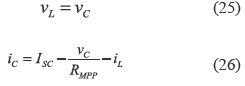
while the equations for the semi-period when the MOSFET is turned off are:
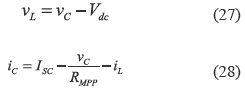
By inductor volt-second and capacitor charge balances [7], the differential equations are:
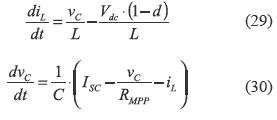
which ones are described in state space format as in (7) and (8), and considering the input capacitor voltage as system output, the system matrices are:
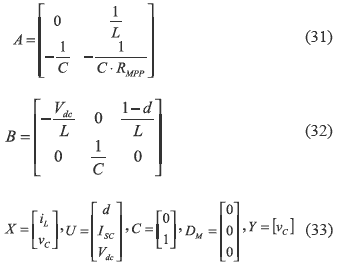
The equilibrium operating point for linealization is calculated from (29)-(30) as:
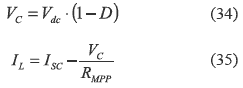
From figure 10 and equations (31)-(35) it is noted that such a power system can be analyzed as a traditional Buck converter with negative current [7], which is a minimum phase system. Therefore, the input voltage controller that regulates VPV was designed using a PID structure (36) to ensure null steady state error, and to provide a damping ratio of 0.707 and a closed-loop bandwidth of 20 kHz within the frequency range where the average model is valid [5].
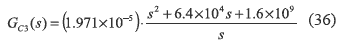
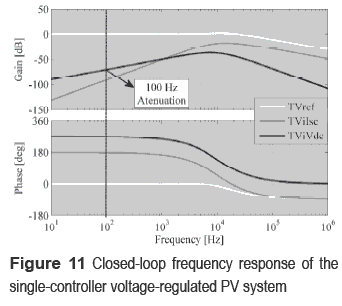
Closed loop transfer functions TVref, TVilsc and TViVdc describe the system dynamics regarding the reference VREF given by the MPPT controller, the short circuit current ISC and the converter output voltage Vdc defined by the inverter. The frequency responses of such transfer functions are shown in figure 11, where the controller tracks the reference in the interesting frequency range [0 kHz - 20 kHz], while a large mitigation of 160 dB in ISC low frequency disturbances is observed, and a satisfactory mitigation of the bulk voltage 100 Hz oscillation of 70 dB is also exhibited. Such a behavior is a significant improvement over traditional solutions [6] since it allows the adoption of non-electrolytic capacitors that generate large bulk voltage oscillations [5].
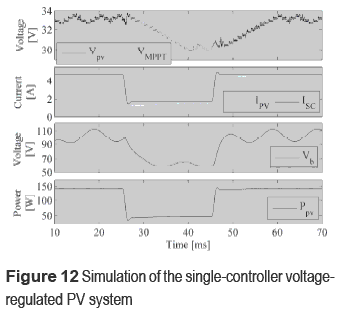
Figure 12 shows the system simulation by using the controller GC3 considering the same operation conditions adopted for the non-regulated inverter case. The simulation is consistent with the analytical results given in figure 11, where the PV voltage accurately tracks the reference provided by the MPPT controller, and satisfactory perturbations rejection is achieved.
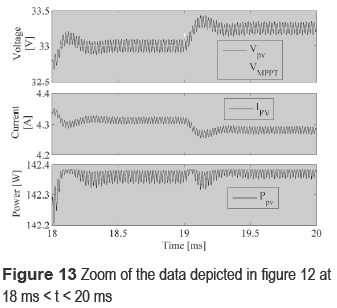
Figure 13 shows a zoom of the data depicted in figure 12 in 18 ms < t < 20 ms, where the new approach provides a PV voltage settling time of 160 µs, while the PV power oscillation generated by the converter is the same than in the previous case. Finally, the solution proposed in this voltage-controlled inverter case presents a better rejection of disturbances, this because the irradiance and bulk voltage perturbations are constrained to 600 Hz, therefore the higher bandwidth of GC3 provides a more efficient PV voltage regulation.
Experimental results
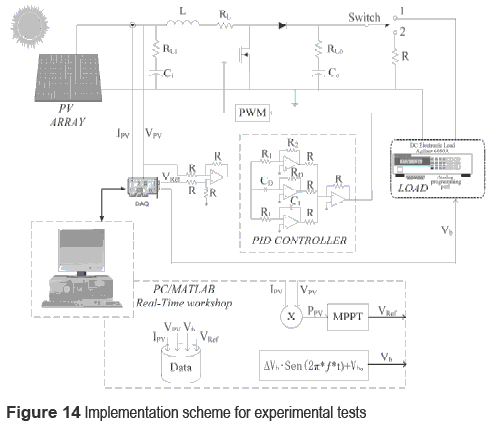
The prototype used for the experimental validation has the same parameters previously considered. The block diagram of the experimental setup is shown in figure 14, where the controller was implemented using operational amplifiers, capacitors and potentiometers, while the perturb and observe MPPT controller was implemented by using the Matlab Real-Time Workshop.
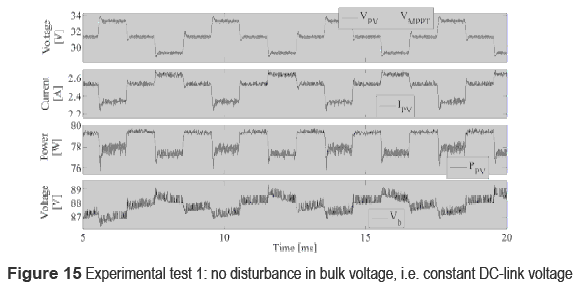
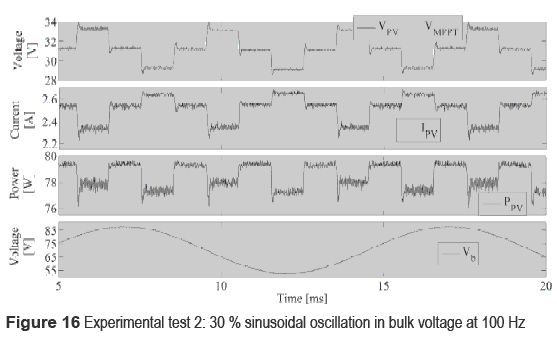
An electronic load was used to test the system in two conditions: under a constant load resistance R = 100 Ω, when the switch is in position 1, to test the operation of the MPPT controller in standard conditions [6], and to verify the controller satisfactory performance by tracking the voltage reference VPV without additional disturbances. The second condition considers the inverter operation emulated by the electronic load imposing a 100 Hz sinusoidal oscillation with 17.5 V amplitude superimposed to a DC-link voltage of 70 V. Such a bulk voltage oscillation corresponds to a 30 % perturbation, which is into the non-electrolytic bulk capacitor conditions since typical electrolytic capacitors causes bulk voltage oscillations between 1 % and 2 % [6]. Such a test requires the switch in position 2, where the electronic load is driven by means of a sinusoidal generator implemented into Matlab. In both tests the GC3 controller was used due to the tests characteristics, and the PV voltage VPV and current IPV, bulk voltage Vb and MPPT controller output VREF were collected by means of a Analog to Digital acquisition card (DAQ).
Figure 15 presents the data obtained from the first test, where the desired performance of the PV controller following the MPPT reference is demonstrated in constant load conditions, and the MPPT controller exhibits the classical 3 points that guarantee stability of the perturb and observe algorithm [4]. This first test also shows the maximum PV power generated of 79.3 W, where 1.3 W PV power oscillations are caused by the MPPT controller operation [4]. Moreover, the bulk voltage DC component is defined by converter steady-state duty cycle imposed by GC3.
Figure 16 depicts the data obtained from the second test, where it is observed the accurate PV voltage regulation in non-electrolytic bulk capacitor conditions, which corresponds to large bulk voltage oscillations up to 30 % at 100 Hz, while the MPPT controller still exhibits the classical 3 points that guarantee stability of the algorithm. In this test is generated the same maximum PV power obtained in the first test. Such a PV power profile characteristics make evident the satisfactory performance of GC3 controller since it effectively rejects the bulk voltage oscillations to extract the same PV power than in the constant load case, i.e. first test.
Conclusions
This paper proposes the unified modeling of the PV panel and DC/DC converter in both bulk voltage regulation and non-regulation conditions for grid-connected PV applications. Such a solution has been designed to mitigate DC- link voltage oscillations caused by the inverter operation, as well as irradiance disturbances caused by clouding or shadowing [4]. The mitigation of the bulk voltage oscillations allows the use of DC-link based on non-electrolytic capacitors, therefore a more reliable PV system can be designed. Moreover, the analytical and simulation results have reported a satisfactory operation in grid-connected applications. Finally, an experimental implementation of the most common grid-connected PV system was developed, and the proposed solution has been successfully validated for non-electrolytic DC- link conditions.
Acknowledgments
This work was supported by GAUNAL group from the Universidad Nacional de Colombia under the projects MECOVA-WIND and SMART-ALEN, COLCIENCIAS under the scholarship 095-2005, and the LAAS-CNRS and TOTAL S.A.
References
1. J. Reynaud, O. Gantet, P. Aloïsi, B. Estibals, C. Alonso. New Adaptive Supervision Unit to Manage Photovoltaic Batteries. In Industrial Electronics IECON. Nov. 2009. pp. 664-669. [ Links ]
2. S. Liu, R. A. Dougal. ''Dynamic multiphysics model for solar array.'' IEEE Transactions on Energy Conversion. Vol. 17. 2002. pp. 285-294. [ Links ]
3. N. Femia, D. Granozio, G. Petrone, G. Spagnuolo, M. Vitelli. ''Optimized One-Cycle Control in Photovoltaic Grid Connected Applications''. IEEE Transactions On Aerospace And Electronic Systems. Vol. 42. 2006. pp. 954-972. [ Links ]
4. N. Femia, G. Petrone, G. Spagnuolo, M. Vitelli. ''Optimization of Perturb and Observe Maximum Power Point Tracking Method''. IEEE Transactions on Power Electronics. Vol. 20. 2005. pp. 963-973. [ Links ]
5. E. Vidal, L. Martinez, J. Calvente, A. Romero. ''An H Control Strategy for Switching Converters in Sliding-Mode Current Control''. IEEE Transactions on Power Electronics. Vol. 21. 2006. pp. 553-556. [ Links ]
6. N. Femia, G. Petrone, G. Spagnuolo, M. Vitelli. ''A Technique for Improving P&O MPPT Performances of Double-Stage Grid-Connected Photovoltaic Systems''. IEEE Transactions on Industrial Electronics. Vol. 56. 2009. pp. 4473-4482. [ Links ]
7. W. Erickson, D. Maksimovic. Fundamentals of Power Electronics. 2nd ed. Ed. Springer. Colorado (USA). 2001. pp. 39-250. [ Links ]
8. G. Petrone, G. Spagnuolo, M. Vitelli. ''Analytical model of mismatched photovoltaic fields by means of Lambert W-function''. Solar Energy Materials & Solar Cells. Vol. 91. 2007. pp. 1652-1657. [ Links ]
9. P. Midya, P. Krein, R. Turnbull, R. Reppa, J. Kimball. ''Dynamic maximum power point tracker for photovoltaic applications. '' In Proc.27th Annu. IEEE Power Electronics Specialists Conf. Vol. 2. 1996. pp. 1710-1716. [ Links ]
10. R. Leyva, L. Martinez-Salamero, H. Valderrama, J. Maixé, R. Giral, F. Guinjoan. ''Linear State-Feedback Control of a Boost Converter for Large-Signal Stability''. IEEE Trans. On Circuits And Systems-I: Fundamental Theory And App. Vol. 48. 2001. pp. 418424. [ Links ]