Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista Facultad de Ingeniería Universidad de Antioquia
versão impressa ISSN 0120-6230
Rev.fac.ing.univ. Antioquia no.66 Medellín jan./mar. 2013
ARTÍCULO ORIGINAL
Accurate calculation of settling time in second order systems: a photovoltaic application
Cálculo preciso del tiempo de estabilización en sistemas de segundo orden: una aplicación fotovoltaica
Carlos Andrés Ramos-Paja, Daniel González, Andrés Julián Saavedra- Montes*
Universidad Nacional de Colombia, Carrera 80 No 65-223, Medellín, Colombia.
*Autor de correspondencia: teléfono: +57 + 4 + 4255297, fax: +57 + 4 + 2341002, correo electrónico: ajsaaved@unal.edu.co (A. Saavedra)
(Recibido el 25 de octubre de 2012. Aceptado el 18 de enero de 2013)
Abstract
A procedure to accurately calculate the settling time of second-order systems for any damping ratio and natural frequency is proposed in this paper. In addition, settling time calculation for second-order systems is reviewed in this paper, illustrating the errors generated by classical approximations reported in textbooks and research papers. Finally, such a procedure is used to precisely design a perturb and observe algorithm in a photovoltaic application.
Keywords: Settling time, accurate calculation, second order systems
Resumen
En este artículo se propone un método para calcular exactamente el tiempo de estabilización de los sistemas de segundo orden. Adicionalmente se ilustran los errores generados cuando las aproximaciones tradicionales son utilizadas para calcular el tiempo de estabilización. Finalmente el método propuesto es utilizado para diseñar un algoritmo del tipo perturbar y observar en una aplicación fotovoltaica.
Palabras clave: Tiempo de estabilización, cálculo exacto, sistemas de segundo orden
Introduction
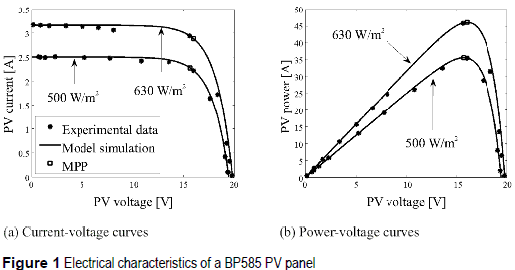
Photovoltaic (PV) modules provide an electrical power that depends on the solar irradiance and temperature acting on the PV module, generating a large amount of possible operating points. Such a condition can be observed in figure 1, where the electrical characteristics of a BP585 PV panel, composed by two PV modules, are reported for two irradiances. Figure 1 also presents the reproduction of the BP585 electrical characteristics by means of the PV model reported in [1]. Moreover, among such current-voltage and power-voltage points exists an optimal condition in which the PV panel produces the maximum power available for the particular environmental conditions, named Maximum Power Point (MPP).The MPP current, voltage, and power change with the irradiance and temperature [1], therefore online optimization techniques have been developed to find such an optimal condition [2, 3], where the Perturb and Observe (PO) algorithm [3] is the most widely adopted due to its simplicity and satisfactory performance.
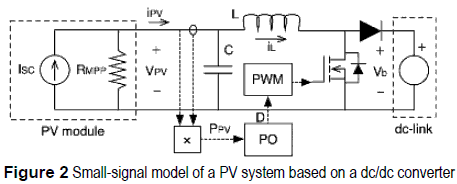
Figure 2 shows a typical PV generation system controlled by a PO algorithm, where the duty cycle D of the dc/dc converter is sequentially modified to find the MPP, maximizing the PV power PPV. The dc/dc converter in figure 2 has a Boost topology due to its extensively use in grid-connected and stand-alone photovoltaic applications. Moreover, the PV module operating at the MPP is modeled by a Norton equivalent, which is an accurate representation as demonstrated in [4]; and the load is modeled by a voltage source as proposed in [4], this because photovoltaic inverters and batteries impose a dc-link voltage at the dc/dc converter output terminals.
To implement the PO algorithm two parameters must be defined: the perturbation period Ta and the perturbation size ΔD. Femia et al. [3] propose a design procedure for the PO algorithm, where Ta is calculated to ensure an optimal three-point behavior on the duty cycle to minimize the power losses in steady-state conditions [2, 3]; while ΔD is calculated to accurately track the MPP in variable irradiance conditions. To guarantee a correct operation of the PO algorithm, the PV voltage must be stable at the instant tPV (tPV = ktpvxTa, ktpv = 1, 2, ...) in which the PO measures the PV power, therefore Ta must be longer or equal than the settling time of the PV system [3].
In [3], Femia et al. propose to calculate the Ta parameter (1), where C represents the input capacitance of the dc/dc converter, and RMPP models the current/voltage derivative of the PV module at the MPP, see figure 2; while ε specifies the acceptable band to consider stable the PV voltage. In [3], the authors use ε = 0.1 or 10 % band, but other settling time bands can be assumed, e.g. 2 % and 5 % bands.
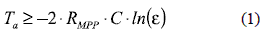
Equation (1) was based on the classical settling time approximation proposed by Ogata [5], which introduces significant errors depending on the damping ratio (ρ) and natural frequency (ωn) of the PV system. Such ρ and ωn parameters were derived from the small-signal model of the PV system (2) reported in [4], where GPV(s) is a second order system with an additional gain -Vb. In such a small-signal model, Vb is the dc-link voltage and L is the inductance of the dc/dc converter.
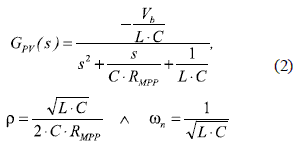
To provide a more precise and reliable PO design it is required an accurate calculation of the PV system settling time. But the settling time calculation procedures reported in classical literature for second-order systems are given for particular bands or damping ratios, introducing also approximations that increase the prediction error [5-12]. In addition, a recent work published in [13] proposes a settling time calculation procedure based on a decomposition of deterministic, random or mixed non-stationary signals in steady-state and transient components. However, such a procedure is intended for sensors and transducers modeling due to the random nature of the input signals, which makes the solution suitable for the particular application, but difficult to apply to different second-order systems.
Such undesirable characteristics make the settling time calculation procedures reported in literature not reliable to accurately design Ta in PO algorithms. This condition must be addressed since the improvement of the PO controllers increase the power extracted from renewable sources, which are extensively used nowadays [14, 15]. Therefore, this paper reviews the settling time calculation for second-order systems, providing information to estimate the errors generated by approximations reported in textbooks and research papers. In such a way, the reported calculation procedures are evaluated to quantify their prediction errors for a wide range of damping ratios and natural frequencies. Moreover, this paper proposes a procedure to accurately calculate the settling time of second-order systems for any damping ratio and natural frequency conditions, which could be implemented in any programming language. Finally, such a procedure is used to precisely design a PO algorithm in a photovoltaic application.
Settling time of second-order systems
The settling time ts, as defined in [5-10], is the time interval required by an output signal of a dynamical system to get trapped inside a band around a new steady-state value after a perturbation is applied to the system. To analyze the settling time of a second- order system, the general G2O(s) expression given in (3) is adopted [5, 8].
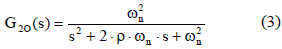
In classical textbooks [5-10] and research papers [3, 11, 12], the settling time analysis is mainly focused on under-damped systems (ρ < 1), providing limited information concerning to critically-damped systems (ρ = 1) and over- damped systems (ρ > 1). In general, the damping ratio of industrial systems could exhibit any value, as in the photovoltaic case (2), therefore all the damping ratio conditions are addressed in the following subsections.
Under-damped systems
Since in ρ < 1 conditions the poles of G2O(s) are complex [5, 8], the inverse Laplace transform of G2O(s) step-response, C(t) = L-1[G2O(s)/s], is:
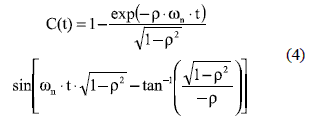
Equation (4) describes the exact time response of the second-order system to a step perturbation depending on ρ and ωn. To isolate the settling time analysis from ωn, the time response of the second-order system is normalized in terms of the variable tN = ωnxt as described in [5, 8]:
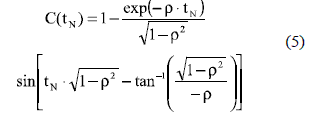
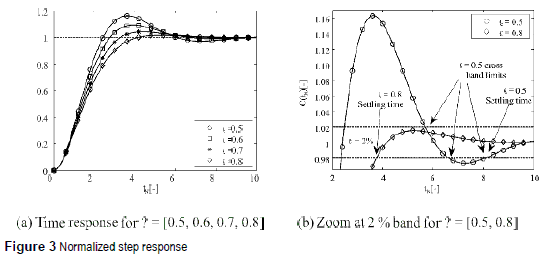
The normalized settling time tsN corresponds to the instant in which C(tN) enters into the band 1±ε to keep trapped inside. From (5) is noted that C(tN) changes depending on ρ as reported in figure 3(a), where ρ = [0.5, 0.6, 0.7, 0.8] conditions were simulated. Performing a zoom to figure 3(a) around the 2% band for ρ = [0.5, 0.8], as in figure 3(b), two types of under-damped systems are differentiated: the systems with more than one cross over the band limits, named m-cross systems, and systems with one cross over the band limits, named s-cross systems.
From figure 3(b) it is noted that ρ = 0.5 defines an m-cross system while ρ = 0.8 defines an s-cross system. The settling time tsN for m-cross systems corresponds to the maximum tN among all the crosses over the band limits, since after the last cross the system gets trapped into the band. In such a way, in m-cross systems the equations C(tN) = 1±ε provide all the crosses over the band limits, where tsN corresponds to the maximum tN value. Instead, in s-cross systems, the settling time corresponds to the tN of the unique cross with the lower band limit, therefore only the equation C(tN) = 1-ε must be solved. Such discrimination allows simplifying the settling time calculation for s-cross systems.
From (5) and figure 3(b) it is noted that s-cross systems are characterized by exhibiting a maximum overshoot lower than the upper band limit 1+ε. Therefore, defining ρs < 1 as the damping ratio in which the maximum overshoot is equal to 1+ε, all second order systems with ρ > ρs are s-cross systems, while ρ ≤ ρs are m-cross systems. The limit ρs can be found from the maximum overshoot time [5, 8] following the procedure proposed by Bert [11] and Piche [12]:
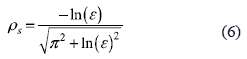
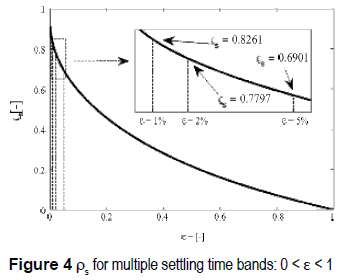
Figure 4 shows the limit ρs for different settling time bands, where the classical 1%, 2% and 5% bands are specified. It is noted that wider bands have lower ρs values and larger ranges of s-cross systems; while narrower bands have higher ρs values with larger ranges of m-cross systems.
From (5) and figure 3(b) it is also noted that ρs specifies a discontinuity in the settling time vs. damping ratio relation, this because in ρ = ρs the settling time corresponds to the tN in which C(tN) =1+ ε (second cross of the band limit); while in a ρ slightly higher than ρs, i.e. ρ = ρs + ξ with ξ 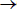 0+, the settling time corresponds to the tN in which C(tN) = 1-ε. Such a difference in C(tN) for ρs and ρs + ξ describes an step-down change in the settling time for consecutive ρ conditions. Moreover, ρ = ρs provides the lower settling time possible for m-cross systems because that condition has a single cross with each band limit, therefore the settling time occurs earlier than in systems with more than two crosses over the band limits. Similarly ρ = ρs + ξ is the minimum ρ for s-cross systems, therefore ρ = ρs + ξ represents the lower settling time possible for s-cross systems because increments in ρ cause increments in the raising time, incrementing the settling time. Finally, due to the step-down change in the settling time for consecutive ρ conditions inside [ρs, ρs + ξ], the settling time for ρ = ρs + ξ is the lowest one for C(tN) on any condition. For practical purposes, such lowest settling time can be found considering ξ = 0 from C(tN) = 1-ε in the condition ρ = ρs as in (7).
0+, the settling time corresponds to the tN in which C(tN) = 1-ε. Such a difference in C(tN) for ρs and ρs + ξ describes an step-down change in the settling time for consecutive ρ conditions. Moreover, ρ = ρs provides the lower settling time possible for m-cross systems because that condition has a single cross with each band limit, therefore the settling time occurs earlier than in systems with more than two crosses over the band limits. Similarly ρ = ρs + ξ is the minimum ρ for s-cross systems, therefore ρ = ρs + ξ represents the lower settling time possible for s-cross systems because increments in ρ cause increments in the raising time, incrementing the settling time. Finally, due to the step-down change in the settling time for consecutive ρ conditions inside [ρs, ρs + ξ], the settling time for ρ = ρs + ξ is the lowest one for C(tN) on any condition. For practical purposes, such lowest settling time can be found considering ξ = 0 from C(tN) = 1-ε in the condition ρ = ρs as in (7).
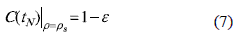
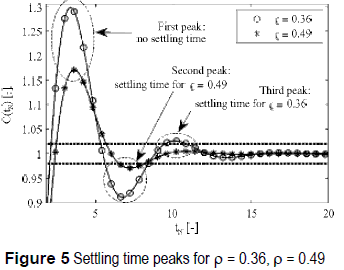
Other discontinuities in the settling time vs. damping ratio relation are generated by the increasing decay of the exponential envelope of (5) when ρ increases, which causes that the last cross over the band limits changes from one peak-zone to a previous one, changing the position of the settling time. Such a condition can be observed in figure 5, where the C(tN) with ρ = 0.36 and ρ = 0.49 have been simulated: it is noted that in ρ = 0.36 the settling time occurs at the third peak, while in ρ = 0.49 the settling time occurs at the second peak. The limit case takes place when the settling time of a system occurs in the peak P of C(tN) with ρ = ρpk,P, because a slightly increment in the damping ratio to ρ = ρpk,P + ξ, with ξ 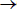 0+, generates a new settling time, which occurs in the previous peak P-1, producing a discontinuity in the settling time vs. damping ratio at ρ = ρpk,P.
0+, generates a new settling time, which occurs in the previous peak P-1, producing a discontinuity in the settling time vs. damping ratio at ρ = ρpk,P.
In this way, (6) can be generalized to find all the discontinuities of the settling time vs. damping ratio relation: such discontinuities occur when the peaks of C(tpN) = 1±ε, where tpN is the normalized peak time given in (8) for the peak n [5, 8], and ρpk,n is the damping ratio to fulfill C(tpN)-1 = ε as in (9) [5, 8], obtaining the critical damping ratios given in (10) where the discontinuities take place.
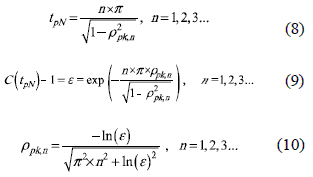
From (10) it is noted that n = 1 corresponds to the first peak, therefore it defines the first discontinuity previously specified by ρs as the limit between m-cross and s-cross systems. In fact, (6) can be obtained by replacing n = 1 in (10), which put in evidence the generality of (10). Moreover, from (10) it is concluded that exist infinite number of discontinuities, but the corresponding limit damping ratio ρpk,n decreases almost inversely proportional to the number of peaks to be analyzed.
In conclusion, the continuous zones of the settling time vs. damping ratio relation can be defined from (10): all damping ratios ρ inside [ρpk,n, ρpk,n + 1], with n =1, 2, 3... and ρ ≤ ρs, generate continuous settling time values, while at ρ = ρpk,n and ρpk,n + 1 a step change on the settling time occurs. Moreover, the settling time of m-cross systems is found by solving C(tN) = 1±ε using (5), selecting the higher tN solution tsN (normalized settling time) and removing the time normalization by calculating ts = tsN/ωn. Similarly, the settling time of s-cross systems is found by solving C(tN) = 1-ε using (5) to find the unique ts solution tsN, removing also the time normalization by calculating ta = tsN/ωn.
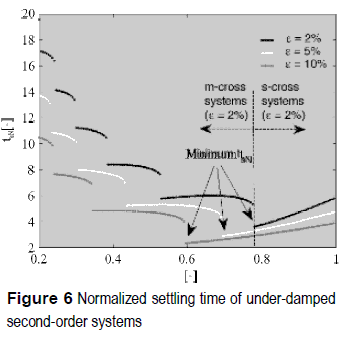
Figure 6 shows the previous analyses results, which have been mathematically condensed in (5-10), for under-damped second-order systems. Such a figure depicts the normalized settling time tsN (tsN = tsxωn) for the classical bands of 2%, 5% and 10%, where the predicted discontinuities on the m-cross systems are observed. Moreover, it is confirmed that no discontinuities occur for s-cross systems. Finally, figure 6 also put in evidence existence of a minimum tsN for each band, which could be used to optimize the response of industrial systems, e.g. a photovoltaic system.
Critically-damped and over-damped systems
The critically-damped systems (ρ = 1) have the poles of G2O(s) equal and real [5, 8]. Therefore, the inverse Laplace transform of G2O(s) step-response, C(t) = L -1[G2O(s)/s], normalized in terms of the natural frequency using tN = txωn, is given by
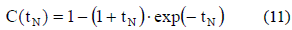
Since (11) has no sinusoidal components, the settling time of a critically-damped system occurs in the same condition than in the s-cross systems: C(tpN) =1-ε.
Similarly, the over-damped systems (ρ > 1) have the poles of G2O(s) different and real [5, 8], and the normalized time response of G2O(s) step-response is given by
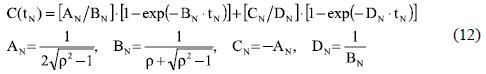
Again, (12) has no sinusoidal components, therefore the settling time of an over-damped system occurs in C(tpN) = 1-ε. From (11) and (12) it is concluded that both critically and over-damped systems have no discontinuities in the settling time vs. damping ratio relation. In addition, since the settling time of s-cross systems is calculated at the same condition than in both critically and over-damped systems, it is evident that ρ ≥ 1 generates larger settling times than ρs < ρ < 1 due to the larger rising time of larger damping ratio conditions.
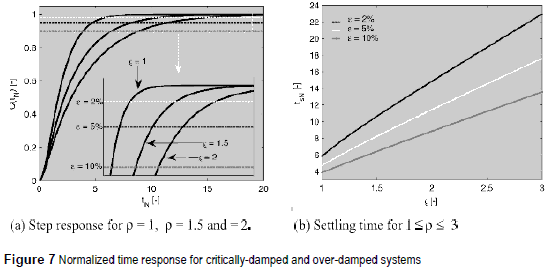
Figure 7 illustrates the previous concepts: figure 7(a) presents the normalized step responses for ρ = 1, ρ = 1.5 and ρ = 2, where the settling time increases with the damping ratio. Also, figure 7(a) contrasts the settling time for 2%, 5% and 10% bands, where it is verified that a single cross with the band limits occurs. In addition, figure 7(b) provides a more general view of the normalized settling time for 2%, 5%, and 10% bands, presenting a sweep on the damping ratio for 1 ≤ ρ ≤ 3.
Figure 7 confirms that both critically and over-damped systems are continuous in the settling time vs. damping ratio relation, also they confirm that increment/decrement in ρ generates an increment/decrement in the settling time.
Evaluation of classical settling time criteria
Taking into account the complexity of solving the implicit relations between normalized settling time tsN and the ρ given in (5), (11) and (12), some authors have proposed calculation procedures to approximate the tsN by means of explicit equations. However, such expressions could introduce significant errors depending on both ρ and ωn. In particular, the widely adopted relation given in (13) was proposed by Ogata [5], which provides a continuous relation that interpolates the intermediate points of figure 6, therefore it is only valid for 0 < ρ < 1. Similarly, Kuo et al. [8] propose the continuous relation given in (14), based on the exponential decay of under-damped systems (5), which again is valid for 0 < ρ < 1 only. Kuo et al. also provide a set of relations for a wider range of ρ (15), which are only applicable to the 5% band (ε= 0.05).
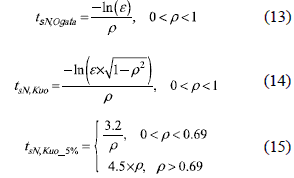
Other interesting relations where proposed by Bert in [11], where (16) approximates the settling time by means of the first two terms of a power series representation of (5). But Bert's expression requires to calculate the constants a and b by means of a precise solution of (5), which reduces its simplicity. In particular, Bert provides a = 2.99 and b = 0.56 for the 5% band. Then, Piche improves Bert's solution by expanding (5) into McLaurin series instead of power series [12], obtaining (17), which provides an equation more general since no external, or offline, parameterization is required to fit any settling time band. In general, Bert and Piche works have the same accuracy if Bert's parameters are externally calculated. Moreover, Bert and Piche are continuous and simple relations applicable to under-damped systems only.
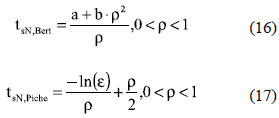
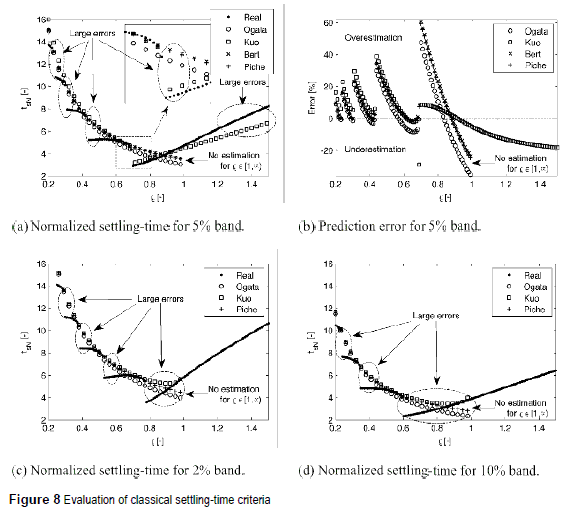
In any case, relations given in (13)-(15) are the most widely adopted ones in control systems textbooks: in example, Carstens [6] and Dorf [7] books use the Ogata relation (13), while Nise [10] and Mandal [9] books use the Kuo relation (14). Figure 8 shows the evaluation of relations (13)-(17) for 2%, 5% and 10% bands. The 5% is evaluated in figure 8(a) and figure 8(b), where large errors are caused by the classical criteria in comparison with the real settling time measured using the exact time response of the system. It is observed that Kuo's criterion is the only one for ρ ≥ 1 using (15), which is valid for ε = 0.05 only. Moreover, figure 8(b) put in evidence the large errors introduced by such explicit equations, which can be up to 60 % at damping ratios around 0.7.
In addition, figure 8(b) also highlights that, classical criteria given in (13)-(17), could either underestimate or overestimate the settling time, it depending on the ρ. Therefore, a system designed with such criteria could exhibit a settling time shorter or larger than the expected one. Figure 8(c) and figure 8(d) show the behavior of the classical criteria for both 2% and 10% bands, where Bert criterion is not presented since a and b parameters are not reported for 2% and 10% bands, and also because Piche criterion is close to Bert approximation. Figure 8(c) and figure 8(d) show the same characteristics than figure 8(a): the classical criteria do not reproduce the settling time vs. damping ratio discontinuities, introducing large errors. Moreover, the settling time is estimated for 0 < ρ < 1 only. Therefore, to perform an accurate design of a second-order system, a more precise settling-time calculation procedure is required.
Method to accurately calculate the settling time in second-order systems
The normalized settling time can be accurately calculated by using (5), (11) or (12), depending on the ρ value, at the cross of C(tN) with the band limits.
In m-cross systems, i.e. 0 < ρ ≤ ρs, the settling time is the higher tN that fulfills C(tN) = 1±ε. From C(tN) expression for m-cross systems given in (5), the settling time is obtained from the solutions of (18). But due to the implicit nature of such an equation, an optimization technique must be used to find the solutions. This paper adopts the Newton-Raphson (NR) method [1], which can be easily automatized.
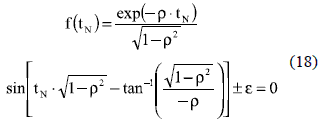
The derivative of (18), given in (19), is equal to zero in multiple points, therefore multiple solutions of f(tN) exist as illustrated in figure 5. Such a characteristic makes impossible to guarantee that the NR algorithm finds all the solutions to select the higher tN, since the NR trajectory and the NR solution depends on the adopted initial condition.
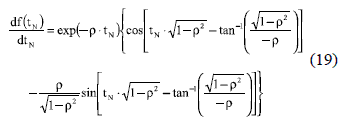
Taking into account that the first relation proposed by Kuo (14) is based on the exponential envelop of C(tN) in (5), it provides a good initial condition for the NR algorithm: relation (14) gives an overestimation of tsN, even for a 5% band where (15) provides underestimations. Therefore, starting from (14), the NR algorithm will find the nearest solution, which corresponds to the maximum tN that fulfills (18), i.e. the settling time tsN. Similarly, in s-cross systems (ρs < ρ < 1) the settling time is obtained from the negative solution of (18), where again the NR initial condition is calculated from (14).
For critically-damped systems (ρ = 1), the settling time is found from C(tN) = 1-ε considering C(tN) expression given in (11). C(tN) = 1-ε in this case corresponds to the solution of (20), which derivative is given in (21). Since in ρ = 1 there is a single cross with the band limits, as previously concluded, the NR algorithm must be able to find the solution starting from any initial condition. This is verified by analyzing (21), which is negative for tN > 0 and zero for tN = 0; hence (20) is a monotonically decreasing function with f(0) = 1-ε > 0. Therefore, (20) has a unique solution and (21) is continuous, which ensures that the NR method will converge to tsN from any initial condition. For practical purposes, the initial condition can be set from (14) with ρ = 1 - ξ and 0 < ξ < 1, where the near ξ to 1- makes faster the convergence of the NR algorithm.
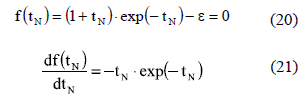
For over-damped systems (ρ > 1), in the same way as in critically-damped systems, there is a single cross with the band limits; hence the NR algorithm must be able to find the solution starting from any initial condition. In this case the settling time is found from C(tN) = 1-ε (22) considering C(tN) expression given in (12). Therefore, a single-solution is obtained from (22). Moreover, from (12) it is noted that 0 < BN <1 due to ρ > 1, therefore the derivative of (22), given in (23), is positive for tN > 0 and zero for tN = 0, which implies that (22) is a monotonically increasing function with f(0) = -1+ε < 0. Such conditions guarantee that (22) has a unique solution, and taking into account that (23) is continuous, the NR method will converge to tsN from any initial condition.
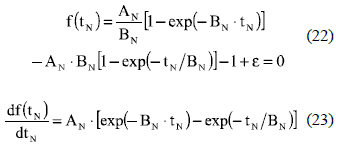
Similar to the critically-damped case, for practical purposes the initial condition of the NR algorithm can be set from (14) with ρ = 1 - ξ and 0 < ξ < 1, this taking into account that over-damped systems have larger normalized settling times than critically-damped systems.
To solve f(tN) given in (18), (20) or (22), selecting the proper one depending on the system damping ratio, the NR method starts from the initial condition tsN = taN0 previously defined. Then, f(tsN) is calculated to evaluate the present value tsN, and the NR algorithm stops if |f(tsN)| ≤ δ, where δ is a threshold to balance the calculation precision and the processing time: smaller δ produces higher precision but longer processing times. If |f(tsN)| > δ, a new tsN value to test is obtained using (24) [1] (non-constant modification to tsN), where tsN,old is the value previously evaluated. New tsN values are sequentially tested until |f(tsN)| ≤ δ is achieved.
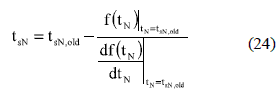
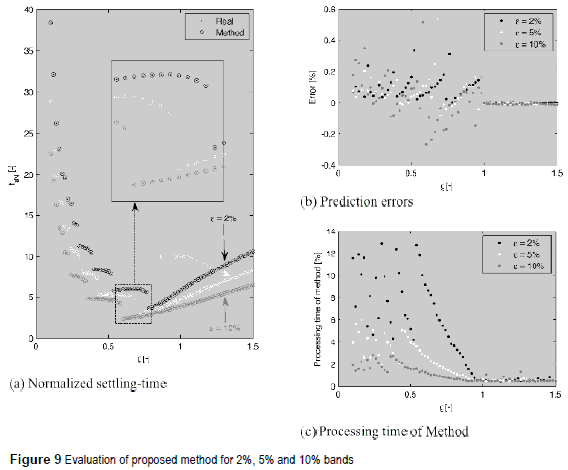
The simplicity of both NR method and relations (18)-(24) allow to implement the proposed solution in any programming language to accurately calculate the settling time. The proposed method (named Method) was implemented in Matlab, where figure 9 shows the comparison between Method and the stepinfo function (named Real) from the Matlab control systems toolbox for 2%, 5% and 10% bands. Figure 9(a) shows the normalized settling time, where the high accuracy of Method is evident.
Such an accurate calculation is verified by the small error between Method and Real data presented in figure 9(b), which is constrained up to 0.6 % for all the bands with an average value of 0.1 %. To perform a fair comparison between the bands, the NR threshold δ was balanced to achieve the same error spectrum: δ was modified proportionally to the band, therefore δ is larger for larger bands. Such a condition is illustrated in figure 9(b), where the errors distribution is similar for all bands tested. Moreover, figure 9(c) presents the processing time required by Method, in comparison with Real, to calculate the settling time. Such results put in evidence the improvement achieved by the proposed solution, in comparison with Matlab stepinfo, since the former requires a small fraction of the time to obtain a small prediction error, which is almost negligible. In such an example, smaller bands use smaller δ to provide comparable prediction errors, which increases the processing time when the band is decreased.
Application example: accurate PO design
To design the Ta parameter of the PO algorithm it is required to define the appropriate irradiance (S) condition. In [3] the authors propose to design at the lowest irradiance in which the PV system will operate. To test such a consideration, the PV system of figure 2 was parameterized with L = 600 μH, C = 100 μF, Vb = 48 V, and considering six BP585 PV panels connected in parallel. Moreover, the PV system was considered with irradiances between 500 W/m2 ≤ S ≤ 1000 W/m2.
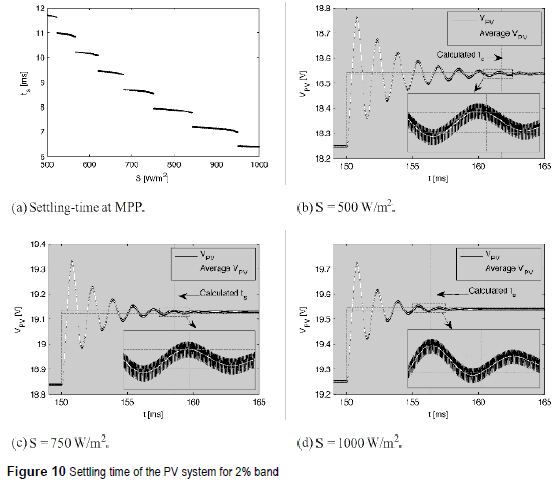
The accurate settling times of the PV system were calculated using Method, and their results are reported in figure 10(a). Those results validate the consideration given in [3] because lower irradiances produce larger settling times. To avoid the condition Ta < ts, Ta must be designed at the lower irradiance required by the application. In this way, figure 10(a) is used to select the accurate Ta for the system.
From Method results, the PV system exhibits a settling time of 11.71 ms at S = 500 W/m2, while at S = 750 W/m2 and S = 1000 W/m2 the settling times are 8.55 ms and 6.40 ms, respectively. Figure 10(b), figure 10(c) and figure 10(d) illustrate the performance of Method for the PO design, where the settling times previously calculated predict the PV system behavior under different conditions. In such figures the settling times are measured in the average PV voltage, since the voltage ripple do not degrade significantly the system power [3]. This application example shows the usefulness and high accuracy of the Method in PV applications.
Conclusios
This paper proposes a method to accurately calculate the settling time in second-order systems. Approximations reported in textbooks and research papers are reviewed illustrating the prediction error generated for those methods. The new method, named Method, was used to calculate the Ta parameter designing a PO algorithm in a PV application. The analytical results show that Method accurately calculates the settling time predicting the PV system behavior. Moreover, due to the accurate results, Method can be used to automatize the settling time calculation in any second order system such as excitation system, operational amplifiers, dc/dc converters, etc.
Acknowledgements
This work was supported by GAUNAL group of the Universidad Nacional de Colombia under the projects SMART-ALEN, VECTORIAL-MPPT and IDENT-EXGEN, and by COLCIENCIAS under the doctoral scholarships 095-2005 and Convocatoria Nacional 2012-567.
References
1. G. Petrone, C. Ramos. "Modeling of photovoltaic fields in mismatched conditions for energy yield evaluations." Electric Power Systems Research. Vol. 81. pp. 1003-1013. 2011. [ Links ]
2. G. Petrone, C. Ramos, G. Spagnuolo, M. Vitelli. "Progress in Photovoltaics: Research and Applications". Granular control of photovoltaic arrays by means of a multi-output Maximum Power Point Tracking algorithm. Article in Press, DOI: 10.1002/pip.2179. 2012. [ Links ]
3. N. Femia, G. Petrone, G. Spagnuolo, M. Vitelli, "Optimization of perturb and observe maximum power point tracking method". IEEE Transactions on Power Electronics. Vol. 20. 2005. pp. 963-973. [ Links ]
4. A. Trejos, D. Gonzalez, C. Ramos."Modeling of step- up grid-connected photovoltaic systems for control purposes". Energies. Vol. 5. 2012. pp. 1900-1926. [ Links ]
5. K. Ogata. Modern Control Engineering. 3rd ed. Ed. Prentice Hall. New Jersey. United States. 2005. pp. 141-159. [ Links ]
6. J. Carstens. Automatic control systems and components. 1st ed. Ed. Prentice Hall. New Jersey. United States. 1990. pp. 219-220. [ Links ]
7. R. Dorf, R. Bishop. Modern control systems. 11th ed. Ed. Prentice Hall. New Jersey. United States. 2008. pp. 281-286. [ Links ]
8. B. Kuo, F. Golnaraghi. Automatic Control Systems. 7th ed. Ed. Prentice Hall. New Jersey. United States. 2002. pp. 398-401. [ Links ]
9. A. Mandal. Introduction to control engineering. 1st ed. Ed. New Age International. New Delhi. India. 2006. pp. 93-99. [ Links ]
10. N. Nise. Control systems engineering. 4th Edition. Ed. Wiley. New Jersey, United States. 2004. pp. 182-201. [ Links ]
11. C. Bert. "Improved approximation for settling time of second-order linear systems". IEEE Transactions on Automatic Control. Vol. AC-31. 1986. pp. 642-643. [ Links ]
12. R. Piche. "Comments, with reply, on 'an improved approximation for settling time of second-order linear systems' by C. W. Bert". IEEE Transactions on Automatic Control. Vol. AC-32. 1987. pp. 747-748. [ Links ]
13. R. Ionel, S. Ionel, A. Ignea. "Calculation of the Second Order Settling Time in SISO Linear Systems". Circuits, Systems, and Signal Processing. Vol. 32. 2013. pp. 375-385. [ Links ]
14. M. Elgendy, B. Zahawi, D. Atkinson. "Assessment of Perturb and Observe MPPT Algorithm Implementation Techniques for PV Pumping Applications". IEEE Transactions on Sustainable Energy. Vol. 3. 2012. pp. 21-33. [ Links ]
15. Y. Xia, K. Ahmed, B. Williams, "Wind Turbine Power Coefficient Analysis of a New Maximum Power Point Tracking Technique". IEEE Transactions on Industrial Electronics. Vol. 60. 2013. pp. 1122-1132. [ Links ]