Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista Facultad de Ingeniería Universidad de Antioquia
versão impressa ISSN 0120-6230
Rev.fac.ing.univ. Antioquia no.67 Medellín abr./jun. 2013
ARTÍCULO ORIGINAL
Spatial super-resolution in coded aperture- based optical compressive hyperspectral imaging systems
Super-resolución espacial en sistemas ópticos hiperespectrales de compresión basados en aperturas codificadas
Hoover Fabian Rueda Chacón, Henry Arguello Fuentes*
School of Systems Engineering and Informatics. Universidad Industrial de Santander. C.P 680002. Bucaramanga, Colombia.
*Autor de correspondencia: teléfono: + 57 + 7 + 634 40 00 ext. 2476, correo electrónico: henarfu@uis.edu.co (H. Arguello)
(Recibido el 14 de Septiembre de 2012. Aceptado el 26 de abril de 2013)
Abstract
The Coded Aperture Snapshot Spectral Imaging system (CAS SI) is a remarkable optical imaging architecture, which senses the spectral information of a three dimensional scene by using two-dimensional coded focal plane array (FPA) projections. The projections in CASSI are localized such that each measurement contains spectral information only from a specific spatial region of the data cube. Spatial resolution in CASSI is highly dependent on the resolution the FPA detector exhibits; hence, high-resolution images require high-resolution detectors that demand high costs. To overcome this problem, in this paper is proposed an optical model for spatial superresolution imaging called SR-CASSI. Spatial super-resolution is attained as an inverse problem from a set of low-resolution coded measurements by using a compressive sensing (CS) reconstruction algorithm. This model allows the reconstruction of spatially super-resolved hyper-spectral data cubes, where the spatial resolution is significantly enhanced. Simulation results show an improvement of up to 8 dB in PSNR when the proposed model is used.
Keywords: Super-resolution, hyper-spectral imaging, compressive sensing, optical imaging, CASSI, multi-shot, coded aperture-based systems
Resumen
El sistema de adquisición de imágenes espectrales basado en apertura codificada de única captura (CASSI) es una arquitectura óptica notable, que permite capturar la información espectral de una escena utilizando proyecciones bidimensionales codificadas. Las proyecciones en CASSI se encuentran ubicadas de tal manera, que cada medición contiene únicamente información espectral específica de una región del cubo de datos. La resolución espacial en el sistema CASSI depende altamente de la resolución del detector utilizado; así, imágenes de alta resolución requieren detectores de alta resolución, que a su vez demandan altos costos. Como solución a este problema, en éste artículo se propone un modelo óptico de súper-resolución para el mejoramiento de la resolución espacial de imágenes hiperespectrales denominado SR-CASSI. Súper-resolución espacial se logra tras solucionar un problema inverso utilizando un algoritmo de compressive sensing (CS), que tiene como entrada las mediciones codificadas de baja resolución capturadas. Éste modelo permite la reconstrucción de cubos de datos hiperespectrales súper resueltos, cuya resolución espacial es aumentada significativamente. Los resultados de las simulaciones muestran un mejoramiento de más de 8 dB en PSNR cuando el modelo propuesto es utilizado.
Palabras clave: Súper-resolución, imágenes hiperespectrales, Compressive Sensing, CASSI, multicaptura, sistemas basados en aperturas codificadas
Introduction
In most applications where digital images are used, are necessary and often required that these exhibit high-resolution. High-resolution refers to a greater number of pixels per unit area in an image, which allows observing a greater amount of detail in images that can be critical and important in different areas such as astrophysics [1], environmental remote sensing [2], microscopy [3], identification of military objectives [4], biomedical image processing [5] and others. Images used in these areas are considered intrinsically multidimensional due to their representation require more than two dimensions; these dimensions include, spectral, time, spatial, etc. Hyper-spectral images are a specific kind of multidimensional images. These are usually captured by spectrometers, which are optical instruments that measure the intensity or polarization of electromagnetic waves across a broad range of wavelengths. They give precise wavelength information of a scene, but spatial information is restricted to the measurement location [6].
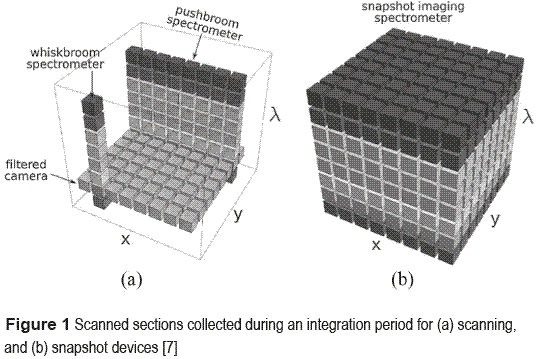
The objective of using spectrometers is to know the information comprised in a three-dimensional scene, in other words, in a hyper-spectral image (two dimensions represent the spatial domain, and the other the spectral or also known as wavelength domain). If a scene or object has many spectral and spatial characteristics, it is necessary to scan the entire object. Figure 1(a) depicts the three different kind of scanning options; one is referred as pushbroom scanning, the second as whiskbroom scanning and the last one as spectral filtering [7]. The former scan the scene pixel by pixel, while the remaining techniques scan the scene line by line; therefore, although the remaining scanning processes are done more rapidly, they are more expensive. On the other side, figure 1(b) shows the snapshot imaging spectrometer; in contrast, it collects the entire datacube information in a single integration period without scanning.
In snapshot spectrometers the scene is encoded both spatially and spectrally using the theory of compressive sensing (CS) [8-10]. For this reason, for a coded aperture-based optical imagery system, the intensity on the detector cannot be directly correlated to spectral density. Instead, the image captured at the detector must be processed using an inverse model that requires some previous knowledge of the optical elements present in the compressive optical system. Spectrometers of this type are referred as spectral or hyper-spectral imagers. The premise to encode spatially and spectrally a hyper-spectral scene is due to hyper-spectral images are well suited for sparse representations as they exhibit high correlation between spectral bands [11, 12].
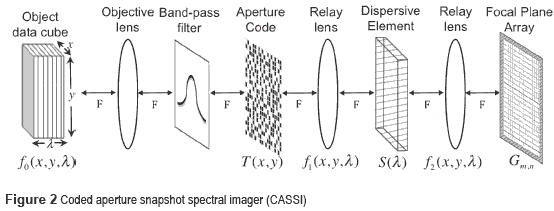
Coded aperture snapshot spectral imager (CASSI) [13-15] is an imaging system that effectively exploits CS principles. In CASSI the coded measurements captured by the FPA are mathematically equivalent to compressive random projections in CS. Notice that in CS, traditional sampling is replaced by measurements of inner products with random vectors. For sensing purpose, CASSI uses a single measurement to capture a complete spatial-spectral data cube. The CASSI instrument is depicted in figure 2.
CASSI is composed by an objective lens that focuses the 3D scene in the plane of the coded aperture, which modulates it spatially. Additionally, a band-pass filter is used between, to limit the spectral range of action. CASSI also has a dispersive element (commonly a prism), which shears horizontally each spectral band respect to its wavelength, and a FPA detector that integrates, and captures the 3D scene. For energy transmission between optics elements detailed above, a set of relay lenses is used.
Recent studies have shown that using multiple CASSI measurements [16-19] instead of a single measurement provides better datacube reconstructions [20-22]. High quality in data cube reconstructions depends directly on the resolution of the detector. However, highresolution detectors demand high costs. Spatial super-resolution in coded aperture-based optical hyper-spectral imaging systems (SR-CASSI) is of high interest because high-resolution reconstructions can be attained from low- resolution/cost detectors. Spectral imaging in infrared (IR) wavelengths is one of the principal examples where FPAs are critical components, because they become very costly when resolution increases [23].
In this paper, we propose the mathematical matrix model for spatial super-resolution in coded aperture-based optical hyper-spectral imaging systems. Spatial super-resolution is attained by solving an inverse problem that accounts for the high-resolution coded aperture, the dispersive element and the decimation induced by the low-resolution detector. Simulations and experiments are performed, obtaining significantly enhancement in spatial data cube reconstructions.
Spatial super-resolution in CASSI
Firstly, it is important to notice the role of CS theory in hyper-spectral image processing, particularly in coded aperture-based optical imaging systems. Formally, a hyper-spectral signal F  RN×M×L, with N and M representing the spatial resolution and L the spectral depth, or its vector representation f
RN×M×L, with N and M representing the spatial resolution and L the spectral depth, or its vector representation f  RN.M.L is S-sparse on some basis Ψ=Ψ1
RN.M.L is S-sparse on some basis Ψ=Ψ1 Ψ2
Ψ2 Ψ3 such that f= Ψθ can be approximated by a linear combination of S vectors from Ψ with S<N.M.L. The operator
Ψ3 such that f= Ψθ can be approximated by a linear combination of S vectors from Ψ with S<N.M.L. The operator 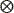 represents the Kronecker product and Ψ the Kronecker basis representation of f [24]. The theory of CS shows that f can be recovered with high probability from m random projections, when m<Slog(N.M.L)<N.M.L. Specially for CASSI, the random projections are given by g=Hf, where H represents the transmission optical function of the system, accounting for the coded aperture and the dispersive element. On the other hand, the random projections for SR-CASSI are given by g=DHf, with D being the decimation due to the low-resolution detector and H representing the effect of the high-resolution coded aperture and the dispersive element.
represents the Kronecker product and Ψ the Kronecker basis representation of f [24]. The theory of CS shows that f can be recovered with high probability from m random projections, when m<Slog(N.M.L)<N.M.L. Specially for CASSI, the random projections are given by g=Hf, where H represents the transmission optical function of the system, accounting for the coded aperture and the dispersive element. On the other hand, the random projections for SR-CASSI are given by g=DHf, with D being the decimation due to the low-resolution detector and H representing the effect of the high-resolution coded aperture and the dispersive element.
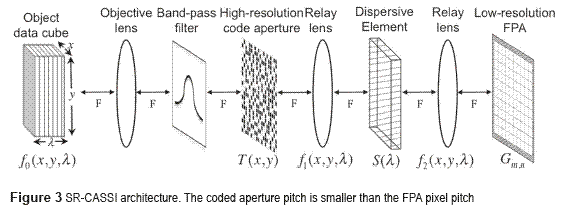
The principal objective in spatial super-resolution is to obtain high-resolution reconstructions from sets of measurements captured by low-resolution FPAs. Figure 3 shows the optical architecture proposed for spatial SR-CASSI to achieve this objective. There, the image source density denoted as f0 (x,y,λ) is first coded by the highresolution coded aperture T(x,y). The resulting coded field f1 (x,y,λ) is subsequently sheared horizontally by a dispersive element before it impinges onto the FPA, resulting in the signal f2 (x,y,λ). The output f2 (x,y,λ) is then optically relayed into the FPA, where the compressive measurements are realized by the integration over the detector's spectral range sensitivity.
Assuming a N×M×N hyper-spectral data cube, the SR-CASSI model is represented as follows. The spatial modulation realized by the coded aperture can be written as in equation (1),
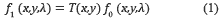
The modulated spatio-spectral information is then sheared horizontally by the dispersive element. Then the signal obtained after dispersion is given by equation (2) as
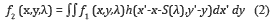
where h(x'-x-S(λ),y'-y) represents the dispersive element operation with S(λ) being the dispersion function which depends on the spectral band wavelength. The measurements across the FPA are realized by the integration of the field f2 (x,y,λ) over the detector's spectral range sensitivity as g(x,y) = ∫f2 (x,y,λ)dλ. Hence, replacing f (x,y,λ) from Eq. (2), we obtain in equation (3),
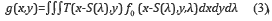
Since the FPA detector is spatially pixelated, the measurement at the (m,n)th pixel is given by the integration of Eq. (3) as presented in equation (4),
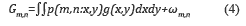
where ωm,n represents additive noise from the capturing process, and p(m,n:x,y) the detector pixelation function given by p(m,n:x,y) = 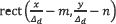 , with Δd being the pixel width of the detector. By replacing equation (3) in equation (4) the (m,n)th measurement can be expressed as in equation (5),
, with Δd being the pixel width of the detector. By replacing equation (3) in equation (4) the (m,n)th measurement can be expressed as in equation (5),
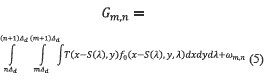
where the FPA pixelation function is replaced by re-defining the spatial integration limits, taking into account the size mismatch between the high-shy;resolution coded aperture features and the low-resolution FPA pixels.
A critical requirement for achieving super-resolution is that the pitch of the modulating coded aperture must be lower than the one of the detector. Letting Δc be the spatial width between elements in the coded aperture, then, the pitch ratio between the coded aperture and the detector is defined as 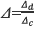 . Assuming the side length of the detector spans an integer number of coded aperture features, the horizontal and vertical spatial super-resolution are thus limited by Δc. Hence, the compressive sensing measurement at the (m,n)th detector pixel can be written in discrete form as in equation (6),
. Assuming the side length of the detector spans an integer number of coded aperture features, the horizontal and vertical spatial super-resolution are thus limited by Δc. Hence, the compressive sensing measurement at the (m,n)th detector pixel can be written in discrete form as in equation (6),
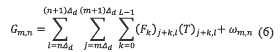
In matrix notation, a snapshot measurement at the detector is represented in equation (7) as,

where, H is a N(M+L-1)×NML matrix representing the transmission function of the system, and D a 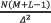 ×N(M+L-1) matrix representing the decimation. Notice that f and g are vector representations of F and G respectively. For a multiple-shot approach, equation (7) changes as stated in equations (8) and (9),
×N(M+L-1) matrix representing the decimation. Notice that f and g are vector representations of F and G respectively. For a multiple-shot approach, equation (7) changes as stated in equations (8) and (9),
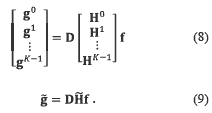
where 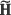
 {0,1}N(M+L-1)K×NML, for K shots. Notice that the coded aperture pattern Ti as given in equation (10) changes for each ith snapshot. The optical transmission function of the system for the ith snapshot in equation (8) can be expressed in matrix form as,
{0,1}N(M+L-1)K×NML, for K shots. Notice that the coded aperture pattern Ti as given in equation (10) changes for each ith snapshot. The optical transmission function of the system for the ith snapshot in equation (8) can be expressed in matrix form as,

with P being a N(M+L-1)×NML matrix representing the dispersive element operation, and Ti a NML×NML block-diagonal matrix accounting for the ith coded aperture as given in equation (11),
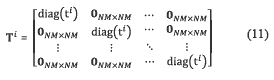
where ti represents the ith N×Mcoded aperture in lexicographical notation, and diag(ti) is a function which places the elements of tiin the diagonal of a matrix. Note that 0NM×NM is a zero-valued matrix with NM rows and columns. Besides, the dispersive element operation when linear dispersion is considered, is represented by a matrix P which is given by equation (12),
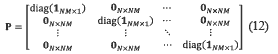
where 1NM×1 is a NM long one-valued column vector. Finally, let define d=[(11×Δ 01×(N-Δ)] and 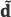 =μΔ
=μΔ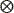 d, where μΔ is a Δ-long one-valued row vector. Then, let define
d, where μΔ is a Δ-long one-valued row vector. Then, let define 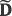 as in equation (13),
as in equation (13),
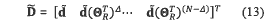
with ΘR being a permutation matrix as in equation (14),
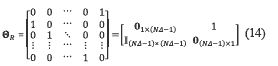
where 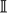 is the identity matrix. Notice, the matrix operation A(ΘRT)k shifts the columns of matrix A, k positions to the right. By using the equation (13) and (14), the decimation operation due to the low-resolution detector can be modeled as given in equation (15),
is the identity matrix. Notice, the matrix operation A(ΘRT)k shifts the columns of matrix A, k positions to the right. By using the equation (13) and (14), the decimation operation due to the low-resolution detector can be modeled as given in equation (15),
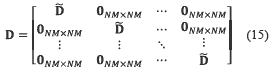
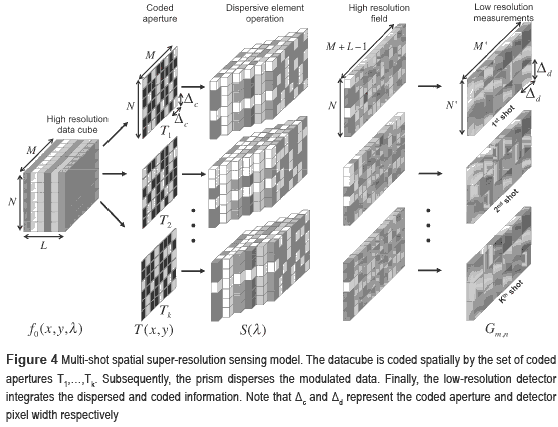
A graphical scheme of the multi-shot approach is depicted in figure 4. There, each coded aperture in a particular shot spatially modulates the data cube. After modulation, the data cube is relayed onto the prism, which shifts horizontally each spectral band S(λ) spatial units. Finally, after the prism shears the modulated data cube, the N'×M' low-resolution detector integrates it. Notice that N' = 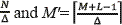 .
.
After detailed the sensing model, an estimation of the hyper-spectral signal can be obtained by solving an inverse problem. Precisely, hyper-spectral image data cube reconstruction 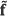 for SR-CASSI can be achieved by solving the optimization problem stated in equation (16),
for SR-CASSI can be achieved by solving the optimization problem stated in equation (16),
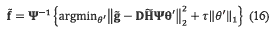
where Ψ represents the projection basis where the hyper-spectral signal becomes sparse, and θ are its representative sparse coefficients (refers to the beginning of spatial super-resolution in CASSI). Furthermore, τ > 0 is a regularization parameter which balances the conflicting tasks of minimizing the least square of the residuals, while at the same time, yielding a sparse solution [25].
Simulations and results
A high-resolution hyper-spectral datacube considered as the digital reality, is experimentally obtained and depicted in figure 5. The acquisition process is performed by using a high-resolution 256×256 FPA detector exhibiting a 9.9 μm pixel pitch, and assuming a linear dispersive element (as in Eq. 12) in the spectral range between 451 nm and 642 nm (the band pass filter allows only visible spectra to pass through the optical system).
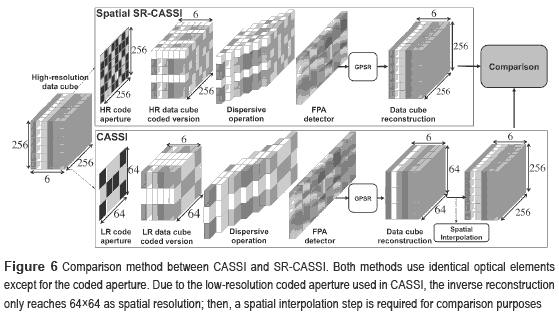
Due to the pixel pitch and the linear dispersion, 24 spectral bands compose the data cube. From the high-resolved data cube (figure 5, right) is obtained a spectrally coarse 256×256×6 version by assuming an integration step of 4 bands; this is considered as the incoming scene for both CASSI and SR-CASSI approaches. Additionally, a 64x69 low resolution FPA is used in all the experimental simulations. Particularly for SR-CASSI, the high-resolution coded aperture exhibits 256×256 pixels as spatial resolution, while on the other hand CASSI uses a 64×64 low-resolution coded aperture matching with the FPA pixel pitch. The entries for both coded apertures as given in Eq. (11) are random realizations of a Bernoulli random variable with parameter p=0.5. In figure 6 is depicted the method used for comparison purposes.
Biological and chemical materials
Notice, the spectral range remains fixed for the high/low resolution, and coarse data cubes. In consequence, the bandwidth of each spectral slice in the high-resolution data cube is 8 nanometers, while the low-resolution data cube exhibits 32 nanometers per band. For datacube reconstructions, the Gradient Projection for Sparse Reconstruction algorithm (GPSR) [26] is used to solve the inverse problem given in Eq. (16), by considering the representation basis Ψ as the Kronecker product [22] of three basis Ψ=Ψ1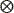 Ψ2
Ψ2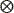 Ψ3, where the combination Ψ1
Ψ3, where the combination Ψ1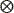 Ψ2 is the 2D-Wavelet Symlet 8 basis, and Ψ3 is the Discrete Cosine basis.
Ψ2 is the 2D-Wavelet Symlet 8 basis, and Ψ3 is the Discrete Cosine basis.
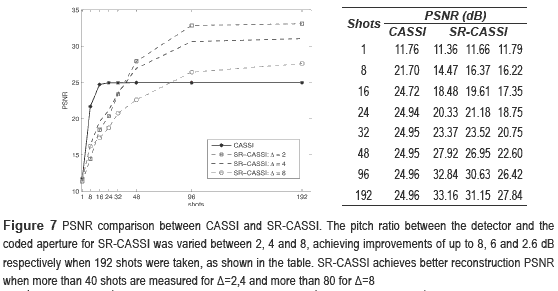
In order to evaluate the efficiency of SRCASSI, the decimation ratio between the highresolution coded aperture features and the low resolution FPA pixels was varied between 2, 4 and 8 (Δ=2,4,8) in Eq. (13). The PSNR of the reconstructed data cubes, as a function of the number of FPA measurements captured, is shown in figure 7. SR-CASSI obtains better PSNR than CASSI when more than 40 FPA measurements are taken for Δ=2,4 and more than 80 for Δ=8. This improvement is approximately 8 dB, 6 dB and 2.6 dB for Δ=2,4,8 respectively. The PSNR in CASSI remains static as number of shots increase, due to the fact that no sub-pixel information can be exploited.
Results in figure 7 show an effectively way to exploit sub-pixel information from the hyper-spectral scene as more shots are captured. Also, it can be seen that even when using extreme pitch ratios as Δ=8, the system continues overcoming CASSI results. SR-CASSI requires at least 40 shots to reach CASSI due to the amount of information collected is less and depends directly on the pitch ratio; as higher it is, more FPA shots are required (dotted square vs. dotted circle SR-CASSI curves). In figure 8 a zoomed version of the six original hyper-spectral bands is shown. Furthermore, in order to show the visual improvement, figure 9 and 10 depict the reconstructed spectral channels when 16 and 192 measurements are captured respectively.
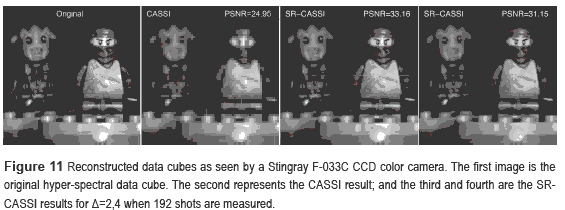
Finally, the complete reconstructed data cubes are integrated and visualized in figure 11 as seen by a Stingray F-033C CCD color camera. The enhancement achieved by using the proposed model can be easily identified.
Conclusions
A super-resolved methodology for coded aperture-based multi-shot hyper-spectral imaging systems has been proposed. The mathematical matrix model was developed to simulate the effect of SR-CASSI optical elements, including the decimation transformation induced by the low-resolution detector. The proposed optical architecture allows exploiting sub-pixel information from the original hyper-spectral signal at the cost of capture multiple FPA measurements. Improvements of 8 dB, 6 dB and 2.6 dB in PSNR were achieved for pixel pitch ratios of 2, 4 and 8, respectively.
References
1. R. Lin, B. Dennis, G. Hurford, D. Smith, A. Zehnder, P. Harvey, D. Curtis, D. Pankow, P. Turin, M. Bester, A. Csillaghy, M. Lewis, N. Madden, H. van Beek, M. Appleby, T. Raudorf, J. McTiernan, R. Ramaty, E. Schmahl, R. Schwartz, S. Krucker, R. Abiad, T. Quinn, P. Berg, M. Hashii, R. Sterling, R. Jackson, R. Pratt, R. Campbell, D. Malone, D. Landis, C. Barrington, S. Slassi, C. Cork, D. Clark, D. Amato, L. Orwig, R. Boyle, I. Banks, K. Shirey, A. Tolbert, D. Zarro, F. Snow, K. Thomsen, R. Henneck, A. McHedlishvili, P. Ming, M. Fivian, J. Jordan, R. Wanner, J. Crubb, J. Preble, M. Matranga, A. Benz, H. Hudson, R. Canfield, G. Holman, C. Crannell, T. Kosugi, A. Emslie, N. Vilmer, J. Brown, C. Johns-Krull, M. Aschwanden, T. Metcalf, A. Conway. ''The Reuven Ramaty high- energy solar spectroscopic imager (RHESSI)''. Solar Physics. Vol. 210. 2002. pp. 3-32. [ Links ]
2. W. Smith, D. Zhou, F. Harrison, H. Revercomb, A. Larar, A. Huang, B. Huang. ''Hyperspectral remote sensing of atmospheric profiles from satellites and aircraft''. Hyperspectral Remote Sensing of the Land and Atmosphere. Vol. 4151. 2001. pp. 94-102. [ Links ]
3. P. Ye, J. Paredes, G. Arce, Y. Wu, C. Chen, D. Prather. Compressive confocal microscopy. Proceeding of International Conference on Acoustics, Speech and Signal Processing. Taipei, Taiwan. 2009. pp. 429-432. [ Links ]
4. C. Stellman, F. Olchowski, J. Michalowicz. War horse (wide-area reconnaissance: hyperspectral overhead real-time surveillance experiment). Proceedings SPIE 4379, Automatic Target Recognition XI. Orlando, USA. Vol. 4379. 2001, pp. 339-346. [ Links ]
5. T. Pham, F. Bevilacqua, T. Spott, J. Dam, B. Tromberg, S. Andersson. ''Quantifying the absorption and reduced scattering coefficients of tissuelike turbid media over a broad spectral range with noncontact fourier-transform hyperspectral imaging''. Applied Optics. Vol. 39. 2000. pp. 6487-6497. [ Links ]
6. D. Kittle. Compressive spectral imaging. Master's thesis. Duke University. Durham, North Carolina, USA. 2010. [ Links ]
7. N. Hagen, R. Kester, L. Gao, T. Tkaczyk. ''Snapshot advantage: a review ofthe light collection improvement for parallel high-dimensional measurement systems''. Optical Engineering. Vol. 51. 2011. pp. 111702-1 - 111702-7. [ Links ]
8. E. Candès, J. Romberg, T. Tao. ''Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information''. IEEE Transactions on Information Theory. Vol. 52. 2006. pp. 489-509. [ Links ]
9. E. Candès, T. Tao. ''Near-optimal signal recovery from random projections: Universal encoding strategies?''. IEEE Transactions on Information Theory. Vol. 52. 2006. pp. 5406-5425. [ Links ]
10. D. Donoho. ''Compressed sensing''. IEEE Transactions on Information Theory. Vol. 52. 2006. pp. 1289-1306. [ Links ]
11. E. Christophe, C. Mailhes, P. Duhamel. ''Hyperspectral image compression: adapting SPIHT and EZW to anisotropic 3D wavelet coding''. IEEE Transactions on Image Processing. Vol. 17. 2008. pp. 2334-2346. [ Links ]
12. P. Dragotti, G. Poggi, A. Ragozini. ''Compression of multispectral images by three-dimensional SPIHT algorithm''. IEEE Transactions on Geoscience and Remote Sensing. Vol. 38. 2000. pp. 416-428. [ Links ]
13. A. Wagadarikar, R. John, R. Willett, D. Brady. ''Single disperser design for coded aperture snapshot spectral imaging''. Applied Optics. Vol. 47. 2008. pp. B44-B51. [ Links ]
14. H. Arguello, H. Rueda, Y. Wu, D. Prather, G. Arce, ''Higher-order computational model for coded aperture spectral imaging.'' Appl. Opt. Vol. 52. 2013. pp. D12-D21. [ Links ]
15. H. Arguello, C. Correa, G. Arce, ''Fast lapped block reconstructions in compressive spectral imaging,'' Appl. Opt. Vol. 52. 2013. pp. D32-D45. [ Links ]
16. Y. Wu, I. Mirza, G. Arce, D. Prather. ''Development of a digital-micromirror-device-based multishot snapshot spectral imaging system''. Optics Letters. Vol. 36. 2011. pp. 2692-2694. [ Links ]
17. H. Arguello, G. Arce. ''Code aperture optimization for spectrally agile compressive imaging''. Journal of the Optical Society of America A. Vol. 28. 2011. pp. 2400-2413. [ Links ]
18. H. Arguello, C. Correa, G. Arce. ''Code aperture optimization by concentration of measure in compressive spectral imaging''. Journal of the Optical Society of America A. USA. 2012. [ Links ]
19. D. Kittle, K. Choi, A. Wagadarikar, D. Brady. ''Multiframe image estimation for coded aperture snapshot spectral imagers''. Applied Optics. Vol. 49. 2010. pp. 6824-6833. [ Links ]
20. H. Arguello, G. Arce. Restricted Isometry Property in coded aperture compressive spectral imaging. IEEE Statistical Signal Processing Workshop. Ann Arbor, MI, USA. 2012. pp. 716-719. [ Links ]
21. H. Arguello, G. Arce. Spectrally Selective Compressive Imaging by Matrix Analysis. OSA Optics and Photonics Congress. Monterey, CA, USA. 2012. pp. CM4B.5. [ Links ]
22. H. Arguello, G. Arce. Code Aperture Agile Spectral Imaging (CAASI). Imaging and Applied Optics Congress (OSA Optics & Photonics Congress). Toronto, Canada, 2011. pp. ITuA4. [ Links ]
23. R. Willett, R. Marcia, J. Nichols. ''Compressed sensing for practical optical imaging systems: A tutorial''. Optical Engineering. Vol. 50. 2011. pp. 072601 1-13. [ Links ]
24. M. Duarte, R. Baraniuk. Kronecker product matrices for compressive sensing. IEEE International Conference on Acoustics Speech and Signal Processing. Dallas, USA. 2010. pp. 3650-3653. [ Links ]
25. H. Arguello, G. Arce. ''Rank minimization code aperture design for spectrally selective compressive imaging''. IEEE Transactions on Image Processing. Vol. 22. 2012. pp. 941-954. [ Links ]
26. M. Figueiredo, R. Nowak, S. Wright. ''Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems''. IEEE Journal of Selected Topics in Signal Processing. Vol. 1. 2007. pp. 586-597. [ Links ]