Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230
Rev.fac.ing.univ. Antioquia no.69 Medellín Oct./Dec. 2013
ARTÍCULO ORIGINAL
Filtrado digital compuesto
Compound digital filter
José de Jesús Medel Juárez1*, Juan Carlos García Infante2, Gonzalo Isaac Duchen Sánchez 2
1Centro de Investigación en Computación. Av. 100 m, esq., Venus, Col. Nueva Industrial Vallejo, C. P. 07738. México D. F., México.
2Escuela Superior de Ingeniería Mecánica y Eléctrica. IPN, Col. San Francisco Culhuacán Del. Coyoacán. México D.F., México.
*Autor de correspondencia: teléfono: + 01 + 52 + 57296000 ext. 56570, correo electrónico: jjmedelj@yahoo.com.mx (J. Medel)
(Recibido el 28 de febrero de 2011. Aceptado el 19 de septiembre de 2013)
Resumen
En este trabajo se describen las características de operación de un Filtro Digital Compuesto, el cual está formado por dos estimadores que intervienen en el filtro de Kalman; el primero de ellos corresponde al gradiente estocástico para obtener la función de transición y el segundo, ajusta la ganancia del proceso de innovación por medio de la lógica difusa. En el proceso de filtrado se cuenta con restricciones de tiempo para que su respuesta ocurra antes de que el sistema de referencia cambie a otro estado. Los resultados obtenidos están desarrollados formalmente a lo largo del documento. Se propone un Modelo Auto-regresivo de Promedios Móviles (MARPM(1,1)) como sistema de referencia. El algoritmo de filtrado fue desarrollado con el programa MatLab® obteniendo las gráficas de su operación, convergencia y respuesta. Concluyendo con un pequeño análisis de los resultados.
Palabras clave: Filtro digital, lógica difusa, tiempo real, identificación, estimación, procesamiento de señales
Abstract
This paper describes the identification by the compound digital filter with two estimators involved in the Kalman filter, the first corresponds to stochastic gradient describing the transition function and the second obtains the innovation process gain through fuzzy logic. The filtering process has time constraints for your response occurring before the reference system changes to another state. The results are formally described throughout the document.
Auto-Regressive Moving Averages model was proposed (ARMA (1, 1)) as the reference system. The filtering algorithm was developed in MatLab® software getting the integrated filter operations illustrated with its graphics of convergence and response, concluding with brief an analysis of the results.
Keywords: Digital filters, fuzzy logic, real-time, identification, estimation, signal srocessing
Introducción
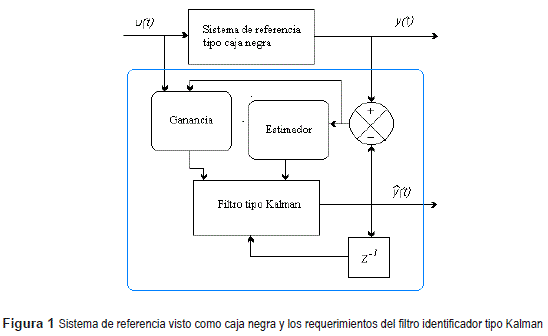
El problema de un filtro identificador en un sistema tipo caja negra, es la estimación de la matriz de transición y de ganancias a través de los estados observables del sistema de referencia (SR), como se observa en la figura 1.
El filtro tipo Kalman es un Filtro Digital Compuesto (FDC) por un filtro identificador con dos estimadores. El primero, es un estimador del tipo gradiente estocástico y se encarga de describir a la función de transición y el segundo, es un estimador por mínimos cuadrados de la ganancia del filtro identificador usando la lógica difusa [1]. En ambos casos el FDC funciona en lazo cerrado y ajusta al identificador, la estimación y las ganancias de acuerdo con el error de identificación (EI) y a sus estados anteriores [2, 3].
En el FDC se conjuntan la lógica difusa y los procesos estocásticos para obtener la convergencia a un punto de referencia que se llama señal observable. Cuenta con el proceso de adaptación a la función de ganancias que afecta al identificador de acuerdo a un grupo de inferencias [4] que sin que se pierdan las condiciones de estabilidad llegue a la condición deseada [5-7].
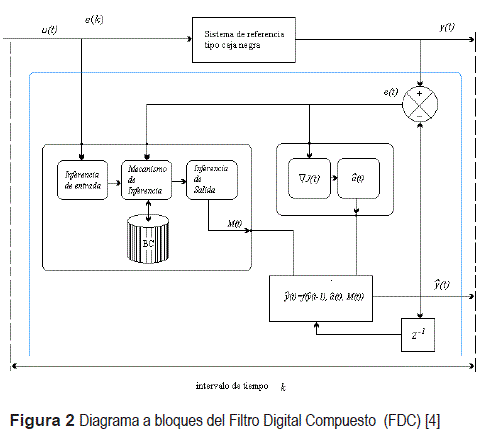
La función de transición del sistema de referencia tipo caja negra se obtiene por medio del estimador de gradiente estocástico [8]. La Lógica Difusa (LD) aplicada para la estimación de la matriz de ganancias del filtro identificador, permite seleccionar los parámetros dentro de la Base de Conocimiento (BC) de acuerdo al rango de la función de distribución del error de identificación ajustando a las Funciones de Membresía (FM) de manera dinámica por medio de sus intervalos, haciendo uso de las reglas de inferencia difusa; para lograr que el error de identificación en el rango seleccionado sea minimizado y que el filtro identificador proporcione una respuesta para una condición específica [1, 9, 10]. El FDC en el diagrama a bloques puede observarse en la figura 2, con el estimador estocástico conjugado con el estimador difuso para integrarse en el identificador de acuerdo con [11, 12].
El Error de Identificación (EI) e(k) permite obtener una función de densidad, dentro de la cual de acuerdo con la LD se obtiene por lo menos una función de membresía que cubre a casi todo el espectro de la función de distribución [13, 14]. Dentro de la propia función de distribución es posible establecer el rango de intervalos requeridos a los que se les llamará n-cil (octil, decil, percentil, entre otros) de acuerdo con la Función Objetivo (FO), previamente establecida; de manera tal que se pueda tener un grupo de Funciones de Membresía (FM) que permitan seleccionar dentro de la Base de Conocimiento (BC) a una ganancia que ajusta la evolución del identificador [15-17].
Desarrollo teórico
En este trabajo se desarrolla el Filtro Digital Compuesto (FDC) considerando: a) al funcional del error J(k) de identificación e(k) := y(k) - ŷ(k), b) el estimador de parámetros por método del gradiente estocástico y, c) el estimador de la ganancia del filtro identificador tipo Kalman utilizando a la lógica difusa. [18, 19]. Lo primero a desarrollar es el funcional del error de identificación de forma recursiva (Teorema 1) ; segundo, el estimador de acuerdo con el gradiente estocástico del funcional del error (Teorema 2); tercero, el estimador estocástico de manera recursiva (Teorema 3); cuarto, la entropía estocástica de manera recursiva (Teorema 4); quinto, la forma en que sería visto el filtro digital compuesto al considerar un sistema de referencia tipo caja negra. En la sección de simulación se consideró un sistema Regresivo de promedios móviles (ARMA, por sus siglas en inglés: Auto Regresive Moving Average) del tipo (1,1). Es así como se presentan las conclusiones y las referencias consideradas a lo largo de este trabajo.
Teorema 1 Sea J(k) el funcional del error de identificación tal que en diferencias finitas y en condiciones estacionarias es descrito de manera recursiva en (1).
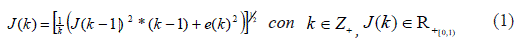
Prueba Sea el funcional de error descrito por el segundo momento de probabilidad del error de identificación (E{e(k)2})1/2 y que en diferencias finitas con condiciones de ergodicidad es descrito de la forma 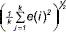 , tomando el último término, y al considerar que la secuencia {e(k)} es estacionaria rígidamente J(k) =
, tomando el último término, y al considerar que la secuencia {e(k)} es estacionaria rígidamente J(k) = 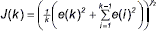 , donde se puede decir, que sus dos primeros momentos de probabilidad son constantes a través del tiempo [9, 20] y
, donde se puede decir, que sus dos primeros momentos de probabilidad son constantes a través del tiempo [9, 20] y 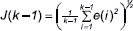 , y permite representar al segundo de J(k) con
, y permite representar al segundo de J(k) con 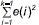 =J(k-1)2(k-1), descripción que es sustituida dentro del funcional del error, obteniendo (1).■
=J(k-1)2(k-1), descripción que es sustituida dentro del funcional del error, obteniendo (1).■
Teorema 2 Sea â(k) el estimador de parámetros óptimo (2) de acuerdo con el gradiente estocástico de (1).
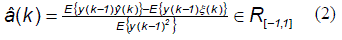
Prueba El funcional del error descrito por el segundo momento de probabilidad del error de identificación tiene la forma J(k) = (E{e(k)2}) en donde el desarrollo del error cuadrático e(k)2 := (y(k) - ŷ(k))2, y al considerar que el modelo de referencia de primer orden del tipo estocástico es en su forma más simple ay(k-1) + ξ(k); el error adquiere la forma e(k)2 := (ay(k-1) + ξ(k) - ŷ(k))2 y que al desarrollar el cuadrado de sus términos e(k)2 :=a2y(k -l)2 +ξ(k)2+ ŷ(k)2 +2ay(k - l)ξ(k) - 2ay(k -1)ŷ(k) - 2ξ(k)ŷ(k). El mínimo del funcional del error se logra por su derivada con respecto al parámetro: 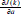 = 2 â(k) E {y(k -1)2} + 2E{y(k -1)ξ(k)} - 2E {y(k -1)ŷ(k)} y al igualar a cero para obtener el estimador del parámetro se obtiene (2).■
= 2 â(k) E {y(k -1)2} + 2E{y(k -1)ξ(k)} - 2E {y(k -1)ŷ(k)} y al igualar a cero para obtener el estimador del parámetro se obtiene (2).■
Teorema 3 El estimador de parámetros (2) de manera recursiva es descrito en (3) al considerar que las señales emitidas por el sistema de referencia son del tipo estacionarias
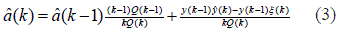
Prueba Ahora considérese que el cociente es descritopor P(k) = E {y(k-l)ŷ(k)} - E {y(k-1)ξ(k)} y Q(k)=E{y(k-1)2}, que en diferencias finitas se tiene con respecto a 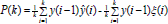 , en donde el último término de la secuencia
, en donde el último término de la secuencia 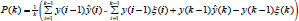 . En condiciones estacionarias
. En condiciones estacionarias 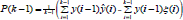 , en donde las sumatorias son
, en donde las sumatorias son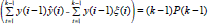 y que al sustituir en,
y que al sustituir en, 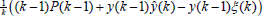 . En condiciones estacionarias el estimador cumple con
. En condiciones estacionarias el estimador cumple con 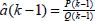 , y al considerarlo en P(k) se tiene
, y al considerarlo en P(k) se tiene 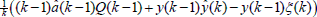 y en el estimador, el cociente es de la forma
y en el estimador, el cociente es de la forma 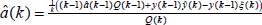 , al agrupar los términos el estimador recursivo es descrito en (3).■
, al agrupar los términos el estimador recursivo es descrito en (3).■
Corolario La forma recursiva de Q(k) en diferencias finitas está descrita por el segundo momento de probabilidad y que corresponde a la matriz de varianzas y que para condiciones estacionarias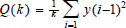 haciendo la expansión
haciendo la expansión 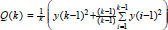 y reduciendo términos se tiene
y reduciendo términos se tiene 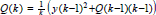 .
.
En los teoremas del 1 al 3, se consideró que las señales de excitación y de respuesta del sistema de referencia tipo caja negra son del tipo estacionario lo que permite utilizar estimadores de primer orden [21]. Se observó que la señal del error de identificación en su estado estacionario queda acotada por una función de distribución y que en cada uno de sus rangos quedarán las Funciones de Membresía (FM) las cuales en su conjunto y de manera ordenada, describirán a la función de distribución en el sentido de Hausdorff [22, 23].
La diferencia entre la función de membresía y la de distribución está limitada en un sentido de distribución por la función de distribución del Funcional de Error de Identificación (FEI) J (k) en su estado estacionario (1) y que de acuerdo con el Conjunto de Reglas Base (CRB), se determina la acción a tomar por el estimador para la selección del rango de su operación que afectará al identificador en su calidad de respuesta [16, 24]. De forma que se considera que el Mecanismo de Inferencia (MI) está delimitado por las variables lingüísticas disponibles aceptando las palabras: bajo, medio, alto, que dentro del sistema digital, cada una de ellas corresponde a un sub-intervalo dentro del intervalo definido en (0,1] en la función de distribución del funcional antes mencionado.
La Base de Conocimiento (BC) en un sentido métrico, está formada por el conjunto de parejas contenidas en (Y(k) × Ŷ(k))  R2 y definida simbólicamente por TN
R2 y definida simbólicamente por TN  R22[1,N ], (también es conocida como el Área de Control de la Base de Conocimiento (ACBC) donde Yd (k) := {y(k)} es el conjunto deseado y Ŷc (k) := {ŷ(k)} es el conjunto de identificación), como se describe en (4).
R22[1,N ], (también es conocida como el Área de Control de la Base de Conocimiento (ACBC) donde Yd (k) := {y(k)} es el conjunto deseado y Ŷc (k) := {ŷ(k)} es el conjunto de identificación), como se describe en (4).
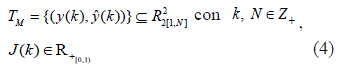
Cada Función de Membresía (FM) establece el valor de correspondencia máximo que hay entre la salida identificada ŷ(k) y la señal deseada y(k), teniendo como objetivo encontrar a través del costo ínfimo del funcional del error de filtrado (inf{J(k)}  δ), la estimación más adecuada así como el estado identificado llevado a una condición deseada. En donde el valor de la entropía de acuerdo con Shannon se encuentra en un estado estacionario [8, 21].
δ), la estimación más adecuada así como el estado identificado llevado a una condición deseada. En donde el valor de la entropía de acuerdo con Shannon se encuentra en un estado estacionario [8, 21].
El Área de Control de la Base de Conocimiento TN de acuerdo con (2) corresponde al conjunto mínimo y se encuentra descrita en (5).
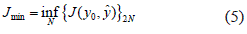
Esto solo puede ocurrir si la entropía en el sentido de probabilidad del funcional del error se encuentra acotada y en forma recursiva en (6).
Teorema 4 La entropía recursiva del funcional del error está descrita en (6)
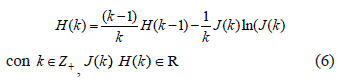
Prueba Considérese que la entropía tiene la forma en diferencias finitas para un sistema estacionario 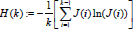 y al desarrollar la sumatoria
y al desarrollar la sumatoria 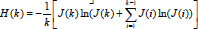 . Las condiciones estacionarias de la entropía
. Las condiciones estacionarias de la entropía 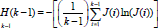 , permite ver
, permite ver 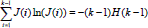 y que al ser sustituida dentro de la entropía se obtiene la forma recursiva descrita en (6).■
y que al ser sustituida dentro de la entropía se obtiene la forma recursiva descrita en (6).■
El 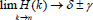 siempre y cuando el funcional del error se encuentre acotado y converja a una región definida
siempre y cuando el funcional del error se encuentre acotado y converja a una región definida 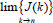
 ε, con (δ±γ*)>0.
ε, con (δ±γ*)>0.
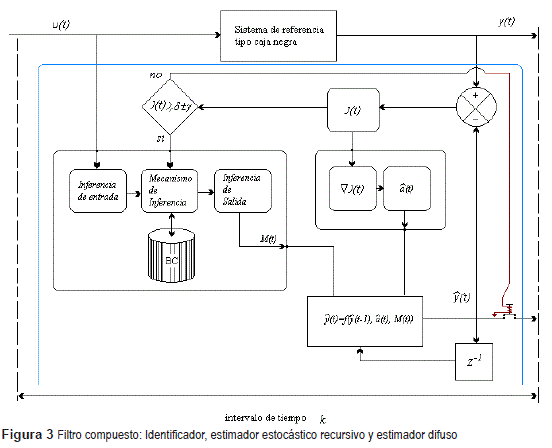
En la figura 3, se muestra el proceso del filtro con el estimador de parámetros y el estimador de la Ganancia obtenida a través de la lógica difusa: proceso integrado por la Estimación, la Estimación Difusa (ED) e Identificación recursiva en el sentido de Kalman (IRFK), enlazados por medio de la adaptación y usando el Mecanismo de Inferencia (MI).
El conjunto de reglas usadas para el estimador de la ganancia del filtro identificador queda acotado en un intervalo de tiempo descrito de manera inversa por dos veces la frecuencia de la evolución del sistema de referencia [25].
En forma simplificada el tiempo de evolución del sistema de referencia (SR) y(k) para el intervalo k es estacionario para lograr una descripción adecuada tanto en tiempo como en calidad de respuesta, significando que en promedio es constante y que para los fines de implementación en los que debe estar un filtro compuesto, resulta muy atractivo, aunque sea del tipo suave contemplando los pequeños retrasos que se pueden generar en un procesador en los cálculos del filtro compuesto. El índice k del tiempo de evolución del sistema de referencia indica de manera simbólica que el sistema tiene un periodo de tiempo en el cual evoluciona a un nuevo estado [11, 21, 26]. De forma que la secuencia de los subprocesos de operación tiene un índice dentro del intervalo k  Z+ en el que éste cambia al siguiente valor en k +1 cuando se ha cumplido con τmín y que corresponde a la frecuencia de evolución del sistema real de acuerdo con [25, 27] y que se describe en (7).
Z+ en el que éste cambia al siguiente valor en k +1 cuando se ha cumplido con τmín y que corresponde a la frecuencia de evolución del sistema real de acuerdo con [25, 27] y que se describe en (7).
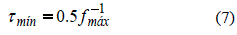
El filtro estimador de las ganancias del identificador {M(k)i} 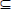 TN; selecciona en cada iteración a la variable difusa, sin perder de vista los Tiempos de Finalizado (TF) {f(k)i} establecidos para el filtro compuesto y que temporalmente de acuerdo con (Medel et al, 2008) quede acotado dentro de los límites descritos en el intervalo [ld(k)i_mín, LD(k)i_máx) y que se cumple μ[ld(k)i_mín, LD(k)i_máx )<τmín.
TN; selecciona en cada iteración a la variable difusa, sin perder de vista los Tiempos de Finalizado (TF) {f(k)i} establecidos para el filtro compuesto y que temporalmente de acuerdo con (Medel et al, 2008) quede acotado dentro de los límites descritos en el intervalo [ld(k)i_mín, LD(k)i_máx) y que se cumple μ[ld(k)i_mín, LD(k)i_máx )<τmín.
El filtrado compuesto ofrece una respuesta local estable ya que el conjunto de ganancias del filtro identificador está dentro de TN, y J(k) de acuerdo con [9, 28] y converge a una región (8) al considerar que el funcional del error decae de forma cuadrática de acuerdo al proceso de adaptación en la estimación de la ganancia.
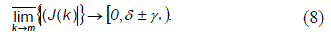
El proceso de filtrado compuesto está delimitado temporalmente en el tiempo de arribo (li (k)), el tiempo de inicio ( si (k) ), el tiempo de ejecución (ci (k)), el tiempo de finalizado (fi (k)) y el límite máximo de tiempo de ejecución (di (k)) de acuerdo con (7) al considerar a τmín como la frontera temporal en la cual el filtro puede entregar un resultado que sea significativo [23].
Simulación
La simulación del filtro compuesto la mejor representación se tiene a través del filtro de Kalman, con una matriz de transición descrita por el estimador e stocàstico y una ganancia obtenida en la BC con respecto al funcional del error J(k) descrito en (1). La caracterización de la estimación difusa considera los niveles de operación ajustables de acuerdo al error de identificación e(k).
Los tiempos de evolución dentro de un sistema del tipo estocástico son los siguientes: Cada iteración con índice k cuenta con un tiempo de evolución de 0,004 ± 0,0002 5 que es menor al tiempo de evolución del sistema de referencia cuya frecuencia es de 100 Hz, cumpliendo con la condición descrita en (5). El modelo de referencia ARMA (1,1) en espacio de estados se describe en (9).
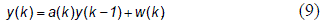
El filtro identificador (10) está descrito de acuerdo al modelo de Kalman.
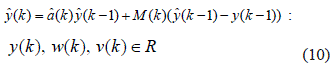
Dónde: {â(k)}es el conjunto de parámetros obtenidos por el gradiente estocástico, {M(k)} es la secuencia de la Ganancia de Kalman obtenida por medio de la lógica difusa, {w(k)} es el conjunto de ruidos que perturban al sistema ( w(k)  N(μw = 0, σ2w < ∞)), {y(k)} es el conjunto de salidas del sistema.
N(μw = 0, σ2w < ∞)), {y(k)} es el conjunto de salidas del sistema.
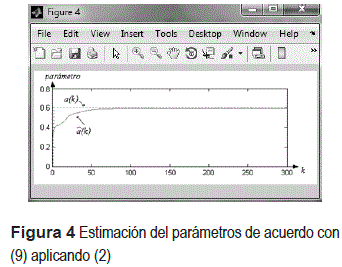
La estimación de la matriz de transición con respecto a (10), está descrita de manera recursiva en (3) y su simulación respectiva se observa en la figura 4.
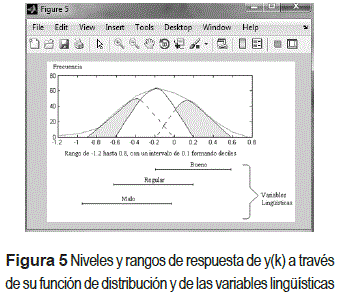
Los diferentes niveles de operación del estimador de ganancia con lógica difusa están construidos al igual que el estimador del gradiente estocástico en un sentido de probabilidad de acuerdo con la función de distribución del funcional del error (1). Cada rango dentro de la función de distribución está identificado por una variable lingüística, y que en el caso presente corresponde a: bajo, medio, alto como puede observarse en la figura 5, en donde se muestran los niveles de respuesta con respecto al filtro de Kalman en un proceso de asignación de matriz de transición de la BC y al grupo de inferencias matemáticas [18].
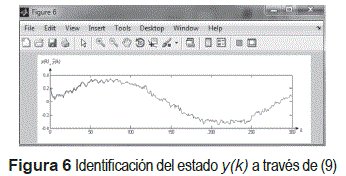
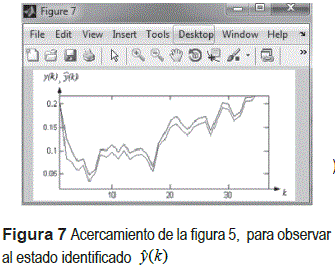
De acuerdo con el error en los niveles de respuesta respecto a la señal deseada expuesta en la figura 4 se obtiene el valor de la ganancia del filtro identificador de acuerdo con (9), y que corresponden a la ganancia del identificador M(k) del Filtro de Kalman. Se usa la lógica difusa de manera adaptiva ya que se encuentran variando dinámicamente con respecto a la función de distribución y que hace desarrollar al filtro de manera adaptable de acuerdo con los cambios que se presenten en el sistema de referencia, ajustando así las FM de la BC(TN), para obtener los valores respectivos de la estimación M(k). Considerando los resultados expuestos en la figura 4, se obtiene la identificación y(k) tomando en cuenta a (2) así como la estimación de M(k) por medio de la lógica difusa, ambos aplicados sobre (9), como se observa en (8) y se ilustra en la figura 6 y con acercamiento en la figura 7.
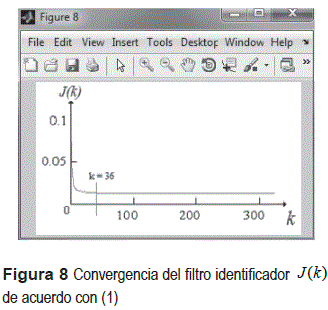
Teniendo los resultados de estimación tanto por el gradiente estocástico y la descripción de la ganancia de Kalman por la lógica difusa; ambos aplicados en la identificación y de acuerdo con la ecuación (9), se obtiene ŷ(k). La figura 8, muestra el funcional descrito en (3) con respecto al filtro identificador, observando en ella la convergencia de filtrado a una región donde la entropía se encuentra acotada y es constante.
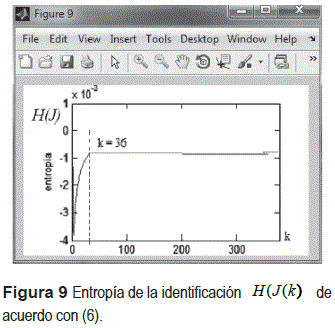
El tiempo de convergencia global se logra con una entropía constante (de acuerdo a la figura 5) a los 69,49 Hz, lo cual es menor a la evolución del propio sistema acotado por la condición LDmax = 24 Hz, cumpliendo con las propiedades de tiempo real descritas previamente. En la figura 9, se puede observar la convergencia del filtro por medio de la entropía descrita en (6).
Se puede observar que el tiempo global de conveigencia del filtro es de 0,1539 s , el cual es menor a la condición de evolución del sistema que es de 0,41653 s , teniendo en cuenta que el tiempo de convergencia propuesto para el sistema se encuentra dentro del intervalo [0,32633; 0,41653]s, y el intervalo de convergencia del filtro [0,1393; 0;1539]s; cumpliendo con la condición de Nyquist, en donde el filtro requeriría de acuerdo con el sistema de un tiempo de evolución de 0,05s y que en la realidad es de 0,004 s . Lo cual que en sus condiciones locales y globales cumple con las propiedades de tiempo-real.
Conclusiones
En este trabajo se realizó la descripción de un filtro identificador con dos estimadores uno realizado de manera estocástica y otro usando la lógica difusa para estimar la ganancia del filtro. El estimador estocástico fue obtenido usando el método del gradiente estocástico que es un estimador óptimo por ser resultado de un punto de equilibrio dentro de la región de estimación. El estimador de la ganancia con lógica difusa, es un estimador del tipo adaptivo y que se basa en la lógica difusa para la selección de la región de operación del error de identificación para lograr que el filtro identificador llegue a la condición deseada.
Referencias
1. B. Kosko. Fuzzy Thinking: The New Science of Fuzzy Logic. Ed. Prentice Hall. New York, USA. 1993. pp. 156-222. [ Links ]
2. T. Amble. Logic Programming and Knowledge Engineering. Ed. Addison Wesley. Boston, US. 1987. pp 281. [ Links ]
3. M. Margaliot, G. Langholz. New Approaches to Fuzzy Modeling and Control Design and Analysis. 1st ed. Ed. World Scientific. Singapore. 2000. pp. 185. [ Links ]
4. G. Feng. ''A survey on analysis and design of model-based fuzzy control systems''. IEEE Transactions on Fuzzy Systems. Vol. 14. 2006. pp. 676-697. [ Links ]
5. J. Jantzen. A tutorial on Adaptive Fuzzy Control. Technical University of Denmark. Copenhagen, Denmark. 2002. pp. 709-719. [ Links ]
6. M. Schneider, A. Kandel. Fuzzy expert systems tools. Ed. Wiley. Chichester, England. 1996. pp. 81-116. [ Links ]
7. K. Tanaka, M. Sugeno. ''Stability Analysis and Design of Fuzzy Control Systems''. Fuzzy Sets and Systems. Vol. 45. 1992. pp. 135-156. [ Links ]
8. L. Manuel. Teoría de la Medida e Integral de Lebesgue. Universidad Nacional de Rosario. Rosario, Argentina. 2003. pp. 60-65. [ Links ]
9. J. García, J. Medel, P. Guevara. ''Real-Time Fuzzy Digital Filter for ARMA Systems''. WSEAS Transactions on Systems and Control. Vol. 2. 2007. pp. 491-496. [ Links ]
10. D. Choi, P. Park. ''H-infinity state feedback controller design for discrete time fuzzy systems using fuzzy weighting- dependent Lyapunov functions''. IEEE Transactions on Fuzzy Systems. Vol. 11. 2003. pp. 271-278. [ Links ]
11. J. García, J. Medel, P. Guevara. ''Evolutive Neural Net Fuzzy Digital Filtering: basic description''. Journal of Intelligent Learning Systems and Applications. Vol. 2. 2010. pp. 43-48. [ Links ]
12. B. Kosko. Fuzzy Engineering. Ed. Prentice Hall. University Michigan. Ann Arbor, USA. 1997. [ Links ]
13. L. Leydesdorff. ''The Construction and Globalization of the Knowledge Base in inter-human communication systems''. Canadian Journal of Communication. Vol. 28. 2003. pp. 267-289. [ Links ]
14. C. Tao, J. Taur. ''Robust Fuzzy Control for a Plant with Fuzzy Lineal Model''. IEEE Transactions on Fuzzy Systems. Vol. 13. 2005. pp. 30-41. [ Links ]
15. C. Park, H. Kang. ''Graphical and Numerical approach to robust stability analysis of fuzzy modeled systems with parametric uncertainty and disturbance''. Fuzzy Sets Systems. Vol. 151. 2005. pp. 99-117. [ Links ]
16. T. Takagi, M. Sugeno. ''Fuzzy Identification of Systems and its Applications to Modelling and Control''. IEEE Transactions and Systems, man, and cybernetics. Vol. 15. 1986. pp. 116-132. [ Links ]
17. L. Zadeh. ''The Concept of a Linguistic Variable and its Applications to Approximates Reasoning''. Information and Control. Vol. 8. 1965. pp. 338-353. [ Links ]
18. D. Marcek. ''Statistical, Classical and Fuzzy Neural Networks, Modeling Decisions for Artificial Intelligence''. Stock Price Forecasting. Ed. Springer Verlag. Berlin, Germany. 2004. pp. 41-48. [ Links ]
19. K. Passino. Fuzzy Control. Ed. Addison Wesley. Boston, US. 1998. pp. 468. [ Links ]
20. S. Hay kin. Adaptive Filtering Theory. 4th ed. Ed. Prentice Hall. Ontario, Canada. 2001. pp. 302-334. [ Links ]
21. R. Ash. Real Analysis and Probability. Ed. Academic Press. New York, USA. 1970. [ Links ]
22. H. Ali. Fundamentals of Adaptive Filters. Ed. John Wiley & Sons. New Jersey, US. 2003. [ Links ]
23. E. Mamdani. ''Applications of Fuzzy Algorithms for Control of Simple Dynamic Plant''. Procedings IEEE. Vol. 121. 1974. pp. 1585-1588. [ Links ]
24. B. Rajen, M Gopal. ''Neuro-Fuzzy Decision Trees''. International Journal of Neural Filters. Vol. 16. 2006. pp. 63-68. [ Links ]
25. M. Shannon. ''Mathematical Theory of Communication''. Bell Systems Technical Journal. Vol. 27. 1948. pp. 379-423, 623-656. [ Links ]
26. S. Mollov, R. Babuska, J. Abonyi, H. Verbruggen. ''Effective Optimization for Fuzzy Model Predictive Control''. IEEE Transactions on Fuzzy Systems. Vol. 12. 2004. pp. 661-675. [ Links ]
27. J. Medel, J. García, P. Guevara. ''Real-time Fuzzy Digital Filters Properties for SISO Systems''. Automatic Control and Computer Sciences AVT. Vol. 42. 2008. pp. 26-34. [ Links ]
28. C. Chen, G. Feng, X. Guan. ''Delay dependent stability analysis and controller synthesis for discrete time TS fuzzy systems with time delays''. IEEE Transactions on Fuzzy Systems. Vol. 13. 2005. pp. 630-643. [ Links ]