Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista Facultad de Ingeniería Universidad de Antioquia
versão impressa ISSN 0120-6230
Rev.fac.ing.univ. Antioquia no.70 Medellín jan./mar. 2014
ARTÍCULO ORIGINAL
Overlapped block-based compressive sensing imaging on mobile handset devices
Sensado comprimido de imágenes por bloques sobrepuestos usando dispositivos móviles
Irene Manotas Gutiérrez, Henry Arguello Fuentes*
Department of Systems Engineering and Informatics, Universidad Industrial de Santander. CP. 680002. Bucaramanga, Colombia.
*Autor de correspondencia: telefax: + 57 + 7 + 634 40 00 ext. 2676, correo eletrónico: henarfu@uis.edu.co (H. Arguello)
(Recibido el 17 de mayo de 2013. Aceptado el 15 de enero de 2014)
Abstract
Compressive Sensing (CS) is a new technique that simultaneously senses and compresses an image by taking a set of random projections from the underlying scene. An optimization algorithm is then used to recover the initial image. In practice, these optimization algorithms have restricted CS techniques to be implemented on high performance computational architectures, such as personal computers or graphical processing units (GPU) due the huge number of operations required for the image recovery. This work extends the application of CS to be implemented in an extremely limited memory and processing architecture such as a mobile device. Specifically, overlapped blocking-based algorithms are developed such that it is possible to reconstruct an image on a mobile device. An analysis of the energy consumption of the block-based CS algorithms is presented. The results show the required computational time for reconstruction and the image reconstruction quality for images of 128x128 and 256x256 pixels.
Keywords: Compressive sensing, sparse recovery, mobile handset devices
Resumen
Compressive Sensing (CS) es una nueva técnica que simultáneamente comprime y muestrea una imagen tomando un conjunto de proyecciones aleatorias de una escena. Un algoritmo de optimización es empleado para reconstruir la imagen utilizando las proyecciones aleatorias. Diferentes algoritmos de optimización se han diseñado para obtener de manera eficiente una correcta reconstrucción de la señal original. En la práctica estos algoritmos se han restringido a implementaciones de CS en arquitecturas de alto rendimiento computacional, como computadores de escritorio o unidades de procesamiento gráfico, debido a el gran número de operaciones requeridas por el proceso de reconstrucción. Este trabajo extiende la aplicación de CS para ser implementado en una arquitectura con memoria y capacidad de procesamiento limitados como un dispositivo móvil. Específicamente, se describe un algoritmo basado en bloques sobrepuestos que permite reconstruir la imagen en un dispositivo móvil y se presenta un análisis del consumo de energía de los algoritmos utilizados. Los resultados muestran el tiempo computacional y la calidad de reconstrucción para imágenes de 128x128 y 256x256 píxeles.
Palabras clave: Compressive sensing, algoritmos de reconstrucción, dispositivos móviles
Introduction
In the acquisition of signals such as image or video, the traditional Nyquist sampling rate imposes that a large amount of data needs to be acquired. Traditionally, the enormous volume of information collected by satisfying the Nyquist criteria needs to be compressed for storing or transmission purposes. This process of first acquiring a large amount of information to then throw away a large portion of this data is inefficient. Conversely, the novel Compressive Sensing (CS) technique [1-3], contrast with the Nyquist process and only acquires relevant components of the underlying image by merging the sampling and compression processes in one step. CS exploits the sparsity property of an image F, or its vector representation f 
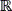 N, to acquire its relevant information using the inner products of the underlying image with random vectors. In CS, only M<<N samples of the image f are acquired. The image is then reconstructed by solving an inverse problem such as a linear program [1] or a greedy pursuit algorithm [2]. An image f is sparse on some basis Ψ
N, to acquire its relevant information using the inner products of the underlying image with random vectors. In CS, only M<<N samples of the image f are acquired. The image is then reconstructed by solving an inverse problem such as a linear program [1] or a greedy pursuit algorithm [2]. An image f is sparse on some basis Ψ
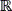 NxN, if f=Ψθ can be approximated by a linear combination of k vectors from Ψ with k<<N, where N represents the dimensions of the image and k represents the sparsity (number of non-zero elements) of the image. The theory of CS states that f can be recovered from M random projections with high probability when M<<k log(N)<<N [3]. The random projections are given by y=Φf=ΦΨθ, where Φ is a MxN random measurement matrix with its rows incoherent with the columns of Ψ, i.e., all the inner products between Φ and Ψ are small [1]. Measurement matrices are selected such that they satisfy the restricted isometry property (RIP) [3], which provides sufficient conditions to ensure near optimal performance of reconstruction algorithms. The literature has proposed several matrices that fulfill the RIP condition, including the independent and identically distributed (i.i.d) Gaussian and Bernoulli matrices. The main advantage of these matrices is that they are universally incoherent with any sparse signal and thus, the number of compressed measurements required for exact reconstruction is minimal [3]. However, those matrices have several drawbacks related to computation time and storage, and therefore need to be analyzed prior to being implemented on limited-resource devices. Some commonly used measurement matrices Φ include the Gaussian ensemble (GE) [4], the symmetric signs ensemble (SSE) [4] and the scrambled block hadamard ensemble (SBHE) [5], among others.
NxN, if f=Ψθ can be approximated by a linear combination of k vectors from Ψ with k<<N, where N represents the dimensions of the image and k represents the sparsity (number of non-zero elements) of the image. The theory of CS states that f can be recovered from M random projections with high probability when M<<k log(N)<<N [3]. The random projections are given by y=Φf=ΦΨθ, where Φ is a MxN random measurement matrix with its rows incoherent with the columns of Ψ, i.e., all the inner products between Φ and Ψ are small [1]. Measurement matrices are selected such that they satisfy the restricted isometry property (RIP) [3], which provides sufficient conditions to ensure near optimal performance of reconstruction algorithms. The literature has proposed several matrices that fulfill the RIP condition, including the independent and identically distributed (i.i.d) Gaussian and Bernoulli matrices. The main advantage of these matrices is that they are universally incoherent with any sparse signal and thus, the number of compressed measurements required for exact reconstruction is minimal [3]. However, those matrices have several drawbacks related to computation time and storage, and therefore need to be analyzed prior to being implemented on limited-resource devices. Some commonly used measurement matrices Φ include the Gaussian ensemble (GE) [4], the symmetric signs ensemble (SSE) [4] and the scrambled block hadamard ensemble (SBHE) [5], among others.
Once the CS measurements in y have been acquired, a recovery process is employed to get an approximation of the original image. This recovery involves finding the approximation vector f satisfying the equation y =Φf. Because y is a M-long vector, where M<<N, there is an infinite number of solutions satisfying that equation. Hence, it is common to search for a vector f optimizing a sparsity measure. The problem of finding a vector with the smallest number of non-zero elements is given by equation (1), where the l0 norm represented by  .
.  0 counts the number of non-zero elements in f, and ε is a tolerance value. Note that (1) is a nonlinear optimization problem, which is shown to be NP hard [2].
0 counts the number of non-zero elements in f, and ε is a tolerance value. Note that (1) is a nonlinear optimization problem, which is shown to be NP hard [2].
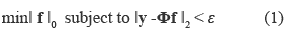
Hence, different sub-optimal strategies have been used to solve the problem described in (1). In practice, the most common strategies to solve (1) include convex relaxation [6], non-convex local optimization [7] and greedy search strategies [2]. These methods find an approximate solution of the original problem with an algorithm of complexity O(MN) or O(NlogM), depending on the approach [2]. Several recovery algorithms using the previously mentioned strategies have been proposed in the literature. Specifically, greedy approaches, which basic operation is to find the supports ofthe unknown image sequentially, have been shown to be relatively fast in comparison with other approaches and are often considered the only practical way to solve very large sparse approximation problems [2]. Iterative hard thresholding (IHT) [8] and orthogonal matching pursuit (OMP) [9] are two examples of recovery algorithms that have demonstrated their potential to recover a compressed signal through the CS technique.
CS has been widely applied in different fields such as imaging (e.g., single-pixel camera [10]), optics (e.g., hyper-spectral imaging [11-12]), and communications (e.g., Wireless Networks [13]). Applications involving the use of CS in embedded devices commonly include transmission of data in Wireless Sensor Networks (WSN) [13], Telecardiology Sensor Networks (TSN) [14] and wireless body sensor networks (e.g., using an iPhone device [15]). However, these works are limited to one-dimensional signals and are mainly centered on the collection of data and the transmission of compressed data. Conversely, there is few research on CS applied on embedded devices like smartphones. Hence, considering the advantages of CS in compressing data and the growing interest in mobile technologies and applications, it is important to analyze the implications of runtime and recovery quality using a CS implementation on a mobile device. This paper develops and analyzes the computational resources and implementation of the compression/recovery processes of an image on a smartphone platform using an overlapped block-based (OBB) CS approach. This paper assumes the incorporation of a CS sensor, such as the single pixel camera [10], on the mobile device to acquire the image measurements. Details about the optical implementations of CS sensors can be found in [16].
The main contributions of this paper are the OBB- CS approach, the extension of CS applied to 2D signals (i.e., images) on mobile devices, and the analysis of the energy consumption of recovery algorithms for CS reconstruction on a smartphone device. The experiments comprise simulations and implementations of the recovery algorithms, which are executed on ARM Cortex architecture, which is a representative design of several kinds of mobile devices such as smartphones.
Sparse recovery algorithms
The theory of CS uses sparse recovery algorithms for the reconstruction of the original image. Different recovery algorithms use varying strategies to find the image that best approximates the original image. Greedy algorithms are a type of sparse approximation algorithms designed to find a solution of the k-sparse optimization problem given by equation (2).
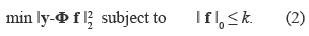
The solution of (2) obtains the best approximation of f using only k columns of the measurement matrix Φ, and were the elements of the image f must be equal or less than a given constant k that determines its sparsity level.
Greedy strategies constitute one class of sub--optimal techniques used in practice to find the vector f with the smallest number of non--zero elements. In general, the reconstruction complexity of the greedy algorithms is lower than that of the l1 minimization methods [2]. Some drawbacks of greedy algorithms are related with the computational cost involved in the computation of the projection operation, which limits the application to small problems. However, greedy strategies efficiently reconstruct signals from compressed sensing observations and succeed with a minimum number of observations [8]. On the other hand, iterative thresholding algorithms, such as the Iterative Hard Thresholding (IHT), are another class of greedy algorithms that has demonstrated good performance and are capable to succeed with a minimum number of observations [8]. IHT relaxes the l0 penalty and replaces it by the l1 penalty, and it is designed to solve the convex problem presented in equation (3), where λ is a regularization parameter which can be adjusted to promote the sparsity of the optimized signal f.
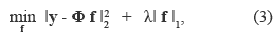
In this paper, greedy methods are studied as they have fast implementations and are less demanding computationally than other strategies such as the Basis Pursuit De- noising (BPDN) method [2] and therefore, more appropriate for mobile devices. In this paper two algorithms are analyzed: Iterative Hard Thresholding (IHT) [8] and Orthogonal Matching Pursuit (OMP) [9].
Iterative Hard Thresholding Algorithm
Iterative Hard Thresholding (IHT) Algorithm is an iterative greedy method that does not require matrix inversion and provides near optimal error guarantees [8]. The algorithm computes the solution f(t) at iteration (t) as f(t+1) in equation (4), where the matrix A is the product of the measurement and representation matrices, A = ΦΨ. Hk (.) is a non-linear operator that sets all but the k largest elements in magnitude of a vector to zero and AT represents the transpose of the matrix A. The parameter λ represents the step size, and f (0) is set to a zero-valued vector.
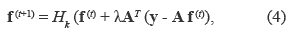
Table 1 column (a) shows the steps required by the IHT algorithm to find the solution f. Two main characteristics of this algorithm include that it converges in linear time due to the fact that it is based on a gradient descend strategy, and the selection of the step size parameter, which needs to be chosen appropriately [6, 17].
Orthogonal Matching Pursuit
Orthogonal Matching Pursuit (OMP) Algorithm is a greedy strategy that iteratively selects the elements in the approximation vector. At iteration (t) the approximation of the image represented by f(t+1) is calculated by equation (5), where Γ represents a set of selected indices based on the inner product of the current residual r(t) and the columns in A. The submatrix A Γ(t) is formed using only the columns of A with indices from r in the iteration (t), and 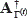 represents the pseudo--inverse of the matrix AΓ(t).
represents the pseudo--inverse of the matrix AΓ(t).

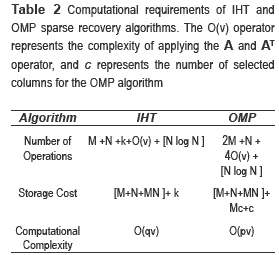
Table 1 column (b) shows the pseudocode of the OMP strategy to find a better approximation vector f in each iteration. Table 2 describes the OMP and IHT algorithms in terms of the number of operations, storage and computational complexity required, where p represents the number of iterations in the OMP algorithm; k denotes the complexity of applying the operator A and AT, which can be O (MN) or O (NlogM) depending on whether the operator is structured (e.g., Gaussian ensemble) or not structured (e.g., the Scramble Block Hadamard Ensemble), and c represents the number of selected columns which varies from 1 to k for the OMP algorithm.
Measurement matrices
The measurement matrix Φ takes the projections of the underlying signal. In general, measurement matrices need to satisfy the Restricted Isometry Property (RIP) defined in [6, 18], as this is a sufficient condition for sparse reconstruction. Random matrices, where the entries are i.i.d. from a normal distribution or a bernoulli process, satisfy the sufficient condition for sparse reconstruction. Popular ensembles of measurement matrices include the Gaussian
Random Ensemble, the Partial Fourier Ensemble (PFE), the Symmetric Signs Ensemble (SSE), the Bernoulli Matrix Family (semi-Hadamard, Partial Hadamard), the Sparse Binary Matrix (SBM) and the Rademacher matrix [4]. Gaussian and Bernoulli matrices have two major drawbacks in practical applications: large memory buffering for storing matrix elements and high computational complexity due to being completely unstructured. Measurement matrices as the SBHE [5] or the SBM [4] are considered more adequate for their implementation than the Gaussian ensemble due to the fact that these measurement ensembles are highly sparse and allow a fast computation compared to the traditional Gaussian ensemble. Considering the limited resource characteristic of mobile devices and the properties of measurement matrices described above, only Gaussian and SBHE matrices are analyzed for the implementation of the CS image system using mobile devices.
Image compression and recovery with overlapped blocks
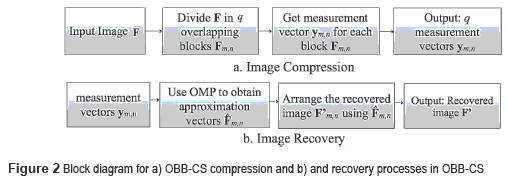
The CS overlapped blocking approach presented in this paper is designed to recover images of higher dimensions on a mobile device by exploiting the image and sensing matrix structures. Given the limited memory of the mobile device, the block approach permits to analyze high-resolution images and extend the results obtained in [19] where images of 32x32 were recovered using CS. Previous work in block-based image CS analysis include the block-based OMP algorithm [20] proposed by Parichat et al, in which the algorithm recovers each block of an image and then rearranges an image of 64x64 pixels using each of the recovered blocks. However, the description of Parichat's block-based approach uses M=N measurements, which leads to no compression of the image due to the number of measurements is equal to the length of the original image. Similarly, Lu Gan proposes a block-based image CS approach in [21], which divides the original image in small non-overlapped blocks of 32x32 pixels. However, the recovery algorithm used in [21] uses a 3x3 Wiener filter to reduce the blocking artifact and smooth the image, which involves more computational requirements to compute the solution and therefore is not suitable for its implementation in a mobile device. Conversely, this paper proposes an overlapped block-based (OBB) CS approach for the reconstruction of images in mobile devices, using different CS configurations and two greedy algorithms. The implementation on mobile devices assumes that the device has a CS camera, which takes the compressed measurements of the image. The main feature of the blocking process is to divide an image into small blocks of b x b pixels. Each predefined block is compressed and stored or transmitted to other device. Then, an iterative process using a Greedy algorithm recovers each block of the image, and an approximation of the original image is obtained rearranging the recovered blocks.
Overlapped Block-Based (OBB-CS)
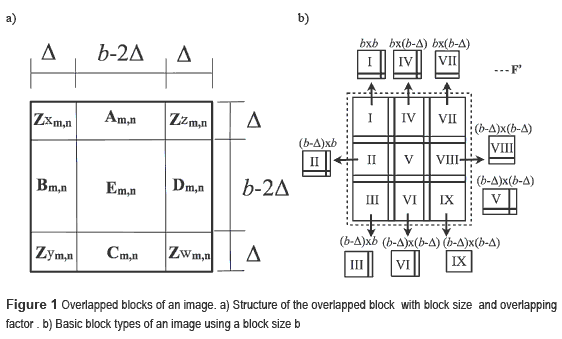
The model presented here uses an Overlapped Block-Based (OBB-CS) strategy that exploits the structure of the sensing matrix Φ for recovering the image from several measurements. The image F is expressed as a qxq ensemble of bxb submatrices Fm,n defined by equation (6), where each submatrix Fm,n is an overlapped block of the image F. The size b of each block is a selectable parameter which must be a non prime number and also a divisor of the total number of pixels N; the rationale behind this selection is to divide the image into a number of overlapped blocks of equal size and avoid zero padding due to blocks with incomplete number of pixels.
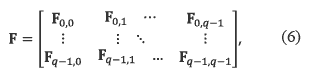
The number of blocks q of the image depends on the total number of pixels N, and the size of the block b; This value is calculated by 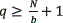 . The overlapping factor Δ defines the amount of overlapped pixels, i.e. pixels shared between consecutive blocks in F. This overlapping factor is calculated by
. The overlapping factor Δ defines the amount of overlapped pixels, i.e. pixels shared between consecutive blocks in F. This overlapping factor is calculated by 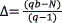 . Figure 1a) shows the structure of an overlapped block Fm,n of the image F. The sections Am,n, Bm,n, Cm,n, Dm,n, Zxm,n, Zym,n, Zwm,n and Zm,n represent the shared parts between consecutive blocks of the image, while the section Em,n represents the unshared region of the block. Each overlapped block Fm,n has a vector representation fm,n
. Figure 1a) shows the structure of an overlapped block Fm,n of the image F. The sections Am,n, Bm,n, Cm,n, Dm,n, Zxm,n, Zym,n, Zwm,n and Zm,n represent the shared parts between consecutive blocks of the image, while the section Em,n represents the unshared region of the block. Each overlapped block Fm,n has a vector representation fm,n 
 (b2)x1, and the measurement vector of each overlapped block ym,n is calculated as ym,n =Aγm,n f γm,n, where Aγm,n
(b2)x1, and the measurement vector of each overlapped block ym,n is calculated as ym,n =Aγm,n f γm,n, where Aγm,n  Rhx(b2) is the block measurement matrix with h=[M/q].
Rhx(b2) is the block measurement matrix with h=[M/q].
Overlapped Block-Based Recovery
The measurement vector ym,n corresponding to each overlapped block Fm,n is used to obtain an approximation block 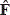 m,n with the OMP and IHT algorithms. The reconstructed block
m,n with the OMP and IHT algorithms. The reconstructed block 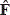 m,n is also in the sections
m,n is also in the sections 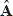 m,n,
m,n, 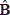 m,n,
m,n, 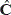 m,n,
m,n, 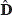 m,n,
m,n, 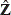 xm,n,
xm,n, 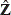 ym,n,
ym,n, 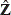 wm,n, and
wm,n, and 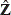 zm,n as indicated in Figure 1. A full size recovered image F' is formed using rearranged versions of the blocks Fm,n. Figure 2 shows the block diagram of the compression and recovery process of the image using the approximation blocks Fm,n. Let the whole recovered image be
zm,n as indicated in Figure 1. A full size recovered image F' is formed using rearranged versions of the blocks Fm,n. Figure 2 shows the block diagram of the compression and recovery process of the image using the approximation blocks Fm,n. Let the whole recovered image be 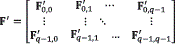 , where F'm,n are the rearranged versions of the blocks
, where F'm,n are the rearranged versions of the blocks 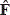 m,n. More specifically, for each rearranged block F'm,n, the average of the shared areas
m,n. More specifically, for each rearranged block F'm,n, the average of the shared areas 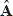 m,n,
m,n, 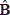 m,n,
m,n, 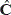 m,n,
m,n, 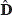 m,n,
m,n, 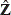 xm,n,
xm,n, 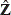 ym,n,
ym,n, 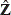 wm,n, and
wm,n, and 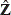 zm,n between subsequent blocks is computed; this average helps to reduce the edge artifacts produced in the recovered image and thus increase the quality of the complete reconstructed image F'.
zm,n between subsequent blocks is computed; this average helps to reduce the edge artifacts produced in the recovered image and thus increase the quality of the complete reconstructed image F'.
Figure 1b) shows an image with nine blocks that represents the types of blocks in the overlapped block structure. The types of blocks are numbered from I up to IX, and each block has an overlapping factor Δ and block size b. For a reduced dimension of the block size b, the total number of blocks increases but the block types illustrated in Figure 1 remain the same.
The average calculation of the shared regions between the rearranged blocks F'm,n depends on the position of the related approximation block 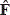 m,n. The estimation of the rearranged blocks
m,n. The estimation of the rearranged blocks 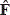 m,n is performed as follows: for the block types I, II, IV and V, the rearranged block F'm,n is expressed by equation (7).
m,n is performed as follows: for the block types I, II, IV and V, the rearranged block F'm,n is expressed by equation (7).
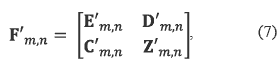
In equation (7), E'm,n, D'm,n, C'm,nand Z'm,n are defined by equations (8) – (11) for the block type I:
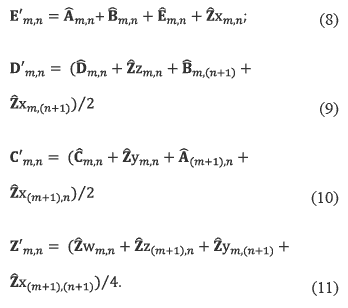
The block type II has a smaller unshared region E'm,n when compared with block type I; thus this section of the block and the shared region D'm,n are computed by equations (12) and (13):
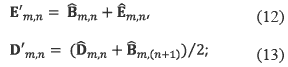
The regions C'm,n and Z'm,n are calculcated as in (10) and (11). The regions E'm,n and C'm,n are calculated for the block type IV as shown in equations (14) and (15).
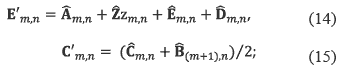
and the regions D'm,n and Z'm,n are computed as in (9) and (11) respectively. The block V has the region E'm,n =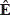 m,n and the shared regions Z'm,n , D'm,n and C'm,n and are computed by equations (11), (13) and (15) respectively.
m,n and the shared regions Z'm,n , D'm,n and C'm,n and are computed by equations (11), (13) and (15) respectively.
For the block types III and VI, the recovered block only shares the section D'm,nwith the adjacent block. Hence, the rearranged block F'm,n is expressed as in equation (16), where D'm,n =( 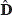 m,n+
m,n+ 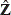 wm,n+
wm,n+ 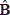 m,(n+1) ,
m,(n+1) , 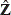 ym,(n+1))/2; E'm,n=
ym,(n+1))/2; E'm,n=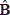 m,n +
m,n + 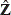 ym,n+
ym,n+ 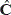 m,n+
m,n+ 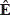 m,n for the block type III, and E'm,n =
m,n for the block type III, and E'm,n = 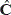 m,n +
m,n + 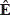 m,n for the block type VI.
m,n for the block type VI.
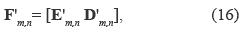
For block types VII and VIII, the rearranged block is calculated by equation (17).
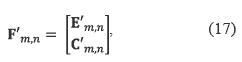
where C'm,n =( 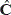 m,n+
m,n+ 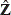 wm,n+
wm,n+ 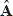 (m+1),n ,
(m+1),n , 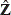 z(m+1),n)/2; E'm,n=
z(m+1),n)/2; E'm,n=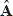 m,n +
m,n + 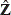 zm,n+
zm,n+ 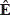 m,n +
m,n +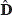 m,n for the block type VII, and E'm,n =
m,n for the block type VII, and E'm,n = 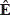 m,n +
m,n + 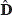 m,n for the block type VIII. Block type IX does not need to compute averages for the recovered image as this portion of the block does not have any subsequent blocks, and therefore any shared regions, thus F'm,n=
m,n for the block type VIII. Block type IX does not need to compute averages for the recovered image as this portion of the block does not have any subsequent blocks, and therefore any shared regions, thus F'm,n=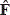 m,n.
m,n.
Simulations and results
The simulations comprise the compression and recovery of two squared standard images, i.e., Lena and Boat, using the OBB-CS approach described in this paper. The resolution of the images is 128x128 and 256x256 pixels. The Wavelet Symmlet of order 8 was used as the representation matrix Ψ because it is one of the best sparse representations for images [5-10]. The images were approximated using different levels of sparsity. Thus, the images were approximated by maintaining only a percentage of the more representative Wavelet coefficients. Two different architectures were used to implement the CS scheme: An iPhone 4 with 512 MB of memory which has an ARM Cortex-A8 with 1 GHz processor (iOS platform); and a PC with 2GB Memory and 2.4 GHz processor, along with the iOS simulator for iPhone (PC platform). The implementation in the PC platform uses the Matlab software and its programming language to ease the CS implementation in the PC. After the PC version of the CS system was tested, the Objective-C language was used to do the implementation in the mobile device. The standard metric Peak Signal to Noise Ratio (PSNR) was used to measure the image quality.
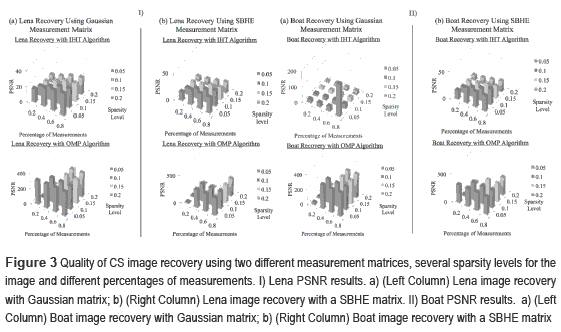
Two random ensembles as measurement matrices were studied for comparison purposes. Figure 3 shows the PSNR of the reconstructed images Lena and Boat when compressed using the Gaussian and SBHE ensembles respectively on the PC platform using Matlab™ and with the IHT and OMP algorithms; the PSNR results are given for different sparsity levels and for different percentage of measurements for the images. Based on the results of figure 3, the SBHE ensemble provided almost the same quality reconstruction as the Gaussian ensemble, but it requires less storage due to its sparse nature, such that SBHE was selected for the CS mobile implementation. Additionally, the results indicate that the OMP algorithm recovers the images with a higher PSNR quality than the IHT algorithm.
Figure 4 shows the original and recovered versions of the Lena and Boat images. This figure shows the results obtained in the PC and iOS platforms described above and using the OBB- CS approach.
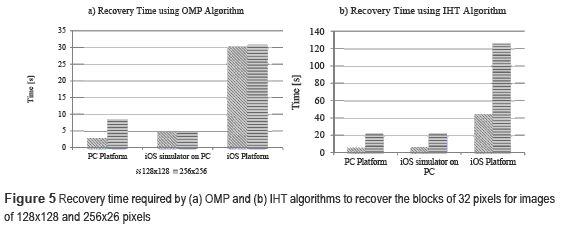
The recovery time required for the OMP and IHT algorithms is illustrated in Figure 5 the required time per iteration for a block of32x32 pixels is 4.9 seconds on the iOS simulator and 30.5 seconds on the mobile device using the iOS platform. As the dimension of the image increases from 128x128 to 256x256 the computational time increases as well since to more blocks need to be processed.
Energy Consumption Analysis
The energy consumption of the recovery algorithms on the mobile device platform was measured using the Instruments application provided by Apple. Instruments provides an Energy Usage Instrument (EUI) to measure the energfry consumption of algorithms on the iOS device. The EUI application takes samples of energy consumption in the mobile device comparing the available amount of battery charge before and after the execution of an application on the device. EUI provides the values of energy usage by each application running on the iOS device in a range from 0, which means no energy consumption, to 20 that indicates that the maximum amount of energy is being consumed by the application.
Figure 6 shows the box plots of the energy consumption levels required by the recovery algorithms implemented for the image compression and recovery process. Comparing the energy consumption on the iOS platform, the OMP algorithm has the largest variability. However, the energy consumption of the OMP and IHT greedy algorithms yield to similar average results.
Conclusions
The mathematical model of the Overlapped Block-Based CS (OBB-CS) strategy to recover images on a Smartphone platform has been presented. The results indicate that the SBHE sensing matrix is more suitable for the mobile implementation. The OMP algorithm presents a higher PSNR image quality reconstruction, a faster reconstruction time, and similar power consumption than the IHT reconstruction algorithm. The image reconstructions on the mobile device using the SBHE matrix, the OMP algorithm, and the OBB-CS block model achieves similar PSNR quality than those on the PC architecture. Additionally, the reconstruction time for images of 256x256 pixels is in the order of 30 seconds on the mobile device.
References
1. D. Donoho. ''Compressed sensing''. IEEE Trans. On Information Theory. Vol. 52. 2006. pp. 1289- 1306. [ Links ]
2. T. Blumensath, M. Davies. ''Gradient Pursuits''. IEEE Transactions on Signal Processing. Vol. 56. 2008. pp. 2370-2382. [ Links ]
3. E. Candes, T. Tao. ''Near optimal signal recovery from random projections: Universal encoding strategies?''. IEEE Trans. On Information Theory. Vol. 52. 2006. pp. 5406-5425. [ Links ]
4. R. Calderban, S. Howard, S. Jafarpour. ''Construction of a Large Class of Deterministic Sensing Matrices That Satisfy a Statistical Isometry Property''. IEEE Journal on Selected Topics in Signal Processing. Vol. 4. 2010. pp. 358-374. [ Links ]
5. L. Gan, T. Do, T. Tran. Fast compressive imaging using scrambled block Hadamard ensemble. Proceedings European Signal Processing Conference (EUSIPCO). Lausane, Switzerland. 2008. pp. 245. [ Links ]
6. T. Cai, G. Xu, J. Zhang, S. Member. ''On Recovery of Sparse Signals Via ^ Minimization''. IEEE Transactions on Information Theory. Vol. 55. 2009. pp. 3388-3397. [ Links ]
7. S. Wright, R. Nowak, M. Figueiredo. ''Sparse Reconstruction by Separable Approximation''. IEEE Transactions on Signal Processing. Vol. 57. 2008. pp. 2479-2493. [ Links ]
8. T. Blumensath, M. Davies. ''Iterative hard thresholding for compressed sensing''. Applied and Computatational HarmonicalAnalysis. Vol. 27. 2009. pp. 265-274. [ Links ]
9. J. Tropp. ''Signal Recovery From Random Measurements Via Orthogonal Matching Pursuit''. IEEE Transactions on Information Theory. Vol. 53. 2007. pp. 4655-4666. [ Links ]
10. M. Davenport, D. Takhar, J. Laska, T. Sun, K. Kelly, R. Baraniuk. ''Single-pixel imaging via compressive sampling''. IEEE Signal Processing Magazine. Vol. 25. 2008. pp. 83-91. [ Links ]
11. H. Arguello, G. Arce. ''Code aperture optimization for spectrally agile compressive imaging''. Journal of the Optical Society of America (JOSA). Vol. 28. 2011. pp. 2400-2413. [ Links ]
12. H. Arguello, C. Correa, G. Arce. ''Fast lapped reconstructions in compressive spectral imaging''. Journal Applied Optics. Vol. 52. 2013. pp. D32-D45. [ Links ]
13. M Balouchestani, K. Raahemifar, S. Krishnan. ''Robust Wireless Sensor Networks with Compressing Sensing theory''. Springer Communication in Comp. and. Inf. Science. Vol. 293. 2012. pp. 608-619. [ Links ]
14. E. Correia, O. Postolache, P. Silva. ''Implementation of compressed sensing in telecardiology sensor networks''. International journal of telemedicine and applications. Vol. 2010. pp. 1-12. [ Links ]
15. K. Kanoun, H. Mamaghanian, A. David. A realtime compressed sensing based personal electrocardiogram monitoring system. Design, Automation & Test in Europe Conference (DATE). Grenoble, France. 2011. pp. 1-6. [ Links ]
16. R. Willett, R. Marcia, J. Nichols. ''Compressed sensing for practical optical imaging systems: a tutorial''. SPIE Optical Engineering. Vol. 50. 2011. pp. 586. [ Links ]
17. T. Blumensath. ''Accelerated iterative hard thresholding''. IEEE Signal Processing Letters. Vol. 92. 2011. pp. 1-10. [ Links ]
18. H. Arguello, G. Arce. Restricted Isometry Property in Coded Aperture Compressive Spectral Imaging. IEEE Statistical Signal Processing Workshop. Ann Arbor, USA. 2012. pp. 716-719. [ Links ]
19. I. Gutierrez, H. Arguello, K. Winbladh. Implementation of Imaging Compressive Sensing Algorithms on Mobile Handset Devices. International Conference on Broadband and Wireless Computing, Communications and Applications. Victoria, Canada. 2012. pp. 252-259. [ Links ]
20. P. Sermwuthisarn, S. Auethavekiat and V. Patanavijit. A Fast Image Recovery Using Compressive Sensing Technique with Block Based Orthogonal Matching Pursuit. International Symposium on Intelligent Signal Processing and Communication Systems (ISPACS). Tokyu, Kanazawa, Japan. 2009. pp. 212-215. [ Links ]
21. L. Gan. Block Compressed Sensing of Natural Images. International Conference in Digital Signal Processing. Cardiff, UK. 2007. pp. 403-406. [ Links ]