Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230
Rev.fac.ing.univ. Antioquia no.75 Medellín Apr./June 2015
https://doi.org/10.17533/udea.redin.n75a10
ARTÍCULO ORIGINAL
DOI: 10.17533/udea.redin.n75a10
Reconfiguration of photovoltaic arrays based on genetic algorithm
Reconfiguración de arreglos fotovoltaicos basada en algoritmo genético
Juan Ramón Camarillo-Peñaranda, Fabio Andrés Ramírez-Quiroz, Daniel González-Montoya, Freddy Bolaños-Martínez, Carlos Andrés Ramos-Paja*
Departamento de Energía Eléctrica y Automática. Universidad Nacional de Colombia (Sede Medellín). Carrera 80 N.° 65-223, Núcleo Robledo. A.A. 568. Medellín, Colombia.
* Corresponding author: Carlos Andrés Ramos Paja, e-mail: caramosp@unal.edu.co
(Received December 02, 2014; accepted April 08, 2015)
Abstract
This paper describes a Genetic Algorithm (GA) implementation devoted to the calculation of reconfiguration patterns for Photovoltaic Arrays (PVs). The proposed solution is compared with the classical Brute Force (BF) approach, which use is very restrictive due to its long processing times. The GA tuning up process is described, and several cases of study, including partial shading profiles for the PV array, are presented. Results show a very superior performance of the GA, when compared to the BF approach. Improvements in output power, as a result of the calculated reconfiguration, are also shown.
Keywords: reconfiguration of PV systems, genetic algorithm, online optimization
Resumen
Este artículo describe una implementación de un algoritmo genético orientada al cálculo de patrones de reconfiguración de arreglos fotovoltaicos. La solución propuesta se compara con el enfoque clásico de fuerza bruta, el cual es muy restrictivo debido a sus tiempos de procesamiento excesivamente largos. Se describe el proceso de puesta punto del algoritmo y se presentan varios casos de estudio, incluyendo perfiles de sombreado parcial para el arreglo fotovoltaico. Los resultados muestran un desempeño muy superior del algoritmo genético en contraste con el enfoque de fuerza bruta. También se presentan las mejoras obtenidas en la potencia de salida como resultado del patrón de reconfiguración calculado.
Palabras clave: reconfiguración de sistemas PV, algoritmo genético, optimización en línea
Introduction
Photovoltaic (PV) systems are an alternative to produce energy without the need of external fuel storage. Such a characteristic makes the PV systems a suitable alternative for mobile applications but also for stand-alone electricity generation in isolated locations [1, 2]. Moreover, PV systems have become an interesting alternative for co-generation in urban environments to supply non-critical loads such as office lighting (light-to-light) [3] and residential comfort devices such as air-conditioned plants [3]. On the other hand, attractive feed-in fees provided by some governments, e.g. Argentina, Ecuador, Nicaragua, Spain, Germany [4], have increased the interest in small PV installations selling power to the grid [1, 3]. Such grid-connected PV systems take advantage of unused rooftop and parking lot spaces in urban environments, but they are also subjected to periodic and unavoidable shades over part of the array caused by adjacent buildings, poles, trees and even other PV panels, it producing non-uniform operation conditions [1].
The mismatched phenomenon, caused by non-uniform conditions, strongly reduces the power generated by the PV system [1]; hence different solutions have been proposed in literature: adopt different static electrical configurations such as Series-Parallel (SP), Total-Cross Tied (TCT) or Bridge-Linked (BL) [5]; isolate every panel using a dedicated dc/dc converter [2, 5]; reconfigure the electrical connections between the PV panels [1]. The first of the above solutions is not reliable since there is not a single static configuration providing the best performance for any shading pattern [1, 2]. The second solution effectively reduces the mismatching effect, but at the expense of additional power stages, which increase significantly the solution cost and complexity due to the requirement of several power stages and controllers. Moreover, those additional dc/dc converters introduce power losses that reduce the energy delivered to the grid in uniform conditions, where the classical single-inverter approach provides higher performance [5]. Finally, the reconfiguration approach provides a low-cost solution to mitigate the mismatching effect without degrading the power production in uniform conditions [2]. Despite the power production in mismatched conditions is lower, when compared to the solution based on dedicated dc/dc converters, the reconfiguration solution requires a single cheap and an almost lossless switching matrix and a single controller.
The main challenge in reconfiguration of PV arrays concerns the large amount of possibilities that must be evaluated to find the best solution. Such a problem has been addressed in literature using multiple approaches: programed configurations (PC) [6], which select a given configuration depending on pre-defined rules; sorting algorithms (SA) [7], which search an acceptable solution that meets a given criterion, e.g. the highest PV current; brute force (BF) algorithm [1], which tests every possible configuration at the cost of very long computation times; and optimization algorithms (OA) [8], which maximize (or minimize) a given cost function to find an acceptable solution. Among those approaches, only the BF solution ensures to find the configuration providing the highest power, but its excessive long processing times make this solution impractical for real-time applications.
This paper proposes the design of a reconfiguration system based on a Genetic Algorithm (GA) aimed to provide the best configuration, or a close one, with a much shorter processing time in comparison with the BF solution. Such a characteristic makes the proposed GA solution suitable for real-time applications. In such a way, the proposed solution is validated using detailed models, parameterized with experimental data taken from commercial PV panels, and under environmental conditions measured in central-west Colombia.
In the following sections, the mismatching phenomenon is explained in detail. Subsequently, the proposed structure for reconfiguring PV systems is introduced. Then, the proposed GA solution is described and its performance is evaluated. Finally, conclusions close the paper.
The mismatching phenomenon
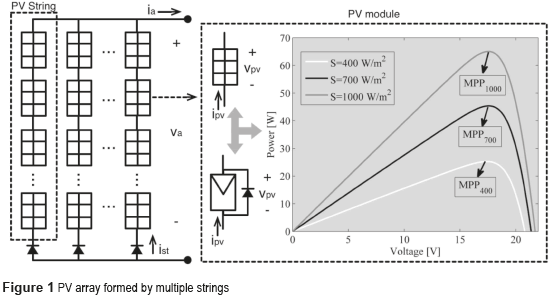
PV generators are, in general, an array of PV modules connected in multiple strings. The size of such strings (number of modules in series) is determined by the voltage requirements of the grid-connected inverter. The number of strings in parallel is determined by the power to be injected into the grid. Figure 1 presents, at the left, the structure of a typical PV array formed by strings, where the strings voltage is the same and equal to the array voltage va, while the strings current is different and the array current ia is equal to the sum of all the strings currents.
Figure 1 also depicts the internal structure of a PV module, which is formed by several cells in series protected by a bypass diode connected in anti-parallel to avoid negative PV voltages that forces the module to consume power. In addition, the figure also presents the electrical behavior of a commercial JS65 PV module from Yingli Solar, where the non-linear behavior of the module is observed: the produced PV power ppv changes depending on the irradiance S and voltage vpv imposed to the module. Moreover, for each irradiance condition there exists an operation point in which the module produces the maximum power, named MPP [5]. Since the irradiance is unpredictable, commercial PV inverters are usually equipped with on-line searching algorithms devoted to track the MPP continuously (named Maximum Power Point Trackers or MPPT).
The electrical behavior of a PV module is modeled using (Eq. 1), where Rs and Rp represent the ohmic losses, iSC represent the photo-induced current depending on the irradiance, i0 represents the saturation current of the junction and vtd represents the thermal voltage depending the module temperature. Those parameters can be calculated from datasheet values and/or experimental measurements by solving the expressions given in [9].
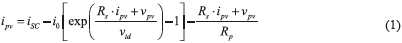
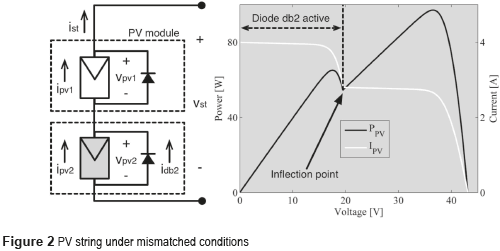
Such an expression and Figure 1 show that a maximum PV current is obtained at short-circuit condition, i.e. vpv = 0 V. Moreover, from (1) it is noted that the photo-induced current is the one powering the PV module; hence PV current is always smaller than iSC. But, since the photo-induced current depends on the effective irradiance reaching the PV module, partial shading across PV strings generate that modules with different irradiation exhibit different iSC values. In a PV string the modules have the same current since they are in series-connection, but if there exists a difference in the values of iSC, a bypass diode will become active to provide a path for the current in excess. Figure 2 illustrates such a case: in a PV string formed by two modules, the upper one is fully irradiated while the module at the bottom is partially shaded, hence it exhibits a lower iSC value. Then, such a string current must to be lower than the photo-induced current of the module at the top (ist < iSC1), but two possible operation conditions appear: if the string current is higher than the iSC value of the module at the bottom (ist > iSC2) the associated bypass diode db2 becomes active to provide a path for the current excess idb2 = ist - iSC2. Such a condition imposes to the module at the bottom almost zero voltage, hence it does not produce power. Instead, if the string current is lower than the iSC value of the module at the bottom (ist < iSC2) the associated bypass diode db2 becomes inactive and the module produces power. Such a bi-state behavior is known as the mismatched phenomenon, and the operation condition in which a bypass diode becomes active is known as inflection point.
Figure 2 presents the main characteristic of a shaded (mismatched) PV string: the power vs. voltage (P-V) curve exhibits multiple local maximum power points (LMPP) due to the activation of bypass diodes. Such a simulation considers the upper module at S1 = 1000 W/m2 and the shaded one at S2 = 700 W/m2, but stronger effects are experimented for larger differences in the irradiances. Moreover, in larger PV arrays, such as the multi-string array depicted in Figure 1, the P-V curve could exhibit a much larger number of LMPP equal to n×m, where n represents the number of modules per string while m represents the number of strings [1].
The main problems introduced by the mismatching phenomenon concern the difficulty to track the best operation condition using traditional MPPT solutions based on following a positive derivative in the power, such as the isolated Perturb and Observe (P&O) technique [5], which keeps trapped on any LMPP. In addition, the position of the shaded modules into the array significantly affects the power, hence it is not possible to predict the best configuration [2, 6].
Reconfiguration of PV arrays
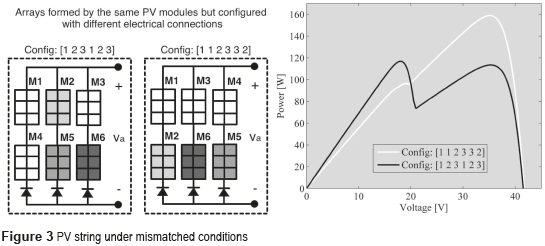
In multi-string PV arrays under partial shading, the power provided by the LMPPs depends on the position of the shaded modules into the array. The position concept does not stand for the physical location of the module but for the electrical connections of the module; for instance, two modules could be physically side-by-side but they could belong to the same string or to different strings depending on the electrical connections among those modules. Figure 3 illustrates such a concept using 6 PV modules: three non-shaded modules (M1, M3 and M4), one module shaded in 25 % (M2), one module shaded in 50 % (M5) and one module shaded in 75 % (M6). Those modules can be connected in different possible connection configurations, where Figure 3 shows 2 of those possibilities, each one of them providing a different P-V curve. The array configuration is described in terms of the strings to which the modules are connected as [M1 M2 M3 M4 M5 M6]; for instance [1 2 3 1 2 3] stands for M1 and M4 connected to the first string, M2 and M5 connected to the second string and M3 and M6 connected to the third string.
In such an example, configuration [1 2 3 1 2 3] provides a maximum power of 117 W at 18 V, while configuration [1 1 2 3 3 2] provides a maximum power of 159 W at 35 V. Hence, for that particular shading profile, it is desirable to configure those modules in [1 1 2 3 3 2]. However, for a different shading profile, another configuration could be the optimal one. Therefore, it is required to reconfigure the PV array continuously to ensure the maximum power production.
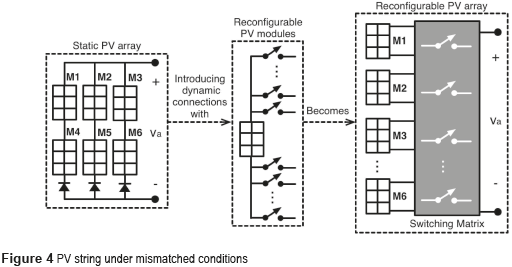
Figure 4 shows both static and reconfigurable PV arrays illustrating the scheme of a reconfigurable PV module. Static arrays, i.e. traditional arrays, have fixed connections between the modules, while reconfigurable PV modules have switches that enable to connect the physical module to any of the strings forming the array.
Therefore, any static PV array can be transformed into a reconfigurable array by introducing dynamics connections using switches. In literature [1], the switches of all the modules are concentrated in a single device named switching matrix, which receives a digital signal from a microprocessor-based controller to reconfigure the array. Then, all the PV modules are connected to the inputs of the switching matrix, while the load (i.e. grid connected-inverted) is connected to the output terminal as depicted in Figure 4.
The control of the switching matrix is simple, because it is only necessary providing the state (ON or OFF) for each switch. The main problem of the reconfiguration system is to find the configuration for such switches, i.e. the best configuration for the PV array, due to the large number of possibilities. Defining n as the number of modules per string and m as the number of strings of the array, each module has (m+1) possible conditions including the disconnection option. Then the number of possible configurations is (m+1)(n×m), where (n×m) corresponds to the number of modules in the array. For instance, the case depicted in Figure 4, with (m+1) = 7 and (n×m) = 6, gives 117649 possible configurations. As described in the introduction, the Brute Force (BF) approach is the only one ensuring to find the best configuration, but it requires to tests all the possibilities. In literature three main solutions have been proposed to evaluate those configurations: estimate the best configuration by equalizing the photo-induced currents [10], measuring the P-V characteristics of each module to interpolate the array P-V curve [11], and use models to predict the P-V curve [2]. The first approach introduces large errors in multi-strings arrays, e.g. SP commercial systems, since it is aimed for single-strings systems such as TCT arrays. The second approach requires acquiring a large amount of data since each module must be experimentally tested for each reconfiguration process, which produces power losses due to the long experimental process. Finally, the model-based approach only requires parameterizing the models regularly to account for the aging, but it requires to compute non-linear models for each possibility, which requires long processing times. Hence, to overcome this final problem, an optimization algorithm must be adopted to avoid testing all the possible configurations.
To evaluate the P-V characteristic of a PV array different PV models have been proposed in literature: simplified fast models exhibiting approximation errors (named Fast) [12], accurate models with long processing times (named Complex) [13], and balanced models with high accuracy but medium processing times (named Tradeoff) [1]. The performances of such models were tested in [1], where the Tradeoff model provides the best balance between accuracy and processing speed: Fast model introduces errors up to 5 %, which could lead to a wrong selection of the optimal configuration; while Tradeoff and Complex models introduce errors smaller than 0.1 %, which is acceptable. Moreover, Tradeoff model requires only 19.65 % of the processing time used by Complex model to achieve an almost identical solution.
Therefore, this paper uses the Tradeoff model described in [1] to calculate the P-V characteristic: for a PV array with m strings of n modules (n×m modules), m equations are formulated by considering that the sum of the modules voltage in each string is equal to the array voltage; moreover (n-1) equations are formulated for each string by considering that all the modules currents are equal. In such a way, a non-linear (n×m) equation system is formed, which is solved using the Newton-Raphson method to find the array current and voltage.
However, testing all the possible configurations will make the reconfiguration impractical for commercial applications. For example, taking into account that the average speed of earth's rotation is 0.25 degrees per minute [14], the shades affecting a PV array also move with the same speed. Then, to account for a change of 1% in the shades, the reconfiguration process must be performed each 7.2 minutes. However, to process a single configuration of a 2´3 PV array, as the one in Figure 4, A PC equipped with an Intel(R) Xeon(R) CPU E5-2620 of 4.0 GHz and 32 GB of RAM requires 20 ms; hence to evaluate the 117649 possibilities it requires 39.22 minutes, which makes impossible to reconfigure the system every 7.2 minutes. Therefore, the following section proposes a genetic algorithm to speed-up the searching of the optimal configuration.
Searching the optimal configuration by using a genetic algorithm
Population–based heuristic algorithms have been used in a plethora of optimization problems with promising results. The population approach has two main advantages over other reported solutions. In the first place, a parallel search is performed through the whole solutions space, where each individual represents a potential optimal, which enable to speed up the performance of the optimization process. Secondly, the search process depends simultaneously on several potential solutions, which allows dealing with local optima issues. Among the many population-based approaches, Genetic Algorithms (GAs) are the most conspicuous option for optimization purposes [15]. A GA deals directly with solutions in a given population, and performs genetic operators over such individuals, such as mutation or crossover. As a result of such operators, the population converges gradually toward an optimal solution, guided by a fitness function.
In this paper, the design of the GA was based on the following parameters for the commercial PV module Yingli Solar JS65 calculated using the procedure described in [9]: i0 = 9.6126e-10 A, vtd = 0.9797 V, Rs = 0.3681 W, Rp = 276.4026 W, and open circuit voltage Voc = 21.7 V. It must be pointed out that iSC values depend of the irradiance reaching the PV modules. Then, using the Tradeoff model, the GA explores the solutions space by generating potential interconnections among the panels. The fitness values guide the exploration, leading toward individuals that provide higher PV powers. The tuning choices of the GA are described below.
Population size
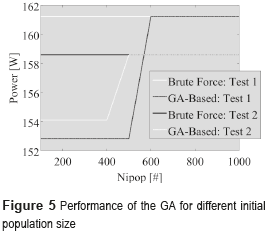
The population size is defined to be dynamic and it depends on two parameters: Nipop that represents the initial population size, and Npop that represents the population size after the first generation. Managing a larger initial population size increases the probabilities of finding the absolute optimum for the optimization problem [15]. Although each optimization problem is unique by nature, after several tests it was found that a population size above 1000 individuals may improve the performance of the GA, for the sake of locating the global optimum [15].
Regarding the initial population size, several tests were performed in order to set such a parameter. Figure 5 shows representative results of such tests, where the GA reaches the BF performance if the initial population size (Nipop) is large enough. Since a population size above 1000 individuals seems to be the best choice, the values of Npop and Nipop were set to the same value, so the population size does not change as the algorithm converges.
Genetic operators
Regarding the genetic operators, a subset of the population, composed by the best Ngood individuals, is chosen to survive for the next generation, and also it is used to produce offspring through crossover. Such offspring competes (in terms of fitness) for complete the remaining individuals of the population. The more suitable a new solution is, the more probable is that such solution survives to the next generation. This feature resembles to the process known as natural selection [15]. Apart from the above, the best Nelite individuals are conserved and precluded from mutation processes, for the sake of not losing good solutions as a result of such an operator.
Constraints
In the GA it is possible to restrict the maximum number of generations, as well as the minimum number of panels connected in series and parallel. Such constraints are represented directly by the bountIte, boundSer, and boundParl parameters, respectively. Similarly, the boundVoltage and boundPower parameters are used to constrain the system voltage and power, respectively. There exists another parameter, named Ndiff, which ensures minimum population diversity. Ndiff represents the number of individuals on a given population which are different from the best solution found so far. Such a parameter is used as stopping criterion.
Fitness and Mating
To ensure a consistent performance of the GA algorithm for any number of modules; the fitness function was designed as a normalized quantity. Eq. (2) describes the proposed fitness function Fcost, where Pcal represents the power delivered by the PV array, Voc represents the open-circuit voltage, ISC(i) represents the short-circuit current of the ith module and NPV represents the number of modules in the system. Then, Fcost provides values in the range [0, 1] to represent the amount of power provided by a configuration as a fraction of the ideal maximum power (without mismatching conditions and without losses) independent of the array size. Therefore, the objective of the GA is to maximize the value of Fcost.
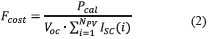
The parents selection process is implemented by a combination of random and tournament strategies. Best results were obtained when half of the parents are chosen randomly, and the remaining individuals are chosen by a tournament process. A two–point crossover was implemented for the problem at hand, and mutations were implemented by changing a single value of the chromosomic representation of a given solution. The number of mutations is controlled by the NMut parameter, where the best results were obtained by setting NMut to 0.2 (20 % of the population size). The selection of individuals subject to the mutation operator was performed in a random fashion, excluding the best Nelite solutions as previously described.
Further settings
Regarding the rest of the tuning of the algorithm, the population's diversity (Ndiff) was set to 20 % of the population size. Constraint parameters boundParl and BoundSer were set to 1 and 2, respectively. The remaining constraints were set to be inactive.
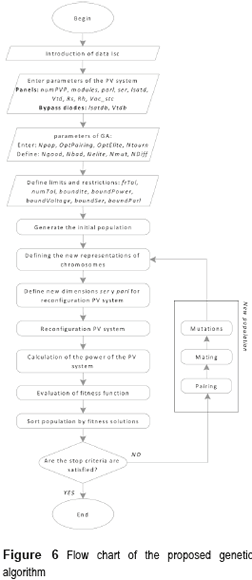
Figure 6 summarizes the GA execution flow. The first section of the algorithm is devoted to the initial settings of the parameters, including those related to the PV system, the GA itself, and the constraints of the optimization problem.
The creation of a new population may occur as a consequence of an initial setting, or as a result of the genetic operators. Since the created solutions are the result of some randomness, it is mandatory to correct their representation, this to avoid redundancy or unreal situations. Once the representation of the solutions is correct, the algorithm evaluates their fitness values. A sorting process is conducted in order to manage elitism and mating issues. If the set of solutions is not yet suitable to the problem at hand, genetic operators create a new population and the iterative process continues. Alternatively, when the population's diversity is low enough, the algorithm stops and delivers the optimized solution.
Performance evaluation
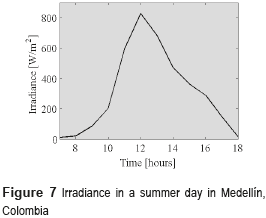
The evaluation of the proposed solution considers the irradiance profile presented in Figure 7, which corresponds to a summer day in Medellin, Colombia. The profile starts at 7:00 and finishes at 18:00, where the maximum irradiance value of 828 W/m2 is achieved at 12:00.
For the parameterized PV modules, the photo-induced current is calculated from the irradiance value S as iSC = S×(iSC,MAX)/SMAX, where iSC,MAX = 4 A and SMAX = 1000 W/m2. Hence, the maximum value of iSC in the given irradiance profile is 3.312 A.
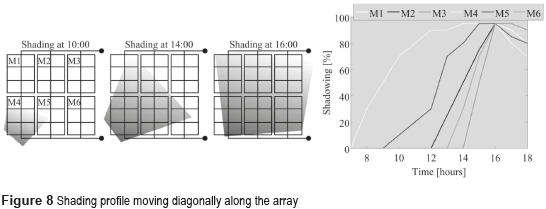
The GA-based solution was tested in two different types of shading profile: a diagonal shade that covers the modules completely after a period of time, and an horizontal shade moving along the array without covering all the modules at the same time. The first shading profile is presented in Figure 8, where the module M4 is the first one in experimenting a shade. The shade moves through the day affecting all the modules by 18:00. The percentage of shading of each module along the day is presented at the right side of Figure 8, which reduces the effective irradiance reaching the corresponding PV module.
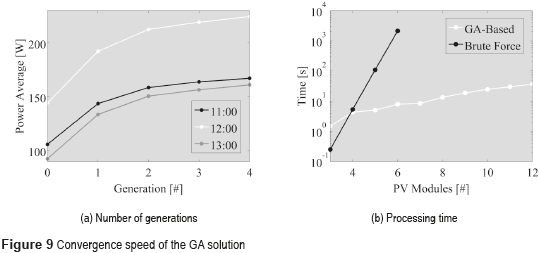
Figure 9 presents the performance of the GA-based solution in detecting the best configuration previously obtained with the classical brute force approach. Figure 9(a) shows that GA solution finds the best configuration in only 4 generations. Such a performance was consistent for multiple trials, where Figure 9(a) presents the evolution of the GA-based reconfiguration in three examples: irradiances at 11:00, 12:00 and 13:00. To provide a scale of the time saving provided by the GA solution, Figure 9(b) compares the processing time required by both brute force and GA approaches to reach the optimal solution for different number of modules between 3 and 12. The results show that for 3 and 4 modules the processing times are comparable, but for 5 modules the brute force requires 2080 % more time that the GA option (109.5 s vs 5.1 s), while for 6 modules the brute force requires 26912 % more time that the GA approach (2134 s vs 7.9 s). In fact, for 6 modules the brute force is not practical to reconfigure each 7.2 minutes to compensate for the rotation of 0.25 degrees per minute of earth, while using the GA-based reconfiguration it is possible. Moreover, Figure 9(b) shows that for 12 modules the GA solution requires 36.5 s to reach the optimal solution, which is within the 7.2 minutes limit. In fact, the GA-based reconfiguration could find the best configuration for PV arrays with up to 36 modules within the 7.2 minutes limit using the processing system adopted in this work. Instead, the brute force approach will require 116 days to achieve the same result.
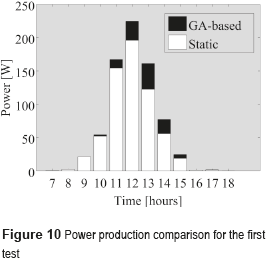
Figure 10 depicts the power production of the GA-based reconfiguration system in contrasts with a classical (static) PV array. It shows that from 10:00 the reconfiguration solution provides higher power, which is due to the stronger shading area covering the modules, as observed in Figure 8. The highest difference between the static and reconfigurable systems occurs at 13:00, where the latter produces 31 % more power (38 W). In the overall profile, the reconfiguration solution provides 17 % more energy than the classical solution, which significantly reduces the time required to recover the investment and improves the economic viability of the PV installation.
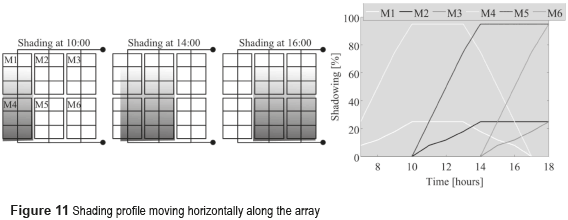
The second test is based on the horizontal shade presented in Figure 11: the shade affects first the modules M1 and M4 at morning, affecting the second and third strings afterwards. At the end of the day the first string is unaffected while second and third strings are partially shaded. The right side of the figure shows the shading profile for each module.
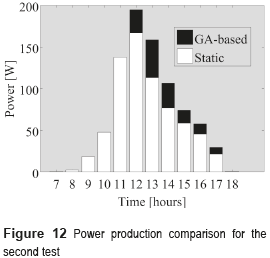
Figure 12 presents the comparison of the power production of both the GA-based and classical (static) solutions. This time the reconfiguration approach produces higher power starting from 12:00 due to the shading profile, and at 13:00 the GA-based reconfiguration produces a peak increment in power of 41 % (46 W). For this shading profile, the GA solution produces 22 % more energy in comparison with the static counterpart.
Those results show the strong improvement provided by the GA-based reconfiguration system, in terms of power production, to any PV system affected by shades. In addition, those results also put in evidence that brute force approaches are not suitable for real-time reconfiguration due to its long processing times, while the GA solution overcomes this limitation.
Conclusions
The design of a GA solution was proposed for the computation of reconfiguration patterns in PV arrays. In terms of performance, the obtained results are very promising, since GA calculations are quite faster than those obtained with the BF approach. The latter is especially true for big-size reconfiguration problems. The proposed GA solution improves the power generated by the PV array, which is the result of the reconfiguration process. However, such improvements require a real-time optimization engine powerful enough to perform practical implementations.
Acknowledgments
This work was supported by the Universidad Nacional de Colombia under the projects RECONF-PV-18789, RECONF-PV-25633 and RECONF-OP-21386, and by COLCIENCIAS under the program ''JÓVENES INVESTIGADORES - 2013'' and the scholarship 567-2012.
References
1. J. Bastidas, E. Franco, G. Petrone, C. Ramos, G. Spagnuolo. ''A model of photovoltaic fields in mismatching conditions featuring an improved calculation speed''. Electric Power System Research. Vol. 96. 2013. pp. 81-90. [ Links ]
2. J. Bastidas, C. Ramos, A. Saavedra. ''Reconfiguration analysis of photovoltaic arrays based on parameters estimation''. Simulation Modelling Practice and Theory. Vol. 35. 2013. pp. 50-68. [ Links ]
3. N. Femia, M. Fortunato, M. Vitelli. ''Light-to-light: PV-Fed LED lighting systems''. IEEE Transactions on power electronics. Vol. 28. 2013. pp. 4063-4073. [ Links ]
4. D. Jacobs, N. Marzolf, J. Paredes, W. Rickerson, H. Flynn, C. Becker, M. Solazo. ''Analysis of renewable energy incentives in the Latin America and Caribbean region: The feed-in tariff case''. Energy Policy. Vol. 60. 2013. pp. 601-610. [ Links ]
5. E. Romero, G. Spagnuolo, L. Garcia, C. Ramos, T. Suntio, W. Xiao. ''Grid-Connected Photovoltaic Generation Plants: Components and Operation''. IEEE Industrial Electronics Magazine. Vol. 7. 2013. pp. 6-20. [ Links ]
6. Y. Zhao, L. Yang, B. Lehman. Reconfigurable solar photovoltaic battery charger using a switch matrix. Proceedings of the IEEE 34th International Telecommunications Energy Conference (INTELEC). Scottsdale, USA. 2012. pp. 1-7. [ Links ]
7. D. Nguyen, B. Lehman. ''An adaptive solar photovoltaic array using model-based reconfiguration algorithm''. IEEE Transactions on Industrial Electronics. Vol. 55. 2088. pp. 2644-2654. [ Links ]
8. M. El-Dein, M. Kazerani, M. Salama. ''Optimal photovoltaic array reconfiguration to reduce partial shading losses''. IEEE Transactions on Sustainable Energy. Vol. 4. 2013. pp. 145-153. [ Links ]
9. J. Accarino, G. Petrone, C. Ramos, G. Spagnuolo. Symbolic algebra for the calculation of the series and parallel resistances in PV module model. Proceedings of the International Conference on Clean Electrical Power (ICCEP). Alghero, Italy. 2013. pp. 62-66. [ Links ]
10. G. Velasco, F. Guinjoan, R. Pique, M. Roman, A. Conesa. ''Electrical PV array reconfiguration strategy for energy extraction improvement in grid-connected PV systems''. IEEE Transactions on Industrial Electronics. Vol. 56. 2009. pp. 4319-4331. [ Links ]
11. J. Storey, P. Wilson, D. Bagnall. ''The optimized-string dynamic photovoltaic array''. IEEE Transactions on Power Electronics. Vol. 29. 2014. pp. 1768-1776. [ Links ]
12. G. Petrone, C. Ramos. ''Modeling of photovoltaic fields in mismatched conditions for energy yield evaluations''. Electric Power Systems Research. Vol. 81. 2011. pp. 1003-1013. [ Links ]
13. G. Petrone, G. Spagnuolo, M. Vitelli. ''Analytical model of mismatched photovoltaic fields by means of Lambert W-function''. Sol. Energy Mater. Sol. Cells. Vol. 91. 2007. pp. 1652-1657. [ Links ]
14. S. Odenwald. Ask the Space Scientist about: Earth - Rotation. NASA/Raytheon. Available on: http://image.gsfc.nasa.gov/poetry/ask/arot.html Accessed: December 15, 2014. [ Links ]
15. R. Haupt, S. Haupt. Practical Genetic Algorithms. 2nd ed. 2. Ed. Jhon Wiley & Sons, Inc. New York, USA. 1998. pp. 27-65. [ Links ]