Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230
Rev.fac.ing.univ. Antioquia no.79 Medellín Apr./June 2016
https://doi.org/10.17533/udea.redin.n79a02
ARTÍCULO ORIGINAL
DOI: 10.17533/udea.redin.n79a02
Estimation of the neuromodulation parameters from the planned volume of tissue activated in deep brain stimulation
Estimación de los parámetros de neuromodulación a partir del volumen de tejido activo planeado en estimulación cerebral profunda
Viviana Gómez-Orozco1*, Mauricio Alexander Álvarez-López1, Óscar Alberto Henao-Gallo1, Genaro Daza-Santacoloma2, Álvaro Ángel Orozco-Gutiérrez1
1Grupo de Automática, Facultad de Ingenierías, Universidad Tecnológica de Pereira. Carrera 27 # 10-02 Barrio Álamos. A. A. 97. Pereira, Colombia.
2Instituto de Epilepsia y Parkinson del Eje Cafetero - Neurocentro. Carrera 9 # 25-20 Torre A Consultorio 418. C. P. 660002. Pereira, Colombia.
* Corresponding author: Viviana Gómez Orozco, e-mail: vigomez@utp.edu.co
(Received May 29, 2015; accepted October 27, 2015)
ABSTRACT
Deep brain stimulation (DBS) is a therapy with promissory results for the treatment of movement disorders. It delivers electric stimulation via an electrode to a specific target brain region. The spatial extent of neural response to this stimulation is known as volume of tissue activated (VTA). Changes in stimulation parameters that control VTA, such as amplitude, pulse width and electrode configuration can affect the effectiveness of the DBS therapy. In this study, we develop a novel methodology for estimating suitable DBS neuromodulation parameters, from planned VTA, that attempts to maximize the therapeutic effects, and to minimize the adverse effects of DBS. For estimating the continuous outputs (amplitude and pulse width), we use multi-output support vector regression, taking the geometry of the VTA as input space. For estimating the electrode polarity configuration, we perform several classification problems, also using support vector machines from the same input space. Our methodology attains promising results for both the regression setting, and for predicting electrode active contacts and their polarity. Combining biological neural modeling techniques together with machine learning, we introduce a novel area of research where parameters of neuromodulation in DBS can be tuned by manually specifying a desired geometric volume.
Keywords: Deep brain stimulation, planned volume of tissue activated, neuromodulation parameters, support vector machines
RESUMEN
La estimulación cerebral profunda (ECP) es una terapia con resultados promisorios para el tratamiento de desórdenes del movimiento. Esta envía estimulación eléctrica por medio de un electrodo a una región específica del cerebro. La propagación espacial de la respuesta neuronal a esta estimulación se conoce como volumen de tejido activado (VTA). Cambios en los parámetros de estimulación que controlan el VTA, como la amplitud, el ancho de pulso y la configuración de polaridad del electrodo pueden afectar la efectividad de la terapia ECP. En este estudio, desarrollamos una metodología novedosa para estimar los parámetros de neuromodulación de ECP adecuados, a partir del VTA planeado, que trata de maximizar los efectos terapéuticos y minimizar los efectos adversos de la ECP. Para la estimación de las salidas continuas (amplitud y ancho de pulso), usamos regresión de soporte vectorial de múltiples salidas, tomando la geometría del VTA como espacio de entrada. Para la estimación de la configuración del electrodo desarrollamos varios problemas de clasificación, también utilizando máquinas de soporte vectorial para el mismo espacio de entrada. Nuestra metodología logra resultados prometedores tanto en el caso de regresión como para predecir los contactos activos del electrodo y su polaridad. Combinando técnicas de modelamiento de neuronas biológicas junto con aprendizaje de máquina, se introduce una novedosa área de investigación donde los parámetros de neuromodulación en ECP pueden sintonizarse manualmente especificando un volumen geométrico.
Palabras clave: Estimulación cerebral profunda, volumen de tejido activo planeado, parámetros de neuromodulación, máquina de soporte vectorial
1. Introduction
Deep brain stimulation (DBS) is a therapy used for the treatment of neurological conditions, such as Parkinson's Disease, essential tremor, and dystonia, among others. It is considered when drug therapy cannot suitably control the movement disorder symptoms. DBS involves the placing of an electrode within a target brain region (the basal ganglia, the thalamus, or other subcortical structures). Although DBS is an effective therapy, understanding the effects of neuronal response to electrical stimulation (its action mechanisms) remains unclear [1-3]. The fundamental purpose of DBS is to modulate neural activity with applied electric fields [4]. In this regard, a measure of the effects of deep brain stimulation is to estimate the volume of tissue activated (VTA), namely, the spatial spread of direct neural response to external electrical stimulation via a deep brain stimulation (DBS) electrode [5, 6].
Once the DBS electrode is implanted, one essential step is the configuration of the neurostimulation parameters. The neurostimulation is carried out by different active contacts in the electrode. Each active contact generates a rectangular pulse function, that shares the same amplitude, pulse width, and frequency. Furthermore, a contact could be active or inactive. If a contact is active, it can behave as a cathode or anode. Therefore, the neurostimulation parameters are the amplitude, pulse width, and frequency of the rectangular pulse function, and each lead contact configuration (cathode, anode or no stimulation). Although the frequency is an important parameter in DBS, it is considered that it does not have an influence in VTA estimation [7]. Accordingly, in this paper, we consider as neurostimulation parameters the amplitude, and pulse width of the rectangular pulse function, and the configuration of each lead contact.
Variations in the electric stimulation parameters affect the spread of the activation, which can have serious consequences on therapeutic effects, or induce side effects when such parameters are not carefully adjusted [8]. The process for manually getting the right parameters can be quite time-consuming since it usually relies on the experience of the medical specialist, commonly demanding several clinical sessions for a successful result. Therefore, in order to achieve the desired therapeutic benefits, and to reduce the amount of time spent by the patient and the specialist in clinical sessions, it is important to find a procedure for optimally adjusting the DBS device parameters.
Although there is a huge amount of literature on the subject of computing the VTA given a specific set of neuromodulation parameters [5-7, 9], the inverse problem, this is, the problem of computing a set of specific neuromodulation parameters given a desired VTA, has received less attention. A previous study about the estimation of VTA uses an approach based on artificial neural networks to characterize the stimulation parameters adjustment effects over DBS [10, 11]. A system is provided in [11], which seeks the correlation between the calculated, and the desired VTA, that allows them to determine the appropriate stimulation parameters for the desired volume. The drawbacks of this approach are that it can not appropriately represent high stimulation parameter values and/or complex electrode configurations (more than two active contacts), and the assumption of an isotropic tissue medium.
In this work, we propose a novel methodology which allows us to find a suitable configuration of the neurostimulation parameters that attempts to maximize the therapeutic benefits, and to minimize the side effects of the VTA for DBS treatment. We first employ a computer simulator of the VTA generation process, where the input data corresponds to different configurations of the neuromodulation parameters, and the output data corresponds to the graphical representation of the VTA. The simulator uses a model to compute the extracellular potential generated by the DBS, plus a model for estimating the neural activation that takes place due to the electrical stimulation. We refer to this step as the direct problem (it is also known as the forward problem). We then solve an inverse problem that takes as input space the graphical representation of the VTA, and the output space corresponds to the values of the parameters that we want to adjust. To solve the inverse problem, we employ a framework based on support vector machines using them either for multi-output regression (for simultaneously tuning the amplitude and the pulse width), or for classification (for tuning the configuration of each contact). The relevance of the SVM underlies in its robustness for generalization, and its ability for easily dealing with high-dimensional input spaces.
To the best of our knowledge, this is the first attempt to compute the neurostimulation parameters for DBS starting from the desired VTA by the specialist. Results are promising and show that the combination of carefully specified physiological models together with machine learning techniques can be used to tackle a novel problem in DBS.
2. Materials and methods
2.1. Direct problem
The key neurostimulation parameters in VTA estimation are amplitude, pulse width and electrode contacts configuration. In this work, we use a clinical DBS electrode (Medtronic DBS 3389 electrode, ACTIVA-RC stimulator [12]) which offers wide neurostimulation parameter ranges. In clinical studies, the DBS amplitude should not exceed a certain value that depends on the neurostimulator, e.g 3.6 Vfor the Soletra, and 5.5 V for the Kinetra neurostimulator. To observe changes in patient response, 0.5 V steps in amplitude levels are also needed [13].
The solution of the direct problem in VTA uses two models, the first one to compute the extracellular potential generated by the DBS electrode, and the second one to estimate the neural activation in response to the electrical stimulation [14]. The model that computes the extracellular potential was implemented in COMSOL Multiphysics 4.2. (Comsol Inc., Stockholm Sweden) [15], and it is used to solve Poisson's equation by means of the finite element method (FEM). The model that estimates the amount of neural activation was computed using Neuron 7.3, configured as a Python module [16, 17]. Figure 1 is a schematic representation of the methodology used to obtain the solution of the direct problem.
In what follows, we briefly explain the extracellular potential model, and the computation of the volume of tissue activated.
Extracellular potential model
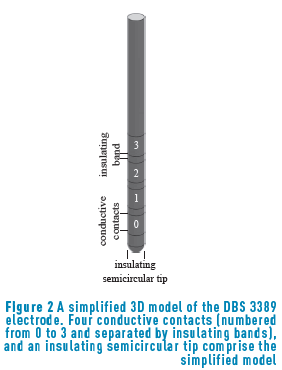
A simplified 3D model of a clinical DBS electrode positioned in the middle of a conductive extracellular medium with an isotropic conductivity [18] was built in COMSOL Multiphysics 4.2., and save as model M-file. The electrode model consisted of four conductive contacts (with a conductivity of 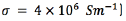 1.27 mm in diameter and 1.5 mm in height separated by insulating bands
1.27 mm in diameter and 1.5 mm in height separated by insulating bands 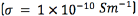 0.5 mm in height, and of an insulating semicircular tip with radius 0.635 mm (Figure 2). The conductor extracellular medium consisted of a sphere of diameter 10 cm. It was assumed to be homogeneous and isotropic with conductivity
0.5 mm in height, and of an insulating semicircular tip with radius 0.635 mm (Figure 2). The conductor extracellular medium consisted of a sphere of diameter 10 cm. It was assumed to be homogeneous and isotropic with conductivity 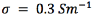 , relative permittivity
, relative permittivity 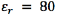 [18], and an encapsulation tissue layer of 0.5 mm around the electrode with conductivity of
[18], and an encapsulation tissue layer of 0.5 mm around the electrode with conductivity of 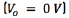 [7, 19]. The DBS pulse was modeled as a rectangular pulse by imposing time dependent Dirichlet boundary conditions on the contacts of the DBS electrode considered as actives. The remaining contacts were left inactive. Dirichlet boundary conditions
[7, 19]. The DBS pulse was modeled as a rectangular pulse by imposing time dependent Dirichlet boundary conditions on the contacts of the DBS electrode considered as actives. The remaining contacts were left inactive. Dirichlet boundary conditions 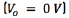 were also imposed on the boundaries of the extracellular medium. Finally, zero current flow conditions were imposed on the surfaces of the non active contacts, and insulating components of the electrode [7]. The Poisson's equation was used to compute the spatial and temporal distribution of the extracellular potential.
were also imposed on the boundaries of the extracellular medium. Finally, zero current flow conditions were imposed on the surfaces of the non active contacts, and insulating components of the electrode [7]. The Poisson's equation was used to compute the spatial and temporal distribution of the extracellular potential.
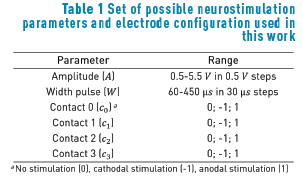
Once the extracellular potential model was built, it was run into Matlab 2012a using COMSOL with Matlab (COMSOL-Matlab LiveLink) [20]. We automated the solution of the Poisson's equation for several possible neurostimulation parameter combinations (Table 1) by using an M-file in Matlab. A random sample of 500 neurostimulation configurations was taken for the available parameter values under study (Table 1), where each configuration described amplitude, pulse width, and the active contacts during the electrode stimulation.
Volume of tissue activated
The gold standard for VTA estimation consists in coupling the electric potential due to DBS with a model of multicompartment myelinated axons distributed around the electrode shaft. The volume of tissue activated is computed as the volume generated by the active axons. To compute the change in the transmembrane potential induced by the stimulation, the multicompartment myelinated axonal model [14, 21] was implemented in Python 2.7 with Neuron 7.3 configured as a Python module. Each axon includes 21 nodes of Ranvier, and 2 myelin attachment segments (MYSA), 2 paranode main segments (FLUT), and 3 internode segments (STIN) between each node. For more detailed information, see [22]. The axonal field was modeled as fibers of 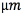 diameter. The straight axons were oriented in four different directions, perpendicular to the axis of the electrode, and positioned at a distance between axons of 0.5 mm in both the vertical and horizontal directions [21]. The electrical potential was interpolated from the elements of the FEM mesh onto each of the sections that integrated the axonal model.
diameter. The straight axons were oriented in four different directions, perpendicular to the axis of the electrode, and positioned at a distance between axons of 0.5 mm in both the vertical and horizontal directions [21]. The electrical potential was interpolated from the elements of the FEM mesh onto each of the sections that integrated the axonal model.
Computer emulator of the simulation model
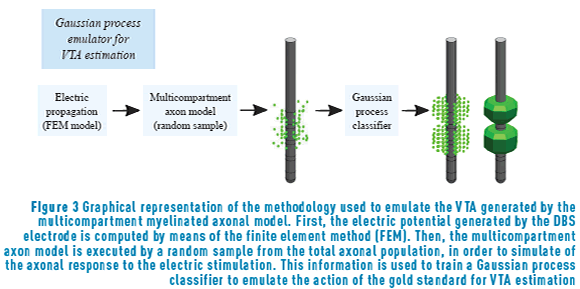
Solving exactly the model for the multicompartment myelinated axons described above is computationally expensive. For each neurostimulation parameter configuration, running the full simulation model takes around one hour. In order to reduce the computational complexity of computing 500 times the direct problem, we used a computer emulator for the simulation model. The computer emulator was based on a Gaussian process (GP) classifier. The GP classifier was trained to emulate the action of the gold standard for VTA estimation, that is, it was trained to determine the spatial extent of neuronal activation, predicting which axons were activated by the applied extracellular stimulus [23]. The GP emulator reduces the computation time to about four mins [23], allowing the complete computation of 500 samples in a reasonable time. The methodology used for emulating the multicompartment myelinated axonal model is summarized in Figure 3. Our final dataset is made of 500 values for the neurostimulation parameters together with the 500 geometrical VTAs generated by each configuration.
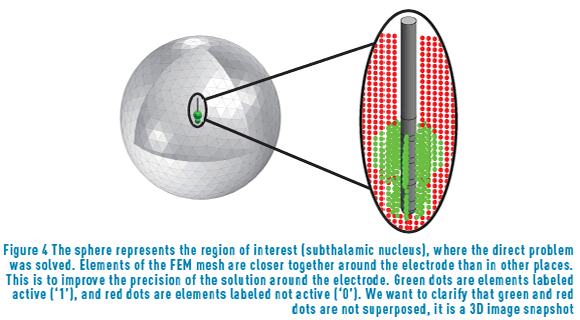
It is important to clarify that each VTA was estimated for the same elements of the FEM mesh with labels {0; 1} that determine which of these elements were not activated (label 0) or were activated (label 1) (see Figure 4). The applied stimulus was different for each sample.
2.2. Inverse problem
Each geometrical representation of the VTA is described using an m-dimensional vector made of zeros, and ones. A value of zero in this vector indicates that the mesh element of the finite element solution (from the direct problem) was inactive due to the particular configuration of the neurostimulation parameters. A value of one in this vector indicates that the mesh element was active. The value of mis determined by the elements of the FEM mesh (in our case, m = 177,924), that is, the elements necessary to cover a spherical volume of 10 cm centered around the subthalamic nucleus, our target brain region for DBS.
As explained in the introduction, we want to map the geometrical representation of the VTA to the neurostimulation parameters that were used for computing that VTA. In short, we want to build a vector-valued function f that maps m-dimensional binary vectors x, to a six-dimensional vector 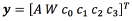 , where A refers to the amplitude of the pulse, W refers to the pulse width, and ck refers to the condition of contact k , with k = 0;1; 2; 3.
, where A refers to the amplitude of the pulse, W refers to the pulse width, and ck refers to the condition of contact k , with k = 0;1; 2; 3.
The space of the brain region that we want to cover with the VTA leads to vectors x with a dimensionality m greater than a thousand, depending of the volume resolution that we aim for the VTA. For building functions in such high dimensional input spaces, we use a framework based on Support Vector Machines, where the computations involved are dependent on the number of samples (in our case, less than 500 for the training stage), and not on the dimensionality of the input space.
For constructing the function 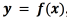 , we use two types of support vector learners. We jointly model the amplitude
, we use two types of support vector learners. We jointly model the amplitude 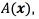 and the pulse width
and the pulse width 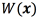 using multiple-output support vector regression through the scheme proposed in [24, 25]. Although, we could use support vector regression for modeling
using multiple-output support vector regression through the scheme proposed in [24, 25]. Although, we could use support vector regression for modeling 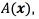 , and
, and 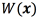 independently, we experimentally found that modeling them jointly offered better results. This result is expected since in generating the VTA, both
independently, we experimentally found that modeling them jointly offered better results. This result is expected since in generating the VTA, both 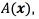 and
and 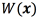 are correlated. We also modeled the contacts
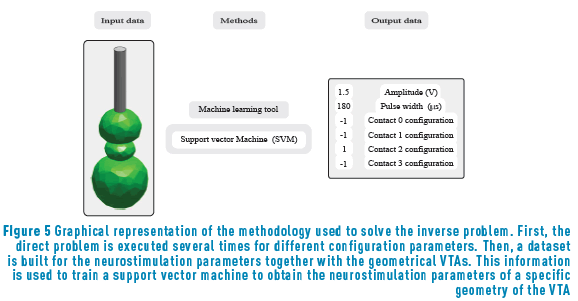
are correlated. We also modeled the contacts 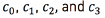 as four different classification tasks, using support vector classifiers for each of them. The methodology employed for solving the inverse problem is depicted in Figure 5.
as four different classification tasks, using support vector classifiers for each of them. The methodology employed for solving the inverse problem is depicted in Figure 5.
The subject of multiple-output regression in the context of SVMs has been less studied in the literature, and in what follows, we briefly summarize the theory behind [24, 25]. The theory behind support vector classifiers is well-known, and it can be found in different machine learning textbooks [26, 27].
For all the SVM configurations (multiple output regression, and the independent classification tasks), we use a kernel function 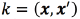 based on a Hamming distance
based on a Hamming distance 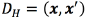 between the binary vectors x, and x', vectors obtained from the mesh given by the FEM model. The Hamming distance measures the number of positions at which the corresponding vectors, x and x', have different symbols. For the SVMs, we also tried the classical radial basis function (RBF) kernel, but the results were extremely poor. The RBF kernel might be useful when the input space is continuous, which is not our case.
between the binary vectors x, and x', vectors obtained from the mesh given by the FEM model. The Hamming distance measures the number of positions at which the corresponding vectors, x and x', have different symbols. For the SVMs, we also tried the classical radial basis function (RBF) kernel, but the results were extremely poor. The RBF kernel might be useful when the input space is continuous, which is not our case.
Support vector regression for multiple outputs
The SVM regression method for multiple outputs that we use in this work is an approach, which defines a hyper-sphere insensitivity zone, that allows us to penalize only once the samples that are not placed inside the insensitivity zone for solving multiple outputs regression problems [24, 25, 28]. Let 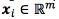 be the input vector, and
be the input vector, and 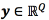 the output vector. The relationship between x , and y is assumed to follow, Eq. (1)
the output vector. The relationship between x , and y is assumed to follow, Eq. (1)
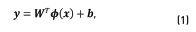
where 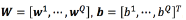 , a regressor
, a regressor 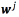 and
and 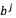 for every output. The function
for every output. The function 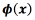 refers to a non-linear transformation to a higher-dimensional space d, where
refers to a non-linear transformation to a higher-dimensional space d, where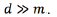
Given a dataset 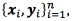 the purpose is to find the set of parameters
the purpose is to find the set of parameters 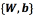 that minimize the objective function (Eq. (2))
that minimize the objective function (Eq. (2))
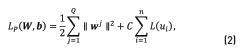
where C is a regularization constant, 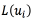 is a loss-function, with
is a loss-function, with 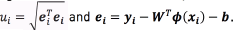 . As a loss function
. As a loss function 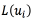 , the authors of [25] use a quadratic loss (Eq. (3)) with respect to an user defined constant
, the authors of [25] use a quadratic loss (Eq. (3)) with respect to an user defined constant 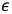
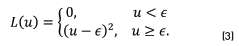
An iteratively reweighted least squares (IRLS) procedure is used to estimate the parameters W, and b.
The solution of the problem above can also be expressed in terms of the vector of coefficients 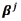 for each output, which relates to the original vectors
for each output, which relates to the original vectors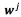 through
through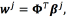 where
where 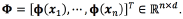 The prediction
The prediction 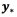 for a new input vector
for a new input vector 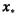 can be computed as
can be computed as 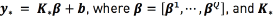 is the kernel between
is the kernel between 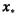 and the training set.
and the training set.
Procedure with SVMs
For all the experiments with SVMs (multi-output regression, and classification), we performed training with seventy percent observations in the dataset, this is, 350 sample points; and testing, with thirty percent of the data, this is, 150 sample points. In the four classification problems (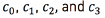 ) we employed the PRTools Matlab toolbox [29], with our own kernel function. For each of these classification problems, the classes considered were three, namely, active contact behaving as anode (label 1), active contact behaving as cathode (label -1), and inactive contact (label 0). The performance measure that we report for classification is the accuracy. For the multi-output regression problem, we use the code provided in [30]. The performance measure that we report for regression is the relative difference between the test value and the predicted value (the relative difference between two values x, and y is defined as
) we employed the PRTools Matlab toolbox [29], with our own kernel function. For each of these classification problems, the classes considered were three, namely, active contact behaving as anode (label 1), active contact behaving as cathode (label -1), and inactive contact (label 0). The performance measure that we report for classification is the accuracy. For the multi-output regression problem, we use the code provided in [30]. The performance measure that we report for regression is the relative difference between the test value and the predicted value (the relative difference between two values x, and y is defined as 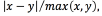 where
where 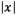 is the absolute value of x, and (x, y)is the maximum value between x, and x). In both cases, the experiments were run 20 times with different training and testing sets to assess the performance.
is the absolute value of x, and (x, y)is the maximum value between x, and x). In both cases, the experiments were run 20 times with different training and testing sets to assess the performance.
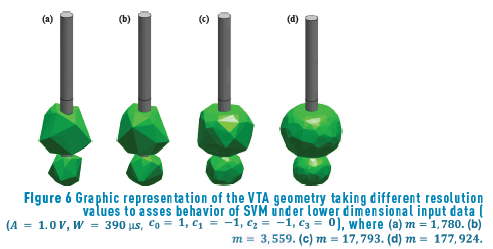
We also evaluate the performance of the different SVM in terms of the dimensionality m of the input vectors x, in other words, in terms of the spatial resolution of the VTA. We start with a dimensionality of m = 177,924 , and then we uniformly subsample each vector by factors of 10; 50, and 100, obtaining input spaces of dimensionalities m = 17,793, m = 3,559 and m = 1,780, respectively. Figure 6 shows an example of the geometries of the VTA for the different input data resolutions considered.
We use different statistical tests to study if there are differences that are significant among the performances obtained in terms of the dimensionality m, for a particular classification task, or for the multiple-output regression task. First, we apply a Lilliefors test for normality over the 20 repetitions of each value of m. If the null hypothesis for normality is rejected, we perform a Kruskal-Wallis test to compare median performances among the values of m, otherwise we use ANOVA. If the null hypothesis for equal medians is rejected, we perform a multiple comparison test using Tukey-Kramer to study further which performances in terms of m are different. All the significance levels are measured at 5%. Details for this procedure can be found in [31].
3. Results
3.1. Direct problem
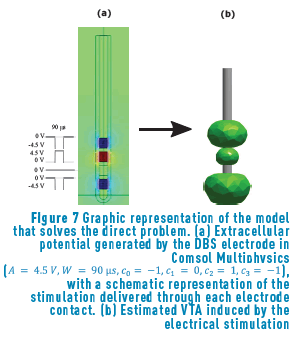
The main objective of the direct problem is to model a DBS electrode inside the brain tissue, onto a region of interest, under ideal assumptions, to modulate the neural activity. The idea is to deliver an electrical pulse to the target region, and then to study the neural response to this stimulation that is well-known as VTA. Figure 7 shows the potential distribution for a specific neurostimulation parameter setting and the corresponding estimated VTA.
3.2. Generated dataset
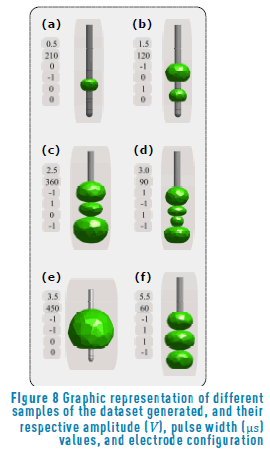
The purpose of the dataset generated was to capture different parameter configurations and their corresponding VTAs. Figure 8 shows six samples of possible parameter combinations (see Table 1), and how they affect the volume that represents the spatial spread of neural activation due to the electric stimulation. A monopolar stimulation, with a low amplitude and a high pulse width value, is represented in Figure 8(a), it shows that high values of pulse width induce a small neural response. A bipolar stimulation, anode-cathode, is described by Figure 8(b), while a cathode-cathode is described by Figure 8(e). The relevance in this configuration is to show how the polarity affects the VTA. The other Figures (Figure 8(c), Figure 8(d) and Figure 8(f)) allow us to see the influence of the parameter variations onto the estimated volume.
3.3. Inverse problem
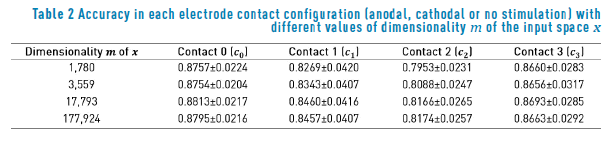
Table 2 summarizes the accuracy obtained for each classification task in terms of the different resolutions of the input data. We obtain a slightly better accuracy for contacts 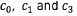 when the dimensionality of the input data is m = 17,793. The best result for contact c2 was obtained when the dimensionality of the input space was equal to m = 177,924. We apply the statistical significance test described in section II-B2 for each classification task, obtaining as a result that the performances for all the contacts are not statistically different in terms of the value of m. This result can be explained by the fact that we are assuming isotropic conductivities for the extracellular potential model, and the shapes for the different VTA generated have regular forms. We expect that if we work with anisotropic conductivities, the shapes generated for the VTA will have irregular forms, and the dimensionality of the input space will become a relevant parameter. Based on the results of Table 2, we conclude that the classification accuracy is in the range of 81%(an error rate of 19%) for contact c2 , and 88% (an error rate of 12%) for contact c1.
when the dimensionality of the input data is m = 17,793. The best result for contact c2 was obtained when the dimensionality of the input space was equal to m = 177,924. We apply the statistical significance test described in section II-B2 for each classification task, obtaining as a result that the performances for all the contacts are not statistically different in terms of the value of m. This result can be explained by the fact that we are assuming isotropic conductivities for the extracellular potential model, and the shapes for the different VTA generated have regular forms. We expect that if we work with anisotropic conductivities, the shapes generated for the VTA will have irregular forms, and the dimensionality of the input space will become a relevant parameter. Based on the results of Table 2, we conclude that the classification accuracy is in the range of 81%(an error rate of 19%) for contact c2 , and 88% (an error rate of 12%) for contact c1.
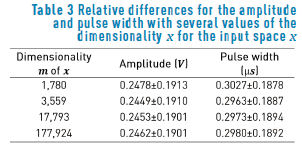
Table 3 shows the relative difference for the amplitude and the pulse width, in terms of the dimensionality m of the input space. Applying the statistical tests described before, we find that the discrepancies among the relative differences are not significant for the amplitude, nor for the pulse width. Again, this could be explained due to the regular forms of the VTA as a consequence of the isotropic conductivities used in the extracellular potential model. The relative difference for the amplitude is about 24%, whereas the relative difference for the pulse width is about 30%.
4. Discussion and conclusions
In this study, we developed a novel methodology to address the problem of finding optimal neurostimulation parameters that increase the effectiveness of the DBS therapy. Our method, first builds a dataset of volumes of tissue activated with their corresponding neurostimulation parameters. This dataset is built with an accurate physiological model that combines an extracellular potential model, and a multicompartment myelinated axonal model. We then use this dataset to design a machine learning algorithm that maps from the space of volumes of tissue activated to the values of the neurostimulation parameters. Since the representation of each VTA is given as a long vector of zeros and ones, in this paper, we use a kernel machine, a SVM, that allows us to handle spaces of high dimensionality. We obtain classification accuracies over 80% for predicting the states of the electrode contacts, and relative differences equal or lower than 30% for the amplitude and the pulse width of the rectangular pulse function. To the best of our knowledge, this is the first attempt in the literature for DBS, that looks to automatically tune the neurostimulation parameters from a previously specified VTA. Although the results shown in this paper may be considered as preliminary, we think these results are promising, and leave plenty of room for further improvement. First, in this paper we solved the classification problems and the regression problems independently. We hope that by solving simultaneously the classification and regression problems, we may improve the performance metrics. This is a foundational idea in successful frameworks like transfer learning or multi-task learning. Second, the choice of the kernel may also help to improve the results. We would like to experimentally test the performance under different distance or similarity measures (other than the Hamming distance), and under different and more sophisticated kernels that exploit the geometric structure of the VTA [32, 33]. Third, the experiments of this paper show that it is possible to reduce the dimensionality of the input space without affecting the performance metrics. Reducing the dimensionality of the input space may ease the design of the machine learning model, improving the performance for classification and regression.
On a different line of work, we would like to apply the methodology for more realistic scenarios, for example, by using anisotropic conductivities for the extracellular potential model, reflecting the properties of the different brain tissues. Such anisotropic conductivities can be obtained from magnetic resonance imaging. For this type of study, it will be important to analyze the performance of the method for different patients.
5. Acknowledgment
The authors would like to thank ''Universidad Tecnológica de Pereira'' for providing us with the computational resources needed to perform the direct problem. This research is developed under the project ''Estimación de los parámetros de neuro modulación con terapia de estimulación cerebral profunda en pacientes con enfermedad de parkinson a partir del volumen de tejido activo planeado'', financed by Colciencias with code 111065740687. The author VGO was also supported by the 645 agreement, ''Jóvenes Investigadores e Innovadores'', funded by Colciencias. The author GDS was partially supported by Colciencias project 499153530997. We would like to thank Iván De La Pava for helping with the direct problem. We would also like to thank the authors of [25] for providing the code of multiple-output regression.
6. References
1. C. McIntyre, W. Grill, D. Sherman and N. Thakor, ''Cellular effects of deep brain stimulation: model-based analysis of activation and inhibition'', Journal of Neurophysiology, vol. 91, no. 4, pp. 1457-1469, 2004. [ Links ]
2. C. McIntyre and P. Hahn, ''Network perspectives on the mechanisms of deep brain stimulation'', Neurobiology of Disease, vol. 38, no. 3, pp. 329-337, 2010. [ Links ]
3. R. So, A. Kent and W. Grill, ''Relative contributions of local cell and passing fiber activation and silencing to changes in thalamic fidelity during deep brain stimulation and lesioning: a computational modeling study'', Journal of Computational Neuroscience, vol. 32, no. 3, pp. 499-519, 2012. [ Links ]
4. A. Chaturvedi, C. Butson, S. Lempka, S. Cooper and C. McIntyre, ''Patient-specific models of deep brain stimulation: influence of field model complexity on neural activation predictions'', Brain Stimulation, vol. 3, no. 2, pp. 65-77, 2010. [ Links ]
5. C. Butson and C. McIntyre, ''Tissue and electrode capacitance reduce neural activation volumes during deep brain stimulation'', Clinical Neurophysiology, vol. 116, no. 10, pp. 2490-2500, 2005. [ Links ]
6. C. Butson, S. Cooper, J. Henderson and C. McIntyre, ''Patient-specific analysis of the volume of tissue activated during deep brain stimulation'', Neuroimage, vol. 34, no. 2, pp. 661-670, 2007. [ Links ]
7. N. Yousif et al., ''Evaluating the impact of the deep brain stimulation induced electric field on subthalamic neurons: a computational modelling study'', Journal of Neuroscience Methods, vol. 188, no. 1, pp. 105-112, 2010. [ Links ]
8. J. Volkmann, J. Herzog, F. Kopper and G. Deuschl, ''Introduction to the programming of deep brain stimulators'', Movement Disorders, vol. 17, pp. 181-187, 2002. [ Links ]
9. N. Yousif, R. Borisyuk, N. Pavese, D. Nandi and P. Bain, ''Spatiotemporal visualization of deep brain stimulation-induced effects in the subthalamic nucleus'', European Journal of Neuroscience, vol. 36, no. 2, pp. 2252-2259, 2012. [ Links ]
10. A. Chaturverdi, J. Luján and C.McIntyre, ''Artificial neural network based characterization of the volume of tissue activated during deep brain stimulation'', Journal of Neural Engineering, vol. 10, no. 5, 2013. [ Links ]
11. J. Luján, A. Chaturvedi and C. McIntyre, ''System and method to estimate region of tissue activation'', U.S. Patent 8589316. Nov. 19, 2013. [ Links ]
12. Medtronic, DBS Lead Kit for Deep Brain Stimulation, 2002. [Online]. Available: http://www.medtronic.com/downloadablefiles/UC199901079bEN.pdf. Accessed on: Dec. 16, 2014. [ Links ]
13. American Association of Neuroscience Nurses (AANN), Care of the Movement Disorder Patient with Deep Brain Stimulation, AANN Clinical Practice Guideline Series, 2009. [Online]. Available: http://www.aann.org/pdf/cpg/aanndeepbrainstimulation.pdf. Accessed on: Dec. 16, 2014. [ Links ]
14. F. Rattay, ''Analysis of models for extracellular fiber stimulation'', IEEE Transactions on Biomedical Engineering, vol. 36, no. 7, pp. 676-682, 1989. [ Links ]
15. COMSOL Multiphysics, COMSOL Multiphysics User's Guide (Version 4.2). Stockholm, Sweden: COMSOL, 2011. [ Links ]
16. M. Hines and N. Carnevale, ''The NEURON simulation environment'', Neural Computation, vol. 9, no. 6, pp. 1179-1209, 1997. [ Links ]
17. M. Hines, A. Davison and E. Muller, ''NEURON and Python'', Frontiers in Neuroinformatics, vol. 3, pp. 1-12, 2009. [ Links ]
18. T. Zhang and W. Grill, ''Modeling deep brain stimulation: point source approximation versus realistic representation of the electrode'', Journal of Neural Engineering, vol. 7, no. 6, 2010. [ Links ]
19. C. Butson, C. Maks and C. McIntyre, ''Sources and effects of electrode impedance during deep brain stimulation'', Clinical Neurophysiology, vol. 117, no. 2, pp. 447-454, 2006. [ Links ]
20. D. Kern and N. Framke, Automation of COMSOL Multiphysics Parameter Studies using the MATLAB Livelink, 2012. [Online]. Available: https://www-user.tu-chemnitz.de/~dker/tutorial_comsol_matlab_livelink.pdf. Accessed on: Dec. 18, 2014. [ Links ]
21. G. Walckiers, ''Bio-electromagnetic model of deep brain stimulation'', Ph.D. dissertation, École polytechnique fédérale de Lausanne, Lausanne, Switzerland, 2009. [ Links ]
22. C. McIntyre, A. Richardson and W. Grill, ''Modeling the excitability of mammalian nerve fibers: influence of afterpotentials on the recovery cycle'', Journal of Neurophysiology, vol. 87, no. 2, pp. 995-1006, 2002. [ Links ]
23. I. Pava et al.,''A Gaussian Process Emulator for Estimating the Volume of Tissue Activated During Deep Brain Stimulation'', in 7th Iberian Conference on Pattern Recognition and Image Analysis (IbPRIA), Santiago de Compostela, Spain, 2015, pp. 691-699. [ Links ]
24. F. Pérez et al., ''Multi-dimensional function approximation and regression estimation'', in International Conference on Artificial Neural Networks (ICANN), Madrid, Spain, 2002, pp. 757-762. [ Links ]
25. M. Sánchez, M. de Prado, J. Arenas and F. Pérez, ''SVM multiregression for nonlinear channel estimation in multiple-input multiple-output systems'', IEEE Transactions on Signal Processing, vol. 52, no. 8, pp. 2298-2307, 2004. [ Links ]
26. B. Scholkopf and A. Smola, Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond, 1st ed. Cambridge, USA: MIT Press, 2001. [ Links ]
27. C. Bishop, Pattern recognition and machine learning, 1st ed. New York, USA: Springer, 2006. [ Links ]
28. D. Tuia, J. Verrelst, L. Alonso, F. Pérez and G. Camps, ''Multioutput support vector regression for remote sensing biophysical parameter estimation'', IEEE Geoscience and Remote Sensing Letters, vol. 8, no. 4, pp. 804-808, 2011. [ Links ]
29. R. Duin et al., PRTools4, A Matlab Toolbox for Pattern Recognition, Delft University of Technology, 2007. [Online]. Available: http://www.prtools.org/files/PRTools4.1.pdf. Accessed on: Jan. 15, 2015. [ Links ]
30. F. Pérez, MSVR: Multioutput Support Vector Regression. [Online]. Available: http://www.uv.es/gcamps/software.html. Accessed on: Jan. 15, 2015. [ Links ]
31. J. Pizarro, E. Guerrero and P. Galindo, ''Multiple comparison procedures applied to model selection'', Neurocomputing, vol. 48, no. 1, pp. 155-173, 2002. [ Links ]
32. F. Bach, ''Graph kernels between point clouds'', in 25th international conference on Machine Learning, Helsinki, Finland, 2008, pp. 25-32. [ Links ]
33. S. Vishwanathan, N. Schraudolph, R. Kondor and K. Borgwardt, ''Graph kernels'', The Journal of Machine Learning Research, vol. 11, pp. 1201-1242, 2010. [ Links ]