ARTÍCULO ORIGINAL

DOI: 10.17533/udea.redin.n79a03

Applicability of semi-supervised learning assumptions for gene ontology terms prediction

Aplicabilidad de las suposiciones del aprendizaje semi-supervisado para la predicción de términos de la ontología genética

Jorge Alberto Jaramillo-Garzón^1,2*, César Germán Castellanos-Domínguez¹, Alexandre Perera-Lluna³

¹Departamento de Ingeniería Eléctrica, Electrónica y Computación, Facultad de Ingeniería y Arquitectura, Universidad Nacional de Colombia. Cra. 27 # 64-60. A. A. 127. Manizales, Colombia.

²Grupo de Automática, Electrónica y Ciencias Computacionales, Facultad de Ingenierías, Instituto Tecnológico Metropolitano. Calle 73 # 76A - 354 Vía al Volador. C. P. 050013. Medellín, Colombia.

³Centro de Investigación en Ingeniería Biomédica, Universidad Politécnica de Cataluña. Edifici U. c/ Pau Gargallo, 5. C. P. 08028. Barcelona, España.

* Corresponding author: Jorge Alberto Jaramillo Garzón, e-mail: jajaramillog@gmail.com

DOI: 10.17533/udea.redin.n79a03

(Received May 30, 2015; accepted January 26, 2016)

ABSTRACT

Gene Ontology (GO) is one of the most important resources in bioinformatics, aiming to provide a unified framework for the biological annotation of genes and proteins across all species. Predicting GO terms is an essential task for bioinformatics, but the number of available labelled proteins is in several cases insufficient for training reliable machine learning classifiers. Semi-supervised learning methods arise as a powerful solution that explodes the information contained in unlabelled data in order to improve the estimations of traditional supervised approaches. However, semi-supervised learning methods have to make strong assumptions about the nature of the training data and thus, the performance of the predictor is highly dependent on these assumptions. This paper presents an analysis of the applicability of semi-supervised learning assumptions over the specific task of GO terms prediction, focused on providing judgment elements that allow choosing the most suitable tools for specific GO terms. The results show that semi-supervised approaches significantly outperform the traditional supervised methods and that the highest performances are reached when applying the cluster assumption. Besides, it is experimentally demonstrated that cluster and manifold assumptions are complementary to each other and an analysis of which GO terms can be more prone to be correctly predicted with each assumption, is provided.

Keywords: Semi-supervised learning, gene ontology, support vector machines, protein function prediction

RESUMEN

La Ontología Genética (GO) es uno de los recursos más importantes en la bioinformática, el cual busca proporcionar un marco de trabajo unificado para la anotación biológica de genes y proteínas de todas las especies. La predicción de términos GO es una tarea esencial en bioinformática, pero el número de secuencias etiquetadas que se encuentran disponibles es insuficiente en muchos casos para entrenar sistemas confiables de aprendizaje de máquina. El aprendizaje semi-supervisado aparece entonces como una poderosa solución que explota la información contenida en los datos no etiquetados, con el fin de mejorar las estimaciones de las aplicaciones supervisadas tradicionales. Sin embargo, los métodos semi-supervisados deben hacer suposiciones fuertes sobre la naturaleza de los datos de entrenamiento y, por lo tanto, el desempeño de los predictores es altamente dependiente de estas suposiciones. En este artículo se presenta un análisis de la aplicabilidad de las diferentes suposiciones del aprendizaje semi-supervisado en la tarea específica de predicción de términos GO, con el fin de proveer elementos de juicio que permitan escoger las herramientas más adecuadas para términos GO específicos. Los resultados muestran que los métodos semi-supervisados superan significativamente a los métodos tradicionales supervisados y que los desempeños más altos son alcanzados cuando se implementa la suposición de cluster. Además se comprueba experimentalmente que las suposiciones de cluster y manifold son complementarias entre sí y se realiza un análisis de cuáles términos GO pueden ser más susceptibles de ser correctamente predichos usando cada una de éstas.

Palabras clave: Aprendizaje semi-supervisado, ontología a genética, máquinas de vectores de soporte, predicción de funciones proteicas

1. Introduction

Proteins are essential for living organisms due to the diversity of molecular functions they perform, which are also related to processes at cellular and phenotypical levels. At molecular level, for instance, binding proteins are capable of creating a wide variety of structurally and chemically deferent surfaces, allowing for recognizing other molecules and performing regulation functions; enzymes use binding plus specific chemical reactivity for speeding up molecular reactions; structural proteins constitute some of the main morphological components of living organisms, building resistant structures and being sources of biomaterials. At the cellular level, proteins perform the majority of functions of the organelles. Structural proteins in the cytoskeleton are responsible for maintaining the shape of the cell and keeping organelles in place; in the endoplasmatic reticulum, binding proteins transport molecules between and within cells; in the lysosome, catalytic proteins break large molecules into small ones for carrying out digestion (for a deeper description of subcellular locations of proteins, see [1]). Phenotypical roles of proteins are harder to determine, since phenotype is the result of many cellular function assemblies and their response under environmental stimuli. However, by the comparison of genes descended from the same ancestor across many different organisms, or by studying the effects of modifying individual genes in model organisms, several thousands of gene products have been associated with phenotypes [2].

The Gene Ontology (GO) project aims to cover the whole universe of protein functions by constructing controlled and structured vocabularies known as ontologies, and applying them in the annotation of gene products in biological databases [3]. The project comprises three ontologies: Molecular function (biochemical activities at the molecular level), cellular component (specific sub-cellular location where a gene product is active) and biological process (events at phenotypical level to which the protein contributes). Recent methods for predicting GO terms employ machine learning techniques trained over physical-chemical and statistical attributes for predicting functional labels that later can be subjected to experimental verification [4]. However, the succesfullness of supervised machine learning strategies relies on the amount and quality of a labelled set of instances needed to train the classifier. Labelled instances are often difficult, expensive, or time consuming to obtain, as they require the e orts of experienced human annotators. Meanwhile unlabelled data may be relatively easy to collect, but there has been few ways to use them [5]. In the particular case of protein function prediction, it is also a known fact that only a small number of proteins have actually been annotated for certain functions. Therefore, it is di cult to obtain sufficient training data for the supervised learning algorithms and, consequently, the tools for protein function prediction have very limited scopes [6]. Besides, it is particularly hard to find the representative negative samples because the available information in the annotation databases, such as GO [3], only provides information about which protein belongs to which functional class but there is no certainty about which protein does not belong to the class [7]. Under such circumstances, semi-supervised learning methods provide an alternative approach to protein annotation [6]. Semi-supervised learning (SSL) is halfway between supervised and unsupervised learning: in addition to labelled data, the algorithm is provided with an amount of unlabelled samples that can be used to improve the estimations.

One significant difference between supervised and semi-supervised methods is that, unlike supervised learning, in which a good generic learning algorithm can perform well on a lot of real-world data sets without specific domain knowledge, in semi-supervised learning it is commonly accepted that there is no ''black box'' solution and a good understanding of the nature of the data is required to achieve successful performance [8]. There are several different semi-supervised learning methods and all of them have to make strong assumptions about the relation of the probability of the feature space and the joint probability of the feature space and the label set. These methods include generative models, graph-based models, semi-supervised support vector machines, and soon [9].

A few semi-supervised methods have been applied for both gene function prediction (over the DNA sequence) and protein function prediction (over the amino acids sequence). [10] used a S³VMs for promoter recognition, improving predictive performance by 55% over the standard inductive SVM results. [11] used a ''co-updating'' schema of two SVMs, each one trained over a different source of data, for discriminating among five functional classes in the yeast genome. For the problem of predicting the functional properties of proteins, [12] conducted an extensive study on the caveats of incorporating semi-supervised learning and transduction for predicting various functional properties of proteins corresponding to genes in the yeast genome, founding that S³VMs significantly decrease performance compared to inductive SVMs. [13] used graph-based semi-supervised learning for functional class prediction of yeast proteins, using protein interaction networks for obtaining the graphs.

More recently, [14] proposes a generative semi-supervised method for protein functional classification and provide experimental results of classifying a set of eukaryotic proteins into seven subcellular locations from the Cellular Component ontology of GO. [6] proposed a new algorithm to de ne the negative samples in protein function prediction. In detail, the one-class SVMs and two-class SVMs are used as the core learning algorithm in order to identify the representative negative samples so that the positive samples hidden in the unlabelled data can be recovered. [15] proposes a method for integrating multiple graphs within a framework of semi-supervised learning and applies the method to the task of protein functional class prediction in yeast. The proposed method performs significantly better than the same algorithm trained on any single graph.

In [16], we presented the prediction of protein sub-cellular localizations with a semi-supervised support vector machine over a database of over 108 Embryophiyta plants, showing that semi-supervised learning significantly outperforms the supervised learning approach in several cases. However, since only one semi-supervised assumption was employed, those results could be subjected to further improvement when several assumptions are considered. Moreover, our previous work only considered the molecular function ontology and, if the other two ontologies are included, the high diversity of data may need diverse tools to be accurately classified.

The present work expands our previous results, presenting an analysis of the applicability of semi-supervised learning assumptions over the three ontologies of Gene Ontology: molecular function, cellular component and biological process. The analysis aims to demonstrate that one semi-supervised assumption is insufficient to classify the whole set of Gene Ontology terms and to provide judgment elements that allow choosing the most suitable tool for protein function prediction among the existing semi-supervised alternatives. The results show that semi-supervised approaches significantly outperform the traditional supervised methods and that the highest performances are reached when applying the cluster assumption. Besides, it is experimentally demonstrated that cluster and manifold assumptions are complimentary to each other and an analysis of which GO terms can be more prone to be correctly predicted with each assumption, is provided.

2. Theoretical background

The main assumption made by semi-supervised learning algorithms is the ''semi-supervised smoothness assumption'' [8].

- Semi-supervised smoothness assumption: If two points x₁,and x₂ in a high-density region are close, then so should be their corresponding label sets y₁, y₂. Note that by transitivity, this assumption implies that if two points are linked by a path of high density (e.g., if they belong to the same cluster), then their outputs are likely to be close. If, on the other hand, they are separated by a low-density region, then their outputs need not be close.

Such assumption originates the two common assumptions used in semi-supervised learning:

- Cluster assumption: If points are in the same cluster, they are likely to be of the same class. This assumption does not imply that each class forms a single, compact cluster, it only means that there are no instances of two distinct classes in the same cluster. The cluster assumption can be formulated in an equivalent way:

- Low density separation: The decision boundary should lie in a low-density region.

- Manifold assumption: The (high-dimensional) data lie (roughly) on a low-dimensional manifold. Instances that are close according to the manifold geodesic distance are likely to be of the same class.

According to each assumption, there are three main families of semi-supervised methods: generative methods (cluster assumption), density-based methods (low density separation), and graph-based methods (manifold assumption). In the following sub-sections, each family of methods will be reviewed, emphasizing on the assumptions made by each one. It should be pointed out that, since semi-supervised learning is a rapidly evolving field, the review is necessarily incomplete. A wider review in this matter can also be found on [9].

2.1. Generative methods

Generative methods follow a common strategy of augmenting the set of labelled samples with a large set of unlabelled data and combining the two sets with the Expectation-Maximization algorithm, in order to improve the parameter estimates [17]. They assume a probabilistic model p(x, y) = p( y) p(x | y), where p(x | y)is an identifiable mixture distribution. The most commonly employed distributions are the Gaussian Mixture Models shown in Eq. (1).

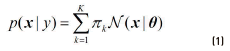
where 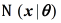is the Gaussian distribution with parameters 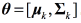, being 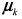the mean vector and Σ_k the covariance matrix of the k −th Gaussian component, and π_k the mixing components such that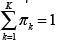for k = 1,2,…,K.

Ideally, only one labelled example per component is needed to fully determine the mixture distribution. In this setting, any additional information on p(x) is useful and the EM algorithm can be used for estimating 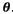A strength of the generative approach is that knowledge of the structure of the problem or the data can naturally be incorporated by modelling it [8]. However, generative techniques provide an estimate of p(x)along the way, although this is not required for classification, and in general this proves wasteful given limited data. For example, maximizing the joint likelihood of a finite sample need not lead to a small classification error, because depending on the model, it may be possible to increase the likelihood more by improving the t of p(x) than the t of 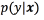[8].

The works of [18, 19], among others, showed to be strong methods for classifying text data. Furthermore, [20] have applied the EM algorithm on mixture of multinomial for the task of text classification, showing better performance than those trained only from the supervised set. [21] extend generative mixture models by including a ''bias correction'' term and discriminative training using the maximum entropy principle. However, anecdotal evidence is that many more studies were not published because they obtained negative results, showing that learning a mixture model will often degrade the performance of a model fit using only the labelled data [22]; one published study with these conclusions is [18]. This is due to the strong assumption done by generative methods: the data actually comes from the mixture model, where the number of components, prior p(x), and conditional p(x | y) are all correct [9].

2.2. Density-based methods

With the rising popularity of support vector machines (SVMs), Semi-Supervised SVMs (S³VMs) emerged as an extension to standard SVMs for semi-supervised learning. S³VMs find a labelling for all the unlabelled data, and a separating hyperplane, such that maximum margin is achieved on both the labelled data and the (now labelled) unlabelled data. As a result, unlabelled data guide the decision boundary away from dense regions. The assumption of S³VMs is that the classes are well-separated, such that the decision boundary falls into a low density region in the feature space, and does not cut through dense unlabelled data [9].

In a similar way to the conventional SVMs, the optimization problem for an S³VMs can be stated as follows shown in Eq. (2).

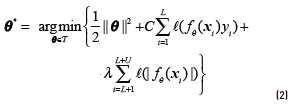
where ℓ(t) = max(0,1 − t ) is the hinge loss function, C is the trade-o parameter and λ is a new regularization parameter. The first two terms in the above equation correspond to the traditional solution for the standard supervised SVM, while the last term puts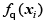of the unlabelled points x_i away from 0 (thereby implementing the low density assumption) [24].

Again, as in the supervised case, the kernel trick can be used for constructing nonlinear S³VMs. While the optimization in SVM is convex and can be solved with QP-hard complexity, optimization in S³VM is a non-convex combinatorial task with NP-Hard complexity. Most of the recent work in S³VM has been focused on the optimization procedure (a full survey in this matter can be found in [24]). Among the proposed methods for solving the non-convex optimization problem associated with S³VMs, one of the first implementations is the S³VM^light by [25], which is based on local combinatorial search guided by a label switching procedure. [26] presented a method based on gradient descent on the primal, that performs significantly better than the optimization strategy pursued in S³VM^light; the work by [22] proposes the use of a global optimization technique known as ''continuation'', often leading to lower test errors than other optimization algorithms; [27] uses the Concave-Convex procedure, providing a highly scalable algorithm in the non-linear case.

Other recent proposals include [28] which focuses on the class-imbalance problem and proposes a cost-sensitive S³VM; [29] which describes Laplacian twin support vector machines; and several approaches to adaptive regularizations like [30, 31].

2.3. Graph-based methods

Graph-based methods start with a graph where the nodes are the labelled and unlabelled data points, and (weighted) edges reflect the similarity of nodes. The assumption is that nodes connected by a large-weight edge tend to have the same label, and labels can propagate throughout the graph. In other words, graph-based methods do the assumption that labels are smooth with respect to the graph, such that they vary slowly on the graph. That is, if two instances are connected by a strong edge, their labels tend to be the same [9].

This family of methods enjoy nice properties from spectral graph theory. They commonly use an energy function as objective in the optimization problem, ensuring that the labels will change slowly through the graph (consequently implementing the manifold assumption) [32].

A graph is represented by the (L + U) × (L + U) weight matrix W, W_ij = 0 if there is no edge between instances x_i and x_j. Once the graph has been defined, a real function over the nodes can be defined 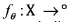. In order to achieve that unlabelled points that are similar (as determined by the edges of the graph) to have similar labels, the quadratic energy function shown in Eq. (3) can be used as objective:

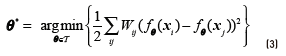
Since this objective function is minimized by constant functions, it is necessary to constrain f_θto take values f_θ (x_i) = y_i , for all the labelled data x_i ∈X_L. Finally, let D be the diagonal degree matrix, where 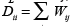is the degree of node x_i. The combinatorial Laplacian ∆ is defined as in Eq. (4).

and it is easy to verify Eq. (5):

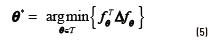
Most graph-based methods are inherently transductive, giving predictions for only those points in the unlabelled set, and not for an arbitrary test point. The simplest strategy for extending the method for unseen data is by dividing the input space into Voronoi cells centered on the labelled instances. From an algorithmic point of view, this strategy is equal to classify instances by its 1-nearest-neighbour. [21] proposed an approach that combines generative mixture models and discriminative regularization using the graph Laplacian in order to provide an inductive model. Laplacian SVMs, proposed by [33], provide a natural inductive algorithm since they use a modified SVM for classification. The optimization problem in this case is regularized by the introduction of a term for controlling the complexity of the model according to Eq. (6):

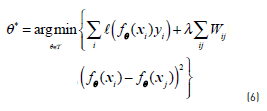
where W_ij is the weight between the i − th andj − th instances in the graph and λ is again a regularization parameter. A lot of experiments show that Laplacian SVM achieves state of the art performance in graph-based semi-supervised classification [29].

3. Proposed methodology: semi-supervised learning for predicting gene ontology terms in Embryophyta plants

3.1. Selected semi-supervised algorithms

In order to test the efficiency of semi-supervised learning in the task of predicting protein functions, two state of the art methods were chosen, each one implementing a different semi-supervised assumption: S³VM following the concave-convex optimization procedure (CCP) [27] (implementing the low-density separation assumption and consequently the cluster assumption) and Laplacian-SVM [34] (implementing the manifold assumption).

- CCP S³VM: The S³VM proposed by [27, 34] was chosen since it provides high scalability in the non-linear case, making it the most suitable choice for the amounts of Embryophyta proteins in the databases used in this work. Consider the set of labelled points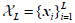 for which labels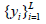are provided, and the points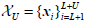the labels of which are not known. The objective function to be optimized in this case, corresponds to Eq. (7):

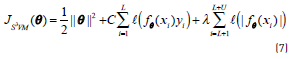
where the function ℓ(t) = max(0,1−|t|) is the hinge loss function. The main problem with this objective function, in contrast to the classical SVM objective, is that the additional term is non-convex and gives rise to local minima. Additionally, it has been experimentally observed that the objective function tends to give unbalanced solutions, classifying all the unlabelled points in the same class. A constraint should be imposed on the data to avoid this problem [26], as shown in Eq. (8):

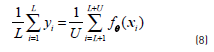
which ensures that the number of unlabelled samples assigned to each class will be the same fraction as in the labelled data. CCP decomposes a non-convex function J into a convex component J_vex and a concave component J_cave. At each iteration, the concave part is replaced by the tangential approximation at the current point and the sum of this linear function and the convex part is minimized to get the next iterate. The first two terms in Eq. (7) are convex, while the third term can be decomposed into the sum of a convex function (Eq. 9) plus a concave one (Eq. 10):

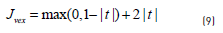
If an unlabelled point is currently classified positive, then at the next iteration, the convex loss on this point will be determined by Eq. (11):

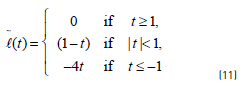
The CCP algorithm for the semi-supervised support vector machines is presented in Algorithm 1 (Table 1).

- Laplacian SVM: Regarding the graph-based algorithms, Laplacian support vector machines (Lap-SVM) were chosen since, according to [29], many experiments show that Lap-SVM achieves state of the art performance among graph-based semi-supervised classification methods. This method, as proposed in [33], uses an objective function that is slightly different to Eq. (6) and can be seen in Eq. (12):

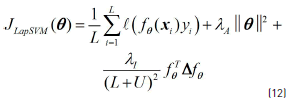
where λ_A and λ_I are two regularizing constants that must be set by the user. [32], also demonstrated a modified version of the Representer Theorem that ensures that the solution function can be given again by linear combination of kernel functions and the Lap-SVMs can be implemented by using a standard SVM quadratic solver.

The S³VM and Lap-SVM were used as base classifiers, both of them with the Gaussian kernel. For the Lap-SVM, the K-NN graph was selected for implementing the manifold regularization term, since there is some empirical evidence that suggests that fully connect graphs performs worse than sparse graphs [9].

All the parameters of the algorithms, including the dispersion of the kernels, the trade-o parameters of the SVMs, the regularization constants of both methods and the number of neighbours for constructing the graph, were tuned with a particle swarm optimization meta-heuristic. The decision making was implemented following the one against-all strategy with SMOTE oversampling for avoiding class-imbalance. Also, the 5-fold cross-validation strategy was implemented for assessing the performance of the predictors.

3.2. Database

The database designed in [4] was used as the set of labeled instances. This database is conformed by all the available Embryophyta proteins at UniProtKB/Swiss-Prot database [35] (file version: 10/01/2013), with at least one annotation in the Gene Ontology Annotation (GOA) project [36] (file version: 7/01/2013). In order to avoid the presence of protein families that could bias the results, the dataset was filtered at several 30% of sequence identity using the Cd-Hit software [37]. The set of labelled instances is then conformed by 3368 protein sequences, from which 1973 sequences are annotated with molecular functions, 2210 with cellular components and 2798 with biological processes [4].

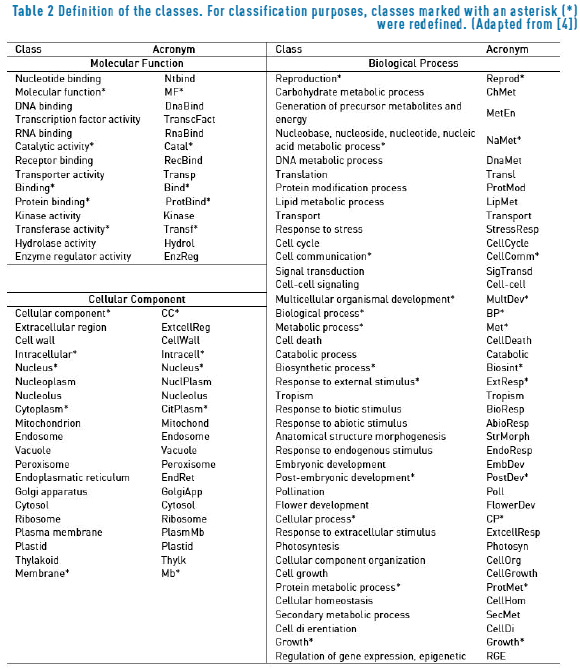
Classes are defined by the plants GO slim developed by The Arabidopsis Information Resource - TAIR [38], (file version: 14/03/2012). Positive samples associated to each GO term are selected by considering the propagation principle of GO: if a protein is predicted to be associated to any given GO term, it must be automatically associated to all the ancestors of that category and thus, it is enough to predict only the lowest level entries. As in [4], in order to explicitly note that some GO terms are not including their descendants categories, such incomplete GO terms are marked with an asterisk throughout the paper. The resulting set comprises 14 GO terms in the molecular function ontology, 20 GO terms in the cellular component ontology and 41 GO terms in the biological process ontology. Table 2 shows the final list of categories, as well as the acronyms used to cite them throughout this paper.

Regarding unlabeled instances, all the available Embryophyta proteins at UniProtKB/SwissProt database that has no entries in the GOA project were added as the core set of unlabeled samples. Also, proteins associated to the nodes in the functional path of a GO term that were not associated to the node itself, were left as unlabeled instances regarding that classifier. Finally, 30000 unlabeled instances were randomly chosen in order to accomplish an approximate relation of ten unlabeled instances per each labeled one.

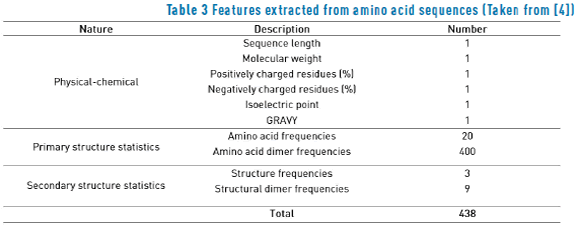
Both labeled and unlabeled sequences were characterized according to the procedure described in section [4] obtaining three types of attributes: physical-chemical features, primary structure composition statistics and secondary structure composition statistics (see Table 3).

4. Results and discussion

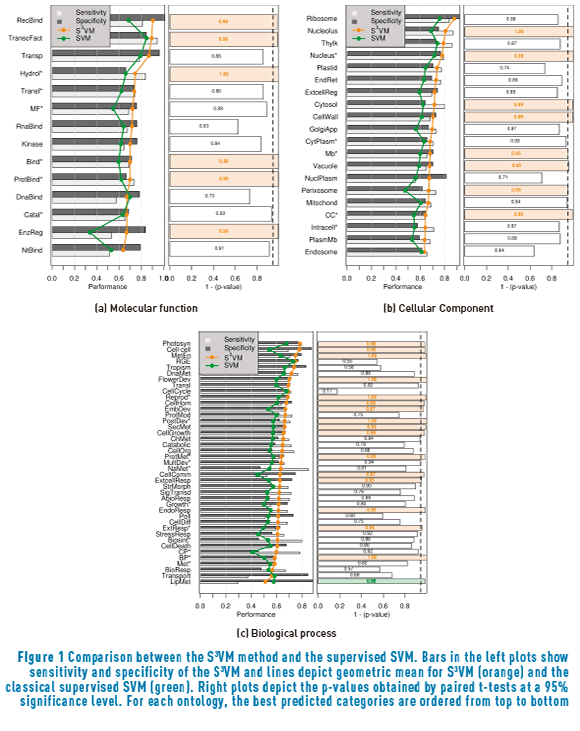
Figure 1 shows a comparison between the results with the S³VM (orange line) and the SVM method presented in [4] (green line). Classes are ordered according to the performance of the SS³VM method from top to bottom. Left plots show sensitivity, specificity and geometric mean achieved with the five-fold cross-validation procedure, while right plots depicts the corresponding p-values obtained from a paired t-test at a 95% significance level. Orange bars show the cases when the S³VM significantly outperforms the supervised SVM and green bars show the opposite case.

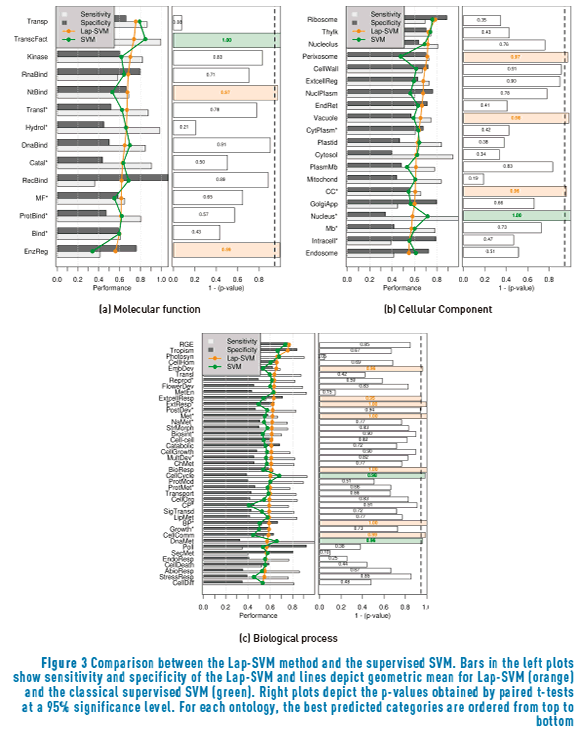
The main purpose of this comparison is to verify whether or not the inclusion of the additional cluster-based semi-supervised term in the training of the SVM improves the performance of the system, thus providing information about the accomplishment of the cluster assumption when the unlabelled data is incorporated to the training process. Figure 1(a) shows that six out of the fourteen molecular functions considered in this ontology were significantly improved. In particular, Receptor binding, Transcription factor activity and Enzyme regulator activity have a special importance, considering that the SVM method was outperformed by BLASTp in those three GO terms when using the supervised model (see [4]). The inclusion of the cluster assumption also improved the performance on Hydrolase activity*, Binding* and Protein binding*. Regarding the Cellular Component ontology (Figure 1(b)), eight cellular components were significantly improved, while other two (Mitochondria and Cytoplasm*) also reached high p-values over 0.9. Finally, sixteen biological processes presented statistically significant improvements when including the unlabelled data with the semi-supervised cluster assumption. Only one biological process, Lipid metabolic process, suffered a statistically significant deterioration, which indicates that the unlabelled data is presenting a misleading cluster structure regarding this GO term.

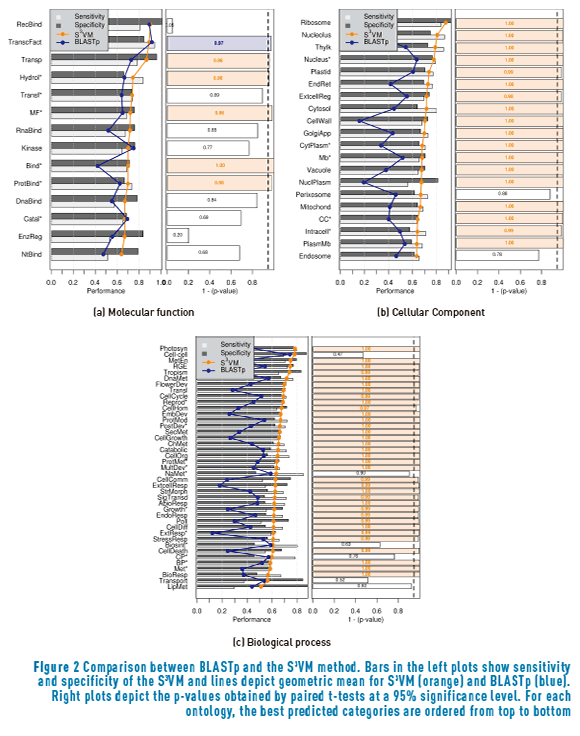
In order to analyse how this improvements affect the system when compared to conventionally used prediction tools, Figure 2 shows a comparison between the results with the S³VM (orange line) and the traditional BLASTp method (blue line). It can be seen from figure 2(a) that the S³VM significantly outperforms BLASTp in five molecular functions, while BLASTp remains better than the S³VM only for Transcription factor activity.

Regarding the cellular component ontology, there are only two cellular components for which there is no statistically significant difference between BLASTp and the S³VM: Perixosome and Endosome. For all the remaining eighteen cellular components, the semi-supervised method obtained superior performance. A similar behaviour is shown at figure 2(c), where the S³VM significantly outperforms BLASTp in 35 out of the 41 biological processes, while the remaining six process showed no statistical difference between the methods.

On the other hand, Figure 3 shows the comparison between the supervised SVM and the Laplacian-SVM. This analysis provides information about the impact of incorporating unlabelled data on the training set but, this time, by implementing the semi-supervised manifold assumption. This time, it is possible to see that there are less GO terms that have been improved by the inclusion of the unlabelled data. For the molecular function ontology (Figure 3(a)), only the Nucleotide binding and Enzyme regulator activity GO terms were significantly improved respecting the supervised SVM; in turn the implementation of the manifold assumption significantly degraded the performance for the GO term Transcription factor activity. Regarding the cellular component ontology (Figure 3(b)), improvements are present for Perixosome, Vacuole and the root node of the ontology, while a decrease is evinced for the Nucleus* GO term. As for the biological process ontology, seven GO terms enhanced their prediction performance (Embryonic development, Response to extracellular stimulus, Response to external stimulus*, Metabolic process*, Response to biotic stimulus, Cell communication and the root node of the ontology), while other two were worsened (Cell cycle and DNA metabolic process).

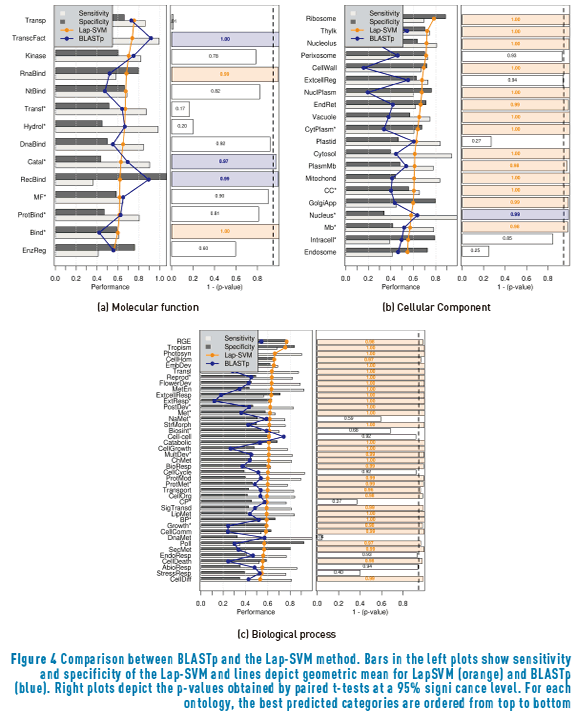
Figure 4 depicts a comparison between the results obtained with BLASTp and the LapSVM method. The first important result that can be inferred from the present analysis is that, in general terms, for the problem of protein function prediction, the semi-supervised cluster assumption holds for many more cases than the semi-supervised manifold assumption. However, the most important aspect to be analyzed here, is how the results in Figure 4 complement the results from Figure 2. Only two molecular functions presented an statistically significant superior performance with the Lap-SVM over BLASTp. One of them, RNA binding, did not show statistical significance when comparing BLASTp and S³VM. The same behaviour is present for the Perixosome cellular component and for the biological processes Transport and Lipid metabolic process. These results indicate that the manifold assumption is best suited than the cluster assumption for this particular GO terms. A few GO terms were not improved by any of the assumptions.

5. Conclusions

In this paper, an analysis of the suitability of semi-supervised methods for the prediction of protein functions in Embryophyta plants was performed. A review of the state of the art of semi-supervised classifiers was presented, highlighting the different assumptions that each method does about the underlying distribution of the data. Two semi-supervised methods were chosen to perform the tests, each representing one of the main semi-supervised assumptions: cluster assumption and manifold assumption. The results show that semi-supervised learning applied to the prediction of GO terms in Embryophyta organisms, significantly outperforms the supervised learning approach, at the same time outperforming the commonly used sequence alignment strategy in most cases. In general terms, the highest performance were reached when applying the cluster assumption. However, several GO terms that were not significantly improved with the cluster assumption, achieved higher performance with the manifold based semi-supervised method, demonstrating that a single assumption is not enough for improving the learning process by the exploitation of the additional unlabelled data. As future work, it is desirable to implement a unified strategy exploiting both assumptions at the same time, in order to achieve high performances in most applications. Also, classifiers devoted to hierarchical classification, such as decision trees, could be used to improve classification performance.

6. References

1. K. Chou and H. Shen, ''Recent progress in protein subcellular location prediction'', Analytical Biochemistry, vol. 370, no. 1, pp. 1-16, 2007.         [ Links ]

2. P. Benfey and T. Mitchell, ''From Genotype to Phenotype: Systems Biology Meets Natural Variation'', Science, vol. 320, no. 5875, pp. 495-497, 2008.         [ Links ]

3. M. Harris et al., ''The gene ontology (GO) database and informatics resource'', Nucleic Acids Res., vol. 32, pp. 258-261, 2004.         [ Links ]

4. J. Jaramillo, J. Gallardo, C. Castellanos and A. Perera, ''Predictability of gene ontology slim-terms from primary structure information in Embryophyta plant proteins'', BMC Bioinformatics, vol. 14, no. 68, pp. 1-11, 2013.         [ Links ]

5. X. Zhu, ''Semi-Supervised Learning Literature Survey'', University of Wisconsin–Madison, Madison, USA, Tech. Rep. TR-1530, Jul. 2008.         [ Links ]

6. X. Zhao, L. Chen and K. Aihara, ''Protein function prediction with high-throughput data'', Amino Acids, vol. 35, no. 3, pp. 517-530, 2008.         [ Links ]

7. X. Zhao, Y. Wang, L. Chen and K. Aihara, ''Gene function prediction using labeled and unlabeled data'', BMC Bioinformatics, vol. 9, no. 57, pp. 1-14, 2008.         [ Links ]

8. O. Chapelle, B. Schölkopf and A. Zien, Semi-supervised learning, 1^st ed. Cambridge, USA: MIT Press, 2006.         [ Links ]

9. X. Zhu and A. Goldberg, Introduction to semi-supervised learning, 1^st ed. Madison, USA: Morgan & Claypool, 2009.         [ Links ]

10. N. Kasabov and S. Pang, ''Transductive support vector machines and applications in bioinformatics for promoter recognition'', in Int. Conf. on Neural Networks and Signal Processing, Nanjing, China, 2003, pp. 1-6.         [ Links ]

11. T. Li, S. Zhu, Q. Li and M. Ogihara, ''Gene functional classification by semisupervised learning from heterogeneous data'', in ACM Symposium on Applied Computing (SAC), Melbourne, USA, 2003, pp. 78-82.         [ Links ]

12. M. Krogel and T. Scheffer, ''Multi-relational learning, text mining, and semisupervised learning for functional genomics'', Machine Learning, vol. 57, no. 1, pp. 61-81, 2004.         [ Links ]

13. H. Shin and K. Tsuda, ''Prediction of protein function from networks'', in Semi-supervised learning, 1^st ed., O. Chapelle, B. Schölkopf and A. Zien (eds). Cambridge, USA: MIT Press, 2006, pp. 339-352.         [ Links ]

14. B. King and C. Guda, ''Semi-supervised learning for classification of protein sequence data'', Scientific Programming, vol. 16, no. 1, pp. 5-29, 2008.         [ Links ]

15. H. Shin, K. Tsuda and B. Scholkopf, ''Protein functional class prediction with a combined graph'', Expert Systems with Applications, vol. 36, no. 2, pp. 3284-3292, 2009.         [ Links ]

16. J. Jaramillo and C. Castellanos, ''Improving protein sub-cellular localization prediction through semi-supervised learning'', in BIOTECHNO: 6^th International Conference on Bioinformatics, Biocomputational Systems and Biotechnologies, Chamonix, France, 2014, pp. 99-103.         [ Links ]

17. F. Cozman, I. Cohen and M. Cirelo, ''Semi-supervised learning of mixture models'', in 20^th International Conference on Machine Learning (ICML), Washington D.C., USA, 2003, pp. 99-106.         [ Links ]

18. D. Miller and H. Uyar, ''A generalized gaussian mixture classifier with learning based on both labelled and unlabelled data'', in Conference on Information Science and Systems, Princeton, USA, 1996, pp. 783-787.         [ Links ]

19. G. McLachlan and T. Krishnan, The EM algorithm and extensions, 2^nd ed. St. Lucia, Australia: John Wiley & Sons, 2007.         [ Links ]

20. K. Nigam, A. McCallum, S. Thrun and T. Mitchell, ''Text classification from labeled and unlabeled documents using EM'', Machine learning, vol. 39, no. 2, pp. 103-134, 2000.         [ Links ]

21. A. Fujino, N. Ueda and K. Saito, ''A hybrid generative/discriminative approach to semi-supervised classifier design'', in 20^th National Conference on Artificial Intelligence (AAAI), Pittsburgh, USA, 2005, pp. 764-769.         [ Links ]

22. X. Zhu and J. Lafferty, ''Harmonic mixtures: combining mixture models and graph-based methods for inductive and scalable semi-supervised learning'', in 22^nd International Conference on Machine Learning (ICML), Bonn, Germany, 2005, pp. 1052-1059.         [ Links ]

23. O. Chapelle, M. Chi and A. Zien, ''A continuation method for semi-supervised SVMs'', in 23^rd international conference on Machine learning (ICML), Pittsburgh, USA, 2006, pp. 185-192.         [ Links ]

24. O. Chapelle, V. Sindhwani and S. Keerthi, ''Optimization techniques for semi-supervised support vector machines'', Journal of Machine Learning Research, vol. 9, pp. 203-233, 2008.         [ Links ]

25. T. Joachims, ''Transductive inference for text classification using support vector machines'', in 16^th International Conference on Machine Learning (ICML), Bled, Slovenia, 1999, pp. 200-209.         [ Links ]

26. O. Chapelle and A. Zien, ''Semi-supervised classification by low density separation'', in 10^th Int. Workshop on Artificial Intelligence and Statistics (AISTATS), Bridgetown, Barbados, 2005, pp. 57-64.         [ Links ]

27. R. Collobert, F. Sinz, J. Weston and L. Bottou, ''Large scale transductive SVMs'', Journal of Machine Learning Research, vol. 7, pp. 1687-1712, 2006.         [ Links ]

28. Y. Li, J. Kwok and Z. Zhou, ''Cost-Sensitive Semi-Supervised Support Vector Machine'', in 24^th Conference on Artificial Intelligence (AAAI), Atlanta, USA, 2010, pp. 500-505.         [ Links ]

29. Z. Qi, Y. Tian and Y. Shi, ''Laplacian twin support vector machine for semi-supervised classification'', Neural networks, vol. 35, pp. 46-53, 2012.         [ Links ]

30. Z. Xu et al., ''Adaptive regularization for transductive support vector machine'', in Advances in Neural Information Processing Systems 22 (NIPS), Vancouver, Canada, 2009, pp. 2125-2133.         [ Links ]

31. Z. Wang, S. Yan and C. Zhang, ''Active learning with adaptive regularization'', Pattern Recognition, vol. 44, no. 10-11, pp. 2375-2383, 2011.         [ Links ]

32. M. Hein, J. Audibert and U. Luxburg, ''From graphs to manifolds-weak and strong pointwise consistency of graph Laplacians'', in 18^th Annual Conference on Learning Theory (COLT), Bertinoro, Italy, 2005, pp. 470-485.         [ Links ]

33. M. Belkin, P. Niyogi and V. Sindhwani, ''Manifold regularization: A geometric framework for learning from labeled and unlabeled examples'', Journal of Machine Learning Research, vol. 7, pp. 2399-2434, 2006.         [ Links ]

34. F. Sinz, O. Chapelle, A. Agarwal and B. Schölkopf, ''An analysis of inference with the universum'', in Conference on Advances in Neural Information Processing Systems 20 (NIPS), Vancouver, Canada, 2007, pp. 1369-1376.         [ Links ]

35. E. Jain et al., ''Infrastructure for the life sciences: design and implementation of the UniProt website'', BMC Bioinformatics, vol. 10, no. 136, pp. 1-19, 2009.         [ Links ]

36. D. Barrell et al., ''The GOA database in 2009-an integrated Gene Ontology Annotation resource'', Nucleic Acids Research, vol. 37, pp. 396-403, 2009.         [ Links ]

37. W. Li and A. Godzik, ''Cd-hit: a fast program for clustering and comparing large sets of protein or nucleotide sequences'', Bioinformatics, vol. 22, no. 13, pp. 1658-1659, 2006.         [ Links ]

38. T. Berardini et al., ''Functional annotation of the Arabidopsis genome using controlled vocabularies'', vol. 135, no. 2, pp. 745-755, 2004.         [ Links ]