Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230
Rev.fac.ing.univ. Antioquia no.79 Medellín Apr./June 2016
https://doi.org/10.17533/udea.redin.n79a05
ARTÍCULO ORIGINAL
DOI: 10.17533/udea.redin.n79a05
A Markov random field image segmentation model for lizard spots
Modelo de segmentación de campos aleatorios de Markov para imágenes de manchas de lagarto
Alexander Gómez-Villa1, Germán Díez-Valencia1*, Augusto Enrique Salazar-Jimenez1,2
1Grupo de Sistemas Embebidos e Inteligencia Computacional (SISTEMIC), Facultad de Ingeniería, Universidad de Antioquia. Calle 67 # 53- 108. A. A. 1226. Medellín, Colombia.
2Grupo de Automática, Electrónica y Ciencias Computacionales (AEyCC), Facultad de Ingenierías, Instituto Tecnológico Metropolitano. Calle 54A # 30-01. C. P. 050013. Medellín, Colombia.
* Corresponding author: German Díez Valencia, e-mail: german.diez@udea.edu.co
DOI: 10.17533/udea.redin.n79a05
(Received June 1, 2015; accepted February 5, 2016)
ABSTRACT
Animal identification as a method for fauna study and conservation can be implemented using phenotypic appearance features such as spots, stripes or morphology. This procedure has the advantage that it does not harm study subjects. The visual identification of the subjects must be performed by a trained professional, who may need to inspect hundreds or thousands of images, a time-consuming task. In this work, several classical segmentation and preprocessing techniques, such as threshold, adaptive threshold, histogram equalization, and saturation correction are analyzed. Instead of the classical segmentation approach, herein we propose a Markov random field segmentation model for spots, which we test under ideal, standard and challenging acquisition conditions. As study subject, the Diploglossus millepunctatus lizard is used. The proposed method achieved a maximum efficiency of 84.87%.
Keywords: Belief propagation, Markov network, Graph Cuts, animal biometrics, Markov random field, Diploglossus millepunctatus
RESUMEN
La identificación de animales para estudio y conservación de la fauna puede ser realizada usando características de apariencia fenotípica como manchas, rayas o forma, teniendo la ventaja de que este enfoque no causa ningún daño al sujeto de estudio. Debido a que la identificación visual debe hacerse a través de la inspección, un experto revisa potencialmente cientos o miles de imágenes. En este trabajo se realiza un análisis con varios algoritmos clásicos de segmentación y preprocesamiento como: binarización, ecualización del histograma y corrección de la saturación. Contra los enfoques clásicos de segmentación, un modelo de segmentación basado en campos aleatorios de Markov para segmentación de manchas es propuesto y probado en imágenes ideales, estándares y desafiantes. Como sujeto de estudio es usado el lagarto Diploglossus millepunctatus. El método propuesto alcanzó una eficiencia máxima de 84,87%.
Palabras clave: Belief propagation, redes Markovianas, corte de grafos, biométrica animal, campos aleatorios de Markov, Diploglossus millepunctatus
1. Introduction
Animal biometrics has increased in recent years, since identifying individual animals and recognizing them at different places and time are important requirements in many biology tasks such as calculating animal population density, survival, analysis of a particular behavior and planning conservation measures [1, 2].
Animal identification strategies usually imply physical labeling using devices that could injure the animal, modify its behavior, or even change the survival possibilities [3]; also marking strategies are not suitable in large populations or extended periods of time.
Non-intrusive approaches include the identification of genetic markers in excrement [4] and Photographic Mark-Recapture (PMR) [5]. The PMR method is based on visual identification using phenotypic appearance features like spots, stripes or morphology. Those features must be stable over time, unique and photographed under different conditions. This method is a two-photo comparison of one target and hundreds of possible subjects to find similarity between patterns. For this reason, the identification of larger animal populations by a human observer is a time-consuming task and, furthermore, the subjectivity, skills or experience of the expert could affect the objectivity of the study [2].
Automatic biometric identification offers an alternative to save time and to provide robustness to the identification process. There are two possible scenarios for a computer vision perspective. First, photos taken in the wild as photo trap framework; this media is commonly cluttered, with low contrast, containing trees, shrubs, other subjects and the target in multiple poses [6]. Another approach is mark-recapture analysis, where the subject is photographed under controlled conditions and position. Additionally to the scenario, both cases present problems in natural appearance of skin, like shininess on reptiles, 3D shape, contamination produced by sand or environmental components, and scars.
Previous semi-automatic approximations include shapes for marine mammals [7-10] and elephants [6]; spots for Serengeti cheetahs [3], giraffes [5], turtles [11], seals [12] and stripes for tigers [1] and zebras [4] which a region of interest (ROI) is manually selected or cut and then, a segmentation is performed giving seeds to an adaptive shape algorithm as deformable shapes or active contours. Another technique avoids pattern segmentation and uses invariant point features such as SURF descriptors, Multi-scale PCA, Scale-Cascaded Alignment, Histogram, SIFT and affine invariant variations to make a direct matching [13].
Our subjects are endangered lizards, Diploglossus millepunctatus, from Malpelo Island (Colombia) [14]. These reptiles, present a unique spot pattern per subject, this pattern are currently studied using mark-based methods. The results achieved show that simple cost functions with Markov Random Fields (MRF) or MRF framework can perform the segmentation of these patterns in multiple illumination variations and under noisy conditions.
2. Related Work
Diploglossus millepunctatus spots do not have the same intensity values throughout the whole subject. This issue is most critical when high amounts of light irradiate the lizard and mask the spots in the illuminated regions. This scenario can be modeled with a MRF that can deal with uncertainty of pixel intensities that belong to a spot in a determinate region based on multiple soft criterions like local intensity, neighborhood relations and a broad number of patterns.
MRFs have been proven to be a suitable method to resolve computer vision tasks like image segmentation. [15] showed that with some seeds set by the user, objects can be segmented using hard constraints and histograms for object and background. In [16], the histograms of user seeds were replaced by Gaussian Mixture Models (GMM), one for background and one for foreground; and also a border matting algorithm was developed to fix transparency on segmented object edges. Another approach is [17], where a shape model was imposed through Layered Pictorial Structures to MRF, which favored specific trained shapes. The method in [18] does not need user interaction, it is based on color values form CIE-L*u*v* color space, and texture features from Gabor filtered images as data term with a GMM parameterized automatically with EM algorithm. In [19], the authors propose a multi-region segmentation method based on geometric interactions between objects that were previously segmented with user interaction or automatic framework.
Our approach uses mono-grid model-based segmentation that targets a specific object (lizard spots) in challenging scenarios. User interaction and previous training is not required. The model uses an appearance model based on RGB color space, gray-level image and smoothness constraints. Segmentation was tested under hard light contamination conditions, with noisy and blurry images, using three types of models and inference algorithms.
3. Methods
To show the insufficiency of classical segmentation methods and to prove the advantages our proposed model offers to cope with the before mentioned challenges, an analysis of lizard spots using several classical techniques was performed. On the basis of these analyses, and to solve the segmentation task, we propose and further explain a preprocessing methodology and a segmentation model based on energy. At the end of this section, three traditional approaches to solve the energy model are explained in more detail.
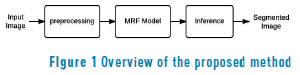
A Diagram of the proposed energy segmentation model is presented in Figure 1. The preprocessing step intends to highlight features, increases spots' contrast, and helps to enhance the model's score. The MRF model block extracts parameters from the input image to feed the mathematical model. Finally, the inference block solves the maximum a posteriori probability (MAP) problem of the MRF model and gives a mask with spots.
3.1. Preprocessing
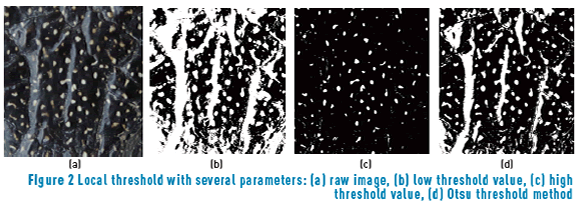
Non-uniform illumination and non-constant color of Diploglossus millepunctatus spots are essential objectives for preprocessing steps, since there is no unique threshold that can separate spots from foreground. A low value in binarization keeps all the spots, but also large amounts of light (Figure 2(b)). Moreover, a high threshold value (see Figure 2(c)) keeps the desired pattern without the presence of light but misses low-intensity spots. There is no prior knowledge about the optimal threshold value on every image. A common solution is Otsu's method, which assumes binarization as bi-class clustering problem and selects a threshold value that minimizes intra-class variation.
Histogram preprocessing techniques used to enhance contrast include histogram equalization and contrast correction. Histogram equalization is a global method that sparse the histogram of an image; however, this approximation does not produce good results (Figure 3(b)), because it masks the spots closest to brightness regions intensities. Then again, contrast correction is a point operation that enhances contrast multiplying intensities of a pixel by a fixed value between 1 and 3 and casting it to a value between 0 and 255. This causes a significant contrast enhancement in dark regions (Figure 3(c)), but gaps among spots and higher intensity regions remain unchanged. Global techniques as histogram equalization or point operations like contrast correction are strategies that use global statistics of an image or just modified pixel values with a constant; they do not observe local variation on contrast and assume equal distribution of intensities in an image.
Local operations like adaptive thresholding (AT) and contrast adaptive histogram equalization (CLAHE) observe a local window in each pixel and calculate the optimum threshold value or intensity to split histogram. Local algorithms depend on window selections and, since intensity, size and distribution of regions are random, windowing size has to vary throughout the image. Results using AT and CLAHE are exhibited in Figure 4(b) and 4(c), both presenting bad choices of correction values, caused by the fixed size of the observed window.
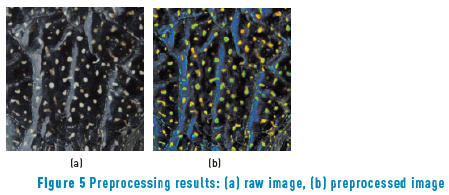
The final implementation must equalize light and let the color values constant to exploit spot color information. This reasoning is done using color spaces that convert RGB color space to representations independent of brightness: HSV, L*a*b* and HSI color spaces. Due to the equalization of aleatory light distribution, a CLAHE was applied after the RGB to L*a*b* conversion in the brightness channel on 3 different color spaces. After that, L*a*b* space showed a more uniform distribution. In order to separate spots from light regions, a saturation correction was implemented. This process highlights Red and Green channels and, hence, spots were turned brighter than the light regions (Figure 5(b)).
Figure 6 shows the final preprocessing method applied. First, CLAHE on the Luminance channel of L*a*b* space is applied, followed by a point operation (saturation correction) in HSI color space, and finally, the image is transformed to RGB space.
3.2. Model
Probabilistic image segmentation approaches try to calculate the probability of a pixel or number of pixels belonging to a certain feasible image class. These classes are modeled as a discrete random variable, taking values in L = {1, 2, .., S}, with S as the maximum number of feasible classes in the image. The set of these labels is a random field, called the label process [18]. Each pixel in the input image is assumed as a random variable Y, which could take a discrete value between 0 and 255. These values constitute the observations Z and are related to the hidden variables X, related to the labels L1and L2 , which correspond to the pixel label either as a spot or as a background. Each pixel is connected to a pixels neighborhood.
In this work, the random variables are related through energy functions that determine whether the pixel belongs to a determined class. The inference process is based on both, the individual values of the pixel or group of pixels and the neighborhood relations. These relations are computed using the cliques [20]. This graph topology allows the interaction of each pixel or group of pixels only with their closer neighborhood which is called a first order Markov blanket.
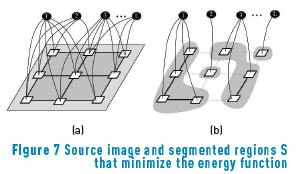
A desirable result of the segmentation process is to find a combination of segmented regions S from the group of all possible combinations of segmented pixels that minimizes the energy function used as the segmentation criteria as shown in Figure 7, based on [15].
There are different ways to define an energy function. One of them is to define an energy function (Eq. (1)) in terms of the disagreement between S and the observed data or Edata and the measurement of the smoothness or Esmooth
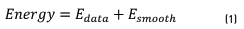
Election of energy functions is a difficult task because different elections in the Esmooth produce different results in final segmented image [21]. For example, in some regularization based approaches [22] Esmooth makes S smooth everywhere. This produces poor results at object boundaries.
The data term energy function could consider different factors as the interaction with the user, the shape or different characteristics of the target object [21]. In non-supervised object segmentation, the introduction of previously known information about the target object in the energy function as foreground specific intensity range of values or background-foreground contrast information could even improve the inference process.
In this work, three different energy functions were tested in order to properly represent the task to solve in the segmentation process. As each pixel in the image is taken as spot or as scale, each energy function is integrated by two terms: The term 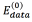 is aware of the membership of the pixel p in the neighborhood P to the class scale and the tern
is aware of the membership of the pixel p in the neighborhood P to the class scale and the tern 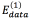 is aware of the membership of the pixel p to the class spot. In those energy functions IGp represents the grayscale intensity value of the pixel p, ILp represents the intensity value of the pixel p after applying a three-label discretization over the image (this discretization is aware of the visual difference between the scales and the spots, which have higher intensity values) and ICp represents the color properties of the spot highlighted in the preprocessing step. Eq. (2) is identified as Function 1, Eqs. (3) and (4) as Functions 2 and 3, respectively.
is aware of the membership of the pixel p to the class spot. In those energy functions IGp represents the grayscale intensity value of the pixel p, ILp represents the intensity value of the pixel p after applying a three-label discretization over the image (this discretization is aware of the visual difference between the scales and the spots, which have higher intensity values) and ICp represents the color properties of the spot highlighted in the preprocessing step. Eq. (2) is identified as Function 1, Eqs. (3) and (4) as Functions 2 and 3, respectively.
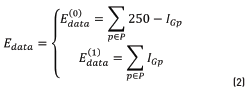
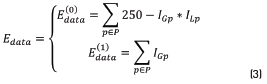
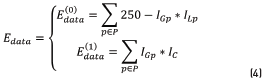
An interesting smooth term energy function is the Potts model, which is the simplest discontinuity preserving model. In this energy function model, discontinuities between any pair of labels are penalized equally and can be reduced to the multi-way minimization problem [15], which is known to be a NP-complete problem, where NP means non-deterministic polynomial time.
In principle, the graphical model of an image can answer different queries about the variables related to the model. Having a set of observations Z, any information about the variables implicit in the model ideally could be obtained based on a conditional probability distribution. Unfortunately, the process to obtain this information is a NP-hard problem even in simple Markov chains. Furthermore, there are loops inside the topology of the model [20] impeding the task of performing the inference process. In order to solve this task, this work uses three algorithms: graph cuts, loopy belief propagation, and dual decomposition; each algorithm has a different approximation to the solution and thus, they show differences in the final result.
The general idea of the graph cuts algorithm is to minimize the energy function through cuts in the probability flow of information inside the model. First, when the set L has cardinality of two, additional nodes called Sink and Source with connections to all nodes in the model, are added. The new graph must be divided or ''Cut'' in two parts, where each part contains one of the added nodes. These cuts are made based on the min cut-max flow theorem [22] claiming that the min cut in the edges of the extended graph of G is the assignation of potentials that maximizes the probability.
The push-relabeling method is a way to perform the min cut task, which maintains a preflow f and a distance labeling d in the graph, and then begins the discharge operation. In the end, the excess at the sink is equal to the minimum cut value. The final stage of the push-relabeling algorithm is to convert f into a flow. This is reached by computing the decomposition of f and reducing f on paths [21].
Loopy belief propagation, as graph cuts, tries to calculate the solution that corresponds to the MAP. It is a message passing-based algorithm where the convergence is secured [23]. The inferences process is performed indirectly and, as the simple belief propagation, few exchanges of messages are sufficient to compute the required probability task.
Loopy belief propagation algorithm defines clusters Cm in all the edges of the graph G with m taken from 1 till the total amount of edges, each cluster sends a message to his Neighbors, this message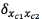 from cluster c1 to cluster c2 connected through a node x2with n taken from 1 till the total amount of nodes are calculated using the factors of each node and the message sent by the Neighbors clusters [20] in an iterative process which calculates the beliefs over the graph G.
from cluster c1 to cluster c2 connected through a node x2with n taken from 1 till the total amount of nodes are calculated using the factors of each node and the message sent by the Neighbors clusters [20] in an iterative process which calculates the beliefs over the graph G.
Dual decomposition algorithm is based on the derivation of a complex problem into simpler and solvable problems where the solution of the whole problem is the solution from these sub-problems. This algorithm is based on the strategy of dividing the graphical model into a different set of slaves or tractable components that try to solve the inference task locally based on neighborhood relations.
We worry about the definition of the problem and the sub-problems. For this purpose, we define a set of subtrees T over the graph G where trees in T should cover at least once every node of G. For each tree T ∈T. We set a smaller MRF defined on the nodes and edges on the tree T, this problem is the decomposition of the big MRF problem into a series of smaller MRF problems (one per each tree T). The relaxation of the coupling constraints by introducing Lagrange multipliers set out the solution of the problem via dual decomposition as shown in [24], where the whole problem is simplified at point of be a group of MRF optimizations over trees T ⊂ G.
4. Experimental Framework
4.1. Dataset
The database was provided from ''Facultad de Ciencias Exactas y Naturales'' from the University of Antioquia and is made up of 450 images of Diploglossus millepunctatus lizards exposed to dust, with differences in light between the images and taken from diverse orientations and distances. Squared samples of 700x700 pixels were randomly taken from 40 raw photos and extracted in three labeled conditions: ideal, standard, and contaminated (see Figure 8). Labeled condition criterions were proposed based on visual perception criteria taking into consideration the light exposure, visual identification of sand or dust and the image resolution. Ideal condition images have a low light exposition, are mostly free of dust and have a resolution that allows the clear observation of the lizard skin. Standard condition includes images with the existence of sand or dust, light exposure and low resolution but in conditions that allow the visual recognition of the spots. Finally, contaminated images have mostly light over exposition as a main characteristic, but also the existence of sand and poor resolution.
4.2. Experiments
Typical lizard spots segmentation processes are performed manually due to the need of an expert criterion of what skin pattern could be considered as a spot. Following the visual criterion, the manual segmentation was taken to create a Ground truth dataset used to confront the accuracy of the experiments performed.
As explained in Section 3, the whole process depends on the variation of the preprocessing step, the smooth term, data term energy function and the inference algorithm.
Based on a literature review, the selected energy term Esmooth functions were Potts, absolute truncated and absolute functions due to good results presented on similar issues. Similarly, the loopy belief propagation, dual decomposition and graph cuts algorithms were implemented as inference algorithms over both, the preprocessing images and the RAW images varying the Edata term of the energy function. The combination of these blocks in the whole process was performed with different inner block parameters and the best results are reported in the next section.
Cost functions were tested with the three different smooth terms previously explained; Potts model was tested with k=1 and discrete values from 0 to 9 for similarity and dissimilarity metrics. The Truncated Square function has a threshold parameter that was moved from 10 to 100 in steps of 10 and a weight that was adjusted from 0.2 to 1 in steps of 0.2. All the experiments were performed using OpenGM [25] library.
5. Results
Tables 1, 2 and 3 show performances of the model with each cost function and inference algorithm. Numbers correspond to mean of efficiency in each condition, where efficiency is calculated as sum of true positives with true negatives terms of confusion matrix. Only Potts model results are presented since truncated absolute difference and absolute different functions always performed worst. In Tables 1, 2, and 3 loopy belief propagation (LBP) is shown; dual decomposition (DD) algorithm shows the same results as LBP and therefore it is not included in the Tables 1, 2, and 3.
The results show that a cost function built with intensity differences, like energy function (2), performs poorly segmentation when the image has low contrast between foreground and background. However, preprocessing enhances this performance significantly pushing the efficiency from 49.60% to 84.87%. Posterization function (3) showed the worst results due to insufficient seed provision. The color-based cost function (4) shows the best results in preprocessed images, owing to color nature of lizard spots and the gain that preprocessing step gives to these color characteristics.
At this point, it is necessary to see how a preprocessing step can improve the segmentation task.
Images that have been passed through the preprocessing step achieve higher performance once the inference process is performed, because the enhancement of the contrast between scales and spots after the preprocessing step. This enhancement makes the data closer to the mathematical model suggested in this work.
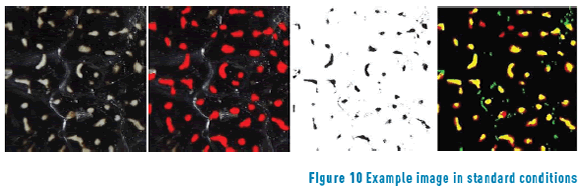
Loopy belief propagation gives better segmentation but is computationally expensive. Due to the optimization of processing time, Graph cuts reach similar percentages in less time. Dual decomposition achieves similar results as Loopy belief propagation, but has the worst inference time. The Figures 9, 10 and 11 show example images of each evaluated condition. The first column is the raw image, the second the ground truth in which the red regions represent the manually marked spots, the third column shows the result of segmentation as black spots, and the final column is a merge in which yellow represents true positives, black true negatives, red false negatives, and green false positives.
As shown, although the proposed model can solve the spot segmentation task under inner image variant illumination conditions, if a single image region is significantly overexposed or the whole image is under conditions where even for the human eye the spots and the brightness are indistinguishable, the model flawed. This imprecision can be observed in the final segmentation of images under contaminated conditions (Figure 11) where under-segmentation occurs. Also, it is common that the model ignores spots that span few pixels and dark spots with intensity similar to the background. Large spots with narrow parts are usually divided into two parts with the narrow part as the break point, as common in energy segmentation approaches.
6. Conclusions
In this paper, a segmentation model for Diploglossus millepunctatus lizards based on MRF is proposed. Extensive experiments using Eqs. (2), (3) and (4) as cost functions, inference methods, loopy belief propagation, dual decomposition and Graph cuts are used. A preprocessing approximation dealing with color spaces, global and local enhancing and segmentation methods is performed. Results show best performance with Potts function as smooth term and intensity build data term (2) with preprocessed images that reach 84.87%, 71.49% and 67.70% of confidence in ideal, standard and contaminated images respectively. In raw images color based data term (4) reaches 69.7%, 64.16% and 58.98% of confidence in ideal, standard and contaminated images respectively. The model shows promising performance to automatize segmentation processes in PMR and to reduce processing time and subjectivity.
In future work, the cost functions will have extra terms that include considerations of shape through pictorial structures concept [17]. Color constraints will be modeled through GMM framework training and specific modeled to Diploglossus millepunctatus spots. The work will be extended to other animals and species. Figure 12 shows the cost function (2) applied to a whale shark dataset [26] to extract spots patterns. Figures 12(b) and 12(d) achieve good performance using the same model as used for Diploglossus millepunctatus.
7. References
1. L. Hiby et al., ''A tiger cannot change its stripes: using a three-dimensional model to match images of living tigers and tiger skins'', Biology Letters, vol. 5, no. 3, pp. 383-386, 2009. [ Links ]
2. H. Kchl and T. Burghardt, ''Animal biometrics: quantifying and detecting phenotypic appearance'', Trends in Ecology & Evolution, vol. 28, no. 7, pp. 432-441, 2013. [ Links ]
3. M. Kelly, ''Computer-aided photograph matching in studies using individual identification: an example from Serengeti cheetahs'', Journal of Mammalogy, vol. 82, no. 2, pp. 440-449, 2001. [ Links ]
4. M. Lahiri, C. Tantipathananandh, R. Warungu, D. Rubenstein and T. Berger, ''Biometric animal databases from field photographs: identification of individual zebra in the wild'', in 1st ACM International Conference on Multimedia Retrieval (ICMR) Trento, Italy, 2011. [ Links ]
5. D. Bolger, T. Morrison, B. Vance, D. Lee and H. Farid, ''A computer‐assisted system for photographic mark–recapture analysis'', Methods in Ecology and Evolution, vol. 3, no. 5, pp. 813-822, 2012. [ Links ]
6. A. Ardovini, L. Cinque and E. Sangineto, ''Identifying elephant photos by multi-curve matching'', Pattern Recognition, vol. 41, no. 6, pp. 1867-1877, 2008. [ Links ]
7. B. Araabi, N. Kehtarnavaz, T. McKinney, G. Hillman and B. Würsig, ''A string matching computer-assisted system for dolphin photo-identification'', Annals of Biomedical Engineering, vol. 28, no. 10, pp. 1269-1279, 2000. [ Links ]
8. C. Gope, N. Kehtarnavaz, G. Hillman and B. Würsig, ''An affine invariant curve matching method for photo-identification of marine mammals'', Pattern Recognition, vol. 38, no. 1, pp. 125-132, 2005. [ Links ]
9. E. Ranguelova and E. Pauwels, ''Saliency detection and matching strategy for photo-identification of humpback whales'', in ICGST International conference on Graphics, Vision and Image Processing (GVIP), Cairo, Egypt, 2005, pp. 81-88. [ Links ]
10. E. Ranguelova, M. Huiskes and E. Pauwels, ''Towards computer-assisted photo-identification of humpback whales'', in International Conference on Image Processing (ICIP), Singapore, Singapore, 2004, pp. 1727-1730. [ Links ]
11. P. Zeeuw, E. Pauwels, E. Ranguelova, D. Buonantony and S. Eckert, ''Computer assisted photo identification of Dermochelys coriacea'', in Int. Conference on Pattern Recognition (ICPR), Berlin, Germany, 2010, pp. 165-172. [ Links ]
12. L. Hiby and P. Lovell, ''Computer aided matching of natural markings: a prototype system for grey seals'', International Whaling Commission, Noordwijkerhout, Netherlands, Report (Special Issue 12), 1990. [ Links ]
13. J. Duyck et al., ''Sloop: A pattern retrieval engine for individual animal identification'', Pattern Recognition, vol. 48, no. 4, pp. 1059-1073, 2015. [ Links ]
14. M. López, ''The lizards of Malpelo (Colombia): some topics on their ecology and threats'', Caldasia, vol. 28, no. 1, pp. 129-134, 2006. [ Links ]
15. Y. Boykov and M. Jolly, ''Interactive graph cuts for optimal boundary & region segmentation of objects in N-D images'' in 8th IEEE International Conference on Computer Vision (ICCV), Vancouver, Canada, 2001, pp. 105-112. [ Links ]
16. C. Rother, V. Kolmogorov and A. Blake, '''GrabCut': Interactive foreground extraction using iterated graph cuts'', ACM Transactions on Graphics, vol. 23, no. 3, pp. 309-314, 2004. [ Links ]
17. M. Kumar, P. Torr and A. Zisserman, ''Obj cut'', in IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), San Diego, USA, 2005, pp. 18-25. [ Links ]
18. Z. Kato and T. Pong, ''A Markov random field image segmentation model for color textured images'', Image and Vision Computing, vol. 24, no. 10, pp. 1103-1114, 2006. [ Links ]
19. A. Delong and Y. Boykov, ''Globally optimal segmentation of multi-region objects'', in 12th International Conference on Computer Vision, Kyoto, Japan, 2009, pp. 285-292. [ Links ]
20. D. Koller and N. Friedman, Probabilistic graphical models: principles and techniques, 1st ed. Cambridge, USA: MIT Press, 2009. [ Links ]
21. A. Goldberg, S. Hed, H. Kaplan, R. Tarjan and R. Werneck, ''Maximum flows by incremental breadth-first search'', in 19th Annual European Symposium, Saarbrücken, Germany, 2011, pp. 457-468. [ Links ]
22. O. Lézoray and L. Grady, Image processing and analysis with graphs: theory and practice, 1st ed. San Jose, USA: CRC Press, 2012. [ Links ]
23. A. Ihler, J. Fisher and A. Willsky, ''Loopy belief propagation: Convergence and effects of message errors'', Journal of Machine Learning Research, vol. 6, pp. 905-936, 2005. [ Links ]
24. N. Komodakis, N. Paragios and G. Tziritas, ''MRF optimization via dual decomposition: Message-passing revisited'', in 11th International Conference on Computer Vision (ICCV), Rio de Janeiro, Brazil, 2007, pp. 1-8. [ Links ]
25. B. Andres, T. Beier and J. Kappes, OpenGM: A C++ Library for Discrete Graphical Models, 2012. [Online]. Available: http://arxiv.org/abs/1206.0111. Accessed on: Mar. 29, 2016. [ Links ]
26. J. Holmberg, B. Norman and Z. Arzoumanian, ''Estimating population size, structure, and residency time for whale sharks Rhincodon typus through collaborative photo-identification'', Endangered Species Res., vol. 7, no. 1, pp. 39-53, 2009. [ Links ]