Redefining the Kanzow Complementarity Function

Redefinición de la función de complementariedad de Kanzo

Favián Arenas
Departamento de Matemáticas, Universidad del Cauca, Popayán - Colombia
E-mail: farenas@unicauca.edu.co

Héctor Jairo Marínez
Departamento de Matemáticas, Universidad del Valle, Cali - Colombia
E-mail: hector.martinez@correounivalle.edu.co

Rosana Pérez
Departamento de Matemáticas, Universidad del Cauca, Popayán - Colombia
E-mail: rosana@unicauca.edu.co

Received: October 14, 2014
Accepted: December 16, 2014

Abstract

In the last years, much work has been done with the aim of finding efficient algorithms to solve nonlinear complementarity problem. A well known way to deal with this problem is to reformulate it as a nonsmooth nonlinear system of equations using a nonlinear complementarity function. In this paper, we consider the complementarity-parameter function proposed in (Kanzow et al., 1998) and we propose a new form of defining it using a quadratic form with symmetric and positive definite matrix. With this new definition, we prove that the function is well defined and some of its properties. We found some bounds that are useful in the development of convergence theory (local and global) of algorithms that solving nonlinear complementarity problem.

Keywords: complementarity function, nonlinear complementarity problem, quadratic form, positive definite matrix, Lipschitz continuity.

Resumen

En los últimos años, ha aumentado la investigación relacionada con la búsqueda de algoritmos eficientes que resuelvan el problema de complementariedad no lineal mediante su reformulación como un sistema de ecuaciones no lineales, no diferenciable, usando las llamadas funciones de complementariedad. En este artículo, consideramos la función de complementariedad uniparamétrica propuesta en (Kanzow et al., 1998) y proponemos una nueva forma de definirla mediante una forma cuadrática, simétrica y definida positiva. Con esta nueva definición, demostramos que la función está bien definida y algunas de sus propiedades. Además, encontramos cotas de gran utilidad en el desarrollo de teorías de convergencia (local y global) de algoritmos que resuelven el problema de complementariedad no lineal.

Palabras clave: función de complementariedad, problema de complementariedad no lineal, forma cuadrática, matriz definida positiva, continuidad Lipschitz.

1. Introducción

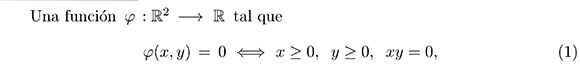
se denomina función de complementariedad. Estas funciones han sido muy utilizadas en los últimos años, para reformular problemas de complementariedad no lineal como sistemas de ecuaciones no lineales, no diferenciables, lo que permite resolver dichos problemas indirectamente (Kanzow et al., 1998; Qi & Sun, 1993; Lopes et al., 1999).Geométricamente, a partir de la equivalencia (1), se infiere que la traza de la función φ obtenida por la intersección con el plano xy, es la curva formada por los semiejes positivos x y y, la cual no es diferenciable en (0, 0). Esta falta de suavidad en la curva implica la no suavidad en la función φ.

En la literatura sobre complementariedad no lineal, existen numerosas funciones de complementariedad, pero las más utilizadas han sido la función mínimo (Pang & Qi, 1993) y la función de Fischer (Fischer & Kanzow, 1996), definidas respectivamente por

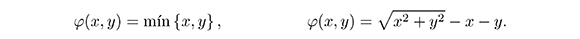
La función mínimo se puede escribir en forma equivalente como

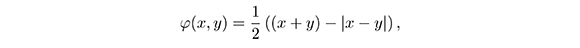que permite observar la no diferenciabilidad que presenta en puntos de la forma (x, x). En cuanto a la función de Fischer, la no diferenciabilidad se presenta en el punto (0, 0).

En 1998, Kanzow y Kleinmichel [11] presentaron la función de complementariedad φλ definida por,

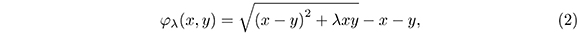
donde el parámetro λ ∈ (0, 4) . En lo que sigue, haremos referencia a esta función como función de Kanzow.

Tanto en la implementación de los algoritmos que utilizan esta estrategia de solución como para el desarrollo de su teoría de convergencia juegan un papel importante las propiedades de la función de complementariedad, entre las que se encuentra el ser Lipschitz continua. Los problemas de complementariedad no lineal surgen en diversas aplicaciones como por ejemplo, problemas de contacto mecánico y fricción (Anitescu et al., 1997), problemas de mecánica estructural y diseño estructural, problemas de lubricación elasto-hidrodinámicos (Kostreva, 1984), problemas de equilibrio de tráfico Chen et al., 2010), así como en problemas relacionados con modelos de equilibrio económico (Ferris y Pang, 1997). Los métodos de homotopía, que son derivados de métodos de punto fijo (Xu & Dang, 2007; Ding & Yin, 2007) y los métodos basados en redes neuronales (Youshen, & Gang, 2007; Liao & Qi, 1999; Liao et al., 2001) también se pueden resolver como un problema de complementariedad no lineal. La importancia de problemas de complementariedad en las áreas de física, ingeniería y economía se debe al hecho de que el concepto de complementariedad es sinónimo de la noción de sistema en equilibrio.

Organizamos la presentación de este documento de la siguiente forma: en la Sección 2, presentamos una forma novedosa de redefinir la función de Kanzow y la usamos para demostrar que en efecto, la función está bien definida, en la Sección 3, a partir de la nueva definición demostramos algunas de sus propiedades de la función de Kanzow y encontramos cotas de gran utilidad en resultados de convergencia de algoritmos que resuelven el problema de complementariedad no lineal. Finalmente, en la Sección 4, hacemos algunos comentarios finales sobre el tema.

2. Una nueva definición de la función Kanzow

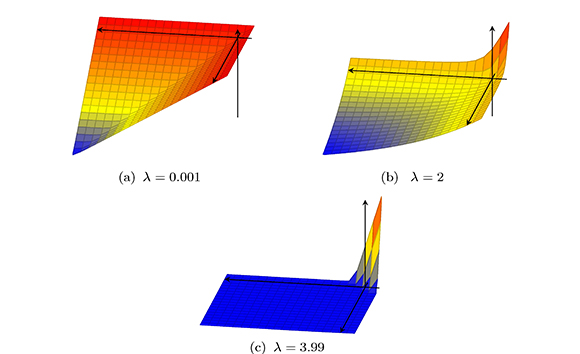
En la definición de φλ dada por (2) observemos que no es conveniente incluir los extremos del intervalo en el que varía λ ya que, la inclusión de λ = 0, aumentaría los puntos de no diferenciabilidad de la función ya que φ0, definida por φ0(x, y) =|x − y|− (x + y) = −2 mín {x, y} no es diferenciable en todos los puntos de la forma (x, x). Para el extremo λ = 4, φ4(x, y) = |x + y|− (x + y) es la función nula, para todo (x, y) con x ≥ 0 y y ≥ 0. En la Figura 1, ilustramos la función de Kanzow para algunos valores de λ.

Figura 1. Función de Kanzow para algunos valores de λ.

Del estudio de la función de Kanzow, observamos que es posible redefinirla en una forma novedosa que presentamos a continuación (Arenas, 2013). Para ello, definiremos una función auxiliar G_λ y notaremos los vectores de ℝ² como vectores columna (matrices de tamaño 2 × 1 ).

Para todo vector x ∈ ℝ² y para todo λ ∈ (0, 4), sea Gλ : ℝ² → ℝ la función definida por

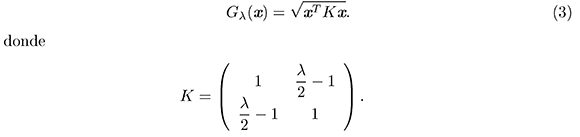
Observemos que la cantidad subradical en (3) coincide con la cantidad subradical en (2):

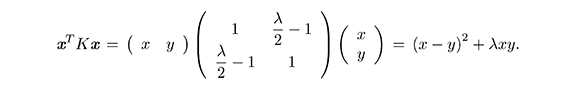
Por otra parte, tenemos que la matriz K es simétrica con valores propios que son funciones de λ, a saber: α1 = α1(λ) = 2 − λ/2 y α2 = α2(λ) = λ/2. Dado que λ ∈ (0, 4), estos valores propios son positivos y, por lo tanto, la matriz K es definida positiva. Así, para todo vector no nulo x en ℝ²

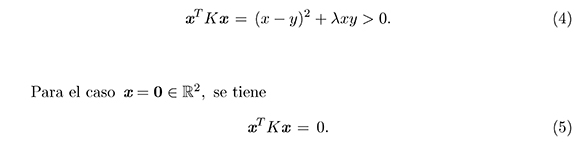
De (4) y (5), tenemos que la función G_λ está bien definida.

Redefinición de la Función de Kanzow. Para todo vector x ∈ ℝ² y para todo λ ∈ (0, 4), redefinimos la función de Kanzow φλ por

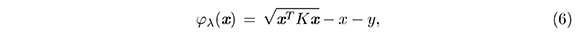
Dado que G_λ está bien definida, concluimos que φλ también está bien definida.

3. Algunas propiedades de la función de Kanzow

En la primera parte de esta sección, demostramos algunas propiedades interesantes de la función G_λ y deducimos algunas cotas relacionadas con esta función; estos resultados los usamos para demostrar que tanto, la función de kanzow, como su gradiente (en los puntos donde existe) son localmente Lipschitz continuos y en cada caso, deducimos la constante Lipschitz.

Lema 1. Sea λ ∈ (0, 4). La función G_λ define una norma sobre ℝ².

Demostración. Por (3), 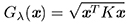= ||x|| . Por lo tanto, G_λ define una norma sobre ℝ², ya que la matriz K es definida positiva [19].

El siguiente resultado es válido puesto que es una forma cuadrática.

Lema 2. La función G_λ definida por (3) satisface las siguientes desigualdades, para todo x ∈ℝ²

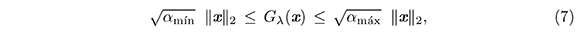
donde α_mín y α_máx son los valores propios mínimo y máximo respectivamente, de la matriz K definida en (4).

Demostración. Teniendo en cuenta que 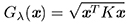y que K, dada por (4),es una matriz simétrica, y α_mín > 0 y α_máx > 0 son sus valores propios mínimo y máximo, respectivamente, concluimos

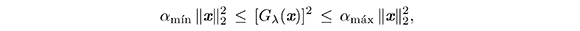
de donde obtenemos las desigualdades (7).

Utilizando la primera desigualdad en (7), obtenemos la siguiente cota para el recíproco de G_λ(x), válida para todo vector no nulo x ∈ℝ²

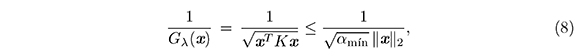
la cual usaremos en la demostración del Lema 5.

Observemos que tanto el valor α_mín como el valor α_máx dependen de λ, en efecto,

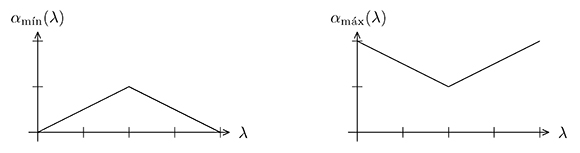
La Figura 2 ilustra las funciones α_mín, y α_máx, para todo λ ∈ (0, 4).+

Figura 2. Funciones α_mín y α_máx

Es importante observar que la función de Kanzow, φλ no es diferenciable en (0, 0). Para cualquier otro vector de ℝ², el vector gradiente de φλ en x está definido por

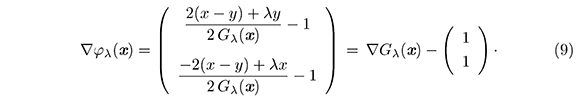
Para su uso posterior, denotaremos las derivadas parciales de G_λ de la sigui- ente manera:

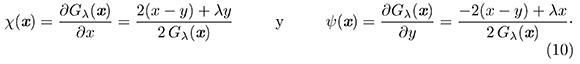
Otro resultado que utilizaremos más adelante es la siguiente desigualdad demostrada en [11],

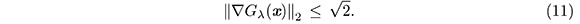
A partir de (9), encontramos una expresión matricial para ∇G_λ(x).

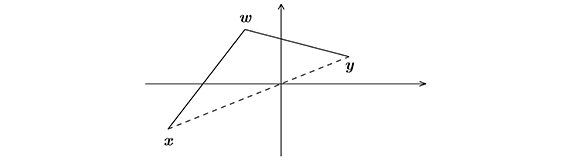
Figura 3. Desigualdad triangular

Puesto que ||K₂|| depende de λ y λ ∈ (0, 4), se tiene que

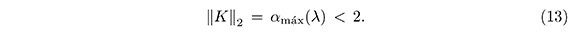
Otra de las propiedades importantes de la función de Kanzow es que es uniformemente continua, más aún, es Lipschitz continua, de acuerdo con el siguiente lema.

Lema 3. La función de Kanzow es Lipschitz continua. Es decir, para todo x, y ∈ℝ²,

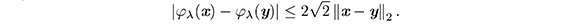
Demostración. Supongamos que el vector cero de ℝ² no está en el segmento [x,y ]. De acuerdo al teorema del valor medio (Apostol, 1976), se garantiza que existe un vector z en el segmento abierto (x,y ) tal que,

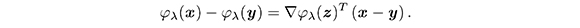
Así, usando la desigualdad de Cauchy-Schwartz, tenemos que |φ_λ(x ) −φ_λ(y )| ≤ ||∇φ_λ(z)||₂ ||x − y||₂. Por (11),

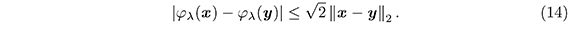
Si el vector cero está en el segmento [x,y], elegimos un vector w que no pertenezca a él y tal que ||x − w||₂ ≤ ||x − y||₂ y ||y − w||₂ ≤ ||x − y||₂, como se indica en la Figura 3. Aplicamos, el resultado (14) a los segmentos [x,w] y [w,y] junto con la desigualdad triangular y obtenemos

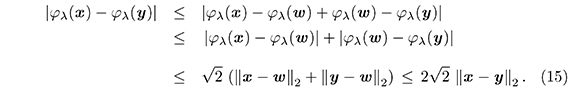
De (14) y (15), φ_λ es Lipschitz continua con constante 2√2.

Corolario 1. La función G_λ es Lipschitz continua. Es decir, para todo x y y en ℝ²,

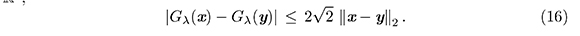
El siguiente lema proporciona cotas para cada una de las derivadas parciales de G_λ y el Lema 2.6 garantiza que el gradiente de φ_λ también es una función localmente Lipschitz continua.

Lema 4. Sea λ ∈ (0, 4). Las derivadas parciales de G_λ definidas en (10) satisfacen las siguientes desigualdades

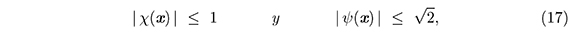
para todo vector no nulo x en ℝ².

Demostración. Iniciamos con el análisis de la función χ. Dado que λ ∈ (0, 4), se tiene que y2λ (λ − 4) ≤ 0, equivalentemente y² λ² − 4y² λ ≤ 0.

Adicionamos los términos 4x² + 4xyλ − 8xy + 4y² y, después de algunas manipulaciones algebraicas, obtenemos las siguientes desigualdades

Lema 5. Sean φ_λ la función de Kanzow, w un vector no nulo de ℝ² , B(w;ε) una bola que no contiene al vector cero, 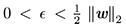. Entonces, existe η λ > 0 tal que para todo x, z ∈ B(w;ε),

Sumamos y restamos la expresión 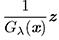para obtener

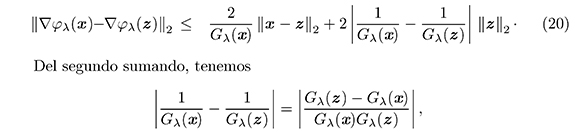
por la continuidad Lipschitz de G_λ (Corolario 2.4),

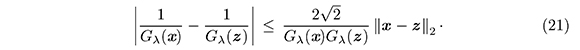
Luego, de las desigualdades (20) y (21), tenemos

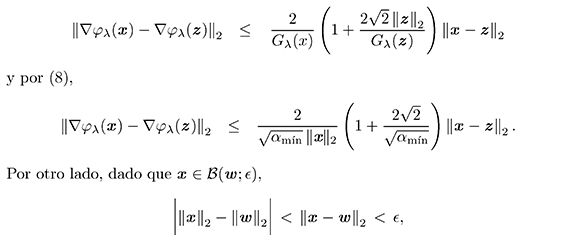
equivalentemente -ε < ||x||₂ − ||w||₂ < π, en particular -ε + ||w||₂ < ||x||₂ , y por la hipótesis, ε ≤ ½ ||w||₂, obtenemos que ||x||₂ > ε.

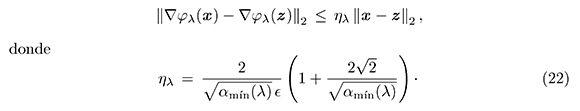
Corolario 2. Las funciones χ y ψ descritas en (10) satisfacen la desigualdades siguientes.

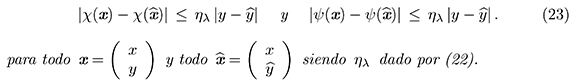
Demostración. Claramente, a partir de (9) y (10),

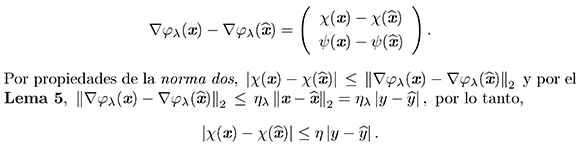
En forma análoga, se demuestra la desigualdad,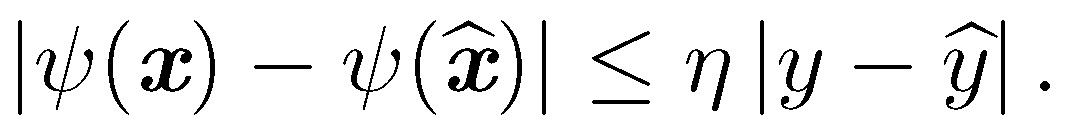

4. Conclusiones

Las llamadas funciones de complementariedad son de gran utilidad para reformular el problema de Complementariedad no lineal como un sistema de ecuaciones no lineales, no diferenciable (De Luca et al., 1996; Kanzow & Kleinmichel, 1998; Qi & Sun, 1993). Una de estas funciones, de amplio uso porque representa una familia de funciones de complementariedad uniparamétrica fue propuesta en 1998 (Kanzow & Kleinmichel, 1998) la cual denominamos función de Kanzow. Dos de las funciones de complementariedad más conocidas y utilizadas son casos particulares de esta familia. En efecto, cuando el parámetro es dos, obtenemos la función de Fisher (Fischer & Kanzow, 1996) y cuando el parámetro tiende a cero, obtenemos un múltiplo de la función mínimo (Pang & Qi, 1993).

En el presente artículo, proponemos una nueva forma de definir la función de Kanzow usando una función cuadrática auxiliar con matriz simétrica y definida positiva. Esta nueva definición nos permitió realizar un estudio detallado de la función, demostrar algunas de sus propiedades y deducir algunas cotas de gran utilidad para demostrar convergencia (local y global) de algoritmos para resolver problemas de complementariedad no lineal (Arenas, 2013; Arias, 2014).

Agradecimientos

A la Universidad del Cauca por proveer tiempo a dos de los autores para la realización de este artículo cuyo contenido hace parte del proyecto de investigación Optimización en Aplicaciones inscrito en VRI ID 3908.

Referencias

Anitescu, M., Cremer, J. F., & Potra, F. A. (1997). On the Existence of Solutions to Complementarity Formulations of Contact Problems with Friction. SIAM Publications (pp. 12-21).         [ Links ]

Apostol, T. M. (1976). Análisis Matemático. Barcelona, España: Reverté         [ Links ].

Arenas, F. (2013). Métodos secantes de cambio mínimo para el problema de complementariedad no lineal. Tesis de Maestría. Universidad del Cauca. Popayán, Colombia.         [ Links ]

Arias, C. A. (2014). Un algoritmo quasi Newton global para problemas de complementariedad no lineal. Tesis de Maestría. Universidad del Cauca. Popayán, Colombia.         [ Links ]

Chen, A., Oh, J. S., Park, D., & Recker, W. (2010). Solving the bicriteria traffic equilibrium problem with variable demand and nonlinear path costs. Applied Mathematics and Computation, 217 (7), 3020-3031.         [ Links ]

De Luca, T., Facchinei, F., & Kanzow, C. (1996). A semismooth equation approach to the solution of nonlinear complementarity problems. Mathematical Programming, 29, 407-439.         [ Links ]

Dieudonné, J. (1969). Treatise on Analysis. New York-London, USA-UK: Academic Press (p. 92).         [ Links ]

Ding, J., & Yin, H. (2007). A new homotopy method for solving non-linear complementarity problems. Numerical Mathematics, 16, 155-163.         [ Links ]

Ferris, M. C., & Pang, J.-S. (1997). Engineering and economic applications of complementarity problems. SIAM Review, 39, 669-713.         [ Links ]

Fischer, A., & Kanzow, C. (1996). On finite termination of an iterative method for linear complementarity problems. Mathematical Programming, 74 (3), 279-292.         [ Links ]

Kanzow, C., & Kleinmichel, H. (1998). A New Class of Semismooth Newton-Type Methods for Nonlinear Complementarity Problems. Computational Optimization and applications, 11 (3) 227-251.         [ Links ]

Kostreva, M. (1984). Elasto-hydrodynamic lubrication: A non-linear complementarity problem. International Journal for Numerical Methods in Fluids, 4(4), 337-397.         [ Links ]

Liao, L.-Z., & Qi, H. (1999). A neural network for the linear complementarity problem. Mathematical and computing modeling, 29, 9-18.         [ Links ]

Liao, L.-Z., Qi, H., & Qi, L. (2001). Solving nonlinear complementarity problems with neural networks. Computational and applied Mathematics, 131, 343-359.         [ Links ]

Lopes, V. L. R., Martínez, J. M., & Pérez, R. (1999). On the local convergence of quasi-Newton methods for nonlinear complementary problems. Applied Numerical Mathematics, 30, 3-22.         [ Links ]

Pang, J.-S., & Qi, L. (1993). Nonsmooth Equations: Motivation and Algorithms. SIAM Journal on Optimization, 3(3), 443-465.         [ Links ]

Qi, L., & Sun, J. (1993). A nonsmooth version of Newton's method. Mathematical Programming, 58, 353-367.         [ Links ]

Watkins, D. S. (1991). Fundamentals of matrix computations. New York, USA: John Wiley and Sons.         [ Links ]

Xu, Q., & Dang, C. (2007). A new homotopy method for solving non-linear complementarity problems. Numerical mathematics, 57, 681-689.         [ Links ]

Youshen, X., & Gang, F. (2007). A neural network for solving nonlinear projection equations. Neural Networks, 5, 577-589.         [ Links ]

Revista de Ciencias por Universidad del Valle se encuentra bajo una licencia Creative Commons Reconocimiento 4.0.