Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista de Ciencias
versão impressa ISSN 0121-1935
rev. cienc. vol.18 no.2 Cali jul./dez. 2014
Lower Bound for the First Steklov Eigenvalue
Óscar Andrés Montaño Carreño
Departamento de Matemáticas, Universidad del Valle, Cali - Colombia
E-mail: oscar.montano@correounivalle.edu.co
Recceived: October 24, 2014
Accepted: December 18, 2014
Abstract
In this paper we find lower bounds for the first Steklov eigenvalue in Riemannian n-manifolds, n = 2, 3, with non-positive sectional curvature.
Keywords: First Steklov eigenvalue, sectional curvature.
1. Introduction
Let (![]() ,g) be a n-dimensional, compact, connected Riemannian manifold with smooth boundary ∂M. The operator L : C∞(∂M) → C∞(∂M) defined by
,g) be a n-dimensional, compact, connected Riemannian manifold with smooth boundary ∂M. The operator L : C∞(∂M) → C∞(∂M) defined by 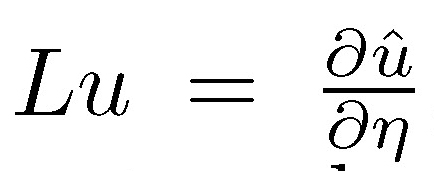 where û is the harmonic extension over M of u and η is the unit outward normal to (∂M) is known as Dirichlet-Neumann operator. The first nonnule eigenvalue (υM) of L is called the first eigenvalue of the Steklov problem and it is variationaly characterized by:
where û is the harmonic extension over M of u and η is the unit outward normal to (∂M) is known as Dirichlet-Neumann operator. The first nonnule eigenvalue (υM) of L is called the first eigenvalue of the Steklov problem and it is variationaly characterized by:
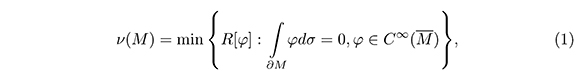
where 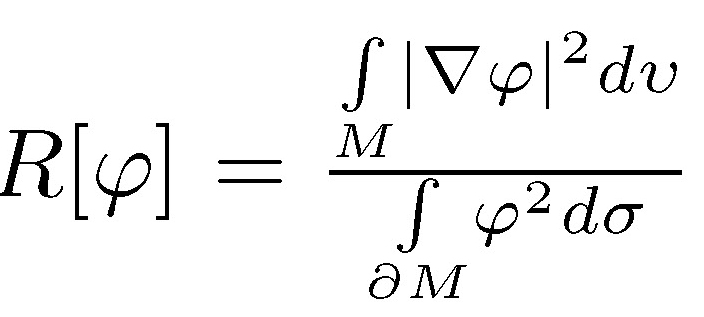 is called Rayleigh quotient. For the Euclidian ball of the radio r > the first eigenvalue is υ 1/r with its own space generated by the coordinate functions. A function φ such taht
is called Rayleigh quotient. For the Euclidian ball of the radio r > the first eigenvalue is υ 1/r with its own space generated by the coordinate functions. A function φ such taht 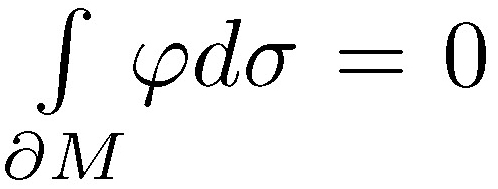 space generated by the Starting from the variational characterization given by (1), if φ is a test function over M then υ (M) ≤ R |φ|.
space generated by the Starting from the variational characterization given by (1), if φ is a test function over M then υ (M) ≤ R |φ|.
In recent years, different authors, among them Weinstock (Weinstock, 1954), Kuttler and Sigillito (1968), Payne (1970), Escobar (1997; 1999; 2000), Wang and Xia (2009; 2010), Illias and Makloul (2011) and Montaño (2013a, 2013b, 2013c, 2014) among others have dealt with the problem of finding geometrical estimates for the first eigenvalue of Steklov.
In this article we find lower bounds for the first eigenvalue of Steklov in geodesic balls and simply connected domain of a Riemannian n-manifold; where n = 2,3, complete of non-positive sectiona curvature.
Our result is extended to Riemannian n-manifolds; where n = 2, 3, the estimate of Kutler-Sigillito for star-shaped domains of the plane (Kuttler & Sigillito, 1968).
2. Preliminaries
For this article, (M,g) will be a Riemannian n-manifold; where n = 2, 3, complete, simply connected and with non-positive sectional K curvature. Since M is complete, then for every p ∈ M the exponential function expp is defined over all TpM. Moreover, since K ≤ 0 over all M the Hadamard theorem (Docarmo, 1992)implies that expp : TpM → M is a difeomorphism, that is, M is difeomorphic to ℝn ≈ TpM, n = 2, 3.
Under the given hypothesis
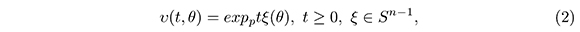
it is a parameterization in geodesic coordinates for M.
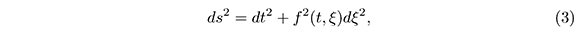
where f(0,ξ) = 0 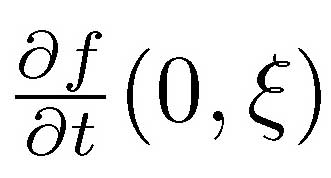 = 1 and dξ2 is the metric of S1 [2]
= 1 and dξ2 is the metric of S1 [2]
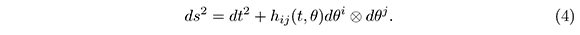
For every t > 0 the boundary of the geodesic ball with center p and radio t, ∂ℜ (p,t), is difeomorphic to S2 andn thus hij (t,θ) dθi ⊗>dθj is a metric over S2 The Uniformization theorem implies that the metric is conformally equivalent to the standard metric over S2 (Escobar 2000, p. 152). Therefore, we can assume that the metric over the 3-manifold is also in the form of
Since the sectional curvature is non-positive, then the Bishop comparison theorem (Chavel, 1984) implies
3. Estimate for the First Eigenvalue over a Geodesic Ball
Theorem 3.1. If ![]() ⊂ M is a geodesic ball with a ratio 1 and center p ∈ M, then the first eigenvalue of Steklov satisfies the inequality
⊂ M is a geodesic ball with a ratio 1 and center p ∈ M, then the first eigenvalue of Steklov satisfies the inequality
where  The equality is achieved only if
The equality is achieved only if ![]() isometric to the Euclidian ball of radio 1.
isometric to the Euclidian ball of radio 1.
Proof. From (6) we have

where δ is the Euclidian metric and  is the gradient over Sn-1. If ∂1 - b is a eigenfunction for υ(
is the gradient over Sn-1. If ∂1 - b is a eigenfunction for υ(![]() , p) and choose the constant b such that ∂: = ∂1 - b serves as a test function for the first eigenvalue of the Euclidean ball υ(
, p) and choose the constant b such that ∂: = ∂1 - b serves as a test function for the first eigenvalue of the Euclidean ball υ(![]() , p) = 1, then
, p) = 1, then
The equality is given only if f(t,ξ) = t, in such ![]() is isometric to the Euclidian ball of radio 1.
is isometric to the Euclidian ball of radio 1.
From the Escobar comparison theorem (Escobar, 2000) and from our estimate, we have
4. Simply Connected Domains
In this section, D is a simply connected domain of TpM and Ω is olso a domaind M such that Ω = expp(D). υ(t,θ) = expptξ (θ) is a parametrization in geodesic cordinates of M, where ξ(θ) is a parametrization of Sn - 1. We suppose that the boundary of D is smooth adn it is given by ∂D = {Rξ : ξ ∈ Sn-1}, where R: Sn-1 → ℝ is a strictly positive smooth function. In geodesic coordinates, the function F(t,θ) = t - R(θ) is such that ∂D and ∂Ω are curves (surfaces) of level 0 of F in the parametrizations tξ(θ) and υ(t,θ) respectively. For this reason the unit normal vectors to each one of the boundaries are given by:
From the previous identities, if we solve the equations cos  and
and 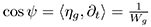 we obtain:
we obtain:
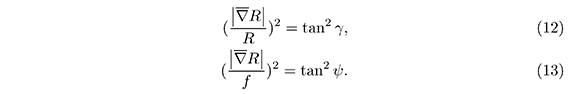
From the inequality 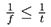 it is deduced that over the boundaries
it is deduced that over the boundaries
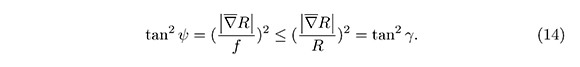
4.1. Estimate for the Integral of the Squared Gradient Over Ω
Let us suppose that the angle γ satisfies the inequality:

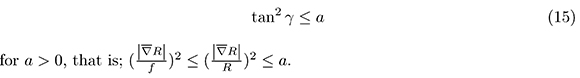
getting the estimate
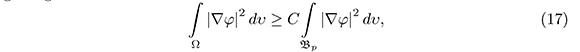
whit
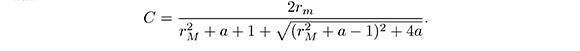
4.2. Estimate for the Integral over the Boundary of φ2

getting the estimate
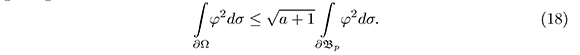
4.3 Estimate for the rst eigenvalue of Steklov over Ω
From the estimates calculated in the previous sections (17), (18), we have the following estimate for the Rayleigh quotient:
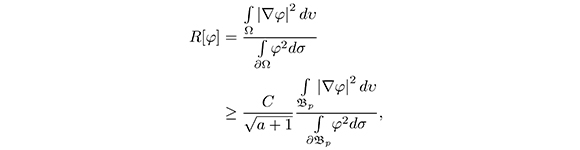
where 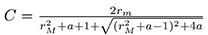 and
and ![]() the geodesic ball over M with center in p and radio 1.
the geodesic ball over M with center in p and radio 1.
If φ is a eigenfunction for the first eigenvalue over Ω and chose the constant b such that φ = φ1 -b erves as a test function for the first eigenvalue of the geodesic ball ![]() , then
, then
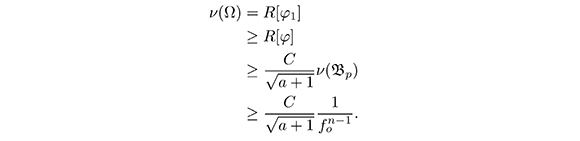
References
Chavel, I. (1984). Eigenvalues In Riemannian Geometry. New York, USA: Academic Press, Inc. [ Links ]
Chavel, I. (2005). Riemannian Geometry A Modern Introduction. Cambridge, USA: Cambridge University Press. [ Links ]
Docarmo, M. P. (1992). Riemannian Geometry. Basilea, Suiza: Birkhauser. [ Links ]
Escobar, J. F. (1997). The Geometry of the first Non-Zero Steklov Eigenvalue. Journal of Functional Analysis, 150, 544-556. [ Links ]
Escobar, J. F. (1999). An Isoperimetric Inequality and the First Steklov Eigenvalue. Journal of Functional Analysis, 165, 101-116. [ Links ]
Escobar, J. F. (2000). A comparison Theorem for the First non-zero Steklov Eigenvalue. Journal of Functional Analysis, 178, 143-155. [ Links ]
Ilias, S., & Makhoul, O. (2011). A Reilly inequality for the first Steklov eigenvalue. Differential Geom. Appl., 5, 699 - 708. [ Links ]
Kuttler, J. R., & Sigillito, V. G. (1968). Lower Bounds for Stekloff and free membrane eigenvalues. SIAM Review, 10, 368-370. [ Links ]
Montaño, O. A. (2013a). The Stekloff problem for rotationally invariant metrics on the ball. Revista Colombiana de Matemáticas, 47(2), 181-190. [ Links ]
Montaño, O. A. (2013b). Cota superior para el primer valor propio del problema de Steklov. Revista Integración, 31(1), 53-58. [ Links ]
Montaño, O. A. (2013c). Cota superior para el primer valor propio de Steklov en el espacio euclídeo. Revista de Ciencias, 17(2), 95-103. [ Links ]
Montaño, O. A. (2014). Métricas rotacionalmente invariantes y el problema de Steklov. Revista Integración, 32(2), 117-128. [ Links ]
Payne, L. E. (1970). Some isoperimetric inequalities for harmonic functions. SIAM J. Math. Anal., 1, 354-359. [ Links ]
Wang Q., & Xia, C. (2010). Inequalities for the Steklov Eigenvalues, arXiv:1006.1154. [ Links ]
Wang, Q., & Xia, C. (2009). Sharp bounds for the first nonzero Steklov eigenvalues. J. Funct. Anal., 257, 2635-2654. [ Links ]
Weinstock, R. (1954). Inequalities for a classical eigenvalue problem. J. Rational Mech. Anal., 3, 745-753. [ Links ]

Revista de Ciencias por Universidad del Valle se encuentra bajo una licencia Creative Commons Reconocimiento 4.0.














