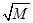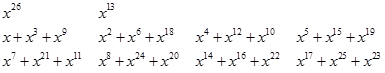1 Introduction
Let 𝑝 be a prime number and 𝔽
q
be a finite field with q = 𝑝
n
elements and let
is an affine plane algebraic curve (over the finite field
In 1940 A. Weil proved the Riemann hypothesis for curves over finite fields. As an immediate corollary he obtained an upper bound for the number of rational points on a geometrically irreducible nonsingular curve ℭ of genus g(ℭ) over a finite field of cardinality q, namely
Where ℭ(𝔽
q
) denotes the set of rational points of the curve ℭ. If the cardinality of the finite field is not a square, the upper bound above was improved by Serre 1 substituting
The interest in curves over finite fields with many rational points with respect to their genera (i.e., with # ℭ.(𝔽 q )) close to known upper bounds; e.g., see tables in 2 and 3 was greatly renewed after algebraic geometry codes (AG codes) were introduced by Goppa in 4. Many constructions of curves over finite fields are often performed by using special polynomials (𝑥) ∈ 𝔽 q [ 𝑥 ]. The essential properties of (𝑥) are sometimes of the following form:
Property I. One has that (𝔽q) ( 𝔽𝑝, and for most elements α ∈ 𝔽q, α is a simple root of 𝑝(𝑥) - 𝑝(α).
Property II. The set
Polynomials satisfying property p (𝔽 q ) ⊆ 𝔽 p are known as (𝔽 p , 𝔽 p )-polynomials. A particular case of (𝔽 q ,𝔽 p )-polynomials, which are studied in detail in 5, are the so-called minimal (𝔽 q ,𝔽 p )-polynomials; i.e., (𝔽 q ,𝔽 p )-polynomials whose degree is ≤ 𝑞 − 1 and whose exponent set is characterized as being the 𝑝-cycles (also introduced in 5) of the integer interval [1, 𝑞 − 1]. We point out that in many cases the exponent set 𝔖 of a minimal (𝔽 q , 𝔽 p )-polynomial has a nice property that has been extensively studied in number theory, namely the 𝑆2 property. More precisely: A subset 𝔖 of integers is an 𝑆2 -set (or has the 𝑆2 property) if all the sums 𝑎 + 𝑎ʹ with 𝑎 ≠ 𝑎ʹ; a, a' ∈ 𝔖 are distinct.
It is known that if 𝔖 ⊆ [1, 𝑀] is an 𝑆2-set, then its cardinality must be asymptotically equal to
The paper is organized as follows: In section 2 we give a brief exposition of some properties of 𝑝-cycles. We show how these can be constructed from a generator element. Section 3 contains some results which allow us to decide when a number 𝑖 ∈ 𝑞−1: = [1, 𝑞 − 1] generates an 𝑆2 𝑝-cycle. We give some criteria to glue some of them and then, obtain sets with a good cardinality. Many examples are included. Section 4 is devoted to study a few particular cases to obtain good 𝑆2 sets. Finally, in section 5 we construct Kummer covers of the projective line over finite fields with many rational points. The idea comes from 7 and that is the construction of rational functions 𝜇(x) ∈ 𝔽 q (x) having the value 1 for many elements 𝛼 ∈ 𝔽 q , such rational functions in our case are induced by (𝔽 p ,𝔽 p )-polynomials whose exponent sets are 𝑆2 sets constructed in section 4.
2 𝑝-Cycles
Let 𝑝 be a prime number and let = 𝑝𝑛 be a non-negative power of 𝑝. The 𝑝-adic expansion of a positive integer 𝑎 in the integer interval 𝐼𝑞−1: = [1, 𝑞−1] is given by:
𝑎 = 𝑘0 + 𝑘1𝑝 + 𝑘2𝑝2 +…+ 𝑘𝑛-1 𝑝𝑛-1,
where the numerals 0 ≤ 𝑘𝑗 < 𝑝 satisfies for j = 0, ··· ,n−1.
If each 𝑎 = 𝑘0 + 𝑘1𝑝 + 𝑘2𝑝2 +…+ 𝑘𝑛-1 𝑝𝑛-1 ∈ 𝐼𝑞−1 is represented by the 𝑛-tuple
𝑎⊓ = 𝑘𝑛-1 + 𝑝𝑘0 + 𝑝2𝑘1 + …+ 𝑝 n-1 𝑘𝑛-2 .
By ⊓𝑘 we will understand the iteration k times the cyclic numeral-permutation. The 𝑝-adic period of 𝑎 is the small natural integer (𝑎) such that
A 𝑝-cycle 𝔍 is an ordered set
Example 2.1 Let 𝑝 = 2 and 𝑛 = 4. The number 3 = 1∙20 + 1∙21 + 0∙22 + 0∙22 corresponds to the 4-tuple (1,1,0,0) therefore 3⊓ = 0∙20 + 1∙21 + 0∙22 = 6, 6⊓ = 12, 12⊓ = 9. Consequently (3,6,12,9) is a 2-cycle of length 4. The element 3 ∈ [1,15] has period 4. On the other hand, if 𝑛 = 7, then the ordered set (3,6,12,24,48,96,65) is a 2-cycle of length 7 and the element 3 ∈ [1,127] has period 7.
Since the process of determining 𝑝-cycles in 𝐼𝑞−1 play an important role in this work, we will study some properties in detail.
Let G = 〈𝜎〉 be the cyclic group of order 𝑛. The group G acts on the set 𝐼𝑞−1 as follows:
ρ: 𝐺 ⨯ 𝐼𝑞−1 → 𝐼𝑞−1
(σ𝑘, 𝑖) ↦ (𝑝𝑘 · 𝑖) 𝑞−1 𝑘 = 0,1,…, 𝑛 −1
where (𝑎) 𝑞−1 is a representative for the residual class of 𝑎 modulus 𝑞−1.
Theorem 2.1
For each 𝑖 ∈ 𝐼𝑞−1, the 𝑝-cycle
Proof: Observe that if 𝑖 = 𝑖0 + 𝑖1𝑝 + 𝑖2𝑝2 +…+ 𝑖 n-1 𝑝 n-1 is the 𝑝-adic expansion of 𝑖, then
𝑖⊓ = 𝑖 n-1 + 𝑖0𝑝 +𝑖1𝑝2 +…+ 𝑖 n-2 𝑝 n-1 .
Hence
𝑝𝑖 − 𝑖⊓ = +𝑖0𝑝 + 𝑖1𝑝2 +…+ 𝑖 n−1 𝑝 n − (𝑖 m−1 + 𝑖0𝑝 + 𝑖1𝑝2 +…+ 𝑖0n−2𝑝n-1)
= 𝑖 n−1 (𝑞 − 1),
consequently 𝑖⊓ ≡ (mod (𝑞 − 1)).
Corollary 2.1 If q = p n and ℑ is a 𝑝-cycle, then 𝑙(ℑ) | 𝑛.
Proof: We known that if G acts on a set 𝑆, then 𝐺𝑥 = {𝑔 ∈ 𝐺 | 𝑔· 𝑥 = 𝑥}
is a subgroup of 𝐺 and the cardinal number of the orbit
Proposition 2.1 Every 𝑝-cycle has the form
ℑ = (i, pi ,..., p k i, (p k+1 i) q−1 ,..., (p ℓ i) q−1 )
where ℓ+1 is the length of ℑ and k > 0 is the smallest integer satisfying p k i < 𝑞−1 ≤ p+1 k+1 i.
Proof: Since
p k+𝑗 i = 𝑟 (𝑞−1) + (p k+𝑗 i) 𝑞−1,
then
p k+𝑗+1 i = 𝑝(p k+𝑗 i) = (𝑟𝑝 + 𝑚)(𝑞−1) + (𝑝(p k+𝑗 i)𝑞−1)𝑞−1
where
(p k+𝑗 i) 𝑞−1 = 𝑚 (𝑞 − 1) + ((p k+𝑗 i) 𝑞−1)−1.
Hence,
(p k+𝑗+1 i)𝑞−1 = ((p k+𝑗 i) 𝑞−1)−1.
Remark 2.1 In accordance with Proposition (2.1), one can see that a 𝑝-cycle ℑ = (i, pi ,..., p k i, (p k+1 i) q-1 ,..., (pℓ i) q-1 ), is nothing but the cyclotomic coset of 𝑖 mod(𝑞 − 1). Cyclotomic cosets mod(𝑁) play an important role in the factorization in 𝔽 p [x] of the polynomial 𝑥𝑁−1 and consequently in coding theory. We refer to 9 for details.
Example 2.2 In the following Tables 1, 2 and 3 we exhibit the different 𝑝-cycles for 𝑝 = 2.3 and 𝑞 = 𝑝𝑛 for some values of 𝑛.
Table 1 2-cycles of length 1, 2, 3 and 6.
| 𝑞 = 26 = 64 | (63) | (21,42) |
| (9,18,36) | (27,54,45) | |
| (1,2,4,8,16,32) | (3,6,12,24,48,33) | |
| (5,10,20,40,17,34 | (7,14,28,56,49,35) | |
| (11,22,44,25,50,37) | (13,26,52,41,19,38) | |
| (15,30,60,57,51,39) | (23,46,29,58,43,53) | |
| (31,62,61,59,55,47) |
Table 2 3-cycles of length 1 and 3.
| 𝑞 = 33 = 27 | (13) | (26) | ||
| (1,3,9) | (2,6,18) | (4,12,10) | (5,15,19) | |
| (7,21,11) | (8,24,20) | (14,16,22) | (17,25,23) |
Table 3 3-cycles of length 1, 2 and 4.
| 𝑞 = 34 = 81 | (40) | (80) | |
| (10,30) | (20,60) | (50,70) | |
| (1,3,9,27) | (2,6,18,54) | (4,12,36,28) | |
| (5,15,45,55) | ((7,21,63,29) | (8,24,72,56) | |
| (11,33,19,57) | (13,39,37,31) | (14,42,46,58) | |
| (16,48,64,32) | (17,51,73,59) | (22,66,38,34) | |
| (23,6947,61) | (25,75,65,35) | (26,78,74,62) | |
| (41,43,49,67) | (44,52,76,68) | (53,79,77,71) |
Observe for example, that for 𝑞 = 64 not all 2-cycle has length 6. The following proposition says when these situations occur. Before that we introduce a convenient notation. Although it is true that we can obtain a 𝑝-cycle from any of its elements, we will say that an integer 𝑖 generates the 𝑝-cycle ℑ if
ℑ = (i, 𝑝i ,..., 𝑝 k i, ( 𝑝 k+1 i) q-1 ,..., (𝑝ℓ i) q-1 ),
and i < (𝑝 k+𝑗 i) q-1 for 𝑗 = 1,…, ℓ− 𝑘. In this case we write ℑ = ⟨ i ⟩.
Proposition 2.2 Let 𝑞 = 𝑝𝑛 with 𝑛 = 𝑚·𝑙. If ℑ = ⟨i⟩, then 𝑙 = (ℑ) < 𝑛 if and only if i is a multiple of
Proof: By definition, ℓ = length(ℑ) if and only if, 𝑝ℓ i= (𝑞 - 1) ℎℓ + i
if and only if,
Proposition 2.3 The greatest integer i ∈ I 𝑞−1 such that i generates a 𝑝-cycle of length 𝑛, is i = 𝑝𝑛 -( 𝑝𝑛-1 + 1). The corresponding 𝑝-cycle is,
(𝑝𝑛 -( 𝑝𝑛-1 + 1), 𝑝𝑛 -( 𝑝0 + 1), 𝑝𝑛 -( 𝑝 + 1), 𝑝𝑛 -( 𝑝2 + 1),…, 𝑝𝑛 -( 𝑝𝑛-2 + 1)).
Proof: First observe that
𝑝i = 𝑝·(𝑝𝑛 - 𝑝𝑛-1 - 1) = (𝑞 - 1)( 𝑝 - 1) - 1 ≡ (𝑞 - 2)(mod 𝑞 - 1).
Hence 𝑝2 i ≡ 𝑞 - 𝑝 - 1 (mod 𝑞 - 1), so in general, 𝑝𝑘 i ≡ 𝑞 - (𝑝𝑘-1 + 1 (mod 𝑞 - 1) which leads to the desired expression. Secondly, each number i < 𝑗 < ?? - 1 can be rewritten as 𝑗 = (𝑞 - 1) - (𝑝𝑛-1 - 𝑘-1) with 0 ≤ 𝑘 ≤ 𝑘 ≤ 𝑝𝑛-1 - 2. Now, the equation 𝑝𝑥 - (𝑞 - 1)t = 𝑗 with 0 ≤ t ≤ 𝑝 - 1 has unique solution in I 𝑞-1 which implies that 𝑗 is the remainder modulus 𝑞 - 1 of some 𝑥 ( I 𝑞-1.
Remark 2.2 Is know that, if 𝛼 = 𝛽 i ∈ 𝔽 q = 𝔽𝑝 (𝛽) and 𝑚𝛼 (𝑥) is its minimal polynomial, then
(Cf 10, Theorem 4.1). Hence one can determine the number of 𝑝-cycles of length 𝑑 | 𝑛 in I 𝑞-1, such number is:
(here (·)is the Moebius function), as many as irreducible polynomials of degree 𝑑 in 𝔽𝑝 [𝑥 ].
3 𝑆 2 - Sets
A subset 𝔖 of integers is an 𝑆2-set if all the sums 𝑎 + 𝑎ʹ with 𝑎 ≠ 𝑎ʹ; 𝑎, 𝑎ʹ; ∈ 𝔖 are distinct. From now on, a set 𝔖 has the 𝑆2 property if 𝔖 is an 𝑆2-set. Similarly, a 𝑝-cycle ℑ = (𝚤1,…, 𝚤𝑙) is an 𝑆2 𝑝-cycle if the underlying set (𝚤1,…, 𝚤𝑙) has the 𝑆2 property. In this section we give some criteria that allows us to decide when a 𝑝-cycle ℑ = ⟨i⟩ has the 𝑆2 property. Also, we give conditions on the generators of a set of 𝑆2-cycles such that the union of these retain this property.
Theorem 3.1 If GCD (i,𝑞 - 1) = 1, then ℑ = ⟨i⟩ is an 𝑆2 𝑝-cycle.
Proof: Assume the contrary, so there exist integers 0 ≤ 𝑟, 𝑠, 𝑢, 𝑣 ≤ 𝑛 -1such that
(𝑝𝑟 i) 𝑞−1 +(𝑝𝑠 i)𝑞−1 = (𝑝𝑢 i)𝑞−1 + (𝑝𝑣 i)𝑞−1 𝑟 < 𝑠, 𝑢< 𝑣, (1)
If 𝑟 = min{𝑟,u}, then (1) implies (𝑝𝑣-𝑟 + 𝑝𝑢-𝑟 − 𝑝𝑠-𝑟 - 1) ≡ (mod 𝑞−1) which is absurd.
Remark 3.1 The reciprocal of Theorem 5.1 is false, in fact if 𝑝 = 3 and = 5, then is easily proved that the 3-cycle generated by the divisor 11 of 242, (11,33,99,55,165) has the 𝑆2 property.
Corrollary 3.1 If 𝑞−1 is a prime number, then any 𝑝-cycle is an 𝑆2-set.
Example 3.1 The Table 4 shows all the 2-cycles of length 5 which, by 3.1 are 𝑆2-sets contained in the integer interval [1.31 ].
Table 4. 𝑆2 2-cycles of length 5.
| 1,2,4,8,16) | (3,6,12,24,17) | (5,10,20,9,18) |
| 7,14,28,25,19) | (11,22,13,26,21) | (15,30,29,27,23) |
The next corollary give us information about the components of a 𝑝-cycle when 𝑖 | 𝑞−1. More precisely.
Corrollary 3.2 Let 𝑖 | 𝑞−1 and Ξ = 〈 i 〉, then all its components are multiples of 𝑖.
Proof: By Proposition (2.1), each component of Ξ has the form (𝑝𝑗𝑖) 𝑞−1 = 𝑝𝑗𝑖 - (𝑞−1) ℎ𝑗.
Remark 3.2 Let us consider the 𝑆2 3-cycle of length 5, Ξ =(11,33,99,55,165) generated by 11, divisor of 242 = 35 − 1 contained in the interval [1,242]. It is clear that its cardinality 5 is very small respect to
Corollary 3.3 Let 𝑖 ∈ [1, 𝑞−1], 𝑑 = 𝐺𝐶D (𝑖, 𝑞−1) and Ξ = 〈 i 〉, The set obtained by canceling the common factor 𝑑 to each component of Ξ has the for:
Proof: It is clear from the uniqueness of the residue.
Example 3.2 If 𝑝 = 2, 𝑛 = 8 and i = 27 ∈ [1,255], then the 2-cycle Ξ, generated by 27, (27,54,108,216,177,99,198,141) is an 𝑆2 2-cycle. Now since (27.255) = 3, then the set 𝔖={9,18,36,72,59,33,66,47} obtained canceling the common factor 3 of each component of Ξ, is an 𝑆2-set. Observe that 𝔖 as a subset of the interval [1,72 has cardinality closed to
On the other hand, since 255/3 = 85 and the first four terms 9,18,36,72 do not exceed 85, but 2 72 ⨯ 72 = 144 ⨯ 1 + 59; 2 ⨯ 59 = 108 ⨯ 1+33 and 2 ⨯ 66 = 112 = 85 ⨯ 1+ 47, then we can generate the new set from 9 taking remainder mod 85.
We emphasize that the set 𝔖 = {9,18,36,72,59,33,66,47} is not the underlying set of the 2-cycle generated by 9, which is {9,18,36,72,144,33,66,132}. This, as 𝑆2-set is very poor respect to
As we can see, there are examples of 𝑝-cycles which have the 𝑆2 property and whose generator 𝑖 is neither prime with 𝑞 - 1 nor divisor of 𝑞 − 1. The following result provides a concrete example.
Proposition 3.1 Let t be an integer number and 𝑛=4t, then the underlying set of the 𝑝-cycle of length 𝑛=4t generated by
is an 𝑆2-set. (Here the hat means that the power 𝑝 t was excluded.)
Proof: First observe that
⟨𝚤⟩ = (𝚤, 𝑝𝚤, 𝑝2𝚤,…, 𝑝 2t-1 𝚤, (𝑝 2t 𝚤)𝑞−1, (𝑝 2t+1 𝚤)𝑞−1 ,…, (𝑝 4t-1 𝚤)𝑞−1)
where (𝑝𝑗𝚤) 𝑞−1 denotes the remainder of 𝑝𝑗𝚤 modulus 𝑞 − 1.
As always, we will suppose that such a set is not an 𝑆2-set, therefore several cases may occur, namely:
Case 1. 𝑝𝑟𝚤 + 𝑝𝑠𝚤 = 𝑝𝑢𝚤 +𝑝𝑣?? with 𝑟, 𝑠, 𝑢, 𝑣 ≤2t − 1.
Case 2.
Case 3.
Case 4.
Case 5.
Case 6.
Our next goal is to determine the number (𝑝 2t+𝑚 𝚤)q−1. For this end, let us denote by 𝚤𝑘, and θ 𝑚 the following natural numbers:
𝚤𝑘,𝑙: = 1 + 𝑝 + ... +
With above notation, the number (𝑝 2t+𝑚 𝚤)𝑞−1 can be written as follows:
As an illustration we consider the case 6. Let us suppose that
For instance, if 0 ≤ 𝑟 < 𝑢 ≤ 2t − 𝑚 < 2t + 𝑚𝑠 < 2t + 𝑚𝑣 with 0 ≤ 𝑚𝑠 ≤ t − 1< 𝑚𝑣, then with the above notation we have:
Now, if 𝑟 = 0 after cancel common terms, we get the following equality
which implies that 𝑝|1.
On the other hand, 𝑟 > 0 implies
if 𝑚𝑠 < 𝑚𝑣 − t and
if 𝑚𝑠 ≥ 𝑣 − 𝑡
If 𝑚𝑠 < 𝑚𝑣 − 𝑡, then 𝑟 > 𝑚𝑠 + 1 implies 𝑝|1; 𝑟 = 𝑚𝑠 + 1, implies 𝑟 = 𝑚 > 𝑡 which is absurd and finally 𝑟 = 𝑚𝑠 + 1 implies
Example 3.3 If 𝑝 = 2 and ?? = 1, then 𝑛 = 8, 𝚤 = 27, Proposition (2.2) says that the 2-cycle (27,54,108,216,177,99,198,141) is an 𝑆2-set contained in [1,256].
Proposition 3.2 If 𝑖 < 𝑝, then the 𝑝-cycle ⟨𝑖⟩ is an 𝑆2 𝑝-cycle.
Proof: If there are different elements 𝑟, 𝑠, 𝑢, 𝑣 such that
𝑝𝑟𝑖 + 𝑝𝑠𝑖 = 𝑝𝑢𝑖 +𝑝𝑣𝑖,
then we would have 𝑝|1.
Corollary 3.4 Let 𝑖, 𝑗 ∈ I 𝑞−1. Then if 𝑖 < 𝑝 and , (𝑗, 𝑞−1) = 1, the 𝑝-cycle Ξ generated by 𝑖𝑗 is an 𝑆2 𝑝-cycle.
Proof: If not, we should have 𝑝𝑟𝑖𝑗 + 𝑝𝑠𝑖𝑗 = 𝑝𝑢𝑖𝑗 + 𝑝𝑢𝑖𝑗 (mod 𝑞−1) for some integers 𝑟, 𝑠, 𝑢, 𝑣, but this congruence contradicts Proposition (3.2).
Proposition 3.3 If 𝑛 is odd, then the 𝑝-cycle generated by 𝑝 +1 is an 𝑆2 𝑝-cycle.
Proof: Observe that such 𝑝-cycle is
(𝑝 + 1, 𝑝2 + 𝑝,…, 𝑝𝑛-2 + 𝑝 𝑛-3, 𝑝 𝑛-1 + 𝑝 𝑛-2, 𝑝𝑛-1 + 1)
First, let us suppose that there exist different integers 1 ≤ 𝑟, 𝑠, 𝑢, 𝑣 ≤ 𝑛 − 1 such that
𝑝𝑛-𝑟+𝑝𝑛-𝑟-1 + 𝑝𝑛-𝑠 + 𝑝𝑛-𝑠-1 = 𝑝𝑛-𝑢 + 𝑝𝑛-𝑢-1 + 𝑝𝑛-𝑣 + 𝑝𝑛-𝑣-1,
then if 𝑠 = max {𝑟, 𝑠, 𝑢, 𝑣} we have 𝑝|1. On the other hand, if there exist different integers 1 ≤ 𝑟, 𝑠, 𝑢 ≤ 𝑛 − 1 such that
𝑝𝑛-𝑟 + 𝑝𝑛-??-1 + 𝑝𝑛-𝑠+𝑝𝑛-𝑠-1 = 𝑝𝑛-𝑢 + 𝑝𝑛-𝑢-1 + 𝑝𝑛-1 + 1, (3)
then since
𝑝𝑛 + 𝑝𝑛-1 -(𝑞 - 1) = 𝑝𝑛-1 + 1,
(3) can be written as
𝑝𝑛-𝑟 + 𝑝𝑛-𝑟-1 + 𝑝𝑛-𝑠+ 𝑝𝑛-𝑠-1 = 𝑝𝑛-𝑢 + 𝑝𝑛-𝑢-1 + 𝑝𝑛 +𝑝𝑛-1 -(𝑞 - 1),
this implies that 𝑝 + 1 divides 𝑞 - 1 which is absurd.
Now we are interested in finding conditions to decide when the union of 𝑆2 𝑝-cycles is an 𝑆2-set. A first approach is given in the following proposition:
Proposition 3.4 If 1 < ?? < 𝑝, then the set
𝔖: ={⟨1⟩ ⋃ ⟨𝑗⟩}
is an 𝑆2-set.
Proof: Assume that 𝔖 is not an 𝑆2-set. Then, there exist ??, 𝑏, 𝑐, 𝑑 ∈ {1, 𝑗} and integer numbers 0 ≤ 𝑟, 𝑠, 𝑢, 𝑣 ≤ 𝑛 - 1 such that,
𝑎𝑝𝑟 + 𝑏𝑝𝑠 = 𝑐𝑝𝑢 + 𝑑𝑝𝑣, (4)
with 𝑟 ≠ 𝑠 if 𝑎 = 𝑏 and 𝑢 ≠ 𝑣 if 𝑐 = 𝑑. The proof is somewhat technical and therefore divided into several cases. To begin suppose that δ = min {𝑟, 𝑠, 𝑢, 𝑣}.
Case 1: If 𝑎 = 𝑏 and 𝑐 = 𝑑, then after canceling 𝑝 δ in (4) we obtain 𝑝|𝑎 or 𝑝|𝑐 which is a contradiction.
Case 2: 𝑎 = 𝑏 and 𝑐 ≠ 𝑑. In this case, if δ = 𝑟 or 𝑠, then after canceling 𝑝 δ in (4) we obtain 𝑝 | 𝑎; if δ = 𝑢 or 𝑣, then 𝑝| or 𝑝|𝑑. The case δ = 𝑢 = 𝑣 leads to 𝑎𝑝 𝑟-δ + 𝑎𝑝 𝑠-δ = 𝑐 + 𝑑, which is again a contradiction. On the other hand, if δ = 𝑟 = 𝑢 = 𝑣 we obtain 𝑎 + 𝑎𝑝 𝑠-δ = 𝑐 + 𝑑, now after to consider the different possibilities for 𝑎, 𝑐, 𝑑, we conclude that 𝑝|1 or 𝑝|𝑗.
Case 3: 𝑎 ≠ 𝑏 and 𝑐 ≠ 𝑑. If 𝑟, 𝑠, 𝑢, 𝑣 are distinct and δ = 𝑟, 𝑠, 𝑢, or 𝑣 then 𝑝|𝑎, 𝑏, 𝑐 or 𝑑 which is a contradiction. If two exponents are equal, for example, 𝑟 = 𝑢 and δ = 𝑟 = 𝑢, then we have 𝑎 - 𝑐 = 𝑑𝑝 𝑣-δ - 𝑑𝑝 𝑠-δ which is absurd. Finally, if three exponents are equal, for example, 𝑢 = 𝑣 = 𝑠 and δ = 𝑢 = 𝑣 = 𝑠, then equation (4) is nothing else but 𝑎𝑝 𝑟-δ + 𝑏 = 𝑐 + 𝑑. Now again after consider all the possibilities for 𝑎, 𝑏, 𝑐, 𝑑, we obtain the same equations and conclusions as in the Case 2.
Example 3.4 If we take 𝑝 = 3, then in this case 𝑗 = 2. We show in the following Table some 𝑆2-sets 𝑆 ⊂ [1, 𝑀 = 3𝑛 − 1] for different values of 𝑛.
As we can see, the first two sets have a reasonable cardinality in respect to
Proposition 3.5 If 1 < 𝑗 < 𝑘 < 𝑝 and 𝑘 + 𝑗 ≠ 𝑝 + 1, then the set
𝔖:= {⟨1⟩ ∪·⟨ 𝑗 ⟩ ∪ ⟨ 𝑘 ⟩}
is an 𝑆2-set.
Proof: Using the notation as in the proof of Proposition (3.4), let us assume that there exist 𝑎, 𝑏, 𝑐, 𝑑 ( {1, 𝑗, 𝑘} and integer numbers 0 ≤ 𝑟, 𝑠, 𝑢, 𝑣 ≤ 𝑛 − 1 such that,
𝑎𝑝𝑟 + 𝑏𝑝𝑠 = 𝑐𝑝𝑢 + 𝑑𝑝𝑣, (5)
with 𝑟 ≠ 𝑠 if 𝑎 = 𝑏 and 𝑢 ≠ 𝑣 if 𝑐 = 𝑑. We distinguish three cases:
Case 1. If 𝑎 = 𝑏 and 𝑐 = 𝑑, then after canceling 𝑝δ in (5) we obtain 𝑝|𝑎 or 𝑝|𝑐 which is a contradiction.
Case 2. 𝑎 = 𝑏 and 𝑐 ≠ 𝑑. In this case, if δ = 𝑟 or 𝑠, then after canceling 𝑝δ in (5) we obtain 𝑝|𝑎; if δ = 𝑢 or 𝑣, then 𝑝|𝑐 or 𝑝|𝑑. The case δ = 𝑢 = 𝑣 leads to 𝑎𝑝𝑟-δ + 𝑎𝑝𝑠-δ = 𝑐 + 𝑑, which is again a contradiction. On the other hand, if δ = 𝑟 = 𝑢 = 𝑣 we obtain 𝑎 + 𝑎𝑝𝑠-δ = 𝑐 + 𝑑. Now after to consider the different possibilities for 𝑎, 𝑐, 𝑑, we obtain the following equalities:
𝑝𝑠-δ + 1 = 𝑗 + 𝑘, + 𝑗??𝑠-δ = 𝑘 +1, 𝑘 + 𝑘𝑝𝑠-δ = 𝑗 + 1. (6)
But 𝑠-δ ≥ 1 implies that none of the above equations are satisfied.
Case 3. 𝑎 ≠ and 𝑐 ≠ 𝑑. If 𝑟, 𝑠, 𝑢, 𝑣 are distinct and δ = 𝑟, 𝑠, 𝑢 or 𝑣, then 𝑝|𝑎, 𝑏, 𝑐 or which is a contradiction. If two exponents are equal, for example 𝑟 = 𝑢 and δ = 𝑟 = 𝑢, then we have 𝑎 − 𝑐 = 𝑑𝑝𝑣-δ − 𝑏𝑝𝑠-δ which is absurd. Finally, if three exponents are equal, for example 𝑢= 𝑣 = 𝑠 and δ = 𝑢= 𝑣 = 𝑠, then equation (5) is nothing else but 𝑎𝑝𝑟-δ + 𝑏 = 𝑐 + 𝑑. Now again after consider all the possibilities for 𝑎, 𝑏, 𝑐, 𝑑, we obtain the same equations and conclusions as (6).
Example 3.5 In the followingTable
we show some 𝑆2 -sets obtained for different values of 𝑀 = 𝑝𝑛-1
With a few modifications at the proof of Proposition (3.5), we have:
Corollary 3.5 If 𝑗 < 𝑘 < 𝑙 < 𝑝 and 𝑘 + 𝑙 ≠ 𝑝𝑗 + 𝑗, then the set
𝑆: = { ⟨𝑗⟩ ∪ ⟨𝑘⟩ ∪ ⟨𝑙⟩ }
is an 𝑆2-set.
Example 3.6 If we take 𝑝 = 7 and 𝑛 = 2, we obtain the Table 7.
Proposition 3.6 If 1 < 𝑎1 < 𝑎2 < 𝑎3 < 𝑝, 𝑎𝑖 + 𝑎𝑗 ≠ 𝑝 + 1 and the set {1, 𝑎1, 𝑎2, 𝑎3} is an 𝑆2-set, then the set
𝔖: = { ⟨1⟩ ∪ ⟨𝑎1⟩ ∪ ⟨𝑎2⟩ ∪ ⟨𝑎3⟩ }
is an 𝑆2-set.
Proof: By Proposition (3.5) in order to prove our assertion, we only have to analyze the equation
𝑝𝑟 + 𝑎1𝑝𝑠 = 𝑎2𝑝𝑢 + 𝑎3𝑝𝑣, (7)
with 0 < 𝑟, 𝑠, 𝑢, 𝑣 < 𝑛. As in the proof of Proposition (3.5) let 𝛿 = min {𝑟, 𝑠, 𝑢, 𝑣}.
1. If δ = 𝑟 = 𝑠 = 𝑢 ≠ 𝑣, then equation (7) becomes 0 < 1 + 𝑎1 − 𝑎2 = 𝑎3𝑝 𝑣-δ which is a contradiction.
2. If ≠ δ = 𝑟 = 𝑠 ≠ 𝑢, we obtain 1 + 𝑎1 = 𝑎2𝑝 𝑢-δ + 𝑎3?? 𝑣-δ which is absurd.
3. The cases δ = 𝑟 with δ ≠ 𝑠, 𝑢, 𝑣 and δ = 𝑟 = 𝑠 = 𝑢 = 𝑣 are trivial.
Example 3.7 If 𝑝 = 11 and 𝑛 = 2, there exist 36 possibilities for 𝑎1, 𝑎2, 𝑎3 which satisfies the hypothesis of the Proposition (3.6), we exhibit in the Table 8 only some of such sets. Before this note that although this example did not give sets whose cardinality is near to
Table 8 Joining 4 11-cycles of length 2.
| 1,2,3,5,11,22,33,55 | 1,2,3,6,11,22,33,66 |
| 1,2,3,7,11,22,33,77 | 1,2,3,8,11,22,33,88 |
| 1,3,5,10,11,33,55,110 | 1,3,6,7,11,33,66,77 |
| 1,3,6,10,11,33,66,110 | 1,3,7,8,11,33,77,88 |
| 1,3,7,10,11,33,77,110 | 1,4,6,7,11,44,66,77 |
| 1,4,6,10,11,44,66,110 | 1,4,7,9,11,44,77,99 |
| 1,4,9,10,11,44,99,110 | 1,5,9,10,11,55,99,110 |
| 1,6,7,8,11,66,77,88 | 1,6,9,10,11,66,99,110 |
| 1,7,8,9,11,77,88,99 | 1,7,9,10,11,77,99,110 |
4 Particular Examples
So far, we have provided some criteria that allow us to glue 𝑆2 𝑝-cycles ⟨𝑖⟩, ⟨𝑗⟩, ⟨𝑘⟩ such that, the resulting set 𝔖: = {⟨𝑖⟩ ∪ ⟨𝑗⟩ ∪ ⟨𝑘⟩} maintains the 𝑆2 property, the condition on their generators 𝑖, 𝑗, 𝑘 is 1 < 𝑖 < 𝑗 < 𝑘 < 𝑝. In this section we will try to go a little further.
4.1 The Case 𝑞 = 𝑝 2
Let us suppose that 1 ≤ 𝑗 < 𝑘 < 𝑝 < 𝑖 are the generators of the 𝑝-cycles (𝑗, 𝑝𝑗), (𝑘, 𝑝𝑘) and (𝑖, (𝑝𝑖) 𝑞−1). As always, we want to establish conditions on their generators so that the resulting set 𝔖: = {⟨𝑖⟩ ∪ ⟨𝑗⟩ ∪ ⟨𝑘⟩} has the 𝑆2 property. Now, observe that for this purpose it is easier to establish conditions for which 𝔖 does not have the 𝑆2 property. Now, observe that for this purpose it is easier to establish conditions for which 𝔖 does not have the S 2 property. In fact, 𝔖: = {𝑗, 𝑝𝑗, 𝑘, 𝑝𝑘, 𝑖 (𝑝𝑖) 𝑞−1} is not an 𝑆2 set if there exist distinct 1, 𝑎2, 𝑎3, 𝑎4 ( 𝔖 such that 𝑎1 + 𝑎2 = 𝑎3 + 𝑎4, then it is evident that this equality leads us to consider a large number of equations. Fortunately many of these equations are not possible, for example it is impossible that 𝑘 + 𝑗 = 𝑝𝑘 + 𝑝𝑗 or 𝑘 + 𝑗 = 𝑝𝑘 +(𝑝𝑖)𝑞−1 or 𝑘 + 𝑗 = 𝑖 +𝑝𝑗. After check all the possibilities, we must consider only the following equations:
1) 𝑖 + (𝑝 + 1) 𝑗 + 𝑘 = 0
2) 𝑖 − (𝑝 + 1) 𝑗 + 𝑝𝑘 = 0
3) 𝑖 − (𝑝 − 1)𝑗 − 𝑝𝑘 = 0
4) 𝑖 + 𝑝𝑗 − (𝑝 − 1)𝑘 = 0
5) 𝑖 − 𝑗 − (𝑝 − 1)𝑘 = 0
6) 𝑖 - 𝑗 = (𝑝 + 1)𝑚
7) 𝑖 + 𝑗 − (𝑝 + 1)𝑘 = 0
8) 𝑖 + 𝑗 = (𝑝 + 1)𝑚
9) 𝑖 + 𝑝𝑗 − (𝑝 + 1)𝑘 = 0
10) 𝑖 − 𝑘 = (𝑝 − 1)𝑚
11) 𝑝𝑖 − (𝑝 − 1)𝑗 - 𝑝𝑘 = (𝑝2 − 1)𝑚
12) 𝑝𝑖 − 𝑝𝑗 − (𝑝 − 1)𝑘 = (𝑝2 − 1)𝑚
13) 𝑝𝑖 + 𝑗 − (𝑝 + 1)𝑘 = (𝑝2 − 1)𝑚
14) (𝑝 + 1)𝑖 − 𝑝𝑗 − ??𝑘 = (𝑝2 − 1)𝑚
Equation 6 corresponds to case 𝑗 + (𝑝𝑖) 𝑞−1 = 𝑖 + 𝑝𝑗, equation 11 corresponds to case 𝑗 + (𝑝𝑖)𝑞−1 = 𝑝𝑗 + 𝑝𝑘 and so on. To illustrate, we consider 𝑝 = 7 and we will to analyze the equations 3, 5, 6, 9, 10 and 12.
The Table 9 contains the solutions:
Table 9 solutions
| Equation | Solutions |
|---|---|
| (3) 𝑖 − (𝑝 − 1)𝑗 - 𝑝𝑘 = 0 | (1,2,20);(1,3,27);(1,4,34);(1,5,39); |
| (1,6,48) | |
| (2,3,33);(2,4,40);(2,5,47) | |
| (3,4,46) | |
| (5) 𝑖 − 𝑗 − (𝑝 − 1)𝑘 = 0 | (1,2,13);(1,3,19);(1,4,25);(1,5,31) |
| (1,6,37) | |
| (2,3,20);(2,4,26);(2,5,32);(2,6,38). | |
| (3,4,27);(3,5,33);(3,6,39). | |
| (4,5,34);(4,6,40). | |
| (5,6,41). | |
| (6) 𝑖 - 𝑗 = (𝑝 + 1)𝑚 | (1,𝑘,9,1) (1, 𝑘,17,2); (1, 𝑘,25,3); |
| (1,,33,4);(1,𝑘,41,5). | |
| (2,𝑘,10,1);(2,𝑘,18,2);(2,𝑘,26,3); | |
| (2,,34,4);(2,𝑘,42,5). | |
| (3,𝑘,11,1);(3,𝑘,19,2);(3,𝑘,27,3); | |
| (3,,35,4);(3,𝑘,43,5). | |
| (4,𝑘,12,1);(4,𝑘,20,2);(4,𝑘,28,3); | |
| (4,,36,4);(4,𝑘,44,5). | |
| (5,𝑘,13,1);(5,𝑘,21,2);(5,𝑘,29,3); | |
| (5,,37,4);(5,𝑘,45,5). | |
| (6,𝑘,14,1);(6,𝑘,22,2);(6,𝑘,30,3); | |
| (6,,38,4);(6,𝑘,46,5). | |
| (9) 𝑖 + 𝑝𝑗 − (𝑝 + 1)𝑘 = 0 | (1,3,11); (1,4,17);(1,5,23);(1,6,29). |
| (2,4,10); (2,5,16);(2,6,22). | |
| (3,5,9);(3,6,15). | |
| (4,6,8). | |
| (10) 𝑖 − 𝑘 = (𝑝 − 1)𝑚 | (𝑗,3,9,1) |
| (𝑗,4,10,1). | |
| (𝑗,5,11,1); (𝑗,5,17,2). | |
| (𝑗,6,12,1);(𝑗,6,18,2). | |
| (12) 𝑝𝑖 - 𝑝𝑗 − (𝑝 − 1)𝑘 = (𝑝2 − 1)𝑚 | (1,2,37,5); (1,3,31,4); (1,4,25,3). |
| (1,5,19,2);(1,6,13,1). | |
| (2,3,32,4);(2,4,26,3); (2,5,20,2). | |
| (2,4,27,3). |
Note that equations containing (𝑝𝑖) 𝑞−1 such that (6), (10) and (12), have as solutions quadruples (𝑗,,,). The value 𝑚 appears because 𝑖 > 𝑝 = 7 and therefore, 𝑝𝑖= (𝑝2−1)+(𝑝𝑖)𝑞−1 = 48𝑚 + (7𝑖). The other equations have as solutions triples (𝑗, 𝑘, 𝑖). The first solution of the equation (6) for example, says that the set 𝔖 = {1, 7, k, 7k, 9, 15} is not an 𝑆2 set for 2 ≤ 𝑘 ≤ 6. The following Table contains all the 𝑆2 sets which were obtained joining three 7-cycles of length 2 whose generators satisfy the condition 1 = 𝑗 < 𝑘 < 𝑝 < 𝑖.
Table 10 𝑆2 sets as union of three 7-cycles of length 2.
| 1,2,7,11,14,29 | 1,4,7,11,28,29 | 1,5,7,26,35,38 |
| 1,2,7,12,14,36 | 1,4,7,13,28,43 | 1,5,7,27,35,45 |
| 1,2,7,14,27,45 | 1,4,7,18,28,30 | 1,5,7,34,35,46 |
| 1,3,7,10,21,22 | 1,4,7,19,28,37 | 1,6,7,10,22,42 |
| 1,3,7,12,21,36 | 1,4,7,26,28,38 | 1,6,7,11,29,42 |
| 1,3,7,13,21,43 | 1,4,7,27,28,45 | 1,6,7,20,42,44 |
| 1,3,7,18,21,30 | 1,5,7,10,22,35 | 1,6,7,26,38,42 |
| 1,3,7,20,21,44 | 1,5,7,12,35,36 | 1,6,7,27,42,45 |
| 1,3,7,21,26,38 | 1,5,7,18,30,35 | 1,6,7,34,42,46 |
| 1,3,7,21,34,46 | 1,5,7,20,35,44 |
The next Table should be read as follows: The two generators 𝑗, 𝑘 that appear in the left-hand column can be put together with exactly one generator 𝑖 in the second column to obtain an 𝑆2 set 𝔖 = {𝑗, 𝑝𝑗, 𝑘, 𝑝𝑘, 𝑖, (𝑝𝑖)48}. for example, line 4 says that the sets 𝔖1 ={2,6,9,14,15,42}, 𝔖2 ={2,6,11,14,29,42}, 𝔖3 = {2,6,14,17,23,42}, 𝔖4 = {2,6,14,20,42,44}, 𝔖5 = {2,6,14,27,42,45}, 𝔖6 = {2,6,9,14,33,39,42}, and 𝔖7 = {2,6,14,41,42,47} are 𝑆2 sets.
Table 11 generators 𝑗, 𝑘 that appear in the left-hand column can be put together with exactly one generator 𝑖 in the second column to obtain an 𝑆2 set 𝔖 = {𝑗, 𝑝𝑗, 𝑘, 𝑝𝑘, 𝑖, (𝑝𝑖)48}
| 𝑗, 𝑘 | 𝑖 |
| 2,3 | 12,17,25,41 |
| 2,4 | 9,11,13,17,19,25,27,33,41 |
| 2,5 | 9,12,19,25,27,33 |
| 2,6 | 9,11,17,20,27,33,41 |
| 3,4 | 5,6,13,17,18,25,26,33,41 |
| 3,5 | 6,10,12,18,20,26,34,41 |
| 3,6 | 10,13,17,20,25,26,34,41 |
| 4,5 | 6,9,18,19,25,26,33,41 |
| 4,6 | 9,11,13,17,19,25,27,33,34,41 |
| 5,6 | 9,10,19,20,25,26,27,33 |
4.2 The Case 𝑞 = 𝑝4𝑡
With the notations as in Proposition 3.1, let 𝑡 be an integer number, 𝑛 = 4𝑡 and
𝚤:= 1 + 𝑝 + 𝑝2 +…+ 𝑝𝑡-1 + 𝑝𝑡 + 𝑝𝑡+1 +…+ 𝑝2𝑡.
With this assumption, we have the following proposition:
Proposition 4.2.1 The set 𝔖 = {⟨1⟩, ⟨𝚤⟩} is an 𝑆2 set.
Proof: As always, we will assume that 𝔖 = {⟨1⟩, ⟨𝚤⟩} has not the 𝑆2 property. If this occurs, then at least one of following equalities is satisfied. For simplicity we write in this prove 𝑝𝑘𝑖 instead of (𝑝𝑘𝑖) 𝑞−1.
1) 𝑝𝑟 + 𝑝𝑠 = 𝑝𝑢 + 𝑝𝑣𝚤
2) 𝑝𝑟 + 𝑝𝑠 = 𝑝𝑢 + (𝑝2𝑡 +𝑚𝑣𝚤)
3) 𝑝𝑟 + 𝑝𝑠 = 𝑝𝑢𝚤 + 𝑝𝑣𝚤
4) 𝑝𝑟 + 𝑝𝑠 = 𝑝𝑢𝚤 + (𝑝2𝑡 +𝑚𝑣𝚤)
5) 𝑝𝑟 + 𝑝𝑠 = (𝑝2𝑡 +𝑚𝑢𝚤) + (𝑝2𝑡 +𝑚𝑣𝚤)
6) 𝑝𝑟 + 𝑝𝑠𝚤 = 𝑝𝑢𝚤 + 𝑝𝑣𝚤
7) 𝑝𝑟 + 𝑝𝑠𝚤 = 𝑝𝑢𝚤 + (𝑝2𝑡 +𝑚𝑣𝚤)
8) 𝑝𝑟 + 𝑝𝑠𝚤 = (𝑝2𝑡 +𝑚𝑢𝚤) + (𝑝2𝑡 +𝑚𝑣𝚤)
9) 𝑝𝑟 + 𝑝2𝑡+𝑚??𝚤) = (𝑝2𝑡 +𝑚𝑢𝚤) + (𝑝2𝑡 +𝑚𝑣𝚤)
We must show that if one of these equations is satisfied, then we obtain a contradiction. We give the proof only for some particular cases of equations 4.7 and 9.
For equation 4, let us suppose that 0 ≤ 𝑢 < 2𝑡 + 𝑚𝑣 = 𝑟 < 𝑠 with 0 ≤ 𝑚𝑣 ≤ 𝑡 − 1, then by (2) the equation defined by item 4, can be rewritten as
𝑝𝑟 + 𝑝𝑠 = 𝑝𝑢𝚤 + θ𝑚𝑣 + 2𝑡 +𝑚𝑣 𝚤𝑚𝑣+1,𝑡(8)
If 𝑢 = 0, after we cancel common powers in (8) we obtain:
𝑝𝑟 · (sum of powers of 𝑝) = 2 + 2𝑝 + 2𝑝2+… + 2𝑝𝑚𝑣 + 𝑝𝑚𝑣+1 +…+ 𝑝2𝑡.
These equalities imply that 𝑝𝑚𝑣+1 | 20𝑚𝑣 which is absurd. On the other hand, 0 < 𝑢 carries us again to the absurd divisibility relation 𝑝𝑢 | 0𝑚𝑣.
Now, suppose that the equation defined by item 7 holds; i.e.,
𝑝𝑟 + 𝑝𝑠𝚤 = 𝑝𝑢𝚤 + (𝑝2𝑡 +𝑚𝑣 𝚤) (9)
Note that implicitly 0 ≤ 𝑠, 𝑢 ≤ 2𝑡 −1. Moreover, we have assumed that 0 < 𝑟 ≤ 4 𝑡 −1 and 0 ≤ 𝑠 < 𝑢 ≤ 2𝑡 −1 < 2𝑡 + 𝑚𝑣 with 0 ≤ 𝑚𝑣 ≤ 𝑡 −1.
Under these hypotheses and using (2), we have 𝑝 | θ𝑚𝑣 which is absurd. On the other hand if 𝑡 ≤ 𝑚𝑣 ≤ 2𝑡 −1, then again by (2) we have:
𝑝𝑟 = 𝑝𝑠𝚤 (𝑝𝑢-𝑠 −1) + 𝑝2𝑡+𝑚𝑣 θ2𝑡−𝑚𝑣−1 + 𝚤2𝑡−𝑚𝑣+1, 𝑚𝑣−𝑡. (10)
And therefore, if 𝑡 < 𝑚𝑣 it is clear that we have a contradiction, but if 𝑚𝑣 = 𝑡 (10) becomes, 𝑝𝑟 = 𝑝𝑠𝚤 (𝑝𝑢-𝑠 −1) + 𝑝2𝑡+𝑚𝑣 θ𝑡−1 + 𝚤𝑡,0 (11)
Now 𝑠 = 0 implies 𝑝 | 𝚤, while 𝑠 > 0 lead us to 𝑝 | θ𝑡−1, both facts being absurd.
Finally, to analyze the equation 𝑝𝑟 + (𝑝2𝑡+𝑚s) = (𝑝2𝑡+𝑚𝑢) + (𝑝2𝑡+𝑚𝑣) defined by item 9, we will assume that 0 < 𝑟 < 4𝑡− 1 and 0 ≤ 𝑚𝑠 < 𝑚𝑢 < ?? ≤ 𝑚𝑣 ≤ 2𝑡− 1. Now again by (2), we have: 𝑝𝑟 + θ 𝑚𝑠 + 𝑝2𝑡+𝑚s = θ 𝑚𝑢 + 𝑝2𝑡+𝑚𝑢 + 2𝑡−𝑚𝑣, 𝑚𝑣−𝑡 + 𝑝2𝑡+𝑚𝑣 θ2𝑡−𝑚𝑣−1 (12)
Now this equality is the same as
𝑝𝑟 + 𝑝2𝑡+𝑚s = 𝑝𝑚s+1θ𝑚𝑢 −𝑚𝑠 −1 + 𝑝2𝑡+ + 2𝑡−𝑚𝑣, 𝑚𝑣−𝑡 + 𝑝2𝑡+𝑚𝑣 θ2𝑡−𝑚𝑣−1 (13)
and consequently 𝑝 |2𝑡−𝑚𝑣,𝑚𝑣−𝑡 which is impossible
Example 4.2.1. Taking 𝑝 = 2 and 𝑡 = 1, we have that 𝚤 = 27 and by Propositions (4.2.1.) and (3.1) the set
𝔖 = {1,2,4,8,16,27,32,54,64,99,108,128,141,177,198,216}
is an 𝑆2 set in the integer interval [1.255]. Note that we have actually provided a good example of an 𝑆2 set which has a nice property: For each element 𝑎𝑗 ∈ 𝔖 the subset S𝑎𝑗 = 𝔖 ∩ I𝑎𝑗 ⊂ 𝔖 is a good 𝑆2 set.
4.3 The Case 𝑞 = 34
The following Proposition provides a criterion to construct 𝑆2 sets in the integer interval [1.80] by joining 𝑆2 3-cycles of length 4. By Theorem (5.1) and Corollary (3.4) we have that the set of generators 𝑆2 3-cycles of length 4 is Λ = {1,2,7,11,13,14,17,22,23,26,41,53} .
Proposition 4.3.1 Let 𝑖, 𝑗 ∈ Λ such that 𝑗 - 𝑖 ≡ 1 (mod 2), then 𝔖 = {⟨ 𝑖 ⟩ ⋃ ⟨ 𝑗 ⟩} is an 𝑆2 set.
Proof: To begin with, observe that 𝔖 is not an 𝑆2 set if and only if there exists (𝑟, 𝑠, 𝑢, 𝑣), with 𝑟 < 𝑠; < 𝑣 and 𝑟, 𝑠, 𝑢, 𝑣 ∈ {0,1,2,3} such that one of the following congruencies is satisfied:
3𝑟 𝑖 + 3𝑠 𝑖 ≡ 3𝑢 + 3𝑣 (mod(80)) (14)
3𝑟 𝑖 +3𝑣 ≡ 3𝑢 + 3𝑠 (mod(80)) (15)
3𝑟 𝑖 +3𝑠 𝑖 ≡ 3𝑢 + 3𝑣 (mod(80)) (16)
If 3𝑟 𝑖 + 3𝑢 𝑗 + 3𝑣 𝑗 (mod (80)) and I =2𝚤. By parity arguments, the congruence (14) is equivalent to:
Now since (3𝑣−𝑢 + 1)/4 is 1 or 7, then (3𝑠−𝑟 + 1)/2 must be equal to 5 and hence 5|2𝑘 +1 which is a contradiction.
On the other hand if i = 2𝜄+1 and keeping in mind that 3𝜇 - 1 =2,8 or 26, then congruence (15) is equivalent to:
This equality implies that (3𝑣−𝑢 − 1)/2 must be even and hence equals to 4, consequently
10𝑡 = 3𝑢 · 2 · 𝑘−3(2+1),
which is again an contradiction.
Finally, congruence (16) is nothing but
80𝑡 = 3𝑟 i (1+3𝑠−𝑟− 3𝑣−𝑟) − 3𝑢 𝑗.
But this is impossible since the RHS is negative.
Example 4.3.1 By Proposition (4.3.1), we can put together the following 3-cycles generated by i and 𝑗 (Table).
Table 12 3-cycles generated by i and 𝑗
| 𝑖 | 𝑗 |
| 1 | 2,14,22,26 |
| 2 | 7,11,13,17,23,41,53 |
| 7 | 14,22,26 |
| 11 | 14,22,26 |
| 13 | 14,22,26 |
| 14 | 17,23,41,53 |
| 17 | 22,26 |
| 22 | 23,41,53 |
| 23 | 26 |
| 26 | 41,53 |
The following Table contains some of these sets:
Table 13 Union of two 3-cycles of length 4.
| 1,2,3,6,9,18,27,54 | 2,6,11,18,19,33,54,57 |
| 2,6,18,53,54,71,77,79 | 7,14,21,29,42,46,58,63 |
| 7,21,22,29,34,38,63,66 | 11,14,19,33,42,46,57,58 |
| 13,22,31,34,37,38,39,66 | 14,42,46,53,58,71,77,79 |
| 17,22,34,38,51,59,66,73 | 22,34,38,53,66,71,77,79 |
| 23,26,47,61,62,69,74,78 | 26,53,62,71,74,77,78,79 |
5 Curves with many rational points over finite fields
We consider the non-singular complete irreducible Kummer curve 𝔈 over 𝔽 q defined by the affine equation:
𝑦𝑟= (𝑥),
Where 𝑟| 𝑞 − 1 and the rational function 𝜇(x) ∈ 𝔽 q (𝑥) satisfies the following conditions:
1. 𝜇 is not the 𝑑-th power of an element 𝑣 ∈ 𝔽 q (𝑥) for any divisor 𝑑 > 1 of 𝑟;
2. 𝜇 = 1 on a substantial subset 𝖅𝜇 of ℙ1 (𝔽 q );
3. (𝑥) has many multiple zeros and poles.
For details about this conditions and proofs we refer 7 and 11. With above notation we have:
Proposition 5.1 (11, Proposition 2.1) The curve 𝔈 over the finite field 𝔽 q given by the Kummer equation 𝑦𝑟= 𝜇(𝑥), where 𝑟 divides 𝑞 − 1 and the rational function 𝜇(𝑥) is not the 𝑑-th power of an element 𝑣(𝑥) ∈ 𝔽 q (𝑥) for any divisor 𝑑 of 𝑟 with 𝑑 > 1, has the following properties:
1.If
2. The set of 𝔽 q −rational points (essentially) satisfies |𝔈 (𝔽 q )| ≥ 𝑟 ∙ |𝖅𝜇|.
Proof: For details and proofs, we refer to the literature on algebraic function fields for instance, 12.
Now, let us explain briefly how construct such rational functions 𝜇: Let ℓ(𝑥) ∈ 𝔽𝑝 [𝑥 ], and we denote by 𝔙ℓ the set { 𝛼∈ 𝔽 q ; ℓ(𝛼)= 0}
1. We split ℓ(𝑥) as ℓ(𝑥) = 𝑓 (𝑥) + 𝑔(𝑥) with 𝑓 (𝑥), 𝑔(𝑥) ∈ 𝔽𝑝 [ 𝑥]. We denote the zero sets (in 𝔽 q ) of 𝑓 (resp 𝑔) by 𝔙𝑓 (resp, 𝔙𝑔), then the rational function
satisfies (𝛼) = 1 for 𝛼 ∈ 𝔙𝓁 \ (𝔙𝑓 ⋃ 𝔙𝑔).
2. Given (𝑥) ∈ 𝔽𝑝(𝑥), we will denote by ℛ (𝑓 (𝑥)) the remainder of the Euclidean division of 𝑓 (𝑥) by ℓ(x). In this way, we have (essentially):
In accordance with above observation, we need consider polynomials ℓ(𝑥) ( 𝔽𝑝 [𝑥] having many roots in 𝔽𝑝.
Definition 5.1 A polynomial (𝑥) ∈ 𝔽 q [ 𝑥 ] is a restricted range polynomial if ??(𝛼) ∈ 𝔙 ⫋ 𝔽𝑝 for some proper subset of 𝔽𝑝 and for all 𝛼 ∈ 𝔽 q . In particular, when 𝔙 = 𝔽𝑝, we say that (𝑥) is a 𝔽 q , 𝔽𝑝-polynomial.
A classic example of restricted range polynomial is the norm polynomial
Definition 5.2 A nonzero (𝔽 q , 𝔽𝑝)−polynomial 𝑓(𝑥) ∈ 𝔽 q [𝑥] will be called minimal, if deg (𝑓(𝑥)) ≤ 𝑞 − 1 and none its proper partial sums is a (𝔽 q , 𝔽𝑝)-polynomial.
We recall briefly some properties of (𝔽 q , 𝔽𝑝)-polynomial. For proofs, we refer to 5 and 13.
Proposition 5.213 (𝔽 q , 𝔽𝑝)-polynomials are subjective.
Theorem 5.15 (Characterization of (𝔽 q , 𝔽𝑝) -polynomials) The exponent sets of the minimal (𝔽 q , 𝔽𝑝)-polynomials are the 𝑝-cycles of set{0,…, 𝑞 − 1}. For each 𝑝-cycle ℑ, all the minimal (𝔽 q , 𝔽𝑝)-polynomials with exponent set ℑ are:
where 𝑖 is an arbitrary but fixed representative of ℑ. In addition, we have all the different (𝔽 q , 𝔽𝑝)-polynomials of less or equal degree to 𝑞−1 by sums of polynomials ??ℑ (𝑥, 𝛼) corresponding to different cycles.
Example 5.1 Using Theorem 5.1 and Example 2.2, we exhibit some (𝔽27: 𝔽3) -polynomials.
Remark 5.1 Proposition 5.2 says that each (𝔽 q , 𝔽𝑝)-polynomial is subjective, hence, we can use this fact to construct appropriate rational functions which leads us to obtain curves over the finite field 𝔽 q with good parameters. The following examples explain how. The reader who is not familiar with the concepts of algebraic function fields (i.e., algebraic curves) as genus, rational points etc is referred to 12.
Example 5.2 The curve ℭ over 𝔽9 given by 𝑦2 = −(𝑥6+ 𝑥5 + 𝑥4 + 2𝑥2+ 2) has 𝑔(ℭ)=2 and 20 rational points. The best value possible, cf 2.
The affirmation is clear. Let us briefly explain how we obtained this equation. Observe that there are 3-cycles of length 2, namely (1,3),(2,6) and (5,7), then set {1,3,5,7} which is not an 𝑆2 set! induces the 𝔽9,𝔽3-polynomial ℓ(𝑥) = 𝑥7 + 𝑥5 + 𝑥3 + 𝑥 which has its roots in 𝔽9. We will take advantage of this fact to construct our curve. In general, given two co-primes polynomials ℓ(𝑥), 𝑓(𝑥) ∈ 𝔽𝑝[ 𝑥] and 𝑟 |𝑞 − 1, the Euclidean division
(𝑥)𝑟 = ℓ(𝑥) ∙ ℎ(𝑥) + ℛℓ(𝑓(𝑥)𝑟),
implies that for each 𝛼 ∈ 𝔽 q root of ℓ(𝑥), ℛℓ (𝑓(𝑥)𝑟)(𝛼) = 𝑓(𝛼)𝑟; i.e. ℛℓ (𝑓(𝑥)𝑟)(𝛼) is an 𝑟-th power in 𝔽 q , therefore the polynomial 𝑦𝑟 = ℛℓ (𝑓(𝑥)𝑟)(𝛼) splits completely en 𝔽 q [𝑦], this means many points. Now in our situation taking (𝑥) = (𝑥 −1) (𝑥 +1) (𝑥4 + 2𝑥 + 2) we have, ℛℓ ((𝑥)2) = −(𝑥6 + 𝑥5 + 𝑥4 + 2𝑥2 + 2), this carry us to our equation.
Example 5.3 The curve ℭ over 𝔽27 given by 𝑦2 = −(𝑥4 + 2𝑥3 + 𝑥2 + 1)3 has 𝑔(ℭ) = 1 and #ℭ (𝔽27) = 38.
By Proposition 3.4, the union of the underlying sets of the 3-cycles (1,3,9) and (2,6,18) is an 𝑆2 set. This set induces the (𝔽27:𝔽3)-polynomial ℓ(𝑥) = 𝑥18 + 𝑥9 + 𝑥6 + 𝑥3 + 𝑥2 + 𝑥 which induces the rational function 𝜇(𝑥) = −𝑥2 (𝑥+1)2 (𝑥4 + 2𝑥3 + 𝑥2 + 1)3 and consequently the algebraic curve ℭ over 𝔽27 defined by the equation:
𝑦2 = −(𝑥4 + 2𝑥3 + 𝑥2 + 1)3.
(Here we split ℓ(𝑥) as ℓ(𝑥) = ℓ1(𝑥) + ℓ2(𝑥) where ℓ1(𝑥) = 𝑥 + 𝑥2 and ℓ2(𝑥) = 𝑥3 + 𝑥6 + 𝑥9 + 𝑥18 = 𝑥3 (𝑥+1)3 (𝑥4 +2𝑥3 + 𝑥2 + 1). Observe that the places corresponding to 𝑥 = 0 and 𝑥 = −1 are unramified.)
It is easy to see that the curve ℭ has genus 𝑔 = 1. For the number of rational points (or places of degree one in the language of algebraic function fields), observe that (ℓ(𝑥), 𝑥27 - 𝑥) = 𝑥 + 𝑥2 + 𝑥4 + 2𝑥5 + 𝑥6 +2𝑥7 + 𝑥9, therefore the curve ℭ has at least 2 ∙ #ℓ−1(0) = 2 ∙ 9 = 18. We use computer program Mathematica to complete the determination of the rational points, we refer to 11, Remark 2.2 for details.
Example 5.4 The 𝑆2 3-cycle of length 3, (17,25,23) induces the minimal (𝔽27:𝔽3)-polynomial ℓ(𝑥) = 𝑥17 + 𝑥25 + 𝑥23 which has 9 roots in 𝔽27, namely the zeros of the polynomial 𝑓(𝑥) = 𝑥 + 𝑥7 + 𝑥9 = 𝑥(1 + 𝑥)(2 + 𝑥)(2+ 𝑥2 + 𝑥3)(1+ 2𝑥2 + 𝑥3). If we split ℓ(𝑥) as ℓ(𝑥) = 𝑥17 + 𝑥23 (𝑥2 + 1) and consider the rational function 𝜇(𝑥) := −𝑥6 (𝑥2 + 1), then for each α root of 𝑓(𝑥), 𝜇(𝛼) = 1.
Now, the curve ℭ over 𝔽27 defined by the Kummer equation
𝑦26 = (𝑥): = −𝑥6 (𝑥2 + 1),
has genus 𝑔 = 24 and 208 rational points. This is the best value know for (𝑞, 𝑔)=(27,24) (see 2).
Example 5.5 We will construct here two maximal curves ℭ1 and ℭ2 over 𝔽49 with (ℭ1) = 1 and (ℭ2) = 3.
In Table 9, we exhibit some 𝑆2 sets 𝔖 ⊂ I48 which was obtained as union of 3 7-cycles of length 2. For this example we consider the set 𝔖 ={1,2,7,11,14,29} = { ⟨1⟩ ∪⟨2⟩ ∪ ⟨11⟩}. This set induces the (𝔽49:𝔽7)-polynomial ℓ(𝑥) = 𝑥 + 𝑥2 + 𝑥7 + 𝑥11 + 𝑥14 + 𝑥29). By Proposition 5.2 there exist a subset 𝔙 ⊂ 𝔽49 such that ℓ(𝔙) = 1 and after some computations we obtain that 𝔙 is the zero set of the polynomial 𝑙(𝑥) = 1+ 𝑥+ 𝑥2 + 6𝑥3 + 𝑥4. We use this polynomial to construct our curves instead of ℓ(x), the reason is that ℓ(x) has high degree compared to |𝔙|. Now we split 𝑙(𝑥) as 𝑙(𝑥) = (1+ 𝑥+ 4𝑥2 + 𝑥4) + (6𝑥3), the polynomial 1+ 𝑥+ 4𝑥2 + 𝑥4 can be factored as 1+ 𝑥+ 4𝑥2 + 𝑥4 = (5 + 𝑥)3 (6 + 𝑥) and therefore we consider the Kummer cover defined by the equation
This algebraic function field has genus 𝑔 = 𝑟 − with 𝑑= 𝐺𝐶𝘋(𝑟,3), this gives, for 𝑟 =2, 𝑔(ℭ1) = 1 and for 𝑟 =4, 𝑔(ℭ2) = 3, the rational points satisfies #ℭ1 = 64 and #ℭ2 = 92 (see tables in 3).