Un ejemplo de articulación de la lógica y la geometría dinámica en un curso de geometría plana^*

An example of the articulation of logic and dynamic Geometry in a plane Geometry course

Carmen Inés Samper de Caicedo^**
Patricia Perry^***
Leonor Camargo^****
Óscar Molina^*****

^*Una versión preliminar de este artículo ha sido publicada en las memorias del XX Encuentro de Geometría y sus Aplicaciones, Universidad Pedagógica Nacional, Bogotá, 23 a 25 de junio de 2011.
^**Universidad Pedagógica Nacional. Bogotá, Colombia. csamper@pedagogica.edu.co
^***Universidad Pedagógica Nacional. Bogotá, Colombia. pperryc@yahoo.com.mx.
^****Universidad Pedagógica Nacional. Bogotá, Colombia. lcamargo@pedagogica.edu.co.
^*****Universidad Pedagógica Nacional. Bogotá, Colombia. ojmolina@pedagogica.edu.co.

Recibido: 15/01/12, Aprobado: 15/11/12

Resumen

En este artículo damos a conocer nuestro punto de vista en relación con el papel de la lógica matemática en los procesos de enseñanza y aprendizaje de la demostración. Ilustramos cómo introducimos temáticas de la lógica en un curso de geometría, para lo cual acudimos a los sucesos del cursillo realizado en el XX Encuentro de Geometría y sus Aplicaciones. Presentamos ejemplos en el los que la geometría dinámica se constituye en un contexto que propicia el acercamiento sugerido a la lógica matemática.

Palabras Clave Lógica matemática, geometría dinámica, formación de profesores, enseñanza y aprendizaje de la demostración.

Abstract

In this paper we present our point of view with respect to the role of mathematical logic in the teaching and learning of proof. We illustrate how to introduce topics of logic in a geometry course. To do so, we rely on results obtained during the workshop developed during the 20º Encuentro de Geometría y sus Aplicaciones. We present examples where dynamic geometry becomes a context that favors the suggested approach to mathematical logic.

Keywords Mathematical logic, dynamic geometry, teacher training, teaching and learning of proof.

Introducción

En la actualidad, se percibe más claramente la problemática compleja en la que está inmersa la construcción de demostraciones por parte de estudiantes de básica secundaria y universidad. Un aspecto que ha sido objeto de discusión entre los investigadores que se han preocupado por los procesos de enseñanza y aprendizaje de la demostración es el papel de la lógica matemática en ellos. Existen posiciones encontradas con respecto a la inclusión del estudio de la lógica matemática en la formación de estudiantes de carreras que tienen un fuerte componente matemático; es el caso de matemáticas, licenciaturas de matemáticas, ingenierías, entre otras. Específicamente, varios estudios se han centrado en determinar cuáles son los temas que se deben incluir y los énfasis que se deben hacer en cursos cuya intención es apoyar a los estudiantes en su transición desde la matemática enfocada en lo procedimental a aquella en la que la demostración cumple un papel crucial (Selden y Selden, 2008; Epp, 2003). A ese respecto, la necesidad del estudio de la lógica matemática ha sido un asunto polémico.

El objetivo de este artículo es dar a conocer nuestro punto de vista en relación con lo anterior e ilustrar la manera de introducir temáticas de la lógica en un curso de geometría. Para la ilustración echamos mano de sucesos del cursillo realizado en el XX Encuentro de Geometría y sus Aplicaciones realizado en 2011 en Bogotá. Además presentamos ejemplos en los que la geometría dinámica se constituye en un contexto que propicia el acercamiento sugerido a la lógica matemática.

Breve revisión de la literatura

Estudio de la lógica matemática

Varios investigadores defienden la tesis de que no es necesario hacer un tratamiento especial de aspectos relacionados con la lógica en los diferentes cursos de matemáticas dado que estudiar matemáticas desarrolla la habilidad de razonar lógicamente. Esta idea es central en la denominada teoría de la disciplina formal y ha sido estudiada por Inglis y Simpson (2008). Otros exponen que el estudio de elementos lógicos elementales (tautologías, conectivos, esquemas de razonamiento válidos, métodos de demostración) no tiene efectos significativos en los resultados de tareas de razonamiento lógico o en la habilidad para hacer demostraciones en geometría (Deer, 1969, citado por Epp, 2003). Así mismo, Hanna y de Villiers (2008, p. 331) manifiestan: "No es claro qué beneficio se desprende de enseñar lógica formal a estudiantes o a futuros profesores, en particular, porque los matemáticos tienden a admitir que rara vez usan la lógica formal en sus investigaciones".

Otros investigadores, conscientes de la complejidad cognitiva implícita en tareas como la determinación del valor de verdad de una proposición y la validación de una afirmación matemática mediante una demostración, consideran que no se puede dar por sentado que los estudiantes, de manera intuitiva y espontánea, las realizan apropiadamente. Por esta razón, señalan la necesidad de tratar de manera deliberada asuntos de lógica mediante la enseñanza, para que los estudiantes puedan tener diversas experiencias en distintos contextos matemáticos en relación con el uso y la comprensión de las respectivas ideas. Al respecto, Selden y Selden (2008, p. 196) hipotetizan la importancia de un curso para aprender a construir demostraciones en el que los asuntos de lógica se aborden cuando al revisar las demostraciones de los estudiantes se vea clara la pertinencia de tratarlos; en el curso se trabaja con teoremas sobre conjuntos, funciones, temas de análisis real, álgebra abstracta, topología, entre otros. Por su parte, Epp (2003) propone también un curso cuyo objetivo es desarrollar las habilidades de razonamiento de los estudiantes; en la unidad inicial del curso se trabajan fundamentos que proporcionan un marco conceptual para poder trabajar con cierta autonomía posteriormente (por ejemplo, lógica, cuantificadores, esquemas de razonamiento), y aboga para que el tratamiento de estos se haga en conexión con el lenguaje y en situaciones de índole tanto matemática como de la cotidianidad; en el resto del curso se traen a colación tales fundamentos para destacar cómo funcionan en la práctica de la demostración.

Finalmente, otros investigadores (Cheng et al., 1986, y Mueller, 1975, citados en Epp, 2003) reconocen el efecto positivo que tiene la enseñanza de la lógica en los procesos de razonamiento de los estudiantes pero abogan porque ésta se desarrolle como unidad temática en los cursos de una disciplina específica, como la geometría, de donde se extraen ejemplos concretos, y que además se usen ejemplos del diario discurrir para explicar principios lógicos.

Nuestra postura didáctica es similar a la de Selden y Selden (2008), Cheng et al. (1986, citado por Epp, 2003) y Mueller (1975, citado por Epp, 2003) en cuanto a que reconocemos que se deben abordar cuestiones de la lógica matemática con cierto formalismo, pero disentimos con los primeros en que ello se haga dentro de un curso cuyo contenido primario sea la demostración. Más bien, nos inclinamos a lo que proponen los últimos dos: mezclar el estudio de la lógica con el de otra disciplina de la matemática, pero vamos más allá. Creemos que se deben tocar los asuntos concernientes a la lógica durante el desarrollo de cualquier curso, en momentos en que ello sea necesario y significativo para los alumnos, porque ello contribuye a la comprensión de un concepto o de un proceso, y no en una unidad especial. Además, abogamos por el uso de la geometría dinámica, entorno que provee elementos tanto para el tema de geometría que se esté estudiando como para el correspondiente de la lógica que se saca a la luz en ese momento.

Geometría dinámica

En la actualidad, se reconoce ampliamente el potencial de la geometría dinámica como mediador instrumental para el aprendizaje de la demostración (Bartolini y Mariotti, 2008). Su uso para resolver tareas que buscan propiciar actividades matemáticas, como la producción de conjeturas, el razonamiento argumentativo y la vinculación de éste con la producción de demostraciones matemáticas, apoya la participación real de los estudiantes en el proceso de conjeturación y de justificación.

Jones (2000) señala que la preparación para la demostración puede hacerse con actividades de enseñanza que lleven a los estudiantes a tener conciencia de la dependencia entre propiedades, y agrega que ello hace que el razonamiento deductivo sea significativo. Olivero (2002) plantea que el aprendizaje de la demostración se favorece mediante procesos, apoyados en la geometría dinámica, que focalizan la atención de los estudiantes en hechos particulares de los cuales van emergiendo las conjeturas y elementos para realizar una demostración. Reconoce además que el papel fundamental del programa de geometría dinámica es constituirse en instrumento con el cual el contexto interno del aprendiz (que incluye el conocimiento previo y su experiencia) se puede hacer explícito y puede ser compartido con otros.

Aunque ninguno de los autores mencionados se refiere explícitamente a la enseñanza o aprendizaje de la lógica, la revisión anterior nos hace suponer la pertinencia de la geometría dinámica como instrumento para sacar a la luz aspectos problemáticos relacionados con el aprendizaje de la lógica, favorecer la construcción de significados asociados a elementos de la lógica, y comprender el trasfondo lógico de la argumentación deductiva, es decir, entender cómo se concluyen propiedades a partir de la información dada.

Asuntos problemáticos

Como se ha visto, no hay una posición unificada de los investigadores frente al papel de la lógica en el aprendizaje de la demostración. No obstante, sí coinciden en reconocer la existencia de asuntos problemáticos estructurales que afectan el mencionado aprendizaje. Consideramos como asuntos problemáticos las acciones de los estudiantes que no obedecen a conceptos o procedimientos matemáticos institucionales, o a las normas socio matemáticas establecidas para el funcionamiento en el aula. Estas últimas son reglas implícitas, o que el profesor declara, relativas al tratamiento que se le dará a la matemática misma y con respecto a las cuales se espera una enculturación de los estudiantes.

A partir de nuestro análisis de las acciones de los estudiantes al construir una demostración, hemos podido agrupar las problemáticas en torno a cuatro asuntos estructurales, dos de los cuales son pertinentes para el tema que nos ocupa: el uso de la lógica matemática como guía y sustento del razonamiento requerido para producir una justificación, y la comprensión y el manejo del enunciado de un teorema¹ (Perry, Camargo, Samper y Rojas, 2006). En el primer asunto se destaca la necesidad de tener el conocimiento conceptual y procedimental de las conectivas lógicas y de las tautologías, y comprender la validez del método de prueba indirecta y poder realizar el respectivo procedimiento. El segundo asunto está relacionado con el trabajo dentro de un sistema axiomático. Tiene que ver, entre otras, con el reconocimiento de la necesidad de formular de manera precisa las definiciones, de verificar el cumplimiento de las condiciones de la hipótesis del hecho geométrico que se pretende usar, de proveer el respaldo teórico explícito y apropiado de las proposiciones que conforman una justificación.

Aproximación metodológica

A partir del estudio cuidadoso de los asuntos problemáticos mencionados, diseñamos estrategias, es decir, planes de acción que la profesora sigue deliberadamente durante el desarrollo de un curso, con el propósito de lograr la respectiva modificación del proceder de los estudiantes, a largo o corto plazo (Samper, Perry, Echeverry y Molina, 2008). En el diseño tuvimos en cuenta, entre otras cosas, la necesidad de: aclarar la estructura lógica de las proposiciones; enfatizar en la realización de acciones de carácter heurístico para favorecer la construcción de conjeturas que establezcan relaciones de dependencia que dan significado a la condicional o de contraejemplos para entender esquemas de razonamiento como la ley de De Morgan y el modus tollendotollens; e identificar el papel que desempeñan las condicionales y el estudio de casos en la construcción de demostraciones formales y en los mecanismos para producir una cadena deductiva. La gestión del contenido que realiza la profesora durante el cursillo al que hacemos referencia en este documento es un reflejo de las estrategias que ella se ha apropiado.

En el diseño de las actividades propuestas en el cursillo se tuvo en cuenta la propuesta de Durand -Guerrier (2003) en el sentido de usar reflexivamente la condicional abierta Px → Qx para ayudar a que los estudiantes tengan mejor comprensión de aspectos lógicomatemáticos y porque ello propicia el desarrollo del razonamiento plausible. Para una condicional abierta, se considera ejemplo cualquier caso en el que el antecedente y el consecuente son verdaderos, mientras que es contraejemplo cualquier caso en el que el antecedente es verdadero y el consecuente falso. Si se aceptan proposiciones contingentes (por ejemplo, aquellas en las que no puede decidirse su valor de verdad) en los cursos de matemáticas, se abre un panorama rico en posibilidades de análisis.

Ejemplo de la gestión de la profesora para establecer conexiones con la lógica

A continuación presentamos una secuencia de tres problemas y el conjunto de sucesos del cursillo realizado en el XX Encuentro de Geometría y sus Aplicaciones, en donde se evidencia cómo la profesora usa las producciones de los participantes, con relación con los problemas presentados, para hacer referencia a aspectos de la lógica.

Diagonales de un cuadrilátero y estructura del enunciado condicional, su tabla de verdad, la negación y la conjunción

El primer problema propuesto es:

Use geometría dinámica para estudiar la relación entre tipo de cuadrilátero y la propiedad "una diagonal es perpendicular a la otra".

• Describa brevemente su construcción y el proceso de exploración.
• Escriba una conjetura.

Esta tarea tiene tres propósitos: el primero, la oportunidad de percatarse de relaciones de dependencia que se manifiestan cuando al arrastrar un elemento básico de la construcción para cumplir una cierta propiedad se dan simultánea y consecuentemente cambios en otros elementos; el segundo, destacar que la conjetura debe reportar esa relación; el tercero, establecer y analizar las definiciones de las figuras geométricas que emergen como resultado de la tarea. Por tanto, apunta a la comprensión de la estructura lógica de la afirmación condicional y de la relación de dependencia entre las condiciones expresadas en el antecedente y aquellas del consecuente, así como a la comprensión de la conjunción de proposiciones y de la negación. Por esta razón, el reporte del proceso de construcción y de exploración realizados es tan importante como la conjetura formulada.

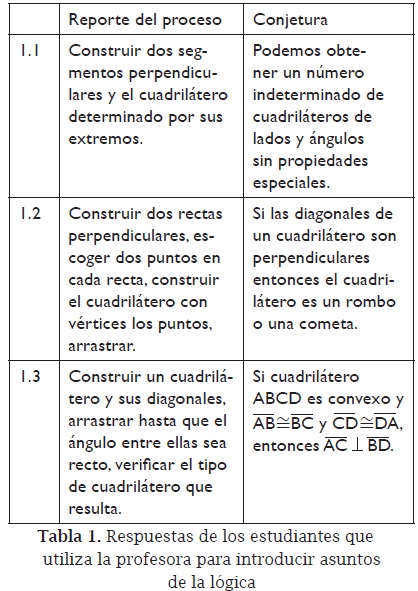
Tres respuestas que la profesora usa para favorecer la comprensión del enunciado condicional, son:

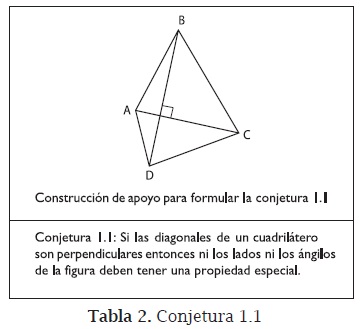
La profesora organiza las conjeturas en el orden en que las va a analizar. Su primer comentario con respecto a la conjetura 1.1 concierne a su formulación: no se ha escrito como una afirmación condicional; en particular, el enunciado que presentan hace referencia a una conclusión, mas no plantea las condiciones a partir de las cuales se obtuvo la conclusión. A partir de ello explica lo que es una condicional, su estructura y lo que se comunica a través de ella.

Aprovecha este momento para indicar que con las herramientas del programa o con el arrastre, la geometría dinámica permite ver las consecuencias (si las hay) de construir una figura con unas determinadas propiedades; éstas conforman la hipótesis de la condicional (figura 1), y lo que se puede inferir de lo que sucede es precisamente la tesis de la condicional. Es decir, el uso de la geometría dinámica permite reconocer situaciones de dependencia.

Teniendo en cuenta la construcción realizada y lo observado en relación con el tipo de cuadrilátero cuando se arrastran los elementos libres de la construcción, entre todos reformulan la conjetura 1.1.

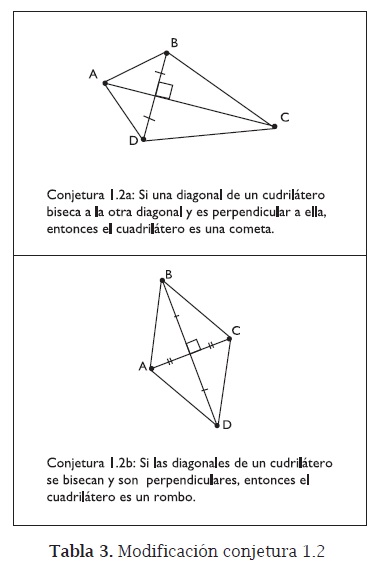
Esta conjetura contradice la propuesta 1.2, hecho que motiva la revisión para determinar si, además de la perpendicularidad de las diagonales, se atribuyeron otras propiedades a la figura, bien en su construcción o al explorarla. Se nota que para obtener la cometa arrastraron el segmento perpendicular construido hasta lograr que el punto medio de la otra diagonal fuera un punto del segmento. Para obtener el rombo, arrastraron uno de los vértices que pertenecen al segmento perpendicular construido hasta lograr que las diagonales se bisequen. La revisión pone de manifiesto que la congruencia de lados adyacentes depende de otras propiedades y que éstas deben ser reportadas en la afirmación condicional. De esta forma surgen dos conjeturas (tabla 3).

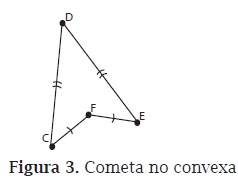
Con la discusión anterior se abre el espacio para precisar la definición de cometa y analizarla trayendo a cuento los respectivos elementos de la lógica de proposiciones. Se propone como definición de cometa: "Una cometa es un cuadrilátero con dos pares de lados adyacentes congruentes y ningún par de lados opuestos congruentes".

En el análisis de la definición, la profesora comienza por destacar la estructura lógica de una bicondicional que involucra una conjunción: c↔(p^q^r^s), donde las proposiciones que la componen son: c: ser cometa, p: ser cuadrilátero, q: tener un par de lados adyacentes congruentes, r: tener otro par de lados adyacentes congruentes y s: tener ningún par de lados opuestos congruentes. Aprovecha esta situación para hablar sobre la conjunción de proposiciones. Con el propósito de establecer la ley de De Morgan para la negación de una conjunción, la profesora plantea la siguiente tarea:

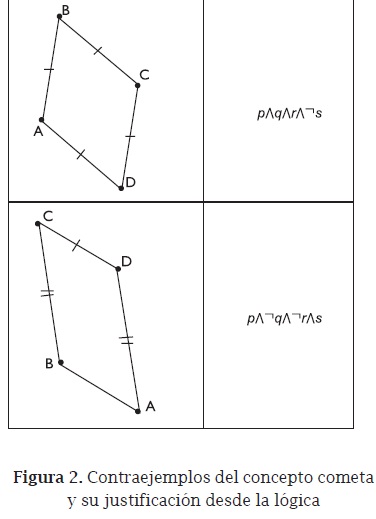
Con geometria dinamica, busque ejemplos de figuras que no son cometa y justifique su respuesta

A medida que se van presentando los diferentes contraejemplos de cometa, la profesora resalta que detrás del proceso de búsqueda está el uso de la siguiente proposición: ¬c↔(¬pv¬qv ¬rv ¬s). Algunos contraejemplos junto con la simbolización de las propiedades de cada figura, con respecto a la definición de cometa, se presentan en la figura 2.

En relación con la conjetura 1.3, la profesora resalta que el proceso de construcción asociado difiere de los dos anteriores, pues la perpendicularidad de las diagonales se obtiene con el arrastre, propiedad que debe incluirse en la hipótesis de la condicional, pero que en la conjetura se reporta en la tesis. Indagando acerca del proceso de construcción y exploración realmente realizadas, es claro para el grupo que el arrastre se usó para obtener la congruencia de dos pares de lados adyacentes, y que se observó la perpendicularidad de las diagonales. Con esta situación, la profesora introduce el concepto de proposición recíproca, pues las conjeturas que se corresponden con el proceso de construcción y exploración son recíprocas de la conjetura reportada:

• Conjetura 1.3a: si un cuadrilátero es cometa entonces una diagonal es perpendicular a la otra y contiene su punto medio.
• Conjetura 1.3b: si un cuadrilátero es rombo entonces las diagonales se bisecan y son perpendiculares.

Frente a la afirmación de la conjetura 1.3, la profesora aprovecha la oportunidad para establecer dos definiciones e introducir la tabla de verdad de la condicional.

Definición: Un polígono es convexo si la región poligonal (el polígono y su interior) es un conjunto convexo.

Definición: Un conjunto de puntos X es convexo si la siguiente propiedad es verdadera: si los puntos A y B pertenecen al conjunto X entonces el AB⊂X.

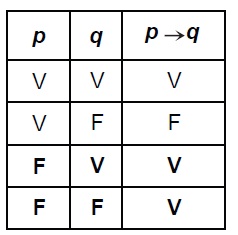
Ella no formula la definición de conjunto convexo como usualmente aparece en los textos (un conjunto de puntos X es convexo si para cualquier par de puntos A y B del conjunto se tiene que el AB⊂X.).A continuación se verá la razón de esta decisión. A través de representaciones figurales, como un triángulo y un círculo, se determina que el primero es un polígono convexo mas no un conjunto de puntos convexo, mientras que el segundo sí es un con-junto convexo. En seguida, la profesora pregunta: "¿Es convexo el conjunto con un solo punto?". La respuesta negativa de muchos de los asistentes y la correspondiente justificación, según la cual el segmento no existe porque hay un solo punto, muestra que es posible que no haya una comprensión real de la definición de conjunto convexo. Por ello, la profesora introduce la tabla de verdad de la condicional a partir del análisis de la proposición p^ ¬q, pues fácilmente es aceptada como equivalente a la negación de una condicional; ello porque se basan en la interpretación de esta última como la expresión de una relación de causa-efecto.

Examinando la tabla para determinar el valor de verdad de la proposición en cuestión, el conjunto unitario es convexo, se obtiene que es verdadera pues su antecedente es falso (el conjunto unitario no tiene dos puntos).

A continuación, la profesora pregunta si la siguiente figura es una cometa:

Aceptar que en efecto lo es, precisamente una cometa no convexa, permite ver la necesidad de transformar la conjetura 1.2a, pues no en todas las comentas se intersecan sus diagonales. Se obtiene entonces la conjetura 1.2a': si una diagonal de un cuadrilátero está contenida en la mediatriz de la otra diagonal, entonces el cuadrilátero es una cometa.

Propiedades de cuadriláteros y enunciados condicionales

En la segunda sesión del cursillo, se presenta el siguiente problema:

Use geometría dinámica para determinar si la respuesta a la pregunta es "Sí", "No" o "No se sabe". Si la respuesta es esta última, indique la condición que debe añadirse para que la respuesta sea afirmativa. a) El cuadrilátero XYZW tiene un ángulo recto y dos lados adyacentes congruentes. ¿Es un cuadrado? b) Las bisectrices de un par de ángulos opuestos de un cuadrilátero se intersecan en más de un punto. ¿El cuadrilátero es una cometa?

Este tipo de ejercicio se propone por su gran riqueza para modificar imágenes conceptuales y acercar a los alumnos a la definición del concepto, para propiciar el desarrollo del razonamiento plausible y para precisar la comprensión de lo que es una condicional.

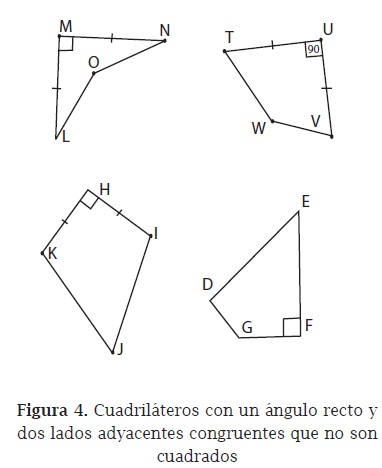
La profesora destaca que la variedad de respuestas a la primera pregunta le permite usar la geometría dinámica para examinar si las condiciones que se agregan o los contraejemplos que se proveen constituyen justificaciones apropiadas para la respuesta dada. Puesto que además de reconocer que el cuadrado es un ejemplo de la figura descrita también se encontraron contraejemplos, la respuesta correcta es "No se sabe". A continuación se muestran cuatro contraejemplos (figura 4), el último de los cuales lo proporciona la profesora con la intención de llamar la atención sobre la representación prototípica que dejan translucir los contraejemplos propuestos (el ángulo recto determinado por lados congruentes).

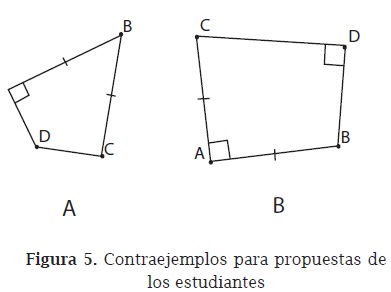
En el problema se solicita además modificar las condiciones iniciales para lograr una proposición condicional verdadera. Una de las propuestas que se analiza es: "Si el cuadrilátero tiene un par de ángulos opuestos rectos y dos lados adyacentes congruentes, entonces es un cuadrado". Con geometría dinámica se desvirtúa la propuesta (figura 5A), y con ello se determina que la condicional es falsa pues no se tienen las condiciones suficientes para que la figura sea un cuadrado.

La profesora usa de nuevo la geometría dinámica en la búsqueda de un contraejemplo (figura 5b) para otro argumento propuesto: "Si un cuadrilátero tiene dos lados adyacentes congruentes, éstos determinan un ángulo recto y el ángulo opuesto también es recto entonces es un cuadrado".

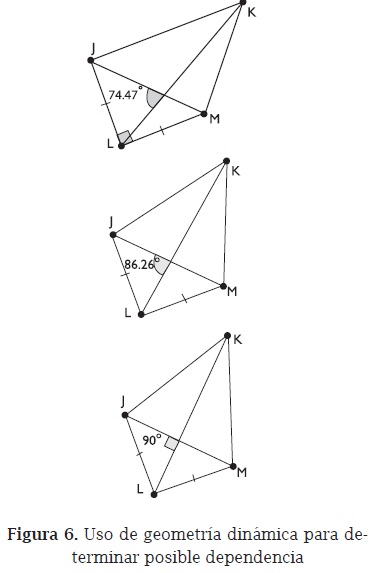
La profesora destaca que la búsqueda de contraejemplos con el apoyo de la geometría dinámica se ha hecho mediante construcciones robustas (Healy, 2000) que satisfacen todas las condiciones que se plantean en el antecedente del enunciado y que permiten ver que no es verdadera la conclusión propuesta en el consecuente. Para analizar una tercera propuesta, "Si un cuadrilátero tiene un ángulo recto, dos lados adyacentes congruentes y diagonales perpendiculares, entonces es un cuadrado", la profesora procede de manera diferente. Hace una construcción blanda (Healy, 2000), en la que se cumplen solo dos de las condiciones planteadas en el antecedente (el ángulo recto y la congruencia de dos lados adyacentes), usa el arrastre para lograr que la construcción blanda cumpla también la tercera condición del antecedente (la perpendicularidad de las diagonales), y durante el arrastre le pide a los asistentes que enfoquen la atención en determinar si hay o no un cambio simultáneo en el tipo de cuadrilátero. El arrastre permite ver que no hay relación de dependencia entre las tres propiedades y la conclusión porque no se evidencia un cambio simultáneo en la figura. Específicamente, la congruencia de los cuatro lados del cuadrilátero no se obtiene al obligar a las diagonales a ser perpendiculares (figura 6).

Con el procedimiento anterior, entre todos se determinan las condiciones bajo las cuales la figura es un cuadrado o una cometa. Es cuadrado si al arrastrar se logra que las dos diagonales se bisequen; es cometa si una de las diagonales está contenida en la mediatriz de la otra. De nuevo, se destaca que hicieron falta condiciones en la hipótesis de la condicional para reportar una verdadera relación de dependencia.

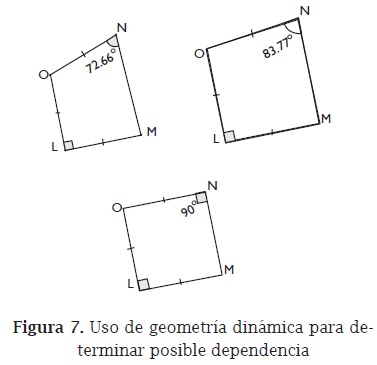
Al examinar una cuarta propuesta, "si el cuadrilátero tiene dos ángulos rectos y tres lados congruentes, entonces es cuadrado", se suscita una discusión en tor-no a si los ángulos rectos mencionados deben ser adyacentes, condición que se había impuesto en el antecedente de otra conjetura presentada. La profesora usa una construcción blanda y el arrastre, y de nuevo la geometría dinámica desempeña un papel importante, pues permite resolver la controversia. Ella construye un cuadrilátero con un ángulo recto y tres lados congruentes, y con el arrastre se logra que el ángulo opuesto al recto también sea recto (figura 7). Además, se observa el cambio simultáneo en la figura: tan pronto el <ONM se hace recto, el NM queda de la misma longitud de los demás segmentos y tanto el <LON como el <LMN se hacen rectos.

El obtener, en efecto, un cuadrado lleva a cuestionar la definición usual de cuadrado (cuatro ángulos rectos y cuatro lados congruentes) y a advertir que ella impone más condiciones de las que realmente se requieren, lo cual muestra que las definiciones son arbitrarias.

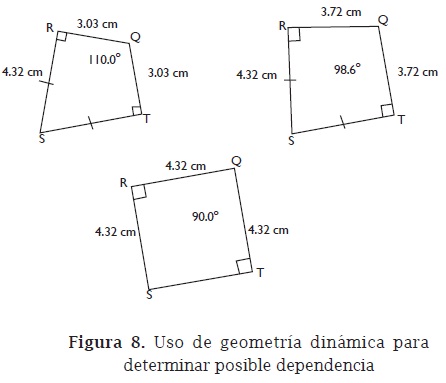
La profesora, al proponer el análisis de la última conjetura propuesta: "Si un cuadrilátero tiene dos lados adyacentes congruentes y tres ángulos rectos, entonces es cuadrado", abrió el espacio para que los asistentes evidenciaran que si uno de los ángulos rectos es el determinado por los lados congruentes, entonces el resultado es un cuadrado. Por otro lado, si el tercer ángulo recto no es aquel determinado por los lados congruentes, la única forma de construir un cuadrilátero con las condiciones exigidas es por medio del arrastre. De nuevo, el resultado es un cuadrado (figura 8).

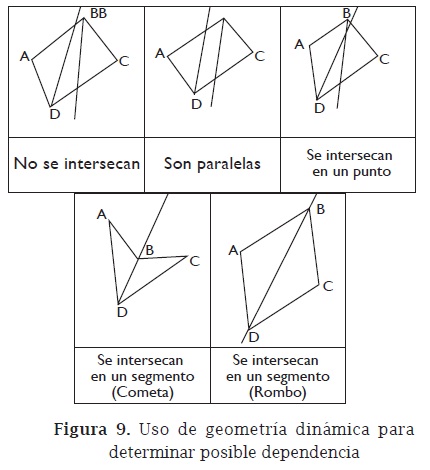
Ahora, la pregunta del ítem (b) de la segunda sesión del cursillo plantea una situación para cuyo abordaje resulta imprescindible la geometría dinámica (al menos así fue para quienes participaron en este cursillo), pues no es fácil imaginar qué relación pueden tener las bisectrices de los ángulos opuestos en un cuadrilátero. Usando geometría dinámica, se observa la relación de dependencia que se genera entre el tipo de cuadrilátero y la relación entre las bisectrices, las cuales pueden ser paralelas, no intersecarse, compartir un punto o compartir un segmento. En este último caso, la figura podría ser una cometa o un rombo y, por tanto, un cuadrado (figura 9).

Ello lleva a que, entre todos se proponga la siguiente conjetura: "Si las bisectrices de un par de ángulos opuestos de un cuadrilátero comparten más de un punto, entonces el cuadrilátero es una cometa o un rombo".

Propiedades de cuadriláteros y esquemas de razonamiento válidos

En la última actividad propuesta en el cursillo, se presentan dos argumentos. Tiene como propósito destacar asuntos problemáticos que suelen surgir cuando se proveen justificaciones. Propicia la discusión sobre los esquemas de razonamiento válidos, modus ponendo ponens y modus tollendo tollens, que si se tienen como referencia contra la cual comparar los argumentos de los participantes, puede ayudar a identificar partes débiles de su comprensión con respecto al uso de la condicional en la deducción. La tarea es:

Para comenzar, se designa cada una de las proposiciones del primer argumento, así:

p: cuadrilátero DEFG tiene diagonales congruentes.

q: cuadrilátero DEFG tiene un ángulo recto.

r: cuadrilátero DEFG es un rectángulo. La primera parte del argumento de Jorge ("Como los rectángulos tienen diagonales congruentes, el cuadrilátero es un rectángulo") quedaría simbolizada como:

[(r→p) ∧p]→r

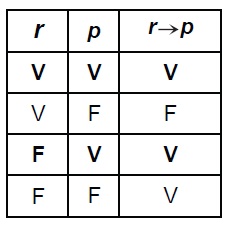
A este asunto problemático lo designamos afirmación del consecuente. Para mostrar por qué el argumento no es válido, la profesora usa la tabla de verdad de la condicional, centrando la atención en las dos filas en que p es verdadera:

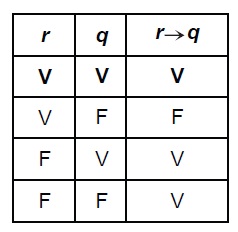
Destaca que el valor de verdad de r, cuando se asume que tanto r →p como p son proposiciones verdaderas, es verdadero o falso y que ello indica que no se puede deducir a r de las dos premisas r→p y p.

La segunda parte del argumento de Jorge ("El cuadrilátero es un rectángulo. Por definición de rectángulo, todos sus ángulos son rectos") se representa así:

[(r→q) ∧r]→q

La profesora muestra que, en este caso, en la tabla de verdad hay un solo caso en el que tanto r → q como r son proposiciones verdaderas y para este, q es una proposición verdadera. Este argumento corresponde al esquema de razonamiento modus ponendo ponens.

En cuanto al argumento presentado en la parte (b) de esta actividad, se representa así:

p: cuadrilátero HIJK es cometa.

q: cuadrilátero HIJK tiene un par de ángulos congruentes.

[(p→q) ∧¬p]→¬q

A este tipo de argumento lo denominamos negación del antecedente. De nuevo, la profesora recurre a la tabla de verdad donde destaca las filas en las que p→q es verdadera y p es falsa:

Nótese que no se puede decidir si la premisa q es verdadera o falsa, razón por la cual no es válido deducir que el cuadrilátero no tiene dos ángulos congruentes.

Comentarios finales

Con la descripción de lo sucedido durante el cursillo, en torno a la incorporación de la lógica matemática en el transcurso de la discusión de problemas de geometría, hemos mostrado cómo creemos que debe ser el estudio de la lógica en la formación de los estudiantes de la Licenciatura en Matemáticas. Ésta se trae a colación en los momentos en los que su uso ayuda aclarar conceptos de la lógica misma, y también conceptos y procesos de la geometría.

En particular, se puede estudiar la negación de una proposición en un contexto especifico, hacer evidente relaciones de dependencia lo cual posibilita acercarse a una concepción de la condicional, estudiar la relación entre la condicional y las proposiciones asociadas a ésta, y mostrar por qué ciertos argumentos no son válidos. No es necesario planear una clase especial para abordar estos temas ni es indispensable usar la geometría dinámica como artefacto mediador; cualquier momento en que se evidencie algún asunto problemático es propicio para abordarlos. Estos suelen surgir en cualquier clase, con cualquier tema. Sin embargo, hemos mostrado cómo el uso de la geometría dinámica es muy útil para indicar errores o incomprensiones razón por la cual se convierte en un elemento que apoya el aprendizaje de los estudiantes. Argumentos como los que se ejemplifican suelen darse en el aula; el profesor debe prestar mucho cuidado a las conjeturas y justificaciones que dan sus estudiantes para identificarlos e indicar al alumno por qué no son válidos.

Pie de página

¹Los otros dos asuntos problemáticos están relacionados con: el trabajo dentro de un sistema axiomático y con prerrequisitos de aritmética de los reales, álgebra y teoría de conjuntos.

Referencias

Bartolini, M.G. y Mariotti, M.A. (2008). Semiotic mediation in the mathematics classroom: Artifacts and signs after a Vygotskian perspective. En: L.D. English (ed.). Handbook of international research in mathematics education (pp. 746-783). NuevaYork: Routledge.         [ Links ]

Durand-Guerrier, V. (2003). Which notion of implication is the right one? From logical considerations to a didactic perspective. Educational Studies in Mathematics, 53(1), 5-34.         [ Links ]

Epp, S.S. (2003). The role of logic in teaching proof. American Mathematical Monthly, 110(10), 886-899.         [ Links ]

Hanna, G. y de Villiers, M. (2008). ICMI Study 19: Proof and proving in mathematics education. ZDM, 40(2), 329-336.         [ Links ]

Healy, L. (2000). Identifying and explaining geometrical relationship: Interactions with robust and soft Cabri constructions. En: T. Nakahara y M. Koyama (eds.), Proceedings of the 24th Conference of the International Group for the Psychology of Mathematics Education (vol. 1, pp. 103-117). Hiroshima, Japón: Universidad de Hiroshima.         [ Links ]

Inglis, M. y Simpson, A. (2009). Conditional inference and advanced mathematical study: Further evidence. Educational Studies in Mathematics, 72(2), 185-198.         [ Links ]

Jones, K. (2000). Providing a foundation for deductive reasoning: Students' interpretation when using dynamic geometry software and their evolving mathematical explanations. Educational Studies in Mathematics, 44(1-3), 55-85.         [ Links ]

Olivero, F. (2002).The proving process within a dynamic geometry environment. Tesis doctoral inédita. University of Bristol, Graduate School of Education.         [ Links ]

Perry, P.; Camargo, L.; Samper, C. y Rojas, C. (2006). Actividad demostrativa en la formación inicial del profesor de matemáticas. Bogotá: Fondo Editorial de Universidad Pedagógica Nacional.         [ Links ]

Samper, C.; Perry, P.; Echeverry, A. y Molina, O. (2008). Aprendizaje de la demostración en geometría euclidiana con el apoyo de un programa de geometría dinámica. Reporte de investigación inédita. Bogotá: Universidad Pedagógica Nacional.         [ Links ]

Selden, A. y Selden, J. (2008). Understanding the proof construction process. En: F.L. Lin; F.J. Hsieh; G. Hanna y M. de Villiers (eds.). Proceedings of the ICMI Study 19 conference: Proof and Proving in Mathematics Education (vol. 2, pp. 196-201). Taipei, Taiwan: The Department of Mathematics, National Taiwan Normal University Taipei.         [ Links ]