Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Cuadernos de Economía
Print version ISSN 0121-4772On-line version ISSN 2248-4337
Cuad. Econ. vol.22 no.39 Bogotá July/Dec. 2003
¿RENOVACIÓN O ELIMINACIÓN DE LOS CLÁSICOS? COMENTARIOS CRÍTICOS A UNA CONTRIBUCIÓN RECIENTE DE H. CUEVAS
José Félix Cataño*
Profesor de la Universidad Nacional de Colombia. Enviar los comentarios al correo: felixcatano@yahoo.fr. Artículo recibido el 5 de septiembre de 2003 y aprobado el 20 de octubre del mismo año.
Resumen
H. Cuevas, a partir de la teoría de la renta, de la medida del valor por medio del trabajo y de la "selecci ón de técnicas", propone una idea de "renovación" del pensamiento clásico diferente a la vía propuesta por la escuela Neo-ricardiana. Aquí se critica esta posición mostrando que esos elementos crean una visión errónea de la evolución de la teoría económica y una deformación de las posiciones centrales de los clásicos, que conducen a que esta "renovación" sea más bien la "asimilación" de sus ideas en el seno de la teoría neoclásica o walrasiana que, por ende, sería reconocida como la adecuada teoría económica general.
Palabras claves: escuela clásica, escuela neoclásica, teoría de los precios, teoría de la renta, historia de la teoría económica JEL : B410
Abstract
H. Cuevas has proposed the idea of "renovating" classical thought from rent theory, from measuring value by means of work and "selecting techniques" in a way different to that proposed by the Neo-Ricardian school. This article criticises this position, showing that these elements create an erroneous view of the evolution of economic theory, deforming the main positions adopted by classical thinkers, leading to such "renovation" being more an "assimilation" of their ideas within the bosom of neoclassical or Walrasian theory than being recognised as an adaptation of general economic theory.
Key words: classical and neoclassical schools, price theory, rent theory, history of economic theory JEL : B410
Résumé
H. Cuevas, en partant de la théorie du revenu, de la mesure de la valeur par l´intermédiaire du travail et de la «sélection de techniques», propose une idée de «rénovation» de la pensée classique différente de la voie proposée par l´école Néoricardienne. Cette position est ici critiquée en montrant que ces éléments créent une vision erronée de l´évolution de la théorie économique et une déformation des positions centrales des classiques, ce qui conduit à que cette «rénovation» soit plutôt l´«assimilation» de ses idées au sein de la théorie néoclassique ou walrasienne, qui par conséquent, serait reconnue comme la théorie économique générale adéquate.
Mots clés: école classique et néoclassique, théorie des prix, théorie des revenus, histoire de la théorie économique JEL : B410
H. Cuevas se ha distinguido en Colombia por proponer interpretaciones y algunas soluciones sobre algunos problemas de la teoría económica pura, principalmente aquellos originados en la tradición clásica y marxista (precios de producción, transformación de valores a precios, mercancía patrón, teoría de la renta). Dada la tradición ya sea pragmática (la teoría ya esta hecha o es muy abstracta, el problema es la aplicación exitosa de alguna idea) o ya sea anti-teórica (la realidad económica se nos da inmediatamente como la luz del día y, por tanto, no hay necesidad de representarla en modelos teóricos) de la mayoría de los economistas colombianos, esta empresa personal y solitaria sólo puede despertarnos un sentimiento de admiración.
Ahora bien, en el capítulo IV de La economía clásica en renovación1, Cuevas plantea la base de una "renovación" de la teoría clásica por fuera de los parámetros trazados por Sraffa y su escuela Neo-ricardiana. Esto ya suscita un gran interés ante la esperanza de poseer nuevas lecturas. El autor comienza haciendo un balance sobre el debate dado en la década de los años ochenta entre defensores del modelo clásico (la tradición Ricardo-Sraffa) en cabeza de los economistas franceses Duménil y Lévy, y el modelo neoclásico (la tradición Marshall y Walras) defendida por F. Hahn [ 1982] . Lo que está en juego allí es decidir cuál de estos modelos podría considerarse más general respecto al otro y, de esta manera, cuál perspectiva es analíticamente más potente. Cuevas comienza dando la razón a F. Hahn ya que considera que Duménil y Lévy se equivocan dado que:
Levantan su modelo, contestatario al de Hahn, sobre el supuesto explícito de una sola tecnología posible [ Cuevas 2000, 33, subrayado nuestro] .
Por ese motivo, estos autores serían incapaces de responder a Hahn, ya que:
[ ...] un solo valor arbitrario, entre muchos posibles, para los coeficientes técnicos convierte al modelo clásico en un caso extremo particular del neoclásico; en que ese procedimiento es incoherente porque tales coeficientes no pueden permanecer fijos, ni ser compatibles con las soluciones, cuando los precios de los insumos, la tasa de beneficio y la tasa de salarios cambian; en que, sin funciones de producción agregadas, el paradigma neoclásico del precio de cada bien de capital determinado por su producto marginal resulta intachable [ Cuevas 2000, 33, subrayado nuestro] .
y por lo tanto,
Con estas coincidencias, el modelo clásico parecería caso juzgado en términos de esas limitaciones [ Cuevas 2000, 33] .
Sin embargo, previene Cuevas:
Pero esto sería, quizá, muy apresurado. Porque, como en todo juicio, es pertinente considerar primero otras evidencias, indicios y posibilidades [ Cuevas 2000, 33] .
Estas otras evidencias son aquellas que permitirían que la "teoría clásica" mostrara sus potencialidades frente a la neoclásica actual. A fin de intentar definir el debate a favor de los primeros, Cuevas introduce tres argumentos o tesis:
Tesis 1. Existe la superioridad histórica y lógica del modelo clásico de precios.
Tesis 2. La vieja teoría del valor trabajo (de Smith, Ricardo y Marx) posee un lugar esencial en el modelo de precios.
Tesis 3. El modelo general de precios de la teoría económica actual podría ser mejorado y ampliado gracias a la antigua teoría clásica de la renta diferencial que facilita la incorporación de la selección (o pluralidad) de técnicas y, de esta forma, se podría asegurar la renovación de la teoría clásica.
Estas tesis son lanzadas con una fuerza y un brío especiales para que merezcan ser tomadas en cuenta y, por tanto, discutidas. Sin embargo, la presente reflexión crítica quiere mostrar que estas tres tesis de Cuevas no tienen una demostración satisfactoria y que, por el contrario, creemos que el verdadero resultado es hacer difícil la identificación sobre lo que es un modelo clásico y, en consecuencia, permitir su absorción por el modelo neoclásico de precios, actualmente dominante.
Para mostrarlo, primero, pondremos en orden la compleja y abigarrada exposición de Cuevas por medio de las siguientes fases: (i) poner a la luz del día las características esenciales de lo que allí se denomina modelo clásico; (ii) aclarar las diferencias propuestas entre el modelo clásico y el neoclásico; y (iii) determinar la lógica que permite plantear una presunta superioridad del modelo clásico.
En segundo lugar, se intentará una crítica global mostrando tres aspectos: (i) No es convincente afirmar que la teoría neoclásica procede (lógicamente) de la generalización de la teoría clásica de la renta. (ii) La versión de Cuevas de la teoría del valor-trabajo, en primer lugar, no representa ni la posición de Ricardo ni la de Marx y tampoco es aplicable en el modelo general que se propone. (iii) No resulta clara ni convincente la tesis sobre que la presunta ampliación del modelo neoclásico provenga de la utilización de la teoría clásica de la renta extensiva.
PRESENTACIÓN DE LAS IDEAS DE CUEVAS
En un principio, Cuevas propone una formulación del modelo clásico que él mismo designa como modelo reducido y que se puede tomar como su interpretación racional de las ideas sobre los precios de Smith, Ricardo y Marx.
El sistema de precios en el modelo reducido
El vector de precios de equilibrio es la solución del siguiente sistema r (así llamado por el autor), que nosotros presentamos en términos matriciales
AX (1+r) + wL = QX
donde A es la matriz de insumos
Q el vector de las producciones
X el vector de precios monetarios
L el vector de trabajos
r la tasa de beneficio
w la tasa de salarios
Los lectores nos encontramos de inmediato frente a un sistema de producción de mercancías por medio de mercancías bastante similar al de Sraffa, donde la única diferencia reside en que, por hipótesis, las magnitudes son monetarias y no físicas2. Así, se introduce en este modelo el rasgo inhabitual de un "deflactor" d que convierte las variables en poderes sobre el trabajo ajeno o en labour commanded, como diría Adam Smith. En este modelo, el número total de incógnitas es, por tanto, n+3 (la tasa de salarios: w, la tasa normal de beneficio: r, y el "deflactor implícito": d), mientras que el número de ecuaciones independientes es n, una por cada industria o proceso.
La solución se logra proponiendo una ecuación para el deflactor de los precios, una ecuación adicional por la división del producto neto entre salarios y beneficios y, finalmente, se toma exógenamente los niveles de w.
Notemos que en este sistema, dejando de lado lo de las magnitudes en dinero, se sigue la tradición clásica en los siguientes puntos: (i) las cantidades están dadas; (ii) los coeficientes técnicos son fijos y (iii) la distribución del ingreso se determina por medio de otras leyes diferentes al precio de las mercancías (la exogeneidad de la tasa de salarios). Ninguno de estos aspectos generales va a ser aceptado por el enfoque neoclásico posterior, y su abandono es una de las rupturas característica de los modelos generales que ellos van a proponer.
Cuevas estudia en su sistema r los efectos sobre los precios cuando ocurren cambios en los niveles paramétricos del salario (que afectan la distribución) y muestra lo que Ricardo y Sraffa habían ya notado: dada las interrelaciones de la producción, una mercancía es al mismo tiempo producto e insumo en la economía y, dado que existen las diferentes composiciones de capital entre los sectores, una variación del salario implica variaciones complejas de los precios lo cual determina que unos precios bajen y otros suban, sin que sea fácil determinar el efecto final. En efecto, Cuevas afirma:
En otros términos, las relaciones capital-trabajo siguen determinando el comportamiento de los precios. Pero es necesario tomar en cuenta no sólo la relación capital–trabajo explícita en un proceso presente, sino también todas las inmersas en la producción de sus medios de producción, en sus fases sucesivas, hasta completar el conjunto de su relación capital-trabajo integral. Y en este momento el problema parece invertirse, pues del comportamiento final de los precios se pueden inferir las relaciones capital-trabajo implícitas. Lo cual conduce a una generalización final [ Cuevas 2000, 46] .
Por lo tanto,
[ ...] la variación del precio de todo producto depende de la distancia entre su propia relación capital-trabajo integral, Ki*, y la relación capital-trabajo integral del sistema en su conjunto, k*. Pero, por si acaso, debe recordarse que en estas mediciones el capital entra a través de su noción clásica, como una magnitud de valor real, dependiente de los precios y la distribución [ Cuevas 2000, 47, cursivas del original] .
Los puntos que Cuevas pretende aquí defender son los siguientes:
1) El modelo clásico enseña que la magnitud del capital y sus composiciones son función de los precios y que, por ende, no es posible hablar de la magnitud física del capital, salvo en casos excepcionales y no significativo3. Esta variación se consigna en la función phi (φ)4, la cual paulatinamente se amplía a más elementos.
2) El trabajo se incorpora como el "numerario correcto" y con esto se pretende incorporar la vieja teoría del valor trabajo de Smith, Ricardo, Marx pero advirtiendo que se trata de una interpretación muy particular5.
3) Los salarios se consideran exógenos y se utilizan como parámetros para estudiar las variaciones eventuales de los precios de los insumos y productos y, por ende, de las estructuras de capital.
Ahora bien, este modelo reducido –que Cuevas atribuye a los clásicos– no es un modelo que se considere completo. En la segunda etapa de la exposición se ponen de presente las características de lo que llamaremos –siguiendo la lógica de exposición– el modelo "ampliado".
El modelo "ampliado"
Si existe modelo "reducido" debe existir un modelo "ampliado". ¿Cuál es? Para Cuevas es el que defiende F. Hahn: el modelo neoclásico general.
En 1982 Hahn sistematizó una crítica a la teoría clásica de los precios, utilizando como blanco el modelo de Sraffa [ 1960] . Sus principales argumentos fueron los siguientes: a) la preocupación por encontrar un patrón de medida invariable, no arbitrario, carece de fundamento teórico; b) el modelo neoclásico no requiere la agregación de los bienes de capital heterogéneos en una sola magnitud escalar; c) las objeciones contra las funciones de producción agregadas y la reversión (reswitching) de tecnologías, aunque válidas, quedan entonces fuera de lugar; d) el precio de cada bien de capital está determinado por su productividad marginal, pero la tasa de interés no está determinada por el producto marginal del capital agregado sino por el equilibrio entre el ahorro y la inversión; e) en el equilibrio neoclásico, cada industria enfrenta un conjunto de alternativas tecnológicas, elige la más rentable y las tasas de beneficio pueden diferir entre industrias; f) en el equilibrio clásico, cada industria opera con una tecnología fija, sin elección entre alternativas, y las tasas de beneficio son idénticas entre industrias; g) los coeficientes Aij de la matriz de insumos son, por tanto, explicados en forma endógena por el modelo neoclásico, mientras constituyen datos exógenos, sin explicación, ni intentos por encontrar alguna, en el modelo clásico; h) si se imponen dos restricciones específicas al modelo neoclásico, a saber: fijación arbitraria de un solo valor, entre todos los posibles, para cada coeficiente Aij; y fijación, igual a cero, de un solo valor, entre todos los valores posibles, para los beneficios extraordinarios en cada industria, se obtienen los precios del equilibrio clásico; i) por consiguiente, el modelo clásico es un caso particular del modelo neoclásico; j) cuando, al final de su análisis, Sraffa introduce en el modelo clásico la problemática de la selección de técnicas, sus resultados son idénticos a los neoclásicos, en particular en lo concerniente a la reversión de tecnologías [ Cuevas 2000, 29-30, subrayado nuestro] .
En resumen, Cuevas apoyándose en F. Hahn sostiene que el modelo neoclásico llena un vacío importante del que adolecía el modelo clásico reducido. ¿Cuál es el "vacío"? Cuevas lo establece claramente:
También dentro de cada subsistema, como derivada parcial, δφ*/ δ∑∑Aijxj), la contribución marginal del capital, en el sentido clásico, depende de los precios reales de los insumos, xj. Y junto con la contribución marginal del trabajo, δφ*/ δ∑Li, sólo pueden ser determinadas si el nivel de producción es determinado. Si esto se postula en forma endógena, entonces, se requiere añadir las respectivas funciones de demanda para cada producto. Y así, dadas las funciones de producción, la cantidad total de cada insumo utilizado, de capital y el nivel global de empleo también quedarían determinados en forma endógena. Lo cual amplía el alcance del sistema y lo expone a complicaciones especiales con la teoría específica del empleo [ Cuevas 2000, 57, subrayado nuestro] .
En resumen, un viejo modelo clásico (o reducido) no es completo por dejar como variables exógenas la distribución, las cantidades y los coeficientes técnicos de las mercancías producidas, con lo cual resulta que estas variables quedan indeterminadas, es decir, inexplicadas. Esto puede ser apenas justo, nos agrega Cuevas, para algunas situaciones especiales (por ejemplo, hechos institucionales o históricos) pero no para una buena teoría general. Por lo tanto, un modelo completo debe incorporar la determinación endógena de las cantidades de bienes, los valores de la matriz A y la distribución de ingresos (salarios, beneficios). En efecto, siguiendo a Hahn, Cuevas piensa que esto se hace introduciendo inicialmente, además de las funciones de producción, las funciones de demanda de los individuos y, además, las contribuciones marginales (en lugar de las tradicionales productividades), evitando así caer en la anomalía abusiva de los capitales físicos homogéneos. Se tendría así un modelo con los mercados completos de la pluralidad de bienes y los múltiples factores.
Por eso Cuevas añade:
Si esta etapa se adicionara, además de soluciones endógenas para las cantidades producidas, los costos de producción se verían afectados en forma indirecta por las demandas, en situaciones distintas de rendimientos constantes a escala. En el caso de estos últimos, las funciones de oferta serían horizontales. Pero tendrían pendiente positiva con rendimientos decrecientes, y pendiente negativa con rendimientos crecientes [ Cuevas 2000, 57, subrayado nuestro] .
En este contexto, entonces, aquellas características de los antiguos clásicos –en las cuales, recordemos, insistió Sraffa– donde la dimensión de la demanda se separa de la determinación de los precios, donde los coeficientes técnicos están dados y donde los salarios son exógenos, serían un caso "reducido" de un caso general neoclásico (esencialmente, el modelo defendido por F. Hahn).
El origen del modelo ampliado
Una vez descrito el modelo "ampliado", Cuevas recurre a una vieja tesis de historia del pensamiento económico. ¿Cómo se llega, históricamente, al modelo ampliado defendido por Hahn? Respuesta: el modelo ampliado se construye gracias a la utilización de la teoría de la renta ricardiana en el momento de la revolución marginalista6.
[ ...] se pueden destacar los siguientes componentes del modelo clásico de la renta intensiva: a) las proporciones específicas en que se combinan los recursos, es decir, los coeficientes de producción, constituyen variables endógenas, cuya solución es simultánea con las de los precios; b) entre muchas alternativas tecnológicas consideradas para cada unidad de producción, entonces, sólo es elegida la que maximiza su rentabilidad; c) esto ocurre cuando el precio de cada recurso se iguala con su contribución marginal; d) considera siempre a la tierra, dentro del análisis, como un recurso constante, mientras los demás se consideran variables. [ ....] El modelo clásico puede generalizarse, por lo tanto, para considerar también a la tierra, dentro del análisis, como un recurso variable. Y esta generalización fue una contribución específica de la revolución marginalista, llegando a constituir un componente fundamental del modelo neoclásico [ Cuevas 2000, 39, subrayado nuestro] .
La idea propuesta es sencilla: los clásicos son valiosos, en primera instancia, porque dieron la idea clave para generar el modelo general que hoy denominamos neoclásico7. Respecto a esto Cuevas nos ilustra que los fundadores del modelo neoclásico (el justo Jevons, el ingrato Walras, el sincero y transparente John B Clark y el refinado e irónico Wicksteed)8 se afanaron –unos más, otros menos– siempre por reconocer sus orígenes, como buenos hijos de decentes familias, en la teoría clásica de la renta. Nosotros, se nos sugiere, debemos hacer lo mismo y no caer en el pecado de la ingratitud como lo harían nuestros contemporáneos F. Hahn y el dúo G. Duménil y D. Lévy9.
En este punto sinteticemos los primeros resultados de Cuevas:
1. No se debe insistir en una diferenciación fundamental entre modelo clásico y neoclásico so pena de cultivar un dogmatismo estéril. Los clásicos propusieron las bases a partir de las cuales se alcanzarían modelos más complejos, que se llamarán "neoclásicos", donde –como las muñecas rusas– los simples son paulatinamente absorbidos por los complejos, sin destruirlos ni desautorizarlos10.
2. El esquema de formación histórica sería el siguiente. A comienzos del siglo XIX, Ricardo logra el modelo reducido utilizando la teoría de la renta únicamente para el factor tierra. La segunda etapa se realiza a finales del mismo siglo, cuando gracias a la generalización de la teoría de la renta al trabajo y al capital, se logra el modelo neoclásico, donde se determinan de manera endógena las cantidades y la explicación de la distribución por las productividades marginales de los factores. Encontramos así la Tesis 1.
3. La tercera etapa estaría compuesta por dos procesos realizados en el siglo XX, a saber: (i) la crítica y la eliminación paulatina de la función de producción agregada (mérito final de los neo-ricardianos en el debate sobre el capital) ya sea como lo hacen los walrasianos en el modelo de Arrow y Debreu11 o, como lo pretende ahora Cuevas, por medio de incorporación de las "contribuciones" marginales –la función phi (φ) de su texto– y (ii) la "corrección" –que Cuevas reivindica– que elimina los numerarios "arbitrarios" y que permite restaurar la teoría del valor trabajo de Smith, Ricardo y Marx.
4. Con estos elementos, a finales del siglo XX se tendría el modelo de precios "ampliado", es decir, aquel donde clásicos (Smith, Ricardo, Marx) y neoclásicos (Arrow-Debreu y Hahn) se reunirían al fin. Este resultado sería especialmente potente dado que coloca al modelo "reducido" de Ricardo y al de los primeros marginalistas como meros casos especiales del más desarrollado.
Llegar a estas tesis ya es un motivo de interés para leer el capítulo IV de Cuevas [ 2001] . Pero su ambición y reflexión no termina allí, pues el modelo "ampliado" no es considerado como suficientemente "completo" o desarrollado. Así como los artesanos y artesanas de Rusia, que al saber hacer una muñeca pequeña son capaces siempre de fabricar una más grande que englobe la primera, el economista teórico de los modelos de precios se considera capaz de plantear un modelo aún más complejo que los anteriores. Tal es el sentido del desarrollo de la teoría de los precios que se nos propone, y que se resume en lo que podemos llamar un modelo de precios completo o desarrollado.
El tercer modelo o modelo desarrollado
Cuevas construye este nuevo modelo siguiendo una línea precisa: introduciendo en el modelo neoclásico la teoría clásica de la renta diferencial. Las justificaciones son las siguientes:
1. El problema de la selección de técnicas se ha limitado tradicionalmente al caso en el cual los cambios de la remuneración de los factores hace que la combinación de factores varíe hasta el punto en que se escoja aquella que rinda el mayor beneficio. Esta selección implica aceptar un proceso de descarte de otras posibilidades hasta lograr en equilibrio la vigencia de una sola técnica para todos los productores12.
2. La vieja teoría de la renta diferencial de la tierra traía el mensaje de la utilización simultánea de varias técnicas para la producción de trigo, donde se produciría una renta diferencial de acuerdo con la estructura de costos de cada unidad productiva de la agricultura. Cuevas muestra que la utilidad de tal idea no se debe limitar a la sola producción agrícola ya que:
Los recursos que generan rentas diferenciales pueden encarnar como dotes naturales de la tierra o de los individuos; como externalidades de localización, aglomeración, congestión, contaminación o conocimiento; o como ventajas de la tecnología, la organización y la capacidad empresarial [ Cuevas 2000, 59-60] .
3. Con las nuevas causas de renta aparecen los beneficios extraordinarios donde el mayor costo actúa como precio regulador al igual que en la vieja teoría de Ricardo. En consecuencia,
El costo de producción del peor proceso —incluido su beneficio normal— actúa como precio regulador. Es decir, el precio de equilibrio no puede ser menor, pues no alcanzaría para el beneficio normal (e1 < O). Ni puede ser mayor, pues sobraría para una extra ganancia positiva (ei > O). Y el flujo de inversiones marginales con rentabilidad decreciente continuaría hasta cuando la ganancia extra sea nula [ Cuevas 2000, 51] .
No tener en cuenta estos hechos (que hacen aparecer los beneficios extraordinarios y la remuneración de recursos especiales) parece ser la deficiencia del modelo ampliado antes visto. Entonces, formalmente, un modelo completo o desarrollado es aquel que le da cabida a una función phi más compleja que la inicial y que toma la forma siguiente: "Una función φ con posibilidad de todas las derivadas parciales así requeridas es, claro está, la suma de todos los procesos del Subsistema e. O sea:
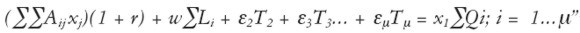 13 13 |
Por lo tanto, un modelo completo es aquel que: (i) contemple las dos vertientes de la teoría clásica de la renta; (ii) incorpore la explicación de los ingresos normales (salarios, beneficios) por medio de las contribuciones marginales bien calculadas (teoría de la renta intensiva); y (iii) explique los beneficios extraordinarios de los recursos especiales.
Ahora la tesis 3 se completa: gracias a la teoría clásica de los dos tipos de renta, se puede construir el modelo ampliado y completo que explicaría todos los precios y todos los ingresos simultáneamente.
LA CRÍTICA A LA CONTRIBUCIÓN DE CUEVAS
La crítica que vamos a proponer a estas tres tesis defendidas por Cuevas se apoya en los siguientes argumentos claves:
1. La Tesis 1 ignora la discusión que hizo Sraffa en 1925 para negar el vínculo entre clásicos y marginalistas por la vía de la teoría de la renta.
2. Deflactar por el salario no significa incorporar la Teoría del valor de Ricardo y Marx en esta evolución sino, precisamente, no tenerlos en cuenta en este punto.
3. El método de selección de técnicas adoptado queda debilitado porque el énfasis de la explicación de la remuneración de los recursos especiales se traslada a la idea de las "contribuciones" marginales y no a la verdadera primera renta de los clásicos.
¿Es el modelo neoclásico una derivación lógica de la teoría clásica de la renta?
Para sustentar la pretendida conexión de la teoría de la renta ricardiana y el desarrollo neoclásico, Cuevas se inspira en la reflexión de algunos primeros neoclásicos de principios del siglo XX (principalmente Clark y Wicksteed) y en la tesis según la cual la teoría de la renta es la base de la teoría de los precios. Sin embargo, fue para rebatir esta posición que Sraffa se levantó con fuerza en 1925.
Teoría clásica de la renta y los neoclásicos
P. Sraffa sustentó su argumentación aprovechando las ideas del mismo Wicksteed que sirve de inspiración a Cuevas, con base en los siguientes argumentos:
Las concepciones de rendimiento decreciente entre clásicos y marginalistas son muy diferentes.Sraffa escribe:
El rasgo característico de la teoría ricardiana [ de los rendimientos decrecientes] (en nuestra opinión fundamental) que consiste en atribuir la productividad decreciente a una causa económica más bien que física fue hábilmente criticada por Wicksteed. Este autor comienza por clasificar las curvas de productividad en dos categorías: las curvas descriptivas y las curvas funcionales. [ ...] Wicksteed construye de la siguiente manera la curva descriptiva, que representa la forma principal de la productividad decreciente en Ricardo: "las diferentes calidades de tierra se llevan sobre el eje X y las fertilidades relativas que se supone ellas tienen, cuando se les aplica cantidades iguales de capital y trabajo, sobre el eje Y. La tierra marginal se sitúa en el extremo derecho. Esta no es una curva funcional: la altura de Y [ la productividad] no depende, de hecho, de la longitud de X [ las cantidades] ya que las unidades se disponen de manera expresa sobre el eje OX de manera a describir un Y decreciente". La definición de la curva funcional es la siguiente: "tome una superficie dada de tierra de una calidad determinada y considere su productividad si en ese punto se aplica una cierta cantidad de trabajo y capital, representada en el eje de las X. Aumente las dosis hasta que un crecimiento suplementario de trabajo y de capital sólo de un acrecentamiento del producto igual al que resultaría si se aplicara a otra fracción de la tierra de calidad igual o diferente o si fuese utilizada en un sector por fuera de la agricultura. El último acrecentamiento efectivamente aplicado es el aumento marginal; el cual mide la fracción del producto que en la distribución es destinada a una unidad del factor variable" [ Sraffa 1976, 15, subrayados y traducción nuestros] .
En seguida, Sraffa saca las primeras conclusiones:
• En la curva funcional –utilizada por la teoría neoclásica– es necesario hacer la hipótesis de que las dosis de cada factor utilizadas sucesivamente son intrínsecamente idénticas. Es decir, en este caso, "es el lugar ocupado por cada dosis lo que determina su productividad: ésta depende estrechamente de la cantidad de dosis utilizadas" [ Sraffa 1976, 16, subrayado nuestro] .
• Por el contrario, en la curva descriptiva –utilizada por la teoría ricardiana antigua– "el lugar ocupado por cada dosis es determinado por su productividad (la cual es independiente de la cantidad de dosis utilizadas)".
• En ambos casos se habla ciertamente de dosis marginales, pero, continua Sraffa:
Wicksteed precisa que en las dos concepciones la expresión asume "significados muy diferentes": en la primera concepción, "se trata de una dosis de calidad mediocre, mientras que en segunda es una dosis cualquiera... [ En esta última] la magnitud de su producto diferencial o marginal no depende de la naturaleza de cada dosis particular sino de la cantidad global" [ Sraffa 1976, 16] .
• La distinción entre las dos curvas es fundamental para la teoría de la distribución: "en las primeras (la descriptiva de los clásicos) las tierras (diferentes) puestas en agricultura en razón del orden de la fertilidad decreciente, reciben remuneraciones diferentes, mientras que en la segunda (la funcional de la teoría neoclásica) las dosis iguales de capital sucesivamente utilizadas en un terreno dado reciben todas la misma remuneración" [ Sraffa 1976, 18].
Así, se indica que en la teoría de la renta diferencial de Ricardo no existe la relación funcional entre la cantidad del factor y su productividad y, por ende, esta renta no se explica por un argumento que anticipe a los neoclásicos. Recordemos aquí que Ricardo muestra que en la última tierra no existe renta, a pesar de que en las tierras menos malas la renta sea positiva. Debe ser evidente que, si la renta ricardiana se explicara por la productividad marginal de la última dosis, esto implicaría la eliminación de las rentas de las otras tierras.
Cuevas parece consciente de la diferenciación anterior ya que advierte que:
La argumentación de Wicksteed es aplicada al caso de intensidades o proporciones variables de los recursos con respecto a una clase homogénea de tierra, detallado por Ricardo en el Capítulo XXIV de sus Principios, y denominado por algunos como renta intensiva o por Marx renta diferencial de tipo II. En cambio, al caso de incrementos de clases heterogéneas de tierra, que generan una renta diferencial "extensiva", o de tipo I, le confirió poco valor. Previno contra la imprecisión de aplicar a este último la noción de productividad marginal, la cual reserva para incrementos de un recurso estrictamente homogéneo. Y degradó el caso heterogéneo al lugar común de que la mercancía mejor comanda un mejor precio [ Cuevas 2000, 38] .
Al mismo tiempo que Wicksteed le confería poco valor al caso descriptivo (o estrictamente clásico), Sraffa nos informa que Ricardo pensaba que la generalidad y la certeza de los rendimientos decrecientes por la vía funcional eran menos claros y que no se podía construir una ley. En efecto,
Ricardo, a pesar de haber analizado las dos formas diferentes de las dos formas de la ley [ de rendimientos decrecientes] preferirá servirse de la primera [ la productividad decreciente debida a tierras distintas] en sus desarrollos posteriores; de esta manera, mientras que él expone el paso de mejores tierras a las tierras menos buenas como una cosa cierta y evidente, él no habla de la productividad decreciente en un terreno dado sino como algo probable, no cierto, y haciendo preceder la exposición de esta última, de frases del tenor "it often and, indeed commonly happens... It may perhaps be found" [ Sraffa 1976, 15] .
Esto nos parece suficiente para afirmar que enarbolar la continuidad entre clásicos y neoclásicos con base en una presunta utilización de la teoría de la renta de Ricardo del caso intensivo, que este último no consideró interesante, es una exageración sin mucho fundamento y que, además, el mismo Wicksteed no propuso.
Frente a este resultado negativo queda por esclarecer la verdadera base para el desarrollo de la teoría de la distribución neoclásica que utiliza la idea de las productividades marginales de los factores, es decir, las relaciones funcionales, donde la derivada parcial se aplica para descubrir el rendimiento marginal del factor homogéneo. Sraffa, quien escribe en 1925,nos da también una pista:
La idea de una interdependencia entre la cantidad producida y el costo de producción de una mercancía en régimen de competencia [ ....] sólo se formó recientemente, de manera indirecta y resulta del desplazamiento del fundamento de la teoría del valor del costo de producción hacia la utilidad. [ ...] . "La función de demanda" se basa en una hipótesis elemental y natural, la de la utilidad decreciente; en la producción, por el contrario, la relación funcional es la resultante de un sistema de hipótesis más complicadas. Pero el hecho permanece: sólo cuando las investigaciones sobre la utilidad marginal concentraron la atención entre la relación entre el precio y la cantidad consumida es que surgió, por analogía, la concepción simétrica de una relación entre costo y cantidad producida [ Sraffa 1976, 4, subrayado y traducción nuestros] .
Según esto, la incorporación de la idea de rendimientos decrecientes en la teoría neoclásica de los precios no nace ni de una admiración ni de una prolongación por la teoría de la renta de Ricardo sino de una evolución interna al enfoque marginalista, el cual, habiendo construido en su primera época la función de demanda, necesita aplicar el análisis marginal a la producción para generar la teoría de la función de oferta y el pago de los factores14.
Fue entonces a posteriori (sobre todo por la insistencia de Clark y los intereses ideológicos en no plantear rupturas históricas sino en buscar retrospectivamente la conciliación con los clásicos) que se vino a promover la idea de la continuidad entre los dos modelos por el lado de la teoría de la renta de Ricardo. Tal como Wicksteed y Sraffa lo mostraron, tal idea se construye deformando la teoría ricardiana de la renta (lo descriptivo se toma como funcional) y, por ende, debe descartarse.
¿Es la teoría de la renta esencial para la teoría de los precios?
En varias ocasiones Cuevas ha promovido esta idea con base en el criterio de que, finalmente, todos los ingresos se pueden explicar como rentas. Pero en este punto nos parece que debe aclararse lo siguiente:
1. Si fuese esto cierto, no podría determinarse los precios clásicos sin renta. Sabemos precisamente que Ricardo "corrige" a Smith mostrando que no son los precios los que dependen de la renta sino que es al revés, la renta depende de la determinación de los precios. Basta ver que en el mismo modelo reducido de Cuevas se determinan los precios sin que se incorpore ninguna clase de renta.
2. Observemos además que tampoco en el modelo neoclásico más avanzado, el de Arrow y Debreu, se utilizan productividades marginales para explicar los beneficios, ya que, como lo explica F. Hahn [ 1983] (el mismo artículo citado por Cuevas):
Notice the meaninglessness of a sentence like "the marginal product of labour determines the real wage". You need to solve nine equations to find either labour’s marginal product or the real wage. This was patiently explained by Roberson [ 1931] and its rather odd that the neo-ricardians continue to assert that in neoclassical theory the rate of profit or anything else is "determined" by marginal productivity [ Hahn 1983, 361] .
Así se explica que, por hipótesis en el modelo Arrow-Debreu (del cual significativamente Cuevas poco habla), los hogares son dueños de las empresas (verdaderas cajas negras) y captan los beneficios que surgen de la diferencia entre ingresos y costos de los proyectos maximizadores que se pueden realizar en equilibrio, y todo esto sin pasar por la idea de productividad o contribución marginal. Frente a este aspecto Geanakoplos [ 1987] , un expositor autorizado del modelo Arrow-Debreu afirma:
There is none the less one aspect of the (Arrow-Debreu) model which these authors (Ricardo and Marx) would greatly approved, namely the shares d hl which allow the owners of firms to collect profits though they have contributed nothing to production Geanakoplos [ 1987, 50] .
Es decir, en el modelo básico y el más general de los neoclásicos (aquel precisamente defendido por Hahn) es la propiedad, y no la productividad de un factor, lo que hace que los beneficios económicos sean atribuidos a los hogares. Esto nos permite confirmar que las teorías de la renta "extensiva" e "intensiva" no hacen parte de la estructura básica de los modelos modernos de precios de las mercancías.
3. En realidad, la teoría de la renta hace parte de la teoría clásica de la distribución del ingreso en lo que tiene que ver con la formación de ganancias extraordinarias que pueden ser captadas por los terratenientes, pero como lo señalaron los fisiócratas, también eventualmente por el Estado. En este caso, la renta hace parte de la teoría de la distribución del ingreso y no de la teoría de los precios y sólo si los ingresos se quieren explicar como precios, se puede afirmar que la renta es parte de los precios. Esto nos permite plantear que en la historia de la teoría económica lo que se ha discutido verdaderamente respecto a este tema es si la distribución del ingreso se puede explicar con la teoría de los precios o necesita una o varias teorías especiales. Por ejemplo, con la teoría del salario con base en una canasta de subsistencias dada y la idea de contradicción entre salarios y beneficios, los clásicos apuntaban a mostrar que son partidarios de la existencia de dos teorías específicas, una para los precios y otras para los distintos componentes de los ingresos. Marx los sigue en esta vía planteando el salario como el precio de una mercancía especial (su pecado fue insistir en que la fuerza de trabajo es una mercancía aunque en letra pequeña anotaba sus peculiaridades) que no se produce en la división social del trabajo y cuyo uso depende de la lucha de clases que fija la jornada laboral; y también Keynes insiste en este punto al comenzar la Teoría General cuando critica, precisamente, la posibilidad de hablar de un "mercado de trabajo" a semejanza de aquel para las mercancías generales ante la ausencia de una curva de oferta de trabajo. La teoría neoclásica estándar ha estado en contra de este proyecto de dos teorías diferentes y pretende poder explicar el salario como un precio de un bien que obedece a los principios de la oferta y la demanda, es decir, a su ley única del valor.
4. Cuevas se aproxima a los neoclásicos en su deseo de endogeneizar, y hacer simultánea la determinación de los precios y los salarios, y esto se corresponde con sus curiosas consideraciones (en contra de la tradición... ¡clásica!) para hacer creer que aceptar un salario institucional es algo que el teórico debe tomar sólo para ciertas situaciones, y no un elemento de la teoría general.
Estas dos argumentaciones nos parecen suficientes para mostrar la debilidad de la Tesis 1 en cuanto a que la continuidad histórica entre clásicos y neoclásicos reside en la teoría de la renta.
Teoría del valor trabajo y el deflactor
De una manera muy personal (y ¡sorprendente!) Cuevas ha considerado en sus diversos escritos que la teoría del valor trabajo (atribuida sin distinción importante a Smith, Ricardo y Marx) se debe reducir a la idea de que el valor agregado real del sistema económico se iguala (mediante un deflactor) al trabajo agregado en el proceso de producción global15. Tal como lo afirmamos en otra parte [ Cataño 1996] la fuente de tal posición parece encontrarse en una lectura especial del capítulo V de la Riqueza de las Naciones donde Smith propone como medida del valor, en lugar de los precios monetarios, los precios de acuerdo con las cantidades de trabajo que puedan adquirir las mercancías. Es decir, su doctrina del labour commanded.
Ricardo rechazó tal procedimiento por considerar que el precio del trabajo no podía servir de patrón invariable de precios, de la misma manera que el precio del oro había sido descartado por Smith. Esto conduce a Ricardo a buscar una medida invariable en una mercancía balanceada de acuerdo con los componentes de capital de tal manera que un cambio en la distribución no altere su propio precio. Sabemos que él no pudo precisar esta solución y le correspondió a Sraffa pensar en una mercancía compuesta y especial para que sirviera de patrón. Por fuera de cualesquiera que sean las posiciones respecto a todas estas investigaciones16, es importante hacer ver que ni Ricardo ni Sraffa ni los neoclásicos aceptan que una teoría del valor se defina por su forma de medir las magnitudes sino con base en cuál es la variable o conjunto de variables que permite determinar cuando un precio es alto o bajo. Que la temperatura se mida en Centígrados o en grados Fahrenheit no indica que esas medidas explican el nivel de calor. Cuevas piensa que una teoría del valor es una cuestión del buen deflactor como si estuviéramos en un problema estadístico de las cuentas nacionales, y no en un problema de determinación de los niveles de los precios en las teorías (abstractas) del valor.
En el caso de Marx, la cuestión es aún más simple. Él nos advertía que:
El error de Ricardo es que sólo se ocupa de la magnitud de valor. De ahí que sólo dirija su mirada a la cantidad relativa de trabajo que representan las mercancías [ ...] Pero el trabajo contenido en ellas debe representarse como trabajo social [ ...] En el precio, esta representación es ideal. Sólo se realiza con la venta. Esta conversión de los trabajos de individuos privados contenidos en la mercancía en trabajos sociales iguales [ ...] este lado cualitativo de la cosa, que se contiene en la representación del cambio como dinero, no aparece desarrollado en Ricardo. Ricardo pasa por alto esta circunstancia: la necesidad de representar como trabajo social igual, es decir, como dinero, el trabajo contenido en ellas [ Marx 1980, 116, subrayados nuestros] .
Si tomamos la interpretación de Cuevas sobre la teoría del valor trabajo, estas ideas de Marx no tienen sentido ni cabida en un modelo "clásico" ni "marxista". Mientras el autor de El Capital reclama que los trabajos privados existentes en la división social del trabajo (independientemente de la existencia de la relación salarial) contenidos en las mercancías, lo que él llama su valor, deben tomar la forma de dinero y presentarse como tal, Cuevas piensa, por el contrario, que son las magnitudes monetarias (inexplicadas por él) las que deben deflactarse para que asuman la expresión de trabajo comandado gracias a la presencia del salario.
Adicionalmente, afirmar que la teoría del valor trabajo se reduce a un problema de medida, impide entender el debate entre clásicos y neoclásicos sobre la determinación del valor de cambio. Si Cuevas tuviera razón, en primer lugar, no podríamos comprender por qué las teorías "reales" del valor deben incorporar siempre un numerario para expresar los valores relativos y, en segundo, lugar, tampoco sería comprensible el esfuerzo de Jevons, de Walras y de Menger de construir una teoría alternativa donde el precio dependa de la oferta y demanda frente a la pretensión de Ricardo (y continuada por Sraffa) de plantear que "es el costo de producción el que debe regular en último término el precio de las mercancías y no, como se ha dicho a menudo, la proporción entre la oferta y demanda" [ Ricardo 1959, 285]17.
Las verdaderas versiones de la teoría del valor trabajo
La teoría del valor trabajo tiene en la literatura internacional contemporánea dos versiones que se resumen en el significado que se le otorga al sistema matemático siguiente.
Supongamos que hay L mercancías diferentes, l = 1,..., L y H individuos, h = 1,..., H.
Las condiciones técnicas de producción están dadas por la matriz A de coeficientes fijos akl, donde akl es la cantidad de la mercancía k necesaria para producir una unidad de la mercancía l. El vector al es el vector de insumos por unidad de producto l. Si ql es la cantidad producida de la mercancía l, el vector de insumos es qlal. En adelante, si suponemos que el producto neto es positivo, se tiene
(I - A)q > 0.
Si agregamos un vector t de trabajo (socialmente necesario) utilizado de magnitud q = 1. Los valores determinados por el trabajo son, entonces:
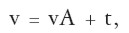 | [1] |
que, si existe (I - A)-1 se convierte en
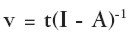 | [2] |
Frente a esta ecuación caben dos interpretaciones. La primera es suponer que el vector t de trabajos está dado por la producción (al igual de los coeficientes técnicos) de acuerdo con la posición de Ricardo y, por ende, una vez dado ese vector se conocen los valores de cambio o proporciones entre los bienes, señalados por el vector v. Aquí, no hay distinción entre trabajo concreto del productor y el trabajo social y, por tanto, la producción es más importante que la circulación. Todo el mundo sabe que esta teoría es válida sólo si las composiciones del capital son iguales y eso explica que los neo-ricardianos y marxistas "ricardianos" la tomen como una teoría antigua deficiente por el evidente fracaso de los métodos de "transformación" de valores a precios y por el simple hecho de que en el modelo de precios de Sraffa el vector t (los trabajos) no aparece.
La segunda versión proviene directamente de Marx cuando éste plantea que el trabajo privado sólo se socializa en el mercado. Es decir, que el vector t no se conoce a priori y, por ende, tampoco el vector v de los valores por fuera de lo que ocurre en la circulación mercantil. En este caso es necesario explicar cómo funciona el mercado para hacer aparecer el valor de estas dos incógnitas a partir de datos anteriores y presentes en el mercado. Esta vía ha encontrado una propuesta de solución en una "teoría monetaria del valor" y su exposición analítica actual se le debe a Benetti y Cartelier [ 1995] .
Ahora bien, si a pesar de todo aceptamos la interpretación de Cuevas de la teoría del valor trabajo, aparecen dos problemas. En primer lugar, Cuevas sostiene al mismo tiempo que las magnitudes iniciales son monetarias y que es válida la posición ortodoxa de que el dinero es neutral. Ahora bien, ¿cuál es la justificación de la presencia del dinero como la inicial unidad de cuenta? ¿cuál es la teoría que autoriza hacer algo diferente a lo que hicieron Sraffa y los neoclásicos? Para estos últimos, antes de afirmar la neutralidad del dinero, lo que propusieron fue su ausencia inicial en un modelo de solo bienes físicos para que después se incorporara una teoría monetaria construida de acuerdo con el modelo de precios.
Para obviar el problema, Cuevas propone una simple ecuación de la teoría cuantitativa del dinero para afirmar que "los impactos nominales dependen de modificaciones institucionales de la velocidad del ingreso y de la emisión monetaria" [ Cuevas 2000, 47] . Es curioso que aquí no se recuerde la debilidad conceptual de la teoría cuantitativa del dinero y que en este punto ya no se cite a Keynes para oponerse a esta teoría (como sucede cuando se quiere oponer a la teoría de la determinación de la tasa de interés propuesta por los neoclásicos). Hace mucho tiempo R. Patinkin mostró que esta ecuación debía explicarse dentro de la teoría económica ortodoxa de su tiempo y a pesar de su intento y el de otros, todavía no se le ha podido dar. ¿No sería menos confuso poner el modelo en términos directamente "reales" (precios directamente relativos) como lo hacen Neo-ricardianos y Neoclásicos, y reconocer que para todos existe la dificultad de integrar el dinero a ese mundo construido sin él?
Además, es fácil ver que "el deflactor" de Cuevas no se puede utilizar y no se necesita en el modelo ampliado. Él lo puede utilizar en el modelo reducido porque la distribución es exógena y, por tanto, puede analizar las modificaciones en los precios de acuerdo con el movimiento externo de los salarios. En estos términos, el conocimiento del deflactor es anterior al estudio de la modificación de los precios, tal como aparece en el modelo reducido. Por el contrario, en el modelo neoclásico (aquel asociado a Hahn) w se vuelve endógeno y depende de todas las interdependencias, entre ellas, la de los mismos precios. Es decir, no se puede plantear la independencia del deflactor respecto a la variación de los precios18. Por lo tanto, la medida del valor en trabajo de Cuevas sólo tiene vigencia en el modelo reducido y es inutilizable en el modelo ampliado y desarrollado. La reliquia atribuida a Ricardo y Marx, que también debía fortalecer la tesis de la superioridad de los clásicos, desaparece al final y queda sólo como un vestigio inútil e insignificante del modelo reducido19.
Por estas razones, debemos descartar de nuevo la interpretación de Cuevas de la teoría del valor trabajo y afirmar que insistir en ella es promover una pésima lectura de una de las teorías del valor más importantes de la historia de la economía política y de grandes pensadores que merecen, de parte de los lectores, ser tomadas con más cuidado.
Pluralidad de técnicas y beneficios extraordinarios
En su planteamiento más original, Cuevas pretende mejorar y establecer un modelo de precios más general al atribuido a los neoclásicos gracias a una extensión de la antigua teoría de la renta diferencial de Ricardo. Como vimos antes, aquí se trata de introducir una idea de selección de técnicas, aunque sería mejor decir, pluralidad de técnicas para un mismo producto, donde en lugar de una selección virtual sobre una función de producción, una mercancía aparece siendo producida al mismo tiempo por medio de varias técnicas con costos diferentes y, en consecuencia, dando cabida a beneficios extraordinarios en algunas producciones muy frecuentes en el mundo real tales como la utilización simultánea de distintas tecnologías, la diversidad de la información, las ciencias, las artes [ Cuevas 2000, 38] , aquello que Cuevas denomina, a secas, "recursos" y cuya retribución depende de la existencia de beneficios extraordinarios tal como en el caso de las tierras de diferente productividad de Ricardo.
Sin duda alguna, intentar incorporar en un modelo económico la retribución de recursos especiales es algo loable y merece todo el interés. Plantearse la cuestión es un mérito que reconocemos a Cuevas.
Sin embargo, nos interesa poner de relieve que existe una gran ambigüedad en el lazo que se establece entre la antigua teoría clásica de la renta y la idea de que los recursos especiales se retribuyen de acuerdo con sus "productividades" o "contribuciones" marginales.
Cuevas quiere mostrar que para estos beneficios extraordinarios se debe aplicar la teoría de la renta diferencial propuesta por Ricardo. Como vimos antes con Wicksteed y Sraffa, aquí la sucesión de las unidades utilizables del factor variable, en este caso la tierra, se hace de la siguiente manera. Primero se utiliza la más productiva y a continuación vienen sucesivamente aquellas que presentan rendimientos paulatinamente decrecientes respecto a esta primera. Esta serie de utilizaciones con sus rendimientos intrínsecos (por las razones que sea) se pueden llevar a un gráfico donde se describa una productividad decreciente a medida que se utiliza otras clases de tierra. Pero aquí los rendimientos no indican rendimientos marginales en el sentido marginalista, es decir, no hay relación funcional entre cantidad del recurso y su contribución, y por ende, el cálculo de su derivada no tiene aquí sentido.
Cuevas quiere trasladar esta idea reemplazando la tierra por algún recurso especial. Supongamos nosotros, a manera de ejemplo, que se trata de un capital humano especial para producir energía eléctrica, indicada por el índice 1 y que utiliza insumos y trabajo normales de las otras firmas que generan electricidad. Sean, entonces, unidades de ingenieros de tipo 1 los recursos especiales que hacen que la firma posea una ventaja respecto a la otra y sea merecedora de una ganancia extraordinaria. En este caso, adaptando la nomenclatura del mismo Cuevas en su parágrafo 3.1 se tendría que el sistema de las dos técnicas para la producción de energía se escribiría, poniendo primero la más productiva a la menos, así:
(a11x1 + a12x2... + a1nXn)(1 + r) + wl1 = x1
(a11x1 + a12x2... + a1nXn)(1 + r) + wl1 + e1 = x1
donde, además de lo ya anotado en el modelo reducido, se tiene: e1: extra ganancias sobre el nivel ordinario, r, gracias a la utilización del ingeniero de tipo 1.
Respecto al proceso sin beneficio extraordinario, el que carece de e positivo, y tal como Cuevas lo recuerda:
El costo de producción del peor proceso –incluido su beneficio normal– actúa como precio regulador [ Cuevas 2000, 51] .
Respecto al segundo, el autor anota:
Si rindiera menos, e1 < 0 y sería eliminado del sistema por las condiciones de información, racionalidad y fluidez. Si rindiera más, entonces ei > 0 y una mayor inversión de capital fluiría hacia el mismo [ Cuevas 2000, 51] .
Se evocan aquí, en realidad, dos hechos distintos: uno es la determinación de las remuneraciones de equilibrio y el otro es qué sucede cuando el sistema no se encuentra en ese punto y los empresarios tienen incentivos para ampliar la producción. Dejemos de lado el segundo tema pues corresponde a la teoría del ajuste competitivo20. El punto que nos interesa es la explicación de la remuneración en equilibrio del ingeniero especial.
Cuevas propone que la nueva explicación se haga, considerando todo el sistema económico, por medio de la ya citada función phi (φ) del parágrafo 3.5.4 [ Cuevas 2000, 53] :
Una función φ con posibilidad de todas las derivadas parciales así requeridas es, claro está, la suma de todos los procesos del Subsistema e. O sea: (∑∑ Aij xj )(1 + r) + w∑ Li + ε2 T2 + ε3 T3... + εμTμ = x1 ;∑Qi ; i = 1...μ.
Que aplicada a nuestro ejemplo daría:
(a11x1 + a12x2... + a1nxn)(1 + r) + wl1 + ε1 T1 = x1Q1
donde ε1 es el costo de arrendamiento o retribución que debe reconocerse a las unidades T1 ingenieros de tipo 1. Es decir, que el valor total de la producción de energía (realizada con dos técnicas distintas) es igual, en equilibrio, a sus costos de capital + beneficios del capital + salarios de los trabajadores normales + retribución de ingenieros de tipo 1.
¿Cómo se determinan los valores de los beneficios y salarios normales? Cuevas lo explica de una manera ambigua. Algunas veces afirma –siguiendo a Clark– que "la contribución marginal del recurso variable determina su tasa de remuneración" [ Cuevas 2000, 37] , y en otras advierte que no se puede hablar en verdad de "determinación", en el sentido de relación causal porque:
El hecho de que, dentro de todo subsistema, las respectivas derivadas parciales de φ, con respecto al trabajo y el capital, sean iguales a w y a r, no significa que la tasa de salarios y la tasa de beneficio estén determinadas por las contribuciones marginales del trabajo y el capital en forma respectiva [ Cuevas 2000, 56, subrayado nuestro] .
Indudablemente, lo correcto es esta segunda posición que indica que la determinación simultánea de las incógnitas hace que las participaciones de los factores normales se hagan idénticas a sus "contribuciones".
¿Cómo se determinan las retribuciones de los recursos especiales? La respuesta se da en dos etapas:
En la primera, se recuerda los presuntos méritos de la renta diferencial, que tras aplicarse originariamente a la tierra, más tarde se pretendieron extender al trabajo y al capital:
Una de las implicaciones cruciales de la teoría clásica de la renta diferencial de la tierra fue la revolución marginalista, la cual exigió [ sic] consecuencia lógica, involucrando los demás insumos, el capital y el trabajo en el mismo análisis de los recursos. En otros términos, la función φ (en 3.5.4), es derivable parcialmente no sólo con respecto a Aijxj sino también con respecto a sus componentes separados, Aij, con respecto a Li y con respecto a Ti, i = 2...μi [ Cuevas 2000, 54, subrayado nuestro] .
En la segunda, Cuevas extiende esta misma idea a "todos los recursos", es decir, a los ingenieros especiales de nuestro ejemplo.
Considerando todos los recursos:
(δ∑Qi /δ∑Ai1 )x1 = x1; (δ∑Qi / δAi2 )x1 = x2 ... (δQi / δAμ)x1 = xμ ; (δQi / δTμ)x1 = εμ
(δQi / δ∑Li )x1 = w; (δQi/ δ∑Ci)x1 = r
Es decir, dentro de cada subsistema e, el valor del producto marginal de cada insumo es igual a su precio; el valor del producto marginal de cada recurso especial es igual a su precio; el valor del producto marginal del trabajo es igual a la tasa de salarios; el valor del producto marginal del capital es igual a la tasa ordinaria de beneficio [ Cuevas 2000, 54, subrayado nuestro] .
¿Y porqué se puede hacer esta extensión? El argumento de Cuevas es este:
Consecuencia lógica en la sustituibilidad: en la teoría clásica de la renta diferencial, la tierra es sustituible por capital para incrementar la producción (surgimiento de la renta intensiva o de tipo II, mediante cambios en las proporciones de los procesos iniciales). Pero el mismo proceso implica un cambio en la cantidad de tierra por unidad de capital, es decir, la sustituibilidad inversa. Además, en el análisis clásico de la maquinaria, las innovaciones y las crisis, la intensidad capital–trabajo es una variable, lo cual implica sustitución. Por consiguiente, la función φ (en 3.6.1), es parcialmente diferenciable por Ti, Aij, Li y Ci [ Cuevas 2000, 54-55, subrayado nuestro] .
El punto esencial que queremos discutir es si efectivamente para dar la explicación de la retribución de los recursos especiales es necesario enarbolar todos estos argumentos, y si de ellos se confirma la idea de renta diferencial de Ricardo, es decir, si la ampliación del sistema de precios resulta efectivamente de la introducción de una idea existente en la economía clásica.
Nuestra apreciación es que Cuevas crea una argumentación que no permite ver claramente la conexión entre sus argumentos y el objetivo esperado y lo más grave que, más bien, invita a que no se tenga en cuenta la originalidad clásica. Veamos porqué:
1. Recordemos que Wicksteed había descrito claramente la diferencia entre la visión de renta diferencial de Ricardo y la utilizada por los marginalistas. Era la diferencia entre la curva descriptiva (aplicada por Ricardo) y la funcional (aplicada por los marginalistas). En el caso descriptivo no existe una relación funcional entre la cantidad de tierra utilizada y su productividad marginal ya que el margen es una cualidad intrínseca del recurso y no una consecuencia de la cantidad de tierra ya utilizada. La idea de factor homogéneo, es en esta última, imposible y, por tanto, tampoco puede existir la productividad marginal de un factor ni organizar una teoría de la distribución con base en sus productividades marginales y hacer creer que allí es utilizable las derivadas parciales. Vimos antes que, afortunadamente, Cuevas reconoce gracias a Wicksteed este punto.
2. Aplicar la teoría de la renta de Ricardo es obligarse a usar curvas descriptivas y no funcionales. Acabamos de ver que Cuevas establece en la función phi (φ), además de las extra-ganancias designadas por e1,una relación funcional entre la utilización de los recursos especiales y su remuneración, y habla entonces de que allí e3... hasta eµ pueden ser obtenidas como el valor del producto marginal de cada recurso Ti.
Con este argumento la confusión se instala ya que de dos cosas una: si el interés era explicar el precio o ingreso del recurso especial por medio de la teoría que Ricardo aplica a las diferentes calidades de tierra no se deben invocar relaciones funcionales. Cada fuente de la extra-ganancia (o mínimamente su proporción) es un dato técnico especial, que va a ser evaluado económicamente resolviendo el sistema de ecuaciones simultáneas. Cuevas oscurece innecesariamente las cosas ya que podría dejar su tesis en el punto 3.2.3 y simplemente apoyarse en el hecho de que añadir todos los e es añadir el mismo número de ecuaciones y el sistema matemático tiene solución que fija los precios de las mercancías y de los recursos merecedores de una ganancia especial. Pero si hubiera procedido así no vale el argumento de que esto es, como él afirma, consecuencia lógica de la sustituibilidad (entre factores).
3. Si por el contrario, se insiste en la sustituibilidad (donde la productividad marginal de unos es simétrica a la productividad marginal de los otros) resulta evidente que ni se respeta ni se aplica el principio de la renta diferencial de Ricardo y, por el contrario, lo que se vuelve a utilizar es la relación funcional entre cantidad utilizada del factor homogéneo y su rendimiento en el caso de recursos especiales. Si es así, sólo se reconocería un tipo de relación, la funcional, entonces lo que se nos escaparía sería lo que pretendíamos introducir, esto es, la curva descriptiva, o sea, ... ¡la renta clásica¡ Todo esto a pesar de que con una buena lectura de Wicksteed y de Sraffa hubiera podido no confundirla.
En resumen, la Tesis 3 no está bien expuesta ya que la explicación de la remuneración de recursos especiales en la función phi (φ) no es una utilización de la teoría ricardiana de la renta sino de una idea general que Cuevas pretende poner en primer lugar: la contribución marginal resultante de derivar una función de producción en precios respecto a los distintos factores.
El problema principal es que si es inaceptable que los ingresos normales sean explicados por productividades físicas de los factores (porque caeríamos en los problemas del retorno de técnicas o porque en realidad no existe esa causalidad como lo recuerda Hahn) tampoco lo es la idea de "las contribuciones marginales".
La experiencia teórica a la que Cuevas nos invita nos parece ser, en definitiva, la siguiente21 : si el capital es concebido como el precio de una colección de objetos (y no como un factor físico homogéneo), su modificación puede provenir de efectos de volúmenes y efectos de precios inextricablemente combinados y difíciles de predecir. Hablar de contribución marginal del capital (con el trabajo fijo) se hace entonces difícil ya que ella es afectada ya sea por la variación de los precios o del volumen. Para hablar de contribución claramente habría que dejar los precios fijos y hacer variar el volumen de los diversos capitales. Su pongamos entonces que los aumentos de capitales son financiados con créditos de acuerdo con una tasa de interés, y cada peso adicional se distribuye en aumentar la masa de capitales sin modificar la cantidad de trabajo. En este momento, se puede afirmar que el valor del incremento en la producción global resultante es la contribución marginal del capital y si esta última decrece regularmente (como lo supone Cuevas), con las sumas de crédito adicionales disponibles valdrá la pena invertir hasta que la contribución marginal se iguale a la tasa de interés de los préstamos. Esta experiencia lógica no significa que la contribución marginal de ese capital "explique" (de manera de causa-efecto) la tasa de interés. De ella tampoco estamos autorizados a decir que cuando una sociedad tiene más capital que otra, ella tendrá menor tasa de interés. En realidad allí sólo se indica que el empresario se endeuda y produce hasta el punto de poder recuperar la tasa de interés que se le impone.
La ironía del asunto aparece cuando el mismo razonamiento lo aplicamos al trabajo dejando el capital fijo. Supongamos una heterogeneidad de trabajos y el empresario que se endeuda para aumentar las cantidades de trabajo. Cada préstamo suplementario que corresponde a una unidad adicional de trabajo se puede hacer corresponder con el incremento de valor del producto resultante. Esta sería la "contribución" marginal de trabajo. Si esta contribución es decreciente, se prestará dinero hasta que la contribución marginal sea igual a la tasa de interés. Lo mismo sucederá con los recursos especiales de la función phi (φ) ampliada de Cuevas.
Ahora la confusión es completa: en el límite, la contribución marginal de los trabajos, de los recursos especiales y la contribución marginal de los capitales son equivalentes a la tasa de interés. Así podemos ver que la idea de las contribuciones del capital y del trabajo no explican los ingresos en un sistema económico y sólo sirven de principio de comportamiento empresarial para el ajuste sobre el equilibrio. Por este motivo pensamos que Cuevas confunde dos cosas de naturaleza distinta22: la teoría de la distribución del ingreso en la posición de equilibrio económico y la trayectoria de los empresarios para alcanzar ese equilibrio y, por eso, se ilusiona con el poder explicativo de las contribuciones marginales de los factores normales o especiales.
CONCLUSIONES
Si son correctas las apreciaciones críticas aquí consignadas nos sorprende ahora, más que ayer, el apego de Cuevas (presente desde sus primeros escritos) en la defensa de la idea de una cierta superioridad del modelo clásico de Smith y Ricardo frente a los neoclásicos. En sus trabajos iniciales se utilizaban siempre modelos de precios sin funciones de demanda donde se incorporaba la extraña versión de la teoría del valor trabajo para diferenciarse del modelo de Sraffa y su mercancía patrón. También es más claro ahora que la antigua simpatía de Cuevas por los clásicos no depende de una adhesión positiva al modelo propuesto por Sraffa y a la visión general de los neo-ricardianos. En realidad, ahora nos parece claro que el único punto compartido con ellos haya sido la satisfacción por el triunfo neo-ricardiano en el debate del reswitching de técnicas, es decir, la crítica a ciertos modelos neoclásicos no walrasianos muy frecuentes en los libros de texto23.
En este último trabajo, Cuevas busca "renovar" la escuela clásica por fuera de Sraffa, reuniendo tres elementos. Primero, acepta (¿tardíamente?) que un modelo a la Hahn (un modelo expresamente neo-walrasiano) no tiene los problemas del reswitching y se regocija que, a diferencia de los antiguos clásicos, incorpore el mercado de trabajo, funciones de demanda, rendimientos diferentes a los constantes y selección de técnicas. Segundo, se aparta de nuevo de Sraffa al apegarse a una forzada historia de la teoría de la renta promovida por algunos neoclásicos y, tercero, insiste en su deflactor salarial.
Ahora bien, si como aquí hemos intentado mostrar, ninguno de estos elementos realmente pertenecen a los clásicos ni tampoco son esenciales para su formulación central, es lógico concluir que la primacía de los clásicos no aparece analíticamente, o en verdad, nunca ha existido, porque más que realidades eran fantasmas o, sería mejor decir, armas retóricas personales para distanciarse de las vulgaridades de algunos libros de divulgación. Por eso pensamos que antes que a una "renovación" de los clásicos (que pudiera rivalizar con todo derecho con la que han propuesto los neo-ricardianos en los últimos 40 años) la propuesta de Cuevas finalmente contribuye a que los lectores se persuadan de que los clásicos no representan un enfoque económico específico sino una mera etapa (la inicial) en la formación de la teoría económica neoclásica que sería la única que merecería el calificativo de general24. Por eso pensamos que a falta de lograr una renovación que lleve las ideas clásicas a nuevos horizontes, Cuevas abre otra vía hacia su eliminación y olvido.
NOTAS AL PIE
1 Cuevas [ 2001, cap. IV: 65-104] reedición de Cuevas [ 2000] .
2 En realidad, Cuevas introduce las variables en términos monetarios, o mejor, nominales por hipótesis y las "deflacta" por medio de un número d. Este truco, que permite presentar las magnitudes en términos de trabajo, altera la medición pero no el contenido intrínseco del modelo.
3 Por esta razón, los modelos que tengan esta neutralidad (los de función agregada o los de Sraffa con mercancía patrón) son particulares y, por ende, quedan descartados y fuera de la polémica.
4 Ver numeral 3.5.4 de Cuevas [ 2000, 53] .
5 "Esta teoría, postulada por Adam Smith, equivale a un análisis de los impactos de la participación de las distintas clases de ingreso sobre el sistema de precios" [ Cuevas 2000, 43] .
6 Esta tesis es un punto común de muchos historiadores simpatizantes del pensamiento neoclásico: por ejemplo Niehans [ 1990, 95] afirma: "Though in his general theory of value Ricardo had nothing substantial to say about scarcity, his theory of rent became fundamental for the understanding of the pricing of scarce resources". Pero es combatida por Sraffa mismo y por historiadores heterodoxos como Deleplace [ 1999] .
7 "Una de las implicaciones cruciales de la teoría clásica de la renta diferencial de la tierra fue la revolución marginalista, la cual exigió consecuencia lógica, involucrando los demás insumos, el capital y el trabajo en el mismo análisis de los recursos" [ Cuevas 2000, 54] .
8 Todas son adjetivos utilizados por el autor para señalar un supuesto carácter de estos pensadores.
9 Estos autores serían aún más culpables porque "[ infortunadamente] olvidan la teoría de la renta diferencial como parte integral y esencial del modelo clásico de los precios" [ Cuevas 2000, 32-33] .
10 Esta visión no antagónica de la evolución de la teoría económica fue inicialmente impulsada por Marshall contra el sectarismo de Jevons frente al ricardianismo, y hoy es un objetivo de los neoclásicos que aceptan la primacía del modelo Arrow-Debreu en tanto plataforma para desarrollar modelos derivados que pongan en escena "imperfecciones" que aparecen como más realistas. No hay que dudar que esta visión es un pilar para defender la idea de una teoría fundamental única para los economistas y para las facultades de economía.
11 Cuevas no lo menciona sino indirectamente mediante la cita de Hahn.
12 En este asunto, se cuenta que Hahn acusa a Sraffa de acercarse a la posición neoclásica, y esto parece aceptable para Cuevas "ya que se trata la relación capital/producto independiente de los precios" [ Cuevas 2000, 30] .
13 Numeral 3.5.4 de Cuevas [ 2000, 53] .
14 Debemos recordar que sobre estas bases es que Sraffa y su escuela han combatido la idea de factor de producción utilizada por los neoclásicos.
15 "[ La ecuación 2.4.1 y simplificando] no conduce a otra vía que a la teoría del valor trabajo, entendiendo por esto la definición de d establecida en 2.4.2. (Valor agregado real = trabajo agregado en el proceso de producción global)" [ Cuevas 2000, 43] .
16 Cuevas ha criticado a Sraffa en este punto aunque otros han considerado infundadas sus consideraciones. Ver Cataño [ 1996] y Supelano [ 1996] .
17 Llama la atención que Cuevas haga aparecer a Hahn diciendo, respecto a la medida invariable, que "la preocupación por encontrar un patrón de medida invariable, no arbitrario, carece de fundamento teórico" cuando en realidad Hahn afirma: "The normalisation [ 5] [ la utilizada por Hahn] also yields invariant standard of value as does any such normalisation [ ....] A numeraire is a numeraire. The price of numeraire can be set equal to one. Sraffa has chosen Standard net product as numeraire and there´s an end to it" [ Hahn 1982, 358] . Afirmar que todo numerario es por definición invariable no significa que no posee "fundamento teórico".
18 Observemos aquí otra ambigüedad de Cuevas: mientras en todos sus escritos ha atacado el tratamiento del capital como una magnitud físicamente dada, siempre ha guardado silencio sobre la magnitud trabajo como si esta sí se pudiera considerar como una magnitud dada antes del mercado, o de los salarios.
19 Podemos anotar también que las otras innovaciones que propone Cuevas no dependen de la idea del deflactor.
20 La mayoría de los economistas teóricos reconocen que sobre la competencia poco se ha podido modelar satisfactoriamente y, por eso, las ideas de convergencias hacia el equilibrio son hoy pura creencia sin fundamento científico.
21 Utilizamos aquí una reflexión crítica de Rebeyrol [ 2000] sobre Clark.
22 El origen de la confusión parece venir de seguir ingenuamente la exposición de Clark.
23 Este punto es hoy aceptado finalmente por el gran vencido en este debate: P.A. Samuelson [ 1998] : "Sraffa was important in teaching me to understand how misleading is this one scalar capital model".
24 Los lectores podrán también comparar el enfoque de Cuevas para definir analíticamente la teoría clásica con el texto colectivo de referencia actual de esa escuela editado por Kurz y Salvadori [ 1998] y Klimovsky [ 2000] .
REFERENCIAS BIBLIOGRÁFICAS
1. Benetti, Carlo y Cartelier, Jean. 1995. "Money, Form and determination of value", Ponencia en el Congreso internacional de Bologna, 1995. Publicado en español en Cuadernos de Economía, v. XVII, n. 28, Universidad Nacional de Colombia, 53-70. [ Links ]
2. Cataño, José F. 1996. "La mercancía patrón en Sraffa", Cuadernos de Economía, v. XV, n. 24, Universidad Nacional de Colombia, 27-40. [ Links ]
3. Cuevas, Homero. 2000. "Selección de técnicas en la teoría de los precios", Cuadernos de Economía, v. XIX, n. 32, Universidad Nacional de Colombia, 27-60. [ Links ]
4. Cuevas, Homero. 2001. "Selección endógena de técnicas", en Economía clásica en renovación, Universidad Nacional de Colombia, cap. IV. [ Links ]
5. Deleplace, Ghislain. 1999. Histoire de la pensée économique, Dunod, París. [ Links ]
6. Geanakoplos, John. 1987. "Arrow-Debreu model of general equilibrium", en The new Palgrave, A Dictionary of economics, Macmillan Press limited. [ Links ]
7. Hahn, Frank. 1982. "The Neo-Ricardians", Cambridge Journal of Economics, v. 6, n. 4, 351-374. [ Links ]
8. Klimovsky, E. 2000. "Modelos básicos de la teoría de los precios", Cuadernos de Economía, v. XIX, n. 32, 77-103. [ Links ]
9. Kurz, H. y Salvadori, N. (eds) 1998. Elgar companion to classical economics, Eduard Elgar, Londres. [ Links ]
10. Mangiovi, G y Petri. F. (eds) 1998. "Value, distribution and capital", Essays in honour of Pierangelo Garegnani, Routledge. [ Links ]
11. Marx, Karl. 1980. Teorías de la historia de la plusvalía, tomo III, Fondo de Cultura Económica, México. [ Links ]
12. Niehans, Jurg. 1990. A history of economic theory. The Johns Hopkins Press Ltd. [ Links ]
13. Rebeyrol, Antoine. 2000. "Repartition, interet et théorie du capital", en La nouvelle histoire de la pensée économique, Beraud y Faccarello (eds), La Decouverte, París. [ Links ]
14. Ricardo, David. 1959. Principios de economía política y tributación, Fondo de Cultura Económica, México. [ Links ]
15. Samuelson, Paul A. 1998. "The special thing I learned from Sraffa", en Mangiovi, G y Petri. F [ 1998]. [ Links ]
16. Sraffa, Piero. 1976. "Sur la relation entre cout et quantité produite", en Ecrits d´économie politique, Economica, París. [ Links ]
17. Supelano, Alberto. 1996. "Bienes básicos, mercancía patrón y tasa de ganancia en Piero Sraffa", [ Links ]














