Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Cuadernos de Economía
Print version ISSN 0121-4772On-line version ISSN 2248-4337
Cuad. Econ. vol.27 no.48 Bogotá Jan./June 2008
PRONÓSTICO Y ESTRUCTURAS DE VOLATILIDAD MULTIPERÍODO DE LA TASA DE CAMBIO DEL PESO COLOMBIANO
Elkin Castaño Vélez*
Karoll Gómez Portilla
Santiago Gallón Gómez
* Elkin Castaño es Magister en Estadística. Se desempaña como docente, investigador y coordinador del Grupo de Econometría Aplicada (GEA) del Centro de Investigaciones y Consultorías Económicas de la Universidad de Antioquia. Igualmente, es docente de la Facultad de Ciencias de la Universidad Nacional (Medellín, Colombia). E-mail: elkincv@gmail.com
Karoll Gómez es Magíster en Economía. Actualmente, es docente de la Facultad de Ciencias Humanas y Económicas de la Universidad Nacional (Medellín, Colombia) e investigadora del Grupo de Econometría Aplicada (GEA) del Centro de Investigaciones y Consultorías Económicas de la Universidad de Antioquia. E-mail: kgomezp@unal.edu.co, karollg@udea.edu.co
Santiago Gallón Magíster en Economía y se desempeña como docente de la Facultad de Ciencias Humanas y Económicas de la Universidad Nacional (Medellín, Colombia). Asimismo, es investigador del Grupo de Econometría Aplicada (GEA) del Centro de Investigaciones y Consultorías Económicas de la Universidad de Antioquia. E-mail: sgallong@unal.edu.co, santiagog@udea.edu.co
Este artículo es producto de una investigación financiada por Bancolombia. Los autores agradecen la colaboración de Johanna Vásquez en el proceso de investigación y de Johanna Marín en la manipulación de la información estadística; así como los valiosos comentarios de los evaluadores anónimos del artículo.
Este artículo fue recibido el 25 de junio de 2007 y su publicación aprobada el 15 de marzo de 2008.
Resumen
El modelo gaussiano GARCH(1,1) ha sido empleado, tradicionalmente, en el estudio de la tasa de cambio; sin embargo, un número importante de estudios recientes (utilizando modelos FIGARCH e HYGARCH) ha encontrado evidencia de persistencia en su volatilidad. En este trabajo, usando una estrategia de modelos anidados, se encontró evidencia a favor del modelo IGARCH bajo una distribución GED. Los pronósticos del modelo IGARCH son usados para calcular la estructura a plazos y la volatilidad multi-período, las cuales permiten conocer las expectativas del mercado sobre la volatilidad de los retornos, en diferentes horizontes de tiempo.
Palabras clave: tasa de cambio, volatilidad, volatilidad multiperíodo, GARCH, IGARCH, FIGARCH, HYGARCH, HYAPARCH, distribución GED. JEL: C22, C51, C52, C53, F31.
Abstract
The Gaussian GARCH (1,1) model has traditionally been used for studying the exchange rate. However, an important number of recent studies, using FIGARCH and HYGARCH models, have found evidence for the persistence of exchange rate volatility. This study, using nested models, found evidence in favor of an IGARCH model under a GED distribution. The IGARCH model forecasts are used to calculate the term structure of multiperiod volatility, which lets us know the expectations of the market about the volatility of returns over different time horizons.
Keywords: exchange rate, volatility, k-period volatility, GARCH, IGARCH, FIGARCH, HYGARCH, HYAPARCH, GED distribution. JEL: C22, C51, C52, C53, F31.
Résumé
Le modèle gaussien GARCH (1,1) a été employé, traditionnellement, dans l'étude du taux de change. Cependant, un nombre important de travaux récents (qui utilisent des modèles FIGARCH et HYGARCH), ont mis en évidence la persistance dans la volatilité du taux d´échange. Dans ce travail, on utilise une stratégie de modèles emboîtés et on repère de résultats en faveur du modèle IGARCH sous une distribution GED. Les pronostics du modèle IGARCH sont utilisés pour calculer la structure avec différentes types d´échéances et la volatilité multi-période, lesquelles permettent de connaître les anticipations du marché sur la volatilité des rendements.
Mot clés : taux de change, volatilité, volatilité multi-période, GARCH, IGARCH, FIGARCH, HYGARCH, HYAPARCH, distribution GED. JEL : C22, C51, C52, C53, F31.
Debido a la naturaleza heterocedástica de los retornos de la tasa de cambio de corto plazo, la modelación de su proceso de volatilidad es de gran importancia en la toma de decisiones macroecónomicas y del mercado financiero. Para modelar la dinámica de dicho proceso, se han propuesto diversos métodos estadísticos, dentro de los cuales la metodología ARCH ha jugado un papel preponderante.
Trabajos como el de Baillie y Bollerslev (1989, 1991), Hsieh (1988, 1989a, 1989b), Diebold y Nerlove (1989), Milhøj (1987), Engle et al. (1990a), Vlaar y Palm (1993), entre otros, han utilizado dicha metodología, siendo el modelo gaussiano GARCH(1,1) el más empleado para estudiar el proceso de volatilidad. Su popularidad radica en la facilidad de estimación, interpretabilidad y en la derivación analítica directa de resultados como la estructura de plazos de la volatilidad, bajo ciertos supuestos. Sin embargo, un número importante de estudios, empleando bases de datos diarias, han encontrado evidencia sobre la persistencia en la volatilidad de las tasas de cambio, aproximando el proceso por medio de modelos IGARCH, FIGARCH e HYGARCH.
Las especificaciones IGARCH y FIGARCH se caracterizan por la no estacionariedad del proceso de volatilidad, lo cual no parece ajustarse bien a las propiedades empíricas de ciertas variables financieras, dado el grado extremo de persistencia que implican los modelos integrados. Davidson (2004) introduce el modelo HYGARCH como una ESPEcificación alternativa más general, suponiendo que el proceso de volatilidad es estacionario de larga memoria. Este autor encuentra evidencia empírica a favor del modelo HYGARCH para tasas de cambio (con respecto al dólar americano) de países asiáticos en el período 1994-2000, aunque para algunos países europeos la encuentra a favor de modelos FIGARCH. Igualmente, otros autores como Tschernig (1994), Baillie et al. (1996) y Hauser (1997), han encontrado evidencia favorable de la larga memoria en los retornos de la tasa de cambio.
En este sentido, este artículo busca encontrar la especificación más adecuada para el proceso de volatilidad de la tasa de cambio del peso colombiano con respecto al dólar americano, para el período comprendido entre enero de 2000 y julio de 2006.
Utilizando una estrategia de modelos anidados, la cual da inicio con el modelo HYAPARCH como el más general, se encontró evidencia a favor del modelo IGARCH bajo una distribución GED. Para confirmar este resultado, se evaluó el comportamiento de la volatilidad pronosticada por los diferentes modelos con respecto a la volatilidad realizada, teniendo en cuenta que ésta puede ser usada como un estimador insesgado y consistente de la volatilidad verdadera, la cual no es observable, Patton (2006). La volatilidad realizada fue obtenida a partir de información intradiaria de la tasa de cambio, utilizando la metodología sugerida por Andersen et al. (2001, 2003).
Buscar el modelo que mejor explica el comportamiento de los retornos de la tasa de cambio, es indispensable para obtener el pronóstico de la volatilidad asociada a los mismos. Dichos pronósticos son necesarios para el cálculo de la volatilidad multi-período y de la estructura de plazos de la volatilidad, las cuales son de gran importancia en la valoración de opciones y otros instrumentos financieros, dado que éstas dependen de la correcta modelación del activo subyacente.
Así mismo, buscar el modelo que mejor explica el comportamiento de los retornos es crucial para medir el riesgo de mercado a través de la medida VaR -Value at Risk-. La importancia financiera de esta medida radica en su utilidad como herramienta de cuantificación del riesgo de mercado y como instrumento de regulación, dado que el entorno de la actividad financiera expone a los precios de los activos financieros a grandes fluctuaciones. En consecuencia, la VaR es ampliamente usada por instituciones financieras, en países donde se ha adoptado el acuerdo de Basilea.
Este documento está organizado en cuatro secciones. En la primera, se describe la información utilizada y se hace un análisis estadístico preliminar de la misma. En la segunda, se presentan los resultados obtenidos a partir de la especificación y estimación de los modelos de la familia GARCH. En el tercer apartado, una vez establecido el modelo más adecuado, los pronósticos de la volatilidad son usados para calcular la estructura a plazos y la volatilidad multi-período, las cuales permiten conocer las expectativas del mercado sobre la volatilidad del retorno de un activo en diferentes horizontes de tiempo. Finalmente, se exponen las conclusiones.
DESCRIPCIÓN DE LA INFORMACIÓN Y ANÁLISIS ESTADÍSTICO PRELIMINAR DE LOS RETORNOS DE LA TASA DE CAMBIO
Descripción de la información
La base de datos empleada en el estudio está compuesta por 1.716 observaciones diarias para el precio de cierre del Peso colombiano con respecto al Dólar americano -COP/USD- correspondientes al período comprendido entre el 3 de enero de 2000 y el 31 de julio de 20061. La información contiene sólo los días comerciales, para las observaciones faltantes correspondientes a los días festivos se utilizó el dato del día comercial inmediatamente anterior. Para las serie de tasa de cambio se calcularon los retornos nominales porcentuales definidos como, rt = (log yt - log yt- 1 )100 , donde yt representa el precio COP/USD en el t-ésimo día.
Análisis estadístico preliminar
Con el fin de comprender el comportamiento de la serie de retornos COP/USD se realizó un análisis estadístico preliminar de la misma. En la Gráfica 1, se presentan la serie del precio del dólar en niveles, sus retornos y sus correspondientes cuadrados y valores absolutos.
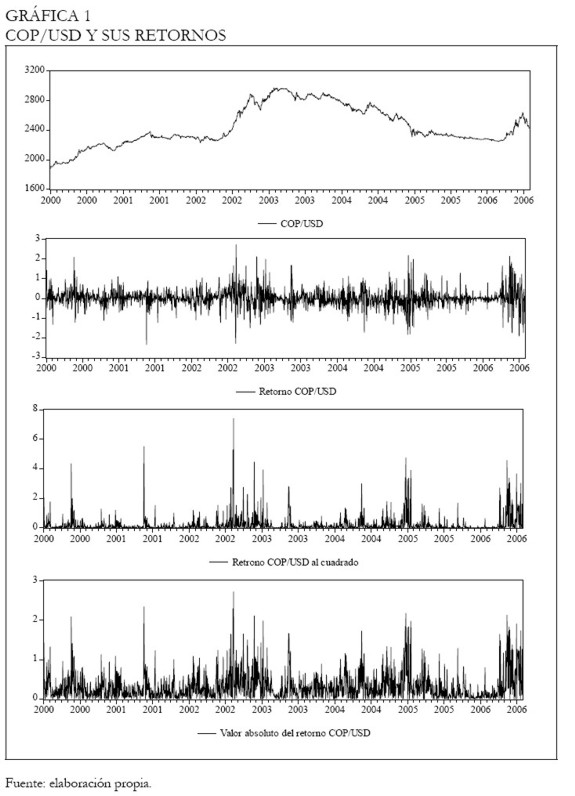 |
La inspección visual de la serie en niveles parece indicar no estacionariedad, mientras que los retornos parecen serlo por lo menos en media. Los retornos al cuadrado y los valores absolutos de los mismos, indican que la volatilidad en el mercado es cambiante en el tiempo y sugieren la existencia de volatilidad por clusters, es decir, grandes (pequeños) cambios en los precios, de cualquier signo, tienden a estar seguidos por grandes (pequeños) cambios de precios. Adicionalmente, la serie nos muestra que los retornos son más volátiles en períodos de devaluación, principalmente, a principios de 2002 y al final del período de estudio.
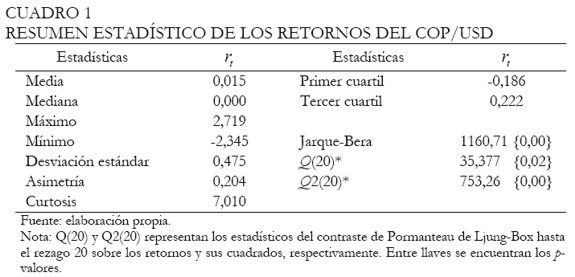
En el Cuadro 1, se presenta el resumen estadístico para los retornos de la tasa de cambio. Se observa que existe un notable exceso de curtosis con respecto a la distribución normal, mientras que el coeficiente de asimetría es positivo y pequeño. En consecuencia, el contraste incondicional de normalidad de Jarque-Bera rechaza la hipótesis nula de normalidad. El estadístico de Ljung-Box evidencia, además, correlación serial significativa al rezago 20, tanto en los retornos como en sus cuadrados, indicando la posible necesidad de modelar la media y la varianza condicionales.
 |
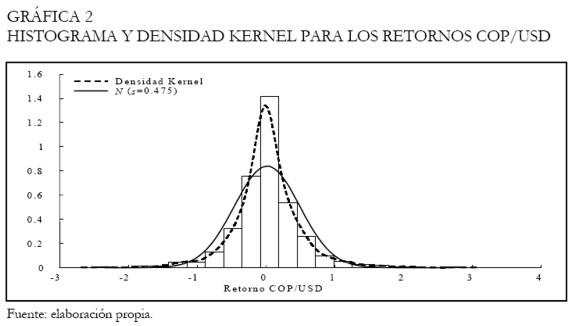
La Gráfica 2, presenta el histograma y el estimador no-paramétrico de la función de densidad de probabilidad de la serie de los retornos (Silverman 1986), los cuales evidencian, nuevamente, el fuerte exceso de curtosis. Esto indica que grandes retornos, tanto positivos como negativos, ocurren más frecuentemente de lo que se podría esperar al compararlos con retornos que distribuyen a partir de una función de distribución normal. El 56% de los retornos son nulos o positivos, con un incremento máximo en el precio de 2,76%, en comparación a caídas en el mismo de 2,32%.
 |
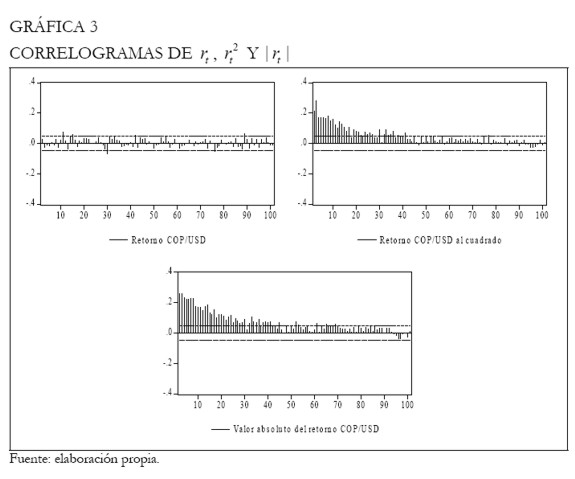
De otra parte, dada la evidencia empírica sobre la existencia de dependencias de larga memoria en datos de series financieras (Lo 1991, Ding et al. 1993, Baillie 1996, y Granger y Ding 1996), se investigó su presencia en los retornos de la tasa de cambio, así como en sus cuadrados y valores absolutos. Para tal fin se emplearon los correlogramas muestrales para los cien primeros rezagos, los cuales se presentan en la Gráfica 3. Para los retornos al cuadrado y los valores absolutos se confirma, aparentemente, la existencia de larga memoria, al presentar patrones de decaimiento hiperbólicos congruentes con un comportamiento de persistencia en el proceso de volatilidad. Sin embargo, no parece existir evidencia a favor de larga memoria en los retornos COP/USD.
 |
Para confirmar la existencia de larga memoria sugerida por los resultados anteriores, se emplearon las pruebas de Geweke y Porter-Hudak -GPH- (1983), de máxima verosimilitud Local de Whittle (Künsch 1987 y Robinson 1995); y los contrastes de Kwiatowski et al. -KPSS- (1992), de rango reescalado de Lo (1991), de Lobato y Robinson (1998), de Harris-McCabe-Leybourne -HML- (2008)2, y de Castaño, Gómez y Gallón (2007) cuyos resultados se reportan en el Cuadro 2.
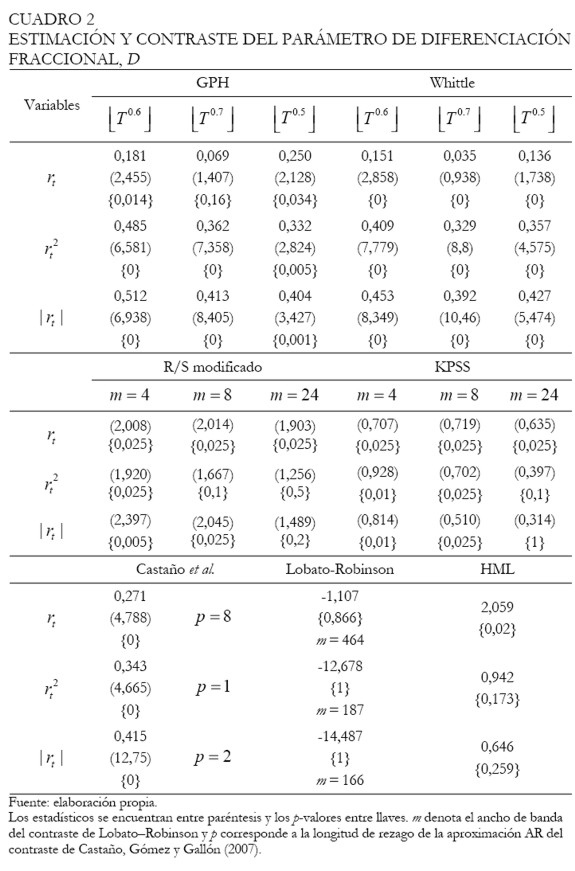 |
Como se observa en el cuadro, la hipótesis nula de corta memoria, H0 : d = 0, para los retornos es rechazada en la mayoría de los casos, excepto para los contrastes de Lobato y Robinson y GPH con un ancho de banda de  T 0.7
T 0.7  . Para los retornos al cuadrado y sus valores absolutos, la hipótesis nula es rechazada, excepto en los contrastes de HML, Lobato y Robinson, rango reescalado ( m = 8 y m = 24 ) y KPSS (m = 24). Estos resultados indican que, al parecer, tanto los retornos como su volatilidad exhiben persistencia o larga memoria.
. Para los retornos al cuadrado y sus valores absolutos, la hipótesis nula es rechazada, excepto en los contrastes de HML, Lobato y Robinson, rango reescalado ( m = 8 y m = 24 ) y KPSS (m = 24). Estos resultados indican que, al parecer, tanto los retornos como su volatilidad exhiben persistencia o larga memoria.
MODELACIÓN DE LOS RETORNOS DE LA TASA DE CAMBIO COP/USD3
Modelo GARCH(1,1)
Un modelo que, tradicionalmente, ha sido empleado en las aplicaciones empíricas para estudiar el comportamiento de los retornos de tasa de cambio es el modelo gaussiano GARCH(1,1), sin componentes ARMA para la media condicional. Su popularidad radica en la facilidad de estimación y de interpretación, así como en la derivación analítica directa de resultados tales como la estructura de plazos de la volatilidad, bajo ciertas condiciones especiales (véase al respecto Baillie y Bollerslev 1989, 1991; Hsieh 1988, 1989a, 1989b; Diebold y Nerlove 1989; Milhøj 1987; Engle et al. 1990a; Vlaar y Palm (1993); Gallón y Gómez (2007), entre otros). La especificación de este modelo está dada por:
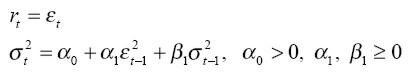 | [1] |
donde ε1 = σ1 zt , zt  i.i.d.N(0,1) y σt > 0 es la desviación estándar condicional al conjunto de información disponible hasta t - 1,
i.i.d.N(0,1) y σt > 0 es la desviación estándar condicional al conjunto de información disponible hasta t - 1,  t - 1. La condición de estacionariedad para el proceso de la varianza condicional está dada por α1 + β1 < 1 . Este modelo captura las regularidades empíricas de volatilidad por cluster, los saltos en volatilidad y la leptocurtosis en los retornos.
t - 1. La condición de estacionariedad para el proceso de la varianza condicional está dada por α1 + β1 < 1 . Este modelo captura las regularidades empíricas de volatilidad por cluster, los saltos en volatilidad y la leptocurtosis en los retornos.
Los resultados de la estimación para la media y la varianza condicional de los retornos se presentan en el Cuadro 34. La segunda, tercera y cuarta columna, muestran las estimaciones del modelo bajo las distribuciones normal, GED y t-Student condicionales. Algunas pruebas de diagnóstico se encuentran en la parte inferior del cuadro. El contraste de Jarque-Bera indica el rechazo del supuesto de normalidad, por lo que esta distribución no es adecuada para la explicación del comportamiento de los retornos. Este resultado está de acuerdo con lo hallado en el análisis descriptivo de los retornos.
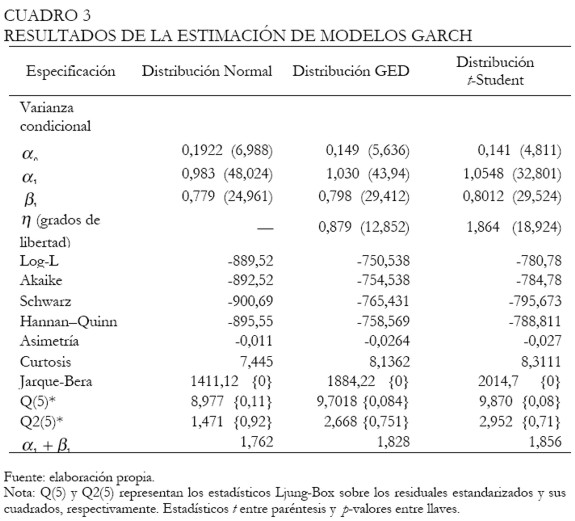 |
En consecuencia, diferentes supuestos fueron probados sobre la distribución condicional del término de error, los cuales incluyen las distribuciones t-Student, t-Student asimétrica y de error generalizado, bajo el modelo GARCH(1,1), encontrándose evidencia a favor de la distribución GED. La tercera columna contiene los resultados de la estimación del modelo bajo esta distribución.
Para los modelos estimados, las pruebas de diagnóstico, basadas en el estadístico de Ljung y Box, parecen indicar el buen comportamiento de los modelos, a un nivel de significancia del 5%. No obstante, la propiedad de estacionariedad se viola al ser la suma de α1 y β1 mayor que 1, indicando que el proceso de volatilidad es no estacionario5 o que es un proceso de larga memoria. En consecuencia, el modelo GARCH(1,1) no parece capturar el proceso de volatilidad de la tasa de cambio adecuadamente. Nótese además que ninguno de estos modelos incorpora el fenómeno de larga memoria detectado en la sección anterior.
Estrategia de modelación: el modelo general ARFIMAHYAPARCH
Para la selección de un modelo de la clase ARCH que más se aproxime a representar el proceso de volatilidad de los retornos, dada la evidencia de larga memoria, se empleó la estrategia de modelos anidados. Con base en un modelo general, se elige la mejor especificación siempre y cuando los parámetros estimados cumplan ciertas restricciones. El modelo general utilizado como base para la selección, es el modelo ARFIMA-HYAPARCH, Schoffer (2003). A continuación se define su especificación y propiedades.
Con el fin de capturar la posible presencia de las principales regularidades empíricas de los retornos de los activos financieros, tales como volatilidad por cluster, leptocurtosis, larga memoria y asimetrías, Schoffer (2003) propone el modelo GARCH de potencia asimétrico hiperbólico -HYAPARCH- como una generalización del modelo GARCH hiperbólico de Davidson (2003, 2004), y del modelo GARCH de potencia asimétrica de Ding et al. (1993). El modelo ARFIMAHYAPARCH (p,d,q) para la media y la varianza condicional de los retornos, está dado por:
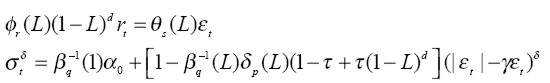 | [2] |
Donde ε1 = σ1 zt , zt  i.i.d.N(0,1), φr (L) = 1 - φ1 L - ... - φr Lr y θs (L) = 1 - θ1 L - ... - θs Ls son los polinomios de la parte autorregresiva y de medias móviles de la media condicional, respectivamente, con todas sus raíces fuera del círculo de unidad y sin factores comunes. δp (L) = 1 - δ1 L -...- δp L p y βq (L) = 1 - β1 L -...- βq L q son los polinomios del proceso de varianza condicional con todas sus raíces fuera del círculo de unidad y sin factores comunes, 0 ≤ τ ≤ 1, 0 ≤ d ≤ 1, δ ≥ 0 y
i.i.d.N(0,1), φr (L) = 1 - φ1 L - ... - φr Lr y θs (L) = 1 - θ1 L - ... - θs Ls son los polinomios de la parte autorregresiva y de medias móviles de la media condicional, respectivamente, con todas sus raíces fuera del círculo de unidad y sin factores comunes. δp (L) = 1 - δ1 L -...- δp L p y βq (L) = 1 - β1 L -...- βq L q son los polinomios del proceso de varianza condicional con todas sus raíces fuera del círculo de unidad y sin factores comunes, 0 ≤ τ ≤ 1, 0 ≤ d ≤ 1, δ ≥ 0 y 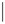 γ
γ 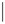 < 1 representan los parámetros de amplitud, memoria, potencia y asimetría, respectivamente, y ( 1 - L)d es el operador de diferencia fraccional, expresado como:
< 1 representan los parámetros de amplitud, memoria, potencia y asimetría, respectivamente, y ( 1 - L)d es el operador de diferencia fraccional, expresado como:
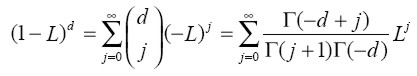 | [3] |
Donde 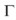 (.) denota la función Gamma. Las condiciones de estacionariedad débil sobre el proceso están dadas por 0 ≤ τ < 1, 0 ≤ d < 1 y (1- β (1))-1 (α0 - δ(1)) > 0 (Davidson 2004 y Schoffer 2003).
(.) denota la función Gamma. Las condiciones de estacionariedad débil sobre el proceso están dadas por 0 ≤ τ < 1, 0 ≤ d < 1 y (1- β (1))-1 (α0 - δ(1)) > 0 (Davidson 2004 y Schoffer 2003).
En el modelo, el parámetro de amplitud determina qué tan grandes pueden ser las variaciones en la varianza condicional, mientras que el parámetro de memoria cuánto persisten o tardan en disiparse los shocks sobre la volatilidad condicional. En cuanto al parámetro de asimetría, éste permite investigar si los shocks "positivos" tienen o no el mismo efecto que los shocks "negativos" sobre la volatilidad. Por su parte, el parámetro de potencia permite capturar patrones de autocorrelación más generales en el proceso estocástico.
Una de las particularidades del modelo HYAPARCH es que anida un gran conjunto de especificaciones entre los cuales están los modelos GARCH, GARCH asimétrico -AGARCH-, AGARCH de potencia -APGARCH-, GARCH integrado -IGARCH-, IGARCH asimétrico -AIGARCH-, AIGARCH integrado de potencia -PAIGARCH-, GARCH fraccionalmente integrado -FIGARCH-, FIGARCH asimétrico -AFIGARCH-, AFIGARCH de potencia -PAFIGARCH- e HYGARCH bajo restricciones sobre los parámetros τ, d , δ y γ resumidas en el Cuadro 4.
 |
Adicionalmente, dado que el modelo APGARCH de Ding et al. (1993) anida a los modelos ARCH de Engle (1982), GARCH de Bollerslev (1986), GARCH de Taylor (1986) y Schwert (1990), GJR de Glosten et al. (1993), TARCH de Zakoian (1994), NARCH de Higgins y Bera (1992) y el log- ARCH de Geweke (1986) y Pantula (1986) como casos especiales del mismo, entonces dichas especificaciones también están incluidas en el modelo HYAPGARCH permitiendo, de este modo, estudiar la presencia de larga memoria en los mencionados modelos.
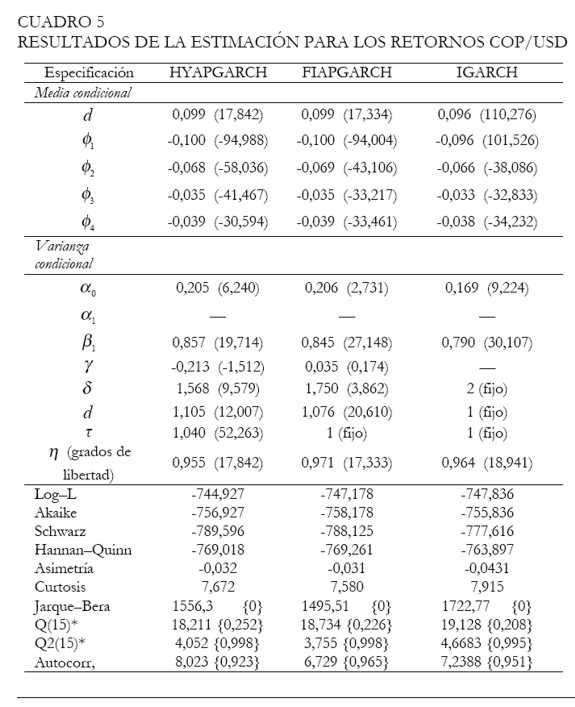
Los resultados de la estimación para la media y la varianza condicional de los retornos partiendo de la especificación más general ARFIMA-HYAPARCH, bajo la distribución condicional GED, se reportan en el Cuadro 5. Para la identificación de la media del proceso, en la sección 2 el procedimiento de Castaño, Gómez y Gallón sugiere la presencia de un modelo ARFIMA, el cual parece ser bien aproximado por un ARFIMA(4,d,0).
 |
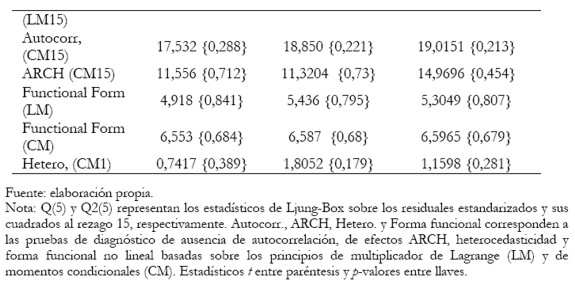 |
Los resultados del Cuadro 5 usan como modelo general un ARFIMA (4,d,0)-HYAPARCH (1,1). Utilizando la estrategia de modelos anidados se contrastaron las diferentes restricciones llegando, finalmente, a un modelo ARFIMA (4,d,0)-IGARCH (1,1). Esta especificación final indica la existencia de larga memoria en el proceso de media y de integración en el proceso de varianza. Ahora bien, a diferencia de la interpretación de un proceso integrado en media, donde un choque sobre la serie no desaparece, Davidson (2004)6 mostró que el proceso IGARCH es un proceso de memoria corta, lo cual implica que un choque sobre el proceso de volatilidad termina desapareciendo en forma exponencial. Por último, no se halló evidencia a favor de asimetría y la forma más adecuada para modelar la volatilidad parece ser en términos de la varianza condicional.
El contraste de Ljung-Box para los residuales estandarizados y sus cuadrados sugieren que no existe correlación serial en la media, ni efectos GARCH adicionales. Los resultados para los diagnósticos de cada uno de los modelos estimados se reportan en la parte inferior del Cuadro 5. Al comparar los resultados de estimación, a partir de los modelos, se encuentra que según los criterios de información de Schwarz y Hannan-Quinn es superior el modelo IGARCH (en el programa TSM, los criterios de información son redefinidos de forma tal que a mayor valor mejor es el modelo). Adicionalmente, comparando el máximo de la función log-verosímil se obtiene evidencia a favor de este mismo modelo. En consecuencia, la volatilidad parece no ser estacionaria. Este resultado concuerda con hallazgos para al menos 10 tasas de cambio de países europeos con respecto al Dólar americano en el período 1980-1996 (Davidson 2004). Aunque para tasas de cambio de países asiáticos con respecto al Dólar americano, Davidson halló evidencia empírica a favor del modelo HYGARCH(1,1), en el período 1994-2000.
Evaluación de los pronósticos
Con el fin de evaluar el efecto de desconocer la larga memoria en el proceso de la media condicional de los retornos de la tasa de cambio, se comparó la capacidad de pronóstico de la volatilidad de los modelos IGARCH (1,1) y ARFIMA-IGARCH (1,1).
Como metodología de comparación entre los modelos se usó la capacidad de pronóstico de cada uno de éstos, medida a partir del Error Cuadrático Medio (ECM) y el Error Absoluto Medio (EAM), utilizando como referencia la volatilidad realizada entre el 16 de abril de 2004 y el 31 de julio de 2006, que actúa como un estimador de la volatilidad que es no observable7. Los resultados arrojan evidencia nuevamente a favor del IGARCH al presentar errores más pequeños y, por tanto, mayor capacidad de pronóstico8.
Adicionalmente, se estimaron regresiones auxiliares de la volatilidad realizada sobre los pronósticos de la volatilidad condicional, con el fin de determinar en cual caso se presentaba mejor bondad de ajuste. Los resultados mostraron un ajuste de 0,237424 en el modelo de la volatilidad realizada sobre los pronósticos de la volatilidad condicional IGARCH frente a 0,227423 para el ARFIMA-IGARCH, confirmándose nuevamente la superioridad del modelo integrado.
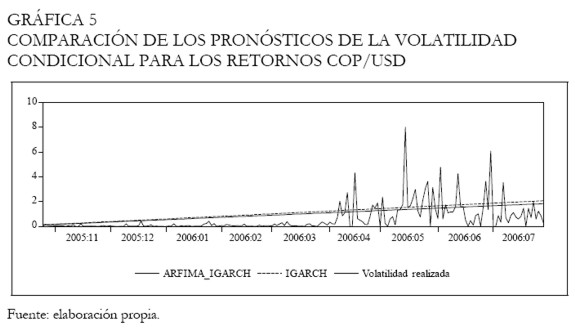
En la Gráfica 5, se presentan los resultados de la comparación de los pronósticos obtenidos para los dos modelos, tomando como referencia la volatilidad realizada. En este se observa que el modelo IGARCH es capaz de predecir el período de exceso de volatilidad que se presentó a partir de abril de 2006. En este sentido, es importante tener en cuenta que la elección y el uso de un modelo erróneo puede conducir a inferencias incorrectas, ausencia o mal diseño de políticas de cubrimiento de riesgo, valoración de activos incorrecta, entre otras.
 |
VOLATILIDAD MULTI-PERÍODO Y ESTRUCTURAS DE PLAZOS
Una vez obtenido el modelo que mejor explica el comportamiento de los retornos de la tasa de cambio, es posible obtener el pronóstico fuera de la muestra de la volatilidad asociada a los mismos. Dichos pronósticos son necesarios para el cálculo de la volatilidad multi-período y la estructura de plazos de la volatilidad, cuyas definiciones se presentan a continuación. Adicionalmente, se presentan los resultados de las estimaciones para las mismas en los siguientes horizontes de pronóstico: diario, semanal, quincenal, mensual, trimestral, semestral y anual.
Definiciones
El log retorno entre los períodos t y t + k, conocido como el retorno k-períodos, está definido como
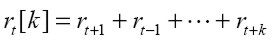 | [4] |
Cuando el proceso para la media condicional de los retornos ( rt ) sigue un proceso tipo ARMA, entonces, el pronóstico de la volatilidad de rt [k ] , comúnmente conocido como volatilidad multi-período, está dado por la varianza condicional del error de pronóstico ( et [k] = rk [k] - E (rk [k]| 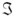 t )),9 cuya expresión es:
t )),9 cuya expresión es:
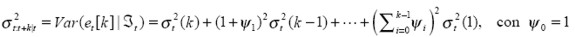 | [5] |
Donde 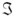 t denota el conjunto de información hasta t, ψi, i ≥ 0 son los coeficientes impulso-respuesta de la representación de medias móviles (MA) del modelo ARMA de la media condicional de la serie de los retornos10 y σ 2 t ( l ) es el pronóstico l-pasos hacia adelante de la volatilidad. Los pronósticos σ 2 t ( l ) dependen del tipo de proceso que sigue la varianza condicional de los retornos (por ejemplo, un proceso de la familia GARCH). Claramente, la volatilidad multi-período crece conforme aumenta el horizonte de tiempo Tsay (2005).
t denota el conjunto de información hasta t, ψi, i ≥ 0 son los coeficientes impulso-respuesta de la representación de medias móviles (MA) del modelo ARMA de la media condicional de la serie de los retornos10 y σ 2 t ( l ) es el pronóstico l-pasos hacia adelante de la volatilidad. Los pronósticos σ 2 t ( l ) dependen del tipo de proceso que sigue la varianza condicional de los retornos (por ejemplo, un proceso de la familia GARCH). Claramente, la volatilidad multi-período crece conforme aumenta el horizonte de tiempo Tsay (2005).
Sin embargo, cuando los retornos son incorrelacionados serialmente, es decir, no existe modelo ARMA, entonces los coeficientes impulso respuesta son nulos ( ψi = 0, 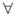 i > 0 ) y, por lo tanto, la ecuación para el pronóstico de la volatilidad de rt[k] se simplifica a
i > 0 ) y, por lo tanto, la ecuación para el pronóstico de la volatilidad de rt[k] se simplifica a
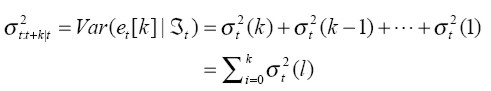 | [6] |
Una práctica muy común en la construcción del pronóstico de la volatilidad de rt[k], es igualar la volatilidad futura a la volatilidad estimada corriente (σ2 t+k | t ≈ σ2 ) y así, bajo el supuesto de retornos serialmente incorrelacionados, el pronóstico de la volatilidad se convierte en la suma sucesiva de los pronósticos de la varianza un período hacia delante, esto es: σ2 t:t+k | t ≈ k σ2. Este resultado es comúnmente conocido como volatilidad escalada. Sin embargo, esto ha sido criticado debido a que puede producir sobreestimaciones de la variabilidad en un horizonte amplio (Diebold et al. 1998).
Una vez obtenido el pronóstico de la volatilidad del retorno k-períodos ( rt[k] ), la correspondiente estructura a plazos de la volatilidad está dada por:
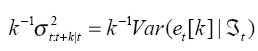 | [7] |
La cual refleja las expectativas de mercado sobre la volatilidad del retorno de un activo para diferentes horizontes de tiempo; indispensable para la valoración de activos y el diseño de estrategias de cobertura de riesgos. A diferencia de la volatilizada multi-período, la estructura a plazos admite tres formas: monótona creciente, monótona decreciente o constante con respecto a la horizonte de tiempo (Xu y Taylor 1994).
Cálculos para los retornos de la tasa de cambio
En el Cuadro 6, se presentan los cálculos de la volatilidad multi-período y de la estructura a plazos de los retornos COP/USD. A partir de los resultados del modelo ARFIMA-IGARCH, se encuentra, por ejemplo, que en un horizonte de un día la variabilidad de los retornos esperados es de 0,79%; es decir, dado que el retorno condicional esperado es igual a cero, se esperaría que el retorno fluctuara entre 0,79% y -0,79%, lo cual en términos de un nivel de tasa de cambio de 2.250 pesos por dólar implicaría una variación de entre 2.232 y 2.267 pesos, para el día siguiente11. Similarmente, según éste mismo modelo se esperaría que en un horizonte de un año la tasa de cambio estuviera entre 1.596 y 2.903 pesos por dólar, correspondiente a una volatilidad acumulada esperada a un año del 29%.
 |
En contraste el modelo IGARCH predice una volatilidad acumulada del 19% para una tasa de cambio entre 1.820 y 2.508 pesos. De otra parte, las expectativas promedio de volatilidad, representadas en la estructura a plazos, aumentan conforme se incrementa el plazo en ambos casos. La expectativa de volatilidad promedio diaria para un año es menor que la obtenida para un día.
En el caso de la volatilidad realizada, se efectuó la conversión de la misma a distintos horizontes de tiempo utilizando la regla de escalamiento típica, es decir, multiplicar la desviación estándar por √k , donde k representa el horizonte de tiempo, bajo el supuesto de retornos independientes e idénticamente distribuidos. En el Cuadro 7, se presentan los resultados.
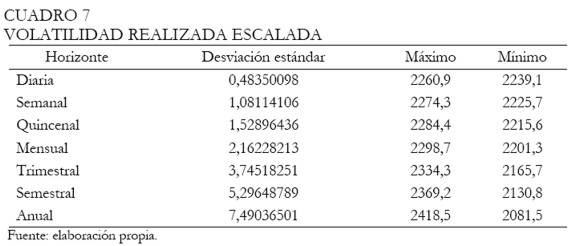 |
En este caso se observa que la volatilidad realizada escalada es menor, en todos los horizontes de tiempo, que la arrojada por el modelo HYGARCH, por lo que ésta arroja predicciones para la variabilidad de los retornos esperados más pequeños. Así, dado que el retorno condicional esperado es igual a cero, el retorno fluctuará entre 0,48% y -0,48%, lo cual en términos de un nivel de tasa de cambio de 2.250 pesos implicaría una variación entre 2.239 y 2.260 pesos, y al cabo de un año una fluctuación entre 2.081 y 2.418.
CONCLUSIONES
En esta investigación se realizó un análisis estadístico, con el fin de comprender el comportamiento de la serie de retornos COP/USD y de sus volatilidades asociadas. Adicionalmente, se construyó el pronóstico tanto de los retornos como de las volatilidades, los cuales fueron los insumos necesarios para la elaboración de las volatilidades multi-período y de las estructuras a plazos de la volatilidad, que a su vez son requeridas en operaciones financieras, tales como la valoración de activos, el cálculo de valoración en riesgo, entre otras.
Del análisis estadístico preliminar, se puede concluir que la serie presenta evidencia de larga memoria en la volatilidad de los retornos, confirmando los resultados que, recientemente, se han hallado para las series de tasas de cambio en otros países. Igualmente, la evidencia empírica mostró que los retornos y las primeras diferencias presentan características que los alejan del supuesto de normalidad. En consecuencia, diferentes supuestos fueron probados sobre la distribución condicional del término de error de los diferentes modelos ajustados, los cuales incluyen las distribuciones t-Student, t-Student asimétrica y de error generalizado -GED-. De acuerdo con lo anterior, utilizando una estrategia de modelos anidados se estimó el modelo HYA PGARCH, el cual permite múltiples regularidades empíricas presentes en las series financieras. En particular, se obtuvo que la especificación que mejor se ajustaba a los datos es la de un modelo IGARCH bajo una distribución GED.
Finalmente, empleando los pronósticos del modelo ARFIMA-IGARCH se construyó la volatilidad multi-período y la estructura a plazos de la volatilidad de los retornos COP/USD. Los resultados indican que asumiendo un nivel de tasa de cambio de 2.250 pesos por dólar, se esperaría que en un horizonte de un año, la tasa de cambio estuviera entre 1.596 y 2.903 pesos por dólar, correspondiente a una volatilidad acumulada esperada anual de 29%. Finalmente, las expectativas promedio de volatilidad, representadas en la estructura a plazos, indican que la expectativa de volatilidad promedio diaria para un año es menor que la obtenida para un día.
NOTAS AL PIE
1Los datos usados para la tasa de cambio corresponden a un período de libre flotación. La fuente de la información estadística fue la página web de Corfinsura [ www.corfinsura.com ] con información suministrada por la Superintendencia Financiera.
2 Para el contraste GPH y de máxima verosimilitud Local de Whittle se emplearon los siguientes anchos de banda recomendados en la literatura:  T 0.6
T 0.6  ,
,  T 0.7
T 0.7  y
y  T 0.5
T 0.5  , donde
, donde  .
.  denota la parte entera del argumento. Para los contrastes de R/S modificado y KPSS se utilizaron los anchos de banda m =
denota la parte entera del argumento. Para los contrastes de R/S modificado y KPSS se utilizaron los anchos de banda m =  4(T / 1000)0.25
4(T / 1000)0.25  y m =
y m =  12(T / 1000)0.25
12(T / 1000)0.25  . Finalmente, para el contraste HML se emplearon k =
. Finalmente, para el contraste HML se emplearon k =  T 0.5
T 0.5  y l =
y l =  2/3 T 12/25
2/3 T 12/25  .
.
3 El programa usado para llevar a cabo los procedimientos de estimación presentados en esta sección y en la siguiente fue el TSM 4.23 de James Davidson.
4 Un conjunto de variables dummy de cierre del mercado debido a días de fiesta que captarán la acumulación de volatilidad durante los días de cierre del mercado y dummies para cada día de la semana con el fin de capturar las posibles diferencias en los retornos o en la volatilidad a través de los días comerciales (Baillie y Bollerlev (1989, 1991), Hsieh (1989b) y Malik (2005)) fueron probadas sin encontrarse evidencia a favor de dichos efectos.
5 Un gran número de estudios, empleando bases de datos diarias, han encontrado evidencia sobre la persistencia de la volatilidad en tasas de cambio, aproximando relativamente bien la volatilidad por un proceso IGARCH.
6 Los modelos IGARCH y FIGARCH han sido descritos en la literatura como de larga memoria, a través de una analogía implícita entre los modelos lineales integrados y fraccionalmente integrados para la media condicional. Sin embargo, tal analogía resulta errónea, dado que el modelo IGARCH es un proceso de corta memoria para el cual la varianza incondicional no existe y el FIGARCH(d) es de corta memoria con d cercano a 1.
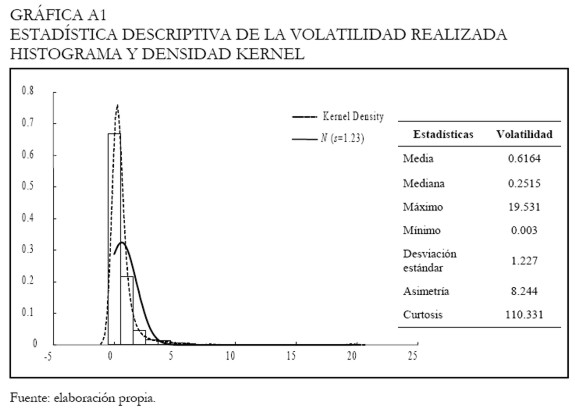
7 A partir de información intradiaria correspondiente a la hora y al precio al que se realizó cada transacción en el mercado, se construyeron retornos cada quince minutos para la tasa de cambio COP/USD, usando una interpolación lineal entre el logaritmo del precio inmediatamente anterior y posterior a cada segundo de referencia. La volatilidad realizada del t-ésimo día se calculó como la sumatoria de los retornos intradiarios cada quince minutos al cuadrado. En los Anexos (Gráfica A1), se presenta el histograma, la estimación de la densidad Kernel y las estadísticas descriptivas que resumen la distribución incondicional de la volatilidad realizada COP/USD.
8 Los errores de pronóstico, respectivamente, para el modelo IGARCH son iguales a 1,186 y 0,83 frente a 1,088 y 0,76 del ARFIMA-IGARCH.
9 El error de pronóstico del retorno rt [k] está dado por:
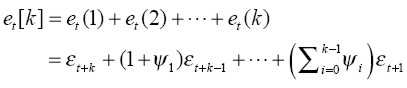
10 La representación MA de un proceso ARMA para la serie de los retornos muestra, explícitamente, el impacto que tienen los shocks aleatorios pasados ( εt-i , i > 0 ) sobre el retorno corriente rt .
11 Este valor corresponde a la tasa de cambio vigente para el día 31 de julio de 2006.
ANEXO 1
 |
REFERENCIAS BIBLOGRÁFICAS
1. Andersen, T.; Bollerslev, T.; Diebold, F.X. y Labys, P. (2001). "The Distribution of Realized Exchange Rate Volatility". Journal of the American Statistical Association, 96: 42-55. [ Links ]
2. Andersen, T.; Bollerslev, T.; Diebold, F.X. y Labys, P. (2003). "Modeling and Forecasting Realized Volatility". Econometrica, 71: 529-626. [ Links ]
3. Baillie, R. (1996). "Long Memory Processes and Fractional Integration in Econometrics". Journal of Econometrics, 73: 5-59. [ Links ]
4. Baillie, R.; Bollerslev, T. y Mikkelsen, H. (1996). "Fractionally Integrated Generalized Autoregressive Conditional Heteroskedasticity". Journal of Econometrics, 74: 3-30. [ Links ]
5. Baillie, R. y Bollerslev, T. (1989). "The Message in Daily Exchange Rates: A Conditional- Variance Tale". Journal of Business and Economic Statistics, 7: 60-68. [ Links ]
6. Baillie, R. y Bollerslev, T. (1990). "Intra-Day and Inter-Market Volatility in Foreign Exchange Rates". Review of Economic Studies, 58: 565-585. [ Links ]
7. Bollerslev, T. (1986). "Generalized Autoregressive Conditional Heteroskedasticity". Journal of Econometrics, 31: 307-327. [ Links ]
8. Bollerslev, T. (1987). "A Conditionally Heteroskedastic Time Series Model for Speculative Prices and Rates of Return". The Review of Economics and Statistics, 69(3): 542-547. [ Links ]
9. Bollerslev, T.; Chou, R. y Kroner, K. (1992). "ARCH Modeling in Finance: A Review of the Theory and Empirical Evidence". Journal of Econometrics, 52: 5-59. [ Links ]
10. Bollerslev, T.; Engle, R. y Nelson, D. (1994). "ARCH Models". En: D. F. MacFadden y R. E. Engle (eds.), Handbook of Econometrics, Vol. 4, Amsterdam: North-Holland. [ Links ]
11. Castaño, E.; Gómez, K. y Gallón, S. (2007). "Identificación de un modelo ARFIMA y una nueva prueba para el orden de diferenciación fraccional", mimeo. [ Links ]
12. Cheung, Y. (1993). "Long Memory in Foreign Exchange Rates". Journal of Business and Economic Statistics, 11: 93-102. [ Links ]
13. Davidson, J. (2004). "Moment and Memory Properties of Linear Conditional Heteroscedasticity Models, and a New Model". Journal of Business and Economics Statistics, 22: 16-29. [ Links ]
14. Diebold, F. y Nerlove, M. (1989). "The Dynamics of Exchange Rate Volatility: A Multivariate Latent Factor ARCH Model". Journal of Applied Econometrics, 4: 1-21. [ Links ]
15. Diebold, F.; Hickman, A.; Inoue, A. y Schuermann, T. (1998). "Converting 1-Day Volatility to h-Day Volatility: Scaling by Root-h is Worse than You Think", Wharton Financial Institutions Center, Working Paper 97-34. [ Links ]
16. Ding, Z.; Granger, C. y Engle, R. (1993). "A Long Memory Property of Stock Market Returns and A New Model". Journal of Empirical Finance, 1: 83-106. [ Links ]
17. Engle, E. (1982). "Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation". Econometrica, 50: 987-1008. [ Links ]
18. Engle, R.; Ito, T. y Lin, W. (1990a). "Meteor Showers or Heat Waves? Heteroskedastic Intra-Daily Volatility in the Foreign Exchange Market", Econometrica, 58: 525-542. [ Links ]
19. Gallón, S. y Gómez, K. (2007). "Distribución condicional de los retornos de la tasa de cambio colombiana: un ejercicio empírico a partir de modelos GARCH multivariados". Revista de Economía del Rosario, 10(2). [ Links ]
20. Geweke, J. (1986). "Modelling the Persistence of Conditional Variances: A Comment". Econometric Review, 5: 57-61. [ Links ]
21. Geweke, J. y Porter-Hudak, S. (1983). "The Estimation and Application of Long Memory Time Series Models". Journal of Time Series Analysis, 4: 221-238. [ Links ]
22. Glosten, L.; Jagannthan, R. y Runkle, D. (1993). "On the Relation between the Expected Value and the Volatility of the Nominal Excess Return on Stocks". Journal of Finance, 48: 1779-1801. [ Links ]
23. Granger, C. W. J. y Ding, Z. (1996). "Varieties of Long Memory Models". Journal of Econometrics, 73: 61-77. [ Links ]
24. Harris, D.; McCabe, B. y Leybourne, S. (2008). "Testing for Long Memory". Econometric Theory, 24(1): 143-175. [ Links ]
25. Hauser, M. (1997). "Semiparametric and Nonparametric Testing for Long Memory: A Monte Carlo Study". Empirical Economics, 22(2) 247-271. [ Links ]
26. Higgins, M. y Bera, A. (1992). "A Class of Nonlinear ARCH Models". International Economic Review, 33(1): 137-158. [ Links ]
27. Hsieh, D. (1988). "Statistical Properties of Daily Exchange Rates: 1974-1983". Journal of International Economics, 24(1-2): 129-145. [ Links ]
28. Hsieh, D. (1989a). "Testing for Nonlinear Dependence in Daily Foreign Exchange Rates". Journal of Business, 62(3): 339-368. [ Links ]
29. Hsieh, D. (1989b). "Modeling Heteroscedasticity in Daily Foreign Exchange Rates". Journal of Business and Economic Statistics, 7(3): 307-317. [ Links ]
30. Künsch, H. R. (1987). "Statistical Aspects of Self-Similar Processes". En Y. Prohorov y V. Sazanov (Eds.) Proceedings of First World Congress of the Bernoulli Soc, 1, 67-74, VNU Science Press, Utrecht. [ Links ]
31. Kwiatowski, D.; Phillips, P. C. B.; Schmidt, P. y Shin, Y. (1992). "Testing the Null Hypothesis of Stationarity Against the Alternative of a Unit Root: How Sure are we that Economic Time Series Have a Unit Root". Journal of Econometrics, 54: 159-178. [ Links ]
32. Lo, A. (1991). "Long-Term Memory in Stock Market Prices". Econometrica, 59: 1279-1313. [ Links ]
33. Lobato, I. y Robinson, P. (1998). "A Nonparametric Test for I(0)". The Review of Economic Studies, 65(3): 75-495. [ Links ]
34. Malik, A. K. (2005). "European Exchange Rate Volatility Dynamics: An Empirical Investigation". Journal of Empirical Investigation, 12: 187-215. [ Links ]
35. Milhøj, A. (1987). "A Conditional Variance Model for Daily Deviations of an Exchange Rate". Journal of Business and Economic Statistics, 5(1): 99-103. [ Links ]
36. Pantula, S. (1986). "Modelling the Persistence of Conditional Variances: A Comment". Econometric Review, 5(1): 71-74. [ Links ]
37. Patton, A. (2006). "Volatility Forecast Comparison using Imperfect Volatility Proxies," Research Paper 175, Quantitative Finance Research Centre, University of Technology Sydney. [ Links ]
38. Robinson, P. M. (1995). "Gaussian Semiparametric Estimation of Long Range Dependence". The Annals of Statistics, 23(5): 1630-1661. [ Links ]
39. Schoffer, O. (2003). "HY-A-PARCH: A Stationary A-PARCH Model with Long Memory". Fachbereich Statistik, Universität Dortmund. [ Links ]
40. Schwert, W. (1990). "Stock Volatility and the Crash of 87". Review of Financial Studies, 3(1): 77-102. [ Links ]
41. Silverman, B. (1986). Density Estimation for Statistics and Data Analysis. Londres: Chapman and Hall. [ Links ]
42. Taylor, S. (1986). Modeling Financial Time Series. New York: Wiley and Sons. [ Links ]
43. Tsay, R. (2005). Analysis of Financial Time Series, 2nd. Edition, Wiley Series in Probability and Statistics. [ Links ]
44. Tschernig, R. (1994). "Long Memory in Foreign Exchange Rates Revisited". Institute of Statistics and Econometrics, Humboldt University of Berlin. [ Links ]
45. Vlaar, P. y Palm, F. (1993). "The Message in Weakly Exchange Rates in the European Monetary System: Mean Reversion, Conditional Heteroscedasticity and Jumps". Journal of Business and Economic Statistics, 11: 351-360. [ Links ]
46. Xu, X. y Taylor, S. (1994). "The Term Structure of Volatility Implied by Foreign Exchange Options". Journal of Financial and Quantitative Analysis, 29(1): 57-74. [ Links ]
47. Zakonian, J.M. (1994). "Threshold Heteroskedastic Models". Journal of Economic, Dynamics and Control, 18: 931-955. [ Links ]














