Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Cuadernos de Economía
Print version ISSN 0121-4772On-line version ISSN 2248-4337
Cuad. Econ. vol.28 no.50 Bogotá Jan./June 2009
APROXIMACIÓN NO LINEAL AL MODELO DE OVERSHOOTING USANDO REDES NEURONALES MULTlCAPA PARA EL TIPO DE CAMBIO DÓLAR-PESO
Jaime Villamil *
Magíster en Matemática Aplicada y Especialista en Estadística. Profesor de la Facultad de Ingeniería. Universidad Nacional de Colombia (Bogotá). E-mail: jalme.villarnil@interbolsa.com. Dirección de correspondencia: Av 82 # 12 -18, piso 3. Este artículo fue recibido el 17 de enero de 2007 y su publicación aprobada el 6 de septiembre de 2008.
Resumen
Desde los años setenta muchos trabajos han intentado elaborar una sustentación empírica de algunos modelos que ofrecieron una explicación lineal de la dinámica de la tasa de cambio de un país, entre ellos el de Dornbusch. Hasta el momento ninguno ha sido concluyente y la caminata aleatoria es considerada como el mejor modelo al que puede ajustarse. De Grauwe ha mostrado que, con la presencia de relaciones no-lineales y heterogeneidad de expectativas de los especuladores, el tipo de cambio puede tener un comportamiento aparentemente aleatorio, pero con explicación determinista. Este trabajo presenta el modelo de Dornbusch en la versión no lineal propuesta por De Grauwe y Dewachter (1993), y una aproximación usando redes neuronales multicapa aplicadas al caso del dólar/peso (USD/COP).
Palabras clave: tasa de cambio, redes neuronales, overshooting. JEL: F31, C45, F37.
Abstract
Since the 1970s much work has been done attempting to provide empirical support for some models that offered a linear explanation for the exchange rate dynamic of a country, including that of Dornbusch. So far none have been conclusive and the random walk is considered the best model to which it can be adjusted. De Grauwe has shown that, with the presence of nonlinear relationships and heterogeneous expectations on the part of speculators, the exchange rate can have an apparently random behavior, but with a deterministic explanation. This article presents the Dornbusch model in the nonlinear version proposed by De Grauwe and Dewachter (1993) and an approximation using multilayer neuronal networks applied to the case of the USD/COP exchange rate.
Key words: exchange rate, neruronal networks. JEL: F31, C45, F37.
Résumé
Dès les années soixante-dix certaines recherches ont essayé de justifier empiriquement quelques modèles offrant une explication linéaire de la dynamique du taux de change d’un pays, parmi eux celui de Dornbusch. Jusqu’à présent aucun n’en a été concluant et la randonnée aléatoire est considérée comme le meilleur modèle du taux de change. De Grauwe a montré que, avec la présence de relations non-linéaires et l’hétérogénéité d’anticipations des spéculateurs, le taux de change peut avoir un comportement apparemment aléatoire, mais avec une explication déterministe. Ce travail présent le modèle de Dornbusch suivant la version nonlinéaire proposée par De Grauwe et De Dewachter (1993), et une approximation en utilisant des réseaux neuronaux multicouche appliqués au cas du taux d’échange USD/COP.
Mot clés: taux de change, réseaux neuronaux, overshooting. JEL : F31, C45, F37.
Hasta 1973 vanas economías industrializadas funcionaron con el sistema tasa de cambio fijo: la moneda de un país se expresaba en términos constantes respecto de una moneda extranjera. En la balanza de pagos tenía una mayor importancia la cuenta corriente: y la cuenta de capitales de largo plazo. en otras palabras. los flujos de capital entre países bajo un régimen de tasa de cambio lijo son graduales y sostenidos. Posteriormente. con el acentuado discurso de liberalización de los mercados. dicha tasa se dejó flotar libremente y la cuenta de capitales de corto plazo empezó a ser relevante. puesto que la reserva ele capital de los países debía convertirse rápidamente según las variacioucx de la tasa de cambio. de esta manera el flujo de capitales tinanciaha el déficit o super.ivit de la cuenta corriente. En estas condiciones. que la economía de un país entrara en crisis. no respondía exclusivamente a la situación de su sector realsino también a la situación de su moneda y de sus reservas de capital.
Las firmas que tienen relaciones comerciales con lax industrias de otras naciones deben realizar los pagos en moneda extranjera y están sujetos al riesgo cambiario. Existe otro tipo de agentes económicos que derivan su ingreso simplemente del arbitraje con la moneda, es decir, "de comprar barato ahora y vender caro después". Estos son los llamados especuladores, sus operaciones son más importantes hoy que hace veinte años cuando los instrumentos financieros no estaban tan desarrollados. En este momento existe una amplia gama de dichos instrumentos como los futuros, los forwards, los swaps, los productos estructurados, los derivados de crédito, entre otros, con los cuales inversionistas o especuladores movilizan grandes cantidades de capital que inciden notablemente en la variabilidad del tipo de cambio y de otras variables fundamentales, que sin duda afectan lo que sucede en el sector real, en parte porque la volatilidad de los precios de los activos no les permite a las empresas estar seguras de su valor.
Con régimen de tasa de cambio flexible las decisiones de los inversionistas juegan un papel crucial en la determinación de la situación rnacroeconómica de los países. Así, por ejemplo, si estos agentes cuentan con poder de mercado -grandes montos de capital-, pueden cambiar la composición de su portafolio (por ejemplo, obteniendo activos denominados en moneda extranjera y no en moneda nacional) creando condiciones para que el gobierno de un país se vea obligado a devaluar la moneda. A esta situación se le conoce como ataque especulativo, uno famoso es el que libró George Soros contra la libra esterlina a principios de la década de los noventa. Con quince mil millones de dólares en libras esterlinas, Soros hizo que el Reino Unido gastará cincuenta mil millones de dólares de sus reservas internacionales con el propósito de defender la estabilidad del tipo de cambio GBP/USD sin otro resultado que el de devaluar. En cuestión de tres semanas Soros había ganado mil mi llones de dólares (Krugrnan 1999). Los especuladores advierten que una economía tarde o temprano va a encontrarse en la necesidad de devaluar y entonces se hace inevitable modificar las posiciones de su portafolio acelerando el proceso de devaluación. casos como éste se observaron en las crisis financieras de algunos países asiáticos a fi nales de los noventa.
Por lo anterior es apremiante la necesidad de desarrollar una herramienta que logre dar cuenta de la dirección de una variable como el tipo de cambio. En los modelos macroeconómicos es usual hablar de los mecanismos de formación de expectativas para referirse a la creencia que una economía en conjunto tiene del comportamiento futuro de una variable fundamental. Muchos de estos mecanismos están basados en el uso de técnicas estadísticas. en particular de las series de tiempo lineales. Esta teoría tiene grandes dificultades para el manejo de las series financieras. puesto que muchas de ellas tienen tendencia estocástica, en particular para las tasas de cambio existe bastante evidencia de que son procesos I(1), La teoría económica ha observado en la inteligencia computacional un gran potencial para manejar las expectativas sobre variables financieras y económicas1.
El presente trabajo utiliza las redes neuronales multicapa con el fin de aproximar la no linealidad en el modelo de Dornbusch (1972) propuesta por De Grauwe y Dewachter (1993), quienes introducen el comportamiento de los especuladores y muestran que éste puede ser el responsable de una dinámica caótica del tipo de cambio, En la primera parte se presenta el modelo de Dornbusch; en la segunda se muestra la modificación de De Grauwe y Dewachter; en la tercera se exponen las redes neuronales multicapa y sus algoritmos de entrenamiento; la cuarta sección se describe la metodología y en la quinta se muestran los resultados.
EL MODELO DE "DESBORDAMIENTO" DEL TIPO DE CAMBIO
Para el caso de los tipos de cambio el marco teórico más destacado es el de Rudiger Dombusch (1976), Este autor ofreció una explicación al comportamiento errático que siguió el dólar después de 1973 con respecto a las divisas más importantes de Europa, Entre 1977 y 1979 el marco se apreció: 33% con respecto al dólar, el franco: 21 % y la libra esterlina 26%. Para el período siguiente, comprendido entre los años 1980 y 1985, Estados Unidos tuvo un gran déficit comercial gracias a la apreciación del dólar, pero la falta de financiamiento interno condujo al país a ser un deudor neto después de 1985. Los años siguientes se caracterizaron por una apreciación sostenida de las tres monedas mencionadas en términos de dólares.
De acuerdo con Dornbusch el diferencial entre las tasas de interés (de los depósitos o inversiones libres de riesgo) de dos países, de alguna manera predice la dirección que tomará la tasa de cambio. Este era el caso de la tasa de interés norteamericana que, a inicios de los ochenta, al ser mucho mayor con relación a las tasas de interés domésticas de Francia y Reino Unido, propició una afluencia de inversiones en activos denominados en dólares que redundó en el fortalecimiento de esta moneda.
El planteamiento de Dombusch pone de manifiesto que en el corto plazo una expansión monetaria eleva los precios internos, disminuye las tasas de interés reales, lo cual presiona una salida de capital que induce a una depreciación inmediata de la moneda nacional (sobre-reacción) y una posterior fluctuación de ésta y de los términos de intercambio. La sobre-reacción es mayor si la oferta agregada del producto nacional permanece inmodificada frente a los cambios en la demanda agregada que imprime el choque monetario. El mecanismo también opera a la inversa. un cambio en la política monetaria que eleve la tasa de interés (por ejemplo la emisión de deuda) produce rápidamente una apreciación de la moneda. En este modelo la política fiscal no genera ningún efecto de sobre-reacción del tipo de cambio, siempre y cuando el gasto público sea financiado con emisión de deuda y no con emisión monetaria.
El modelo de Dornbusch se basa en los siguientes supuestos:
1. Perfecta movilidad de capital.
2. Los mercados de bienes se ajustan más lentamente que los mercados de activos financieros.
3. Los activos financieros nacionales e internacionales son substitutos perfectos.
4. Se asume que frente a desequilibrios en el mercado de activos financieros la velocidad de ajuste de la tasa de cambio nominal es instantánea. entre tanto frente a desequilibrios en el mercado de bienes la velocidad de ajuste del nivel de precios doméstico es gradual.
Este modelo se formula en tiempo continuo. Las variables se encuentran en escala logarítmica. La economía doméstica es un país pequeño, por lo tanto los fundamentales de la economía extranjera se toman como variables cxógenas. Se da por sentado la validez de la paridad no cubierta de tasas de interés que implica la substituibilidad perfecta entre activos denominados en moneda doméstica o extranjera y que se expresa corno:2
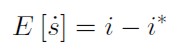 [1]
[1]
Es decir. el valor esperado de la variación de la tasa de cambio nominal obedece a los diferenciales de tasa de interés entre las dos economías. Si existe perfecta movilidad de capital y substituibilidad de activos, las inversiones tienden a desplazarse a las economías que ofrecen mayor rentabilidad.
Se asume que el valor esperado finalmente se cumple, a esto se llama previsión perfecta:3
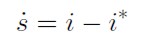 [2]
[2]
Se considera el control del dinero en manos del banco central quien sigue la regla:
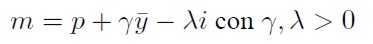 [3]
[3]
Donde 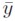 es el nivel de producto de equilibrio, que también se llama producto de pleno empleo o producto potencial.
es el nivel de producto de equilibrio, que también se llama producto de pleno empleo o producto potencial.
En (3) se muestra que la cantidad de dinero que el banco central mantiene en el mercado debe ser proporcional a la cantidad de bienes que se producen. Si la producción de equilibrio sube, la economía debe contar con un mayor monto de dinero para respaldar las transacciones por este producto sin que la inflación aumente. De otro lado, el banco central puede reducir el monto de dinero circulante emitiendo bonos de deuda pública interna con tasas de rendimiento superiores a las de captación de los bancos comerciales para que su compra sea atractiva. Los bancos. que también compiten por recursos. suben sus tasas de interés y. por medio de esta alza. el público desea mantener mayor parte de su dinero en los bancos o en compra de bonos de deuda y no en efectivo. esto explica la relación inversa que existe en (3) con respecto a la tasa de interés.
La velocidad de ajuste del nivel de precios doméstico es directamente proporcional a la diferencia entre la demanda agregada y el producto de equilibrio:
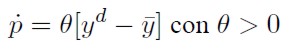 [4]
[4]
La demanda agregada doméstica viene linealmente determinada por el tipo de cambio real (e = s + p* - p). la tasa de interés doméstica y el producto de pleno empleo:
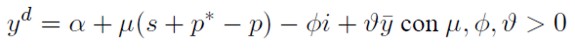 [5]
[5]
Donde α es una constante positiva que representa el componente autónomo de la demanda que incluye el gasto del gobierno. Si la tasa de cambio nominal aumenta, esto es, si ocurre una depreciación de la moneda nacional, habrá mayor demanda por productos nacionales que por productos extranjeros, lo mismo ocurre si el precio de un producto de importación crece. Ahora, si la tasa de interés doméstica es mayor, aumenta el dinero en depósitos en los bancos y en consecuencia habrá menos efectivo para demandar bienes.
Dado que la economía doméstica se supone igual a la de un país pequeño, se asume el nivel de precios extranjero determinado exógenamente y se normaliza en uno. por lo tanto p* = ln P* = ln 1 = 0, esto reduce la ecuación (5) a:
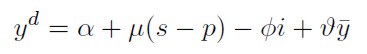 [6]
[6]
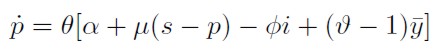 [7]
[7]
La tasa de interés doméstica compatible con el producto de pleno empleo se obtiene despejando de (3):
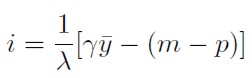 [8]
[8]
Reemplazando (8) en (7) se obtiene una expresión explícita para la ecuación de ajuste que relaciona la inflación con los excesos de demanda:
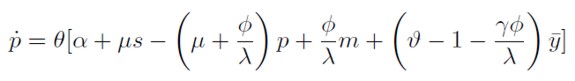 [9]
[9]
Reemplazando (8) en (2) se llega a una ecuación para el comportamiento del tipo de cambio:
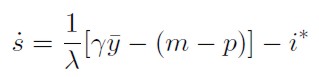 [10]
[10]
Las ecuaciones (9) y (10) conforman un sistema de ecuaciones diferenciales lineales que en notación matricial se escribe de la forma:
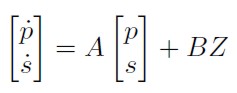 [11]
[11]
Donde:
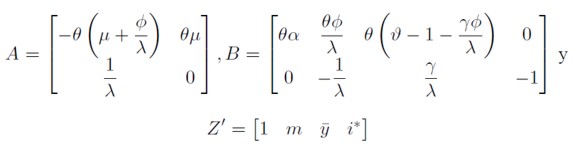
Los valores de equilibrio de largo plazo de las variables endógenas (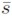 ,
, 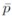 ) en el sistema (11) se obtienen cuando
) en el sistema (11) se obtienen cuando 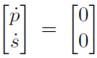 , luego los valores de equilibrio satisfacen:
, luego los valores de equilibrio satisfacen:
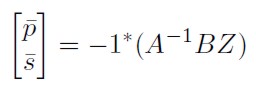 [12]
[12]
Los valores de equilibrio de (11) sólo existen si det(A) ≠ 0. El valor del determinante de la matriz de coeficientes para las variables endógenas es diferente de cero y negativo det(A) = - θµ / λ < O. Luego existe el equilibrio y la dinámica alrededor de éste es del tipo punto de silla.
De (12) se conoce que BZ = - 1* A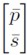 , reemplazando este valor en (11) se obtiene un nuevo sistema con respecto a las desviaciones del nivel de precios y de la tasa de cambio de equilibrio:
, reemplazando este valor en (11) se obtiene un nuevo sistema con respecto a las desviaciones del nivel de precios y de la tasa de cambio de equilibrio:
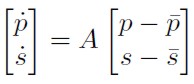 [13]
[13]
Ya se vio que el determinante de es negativo por lo que la estabilidad del nuevo sistema (13) está representado también por un punto de silla. El punto de equilibrio en este nuevo sistema se obtiene haciendo 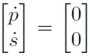 en (13), de esta condición se hallan las siguientes ecuaciones:
en (13), de esta condición se hallan las siguientes ecuaciones:
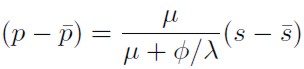 [14]
[14]
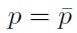 [14b]
[14b]
De la ecuación (14a) se observa que los valores p de equilibrio son dibujados en el plano (s, p) por una línea con pendiente positiva µ / Φ / λ. Siguiendo el mismo razonamiento para la ecuación (14b) se tiene que los valores de la tasa de cambio de equilibrio quedan descritos por la función constante p = 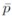 que es una línea horizontal en el plano (s, p). La intersección de estas dos curvas se logra en el punto
que es una línea horizontal en el plano (s, p). La intersección de estas dos curvas se logra en el punto 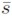 ,
,  . En la Gráfica 1 se dibuja el comportamiento cualitativo del sistema (13).
. En la Gráfica 1 se dibuja el comportamiento cualitativo del sistema (13).
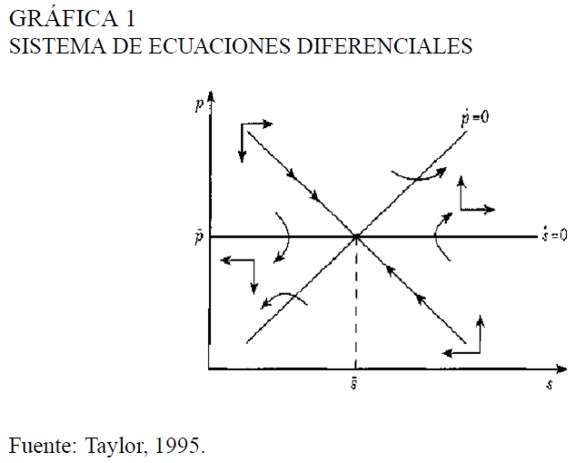
Suponiendo que el banco central repentinamente emprende una política monetaria contraccionista y mediante colocación de deuda pública restringe los medios de pago de m0 a m1, esto obliga en el largo plazo a un descenso en la misma proporción -por la expresión (3)- del nivel de precios doméstico. y a una disminución en la misma proporción (debido a que s = e - p* + p) de la tasa de cambio nominal.
En el sistema dinámico de las ecuaciones (14a) y (14b), el nivel de precios de equilibrio 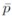 ya no sería p0 sino p1 y este menor nivel de precios debe coexistir con un menor nivel de la tasa de cambio nominal, que pasa de s0 a s1. En la Gráfica 2 se observa que si la economía inicialmente se encontraba en el equilibrio del punto A, la política monetaria fija como meta de largo plazo el equilibrio del punto B.
ya no sería p0 sino p1 y este menor nivel de precios debe coexistir con un menor nivel de la tasa de cambio nominal, que pasa de s0 a s1. En la Gráfica 2 se observa que si la economía inicialmente se encontraba en el equilibrio del punto A, la política monetaria fija como meta de largo plazo el equilibrio del punto B.
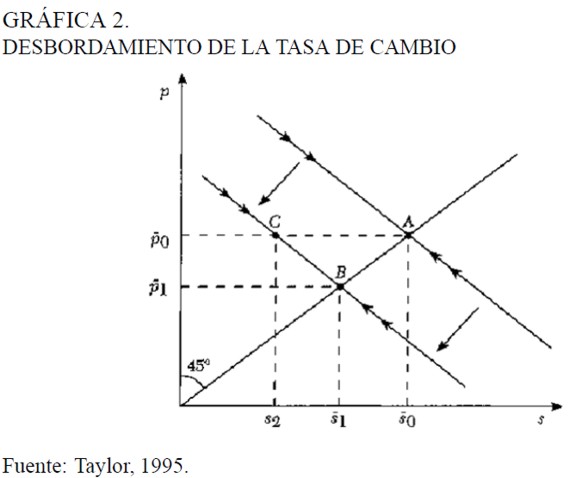
Sin embargo en el corto plazo existe dificultad para que los precios nacionales se modifiquen. por lo que se mantiene el nivel de precios en p0, esto produce una apreciación de la moneda nacional (un descenso de s) mayor que el valor de equilibrio de largo plazo s1. Esta situación de desequilibrio corresponde al punto C de la Gráfica 2.
Este modelo es cuestionado por su falta de realismo, porque además de los agregados económicos que se describieron arriba, los inversionistas tienen en cuenta otro tipo de información, por ejemplo, el número de empleos que una economía crea, si este número es favorable fortalece la moneda nacional. También se hace énfasis en los aspectos políticos, si existe un conflicto bélico con un país productor de petróleo, es posible un desabastecimiento de combustible que perjudique a economías dependientes de este insumo como la norteamericana, esto produce alza en los precios de la gasolina procurando así una inflación mayor y un posterior debilitamiento de dólar.
Pese a la acogida que tuvo la explicación de Dombusch en la teoría económica. la estimación estadística de los parámetros del sistema dinámico para diversos países no se ha mostrado concluyente (Nelly y Sarno 2002). Otros autores argumentan que el fracaso del modelo de Dornbusch posiblemente se deba a su linealidad implícita. De Grauwe y Dewachter (1993) Y Da Silva (2001) reemplazan las ecuaciones del modelo de desbordamiento por expresiones no-lineales e introducen el papel de los especuladores. quienes buscan valores de algunos de los parámetros de los nuevos sistemas que generen un comportamiento aparentemente aleatorio. pero con explicación determinista.
MODELO NO-LINEAL DE DESBORDAMIENTO DEL TIPO DE CAMBIO
El modelo que proponen De Grauwe y Dewachter (1993) se formula en tiempo discreto y al igual que el de Dornbusch utiliza variables en escala logarítmica. La ecuación (1) se escribe como:
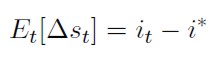 [15]
[15]
Existe una condición de equilibrio en el mercado de bienes que garantiza el cumplimiento de la paridad de poder de compra dada por:
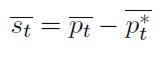 [16]
[16]
Se mantiene la regla del banco central semejante a la vista en la ecuación (3):
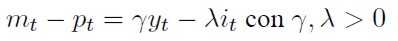 [17]
[17]
La dinámica del nivel de precios descrita en (4) se expresa como:
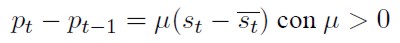 [18]
[18]
La lógica detrás de (18) es la siguiente: los incrementos del tipo de cambio nominal por encima de su valor de equilibrio estimulan la demanda interna de bienes, que se traduce en un incremento del nivel general de precios.
Se asume. otra vez. que la economía nacional es una economía pequeña por lo que se puede suponer que las variables extranjeras son constantes dadas exógenamente. Para simplificar. el nivel de precios de equilibrio y la tasa de interés extranjeros se hacen iguales a uno por lo que se tiene que 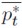 y i*t son cero.
y i*t son cero.
Asumiendo que el nivel de precios es el de equilibrio. se reemplaza (16) en (18) y se despeja 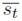 . De esta forma se llega a:
. De esta forma se llega a:
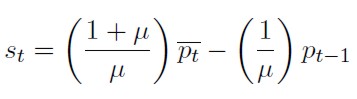 [19]
[19]
Se reemplaza (17) y el valor de la tasa de interés doméstica de (15) en (19). Reordenado términos se obtiene una expresión del tipo de cambio en función de los fundamentales y de las expectativas de variación del tipo de cambio:
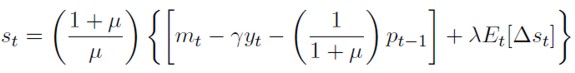 [20]
[20]
Existen 2 enfoques usados por los especuladores que se resisten a aceptar la hipótesis de Fama4. Uno de ellos se llama análisis fundamental y el otro análisis técnico. El primero afirma que el movimiento de los precios de los activos financieros tiene explicación en variables relevantes del desempeño macroeconómico de un país, el segundo insiste en que existen patrones de comportamiento en el pasado que posibilitan el pronóstico del futuro.
Una de las estrategias de uso más frecuente entre especuladores del análisis técnico -que se llamarán en adelante chartistas- es el MACD (siglas en inglés de convergencia-divergencia del promedio móvil) que consiste en la construcción de dos promedios móviles. Uno de corto plazo que da más importancia a los valores más recientes de los precios y, otro de largo plazo, que privilegia valores más lejanos. Los dos promedios producen series más suaves (con menor variabilidad) que la original. El promedio de largo plazo es más suave que el de corto plazo.
El MACD es la diferencia entre el promedio de corto y el de largo plazo. fue propuesto por Gerald Appel y produce señales de compra y venta5. Después del corte de ambos promedios, si el MACD es positivo. existe un indicio de que el precio del activo subirá (y los inversionistas deben comprar), y si es negativo indica que el precio caerá (y los inversionistas deben vender). La estrategia de negociación óptima basada en el indicador MACD busca los promedios móviles que maximicen la rentabilidad de las ncgociaciones en un tiempo dado.
En la Gráfica 3 se ilustra como opera el MACD. La línea negra es la diferencia entre el promedio de corto plazo con respecto al de largo plazo, cuando esta línea corta el eje de las abscisas se genera una señal de negociación: se trata de una señal de compra si posterior a este corte la línea negra es creciente, y se habla de una señal de venta si ocurre lo contrario. En la Gráfica 3 se ilustra un periodo de negociación en el cual se produjeron tres señales de compra y dos de venta.
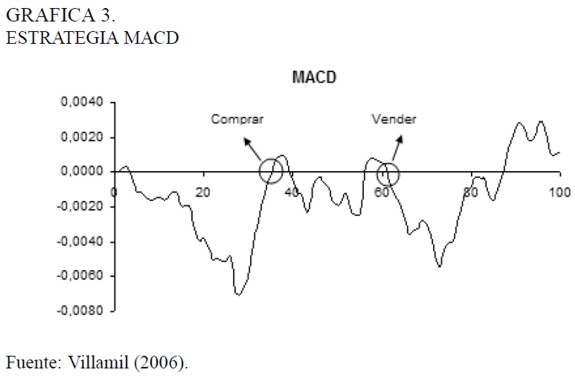
De Grauwe y Dewachter (1993) introducen las expectativas de variación del tipo de cambio como un promedio ponderado de las expectativas de los especuladores fundamentalistas (f) y de los chartistas (c).
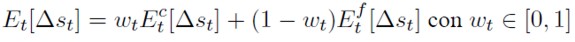 [21]
[21]
Las expectativas de los chartistas son directamente proporcionales al valor del MACD y las de los fundamentalistas al ajuste del tipo de cambio nominal respecto de su valor de equilibrio. Ambos tienen diferentes conjuntos de información (el de los chartistas. por ejemplo. no incluye toda la información disponible de la tasa de cambio) y sus expectativas no son racionales. para ello necesitarían conocer el modelo y el mecanismo de formación expectativas de los demás especuladores.
El promedio de cono plazo (PCP) ele los chartistas se supone que considera sólo el cambio del periodo inmediatamente anterior. entre tanto el promedio de largo plazo (PLP) involucra la media de los cambios en los dos periodos precedentes, respectivamente:
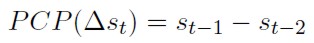 [22]
[22]
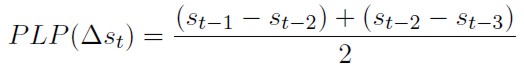 [23]
[23]
El MACD viene dado. entonces. por:
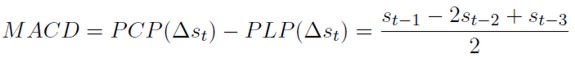 [24]
[24]
La expresión (25) describe la formación de expectativas de los chartistas (se multiplica por dos para simplifican. Cuando el MACD es positivo los chartistas tienen una expectativa de devaluación del tipo de cambio. Si es negativo, esperan una revaluación.
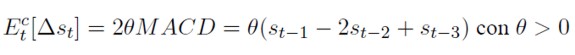 [25]
[25]
La expresión con la que se dibuja la formación de expectativas de los fundamentalistas es:
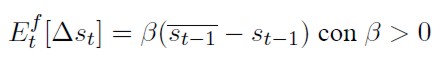 [26]
[26]
En (26) se plantea que una devaluación respecto del tipo de cambio de equilibrio se traduce, para los fundamentalistas, en expectativas de revaluación, y a la inversa, una apreciación implica que deberían esperar una corrección por medio de la depreciación futura.
Reemplazando (25) y (26) en (21) se llega a una expresión para la formación de expectativas del conjunto de la economía:
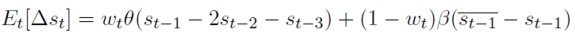 [27]
[27]
La ponderación de la expresión (27) se hace endógena al modelo por medio de la ecuación (28) que resume la siguiente intuición; si el tipo de cambio nominal no es muy diferente del valor de equilibrio estimado por los fundamentalistas, entonces la variación esperada de esta variable que tienen ellos es cercana a cero, y no existirá tanta participación de este tipo de especuladores en el mercado de divisas (wt toma valores próximos a uno). Por el contrario, si la divergencia en un sentido o en otro es considerable, su participación en el mercado es mucho mayor, reduciendo así la importancia de los chartistas (wt toma valores cercanos a cero).
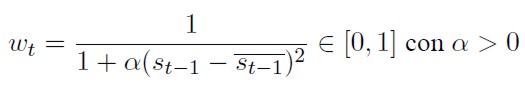 [28]
[28]
Reemplazando (27) en (20) y organizando términos se tiene una ecuación en diferencias no lineal para el comportamiento del tipo de cambio nominal, así:
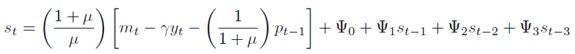 [29]
[29]
Donde:
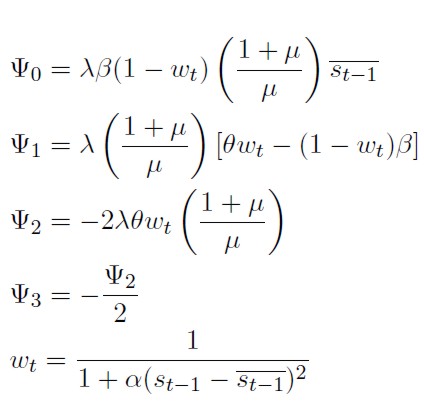
En la expresión (29) las implicaciones fundamentales del modelo de Dorn-busch se mantienen. El factor 1 + µ / µ es siempre mayor que uno, esto indica que la tasa de cambio responde más que proporcionalmente a la política monetaria del banco central.
De Grauwe y Dewachter, H. (1993) hacen que el valor de la tasa de cambio de equilibrio sea una constante y lo normalizan en uno. El comportamiento caótico de la tasa de cambio se puede obtener de la expresión (29) con una combinación particular de los parámetros (γ, λ, µ, β, θ, α). La existencia de sistemas caóticos en macroeconomía tiene dos consecuencias. La primera de ellas es el cuestionamiento al enfoque de las expectativas racionales, en un modelo se puede suponer conocimiento perfecto por parte de los agentes de cada una de las ecuaciones y de los valores pasados de la variable, pero dado que los sistemas caóticos son inestables, la predicción que hacen los agentes de valores futuros (de largo plazo) pueden ser muy diferentes. La segunda, es la posibilidad de explicar las fluctuaciones de agregados económicos sin que intervenga la idea de un choque externo que se modela siempre mediante un término aleatorio.
LAS REDES NEURONALES MULTICAPA
Las redes neuronales son sistemas de procesamiento de información inspirados en el funcionamiento del cerebro humano. Se sabe que el cerebro está conformado por neuronas y que en la medida que se ve enfrentado él resolver tareas complejas. éste requiere ele un mayor número de neuronas activadas procesando información, La primera representación de una neurona biológica fue ofrecida en 1911 por Santiago Ramón y Cajal. En la Gráfica 4 se observa un dibujo de una neurona biológica, esta es en general una célula nerviosa provista de un núcleo que genera un impulso eléctrico dependiendo de un grado de excitación (por ejemplo, la dificultad de la tarea), unas prolongaciones que se conocen como axón y, finalmente, las dendritas.
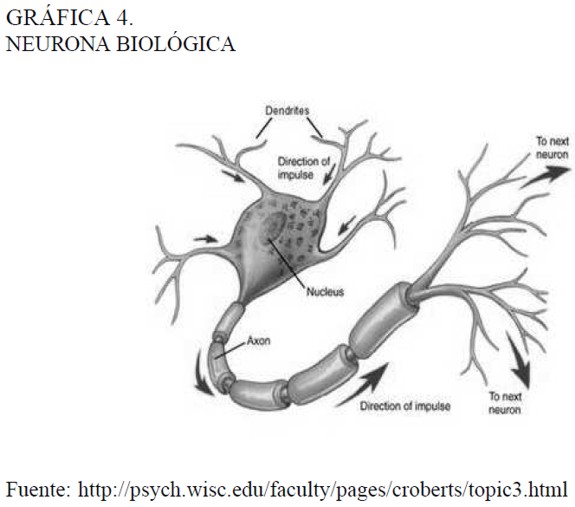
Es por medio de las ramificaciones más pequeñas derivadas del axón, las dendritas, que unas neuronas se comunican con otras. Esta conexión no es física. las dendritas de una neurona están cerca de las dendritas de otra. pero ambas terminaciones se encuentran inmersas en una sustancia neurotransmisara que, dependiendo de la intensidad del impulso eléctrico que viene de una neurona, le es comunicado a las neuronas contiguas, a este espacio entre dendritas se le conoce como sinapsis, La intensidad del impulso eléctrico que permite la activación de las neuronas vecinas está determinada por un umbral, si el impulso es mayor a éste. entonces se transmite a la demás, de lo contrario no. En 1943 el esquema de funcionamiento neurofisiológico de la neurona fue emulado matemáticamente por McCulloch y Pitts mediante una representación como la presentada en la Gráfica 5, a la cual se conoce como neurona artificial o perceptron.
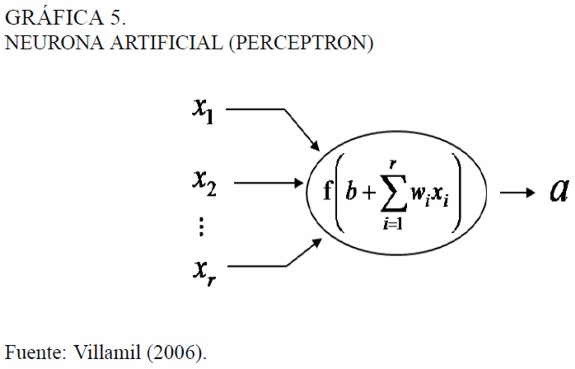
En la Gráfica 5 existe un vector Xr x 1 con r variables de entrada, un vector Wl x r que consta de ponderadores (que son ajustables) para cada variable de entrada y, además, se involucra un parámetro escalar b llamado umbral. La activación (el impulso eléctrico representado por la letra a) de la neurona se expresa por medio de la función de activación6 f, cuyo argumento es el producto interno de los vectores W y X más el parámetro b (también ajustable si se desea).
En principio se usó como activación de funciones escalonadas. Por ejemplo, para un resultado positivo de la suma entre el umbral y la combinación lineal entre ponderadores y valores se dice que la neurona se activa y envía un impulso a las demás neuronas, si el resultado es menor o igual que cero no hay activación.
En breve, una red neuronal se define como una interconexión en paralelo de neuronas, donde las salidas de una sirven de entrada a otras. La red neuronal es capaz de aprender cuál es la asociación entre variables explicativas y explicadas. El modo en que estas conexiones se presentan se llama arquitectura de la red. Y al proceso gradual de ajuste de los pesos y umbrales a valores que se adecuan a un correcto aprendizaje de la tarea presentada se llama entrenamiento.
Las redes neuronales se diferencian de la máquina de John Von Neumann en varios aspectos. los más importantes son:
1. La máquina de Von Neumann opera secuencialmente, es decir, que si existe una falla en la cadena de secuencias la máquina falla. Por el contrariu. las redes neuronales funcionan en paralelo, de modo que son tolerantes a fallos.
2. El "conocimiento" en una red neuronal no reside en un listado de instrucciones como en el caso de la máquina de Van Neumann, sino que ésta "aprende". Es decir, cuando a la red se le presenta un conjunto de patrones (datos de entrada con los datos deseados de salida), mediante un mecanismo de actualización iterativo la red encuentra los valores de los pesos de cada neurona que producen una mejor salida deseada. Esto hace que las redes sean "flexibles" a los ambientes que las rodean, que no necesiten ser programadas nuevamente frente a cambios en el entorno.
3. Gran cantidad de problemas reales son no lineales. La combinación de varias neuronas artificiales configuradas en paralelo arroja una función altamente no lineal no sólo en variables sino también en los parámetros. Los modelos lineales generalizados (regresión logística, de Poisson. de Cox, etcétera) pueden ser no lineales en variables, pero si en parámetros. "A diferencia de los modelos estadísticos tradicionales, los cuales intentan ´ajustar los datos a un modelo´, las redes neuronales ´fabrican un modelo que se ajuste a los datos´. El enfoque de la computación neuronal es diametralmente opuesto" (Alfonso y Torres. 1992)7.
Pero las redes neuronales también tienen desventajas:
1. Para quienes quieren encontrar una relación explícita entre las variables de entrada y la respuesta, el modelo neuronal produce una expresión altamente no lineal donde los pesos que se optimizan en el entrenamiento no tienen interpretación alguna: mientras que los coeficientes de un modelo estadístico si la tienen.
2. Las redes neuronales han recibido muchas críticas porque su entrenamiento es un proceso de "ensayo y error" que consume demasiado tiempo, este se hace más grande si la red es muy compleja (tiene bastantes neuronas ocultas) y si además el tamaño de muestra para entrenamiento también es grande.
3. No existe un procedimiento respaldado teóricamente para determinar el número de neuronas en capa oculta ni las variables de entrada con mayor relevancia, y no se puede hacer inferencia estadística para medir la importancia de los pesos, aunque ya hay trabajos que estudian esta posibilidad (Sarle 1994).
4. La superficie del error para una red compleja está formada por muchos mínimos locales haciendo que sea muy probable que el algoritmo de propagación inversa quede atrapado en uno de ellos.
Perceptron y la separabilidad lineal
La investigación en redes neuronales, después del hallazgo de Minsky y Papert (1969), entró en un estado de abandono hasta finales de los ochenta. El resultado de estos autores señaló que, sin importar la función no lineal usada como función de activación, un perceptron con solamente la capa de salida, tiene éxito en tareas de clasificación de patrones sólo si estos son linealmente separables. El ejemplo clásico para ilustrar esta idea ha sido el aprendizaje de la función lógica o exclusiva (XOR). Esta operación lógica entre valores ele verdad ele dos proposiciones se representa mediante la siguiente tabla.

El valor 0 indica falsedad y el valor 1 lo contrario. De esta manera la operación lógica o exclusiva entre dos proposiciones es verdadera sólo si alguna de las dos proposiciones es verdadera, pero no ambas.
Supongamos un perceptrun (ver Gráfica 5) se comprende con dos entradas y una función de activación logística que se define por f(x) = 1 1 + e- x. Las dos entradas son los valores de x1 y x2 del Cuadro 1 multiplicados por los ponderadores w1 y w2, respectivamente y sumados a un umbral θ, este resultado es el argumento de la función logística.
El problema del reconocimiento de las salidas de la operación XOR al que se enfrenta el perceptron descrito arriba consiste en encontrar los valores adecuados de w1, w2 y θ, Es un problema ele optimización donde no es posible encontrar valores satisfactorios.
La dificultad para resolver el problema reside en el hecho de que los patrones no son linealmente separables; es decir, que no existe una línea recta que permita separar el espacio de patrones8. En la Gráfica 6 se representan los valores del Cuadro 1, en las abcisas van los valores de x1 y en las coordenadas los de x2, con el punto blanco se representa un valor verdadero (1) de la proposición x1 XOR x2 y con el punto negro un valor falso (0). Se observa en dicha gráfica que no es posible trazar una línea recta que divida las respuestas falsas de las verdaderas.
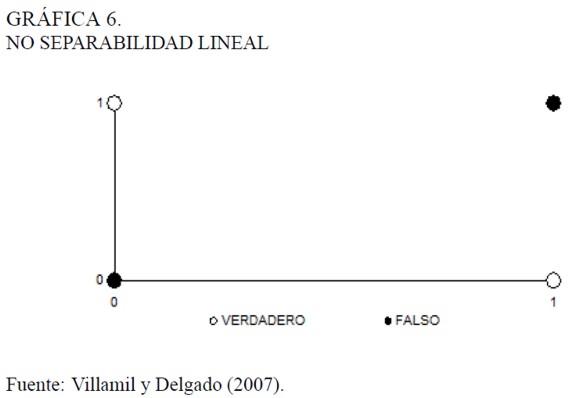
La forma en la que se pueden hacer separables las respuestas de la Gráfica 6 es mediante una o varias capas de funciones no lineales entre las entradas y las salidas de un perceptron. a esta configuración se le llama perceptron multicapa. Éste, según la demostración Funahashi (1989)9 es capaz de aproximar cualquier asociación no-lineal entre variables.
Perceptron Multicapa
La red neuronal más sencilla es el perceptron multicapa, este consiste en un arreglo de neuronas por capas: la capa de neuronas para las variables de entrada se llama capa de entrada, una o varias capas intermedias se llaman capas ocultas, y una capa de neuronas para las variables de salida se llama capa de salida, las interconexiones que son permitidas entre neurona sólo van de una neurona de una capa a las neuronas de la capa siguiente, es posible que uno o varios ponderadores sean cero. Esta es la principal característica de las redes multicapa o estáticas, no existe retroalimentación, es decir, no se permite que la salida de una capa vaya como entrada a una capa anterior. Cuando se admite la retroalimentación se habla de redes recurrentes o dinámicas. La notación abreviada para la arquitectura de una red neuronal multicapa es (ni, nj, nk). Donde ni y nk son el número de variables de entrada y de salida respectivamente, en tanto que nj es el número de neuronas en la capa oculta. En la Gráfica 7 se ilustra una red neuronal multicapa con arquitectura (4, 3, 3, 2).
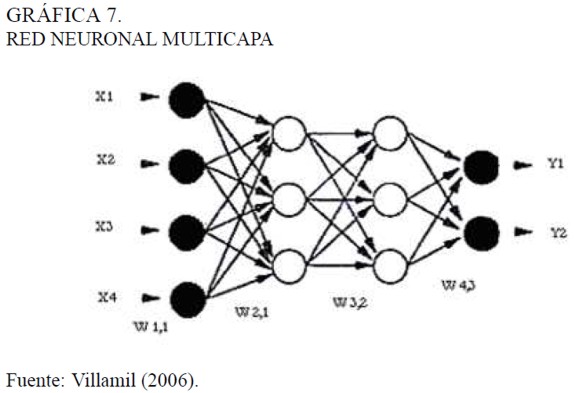
Toda red multicapa se encuentra definida en términos de su arquitectura, sus funciones de activación, los umbrales y los pesos. Estos últimos son las variables de ajuste en el momento de utilizar un algoritmo de entrenamiento para que la red aprenda. En el entrenamiento, además de ajustar los pesos y los umbrales, es preciso optimizar el número de neuronas que la conforman porque de esto depende la velocidad que adquiere la red para aprender.
El entrenamiento de una red multicapa es de dos tipos: incremental si el aprendizaje se da al presentarle a la red cada entrada (variables explicativas) con su respectiva salida (variables explicadas), o batch cuando el aprendizaje de la red ocurre sólo después de haberle presentado todo el conjunto de datos de entrada y salida. El objetivo del entrenamiento es minimizar una función de pérdida o costo, la que se usa con frecuencia es el error cuadrático medio.
Una función de pérdida L debe satisfacer las siguientes propiedades (Jalil y Misas (2006):
i. L(e) ≥ 0 ∀ e ≠ 0
ii. L(0) = 0
iii. L(e) = L(-e)
iv. L(ei ) ≥ L(e´i ) ∀ |ei | > |e´i |
Donde e son los residuales entre las salidas deseadas y las simuladas por el modelo.
Dos de las funciones que cumplen estas condiciones son:
- El error cuadrático medio (ECM). L(e) = αe2 con α > 0. Se usa con frecuencia α = 0,5.
- La función LINEX. L(y - y*) = 1/φ2 {exp [φ (y - y*)] - φ(y - y*) -1} con φ ≠ 0. En la cual y* es el valor pronosticado. Existen dos posibles casos: uno en el que φ > 0 donde las sub-predicciones y - y* > 0 son mucho más costosas. Y otro, en el que φ < 0, donde se presta más atención a las sobre-predicciones y - y* < 0. Cuando φ es muy cercano a cero esta función tiende a parecerse al ECM.
El algoritmo de propagación inversa (BP)
Para deducir el mecanismo de actualización de los pesos como lo plantea el algoritmo de propagación inversa (back propagation) se emplea la siguiente notación -siguiendo la exposición de Haykin (1994). Sea una capa I de entrada, una capa de neuronas ocultas J y una capa de salida K donde sólo se permiten conexiones entre las neuronas de una capa con las neuronas de la capa siguiente, se dice que:
a) i es la i-ésirna neurona en la capa I, j es la j-ésima neurona en la capa J y k es la k-ésima neurona en la capa K.
b) n es la n-ésima iteración realizada por el algoritmo cuando se le presenta el n-ésimo patrón del conjunto de entrenamiento.
c) yj(n) y yk(n) son las salidas de las neuronas j y k respectivamente para la n-ésima iteración. yk es el valor de salida que simula la red.
d) dk(n) es el k-ésimo elemento en el vector de patrones de salidas (deseadas) para la n-ésima iteración.
e) ek(n) = dk(n) - yk(n) es el error de aproximación de la red a la respuesta deseada dk(n).
f) yi(n) es el i-ésimo elemento en el vector de patrones de entrada en la n-ésima iteración.
g) N es el número de patrones de entrenamiento: las filas de variables de entradas con sus respectivas salidas.
h) wij(n) es el peso de la neurona j (de la capa oculta) que multiplica a yi(n).
i) wkj(n) es el peso de la neurona k (de la capa oculta) que multiplica a yj(n).
j) wj0(n) es el umbral de la neurona j y wk0(n) es el umbral de la neurona k en la n-ésima iteración.
k) Δwij(n) es la corrección aplicada al peso wij(n) en la n-ésima iteración, Δwkj(n) tiene la misma interpretación.
l) sj(n) = ∑ i ∈ I wji(n)yi(n) es el nivel de actividad interna neta de la neurona j.
m) sk(n) = ∑ j ∈ J wkj(n)yj(n) es el nivel de actividad interna neta de la neurona k.
n) fj (⋅) es la función de activación de la neurona j. Esta genera la salida yj que se obtiene de yj = fj (sj (n)).
o) De la misma manera se interpreta la salida de la neurona k de la capa de salida yk = fk (sk (n)).
p) E(n) = 1/2 ∑ k ∈ K ek2 (n) es la suma de errores cuadrados en la n-ésima iteración.
q) El error cuadrado medio es E C M = l / N ∑n= 1 N. El E C M es la función de costo o pérdida que muestra el desempeño del entrenamiento, un valor muy pequeño indica que la red ha aprendido la relación entre los vectores de entrada y los vectores de salida para los N patrones de entrenamiento10.
BP fue inicialmente propuesto en la tesis doctoral de Werbos (1974), es el algoritmo de entrenamiento más conocido, éste debe buscar valores óptimos de wkj(n), wji(n), wk0(n) y wj0(n) que minimicen el valor de la función de pérdida. Se parte de unos valores iniciales de todos los pesos y umbrales que son generados aleatoriamente (a esta etapa se le conoce como la inicialización de los pesos). Los pesos de una iteración a otra se actualizan con base en una corrección Δw(n) de esta manera:
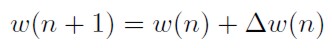 [30]
[30]
El proceso iterativo se realiza desde la última capa de neuronas hasta la primera en la medida que cada patrón es presentado a la red. En virtud de que el aprendizaje se hace con base en la repetición, no sólo es necesario presentarle a la red una lista de datos (patrones) disponibles en la muestra de entrenamiento, sino que es preciso mostrárselos varias veces hasta que la red aprenda. A cada listado de patrones se llama época. El número de iteraciones del algoritmo BP es igual al número de épocas multiplicado por el número de patrones disponibles en la muestra de entrenamiento.
La corrección Δw(n) es igual a una constante de proporcionalidad η (llamada tasa de aprendizaje) que multiplica el cambio de dirección de la suma de errores cuadrados con respectos a los pesos, es decir:
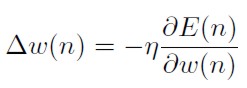 [31]
[31]
La expresión (31) es necesario examinarla por separado en la capa de salida y en la capa oculta, debido a que en esta última no existen unos valores deseables que puedan ser observados y con los cuales medir los errores de salida de las neuronas en esa capa.
Caso 1. La capa de salida
Reemplazando las expresiones e) y o) en p) puede verse que la suma de errores cuadrados se expresa como:
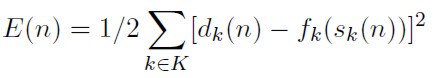 [32]
[32]
Aplicando la regla de la cadena, la derivada en la ecuación (31) se expresa así:
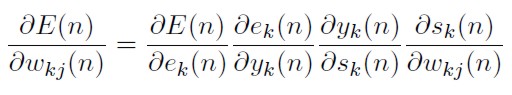 [33]
[33]
Derivando a ambos lados la definición p) con respecto al error de salida en la neurona k:
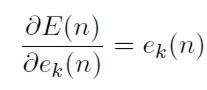 [34]
[34]
Derivando a ambos lados la definición e) con respecto a la salida de la neurona k:
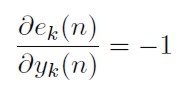 [35]
[35]
Derivando a ambos lados la definición o) con respecto al nivel de actividad interna neta en la neurona k:
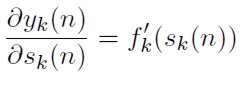 [36]
[36]
Derivando a ambos lados la definición m) con respecto a los pesos en la neurona k:
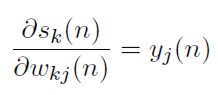 [37]
[37]
Reemplazando (34), (35), (36) y (37) en (33) se obtiene:
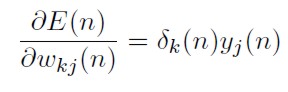 [38]
[38]
Donde δk(n) = ∂ E(n) / ∂ sk(n) = -ek (n) f´k (sk (n)) y se llama gradiente local.
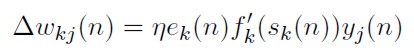 [39]
[39]
Reemplazando (39) en (30) obtenernos la regla de actualización de pesos en la capa ele salida del perceptron rnulticapa:
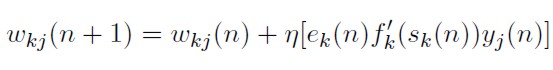 [40]
[40]
Caso II. La capa de oculta
En la capa oculta es necesario buscar que la regla de actualización de los pesos involucre el error en la capa de salida, puesto que no hay salidas deseables a priori para la capa oculta. Reemplazando la definición m) en (32), la suma de errores cuadrados en la capa de salida se expresa como:
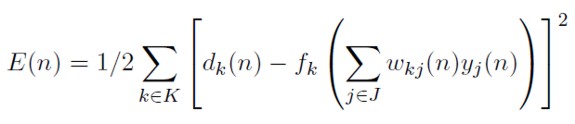 [41]
[41]
De aquí es claro que E(n) es una función de las salidas en la capa oculta yj(n). Usando nuevamente la regla de la cadena, el cambio de dirección de la suma de errores cuadrados con respecto a los pesos en la capa oculta puede escribirse así:
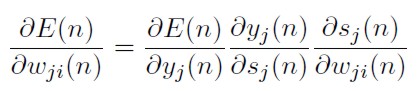 [42]
[42]
Donde δj(n) = ∂ E(n) / ∂ sj(n) es el gradiente local respectivo.
Aplicando la regla de la cadena se deriva (41) a ambos lados con respecto a yj(n):
 [43]
[43]
Derivando la definición m) con respecto a yj(n):
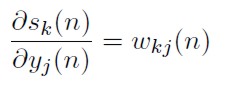 [44]
[44]
Reemplazando (35), (36), (44) en (43) se obtiene:
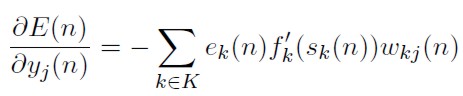 [45]
[45]
Derivando a ambos lados la definición n) con respecto al nivel de actividad interna neta en la neurona j:
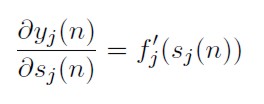 [46]
[46]
Derivando a ambos lados la definición l) con respecto a los pesos en la neurona j:
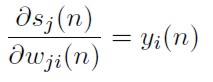 [47]
[47]
Reemplazando (45), (46) y (47) en (42) se obtiene:
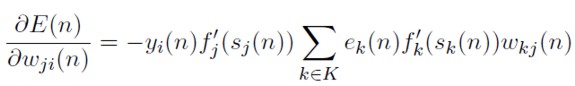 [48]
[48]
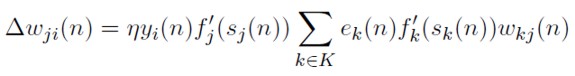 [49]
[49]
Reemplazando (49) en (30), la regla de actualización de pesos en la capa oculta queda como:
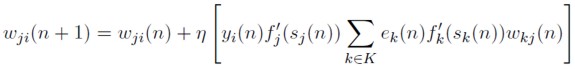 [50]
[50]
Las ecuaciones (40) y (50) conforman el ajuste iterativo de los pesos en la capa de salida y oculta respectivamente.
El algoritmo BP se ha cuestionado porque con una tasa de aprendizaje muy pequeña el entrenamiento es demasiado lento, y considerando una tasa muy alta. el algoritmo es inestable. Otro comentario consiste en que los pesos con los que se inicializa el entrenamiento puede ubicar al gradiente en una zona donde se converja a un mínimo local y no a uno global. En consecuencia el entrenamiento mediante BP es un ejercicio de ensayo y error que resulta algo engorroso. por esta razón se han propuesto algunas modificaciones del algoritmo. En Villamil (2006) se enuncian mecanismos tanto formales como heurísticos de selección de la "mejor" red neuronal.
La primera modificación involucra en la regla de actualización de pesos un término de ajuste α (llamado momentum) respecto al cambio entre los pesos conseguidos en una iteración y la siguiente, como se muestra en la siguiente ecuación:
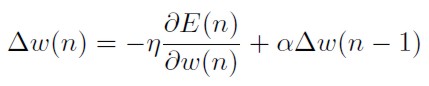 [51]
[51]
Algunos autores han sugerido que la tasa de aprendizaje no fuera fija sino dinámica y algunos se han enfocado en emplear algoritmos de optimización diferentes, como el de Levenberg-Marquart, Newton, de gradiente conjugado, etcétera; no obstante, el algoritmo BP es el más usado11. Otros, por su parte, recomiendan entrenar el perceptron varias veces con diversos valores de los pesos iniciales (generados aleatoriamente), esto se hace con el fin de reducir la posibilidad de que el algoritmo converja a un mínimo local. Una práctica frecuente es realizar el primer entrenamiento con una tasa de aprendizaje de 0, 9, guardar los pesos y entrenar nuevamente usando estos pesos con una tasa de aprendizaje menor, y así sucesivamente. En la etapa en la que se encuentre el menor valor del error cuadrado medio se selecciona la red. Para el estudio de series muy complicadas, si los ajustes no son buenos mejorando el procedimiento de optimización, se ayuda a la red modelando su error de predicción con un proceso ARIMA (p, i, q).
No es aconsejable entrenar la red con los datos en sus valores originales, con frecuencia se recomienda el re-escalamiento de los datos o patrones a intervalos semejantes al dominio para el cual la función de activación logra sus valores máximo y mínimo. Se afirma que este procedimiento es necesario para evitar la saturación de las funciones de activación, es decir, que las salidas de las neuronas se ubiquen siempre o en su valor máximo o en su valor mínimo. El re-escalamiento consiste en una regla tres; para transformar, por ejemplo, los valores de z a valores de una variable y que se mueve en el intervalo [a, b], se aplica la siguiente expresión:
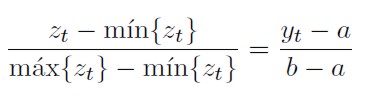 [52]
[52]
También se puede re-escalar los datos normalizando. restando a cada dato el promedio de la serie y dividiendo por la desviación estándar.
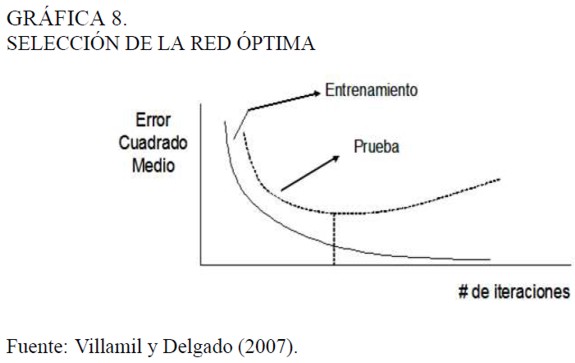
El objetivo del algoritmo de entrenamiento es minimizar la función de pérdida. pero la experiencia ha demostrado que las redes tienden a sobreajustar los datos y mostrar muy buenos resultados. Por esta razón es usual destinar el 70% de la muestra para el entrenamiento y el 30%{ para la prueba del modelo. La selección de la mejor red se realiza con base en la arquitectura que obtenga el menor valor de la función de pérdida en el conjunto de prueba. En la Gráfica 8 se muestra el comportamiento de la función a medida que el algoritmo avanza en cada iteración, se aprecia que en el conjunto de entrenamiento este valor siempre decae con el número de iteraciones, pero para seleccionar la red óptima sólo hay un número de iteraciones que hace mínimo su valor en el conjunto de prueba. De ese número de iteraciones en adelante se representan arquitecturas que se ajustan muy bien en el entrenamiento. pero muy mal con los valores de prueba. Por lo anterior el modelo se selecciona cuando se obtiene el menor valor de la función objetivo con los datos de prueba.
Chemotaxis
Algunos organismos unicelulares, por ejemplo las bacterias, responden al estímulo de las sustancias químicas que le sirven ele nutrientes. El movimiento de estos organismos se conoce como chemotaxis. De la observación de la bacteria intestinal Escherichia Coli (especies que se nutre de arninoacidos), investigadores como Berg y Brown (1972)12 establecieron que su desplazamiento ocurre inicialmente de forma aleatoria hasta que paulatinamente encuentra una mayor concentración de su sustancia alimenticia13.
El entrenamiento de una arquitectura neuronal, como se había mencionado, es un problema de optimización, que consiste en encontrar los pesos adecuados en las funciones de activación (neuronas). El algoritmo BP para resolverlo se basa en el cambio de la función de pérdida con relación a los pesos en la capa oculta y de salida. Bremermann y Anderson (1991) propusieron entrenar redes neuronales artificiales usando el mecanismo de chernotaxis, ellos señalan que la principal ventaja en comparación con BP es su fácil implementación y que este algoritmo no usa el gradiente del error, simplificando así el número de cálculos a realizar.
En ocasiones el interés no reside en el ajuste de la salida de una red en comparación con una salida deseada, sino de una función de pérdida mucho más compleja para la cual el cálculo del gradiente es difícil o imposible de realizar. El algoritmo de entrenamiento con base en el mecanismo de chemotaxis se reduce a una caminata aleatoria sesgada por el espacio de parámetros de la función que se quiere optimizar. El algoritmo tiene la siguiente secuencia (ver Delgado 2000):
i) Se inicia con una matriz arbitraria de pesos14 W0.
ii) Los pesos iniciales de i) son perturbados por un término ΔW que sigue una distribución normal estándar. Wt = W0 + h* ΔW. donde h es una constante similar a la tasa de aprendizaje en el algoritmo BP y toma valores entre cero y uno.
iii) La función objetivo de interés a ser optimizada se evalúa con los nuevos pesos f(Wt). Si los nuevos pesos disminuyen (en el caso que se desee minimizar) o aumentan (en el caso que se desee maximizar) la función de pérdida con relación al resultado que se obtiene con los pesos iniciales f(W0), se toman estos nuevos pesos como referencia y se vuelve al paso ii), de lo contrario se regresa a i).
iv) Durante el ciclo de iteraciones el valor de h es ajustado de la siguiente forma: después de s pasos exitosos el nuevo valor es h + δ, es decir, se hace más rápido el aprendizaje. Después de f pasos fallidos el nuevo valor es h - δf, lo que significa que el aprendizaje es más lento15.
El algoritmo se detiene fijando un número de iteraciones máximo o un valor aceptable de la función objetivo. En la siguiente sección se instrumenta los modelos descritos anteriormente con cifras de cierre del mercado del USD/COP y algunas variables macroeconómicas con el fin de encontrar respaldo empírico a las formulaciones teóricas.
METODOLOGÍA
Se construye una muestra de 78 observaciones en frecuencia tri mestral del tipo de cambio USD/COP, de los medios de pago. del producto interno bruto (desestacionalizado) y del índice de precios al consumidor (IPC) con base en 1998. desde el cuarto trimestre de 1986 hasta el primer trimestre de 2006. Todas las series se transforman a escala logarítmica. Se reserva el 70% de los datos de la muestra para el ajuste de los modelos y las cifras restantes se emplean en su validación.
El primer modelo (DD -De Grauwe y Dewachter-) resulta de la estimación de los parámetros de la ecuación (29) usando corno función de pérdida el ECM y empleando el algoritmo de programación cuadrática secuencial (PCS) con diferentes valores de parámetros iniciales generados de una distribución uniforme en el intervalo [0, 1]. Se seleccionan los parámetros finales que reportan un menor valor de la función de pérdida.
En la ecuación (29) los medios de pago y el producto se encuentran en el mismo tiempo que la variable a pronosticar. esto implicaría tener dos expresiones que las pronostiquen. para simplificar se consideran los valores de estas variables rezagados un periodo. Además. a diferencia de De Grauve y Dewachter (1993), no se asume que la tasa nominal de equilibrio sea constante, sino que se estima a través del filtro de Hodrick-Prexcott con parámetro λ = 100. Dada una serie de tiempo {xt}, este filtro extrae una tendencia estable x*t , aislada del comportamiento volátil, minimizando la siguiente expresión:
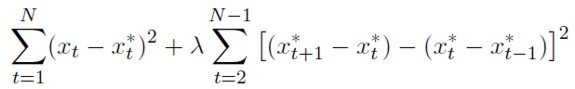 [53]
[53]
Donde N es el número de observaciones.
Haciendo: z = (st - 1 - st)2 y x = st - 1 - 2st - 2 - st - 3, la ecuación (29) conviene re-expresarla como (54) para evitar la sobre-pararnetrización y simplificar la función a estimar por PCS. Este algoritmo permite restringir los parámetros fe la función a valores deseados, para este caso, se exige que los parámetros sean no-negativos de acuerdo con los valores que se espera de las ecuaciones presentadas en la segunda parte.
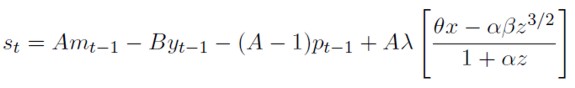 [54]
[54]
Donde A = 1 + µ / µ y B = γ A.
El segundo y tercer modelo se obtienen del entrenamiento de una red multicapa que aproxime la ecuación (29) del modelo no-lineal de sobre-reacción del tipo de cambio nominal. Las variables de entrada se re-escalan en el intervalo [0, 1] mediante la expresión (52). Igual que en el primer modelo se introducen el producto y los medios de pago rezagados un período.
Las redes usan como activación la función logística y la Gumbel (doble exponencial). Se llaman LL a las redes con función logística en ambas capas, GG a las que tienen activación Gumbel y LG a las que tienen función logística en la capa oculta y Gumbel en la capa de salida. La arquitectura de los perceptrones es (6, nj, 1) y el número de neuronas en capa oculta varía ente uno y veinte.
El segundo y tercer modelo son redes neuronales, pero una de ellas es entrenada por BP y con función objetivo ECM ó Indice de Theil y la otra por Chemotaxis con función objetivo LINEX. El entrenamiento por BP usa los siguientes valores de los parámetros: 0,4 para la tasa de aprendizaje, 0,5 para el momentum de primer orden, 400 para el número de épocas.16 El algoritmo de Chemotaxis se emplea con los siguientes parámetros: 0,4 para la tasa de aprendizaje, 100 para el contador de pasos fallidos y exitosos (s = f = l00), 0,05 para el ajuste de la tasa de aprendizaje (δs = δf = 0,05), l00.000 para el número máximo de iteraciones y se usa la función de pérdida LINEX con parámetro Φ = 1.17 Los pesos iniciales se generan de una distribución uniforme en el intervalo [0, 1]. Por último. se comparan los pronósticos de los tres ajustes con los datos de validación.
RESULTADOS
En el Cuadro 2 se encuentra la combinación de valores finales de los parámetros asociados a la estimación no lineal de [54] que producen el menor valor del ECM.
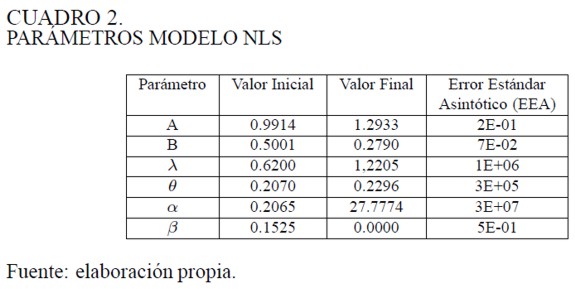
Los coeficientes que acompañan a los fundamentales son asintóticamente estables a juzgar por los valores de los EEA para A y B. El incremento en un peso de los medios de pago significa más o menos 1,29 pesos en los que puede aumentar el tipo de cambio nominal (A = 1,29). La respuesta con respecto al comportamiento de los especuladores es un poco mayor, un valor esperado en la variación del tipo de cambio de un peso por parte de ellos, se puede traducir en un aumento de la tasa de cambio en 1,58 pesos (Aλ = 1,58). No obstante. esta afirmación no es concluyente. puesto que el EEA para λ es bastante grande.
A partir de la estimación del parámetro α se puede construir el comportamiento de la participación de los especuladores con inclinación por el análisis técnico. En la Gráfica 9 se ve que estos son mucho más importantes que aquellos que siguen el análisis fundamental. Nuevamente, esta observación no es concluyente, porque el EEA del parámetro α es un número muy grande.
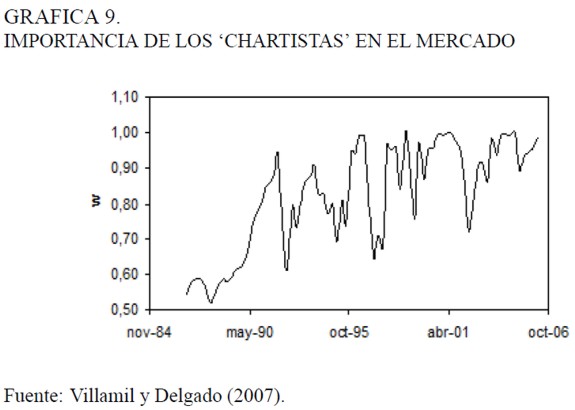
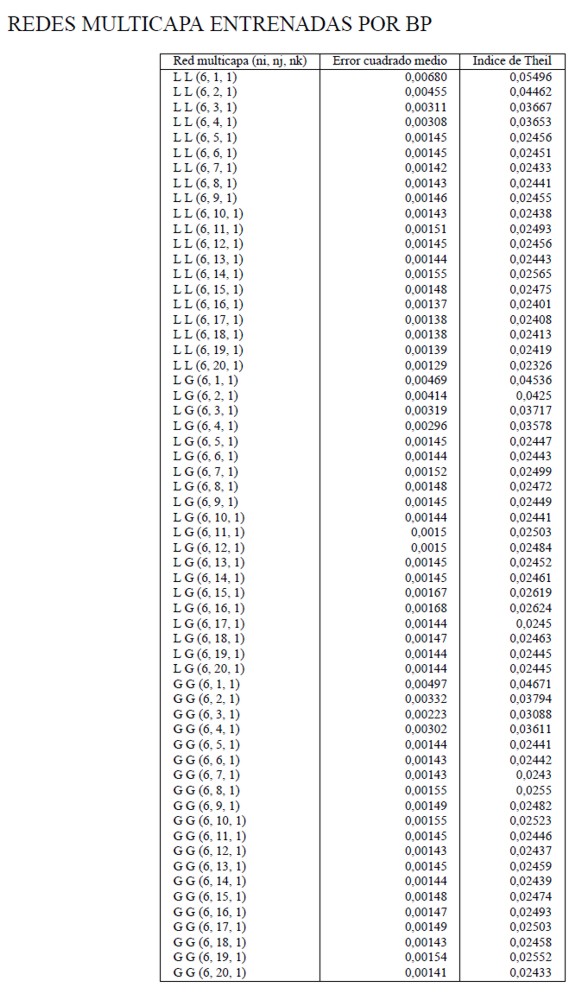
En el Anexo 1 se muestra el ajuste de 60 redes neuronales entrenadas por BP en términos del error cuadrado medio y del índice de Theil, que toma valores cercanos a cero a medida que el poder predictivo de la red se incrementa. A diferencia de ECM, este indicador no depende de la escala en la que se encuentre la variable a predecir yt y se define por la siguiente expresión:
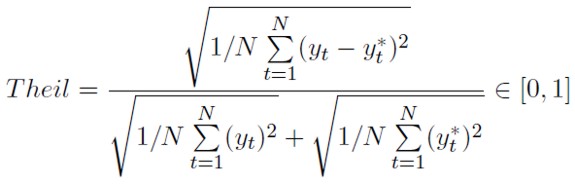 [55]
[55]
Donde N es el número de observaciones.
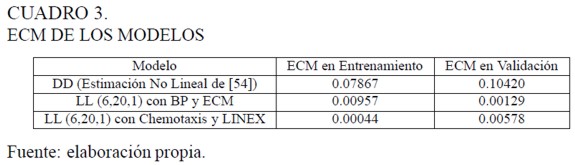
Se observa en el Cuadro 3 que la mejor red entrenada por BP -Ia que produce los menores valores de ECM y Theil con los datos de validación- es la LL (6, 20, l). A su vez. la mejor red entrenada por chernotaxis y usando la función LINEX es la LL (6, 20, 1), esto habla bien de la utilidad de chernotaxis en relación con BP; pero con los datos de validación es superior el ajuste de la misma red entrenada por BP. El modelo DD tiene un mal desempeño tanto con el conjunto de entrenamiento como con el de prueba, esto hace que sea preferible su aproximación usando redes multicapa. En Villamil y Delgado (2007) se explica la importancia que tiene la técnica estadística de componentes principales en la consecución de los mejores modelos cuando se está interesado en alcanzar más de un objetivo (por ejemplo, un buen ajuste medido por el criterio de Akaike, pero también en términos de rentabilidad si se contempla un modelo de pronóstico para negociación).
En la Gráfica 10 se comparan los pronósticos de los tres modelos. Se observa que con los datos de prueba la red entrenada por BP sigue "más de cerca" el comportamiento del UDS/COP que el modelo DD y la red con función de pérdida asimétrica entrenada por chemotaxis. Se puede afirmar, por lo menos en este caso, que optimizar la red con una función de pérdida que "castigue" las sub-predicciones no garantiza que, con datos que nunca fueron presentados a la red, surja este tipo de pronóstico. Como se ilustra en la Gráfica 10 con los datos de validación, la red entrenada con la función LlNEX procura mayores sub-predicciones en comparación con la que se entrenó con el ECM.
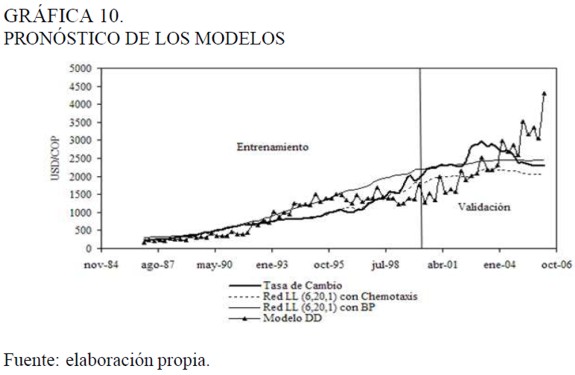
Otra observación importante se relaciona con el tiempo computacional empleado en cada uno de los entrenamientos, que es una función directa con respecto a la cantidad de observaciones en el conjunto de datos de entrenamientos y de el número de neuronas en capa oculta, lo cual se traduce en un mayor número de parámetros bien sea de la función logística o Gurnbel que tienen que estimarse. El tiempo promedio de los modelos entrenados con el mayor número de neuronas contemplado (veinte) por BP fue de 25 minutos, mientras que el mismo modelo entrenado por Chernotaxis requería entre 10 y 15 minutos adicionales.
CONCLUSIONES
Nelly y Samo (2002) han mostrado que varios de los modelos que usan variables fundamentales no permiten explicar el comportamiento de la tasa de cambio. Una afirmación ya generalizada, es que los fundamentales ayudan en la explicación de la dinámica de largo plazo de esta variable, pero no lo hacen en el corto y mediano plazo. Rowland (2002) muestra que ninguno de los modelos monetarios que él ajusta para el USD/COP es superior a la caminata aleatoria.
Las explicaciones que incorporan la interacción entre diversos tipos de especuladores argumentan que la diversidad de opiniones sobre el valor futuro de la tasa de cambio es la responsable de las variaciones de corto plazo. De Grauwe y Oewachter (1993) se ubican en esta línea al proponer dos categorías de especuladores, los fundamentalistas que toman posiciones (de compra o venta) de acuerdo con la distancia que tenga la tasa de cambio respecto de su valor de equilibrio (esta a su vez se determina por los fundamentales de la economía), y los chartistas que utilizan indicadores sobre la serie histórica de precios. Cuando no hay una distancia notable entre la tasa de cambio y su nivel de equilibrio, son los chartistas quienes tienen mayor responsabilidad en las fluctuaciones de la tasa de cambio.
En este documento se estimó la ecuación de comportamiento no-lineal propuesta por Grauwe y Dewachter (1993). Con los parámetros se mostró que la especulación tiene una incidencia un poco mayor sobre la tasa de cambio que la política monetaria y que la actividad de los especuladores que siguen el análisis técnico es más importante que la de quienes se guían por los fundamentales. Sin embargo, estas conclusiones son débiles debido a los altos errores de estimación.
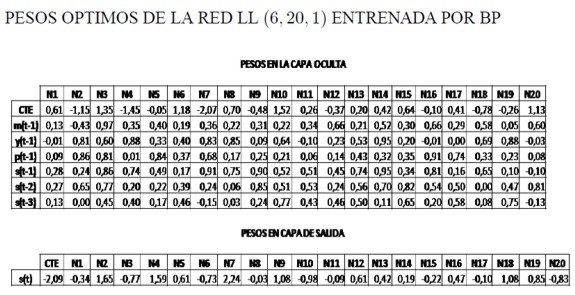
La estimación de expresiones no lineales como la de Grauwe y Dewachter tiene bastantes dificultades, la más importante es la inestabilidad de los parámetros. Por esta razón se sugiere las redes multicapa como una metodología de aproximación de formas funcionales no lineales que goza de la propiedad de "generalivación", es decir, que aprende la relación no lineal que subyace a unas variables explicadas con unas explicativas con base en unos patrones que se le presentan (el conjunto de datos de entrenamiento), y que es capaz de reconocer y reproducir esta misma asociación para unos datos que no se le han presentado (el conjunto de validación). Para las cifras usadas en este documento se mostró cómo el ajuste de las redes neuronales supera, en términos de error cuadrado medio, la estimación directa por mínirnos cuadrados no lineales de la expresión de Grauwe y Dewachter. No obstante, la red tiene la dificultad de que ninguno de sus parámetros tiene interpretabilidad estadística (los pesos de la red multicapa LL (6, 20, 1) entrenada por BP se encuentran en el Anexo 2), por esta razón se acostumbra a llamarle a la arquitectura con los parámetros óptimos "caja negra",
Es necesario destacar algunos aspectos que orientan el rumbo actual del modelamiento macroeconómico:
1. Pese a que la utilización de la gráfica del agente representativo puede simplificar su presentación, también puede ocultar interacciones importantes a nivel micro que inciden en los agregados, en este caso, la interacción entre especuladores heterogéneos tiene relevancia en la explicación del comportamiento de corto plazo del tipo de cambio.
2. La psicología es más importante que la racionalidad del mercado, siendo más indicado el concepto de racionalidad acotada. En este caso los especuladores que se llamaron chartistas no disponían de información completa y desconocían el mecanismo de formación de expectativas de los fundamentalistas, sus pronósticos los obtenían por reglas intuitivas como el cruce de dos promedios móviles.
3. Los sistemas no lineales ofrecen explicaciones en las cuales no intervienen términos aleatorios y pueden dar cuenta, a partir de expresiones deterrninísticas, de comportamientos erráticos como el de las tasas de cambio .
4. Los tres elementos anteriores complican bastante el desarrollo analítico de un modelo no dejando otra alternativa que la utilización de métodos computacionales, aquellos que son bio-inspirados (redes neuronales, lógica borrosa y algoritmos genéticos) y que se han agrupado bajo el nombre de inteligencia computucional. Sargent (1993) ilustra extensamente sus aplicaciones en economía.
NOTAS AL PIE
1 En Colombia existe aplicaciones de las redes neuronales para el comportamiento de la inflación y del efectivo (Misas et al., 2002 y 2003). Para referencias internacionales puede consultarse el texto de Sargent (1993).
2 Las variables con asterisco simbolizan agregados macroeconornicox de la economía extranjera, s es el tipo de cambio nominal (el número de unidades de moneda doméstica que se da a cambio por una unidad de moneda extranjera), e es la tasa de cambio real (el precio de una canasta de bienes extranjeros expresado en términos de los mismo bienes nacionales), i es la tasa de interés, y es el producto interno bruto, m es el dinero líquido que circula en la economía y p es el nivel general de precios.
3 Este supuesto es importante no sólo en teoría económica sino en finanzas. Muchas de las elaboraciones de modelos de pricing y valoración en finanzas están construidas con base en este supuesto restrictivo, un ejemplo de ello es la idea de las tasas forward. Como en economía esta hipótesis es objeto de fuertes cuestionamientos, los modelos más importantes son hechos por Soros (2008) con su teoría de la reflexividad y Taleb (2005) con su idea del "Cisne Negro".
4 La hipótesis de los mercados eficientes, formulada por Eugene Fama (1969 Y 1970), sostiene que los mercados en los que se transan activos financieros se caracterizan por, que cualquier nueva información es incorporada inmediatamente por los negociadores en sus decisiones de compra y venta. De lo anterior se desprende que no es posible que un especulador anticipe estas decisiones y que, en promedio y de manera sistemática, obtenga ganancias superiores a las del mercado. En otras palabras, estos mercados no son predecibles, el conocimiento del comportamiento del precio en el pasado no aporta información para dilucidar su nivel futuro.
5 Para más indicadores del análisis técnico puede consultarse Kaufrnan (1987).
6 La función de activación se usa para acotar el rango de su respuesta o salida (a) entre dos valores deseables. Las funciones de activación más usadas son la función logística que garantiza valores en el intervalo (0, 1) y la función tangente hiperbólica que garantiza valores en el intervalo (-1, 1).
7 En el caso de las variables financieras se ha usado para su modelamicnto las series de tiempo lineales y las no-lineales, estas últimas buscan una forma especifica de relación funcional no-lineal entre los datos. Para ambas técnicas la validez estadística del modelo global, de cada uno de sus parámetros y la verificación de sus supuestos es de vital importancia. En el caso de las redes multicapa, que simulan series de tiempo, se busca la forma funcional y no se impone a los datos, y los parámetros (los pesos) sólo importan en tanto sean los que reflejan el aprendizaje de la red.
8 Cuando se tiene n variables de entrada la no separabilidad lineal consiste en que no es posible que un hiperplano separe dos hipervolúmenes.
9 Citado en Delgado, (1998).
10 Krõse y Van der Smagt (1996) señalan que el valor de la función de pérdida en el conjunto de entrenamiento debe converger al valor de ésta en el conjunto de prueba. para garantizar que el algoritmo ha encontrado un mínimo global.
11 Sarle (1994, 3) hace la siguiente afirmación: "Considering how tedious unreliable standard backprop, it is difficult to understand why it is used so widely. [ ... ] For small networks (tens of weights), a Levenberg-Marquardt algorithrn is usually a good choice. For a medium size network (hundreds of weights), quasi-Newton rnethods are generally faster. For large networks (thousands of weights), memory restrictions often dictate the use of conjugare gradient methods".
12 Citado en Müller et al. (2002).
13 "Bacteria are too smlall to be ahle to measure spatial concentration gradients of chemoattractats. When swimming in a medium with varying concentrations they generate ramdom directions instead and keep going as long as concentartion increases. lf attractant concentration does not or no longer increases, then they stop, tumble, then emerge in a new direction at random angles to the old dircetion. In this way they move towards larger and larger concentration values of the attractant. In othcr words, they optimize the function that describes the concentration of the chemoattractant in the medium". Bremermann y Anderson (1991, 127).
14 En el caso de los perceptrones multicapa se parte de dos matrices: una en la capa oculta y otra en la de salida.
15 Esta es otra ventaja que Bremmerman y Anderson (1991) destacan del algoritmo chemotaxis en comparación con el de propagación inversa. en este último la tasa de aprendizaje (y los momentum) deben ser ajustados empíricamente, por el contrario con chemotaxis el ajuste de este parámetro se hace automáticamente.
16 Teniendo en cuenta que el algoritmo de retropropagucion puede quedarse atrapado en mínimos locales, de la función ECM, los pesos de la mejor red encontrada por BP pueden utilisarse como pesos iniciales para un entrenamiento posterior usando el algoritmo de chemotaxis (pues este se basa en saltos aleatorios y no en el criterio de la primera derivada).
17 De acuerdo con Jalil y Misas (2006, 28) "[Las] sub-predicciones (pronosticar por debajo del valor efectivamente observado) significan mucho dinero perdido para el sistema financiero".
ANEXOS
REFERENCIAS BIBLIOGRAFICAS
1. Alfonso, J.N. y Torres, S.L. (1992). Análisis de Series de Tiempo con Redes Neuronales Aplicado a Descargas Atmosféricas. Monografía de pregrado no publicada, Departamento de Ingeniería Eléctrica, Universidad Nacional de Colombia. Sede Bogotá [ Links ]
2. Berg, H.C. y Brown, D.A. (1972). Chemotaxis in Escherichia Coli Analyzed by Three-Dimensional Tracking. Nature, 239, 500-504. [ Links ]
3. Bremermann H. J. y Anderson, R. W. (1991). How the Brain Adjusts Synapses Maybe. En: Robert S. Boyer (Ed.). Automated Reasoning. Essays in Honor of Woody Bledsoe. Boston: Kluwer Academic Publishers. [ Links ]
4. Da Silva, S. (2001). The Dornbusch Model with Chaos and Foreign Exchange Intervention (Working Paper, Department of Economics). Porto Alegre: Universidade Federal do Rio GrandeDo Sul. Disponible en http://ideas.repec.org/p/wpa/wuwpif/0405017.html [ Links ]
5. De Grauwe, P. y Dewachter, H. (1993). A Chaotic Model of the Exchange Rate: The Role of Fundamentalists and Chartists. Open Economies Review, 4(4), 351-79. [ Links ]
6. Delgado, A. (1998). Inteligencia Artificial y MiniRobots. Bogotá: Ecoe Ediciones. [ Links ]
7. Delgado, A. (2000). Control of Non-Linear Systems Using a Self-Organising Neural Network. Neural Computing y Applications, 9, 113-123. [ Links ]
8. Dornbusch, R. (1976). Expectations and Exchange Rate Dynamics. Journal of Political Economy, 84(6), 1161 - 1176. [ Links ]
9. Fama. E. (1969). The Behaviour of Stock Market Prices. Journal of Business, 38, 34-105. [ Links ]
10. Fama. E. (1970). Efficient Capital Markets: A Review of Theory and Empirical Work. Journal of Finance, 25, 383-417. [ Links ]
11. Funahashi, K.Y. (1989). On the Approximate Realization of Continuous Mapping by Three Neural Networks. Electronics and Communications in Japan. 3(73), 61-68. [ Links ]
12. Haykin, S. (1994). Neuronal Networks: A Comprehensive Foundation. New York: Mcmillan College Publishing Company. [ Links ]
13. Jalil, M. y Misas, M. (2006). Evaluación de Pronósticos del Tipo de Cambio utilizando Redes Neuronales y Funciones de Pérdida Asimétricas (Borradores de Economía 376). Bogotá: Banco de la República. [ Links ]
14. Krugman, P. (1999). El teórico accidental: y otras noticias de la ciencia lúgubre. Barcelona: Editorial Crítica. [ Links ]
15. Kaufman, P. (1987). The New Commodity Trading Systems and Methods. New York: John Wiley and Sons. [ Links ]
16. Kröse, B. y Van der Smagt, P. (1996). An Introduction to Neural Networks. Amsterdam: The University of Amsterdam. Disponible en: http://citeseer.ist.psu.edu/ose96introduction.html. [ Links ]
17. McCulloch,W.S. y Pitts, W. (1943). A Logical Calculus of the Ideas Immanent in Nervous Activity. Bulletin of Mathematical Biophysics, 5, 115-133. [ Links ]
18. Minsky, M. y Papert, S. (1969). Perceptrons: An Introduction to Computacional Geometry. Cambridge: MA. MIT Press. [ Links ]
19. Misas, M., López, E. y Querubín, P. (2002). La Inflación en Colombia: Una Aproximación desde las Redes Neuronales (Borradores de Economía 199). Bogotá: Banco de la República. [ Links ]
20. Misas, M., E. López, C. Arango y N. Hernández. (2003). La Demanda de Efectivo en Colombia: Una Caja Negra a la Luz de las Redes Neuronales (Borradores de Economía 268). Bogotá: Banco de la República. [ Links ]
21. Müller, S., Marchetto,J., Airaghi, S. y Koumoutsakos, P. (2002). Optimization Based on Bacterial Chemotaxis. IEEE transactions on Evolutionary Computation, 6(1): 17-19. Disponible en: http://www.icos.ethz.ch/cse/research/publications/bacteria_chemotaxis.pdf. [ Links ]
22. Nelly, C. y Sarno, L. (2002). How Well Do Monetary Fundamentals Forecast Exchange Rates? (Review of Federal Reserve Bank of St. Louis). St. Louis: Federal Reserve Bank of St. Louis. Disponible en: http://research.stlouisfed.org/publications/review/02/09/51-74Neely.pdf. [ Links ]
23. Rowland, P. (2002). Forecasting the USD/COP Exchange Rate: A Random Walk with a Variable Drift. Borradores. (Borradores de Economía 254). Bogotá: Banco de la República. [ Links ]
24. Sarle, W.S. (1994). Neural Networks Implementation in SAS. Proceedings of the Nineteenth Annual SAS Users Group International Conference. Cary, NC: SAS Institute. [ Links ]
25. Sargent, T. (1993). Bounded Rationality in Macroeconomics: The Arne Ride Memorial Lectures. Oxford: Clarendon Press. [ Links ]
26. Soros, G. (2008). The New Paradigm For Financial Markets: The Credit Crisis of 2008 and What It Means. New York: Public Affairs. [ Links ]
27. Taleb, N. (2005). Fooled by Randomness. The Hidden Role of Chance in Life and in the Markets. London: Texere. [ Links ]
28. Taylor, J. (1995). The Economics of Exchange Rates. Journal of Economic Literature, 33(1), 13-47. [ Links ]
29. Villamil, J. y Delgado, A. (2007). Entrenamiento de una Red Neuronal Multicapa para la Tasa de Cambio Euro-Dólar (EUR/USD). Ingeniería e Investigación, 27(3), 106-117. [ Links ]
30. Villamil, J. (2006). Entrenamiento de una Red Neuronal Multicapa para la Tasa de Cambio Euro-Dólar (EUR/USD). Tesis de Maestría en Matemática Aplicada, Facultad de Ciencias. Universidad Nacional de Colombia, Sede Bogotá. [ Links ]
31. Werbos, P.J. (1974). Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences . Cambridge. M.A.: Harvard University. [ Links ]












