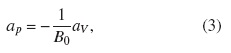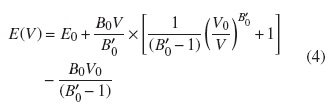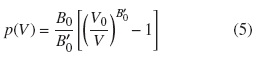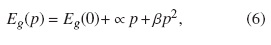Analysis of the Performance of the mBJLDA Potential Considering Pressure Effects

Análisis del rendimiento del potencial mBJLDA considerando efectos de presion

J. A. Camargo-Martínez^a,*
L. J. Correa-Higuera^a
R. Baquero^b

^a Grupo de investigación en Ciencias Básicas Aplicación e Innovación (CIBAIN). Fundación Universitaria Internacional del Trópico Americano -Unitrópico. Casanare, Colombia.
^* Autor de correspondencia: jcamargo@unitropico.edu.co
^b Departamento de Fisica CINVESTAV-México.

Recepción: 11-jul-14 Aceptación: 16-nov-14

Abstract

In this paper a detailed analysis of the performance of the modified Becke-Johnson potential (mBJLDA) considering hydrostatic pressure effects is reported. The band gap was calculated for a set of semiconductors using the mBJLDA potential. These results were compared with those obtained by other methods of calculation, in order to have an objective judgement of this potential. It was found that the GW approximation (GWA) gives the most accurate predictions. The mBJLDA potential is slightly less precise, in general. The hybrid functionals are less accurate, on the overall. In 88% of the semiconductors considered the error was less than 10 %. Both, the GWA and the mBJLDA potential, reproduce the band gap of 15 of the 27 semiconductors considered with a 5 % error or less. Next, the behavior the mBJLDA potential was analyzed to describe the hydrostatic pressure effects. The pressure coefficients were calculated and also the volume deformation potential for a set of semiconductors using this potential. The calculated values correlate quite well with other theoretical reports. With these results, it was concluded that the mBJLDA potential performs reasonable well in describing the hydrostatic pressure effects on the band gap of semiconductors.

Key words: Band Gap Problem, GW Approximation, Hybrid Functionals, Hydrostatic Pressure, mBJLDA Potential, Wien2k Code.

Resumen

En este artículo se presenta un análisis detallado del rendimiento del potencial modificado de Becke-Johnson (mBJLDA), considerando los efectos de la presión hidrostática. La brecha de energía prohibida fue calculada para un grupo de semiconductores usando el potencial mBJLDA. Estos resultados se compararon con los obtenidos por otros métodos de cálculo, para lograr un juicio objetivo de este potencial. Se encontró que la aproximación GW (GWA) brinda las predicciones más precisas. El potencial mBJLDA es, en general, un poco menos exacto. Los funcionales híbridos son menos precisos. En el 88% de los semiconductores tenidos en cuentra, el error fue menor del 10%. Tanto GWA como el potencial mBJLDA reproducen la brecha de energía prohibida de 15 de los 27 semiconductores considerados, con un error del 5 % o menor. Enseguida, se analizó el comportamiento del potencial mBJLDA para describir los efectos de la presión hidrostática. Se calcularon los coeficientes de presión y el potencial de deformación volumetrica para un grupo de semiconductores utilizando este potencial. Los valores calculados se correlacionan muy bien con otros informes teóricos. Con estos resultados se concluyó que el potencial mBJLDA opera razonablemente bien en la descripción de los efectos de la presión hidrostática sobre la brecha de energía prohibida de los semiconductores.

Palabras clave: Problema de la brecha de energía prohibida, Aproximación GW, Funcionales híbridos, Presión hidrostática, Potencial mBJLDA, Código Wien2k.

1. Introduction

Khon-Sham equations [1] are central to the practical application of Density Functional Theory (DFT). To solve them, an approximation to the exchange and correlation energy is required from which an exchange and correlation potential is derived. The way in which this term is approximated is crucial to the proper description of the band structure of solids. The Local Density Approximation (LDA) [2], the Generalized Gradient Approximation (GGA) [3 5] and the meta-GGA [3, 6], among others, describe very well the electronic band structure of even complicated metallic systems. They fail, nevertheless to account for the band gap value of semiconducting systems, a short come known for several years now [7]. Efforts to solve this problem were done since long ago. Approximations as the "scissor operator" [8], the Local Spin Density Approximation, LSDA+U [9] and methods based on the use of Green's functions and perturbation theory as the GW approximation, GWA [10, 12], were proposed. In the last ten years, these efforts gave rise to substantially improved results. Some of the new proposals include, the screened hybrid functional of Heyd, Scuseria and Ernzerhof (HSE) [13 -15] and the middle-range exchange and correlation hybrid functional of Hender-son, Izmaylov, Scuseria and Savin (HISS) [16, 17]. Another recent proposal is an empirical potential the modified Becke Jonhson potential (mBJLDA) proposed by Tran and Blaha [18]. This potential was introduced to the Wien2k code [19] in 2010.

2. The Band Gap: Calculation Methods

Recently, a detailed analysis of the mBJLDA potential was made based on the calculation of the electronic band structure of 41 semiconductors [20]. This paper is a continuation of that work. It was found an important improvement in the predictions of the band gap as compared to the experiment. The mBJLDA is an empirical potential that cannot be derived from an exchange and correlation energy term in the usual way. For that reason it requieres that the lattice parameter is optimized with a previous procedure that considers LDA or GGA as the authors advice [18]. The possibility of using the averaged value as the lattice parameter, α_Avg was used, where α_Avg = (a_LDA + α_GGA)/2. Here α_LDA(a_GGA) is the lattice parameter obtained from an LDA (GGA) optimization procedure. When α_Avg is used as input into the Wien2k code implemented with the mBJLDA potential, a better agreement of the band gap value with experiment is obtained, as compared to the results with either α_LDA or α_GGA. So this procedure turns out to give better results than the one recommended by Tran and Blaha [18] and its extra computational cost is relatively low. A surprising result was, nevertheless, obtained when the experimental low temperature lattice parameter, α_LT , was introduced instead. Unexpected deviations of the band gap value from experiment as big as 48 % were obtained [20]. This is a disturbing result since the lattice parameters obtained from any optimization procedure, are judged to be as good as the small deviation from the experimental lattice parameter value, and so one expects to get the best result (the minimum deviation of the predicted band gap value from the experiment) when the experimental lattice parameter is used. This is not the case. This fact throws doubts on the meaning of the optimization procedure altogether, when the empirical mBJLDA potential is employed. Nevertheless, it is stressed that the results obtained for the band gap value of semiconductors using the mBJL-DA potential, represents a relevant improvement at relatively low computational cost, a fact that we will emphasize below.

Another methods to calculate the band structure of semiconductors are the hybrid functionals which are a linear combination of Hartree-Fock (HF), LDA and GGA terms, and were proposed initially with the aim of improving LDA and GGA in the calculation of the energy bands of molecules [21, 22]. More recently, hybrid functionals were used as an effort to improve the old-standing problem of the band gap of semiconductors; they include among others, the Heyd-Scuseria-Ernzerhof (HSE) functional [13] proposed in 2003. It combines a screened short-range HF term and a screened short-and longrange functional proposed by Perdew, Burke and Ernzerhof (PBE) [4]. The functional form of HSE is based on the hybrid functional of Perdew, Burke and Ernzerhof (PBEh) [23] (also known in the literature as PBE1PBE and PBE0) [24, 25]. In the literature, the functional HSE appears as HSE03 and HSE06. The difference is in the choice of the para-meter value a parameter. The HSE03 will be refered simply as HSE, in this work. In 2005, Heyd et al. [14] reported a study of the band gap and lattice parameters of semiconductor compounds using the HSE functional. Comments on these results will be given below. Recently, Marques et al. [26] have proposed to relate the mixing constant that appears in the method, a, to dielectric properties of the solid. They introduced this parameter into the hybrid functionals PBE0 and HSE06, respectively, and got an improved result. These proposals improve the performance of the hybrid functionals at no extra cost, but as will see below, their results are not the best ones at the moment. Another kind of hybrid functional is the middle-range hybrid exchange and correlation Henderdon-Izmaylov-Scuderia-Savia functional (HISS) [16, 17]. It also uses the PBE potential but in a different way. In 2012, Lucero et al. [27] reported their study of the band gap and lattice parameters of some semiconductor compounds using HISS.

An alternative way to deal with the band gap problem is the GW approximation (GWA). It is derived from many-body perturbation theory [28]. The form of the self-energy in the GWA is the same as in the Hartree-Fock Approximation (HFA) but the Coulomb interaction is dynamically screened remedying the most serious deficiency of the HFA. The corresponding self-energy is therefore non-local and energy dependent. The Green function is obtained from a Dyson equation of the form G = G₀ + G₀ΣG whereG₀ describes the direct propagation without the exchange and correlation interaction and Σ contains all possible exchange and correlation interactions with the system that an electron can have during its propagation. The GWA may be regarded as a generalization of the HFA but with a dynamically screened Coulomb interaction. For details see ref. [11]. In 2005, Rinke et al. [29] using the so called OEPx(cLDA)+GW approximation obtained a reasonable agreement with experiment when calculating the band gap of a certain number of semiconductors. In 2007, Shishkin et al. [30, 31] using a self-consistent GWA (GWA + DFT), and the self-consistent GW approximation with attractive electron-hole interaction, scGW(e-h) accounted quite well for the experimental band gap of several semiconductors.

Now an analysis on some of the different offers in the literature, in what the calculation of the band gap of semiconductors is concerned, is the procedure to follow and a comparison of their results among themselves and with experiment. The goal is to have an objective judgment of the improvement represented by the mBJLDA empirical potential.

3. Analysis

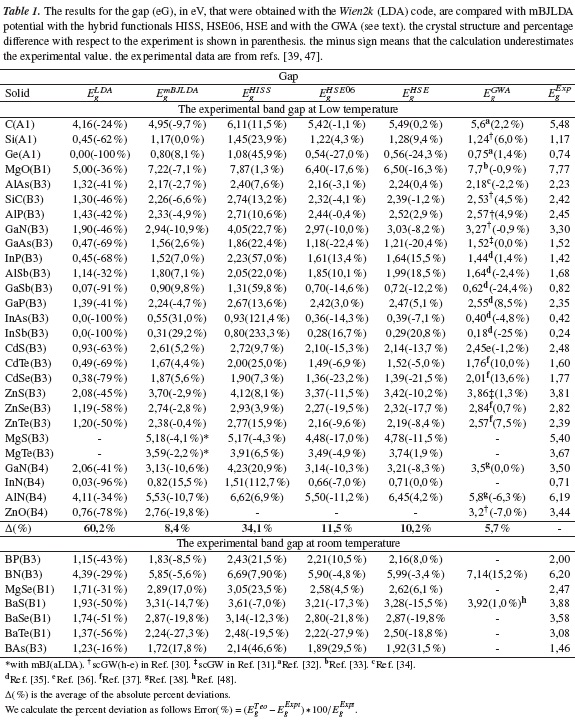
In Table 1, in the first column, the semiconductor and its crystal structure are identified. The next two columns refer to our calculation using the Wien2k code with LDA and mBJLDA potential. In this last calculation, the average of the values obtained from an LDA and a GGA optimization was used as lattice parameter, which gives the best results for the gap [20]. In the next columns, the values obtained with the hybrid functional HISS, HSE06 [27], HSE [13, 14] and GWA are reported. The column denoted as GWA includes the most precise predictions for the gap reported in the literature, using either the self consistent GW (scGWA) [31 -38] or the scGWA with attractive electron-hole interaction, scGW(e-h) [30].

The results of the predictions obtained with the GWA are the most accurate with an averaged error of 5,7 %. The mBJLDA potential produces results with an averaged error of 8,4%. Next, the errors obtained with the HSE functional result in an averaged error of 10,2%, HSE06 (11.5%) and HISS (34,1%). The GWA, the mBJLDA potential, and HSE functional have the better agreement than the ones reported by Marques et al. [26]. They get results with averaged errors 16,5%, 14,4% y 10,4% using the hybrid functional PBE0 ǫ∞, PBE0 mix and HSE06 mix, respectively. Notice that this last result compares well with the one reported by Marques et al. with the HSE functional which we consider the third best method of calculation. The performance of the GWA is highly accurate, 88% of the calculated results recorded here show less than 10% error. This is to be compared to the one obtained when using mBJLDA (74%), HSE (54%), HSE (42%), HISS (35%). On the other hand, more than a 20% deviation from experiment occurs when using mBJLDA in 7% of the cases, and with the GWA in 8% of the semiconductors studied, which is to be compared with HSE (15%), HISS (46%). All together, the best results are obtained when using the GWA; mBJLDA is next, but also HSE gives results with acceptable accuracy. A special case is the very-low-gap InSb. In this case none of the methods give less than a 20% error although it would be more reasonable to judge these results from the absolute deviation in electron-volts rather than from the percent deviation (see Table 1). It is important for the overall picture, to stress that the GWA and our calculations with the mBJLDA potential present deviations are less than 5% in 15 of the 27 semiconductors considered. When the HSE functional is considered, 12 of the 27 semiconductors present deviations are less than 5%.

Another remark. In the previous analysis only low temperature band gap data was taken into account. In Table 1, some calculations are presented, for which no experimental reports at low temperature were found. Since the calculations are done at 0 K, room temperature measurements require extrapolation either using Varshni's law or a quadratic fit or any other suitable method which, in any case, generates an extra incertitude in the obtained 0 K data. If the high temperature data is rather used, the HSE functional gives a better agreement with experiment. But the theoretical calculations are done at 0 K.

4. The Hydrostatic Pressure Effects

The mBJLDA potential performs well as compared to other methods as were just described. Now, its ability to describe the hydrostatic pressure effects need to be further explored. These effects can be quantified by calculating the pressure coefficients and the volume deformation potential, whose experimental values have been reported extensively in the literature [39, 49]. The pressure coefficient, a_p, of an interband transition (e.g., Γv → Γc, Γv → Lc,

where E_g is the band gap of an interband transition and p is the pressure. The volume deformation potential, aV , of an interband transition is:

where V is the volume. These parameters are related through the relation:

where B₀ is the bulk modulus.

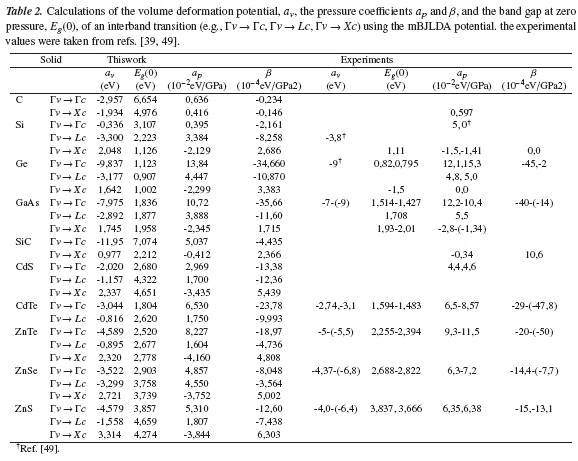
The band-gap pressure coefficients and the volume deformation potential calculated using the mBJLDA potential, are presented for a set of semiconductors. To obtain these parameters, the equilibrium structural properties of the system are first calculated, also, the minimum of the total energy, E₀, the Bulk modulus B₀, its derivative with respect to pressure, B'⁰, and the equilibrium volume at zero pressure, V₀, by fitting the calculated total energy to the Murnaghan equation of state [50]:

With these parameters, the pressure is determined using the corresponding Murnaghan equation of state:

This calculation was done using the local density approximation, LDA. These parameters cannot be obtained via the empirical mBJLDA potential [18 20]. At low pressure, E_g(p) can be fit to a quadratic function [51]:

where E_g(0) is the band gap at zero pressure, α and β are the pressure coefficients of an interband transition. They can be determined as α= ap = dE_g/dp

Análisis del rendimiento del potencial mBJLDA considerando efectos de presion and β= d²E_g/dp². The experimental values for these blende phase was maintained (see refs. [39, 49]). In parameters are known [39, 49]. Column 1 the semiconductor compounds and their respective interband transition are shown. Columns

In Table 2, the calculations of the volume defor2-5 show results of this work and in columns 6-9 mation potential, aV, the pressure coefficienst ap and the experimental values. From this Table it can be β using the mBJLDA, and experimental values for seen that, as a general trend, the calculation with the 10 semiconductors with zinc blende structure are mBJLDA potential gives values in the right order reported. The experimental values were obtained at of magnitude, as compared with the experimental room temperature and pressures for which the zinc values for all the calculated parameters. The pressure coefficient, ap, is calculated with one absolute difference from the experimental values of 0,1 - 2x10^-2 eV/GPa, for β of 0,3 - 3x10^-4 eV/GPa²( and the E_g(0) present differences between 0,02 - 0,3 eV.

The calculated volume deformation potentials, aV, are in good agreement with experiment for all but Si, ZnTe and ZnSe which are about 0,5 eV below the experimental values. The calculated values in this work correlate, in general, quite well with other theoretical reports [39, 51]. In the ref. [51], the authors used the Linear Density approximation (LDA) which deviates sometimes strongly, from the experimental values of the band gap at zero pressure [21]. It is concluded from the above work, that the mBJLDA potential performs reasonable well in describing the hydrostatic pressure effects, on the band gap of semiconductors.

5. Conclusions

The accurate calculation of the band gap of semiconductors, is a difficult task that has been the object of intense research, with the result of important progress during the last approximately ten years. As a continuation of our previous work [20] an objective judgment of the quite improved performance of the mBJLDA potential by comparing it, to other methods in the literature was intended. A group of 27 semiconductors (see Table 1) for which low temperature data was found on the band gap value were considered. The results of the GWA, the Wien2k code implemented with the mBJLDA potential, and codes using a hybrid functional, HSE, and HISS were taken into consideration. The results reported by Marques et al. [26] were found to be less accurate than the ones just mentioned. The GWA was found to give, all together the best results. The mBJLDA potential produces results slightly less accurate and HSE comes next. The two first methods give quite good results (prediction better than 5% for 15 of the 27 semiconductors studied). It is important to stress the empirical character of the mBJLDA potential, because it prevents the consistent definition of the optimization procedure, which contrasts with the sound theoretical bases of the GWA. Even with the several theoretical non-properly solved issues, the mBJLDA potential gives rise to acceptable predictions of the band gap value, as compared to experiment. An extra factor to be taken into account is the computational cost. If one would seek for precision without taking this factor into account, the GWA is the method to use. If one would prefer to sacrifice a little the precision obtained against the savings in computational cost, the mBJLDA potential seems the appropriate method. In conclusion, the state of matters with respect to the calculation of the band gap of semiconductors can be typified as follows. A quite precise method does exist, the GWA approximation. Its computational cost is higher. A relatively quicker code, the Wien2k implemented with the mBJLDA potential, gives somehow less accurate results, but quite acceptable at lower computational cost. Other methods do exist but are less accurate. Very recently, the new approximation announced in the ref [52] was implemented in the Wien2k 12.1 code implemented for public use. The new hybrid functional YS-PBE0 is "equivalent" to the HSE one, according to the authors.

Based on the conclusions just presented, the behavior of the mBJLDA potential was analyzed to describe the hydrostatic pressure effects (see Table 2). The volume deformation potential was calculated, al-so the pressure coefficients and the band gap at zero pressure for a set of semiconductors. As a general trend, the calculation in this work gives values in the right order of magnitude as compared with the experimental values. The pressure coefficient, ap, is calculated with absolute differences below to 2x10⁻² eV/GPa with experiment, which is an acceptable result. The calculated volume deformation potentials, aV, are in good agreement with the experiment; our calculation gives values with differences below 0,5 eV. These results agree, in general, quite well with other theoretical reports [39, 51]. From this analysis it was concluded that the mBJLDA potential can account for the hydrostatic pressure effects in semiconductors reasonably well.

Acknowledgments

The calculations in this work, were done on the Hybrid Cluster Supercomputer "Xiuhcoatl" at CGSTIC, Cinvestav, Mexico City. It is also acknowledged the interest of R. de Coss (Cinvestav Mérida, México) on this work. The authors acknowledge to Dr. Martínez (Idaho State University, USA) for a critic reading of the manuscript and his valuable comments.

References

[1] W. Khon and L. J. Sham, Phys. Rev., 140, A1133, 1965.         [ Links ]

[2] J. P. Perdew and Y. Wang, Phys. Rev. B, 45, 13244, 1992.         [ Links ]

[3] J. P. Perdew, S. Kurth, A. Zupan, P. Blaha, Phys. Rev. Lett., 82, 2544, 1999.         [ Links ]

[4] J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 77, 3865, 1996.         [ Links ]

[5] J. P. Perdew, S. Kurth, A. Zupan, P. Blaha, Phys. Rev. Lett., E78, 1396, 1997.         [ Links ]

[6] J. Tao, J. P. Perdew, V.N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 91, 146401, 2003.         [ Links ]

[7] J. P. Perdew, Int. J. Quantum Chem., 30, 451, 1986.         [ Links ]

[8] G. A. Baraff, M. Schluter, Phys. Rev. B, 30, 3460, 1984.         [ Links ]

[9] V. I. Anisimov, J. Zaanen, and O. K. Andersen, Phys. Rev. B, 44, 943, 1991.         [ Links ]

[10] L. Hedin, Phys. Rev., 139, A796, 1965.         [ Links ]

[11] F. Aryasetiawany and O. Gunnarssonz, Rep. Prog. Phys., 61, 237, 1998.         [ Links ]

[12] W. G. Aulbur, L. Jonsson, and J. W. Wilkins, Solid State Phys., 54, 1, 2000.         [ Links ]

[13] J. Heyd, G. E. Scuseria, and M. Ernzerhof, J. Chem. Phys., 118, 8207, 2003.         [ Links ]

[14] J. Heyd, J. E. Peralta, G.E. Scuseria, and R. L. Martin, J. Chem. Phys., 123, 174101, 2005.         [ Links ]

[15] J. Heyd, G. E. Scuseria, and M. Ernzerhof, J. Chem. Phys., 124, 219-906, 2006.         [ Links ]

[16] T. M. Henderson, A. F. Izmaylov, G. E. Scuseria and A. Savin, J. Chem. Phys., 127, 221103, 2007.         [ Links ]

[17] T. M. Henderson, A. F. Izmaylov, G. E. Scuseria and A. Savin, J. Theor. Comput. Chem., 4, 1254, 2008.         [ Links ]

[18] F. Tran and P. Blaha, Phys. Rev. Lett., 102, 226401, 2009.         [ Links ]

[19] P. Blaha, K. Schwars, G.K.H. Madsen, D. Kvasnicka, and J. Luitz, WIEN2K: Full Potential Linearized Augmented Planewaves and Local Orbital Programs for Calculating Crystal Properties, edited by K. Schwars, Vienna University of Technology, Austria, 2001.         [ Links ]

[20] J. A. Camargo-Martínez and R. Baquero, Phys. Rev. B, 86, 195106, 2012.         [ Links ]

[21] A. D. Becke, J. Chem. Phys., 98, 1372, 1993.         [ Links ]

[22] A. D. Becke, J. Chem. Phys. , 98, 5648, 1993.         [ Links ]

[23] C. S. Wang and B. M. Klein, Phys. Rev. B, 24, 3393, 1981.         [ Links ]

[24] M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 110, 5029, 1999.         [ Links ]

[25] C. Adamo and V. Barone, J. Chem. Phys. 110, 6158, 1999.         [ Links ]

[26] M. A. L. Marques, J. Vidal, M. J. T. Oliveira, L. Reining, S. Botti, Phys. Rev. B 83, 035119, 2011.         [ Links ]

[27] M. J. Lucero, T. M. Henderson, and G. E. Scuseria, J. Phys.: Condens. Matter, 24, 145504, 2003.         [ Links ]

[28] A. L. Fetter and J. D. Walecka, Quantum Theory of Many-Particle Systems. Courier Do-ver Publications, 2003.         [ Links ]

[29] P. Rinke et al., New J. Phys., 7, 126, 2005.         [ Links ]

[30] M. Shishkin, M. Marsman, and G. Kresse, Phys. Rev. Lett., 99, 246403, 2007.         [ Links ]

[31] M. Shishkin and G. Kresse, Phys. Rev. B, 75, 235102, 2007.         [ Links ]

[32] M.S. Hybertsen and S. G. Louie, Phys. Rev. B, 34, 5390, 1986.         [ Links ]

[33] U. Schonberger and F. Aryasetiawan, Phys. Rev. B, 52, 8788, 1995.         [ Links ]

[34] R. W. Godby, M. Schluter and L. J. Sham, Phys. Rev. B, 37, 10159, 1988.         [ Links ]

[35] X. Zhu and S. G. Louie, Phys. Rev. B, 43, 14142, 1991.         [ Links ]

[36] M. Rohlng, P. Kruger and J. Pollmann, Phys. Rev. Lett., 75, 3489, 1995.         [ Links ]

[37] O. Zakharov, A. Rubio, X. Blase, M. L. Cohen and S. G. Louie, Phys. Rev. B, 50, 10780, 1994.         [ Links ]

[38] A. Rubio, J. L. Corkill, M. L. Cohen, E. L. Shirley and S. G. Louie, Phys. Rev. B, 48, 11810, 1993.         [ Links ]

[39] S. Adachi, Handbook on Physical Properties of Semiconductors, Vols. I, II and III. Kluwer Academic Publishers, 2004, and references therein.         [ Links ]

[40] O. Madelung, Data in Sciene and Technology, Semiconductors Group IV Elements and II-V Compounds. Ed. Springer-Verlag, 1991.         [ Links ]

[41] O. Madelung, Semiconductors: Data Handbook CD-ROM. Ed. Springer-Verlag, 2003.         [ Links ]

[42] D. Wolverson, D. M. Bird, C. Bradford, K. A. Prior, B. C. Cavenett, Phys. Rev. B, 64, 113203, 2001.         [ Links ]

[43] K. Watanabe, M. Th. Litz, M. Korn, W. Ossau, A. Waag et al. J. Appl. Phys., 81, 451, 1997.         [ Links ]

[44] M. Feneberg, J. Daubler, K. Thonke, R. Sauer, P. Schley, R. Goldhahn, Phys. Rev. B, 77, 245207, 2008.         [ Links ]

[45] H. Morkoc, Handbook of Nitride Semiconductors and Devices, Ed. Wiley-VCH, 2008.         [ Links ]

[46] D. M. Roessler and W. C. Walker, J. Phys. Chem. Solids, 28, 1507, 1967.         [ Links ]

[47] G. Ramírez-Flores, H. Navarro-Contreras, A. Lastras-Martínez, R. C. Powell and J. E. Greene, Phys. Rev. B, 50, 8433, 1994.         [ Links ]

[48] L. Tie-Yu, C. De-Chan and H. Mei-Chun, Chinese Phys. Lett. 23, 943, 2005.         [ Links ]

[49] W. Paul, J. Appl. Phys. 32, 2082, 1961.         [ Links ]

[50] F. D. Murnaghan, Proc. Natl. Acad. Sci. USA 30, 244, 1944.         [ Links ]

[51] S-H. Wei and A. Zunger, Phys. Rev. B 60, 5404, 1999.         [ Links ]

[52] F. Tran and P. Blaha, Phys. Rev. B, 83, 235118, 2011.         [ Links ]