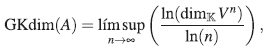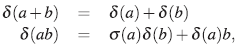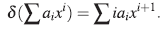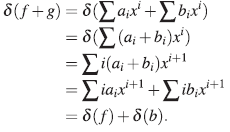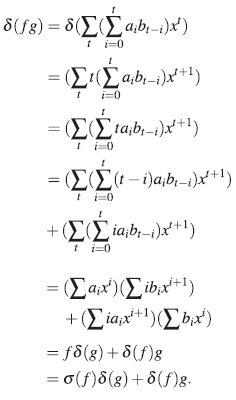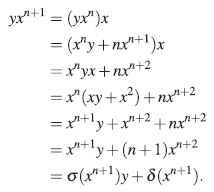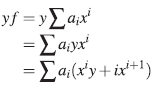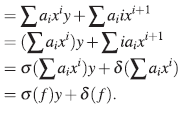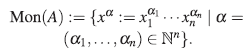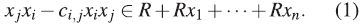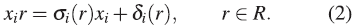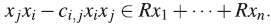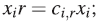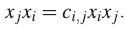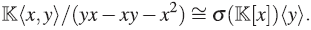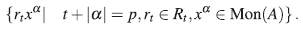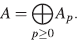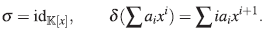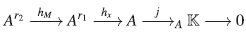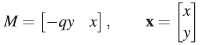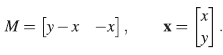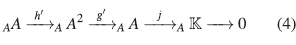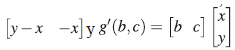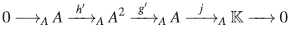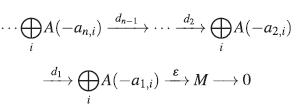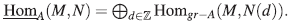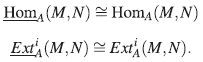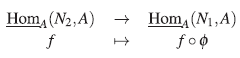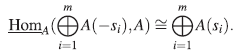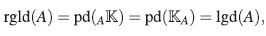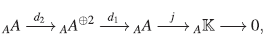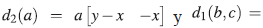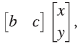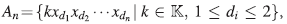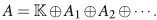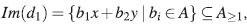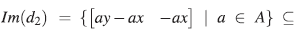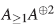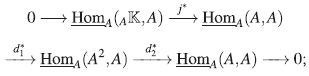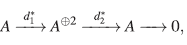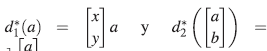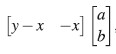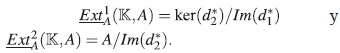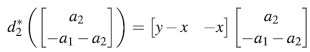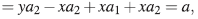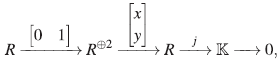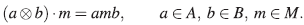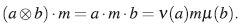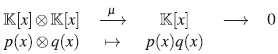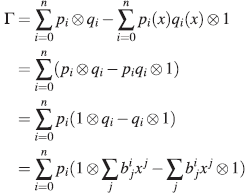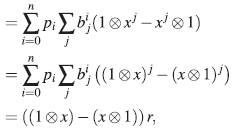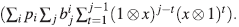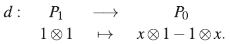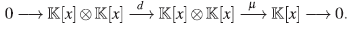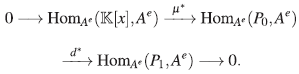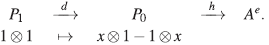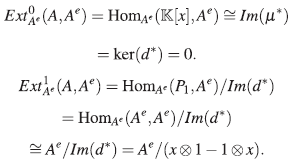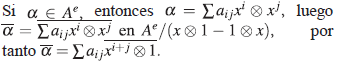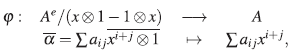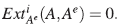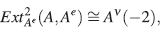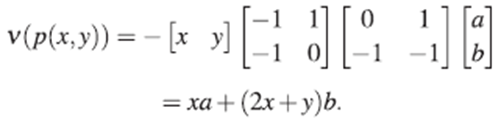1. INTRODUCCIÓN
Existen varias versiones sobre el origen del plano de Jordan: en [2] afirman que el plano de Jordan fue definido por primera vez en [10]; posteriormente en [3] afirman que la denominación de Jordan proviene de [5]; otros autores afirman que el plano de Jordan lo introdujo Korenskii en [13]. El plano de Jordan aparece en diferentes contextos en matemáticas y física y es uno de los ejemplos básicos en los orígenes de la geometría algebraica no conmutativa, siendo uno de los ejemplos básicos de anillos graduados no conmutativos de crecimiento cuadrático. En 1987 Artin y Schelter definieron las álgebras Artin-Schelter regulares (véase [4]) y afirmaron que el plano de Jordan (sin darle este nombre) es una de las dos álgebras regulares de dimensión global dos. Las álgebras Calabi-Yau fueron introducidas por Ginzburg en [7] y posteriormente hicieron una generalización de estas álgebras, denominadas álgebras Calabi-Yau torcidas. Las extensiones PBW torcidas fueron definidas por Gallego y Lezama en [6].
El plano de Jordan ha sido ampliamente estudiado, por ejemplo: es el álgebra de Nichols asociada a un espacio vectorial trenzado de dimensión 2 en la categoría de módulos de Yetter-Drinfeld con dimensión de Gelfand-Kirillov 2, se conocen sus representaciones, su homología y cohomología de Hochschild, entre otras propiedades (véase por ejemplo [1,2,3,12,18]). Esta es un álgebra de Koszul (véase [23], página 208), Artin-Schelter regular (véase [4], página 172) y es un álgebra Calabi-Yau torcida que no es Calabi-Yau (véase [17]). Aunque estos resultados son ampliamente conocidos en la literatura (véase por ejemplo [4,17,21,22,24]), el objetivo de este artículo es mostrar que el Plano de Jordan satisface tales propiedades usando el hecho que tal álgebra puede presentarse como una extensión de Ore (véase [17], página 16) y como una extensión PBW torcida (véase [25], página 185). Las álgebras de Koszul, Artin-Schelter regulares, Calabi-Yau y las extensiones PBW torcidas juegan un papel importante en estudios recientes, especialmente en geometría algebraica no conmutativa (véase por ejemplo [16,21]).
En la sección 2 se presentan algunos preliminares y se muestra que el plano de Jordan es un álgebra cuadrática, finitamente graduada y finitamente presentada. En la sección 3 se muestra que el plano de Jordan es una extensión de Ore del anillo de polinomios 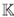 [x] y es una extensión PBW torcida graduada biyectiva y pre-conmutativa. En la sección 4 se presenta una resolución proyectiva de
[x] y es una extensión PBW torcida graduada biyectiva y pre-conmutativa. En la sección 4 se presenta una resolución proyectiva de 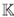 como A-módulo, donde A es el plano de Jordan y se demuestra que el plano de Jordan es un álgebra Artin-Schelter regular de dimensión global 2. Usando los resultados de las secciones anteriores, se muestra que en efecto el plano de Jordan es un álgebra Calabi-Yau torcida de dimensión 2 y se calcula su automorfismo de Nakayama.
como A-módulo, donde A es el plano de Jordan y se demuestra que el plano de Jordan es un álgebra Artin-Schelter regular de dimensión global 2. Usando los resultados de las secciones anteriores, se muestra que en efecto el plano de Jordan es un álgebra Calabi-Yau torcida de dimensión 2 y se calcula su automorfismo de Nakayama.
2. PRELIMINARES
Para lo que sigue del artículo fijaremos la siguiente notación: todos los anillos tienen identidad, 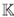 es un cuerpo, todas las álgebras son ℝ -álgebras y el símbolo ⊗indicará ⊗
es un cuerpo, todas las álgebras son ℝ -álgebras y el símbolo ⊗indicará ⊗ 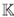 .
.
Un álgebra A es finitamente generada como álgebra si existen elementos α1,...,αη∈ A tal que el conjunto {ai1ai2…aim │1│≤ij≤n,m≥ 1} U{1} genera a A como un 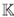 -espacio vectorial. Un álgebra ℕ es N-graduada si tiene una descomposición en
-espacio vectorial. Un álgebra ℕ es N-graduada si tiene una descomposición en 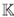 -espacios vectoriales A = ⊗n≥
0
A
n
tal que A
¡
A
j
⊆ A
¡+j
, para todo i, j ≥ 0. Se dice que A es conexa si A0 = ℝ. Un elemento x en A es homogéneo si x∈Α
n
para algún n. Un ideal izquierdo I de A es llamado homogéneo o graduado si es generado por elementos homogéneos, o equivalentemente, si I = ⊗
n≥0
(I ∩ A
n
). En el álgebra libre A =
-espacios vectoriales A = ⊗n≥
0
A
n
tal que A
¡
A
j
⊆ A
¡+j
, para todo i, j ≥ 0. Se dice que A es conexa si A0 = ℝ. Un elemento x en A es homogéneo si x∈Α
n
para algún n. Un ideal izquierdo I de A es llamado homogéneo o graduado si es generado por elementos homogéneos, o equivalentemente, si I = ⊗
n≥0
(I ∩ A
n
). En el álgebra libre A =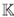 〈x1,...,x
n
〉, la longitud de una palabra xilxi2…x¡
m
es m y la longitud de 1 es 0. Notemos que A es ℕ -graduada conexa, donde Ai es el
〈x1,...,x
n
〉, la longitud de una palabra xilxi2…x¡
m
es m y la longitud de 1 es 0. Notemos que A es ℕ -graduada conexa, donde Ai es el 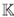 -subespacio generado por todas las palabras de longitud i. Por simplicidad en la escritura, para m≥0, la suma ⊗
n
≥
m
A
n
se notará como A>
m
.
-subespacio generado por todas las palabras de longitud i. Por simplicidad en la escritura, para m≥0, la suma ⊗
n
≥
m
A
n
se notará como A>
m
.
Dada A un álgebra ℕ -graduada conexa finitamente generada, se dice que A es finitamente presentada si existe un ideal homogéneo I generado por finitos elementos homogéneos, I=(f
1,..., f
m) tal que A ≅ 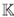 , 〈x1,…,xn〉/I. Al cociente
, 〈x1,…,xn〉/I. Al cociente 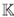 〈x
1
,...,x
n
〉/(f1,...,f
m
) se le llama una presentación de A con generadores x
1
,...,x
n
״ y relaciones f
1,…, f
m
· Las álgebras finitamente graduadas fueron definidas por Rogalski en [21], un álgebra A es finitamente graduada si A es ℕ ℕ -graduada conexa y finitamente generada como un álgebra.
〈x
1
,...,x
n
〉/(f1,...,f
m
) se le llama una presentación de A con generadores x
1
,...,x
n
״ y relaciones f
1,…, f
m
· Las álgebras finitamente graduadas fueron definidas por Rogalski en [21], un álgebra A es finitamente graduada si A es ℕ ℕ -graduada conexa y finitamente generada como un álgebra.
Sea A un álgebra ℕ -graduada. Un A-módulo M es graduado si M tiene una descomposición en 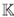 -espacios vectoriales M = ⊗
n∈ ℤ
M
n
tal que AjMi ⊆ M
¡+j
para todo ¡ ∈ ℤ,j∈ ℕ. Dado un A-módulo graduado M se define M(i), i ∈ ℤ, como el módulo graduado que es isomorfo a M como un A-módulo, el cual tiene una graduación dada por M(i)
n
- M¡
+n
. De forma análoga, dada un álgebra graduada A, se define el álgebra graduada A(i), con i ∈ ℤ. Si M y N son A-módulos, el conjunto de los A-homomorfismos de M en N se denotará como Homa(M, N). Si M y N son graduados, para un l∈ ℤ, se dice que f es un homomorfismo l-graduado si f(M
n
) ⊆ N
n+
l para todo n. Si l = 0, se dice simplemente que f es graduado.
-espacios vectoriales M = ⊗
n∈ ℤ
M
n
tal que AjMi ⊆ M
¡+j
para todo ¡ ∈ ℤ,j∈ ℕ. Dado un A-módulo graduado M se define M(i), i ∈ ℤ, como el módulo graduado que es isomorfo a M como un A-módulo, el cual tiene una graduación dada por M(i)
n
- M¡
+n
. De forma análoga, dada un álgebra graduada A, se define el álgebra graduada A(i), con i ∈ ℤ. Si M y N son A-módulos, el conjunto de los A-homomorfismos de M en N se denotará como Homa(M, N). Si M y N son graduados, para un l∈ ℤ, se dice que f es un homomorfismo l-graduado si f(M
n
) ⊆ N
n+
l para todo n. Si l = 0, se dice simplemente que f es graduado.
El plano de Jordan aparece en diferentes contextos en matemáticas y física, además de presentarse como un ejemplo básico en los inicios de la geometría algebraica no conmutativa.
Definición 1. El Plano de Jordan es el álgebra libre 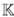 〈x,y〉, sujeta a la relación yx = xy+x
2
, es decir, A =
〈x,y〉, sujeta a la relación yx = xy+x
2
, es decir, A =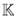 〈x, y〉/(yx - xy - x2), donde (yx - xy - x2) es el ideal bilátero de
〈x, y〉/(yx - xy - x2), donde (yx - xy - x2) es el ideal bilátero de 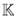 〈x,y〉 generado por el polinomio yx - xy - x
2
〈x,y〉 generado por el polinomio yx - xy - x
2
Proposición 2. El plano de Jordan A =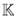 〈x,y〉 I (yx - xy - x
2
) es un álgebra finitamente graduada y finitamente presentada.
〈x,y〉 I (yx - xy - x
2
) es un álgebra finitamente graduada y finitamente presentada.
Demostración. El álgebra libre 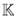 〈x,y〉 es finitamente generada como álgebra, además de ser graduada y conexa. El ideal de relaciones I = (yx - xy- χ
2
) es homogéneo de grado 2, luego el cociente -es decir, el plano de Jordan-resulta finitamente generado, graduado y conexo. Como I es finitamente generado, el álgebra A es además finitamente presentada.
〈x,y〉 es finitamente generada como álgebra, además de ser graduada y conexa. El ideal de relaciones I = (yx - xy- χ
2
) es homogéneo de grado 2, luego el cociente -es decir, el plano de Jordan-resulta finitamente generado, graduado y conexo. Como I es finitamente generado, el álgebra A es además finitamente presentada.
Definición 3. Si A es un álgebra finitamente generada, la dimensión de Gelfand-Kirillov (GK-dim) de A se define como
donde V es un 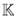 -subespacio de dimensión finita de A, que genera a A como un álgebra y 1∈v
-subespacio de dimensión finita de A, que genera a A como un álgebra y 1∈v
En [14] se encuentran las propiedades básicas de la dimensión de Gelfand-Kirillov. Una de estas propiedades es la no dependencia en la elección de V [14, Lema 1.1 y Lema 2.1].
El siguiente resultado es de gran utilidad para decidir si algunas álgebras son dominios o cumplen la condición de ser noetherianas. Recordemos que un elemento x∈A es normal si xA- Ax.
Lema 4 ([21], Lema 1.11). Sean A un álgebra finitamente graduada y x∈Ad un elemento normal homogéneo, para algún d ≥ 1.
(i) Dado x un elemento no divisor de cero en A, si A/Ax es un dominio entonces A es un dominio.
(ii) Si A/Ax es noetheriana, entonces A es noetheriana.
Un álgebra A = ⊗n≥0An es generada en grado uno si A es generada por A1. Un álgebra generada en grado uno es llamada cuadrática si el álgebra está determinada por relaciones pertenecientes a A1 ⊗A1. Por lo tanto, un álgebra cuadrática A está determinada por un espacio vectorial de generadores V = A1 y un subespacio arbitrario de relaciones cuadráticas I ⊂zA1 ⊗A1.
Proposición 5. El plano de Jordan A = 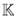 〈x,y〉/(yx-xy- x
2
) es un álgebra cuadrática.
〈x,y〉/(yx-xy- x
2
) es un álgebra cuadrática.
Demostración. Como A1 es el espacio vectorial generado por x, y, entonces A es generada en grado uno. Además, yx - xy-x 2 ∈A 1 ⊗A1 =A2, luego el plano de Jordan es un álgebra cuadrática.
3. EXTENSIONES DE ORE Y EXTENSIONES PBW TORCIDAS
En esta sección se presentan las nociones y algunas propiedades de las extensiones de Ore y de las extensiones PBW torcidas de un anillo R. Adicionalmente, se muestra que el plano de Jordan puede ser visto como una extensión de Ore y como una extensión PBW torcida del anillo de polinomios 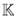 [x].
[x].
3.1 Extensiones de Ore
Se dice que A es una extensión de Ore del anillo R si se cumplen las siguientes condiciones:
(i) R es un subanillo de A.
(ii) Existe en A un elemento x tal que A es un R-módulo libre a izquierda con base {·xk}k≥0, es decir, cada elemento de A se expresa unívocamente como una suma finita Σi r i x i con r¡ ∈ R.
(iii) xr ∈Rx+R , es decir, xr = σ (r)x+ δ(r) para algunos σ (r), δ (r) ∈ R, con r∈R.
De (iii) se obtiene que σ : R → R es un endo-morfismo de anillos, mientras que δ : R → R es una σ - derivación; es decir:
En particular, σ(1) = 1γδ(1)=0. La extensión de Ore del anillo R se nota por A = R[x; σ, δ].
Proposición 6. El plano de Jordan A =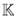 〈x,y〉/ (yx - xy - x
2
) es una extensión de Ore del anillo de polinomios
〈x,y〉/ (yx - xy - x
2
) es una extensión de Ore del anillo de polinomios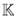 [x].
[x].
Demostración. Sean σ : 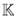 .[x] →
.[x] → 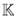 .[x], con σ = id
.[x], con σ = id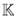 [x], y δ:
[x], y δ: 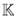 [x] →
[x] → 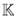 .[x], tal que
.[x], tal que
Sean f,ge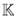 [x], entonces f = Σa
i
x
i
, y g= Σb
i
x
i
, así
[x], entonces f = Σa
i
x
i
, y g= Σb
i
x
i
, así
luego, δ es una σ-derivación.
Sea
A=
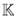 〈x,y〉/(yx-xy - x
2
), si consideramos en A el elemento yx - xy - x
2
- 0, se tiene que yx = xy + x2. Si σ, δ :
〈x,y〉/(yx-xy - x
2
), si consideramos en A el elemento yx - xy - x
2
- 0, se tiene que yx = xy + x2. Si σ, δ : 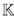 〈x,y〉 →
〈x,y〉 → 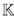 〈x,y〉son como antes, entonces σ(x) = x y δ(x) = x
2
y así yx = σ(x)y + δ(x).
〈x,y〉son como antes, entonces σ(x) = x y δ(x) = x
2
y así yx = σ(x)y + δ(x).
Sea n ∈ ℕ tal que yx n = σ(x n )y + δ(x n ), es decir yx n = x n y + /nxn+1, entonces,
Por tanto, para f = ⅀a¡xi ∈ 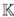 .[x], se tiene que:
.[x], se tiene que:
Por lo anterior se puede concluir que:
(i) 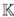 [x] →
[x] →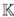 〈x,y〉/(yx - xy- x
2
).
〈x,y〉/(yx - xy- x
2
).
(ii) Existe en 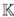 〈x,y〉/(yx - xy- x
2
) un elemento y tal que
〈x,y〉/(yx - xy- x
2
) un elemento y tal que 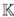 〈x,y〉/(yx - xy- x
2
) es un
〈x,y〉/(yx - xy- x
2
) es un 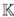 [x]
-
módulo libre a izquierda con base{yk}k≥0
[x]
-
módulo libre a izquierda con base{yk}k≥0
(iii) yr∈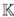 [x]y +
[x]y + 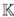 [x], es decir, yr = σ (r)y + δ (r), para algunos σ (r), σ δ (r) ∈
[x], es decir, yr = σ (r)y + δ (r), para algunos σ (r), σ δ (r) ∈ 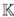 [x] con r ∈
[x] con r ∈ 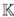 [x].
[x].
Con lo cual,
3.2 Extensiones PBW torcidas
Definición 7. Sean R y A dos anillos. Se dice
que A es una extensión PBW (Poincaré-Birkho-ff-Witt) torcida de R si cumple las siguientes condiciones:
(i) R⊆A;
(ii) Existen elementos x 1 ,...,x n ∈ A tal que A es un R-módulo libre a izquierda, con base el conjunto Mon(A) de los monomios estándar,
(iii) Para cada 1 ≤ 1 ≤ n y cada r ∈ R\{0}, existe un elemento ci,r ∈ R \ {0} tal que x ¡ r - c i,r Xi ∈ R.
(iv) Para l≤i,j≤n existe ci,j ∈R\{0} tal que
Bajo estas condiciones A se denota como A = σ (R)(x1,...,x n ). También denotaremos | α | := α 1 + α 2 + ··· + α η .
Proposición 8 ([6], Proposición 3). Sea A una extensión PBW torcida de R. Para cada 1 ≤ i ≤ n, existe un endomorfismo inyectivo σi: R→R → R y una σi־ -derivación δ i : R → R tal que
Definición 9 ([25], Definición 2.3). Sea A una extensión PBW torcida de 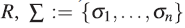 y Δ := {δ1,..., δη}, donde σ־ y δi
(1≤i≤ n) son como en la proposición anterior.
y Δ := {δ1,..., δη}, donde σ־ y δi
(1≤i≤ n) son como en la proposición anterior.
(a) A es llamada pre-conmutativa si la condición (iv) en la Definición 7 es reemplazada por: para cualesquiera 1 ≤ i, j ≤ n, existe c¡j ∈ R\{0} tal que
(b) A es llamada cuasi-conmutativa si las condiciones (iii) y (iv) en Definición 7 son reemplazadas por
(iii) para cada 1≤i≤n y todo r ∈ R\{0}, existe c i,j ∈ R\{0} tal que
(iv') para cualesquiera 1 ≤ i,j ≤ n, existe c ¡,j G R\{0} tal que
(c) A es llamada biyectiva si σ־ es biyectivo para cada σi־ ∈ Σ y ci־ j es invertible para cada 1 < י ≤ j <n.
(d) Si σ i , = id R para cada σ i e ∈י se dice que A es una extensión PBW torcida de tipo derivación.
(e) Si δί = 0 para todo δ i ∈ Δ, se dice que A es una extensión PBW torcida de tipo endomorfismo.
(f) Un elemento r de R tal que σi־(r) = = ry δi (r) = 0 para todo 1 ≤i≤n será llamado una constante. A es llamada constante si todo elemento de R es constante.
(g) A es llamada semi-conmutativa si A es cuasi-conmutativa y constante.
Estas extensiones y sus subclases han sido bastante estudiadas recientemente (véase por ejemplo [6,8,16,19,22,23,24,25]).
3.3 El plano de Jordan como una extensión PBW torcida
Proposición 10. El plano de Jordan es una extensión PBW torcida biyectiva y pre-conmutativa.
Demostración. Considérese el plano de Jordan A = (x,y)/(yx-xy - x
2
), entonces se tiene que:
(x,y)/(yx-xy - x
2
), entonces se tiene que:
(ii) Existe y ∈ A tal que A es un  [x]-módulo con base {y
n
|n ∈ ℕ }.
[x]-módulo con base {y
n
|n ∈ ℕ }.
(iii) Como en A se tiene que yx - xy - x
2
= 0, entonces yx - xy - x
2
∈ ־ [x].
[x].
Por tanto el plano de Jordan puede expresarse como una extensión PBW torcida, es decir,
Además, como yx - xy + x
2
, se debe tener que para el endomorfismo σ y la σ-derivación δ de la Proposición 8, σ(χ) - xy δ(χ) - x
2
, coincidiendo con el automorfismo σ y la σ -derivación σ del plano de Jordan como extensión de Ore del anillo  [x]. Así, se puede concluir que el plano de Jordan es una extensión PBW torcida biyectiva y pre-conmutativa.
[x]. Así, se puede concluir que el plano de Jordan es una extensión PBW torcida biyectiva y pre-conmutativa.
3.4 Extensiones PBW torcidas graduadas
Como una generalización de las extensiones de Ore iteradas graduadas, en [22] fueron definidas las extensiones PBW torcidas graduadas.
Proposición 11 ([22], Proposición 2.7). Sea R = ⊗m ≥ 0 R m un álgebra ℕ -graduada y sea A = σ (R) 〈x\,...,x n 〉 una extensión PBW torcida biyectiva de R que satisface las siguientes condiciones:
(i) σ ¡ es un homomorfismo de anillos graduados y δί : R(-l) → R es una σ ¡ - derivación para todo 1 ≤ i ≤ n, donde σ ¡ y δ i son como en la Proposición 8.
(ii) x j x i - C i,j x i x j ∈R 2 + R 1 x 1 +…+-----R 1 x n , como en (1) y c ¡,j ∈R 0.
Para p ≥ 0, sea A
p
el -espacio generado por el conjunto
-espacio generado por el conjunto
Entonces A es un álgebra ℕ-graduada con graduación
Definición 12. Sea A = σ (R)(x1,...,xn) una extensión PBW torcida biyectiva de un álgebra N-graduada R = ⊗m ≥0Rm Se dice que A es una extensión PBW torcida graduada si satisface las condiciones (i) y (ii) en la Proposición 11.
Proposición 13. El plano de Jordan es una extensión PBW torcida graduada.
Demostración. Por la Proposición 10 tenemos que el plano de Jordan  〈x,y〉/(yx-xy - x
2
) es una extensión PBW torcida biyectiva y pre-conmutativa de
〈x,y〉/(yx-xy - x
2
) es una extensión PBW torcida biyectiva y pre-conmutativa de  [x], que resulta ser un álgebra N-graduada, con la graduación usual dada por el grado de los monomios. Además, el endo-morfismo σ y la σ-derivación δ de la Proposición 8 están dados por
[x], que resulta ser un álgebra N-graduada, con la graduación usual dada por el grado de los monomios. Además, el endo-morfismo σ y la σ-derivación δ de la Proposición 8 están dados por
Luego, σ es un homomorfismo de anillos graduados y δ :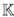 [x](-1) →
[x](-1) →  [x] es una σ-derivación. Por tanto,A=
[x] es una σ-derivación. Por tanto,A=  〈x,y〉/(yx-xy - x
2
) es una extensión PBW torcida graduada de
〈x,y〉/(yx-xy - x
2
) es una extensión PBW torcida graduada de  [x].
[x].
4. ÁLGEBRAS ARTIN-SCHELTER REGULARES VERSUS ÁLGEBRAS CALA-BI-YAU TORCIDAS
Reyes, Rogalski y Zhang en [20, Lema 1.2] demostraron que en el caso de álgebras graduadas conexas, las álgebras Calabi-Yau torcidas y las álgebras Artin-Schelter regulares coinciden.
4.1 Álgebras Artin-Schelter regulares
Las álgebras Artin-Schelter regulares son una clase de álgebras graduadas introducidas por Artin y Schelter en [4]. En tal artículo los autores clasificaron las álgebras Artin-Schelter regulares generadas en grado uno y de dimensión global menor o igual a 3.
Definición 14. Sea A = ⊗A
1
⊗A
2
⊗… un álgebra graduada finitamente presentada. El álgebra A se dice Artin-Schelter (AS) regular si satisface:
⊗A
1
⊗A
2
⊗… un álgebra graduada finitamente presentada. El álgebra A se dice Artin-Schelter (AS) regular si satisface:
(i) A tiene dimensión global finita d, es decir, todo A-módulo graduado tiene dimensión proyectiva menor o igual a d.
(ii) A tiene dimensión de Gelfand-Kirillov finita.
(iii) A es Gorenstein, es decir, 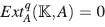
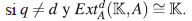
En la definición anterior se considera a  como un A-módulo, de la siguiente manera: dado α∈A, α=k
0+ α
d1
+… α
dr
con k
0 ∈
como un A-módulo, de la siguiente manera: dado α∈A, α=k
0+ α
d1
+… α
dr
con k
0 ∈  y α
di
∈ A
di Entonces para k∈
y α
di
∈ A
di Entonces para k∈ y a∈ A se define a-k:= k
o
k.
y a∈ A se define a-k:= k
o
k.
Sea A como en la definición anterior. Podemos definir el homomorfismo canónico de A-módulos j :A→y , con j(α) := k
o
para cada a a ∈ A.
, con j(α) := k
o
para cada a a ∈ A.
Proposición 15 ([4], Página 173). La sucesión de A-módulos
es exacta.
A continuación se presentan dos ejemplos de sucesiones exactas de A-módulos del cuerpo  como A-módulo, las cuales serán de utilidad para mostrar ejemplos de álgebras Artin-Schelter regulares.
como A-módulo, las cuales serán de utilidad para mostrar ejemplos de álgebras Artin-Schelter regulares.
Ejemplo 16. Considérese la  -álgebra A =
-álgebra A = 〈x,y〉 sujeta a la relación xy = qyx, con q ∈
〈x,y〉 sujeta a la relación xy = qyx, con q ∈  *, es decir, A -
*, es decir, A -  〈x,y〉/(xy - qyx) (A es conocida como el plano cuántico). Entonces r
1
=2,y r
2
= 1, con f
1
=xy- qyx.
〈x,y〉/(xy - qyx) (A es conocida como el plano cuántico). Entonces r
1
=2,y r
2
= 1, con f
1
=xy- qyx.
Sean 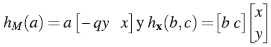 para todo a, b, c ∈ A. Por tanto
para todo a, b, c ∈ A. Por tanto
es una sucesión exacta de A-módulos proyectivos de  como A-módulo. Además dado que A/Ax≅
como A-módulo. Además dado que A/Ax≅  [y] es un dominio noetheriano, por el Lema 4 se tiene que A es un dominio noetheriano y por tanto h
M
resulta ser inyectiva, con lo cual
[y] es un dominio noetheriano, por el Lema 4 se tiene que A es un dominio noetheriano y por tanto h
M
resulta ser inyectiva, con lo cual
es una resolución proyectiva de  como A-módulo.
como A-módulo.
Ejemplo 17. Sea A =  〈x,y〉/(yx-xy - x
2
)el plano de Jordan. Entonces r1 = 2 y r
2
= 1, con f
1 = yx - xy - x2.
〈x,y〉/(yx-xy - x
2
)el plano de Jordan. Entonces r1 = 2 y r
2
= 1, con f
1 = yx - xy - x2.
Por tanto
es una sucesión exacta de A-módulos pro-yectivos de  como A-módulo, donde h'(α) = α
como A-módulo, donde h'(α) = α
Análogo al plano cuántico, A/Ax ≅ 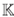 [y] es un dominio noetheriano, luego h' resulta ser inyectiva, y por tanto
[y] es un dominio noetheriano, luego h' resulta ser inyectiva, y por tanto
es una resolución proyectiva de 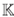 como A-módulo.
como A-módulo.
El cálculo hecho en el Ejemplo 17 es similar al realizado en [21, Ejemplo 1.25], salvo que la resolución allí obtenida es de módulos libres graduados.
Sea A un álgebra finitamente graduada y M un A-módulo graduado acotado a izquierda, es decir, M n = 0 para n«0. Sea {mi} ⊆Mun conjunto de elementos homogéneos que generan a M minimalmente como A-módulo. Entonces, existe un A-homomorfismo graduado sobreyectivo Φ י ⊗ i A(-di) → M, con di: = deg(mi־) (i.e.,mi es un elemento homogéneo de grado d¡. En tal caso φ es llamada una sobreyección minimal de un módulo libre graduado sobre M.
Una resolución libre graduada de un A-módulo M de la forma
es llamada minimal si cada d i es una sobreyección minimal en Im(d ¡ ) para todo i ≥ 1 y ε : ⊗i¿A(-α1,i) → M es una sobreyección minimal sobre M (véase [21, Página 9]).
Proposición 18. ( [21] , Lema 1.24) Una resolución libre graduada P. de M es minimal si y solo si para todo i≥1 se tiene que Im(di) ⊆ A≥1P i .
Definición 19. Sean A un álgebra finitamente graduada y M,N A-módulos Z-graduados.
• Hom gr - A (M,N) := {f : M → N|f es un A-homomorfismo graduado}.
• ExtiA(M,N) es definido tomando un resolución libre graduada de M, aplicando el funtor HomA(-,N) y calculando la i-ésima homología.
En la definición anterior Homg,._A (M, N) es un grupo abeliano; más aún, si f ∈ Homgr_A(M,N) y k ∈ 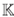 , entonces se define (k f) (m) := k · f(m), para m∈ M, con lo cual Homgr-a(M,N) resulta ser un
, entonces se define (k f) (m) := k · f(m), para m∈ M, con lo cual Homgr-a(M,N) resulta ser un 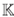 -espacio vectorial.
-espacio vectorial.
Sean S := Homgr_A(M,N) y sd:= Homgr-A (M,N(d)), para cada d ∈ ℤ, fácilmente se muestra que la colección {Sd}d∈ℤ define una graduación de S.
Observación 20 ([21], Página 10). Sean A un álgebra finitamente graduada A y M, N A-módulos Z-graduados.
(i) Existe una inclusión natural HomA (M,N) → HomA (M,N).
(ii) Si M es finitamente generado, entonces
Es importante entender la acción del funtor HomA(-,A) en funciones entre módulos libres graduados. Si N es un módulo graduado sobre el álgebra finitamente graduada A, entonces HomA(N,A) es un A-módulo izquierdo vía [α-ψ](x) =αψ(x). Dado un homomorfismo de A-módulos graduados φ : Ni → N2, entonces induce el homomorfismo de A-módulos
A continuación presentamos algunos resultados preliminares que se usan en la demostración de la Proposición 24.
Lema 21 ([21], Lema 1.28). Sea A un álgebra finitamente graduada.
(i) Para cada módulo libre graduado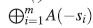 , existe un isomorfismo de A-módulos graduados canónico
, existe un isomorfismo de A-módulos graduados canónico
(ii) Sea 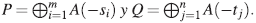 Dado un homomorfismo de A-módulos graduados Φ : Ρ →Q, representado por la multiplicación por la matriz M, entonces aplicando HomA(-,A) se obtiene un homomorfismo de módulos Φ * : HomA(Q,A) → HomA(P,A), el cual puede ser identificado canónicamente con una función de módulos graduados
Dado un homomorfismo de A-módulos graduados Φ : Ρ →Q, representado por la multiplicación por la matriz M, entonces aplicando HomA(-,A) se obtiene un homomorfismo de módulos Φ * : HomA(Q,A) → HomA(P,A), el cual puede ser identificado canónicamente con una función de módulos graduados 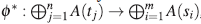 usando (i). Entonces Φ * es definido bajo la multiplicación por la misma matriz M.
usando (i). Entonces Φ * es definido bajo la multiplicación por la misma matriz M.
Proposición 22 ([21], Proposición 1.30). Sea A un álgebra finitamente graduada. Entonces
y este número es igual a la longitud de la resolución minimal libre graduada de
A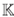 .
.
Proposición 23 ([24], Proposición 3.5). Sea a = σ (R) (x i , … ,X n ) una extensión PBW torcida graduada de un álgebra conexa R. Si R es noe-theriana con dimensión global finita graduada, entonces A tiene dimensión global finita graduada y GKdim(A) < ∞,
4.2 El plano de Jordan como un álgebra Artin-Schelter regular
En [4] fueron clasificadas las álgebras Artin-Schelter regulares de dimensión global 3 y afirman que las únicas álgebras Artin-Schelter regulares de dimensión global 2 son el plano cuántico y el plano de Jordan. En esta subsección presentamos una demostración detallada de la propiedad Artin-Schelter regular del plano de Jordan, usando el hecho que el plano de Jordan se puede expresar como una extensión PBW torcida graduada (Proposición 13).
Proposición 24. El plano de Jordan es un álgebra Artin-Schelter regular de dimensión global 2.
Demostración. Sea
A =
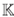 〈x,y〉/(yx-xy - x2) el plano de Jordan y consideremos la resolución de
〈x,y〉/(yx-xy - x2) el plano de Jordan y consideremos la resolución de 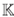 dada en (4)
dada en (4)
Nótese que:
Por la Proposición 18, se sabe que la resolución para A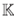 es minimal. Así, de la Proposición 22 se sigue que la dimensión global de A es 2.
es minimal. Así, de la Proposición 22 se sigue que la dimensión global de A es 2.
Aplicando el funtor Hom
A
(-,A) a la resolución minimal de 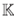 , obtenemos la sucesión
, obtenemos la sucesión
por el Lema 21 (i), esta última puede reescribirse como
En consecuencia
Veamos que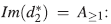 : la contenencia
: la contenencia 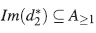 es inmediata. Sea α ∈ A≥1, entonces a puede escribirse de la forma α = x α1 +yα2, con α1,a2∈A. Sea
es inmediata. Sea α ∈ A≥1, entonces a puede escribirse de la forma α = x α1 +yα2, con α1,a2∈A. Sea 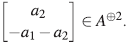 .Tenemos
.Tenemos
por 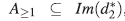 , con lo que
, con lo que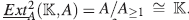 . De la Proposición 20 se tiene que
. De la Proposición 20 se tiene que 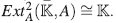
Por otra parte, note que 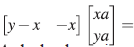
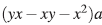 para todo a ∈ A, de donde se sigue que
para todo a ∈ A, de donde se sigue que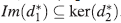 .
.
Sea [a b] ∈ ker(d*
2)> entonces ya - xa - xb= (yx - xy - x2)f para algún f∈A. Luego α = xf y b = yf, por lo cual [a b]
=
[xf yf] ∈ Im(d
*
1
). Así, Im(d
*
1
) = ker(d
*
2
) y además Ext
1
A
(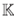 ,A) = 0.
,A) = 0.
Finalmente, Ext
0
A
(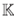 ,A) = Hom
A
(
A
,A) = Hom
A
(
A
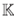 ,A) = Im(j*) =
ker(d
*
1
)
= 0.
,A) = Im(j*) =
ker(d
*
1
)
= 0.
Para concluir que el plano de Jordan es un álgebra Artin-Schelter regular, hace falta ver que tiene dimensión Gelfand-Kirillov finita. Considérese a
R = ־
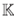 [x] ≅
[x] ≅ 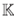 〈x,y〉 / (y), por la Proposición 15 se tiene que la sucesión de
〈x,y〉 / (y), por la Proposición 15 se tiene que la sucesión de 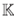 [x]-módulos proyectivos,
[x]-módulos proyectivos,
es exacta. Además, como R es un dominio se tiene una resolución proyectiva de longitud 2. Por tanto la dimensión proyectiva de 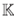 como R-mó-dulo es menor o igual a 2. Por la Proposición 22, se tiene que
como R-mó-dulo es menor o igual a 2. Por la Proposición 22, se tiene que 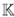 [x] tiene dimensión global finita. Dado que
A =
[x] tiene dimensión global finita. Dado que
A =
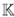 〈x,y〉/(yx - xy - x
2) es una extensión PBW torcida graduada de
〈x,y〉/(yx - xy - x
2) es una extensión PBW torcida graduada de 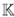 [x] donde
[x] donde 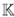 [x] tiene dimensión global finita, se sigue de la Proposición 23 que GKdim(A) < ∞. Por tanto el plano de Jordan es un álgebra Artin-Schelter regular de dimensión global 2.
[x] tiene dimensión global finita, se sigue de la Proposición 23 que GKdim(A) < ∞. Por tanto el plano de Jordan es un álgebra Artin-Schelter regular de dimensión global 2.
Notemos que el plano de Jordan tiene la misma serie de Hilbert que el anillo de en polinomios en dos variables, lo cual implica, en particular, que GKdim(A) = 2 (véase [15]).
4.3 Álgebras Calabi-Yau torcidas
Si A es un álgebra, el álgebra opuesta A° es el álgebra tal que A° = A como 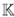 -módulo con producto a * b := ba.
-módulo con producto a * b := ba.
Un A-B-bimódulo M puede ser identificado como un A⊗ B° -módulo izquierdo, definiendo
El álgebra envolvente de A es Ae := A ⊗A°. Como A es naturalmente un A-bimódulo, entonces A es un Ae-módulo.
Sea M un A-bimódulo, ν,μ :A →A dos au-tomorfismos, el A-módulo torcido νΜμ es igual a M como un 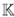 -espacio vectorial con a-m-b:= ν(α)mμ(b). Así, M es un Ae - módulo con el producto dado por
-espacio vectorial con a-m-b:= ν(α)mμ(b). Así, M es un Ae - módulo con el producto dado por
Definición 25. Una 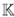 -álgebra A es llamada ν-Calabi-Yau torcida de dimensión d, para algún automorfismo ν de A y para algún entero d ≥ 0, si se cumplen las siguientes dos condiciones:
-álgebra A es llamada ν-Calabi-Yau torcida de dimensión d, para algún automorfismo ν de A y para algún entero d ≥ 0, si se cumplen las siguientes dos condiciones:
(i) A es homológicamente suave; es decir, A tiene una resolución finita de A-bimódulos pro-yectivos finitamente generados;
(ii) 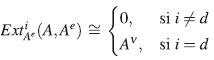 (isomorfismo de Ae - módulos).
(isomorfismo de Ae - módulos).
La condición (ii) es llamada la condición Calabi-Yau torcida. En este caso ν es llamado el automorfismo de Nakayama de A. Si el automorfismo ν es interno, es decir, v(x) = α-1χα, para algún elemento invertible a ∈ A, se dice que A es Calabi-Yau.
Ejemplo 26. A = 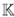 [x] es un álgebra Calabi-Yau. En efecto: una base como espacio vectorial de A
e
= A⊗A° =A⊗A es el conjunto {x
i
⊗>x
j
| i,j ≥ 0}· Consideremos la siguiente sucesión
[x] es un álgebra Calabi-Yau. En efecto: una base como espacio vectorial de A
e
= A⊗A° =A⊗A es el conjunto {x
i
⊗>x
j
| i,j ≥ 0}· Consideremos la siguiente sucesión
donde μ denota la multiplicación en el álgebra A. Note que esta resulta ser exacta dado que μ es un homomorfismo sobreyectivo.
Sea 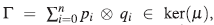 entonces
entonces 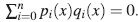 Como (1 ⊗x)
J
= 1 ⊗xj,
Como (1 ⊗x)
J
= 1 ⊗xj,
Por lo tanto, ker (μ) = (1 ⊗x-x⊗ 1) = (x⊗1-1⊗ x).
Sean 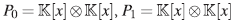 y considere el siguiente homomorfismo
y considere el siguiente homomorfismo
Se tiene entonces la sucesión exacta corta
Aplicando el funtor HomA־(-,Ae), se obtiene el complejo
Sea h ∈ ker(d*), es decir hod = 0, donde
Así, 0 = d*(h)(1⊗1)=h(d/(1⊗1)) = h(χ⊗1 - 1⊗x), luego h(x⊗ 1) = h(í ⊗ x) por tanto h = 0.
Entonces ker(d*) = {0}.
Ahora,
Por lo tanto,
es un isomorfismo de módulos y se sigue que 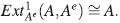
En consecuencia, el anillo de polinomios 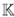 [x] es un álgebra Calabi-Yau torcida de dimensión 1, con automorfismo de Nakayama ν = id, y como este automorfismo es trivialmente un automorfismo interno, se sigue que
[x] es un álgebra Calabi-Yau torcida de dimensión 1, con automorfismo de Nakayama ν = id, y como este automorfismo es trivialmente un automorfismo interno, se sigue que 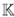 [x] es Calabi-Yau.
[x] es Calabi-Yau.
4.4 El automorfismo de Nakayama del plano de Jordan
Como el plano de Jordan es una álgebra finitamente graduada (Proposición 2) y Artin-Shelter regular (Proposición 24), es inmediato que esta resulta ser también Calabi-Yau torcida ([20, Lema 1.2]). El objetivo de esta última subsección es usar lo hecho atrás para mostrar que, en efecto, el plano de Jordan es Calabi-Yau torcida de dimensión 2, y calcular efectivamente su automorfismo de Nakayama.
Teorema 27 ([17], Teorema 3.3). Sea R un álgebra y A = R[x;σ, δ] una extensión de Ore. Suponga que R es ν-Calabi-Yau torcida de dimensión d. Entonces A es Calabi-Yau torcida de dimensión d + 1 y el automorfismo de Nakayama V׳ de A satisface que V'| R = σ_1ν y ν׳(x) = ux+b con u,b ∈ R y u invertible.
Observación 28 ([17], Observación 3.4). Si en el Teorema 27 tomamos σ = id se sigue que v'(x) = x+b. Por otra parte, si δ = 0 entonces v'(x) = ux.
Observación 29 ([11], Página 338). Sea A un álgebra ℕ -graduada, generada en grado uno. Si A es Artin-Schelter regular de dimensión global 2, entonces A ≅ 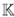 〈x1 ,...,x
n
〉/(f), donde (f) es el ideal bilátero generado por el elemento f, con f de la forma f =[x1,...,xn]M[x,…,xn]
t
M es una matriz invertible con entradas en
〈x1 ,...,x
n
〉/(f), donde (f) es el ideal bilátero generado por el elemento f, con f de la forma f =[x1,...,xn]M[x,…,xn]
t
M es una matriz invertible con entradas en 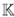 .
.
Aunque en [17] se presenta el automorfismo de Nakayama de una extensión de Ore de un álgebra Calabi-Yau torcida, en su demostración no es posible obtener una forma para calcularlo, por esta razón el Teorema 30 nos ayuda a calcular este automorfismo en el caso específico en que el álgebra sea el cociente entre un álgebra libre y el ideal bilátero generado por un polinomio.
Teorema 30 ([11], Proposición 3). Sean A = 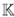 〈x1,...,x
n
〉/(f) y M como en la Observación 29. Entonces Ext
A
i
e
(A,A
e
) = 0 para i≠2, y
〈x1,...,x
n
〉/(f) y M como en la Observación 29. Entonces Ext
A
i
e
(A,A
e
) = 0 para i≠2, y
donde ν es un automorfismo definido por v(g) =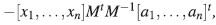 para g = α
1
x
1
+…+ a
n
x
n
.
para g = α
1
x
1
+…+ a
n
x
n
.
Nótese que si en el teorema anterior A es Ca-labi-Yau torcida de dimensión 2, entonces el automorfismo ν es el automorfismo de Nakayama de A.
Proposición 31. El plano de Jordan es un álgebra Calabi-Yau torcida, con automorfismo de Nakayama ν dado por ν(x) = x y ν(y) = 2x + y.
Demostración. Sea A =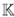 〈x,y〉/(yx - xy - x2) el plano de Jordan. Por la Proposición 6 el plano de Jordan es una extensión de Ore de
〈x,y〉/(yx - xy - x2) el plano de Jordan. Por la Proposición 6 el plano de Jordan es una extensión de Ore de 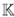 [x], con σ(x) = χ y δ(χ) = χ
2
. Como
[x], con σ(x) = χ y δ(χ) = χ
2
. Como 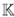 [x] es Calabi-Yau (en particular es Calabi-Yau torcida), entonces del Teorema 27 se tiene que el plano de Jordan es un álgebra Calabi-Yau torcida. Como σ = entonces por la Observación 28 se tiene que el automorfismo de Nakayama de A es de la forma v(x) =xy v(x) =x y v(y)+ p con ρ Ε
[x] es Calabi-Yau (en particular es Calabi-Yau torcida), entonces del Teorema 27 se tiene que el plano de Jordan es un álgebra Calabi-Yau torcida. Como σ = entonces por la Observación 28 se tiene que el automorfismo de Nakayama de A es de la forma v(x) =xy v(x) =x y v(y)+ p con ρ Ε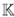 [x].
[x].
Sea f = yx - xy -x 2 , entonces f puede ser
reescrito de la forma 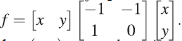 Por el Teorema 30, dado p(x,y) = ax+by∈A, se tiene que
Por el Teorema 30, dado p(x,y) = ax+by∈A, se tiene que
Como v es un automorfismo de A, necesariamente ν (k) - k, para todo k∈־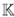 . Pero x - 1x+0y, entonces v(x) -x+(2x + y)0 = x, y al ser y = 0x+ 1y, se sigue que v(y) -x0 + (2x+y)1=2x+y.
. Pero x - 1x+0y, entonces v(x) -x+(2x + y)0 = x, y al ser y = 0x+ 1y, se sigue que v(y) -x0 + (2x+y)1=2x+y.
Notemos que el plano de Jordan no es Cala-bi-Yau, pues ν no es un automorfismo interno.
Observación 32. Si A es un álgebra Cala-bi-Yau torcida, entonces A puede ser extendida a un álgebra Calabi-Yau, es decir, si A es Cala-bi-Yau torcida con automorfismo de Nakayama σ, entonces Α[ζ;σ] es Calabi-Yau (véase [9, Teorema 1.1 y Observación 5.1]).
Ejemplo 33. Sea A el plano de Jordan con automorfismo de Nakayama ν como en la Proposición 31, entonces
es una extensión de Ore de A. Por Teorema 27, B es Calabi-Yau torcida con automorfismo de Nakayama v׳ tal que v׳(x) =xy v׳(y) =y y podemos escribir el álgebra B como Β =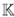 |x,z| [y; δ] donde δ(x) = x
2
. Por otro lado, en Β =A[z;v] tenemos que zy= v(y)z= (y + 2x)z=yz + 2xz, mientras que en B =
|x,z| [y; δ] donde δ(x) = x
2
. Por otro lado, en Β =A[z;v] tenemos que zy= v(y)z= (y + 2x)z=yz + 2xz, mientras que en B =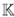 [x,z] [y;δ] vale yz = zy + δ(ζ). Así, yz -δ(ζ) = 2xz+yz y por lo tanto, δ(ζ) = -2xz. Entonces, yz = zy-2xz = v׳(z)y + δ(ζ), es decir, v'(z) = z. Por lo tanto v׳ = i
B
es un automorfismo interno y B resulta ser Calabi-Yau.
[x,z] [y;δ] vale yz = zy + δ(ζ). Así, yz -δ(ζ) = 2xz+yz y por lo tanto, δ(ζ) = -2xz. Entonces, yz = zy-2xz = v׳(z)y + δ(ζ), es decir, v'(z) = z. Por lo tanto v׳ = i
B
es un automorfismo interno y B resulta ser Calabi-Yau.