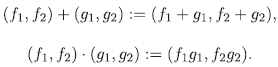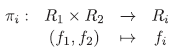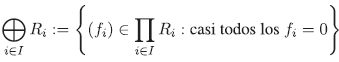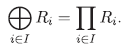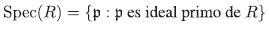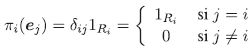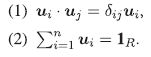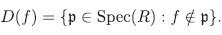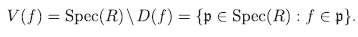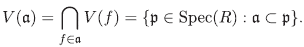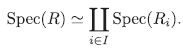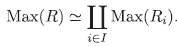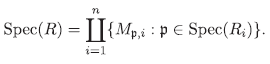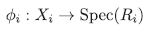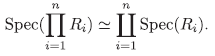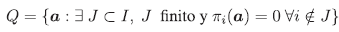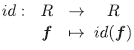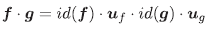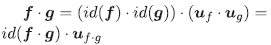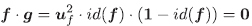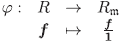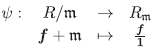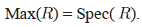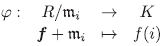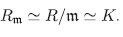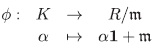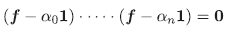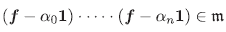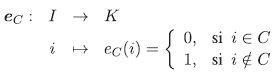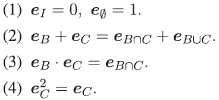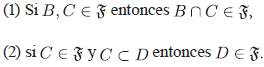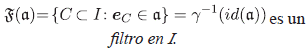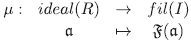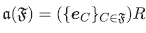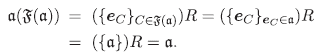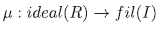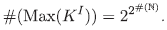Spanish (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
1. INTRODUCCIÓN
Sean R¡ y R 2 anillos conmutativos con unidades e1 y e2 respectivamente. El producto cartesiano R1 χ R2 tiene estructura de anillo con las operaciones suma y producto componente a componente:
Además, R1 XR2 es un anillo conmutativo con unidad e = (e1, e2). Todo producto cartesiano, R1 xR2 tiene asociado sus proyecciones
con i = 1, 2.
Por otra parte, el producto cartesiano X1 x X2 de los conjuntos X1 y X2 satisface la propiedad universal: para todo conjunto Z y para todas las aplicaciones φι : Ζ → X 1 y φ 2 : Ζ → X2, existe una única aplicación φ : Ζ → Χ 1 x Χ 2 tal que φ 1 = π1 ο φ, φ 2 = π2 o π. El producto cartesiano R1 χ R2 de los anillos R1 y R2 satisface la propiedad universal análoga en la categoría de anillos conmutativos. Por tanto, el producto cartesiano de anillos conmutativos es también producto en el sentido de categorías (véase [6]).
Al igual que en conjuntos, podemos considerar el producto cartesiano de una familia de anillos: sea I un conjunto arbitrario y {R i } i ∈I una familia de anillos conmutativos con unidad, su producto cartesiano Π i ∈I Ri es un anillo conmutativo con unidad con las operaciones suma y producto componente a componente. El producto cartesiano Π i ∈I Ri satisface la propiedad universal del producto.
En la categoría de anillos conmutativos se tiene también un producto directo y una suma directa de anillos. Es decir, dada la familia de anillos {R i } i∈i , existe un anillo R = Π i ∈I Ri junto con los homomorfismos de anillos : i i : R i →R,i∈ I, tal que para todo anillo S y para todos los homomorfismos φ i : R i → S, existe un único homomorfismo φ i : R → S con φ ί = φ o i ί (véase [1,2,6]).
La suma directa de la familia anterior es el conjunto
donde por "casi todos" queremos decir "todos, excepto un número finito". La suma directa así definida no posee unidad, de tal forma que esta suma no pertenece a la categoría de anillos conmutativos con unidad. En cambio, si se considera el producto tensorial de anillos (vistos como álgebras sobre el anillo de los enteros), entonces este producto tensorial si es el coproducto (también llamado suma directa) en el sentido categórico además las inyecciones canónicas son homomorfismos en la categoría de anillos conmutativos con unidad.
Observe que si el conjunto de índices I es finito, entonces
El producto de anillos es un tema de investigación en la actualidad en el área de álgebra conmutativa (véase [9,10,15,19]). Nuestro interés en este tema se basa en un problema abierto de geometría proyectiva, el cual consiste en caracterizar la recta proyectiva sobre anillos, en particular sobre anillos totales de fracciones. El producto de anillos conmutativos es un anillo total de fracciones (véase [10]). Para alcanzar este fin, en [11] hemos estudiado las K-álgebras finitas conmutativas con unidad, pues ellas también son anillos totales de fracciones.
Las rectas proyectivas sobre las R-álgebras bidimensionales 
generan las tres geometrías clásicas del plano, Moebius, Laguerre y Minkowski (véase [12]). Existen trabajos recientes sobre las rectas proyectivas sobre anillos, pero en general es una teoría muy incompleta. [13] es un trabajo sobre la geometría correspondiente a la R-álgebra tridimensional 
y [10] es un estudio inicial de las rectas proyectivas sobre anillos totales de fracciones, sin embargo estudiar la geometría de la recta proyectiva sobre anillos es un problema abierto.
Dado un anillo conmutativo con unidad R, podemos asociar a R un espacio topológico
llamado el espectro primo de R. El espectro primo de un anillo conmutativo relaciona dos áreas de la matemática, el álgebra conmutativa y la topología.
En la sección dos se describe el conjunto de ideales primos y maximales de un producto de anillos, en particular, se muestra que en el caso de productos finitos el espectro de un producto es el producto de los espectros en el sentido topológico. En la tercera sección se estudia el caso particular del producto directo de cuerpos donde usamos el anillo de fracciones por un ideal maximal m, Rm. Mostramos que si Π i ∈I Ri donde Ri es cuerpo, entonces los cuerpos R/m y Rm, m ∈ Max(R), son isomorfos. Además, si R = KI con Κ cuerpo e I finito, entonces los cuerpos R/my Rm,, m ∈ Max(R), son isomorfos a Κ. De igual forma se tiene este isomorfismo si R = K1 con Κ un cuerpo finito e I un conjunto arbitrario. En la sección cuatro se alcanza el objetivo principal del artículo, el cual consiste en hacer una estimación del cardinal del espectro maximal de un producto infinito de cuerpos para esto se estudian los filtros y ultrafiltros asociados al espectro.
2. PRELIMINARES
Sean I un conjunto arbitrario y {Ri}i∈I una familia de anillos conmutativos con unidad. Consideremos el anillo producto Π i ∈I Ri con las operaciones suma y producto componente a componente. Decimos que f ∈ R es idempotente si f2 = f. Sea Πi : R →Ri la proyección i-ésima, es decir para f = (f (i))i∈I ∈ R, Πi.( f) = f (i)
Proposición 2.1 Sean R= Π i ∈I Ri y f ∈ R Entonces
(1) f es inversible si y solo si, para todo i ∈ I, Πi(f) = f(i) es inversible.
(2) f es divisor de cero si y solo si existe i ∈ I tal que Πi (f) = f(i) es divisor de cero.
(3) f es idempotente si y solo si, para todo i ∈I, Πi (f) = f(i) es idempotente.
Demostración. Se sigue de las definiciones.
Corolario 2.2 Sean R= Π i ∈I Ri y f ∈R. Si para todo i ∈I, Ri es un cuerpo, entonces
(1) f es inversible si y solo si f(i) ≠ 0 para todo i ∈ I.
(2) f es divisor de cero si y solo si existe i ∈ I tal que f(i) - 0.
(3) f es idempotente si y solo si f(i) es cero o uno para todo i ∈ I.
Demostración. Consecuencia de la Proposición 2.1 ya que Ri es cuerpo para todo i ∈ I.
Para cada j∈ I definimos ej ∈ R= Π i ∈I Ri como
donde 1.Ri es la unidad en Ri y es la función delta de Kronecker. En la proposición siguiente mostramos las propiedades elementales.
Proposición 2.3 Sean R= Π i ∈I Ri y ei ∈ R con i ∈ I. Entonces
(1) e2i = ei.
(2) ei · ej = 0 para todo j ≠i.
(3) f ei = f(i) ei para todo f ∈ R.
(4) (f ־ f(i)ei) ei = 0 para todo f ∈ R.
Demostración. Son consecuencia directa de la definición de ei.
El lema siguiente muestra una equivalencia para un producto finito de anillos. En ([2], pág. 98), podrá encontrar una versión del Lema 2.4 y otras equivalencias que no trataremos en este trabajo.
Lema 2.4 Sea R un anillo con unidad 1R R- es producto de una familia finita de anillos si y solo si existen u1,...,un ∈R idempotentes tales que
El conjunto de idempotentes del lema anterior es llamado conjunto ortogonal de idempotentes (véase [2]). Para todos f,g ∈ R idempotentes se tiene que f · g es idempotente y que 1 - f es idempotente.
2.1 Espectro primo y maximal
Exponemos a continuación algunas definiciones y resultados en el lenguaje de espectros que usaremos más adelante.
Un ideal ρ de un anillo R es primo si ρ ≠ (1) y si ab ∈ p entonces a∈p o b ∈p, y un ideal m de R es maximal si m ≠ (1) y no existe ningún ideal a tal que m⊂ α⊂ (1). Esto es equivalente a decir:
p es primo si y solo si R/p es dominio entero, m es maximal si y solo si P/m es cuerpo.
Por tanto un ideal maximal es primo pero el recíproco no es cierto en general. El ideal cero es primo si y solo si R es un dominio entero. Cada elemento de R que no es unidad está contenido en un ideal maximal (véase [4,18]).
A cada anillo R se asocia un espacio topológico
Spec(R) = {p : ρ es ideal primo de R}
dotado de la topología de Zariski con base de abiertos {D(f)}f∈R, donde
El complemento de D(f) se llama variedad de f
Si α es un ideal de A, entonces
Se verifican las siguientes propiedades
(1) V(0) = Spec(R), V(R) = Φ.
(2) Si a⊂ b son ideales de R, V(α) ⊃ V(b).
(3) Si α, b son ideales de R, V(α ∩ b) = V(αb) = V(α) ∪V(b).
(4) Si {α}i∈I es una familia de ideales de R, V(∪i∈I α i.) = V Σ i∈I α i)= ∩ i∈IV(αi.).
Note que D(1) = V(0) = Spec(R) y también que el espacio Spec(R) es compacto (véase [4,8,16,21]).
En la proposición siguiente vamos a caracterizar el espectro primo y el maximal de una suma directa de anillos conmutativos con unidad.
Proposición 2.5 Sea R = Π i ∈I Ri y consideremos la proyección i-ésima Πi : R →Ri definida por Πi (f) = f(i).
(1) Si para cada p ∈ Spec(Ri) consideramos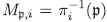 
, entonces Mp,i es un ideal primo de R dado por 
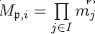con m
j
= R
j
para todo j ≠ί,ym
ί
= ρ.
(2) Si para cada m ∈ Max(R i) consideramos Mm,i = Π -1 i(m), entonces Mm,i es un ideal maximal de R dado por Mm,i = Π m j con mj = Rj para todo j ≠ι, y m i = m. j∈I
(3) Si Ρ es un ideal primo de R y existe i ∈ I tal que ei ∉ Ρ entonces ej ∈ Ρ para todo j φ i y en consecuencia ¿ es único. Además si I es finito, entonces existe i ∈ I tal que ei ∉P.
(4) Sea Ρ un ideal. Entonces, ei ∈ P si y solo si Πi(P) = R i.
(5) Si I es finito, entonces los ideales primos de Ρ son los M P,i con p ∈ Spec(Ri).
(6) Si I es finito, entonces los ideales maximales de R son los M m,i con m ∈ Max(Ri).
(7) Si I es finito, entonces
(8) Si I es finito, entonces
(9) Si I es infinito, entonces existen ideales maximales y por tanto primos de R que no son de la forma M mi .
Demostración. (1) Como Πi es un homomorfismo de anillos y p ∈ Spec(R i), entonces Πi -1 (p) =Mp,i es un ideal primo de R.
(2) Puesto que Πi es sobreyectiva y m ∈ Max(Ri), entonces Πi -1 (m) = Mm,i es un ideal maximal de R.
(3) Como ei · e
j
= 0 para todo i ≠ j, ei · ej ∈ Ρ y si existe i∈ I tal que ei ∉ P entonces ej∈ P para todo j ≠ i luego ei es único. Además, si I es finito y ei ∈ P para todo i ∈ I entonces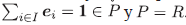 
. Por tanto existe i ∈ I tal que ei ∉ P.
(4) Sea Ρ un ideal. Si ei ∈ Ρ, entonces 1 = Πi (ei) ∈ Πi (P) y como Πi es sobreyectiva, Πi (P) es un ideal, luego Πi (P) = Ri. Recíprocamente, si Πi (P) = P¿, entonces existe α ∈ Ρ tal que Πi (α) = 1 luego Πj (ei · α) = 1 y Πi (ei · α) = 0 para todo j ≠ i por tanto ei α = ei. Como α Ε P se tiene que ei ∈ P.
(5) Si P es un ideal primo de P se tienen dos casos:
(a) existe i Ε I tal que Πi (P) ≠ Ri.
(b) Πi (P) = Ri, para todo i ∈ I.
Si se verifica (a), existe i ∈ I tal que Πi (P) ≠ Ri, entonces Ρ = Πi -1(Πi (Ρ)).
En efecto, P ⊂ Πi -1 (Πi (Ρ)) y si α ∈ Πi -1 (Πi (Ρ)) entonces Πi (α) ∈ Πi (P) luego existe b ∈ Ρ tal que Πi (α) = Πi (b) por tanto (α - b)ei = OEP.
Como ei∉P,a - b∈P y en consecuencia α ∈ Ρ ya que b∈ P.
Por el ítem (3), el caso (b) no puede darse si I es finito.
(6) Si Me s un ideal maximal de Ρ entonces Me s primo y por el ítem (5), M = MP,i con p ∈ Spec(Ri).
Si p no es maximal entonces existe m ∈ Max(Ri) tal que pera⊂ m por tanto 
(m) lo cual es absurdo pues M es maximal de R. Entonces p es maximal.
(7) Si se considera en R =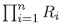
los ideales primos, MP,i. Por el ítem (2),
Para todo i se define Xi = {M p,i : ρ ∈ Spec(R i )} se considera la aplicación
definida por φ i(MP1) = Πi (MP,i) = p. Así, Φ i es inyectiva pues si ρ = q entonces M p , i = Mq,i y φί es sobreyectiva pues Πi es sobreyectiva, y Φ i es continua ya que Φ i -1 (V(p))= {Mq,i∈ Spec(R): P c q} y {M q ,i ∈ Spec(R) : p c q} = V(M p,i ), donde V(p) denota el cerrado de Zariski del ideal p. De igual forma, φ- i 1 es continua y por tanto Xi es homeomorfo a Spec(Ri). En consecuencia,
(8) La demostración es similar a la del ítem (7), solo lo cambiamos p ∈ Spec(Ri) por m ∈ Max(R i) y Spec(R) por Max(R).
(9) Sea I infinito y consideremos
es decir, ⊗ i∈I = R i Entonces Q es un ideal de R i . En efecto, sean a,b ∈ Q entonces existen J 1 ,J 2 CI finitos tales que Πi (α) - 0y Πj(b) = 0 para todos i ∉J 1 y J 2 CJ 2 respectivamente. Luego para todo i ∉ J1 U J2, Πi (α + b)= 0 y J1UJ 2 es finito. Así, α+b ∈ Q. Además, si λ∈ R, entonces Πi (λ-α) = 0 para todo i ∉ J1 y como J1 es finito, Xa∈ Q. Por otra parte, como todo ideal está contenido en un ideal maximal entonces existe un ideal maximal M y por tanto un ideal primo de R que contiene a Q y que cumple que Πi (M) = Πi (Q) = Ri para todo i ∈ I. Lo que contradice que M tiene la forma del ítem (6).
En la Proposición 2.5(9) Q no es primo, por ejemplo, sea R = A ℕ con anillo. Sean a y b divisores de cero de A tales que ab = 0. Si definimos Πi (α) = αy Πi (b) = 6 para todo i = Ι,.,.,η entonces a b = 0 ∈ Q pero a a∉ Q y b∉ Q.
Proposición 2.6 Si Ies finito, entonces los ideales primos minimales de R son los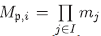 
con mj = Rj para todo j ≠i, y m
i
= p donde p ideal primo minimal de R
¡
.
Demostración. Se tiene por la Proposición 2.5(5).
3. PRODUCTO DE CUERPOS
Sean I un conjunto arbitrario y {R 1 } i∈I una familia de cuerpos. Consideremos el anillo producto de cuerpos R = Π i∈I R i
La proposición siguiente muestra que todo elemento de un producto de cuerpos es producto de un elemento idempotente y un elemento inversible. Esta propiedad también se puede probar definiendo los anillos regulares (o anillos regulares de von Neumann) ya que un cuerpo es un anillo regular y un producto de anillos regulares es anillo regular (véase [20]).
Proposición 3.1 Para todo f ∈ R, existen u f inversible y α f idempotente tal que u f - αf uf. Además, α es único y, αf - 1 si y solo si f es inversible.
Demostración. Definimos la aplicación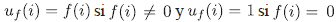 
y la aplicación 
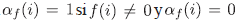si f(i) = 0Asi uf es inversible, αf es idempotente y f = uf α f. Note que uf no es único pues la construcción es válida con uf(i) ≠ 0 si f=0. Además, α f está unívocamente determinado por f. En efecto, f(i) = uf(i) αf(i) y uf(i) ≠ 0 para todo i pues uf es inversible. Luego f(i) = 0, entonces α f (i) = 0 y si f(i) ≠ 0 entonces αf{i) ≠ 0 y por tanto αf(i) = 1 ya que αf es idempotente. En particular, α.f = 1 si y solo si f es inversible.
Para cada ideal α de R definimos el conjunto de idempotentes de α como
id(α) = {f ∈ α: f es idempotente}.
En particular id(R) = {f∈R:f es idempotente}.
En la Proposición 3.1, como αf ∈ id(R) es único, se llama a α f el idempotente asociado a f y es denotado por id(f). Se define así la aplicación
y se tienen las propiedades siguientes:
Proposición 3.2 (1) Sean f,g∈:R entonces id(f g) = id(f)-id(g).
(2) Para todo ideal α se tiene que id(α) ⊂ α.
(3) Para todo f ∈ R, f∈ α si y solo si id(f) ∈ id(α).
(4) Sean α, b ideales de R. α = b si y solo si id(α) = id(b).
Demostración. (1) Por la Proposición 3.1
además el producto de idempotentes es idempotente y el de inversibles es inversible luego
donde id(f · g) = id(f) id(g) ya que el idempotente es único.
(2) Para todo f ∈ R, f = αf uf. Luego, si f∈ α entonces αf =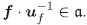
(3) Inmediato.
(4) Por el item (3).
Proposición 3.3 Sea f ∈R, f no es inversible si y solo si existe g ≠ 0 tal que f g = 0 y f + g es inversible.
Demostración. Si f no es inversible, por la Proposición 3.1, f = id(f) uf y 1-id(f) ≠ 0. Entonces se define g - uf(1 - id(f)) y de esta forma, g ≠ 0,
y f+ g = uf es inversible. Recíprocamente como f g = 0y g≠0, f es no inversible.
Proposición 3.4 Sean m ∈ Max(R) y f ∈ R. Entonces f∈ m si y solo si existe h ∉ m tal que f · h = 0.
Demostración. Si existe h ∉ m tal que f h = 0 entonces f ∈ m pues m es primo. Recíprocamente, si f ∈ m, f no es inversible y por la Proposición 3.3, existe h ≠Ο tal que f h=0 y f + h es inversible entonces h ∉ m ya que f ∈ m y f + h ∉ m.
La proposición siguiente muestra un isomorfismo entre el cuerpo R/m, m ∈ Max(R) y el anillo de fracciones o localización R m .
Proposición 3.5 Para todo m ∈ Max(R), los cuerpos R/m y Rm son canónicamente isomorfos.
Demostración. Consideremos el homomorfismo canónico
Veamos que para todo f ∈ -R, f ∈ m si y solo si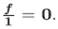 
. En efecto, si f ∈ m entonces f no es inversible y por la Proposición 3.3, existe g ≠ 0 tal que f g = 0 y f + g = 1. Por tanto g ∉ m y 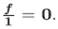. Recíprocamente, si 
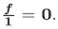, entonces existe g ∉ m tal que f g = 0. Luego f g∈ m y por tanto f ∈ m. En consecuencia, φ induce un homomorfismo inyectivo
Veamos ahora que Ψ es sobreyectivo. Es decir, si para todo f ∈ R y para todo g ∉ m existe h ∈ R tal que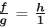 
y esto es equivalente a que existe t ∉ m tal que (f - g h) t = 0 pero por la Proposición 3.4, f
-gh∈m. Por tanto, hay que demostrar que para todo f ∈ R y para todo g ∉ m existe h ∈ R tal que f - g h ∈ m. Como g ∉ m, entonces g + m≠0 en el cuerpo R/m luego existe h + m ∈ P/m tal que (g + m) (s + m) = 1 + m y esto es equivalente a que 1 - g s ∈ m. Por tanto, f -g (f s) ∈ m.
Proposición 3.6 Si p es un ideal primo de P entonces p es maximal.
Demostración. Supongamos que p es un ideal primo contenido estrictamente en un ideal maximal m, entonces existe f ∈ mtal que f ∉ p. Como f no es inversible, por la Proposición 3.3, existe g ≠Ο tal que f g = 0 y f + g es inversible. Por tanto, f g ∈ p y como f ∉ p, g ∈ p.Pero p ⊂ m entonces f + g∈ m y f + g׳ es inversible, entonces m = R.
En consecuencia, si R es un producto de cuerpos, entonces
Es decir, el espectro de un producto de cuerpos es T1, equivalentemente, es Hausdorff. Por otra parte, se puede afirmar que R tiene dimensión de Krull cero (véase [2,4,5,7,17]).
La Proposición 3.6 también se puede demostrar utilizando herramientas de anillos con dimensión de Krull cero o anillos 0-dimensionales ya que un cuerpo es 0-dimensional y el producto de cuerpos es 0-dimensional (véase [3]). Además el resultado de la Proposición 3.6 no es cierto para el producto de anillos conmutativos, para estudiar este caso se puede ver [9].
Corolario 3.7 Sean Kun cuerpo, I un conjunto finito y R = K I . Entonces
(1) Spec(R) = Max (R) = {mi} i∈I donde mi = {f∈R:f(i) = 0},
(2) R/m i ≃ Rm i ≃ Κ para todo i.
Demostración. (1) Es inmediato ya que, por la Proposición 2.5 (6), todos los ideales maximales de R son de la forma { m i } i∈I donde m i = {f∈R: f (1) = 0}.
(2) Por la Proposición 3.5, basta mostrar que para todo m ∈ Max(P), R/m ≃ K. Pero para todo i ∈ I el homomorfismo : R → K definido por ψ(f) = f(i) es sobreyectivo y Ker(ψ) = m i entonces
es un isomorfismo.
Proposición 3.8 Sean K un cuerpo finito, I un conjunto arbitrario y R = KI . Para todo m ∈ Max(R),
Demostración. Por la Proposición 3.5, basta demostrar que R/m ≃ Κ para todo m ∈ Max(R). Sean Κ - {α0,..., αn} y consideremos la aplicación
φ es inyectiva ya que si α ∈ K y α1 ∈ m entonces α = 0 pues si α ≠ 0, por la Proposición 2.1, α1 es inversible en R. Veamos que φ es sobreyectiva. Sea f ∈ R, para todo i ∈ I, f(i) ∈ { α0,.. ., α n } y
ya que para todo i ∈ I existe j ∈ {0,1,... ,n} tal que f(i) = a¡, es decir (f - αj1)(i) = 0. Entonces
y por tanto existe j∈{1,...,n} tal que f- αj1 ∈ m. Así φ es sobreyectiva.
En la siguiente sección se muestra que el resultado anterior no es cierto si K es un cuerpo infinito, I un conjunto infinito y R = KI.
4. FILTROS Y ULTRAFILTROS DE I
Hemos visto en la Proposición 2.5(9) que existen ideales maximales de K 1 , con I arbitrario, que no son de la forma mi. Sobre estos ideales hay mucha literatura (véase [15,19]), pero aquí nos limitaremos a estimar el cardinal del conjunto que forman usando filtros y ultrafiltros.
Sean R = K I , I un conjunto arbitrario y K un cuerpo. Para todo C⊂I, definimos la aplicación
Proposición 4.1 Sean B,C ⊂I. Entonces se tiene que:
Demostración. Consecuencia directa de la definición de e C .
Veamos que existe una correspondencia biunívoca entre el conjunto de partes de I, P(I), y el conjunto de los elementos idempotentes de R, id(R).
Proposición 4.2 Sean I un conjunto arbitrario y R = K I . Entonces la aplicación
es una biyección.
Demostración. ү es inyectiva pues si e B = e C entonces e B (i) =e c (i), para todo i ∈ I. Luego e B (j) = 0 con j ∈ B si y solo si ec(j) - 0 con j ∈ C. Por tanto B = C. Además, ү es sobreyectiva pues si f ∈ id(R), f(i) - 0 o f(i) - 1, para todo
i ∈ I, entonces C = {i ∈ I : f(i) = 0} cumple que ү(C) = f.
Definición 4.3 Un filtro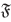 
sobre un conjunto I es una familia no vacía de subconjuntos no vacíos de I, que satisfacen:
Proposición 4.4 Si a es un ideal propio de R, entonces
Demostración. Veamos que 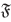(α) cumple las condiciones de filtro. Puesto que e
I
= 0 ∈ α, entonces I ∈ 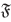(α) y por tanto 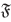(α) es no vacío. Ahora si B, C ∈ 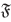(α) entonces es, eB, ec ∈ α y como a es ideal, e
B
+ ec - · e
B
= e
B
n
C
∈ α, por tanto Β ∩ C ∈ 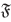(0). Por último, si C∈ 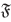(0) y C ⊂ D entonces ec-e
D
= ecu
D
= e
D
∈ α. Luego D ∈ 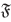(α).
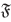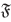Lema 4.5 Sean α y b ideales de R. Entonces R si y sólo si (α) ⊂ (b).
Demostración. Sea C ⊂ I tal que C ∈ 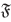(α) entonces ec ∈ α ⊂ b, luego ec ∈ b por tanto C ∈ 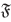(b). Recíprocamente, si ec ∈ α entonces 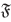C ∈ (α) C 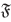(b), luego C ∈ 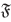(b) y por tanto ec ∈ b.
Ahora se muestra que existe una correspondencia biunívoca entre el conjunto de ideales de R, idea/ (R), y el de los filtros en I,fil(I).
Proposición 4.6 Sean R = KI con I un conjunto arbitrario. Entonces la aplicación
Demostración. Por el Lema 4.5, α = b si y solo si 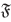(α) = 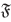(b). Por tanto, μ está bien definida y es inyectiva. Veamos que μ es sobreyectiva. Dado un filtro 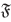de I, el ideal propio de R asociado a 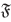es
ya que
Definición 4.7 Un ultrafiltro es un filtro maximal con respecto a la relación de contenido.
Proposición 4.8 La correspondencia
relaciona biunívocamente los ideales maximales de R con los ultrafiltros de I.
Demostración. Por la Proposición 3.6, todo ideal primo de R es maximal. Además, por el Lema 4.5 y la Proposición 4.6, μ es una aplicación biyectiva que preserva la relación de contenido, por tanto los ideales maximales de R son enviados en los ultrafiltros de I.
Lema 4.9 (1) Si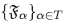 
es una familia no vacía de filtros de I, entonces 
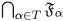es un filtro de I.
(2) Si C =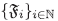 
es una cadena, es decir, 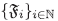es una familia no vacía de filtros de I tal que 
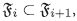entonces ∪C =
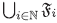es un filtro de I.
Demostración. (1) Se deduce de la Proposición 4.6 y el hecho que la intersección de ideales es un ideal.
(2) Veamos que 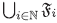cumple las condiciones de un filtro de I. 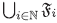≠Ф ya que 
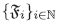es una familia no vacía. Además si B,C ∈ 
como 
existe i tal que B,C ∈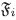 
y por tanto Β ∩ C ∈ 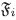, luego Β ∩ C ∈ 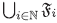Por último, si C∈ 
y C CD, existe i tal que C ∈ 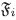y C CD, luego D ∈ 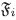y por tanto D ∈
Lema 4.10 Todo filtro puede extenderse a un ultrafiltro.
Demostración. Sea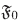 
un filtro en I. Supongamos Ρ el conjunto de todos los filtros 
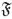en I tales que 
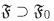y consideremos el conjunto parcialmente ordenado (P, C). Si C es una cadena en P, por el Lema 4.9(2), ∪C es un filtro y por tanto una cota superior de C en P. Por el lema de Zorn existe un elemento maximal 
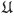en Ρ y por definición, 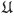es un ultrafiltro.
Proposición 4.11. [14, Theorem 7.6] Existen exactamente 2 2 # (I) ultrafiltros de I.
Ejemplo 4.12. Si I = N y K = Z/(2), por las Proposiciones 4.8 y 4.11,
Como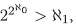 
hay una cantidad de ideales maximales de K
I
que no se pueden describir pero hay una cantidad numerable de la forma m
i
.
