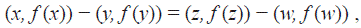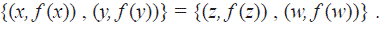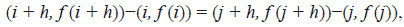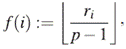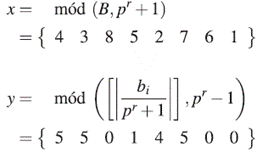Español (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Citado por Google 
Similares en
SciELO 
Similares en Google 
Permalink
1. INTRODUCCIÓN
Las secuencias sonar fueron introducidas por Golomb y Taylor [4] como ejemplos de patrones de sincronización dos dimensional de mínima ambigüedad. Una secuencia sonar m x n es un arreglo de puntos y espacios que tienen m filas y exactamente un punto en cada una de sus n columnas, sujeto a la restricción que cada par de puntos determinan vectores distintos.
El problema de estudio actualmente de las secuencias sonar es el siguiente: para m fijo encontrar el mayor n para el cual existe una secuencia sonar m x n;
Un arreglo Costas de orden n se puede considerar geométricamente como un conjunto de n puntos situados en los cuadrados de un tablero de ajedrez de tamaño n x n, tales que cada fila o columna contiene un sólo punto y los 
vectores de desplazamiento, entre cada par de puntos, son distintos.
Los arreglos Costas aparecen por primera vez en 1965 en el contexto de la detección sonar [1] cuando J. P. Costas decepcionado por los malos resultados de los sistemas sonar, los usó para describir un nuevo patrón de saltos de frecuencia [10] para los sistemas sonar con óptimas propiedades de autocorrelación. J. Costas encontró arreglos Costas hasta de orden 12 utilizando lápiz y papel, pero no pudo continuar, mucho menos pudo encontrar una técnica general de construcción de los mismos. Golomb desarrolló dos técnicas de generación de arreglos Costas, ambas basadas en la teoría de Campos Finitos, conocidos hoy en día como Método Welch y Método Golomb [11,3,2]. Además, éstas construcciones son las únicas que se conocen en la actualidad, pese a los esfuerzos de muchos investigadores.
Los arreglos Costas se han estudiado durante varios años y muchas de las preguntas básicas referentes a su construcción aún permanecen abiertas. Por ejemplo, la generación de algunos métodos produce arreglos Costas para infinitos n, pero no para todo n. La primera pregunta planteada por J. Costas, que aún sigue abierta, es la siguiente:
¿Existen arreglos Costas de orden n, para todo n?
Los dos primeros n para los cuales no se conoce nada son n = 32 y n = 33.
2. FUNCIÓN SIDON, SECUENCIAS SONAR Y ARREGLOS COSTAS.
Un conjunto de enteros positivos se llama conjunto de Sidon si las sumas de dos elementos del conjunto son todas distintas, excepto por la conmutatividad. Esta definición se puede extender a cualquier grupo aditivo, en particular podemos definir conjuntos de Sidon en dimensión dos; por ejemplo las secuencias sonar y los arreglos Costas son un tipo de conjuntos de Sidon en dimensión dos. Para dar la definición formal de éstos conceptos, vamos a definir lo que es una función Sidon. En lo que sigue, consideremos G1 y G2 dos grupos conmutativos finitos notados aditivamente, A ⊆ G 1 , B ⊆ G 2 , f : A → B, una función. Recordemos que el grafo de f es el conjunto
Definición 2.1. f : A → B, es una función Sidon si
es un conjunto de Sidon en el grupo G
1
x G2.
Definición 2.2. Una secuencia sonar de orden m x n, es una función Sidon f : A → B, donde |A| = n y |B| = m.
Debido a que las secuencias sonar tienen diversas aplicaciones, también presentamos la definición clásica de secuencia sonar [5], pero antes definimos los siguientes conceptos.
Definición 2.3. Sean n, m ∈ ℕ y f : [1, n] → [1, m] una función. Se dice que f tiene la propiedad de diferencias distintas si para todo i, j, k tales que 1 ≤ k ≤ n - 1, 1 ≤ i, j ≤ n - k, se cumple que :
Equivalentemente, se tiene el siguiente resultado, el cual no es difícil de verificar.
Proposición 2.4. f tiene la propiedad de diferencias distintas si y sólo si el grafo de f, G f : = {(x, f (x)) : x ∈ [1, n]}, es un conjunto de Sidon en el grupo aditivo ℤ x ℤ.
Demostración. (⇒) Sean x, y, z, w ∈ [1, n] tales que
esto implica que
Entonces sin pérdida de generalidad podemos considerar x-y = z-w>0, pues el caso negativo se analiza de manera similar, así tenemos que x>y, z>w, luego existen enteros positivos a, b tales que x = y + a, z = w + b, luego como x - y = z - w entonces a = b, por lo tanto reemplazando x = y + a y z = w + b en (2) tenemos
y como por hipótesis f satisface la propiedad de diferencias distintas entonces y = w y en consecuencia x = z. Así,
(⇐) Supongamos que G f es un conjunto de Sidon entonces para todo x, y, z, w ∈ [1, n], si (x, f (x)) - (y, f (y)) = (z, f (z)) - (w, f (w)) , implica que {x, y} = {z, w}. Luego si consideramos 1 < h ≤ n - 1 y 1 ≤ i, j ≤ n - h entonces i + h y j + h son elementos de [1, n], luego por la hipótesis que G f es un conjunto de Sidon, tenemos que
lo que implica que {i + h, i} = {j + h, j}. Por lo tanto, i = j o h = 0.
En consecuencia, para 1 ≤ h ≤ n - 1 y 1 ≤ i, j ≤ n - h tales que
implica que i = j y por lo tanto f satisface la propiedad de diferencias distintas.
En el caso cuando se cambia [1, m] por ℤ m se dice que la función f satisface la propiedad de diferencias distintas modulares.
Definición 2.5. Una función Sidon modular, es una función f : [1, n] - ℤ m tal que tiene la propiedad de diferencias modulares distintas; esto es, si para todo h, i, j con 1 ≤ h ≤ n - 1 y 1 ≤ i, j ≤ n - h, se cumple que:
Definición 2.6. Una secuencia sonar de orden m x n es una función f: [1, n] → [1, m] que tiene la propiedad de diferencias distintas.
Definición 2.7. Una secuencia sonar modular m x n es una función f : [1, n] → ℤ m con la propiedad de diferencias modulares distintas.
El problema principal en el caso entero de las secuencias sonar es el siguiente: dado m fijo, encontrar
S(m) = máx{n: existe una secuencia sonar m x n},
y para el caso modular el problema es determinar si existen secuencias sonar modulares m x m, para todo m entero positivo.
Definición 2.8. Un arreglo Costas de orden n, es una función Sidon biyectiva f : A → B, donde A| = B| = n.
De manera equivalente, un arreglo Costas lo podemos definir en términos de función que satisface la propiedad de diferencias distintas, así:
Definición 2.9. Un arreglo Costas de orden n es una permutación f: [1, n] → [1, n] que tiene la propiedad de diferencias distintas.
Si
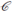(n) cuenta el número de arreglos Costas de orden n, entonces el problema principal de estudio en los enteros para el caso de los arreglos Costas es determinar si
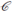(n) > 0, para todo n. El primer n para el cual no se conoce es n = 32.
2.1. Construcciones de Secuencias Sonar
Ahora vamos a describir algunas construcciones conocidas de secuencias sonar [5], consideremos p un número primo, r un entero positivo y q = p
r, sea además
el campo finito con q elementos.
Teorema 2.10 (Construcción cuadrática). Sean p un primo impar, y a, b, c enteros tales que a ï 0 (mód p). La función f: [1, p + 1] → ℤ p definida por f (i) = ai2 + bi + c es una secuencia sonar modular p x (p + 1).
Teorema 2.11 (Construcción Shift). Sean q = p
r
una potencia prima, a un elemento primitivo de
2 y ß un elemento primitivo de
. La función f: [1, q] → ℤ
p-1
definida por f (i) = log
ß
(α
iq
+ α
i
) es una secuencia sonar modular (q - 1) x q.
Teorema 2.12 (Construcción Welch Exponencial). Sean α un elemento primitivo modulo p. La función f: [0, p - 1] → ℤ p definida por f (i) = α i es una secuencia sonar modular p x (p - 1).
Teorema 2.13 (Construcción Welch Exponencial Extendida). Sean a un elemento primitivo modulo p y s un entero. La función f : [0, p - 1] → ℤ p definida por f (i) = α i+s es una secuencia sonar modular p x p.
Teorema 2.14 (Construcción Welch Logarítmica). Sea α un elemento primitivo modulo p. La función f : [1, p - 1] → ℤ p-1 definida por definida por f (i) = logα i es una secuencia sonar modular (p - 1) x (p - 1).
Teorema 2.15 (Construcción Golomb-Lempel). Sea q una potencia prima mayor que 2, y sean α, ß elementos primitivos de
. La función f: [1, q - 2] → ℤp-1
definida por definida por f (i) = j si y sólo si α
i
+ ß
i
= 1 es una secuencia sonar modular (q - 1) x (q - 2). Si α = ß esta construcción se conoce con el nombre de construcción Lempel.
En el artículo [7], se presentan nuevas construcciones de secuencias sonar que provienen del análisis de ciertas propiedades que satisfacen los conjuntos de Sidon de tipo Bose y Ruzsa.
Teorema 2.16. Sean m, b ⋲ ℕ y
= {α
1,..., α
n
} un conjunto de Sidon en el grupo aditivo ℤ
mb
. Si
mód b: = {α mód b : α ⋲
} = [1, n], entonces la función f : [1, n] → ℤ
m
definida por f (i) =
, es una secuencia sonar m × n , donde α
i
es el único elemento en
tal que α
i
≡ i mód b.
El siguiente corolario viene de la construcción tipo Bose de conjuntos de Sidon.
Corolario 2.17. Sean q una potencia prima, θ un elemento primitivo del cuerpo finito
y B(q, θ) = {log
θ
(θ + α): α ⋲
}, un conjunto de Sidon tipo Bose en el grupo aditivo ℤq2-1. La función f: [1, q] → ℤq-1
definida por
es una secuencia sonar modular (q - 1) x q, donde b. es el único elemento en B(q, θ) tal que b i = i mód (q + 1).
Corolario 2.18. Sean p un número primo, θ un elemento primitivo del cuerpo finito
y R(p, θ) = {ip - θ
i
(p - 1)/ 1 ≤ i ≤p - 1} un conjunto de Sidon tipo Ruzsa en el grupo aditivo ℤ
p2-p
. La función f : [1, p - 1] → ℤ definida por
es una secuencia sonar modular (p - 1) x (p - 1), donde r i es el único elemento en R(p, θ) tal que r i = i mód p.
Corolario 2.19. Sean p un número primo, 6 un elemento primitivo del cuerpo finito
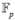y R(p, θ) = { ip - θ
i
(p - 1)/ 1 ≤ i ≤ p - 1} un conjunto de Sidon tipo Ruzsa en el grupo aditivo ℤ
p2-p
. La función f : [1, p - 1] → ℤ definida por
es una secuencia sonar modular p x (p - 1), donde r i es el único elemento en R(p, θ) tal que r. = i mód (p - 1).
Ejemplo 2.20. Sean q=9, q 2 - 1 = 80 = 10 x 8. Un conjunto de Sidon de tipo Ruzsa con 9 elementos es
Usando la función f : [1, 9] → ℤ8 , definida por f (i) = └bi/8┘, donde bi ⋲ B(9, θ), del Corolario 2.17 tenemos una secuencia sonar modular 8 × 9 dada por {(1, 0), (2, 6), (3, 5), (4, 0), (5, 5), (6, 7), (7, 3), (8, 3), (9, 4)}.
Ejemplo 2.21. Sean p = 7, p 2 - p = 42 = 6 x 7. Un conjunto de Sidon de tipo Ruzsa con 6 elementos es
Usando la función f : [1, 6] → ℤ6 , definida por f (i) = └ri/7┘, donde ri ⋲ R 1 , del Corolario 2.18 tenemos una secuencia sonar modular 6 × 6 dada por
Ejemplo 2.22. Sean p = 13, p2 - p = 156 = 13 x12. Un conjunto de Sidon de tipo Ruzsa con 12 elementos es R2 = {10, 16, 57, 59, 90, 99, 115, 134, 144, 145, 149, 152}.
Usando la función f: [1, 12] → ℤ13 , definida por f (i) = └r i /12┘, donde r i ⋲ R 2 , del Corolario 2.19 tenemos una secuencia sonar modular 13 × 12 dada por {(1, 12), (2, 12), (3, 11), (4, 8), (5, 1), (6, 12), (7, 7), (8, 9), (9, 12), (10, 4), (11, 0), (12, 4)}.
3. EJEMPLO DE UNA CONSTRUCCIÓN DE LA SECUENCIA BOSE CON AYUDA DEL SOFTWARE MATLAB
Para entender la construcción de la secuencia sonar Bose presentada a continuación, lo primero que debemos notar es un polinomio en forma vectorial. A manera de ejemplo, el polinomio P(x) = 1 + 2x2 + 3x4 será interpretado vectorialmente como [1 0 2 0 3].
Mostraremos una secuencia sonar tipo Bose para p = 2 y r = 3 por medio de los siguientes pasos:
1. Para calcular todos los polinomios primitivos del cuerpo
empleando Matlab se puede hacer con el comando Pk=gfprimfd(k,'all',p). Escogemos un polinomio primitivo sobre cada cuerpo de Galois
p2r y
pr arbitrarios. En el caso del cuerpo
los dos polinomios primitivos están conformados por las filas de la matriz:
y seleccionamos uno arbitrario, por ejemplo tomamos la segunda fila P = [1 0 1 1]. Análogamente, calculamos los polinomios primitivos en
:
y escogemos uno arbitrario, por ejemplo el de la primera fila:
Q = [1 1 0 0 0 0 1]
2. Para calcular las raíces del polinomio P sobre el cuerpo
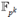se puede hacer mediante la siguiente función [potencia,raiz]=gfroots(P,k,p). El polinomio Q = [1 1 0 0 0 0 1] tendrá 2x3 raíces como se muestran en las filas de la matriz:
Posteriormente escogemos un elemento primitivo arbitrario sobre
. Por ejemplo la quinta fila, α = [1 1 0 0 " 1 0].
3. Calculamos todas las potencias de α desde k = 0, 1, 2, ... p 2r - 2, lo que nos genera un grupo cíclico de orden k = p 2r - 1 como se muestra en la Tabla 1.
4. Resolvemos la ecuación P(α
k
) = 0 sobre
p2r, donde P es el polinomio primitivo en
pr y obtenemos las siguientes potencias:
Escogemos arbitrariamente un elemento primitivo β sobre
pr. A manera de ejemplo tomamos β = α
9 = [ 1 1 1 1 0 0 ] y calculamos las potencias de β para formar el grupo cíclico < β > de orden k = 23 − 1
5. Se construye el conjunto
dado en el Teorema 2.16 como:
6. Buscamos las potencias de α en la Tabla 1 del paso 3 que coinciden con los elementos del paso 6 para construir el conjunto
B = {bi} = {49 48 8 14 38 52 6 1}
7. Se calculan los valores de x e y como en el Corolario 2.17:
y finalmente se organiza la secuencia mediante el orden de x para obtener la secuencia sonar Bose: SB
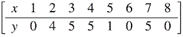
Podemos notar en el gráfico que los vectores diferencia entre cada par de puntos de la secuencia son distintos en magnitud y dirección, lo que hace que no se generen paralelogramos; propiedad que cumplen los conjuntos de Sidon en dimensión dos. Para observar esto calculamos el conjunto diferencia SB-SB = {(x1 - x2, y1 - y2) :
,y
i
) ⋲ SB, i = 1, 2} y verificamos que el tamaño del conjunto diferencia sea
. En efecto, calculamos las matrices antisimétricas X y Y de diferencias en x e y respectivamente:
y conformamos el conjunto de todas las parejas (X i ,Y i ), contando solamente una vez a la pareja (0, 0). De esta forma se generan 57 puntos como se muestran en la Figura 2
Se puede evidenciar que manteniendo los polinomios primitivos P y Q fijos y seleccionando dos elementos primitivos diferentes en los cuerpos
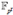y en
, la secuencia sonar Bose será la misma, por ejemplo al tomar α = [0 0 1 0 0 0 ] y β = [0 0 0 1 1 0], se obtiene la misma secuencia sonar presentada en la Figura 1. Ahora al cambiar los polinomios primitivos, podemos obtener otra secuencia sonar tipo Bose como se muestra en la Figura 3, lo cual evidencia que se puede obtener más de una secuencia sonar para cada valor de p y r.
3.1 Representación de la secuencia Sonar Bose
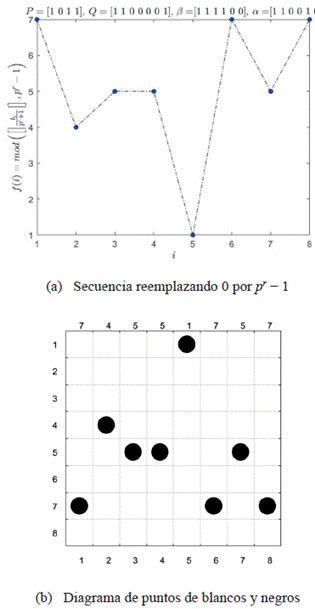
La secuencia Sonar Bose es el conjunto de puntos de la forma (i, f (i)) donde i ⋲ {1, 2, ..., pr} y f (i) es la correspondiente imagen de la secuencia en el punto i. Para efectos computacionales es conveniente cambiar el cero de la secuencia por su correspondiente valor p r - 1, esto se aplica en el cálculo de la matriz de energía y posteriormente realizar correlaciones de secuencias. En la Figura 4(a) se presenta la secuencia de la Figura 1 reemplazando el 0 por el 7 y en la Figura 4(b) se presenta el diagrama de puntos de blancos y negros como se hace en [6], la numeración inferior representa los valores de i mientras la numeración lateral izquierda representa las imágenes f (i) de la secuencia, la numeración superior representa la secuencia simplificada, la cual significa que el primer valor es f (1), el segundo f (2) y así hasta el valor f (p r ). En el diagrama de puntos de blancos y negros se puede evidenciar que no se forman paralelogramos entre los puntos, en este diagrama se puede verificar fácilmente si la secuencia es biyectiva, basta con observar si en cada fila o columna aparece un sólo punto. En el caso en que sea biyectiva se obtienen arreglos Costas. La construcción de la secuencia sonar Bose no es biyectiva pues es de orden (pr-1) x p r lo que garantiza que se va a repetir en alguna fila un punto.
De la secuencia sonar Bose de orden (pr-1) x pr se puede extraer la matriz de energía A del mismo orden, definida como A( f (i), i) = 1 y el resto de las componentes en cero. La matriz de energía de la secuencia presentada en la Figura 4(b) viene dada por:
Se considera la función de correlación de dos matrices de energía A y B como se define en [11], Ψ AB (u, v) = |{A(i, j) = B(i + u, j + v)}|, que representa el número de coincidencias de puntos de la matriz A con la matriz B trasladada por u filas y v columnas. Para el caso de la secuencia sonar se analiza la función de autocorrelación, es decir B = A que genera una superficie de autocorrelación donde la característica principal es que al sobreponer una matriz con la otra al trasladarla u filas y v columnas el número de coincidencias es a lo más uno, salvo cuando las dos matrices coinciden para cierta traslación como se puede observar en la Figura 5.
4. DISCUSIÓN
La metodología presentada en este artículo puede ser implementada para la obtención de otros tipo de secuencia sonar generadas por otras construcciones, ya que provienen de la teoría de cuerpos finitos. Del trabajo presentado se evidencia que al cambiar la elección del polinomio primitivo la secuencia sonar cambia, pero al cambiar el elemento primitivo se mantiene, esto sugiere realizar un análisis más detallado de la construcción del conjunto tipo Bose y su secuencia sonar correspondiente.
Por otra parte, los gráficos de superficie de autocorrelación permiten identificar si dada una secuencia arbitraria cumple la propiedad de ser secuencia sonar, para de esta manera obtener otros tipos de secuencias que no provienen de las secuencias conocidas. Respecto al costo computacional se pudo evidenciar que es elevado cuando p y r lo son, es interesante proponer otra metodología que permita reducir los costos computacionales.
Un problema interesante surge a partir de que la secuencia sonar tipo Bose no es biyectiva, ¿será posible conseguir un arreglo Costas de menor tamaño al eliminar un punto de la secuencia sonar tipo Bose para que sea una secuencia sonar biyectiva?, estas preguntas sugieren investigar más sobre nuevas técnicas sonar y sus propiedades.
