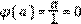1. Introducción
La construcción de los anillos de fracciones es similar a la de los números racionales a partir de los números enteros, desde el punto de vista del álgebra conmutativa esta construcción tiene mucha importancia porque relaciona dos áreas de la matemática, el álgebra y la geometría.
En 1926, H. Grell, un alumno de E. Noether, definió el anillo de fracciones de un dominio entero; su extensión a anillos noetherianos se dio en 1944 por Chevalley y en 1948, Uzkov la definió en el caso general [4]. En adelante, se entiende por anillo a un anillo conmutativo con unidad. Sean R un anillo y S un subconjunto multiplicativo de R, es decir, 1 ∈ S y si s, t ∈ S entonces st ∈ S. Se define en R x S la relación de equivalencia (f, g) ~ (u, v) ⇔ (fv - gu)s = 0 para algún s ∈ S. En el conjunto cociente RS: = (R x S)/ ~, se denota a la clase de equivalencia de (f, g) como f g y se definen las operaciones suma y producto así:
Estas operaciones están bien definidas y hacen de RS un anillo conmutativo con unidad, donde el cero es
La relación del anillo total de fracciones con otros anillos es un tema de investigación en álgebra conmutativa [2,10]. En este artículo se estudia la relación de los anillos totales de fracciones con los dominios euclídeos, los productos directos de cuerpos y las K-álgebras finitas. Se entiende por K-álgebra finita a una álgebra conmutativa con unidad y de dimensión finita como K-espacio vectorial. Además, los anillos de Hermite son de interés permanente entre los investigadores para resolver la conjetura relacionada con estos anillos [12,13,15,16,17]. Aquí se muestra que los anillos locales, las K-álgebras finitas y el producto directo de cuerpos son anillos de Hermite. Nuestro interés por estos anillos se basa en un problema abierto en geometría proyectiva, el cual consiste en caracterizar la recta proyectiva sobre anillos [6,9,11]. Más exactamente, queremos caracterizar las rectas proyectivas sobre anillos totales de fracciones y sobre anillos de Hermite. En dirección a este fin, se han estudiado las K-álgebras finitas en [7] y [6] es un estudio inicial de la recta proyectiva sobre anillos totales de fracciones.
En la sección siguiente se define el anillo total de fracciones de forma un poco distinta a la enunciada arriba, se muestra la relación de estos anillos con los dominios euclídeos y se prueba que el producto directo de anillos totales de fracciones es un anillo total de fracciones. En la tercera sección se estudian los anillos de Hermite y se muestra que los anillos locales y el producto directo de anillos de Hermite son anillos de Hermite. En consecuencia, se tiene que el producto directo de cuerpos es ejemplo tanto de anillo total de fracciones como anillo de Hermite. Finalmente, en la cuarta sección se muestra que las K-álgebras finitas son anillos totales de fracciones y también anillos de Hermite.
2. Anillo total de fracciones
Definición 2.1. Un anillo R es un anillo total de fracciones si sus elementos son invertibles o divisores de cero.
Ejemplo 2.2. Un cuerpo es un anillo total de fracciones y un dominio entero que no es un cuerpo no es anillo total de fracciones. En particular, el anillo K[x] de polinomios con coeficientes en un cuerpo K no es un anillo total de fracciones, pues x no es ni invertible ni divisor de cero en K [x].
Definición 2.3. Se dice que un anillo R es un dominio euclídeo si R es un dominio entero y existe una aplicación δ: R - [0] → ℕ tal que
1. δ(a) ≤ δ (ab) para todos a, b ∈ R - [0].
2. Si a ∈ R - [0], para cada b ∈ R existen c, r ∈ R tales que b = ac +(r) < δ(a) ó r = 0. r, δ
Ejemplo 2.4. Los siguientes son ejemplos de anillos ecuclídeos:
El anillo de números enteros ℤ con δ(n) = |n|,
El anillo K [x] de polinomios con coeficientes en el cuerpo K con δ(p(x)) = gr(p(x)).
Como todo ideal de un anillo euclídeo R es principal, entonces fR + gR = dR si f,g ∈ R y d = mcd(f, g). Luego, se tiene la identidad de Bézout.
Identidad de Bézout:
d = λf + μg donde λ, μ ∈ R.
La Proposición 2.5 relaciona el dominio euclídeo con el anillo total de fracciones y permite mostrar otros ejemplos.
Proposición 2.5. Si R es un dominio euclídeo y 0 ≠ f ∈ R, entonces R/(f) es un anillo total de fracciones.
Demostración. Sea g + (f) ∈ R/(f) y supongamos que d = mcd(f, g). Por la identidad de Bézout, existen λ, μ ∈ R tales que λf + μg = d. Por tanto,
(g + (f))(μ + (f)) = gμ + (f) = gμ + λf + (f) = d + (f).
Consideremos los dos casos siguientes:
1. Si d es invertible en R, entonces d + (f) es invertible en R/(f) y por tanto g + (f) también lo es.
2. Si d no es invertible, como d| f y d|g, existen c1, c2 ∈ R tales que f = c1d, g = c2d. Luego c1 + (f) ≠ 0 ya que f no divide a c1 pues d no es invertible. Ahora, como (g+(f))(c1 + (f)) = gc1 + (f) = c2dc1 + (f) = 0 + (f), entonces g + (f) es divisor de cero.
Por la Proposición 2.5 se tienen los ejemplos:
1. Consideremos el anillo ℤ y 0 ≠ n ∈ ℤ. Entonces el anillo ℤ/(n) es un anillo total de fracciones.
2. Sea K [x] el anillo de polinomios con coeficientes en el cuerpo K. Entonces los anillos K[x]/(f(x)), con f(x) ≠ 0, son anillos totales de fracciones, en particular, el cuerpo complejo
el anillo de los paracomplejos
y el anillo de los números duales
son anillos totales de fracciones.
Proposición 2.6. Si R es un anillo total de fracciones, entonces
es anillo total de fracciones.
Demostración. Sean
Como R es anillo total de fracciones, tenemos dos posibilidades:
1. a + bγ ∈ A es invertible si y sólo si a ∈ R es invertible. En efecto, si a ∈ R es invertible entonces existen c, d ∈ R, (c, d) ≠ (0, 0) tales que ac = 1 y bc + ad = 0, luego a es invertible en R. Recíprocamente, si a es invertible en R,
Luego a + bγ es invertible.
1. a + bγ ∈ A es divisor de cero si y sólo si a ∈ R es divisor de cero. En efecto, si a + bγ ∈ A es divisor de cero, existen c, d ∈ R, (c, d) ≠ (0,0) tales que ac = bc + ad = 0. Así, si c es divisor de cero, a es divisor de cero de R; y si c = 0 entonces ad = 0 luego a es divisor de cero. Recíprocamente, si a es divisor de cero en R, existe c ≠ 0 con ac = 0 y bc + ad = 0. En consecuencia, a + bγ ∈ A es divisor de cero.
Proposición 2.7. Sean R un anillo, S ⊂ R un subconjunto multiplicativo y
Entonces
1.
2
(i) bv ≠ 0 para todo v ∈ S,
(i) existe u ∈ S con abu = 0.
3. a ∈ Ker(φ) si y sólo si existe s ∈ S con as = 0.
Demostración. 1.
2.
3. Inmediato.
Observación 2.8. Si a es invertible en R, lo es en S-1R porque aa-1(1) = 1 ∈ S. Pero si a es divisor de cero en R no necesariamente lo es en S-1R e incluso puede ser invertible en este anillo. Por ejemplo, en R = ℤ/(6), 2 es divisor de cero en R pero si S = 1, 2, 4 entonces S es un subconjunto multiplicativo y 2 ∈ S luego 2 es invertible en S -1 R = 0,1, 2. Recíprocamente, a puede ser invertible en S -1 R sin serlo en R y si a es divisor de cero en S -1 R entonces a es divisor de cero en R.
Proposición 2.9. Sea S el subconjunto multiplicativo de los no divisores de cero de un anillo R. Consideremos el anillo
1. Σ es un anillo total de fracciones.
2. Existe un homomorfismo
tal que para todo anillo total de fracciones Δ y todo homomorfismo f: R → Δ existe un único homomorfismo f: Σ → Δ con el cual el diagrama siguiente es conmutativo:
Demostración. 1. Sea
2. Es consecuencia de la propiedad universal de los anillos de fracciones ya que todo homomorfismo unitario de anillos transforma elementos invertibles en invertibles.
El homomorfismo φ, de la Proposición 2.9, es inyectivo. En efecto, si
Definición 2.10. El anillo
Proposición 2.11. Un anillo Σ es anillo total de fracciones si y sólo si existe R, no necesariamente único, tal que Σ es el anillo total de fracciones de R.
Demostración. Si Σ es un anillo total de fracciones entonces Σ es el anillo total de fracciones de Σ. Recíprocamente, si Σ es el anillo total de fracciones de un anillo R, por la Proposición 2.9, Σ es un anillo total de fracciones. El anillo R no es único pues si Σ es el anillo total de fracciones de un anillo R ≠ Σ, se tiene que Σ también es el anillo total de fracciones de Σ.
El siguiente es otro ejemplo de anillo total de fracciones.
Ejemplo 2.12. Sean K un cuerpo y
1.
2. R es un anillo total de fracciones ya que los elementos que no están en el maximal 𝔪 son
3. Los elementos de R admiten una escritura única como
Observación 2.13. Si R es un anillo total de fracciones y a es un ideal de R, entonces
2.1. Producto directo de anillos
Consideremos el producto directo de una familia de anillos
La suma directa de la familia anterior es el conjunto
donde por "casi todos" queremos decir "todos, excepto un número finito".
Observe que si el conjunto de índices I es finito, entonces
La Proposición 2.14 caracteriza los elementos invertibles y los divisores de cero de un producto directo de anillos, ver [7]. Sea
Proposición 2.14. Sean
(1) f es invertible si y sólo si, para todo
(2) f es un divisor de cero si y sólo si existe
Demostración. Se sigue de las definiciones.
El Corolario 2.15 muestra que el producto de anillos totales de fracciones es anillo total de fracciones y, en particular, el producto directo de cuerpos es anillo total de fracciones.
Corolario 2.15. Si para todo
Demostración. Consecuencia de la Proposición 2.14 ya que Ri es anillo total de fracciones para todo
Corolario 2.16. Sean
1. f es invertible si y sólo si f(i) ≠ 0 para todo
2. f es un divisor de cero si y sólo si existe
3. R es un anillo total de fracciones.
Demostración. Las dos primeras afirmaciones se tienen por la Proposición 2.14 y la tercera por el Corolario 2.15.
Corolario 2.17. Si, para todo
Demostración. Consecuencia de la Proposición 2.14 ya que R es anillo total de fracciones.
3. Anillo de Hermite
Si M es un R-módulo libre, toda base
Definición 3.1. Sean M un R-módulo libre y
(Wi>iei )R = (Wi>iei ).
Proposición 3.2. I (a) es independiente de la base
Demostración. Sea
Además, como
Definición 3.3. Sea M un R-módulo libre de rango finito.
1. Un elemento α ϵ M se dice unimodular si I (α) = R.
2. Un elemento α ϵ M se llama complementable si existe una base de M que contiene a α.
3. Un anillo R se llama anillo de Hermite si para todo M, R-módulo libre de rango finito, cada elemento unimodular es complementable.
Observación 3.4. Sea M = R n .
1. Un vector fila (a1,..., an) ϵ Rn es unimodular si y sólo si existen λ1,..., λn ϵ R tales que λ1 a1 + … + λnan = 1.
2. Un elemento (a1,..., an) ϵ Rn es complementable si y sólo si existe una matriz λ invertible de tamaño n x n cuya primera fila es (a1,..., an).
3. Un anillo R es Hermite si y sólo si, para todo n, todo vector (a1,..., an) ϵ Rn unimodular es complementable.
En 1.976 la conjetura de los anillos de Hermite se enunciaba como (ver [13,12,17]): Si R es un anillo de Hermite, entonces R[x] es también un anillo de Hermite. Esta conjetura es equivalente a que si R es un anillo conmutativo y v = (v0(x),…,vn(x)) es una fila unimodular sobre R[x] tal que v(0) = (1,0, …,0) entonces v puede ser complementada a una matriz en GLn+1(R[x]). Mnif y Yengui en [15] presentan un algoritmo para complementar filas unimodulares sobre anillos noetherianos pero finalmente Yengui en [17] prueba la conjetura en el caso en que R tiene dimensión de Krull menor o igual a 1, y su demostración depende en gran medida de Roitman [16].
Ejemplo 3.5. Un cuerpo y el dominio ℤ son ejemplos de anillos de Hermite. Además, el anillo de polinomios K [x1,..., xn], con K cuerpo, es ejemplo de anillo de Hermite debido al Teorema de Quillen-Suslin.
Veamos un ejemplo de un anillo que no es Hermite [16].
Ejemplo 3.6 (Una fila unimodular que no es complementable). Consideremos el anillo de polinomios reales sobre la 2-esfera S2,
Entonces
Supongamos que
Considere B = (Qt)-1 entonces BQt = I 3 y
Entonces, la aplicación
es un campo vectorial analítico sobre S2 tal que nunca se anulan las tres componentes al mismo tiempo, pues es una fila de una matriz invertible y esto no es posible por la topología de S2.
En la Proposición 3.7 vemos otro ejemplo importante de anillo de Hermite.
Proposición 3.7. Sea R un anillo local, es decir, R tiene un único ideal maximal. Entonces R es anillo de Hermite.
Demostración. Sea m el ideal maximal de R. Para toda fila unimodular (a1,..., an) ∈ Rn existen x
1
,...,x
n
∈ R tales que a
1
x
1
+…+ a
n
x
n
= 1. Entonces el ideal generado por x1,...,xn cumple que (x1,..., xn)
Note que λxi = 1 si λ = (-1)i+1xi -1 . En consecuencia R es un anillo de Hermite.
Observe que un anillo local es Hermite pero no es necesariamente anillo total de fracciones. Por ejemplo, ℤ =(6) es un anillo total de fracciones y no es anillo local, de igual forma existen anillos locales que no son anillos totales de fracciones.
Proposición 3.8. Sea
Demostración. Consideremos la proyección i-ésima,
Luego la matriz M tiene determinante uno ya que
Corolario 3.9. Un producto directo de cuerpos es anillo de Hermite.
Observación 3.10. Un subanillo de un anillo de Hermite no es en general Hermite y un cociente de un anillo de Hermite tampoco es Hermite. Por ejemplo, el anillo del Ejemplo 3.6 es un dominio entero por tanto s
4. Álgebra finita sobre un cuerpo K
Considere A una K-álgebra finita, es decir, A es una álgebra conmutativa con unidad y de dimensión finita como espacio vectorial sobre un cuerpo K, su dimensión se denota por dimK A. En [7] hemos estudiado con más detalle las K-álgebras finitas. Existen, salvo isomorfismos, tres álgebras de dimensión 2 sobre
Esto es debido a que en una extensión de grado 2 de
se pueden dar tres casos según x2 + bx + c tenga dos raíces imaginarias, dos raíces reales distintas o una raíz doble. Los conjuntos
Las rectas proyectivas sobre las
Proposición 4.1. ([7], Proposición 2.2). A es una K-álgebra finita si y sólo si A es una suma directa de K-álgebras finitas locales.
Proposición 4.2. Toda K-álgebra finita es un anillo total de fracciones.
Demostración. Sean A una K-álgebra finita y dimK A = n. Para todo u ∈ A, existe r < n tal que 1, u,..., ur son linealmente independientes y ur+1 depende linealmente de 1, u,..., ur luego existen b0, b1,..., br ∈ K tales que ur+1 = brur + … + b01 y tenemos dos casos:
1. Si b0 = 0 entonces 0 = ur+1 - br ur - … -b1u = u(ur- … -b2u - b11), luego, u es divisor de cero. Note que ur - … - b2u - b11 ≠ 0 ya que 1 , u, . . . , ur son linealmente independientes.
2. Si b0 ≠ 0 entonces 1 = b0 -1u(ur - … - b2u - b11) , por tanto, u es invertible.
En consecuencia, A es un anillo total de fracciones.
El ejemplo más simple de las K-álgebras finitas es el de las K-álgebras
Ejemplo 4.3. (Un anillo total de fracciones con maximal no nilpotente)
Sea
Note que los elementos de R satisfacen que
donde
1. Si a ≠ 0 entonces
donde
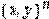 tal que
tal que
2. Si a ≠ 0 entonces
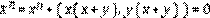 es un divisor de cero. En efecto, si a = 0 entonces existe
es un divisor de cero. En efecto, si a = 0 entonces existe
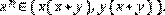 tal que
tal que
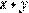
Note que R es anillo local con ideal maximal (x; y) pues está formado por las no unidades de R. Además, R no es nilpotente pues si lo fuera existiría n 2 N tal que (x; y)n y en particular existiría n 2 N tal que xn = 0. Como x = x + (x(x + y); y(x + y)) entonces xn = xn + (x(x + y); y(x + y)) = 0 esto es xn 2 (x(x + y); y(x + y)). Luego x + y divide a xn y esto es absurdo. En consecuencia, R es un anillo total de fracciones y anillo local pero no es R-álgebra finita. Además, por la Proposición 3.7, R es anillo de Hermite.
Proposición 4.4. Toda K-álgebra finita es un anillo de Hermite.
Demostración. Sea A una K-álgebra finita. Por la Proposición 4.1, existen A1,..., A r K-álgebras locales finitas tales que A = A1 x … x A r . Puesto que A 1 ,...,A r son anillos locales, por la Proposición 3.7, A 1 ,...,A r son anillos de Hermite y por la Proposición 3.8, el producto de anillos de Hermite es un anillo de Hermite. En consecuencia, A es un anillo de Hermite.
5. Conclusiones
En este artículo se han estudiado propiedades generales de anillos totales de fracciones y anillos de Hermite. Se consideran las K-álgebras finitas para probar que estas son anillos totales de fracciones y anillos de Hermite. Además, se mostró que el producto directo de cuerpos es también un anillo total de fracciones y anillo de Hermite.
La relación del anillo total de fracciones con otros anillos es un tema de investigación en la actualidad en álgebra conmutativa [2,10]. Además, resolver la conjetura de los anillos de Hermite es de interés permanente entre los investigadores [12,13,15,16,17]. Nuestro interés en estos dos anillos se basa en un problema abierto en geometría proyectiva, el cual consiste en caracterizar la recta proyectiva sobre anillos [6,9,11]. Existen trabajos recientes sobre este tema pero en general es una teoría muy incompleta. [11] es un trabajo sobre la geometría correspondiente a la
 . Más exactamente, queremos caracterizar las rectas proyectivas sobre anillos totales de fracciones y anillos de Hermite. Para alcanzar este fin, se han estudiado las K-álgebras finitas en [7] y [6] es un estudio prelimimar de la recta proyectiva sobre anillos totales de fracciones.
. Más exactamente, queremos caracterizar las rectas proyectivas sobre anillos totales de fracciones y anillos de Hermite. Para alcanzar este fin, se han estudiado las K-álgebras finitas en [7] y [6] es un estudio prelimimar de la recta proyectiva sobre anillos totales de fracciones.