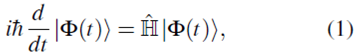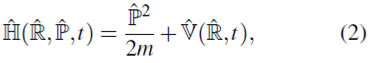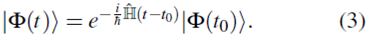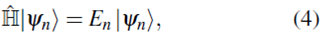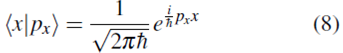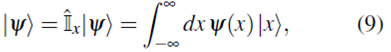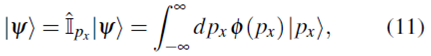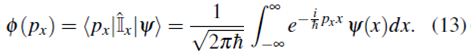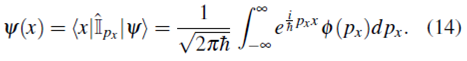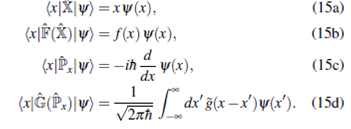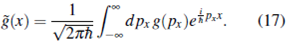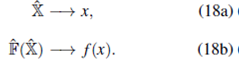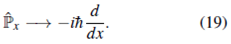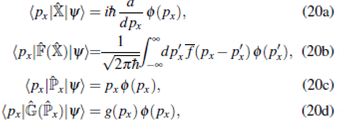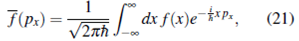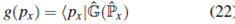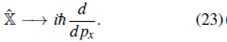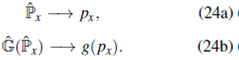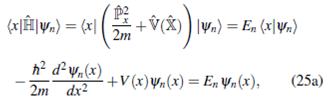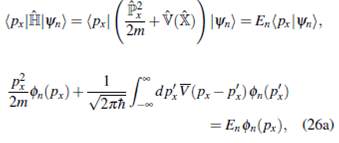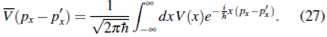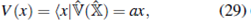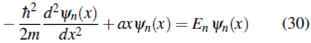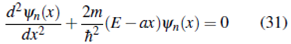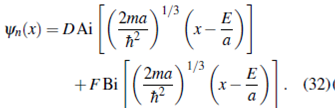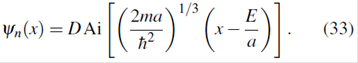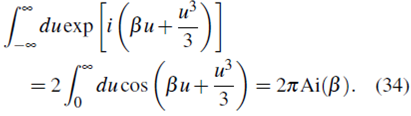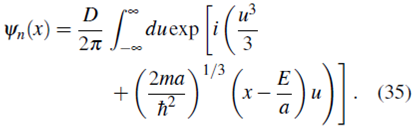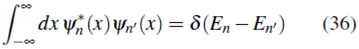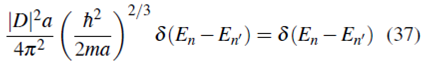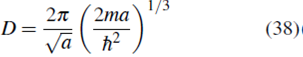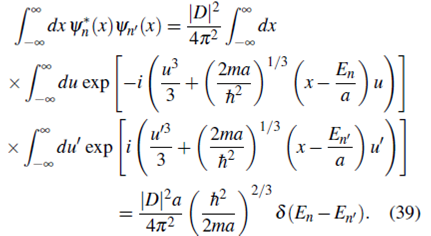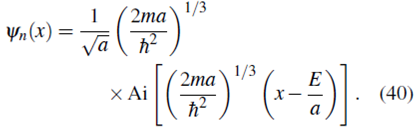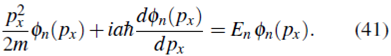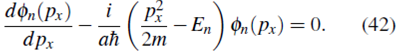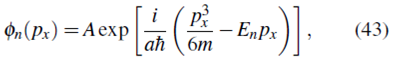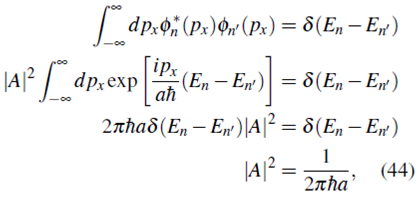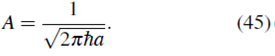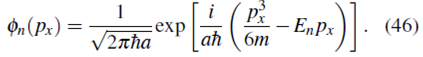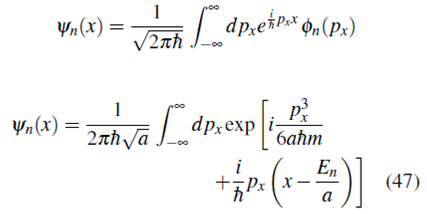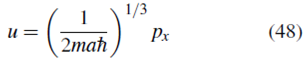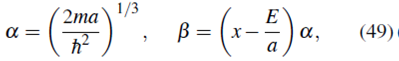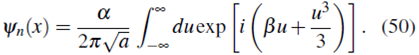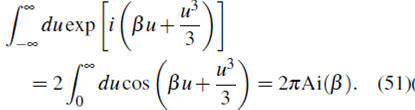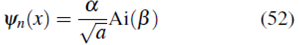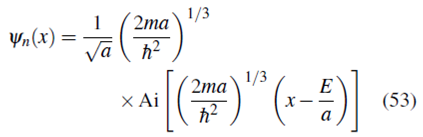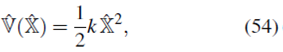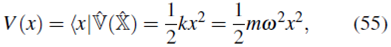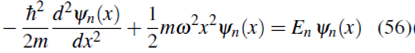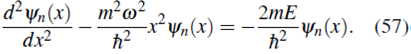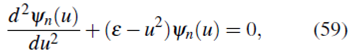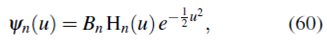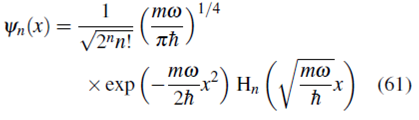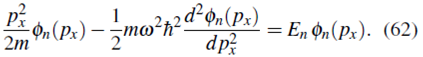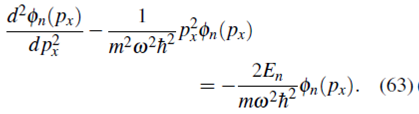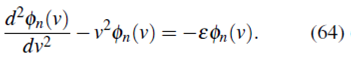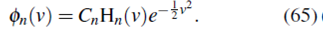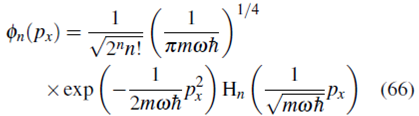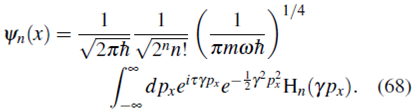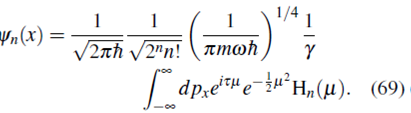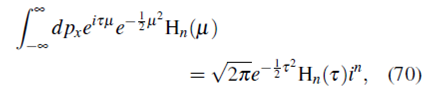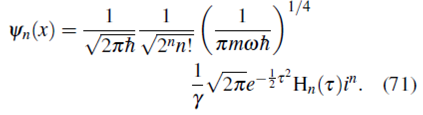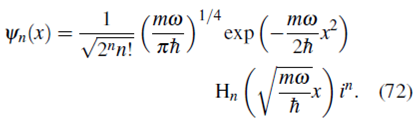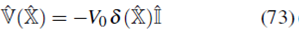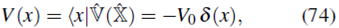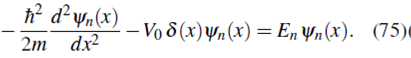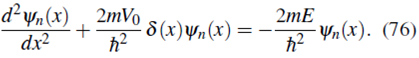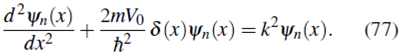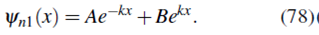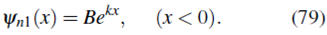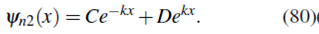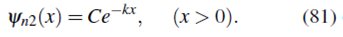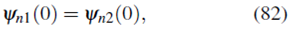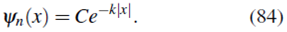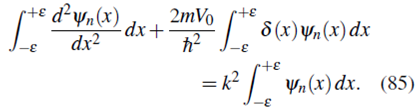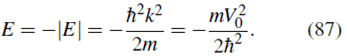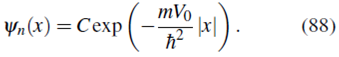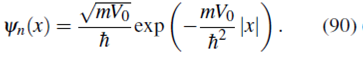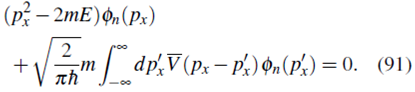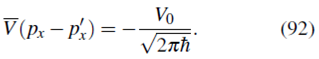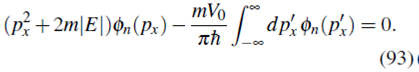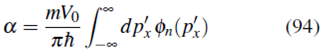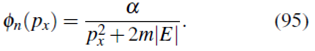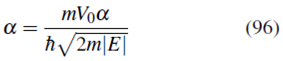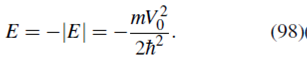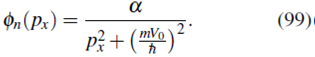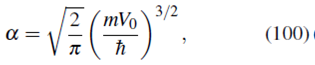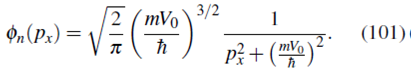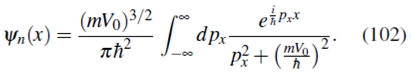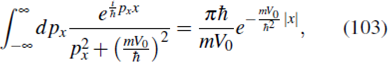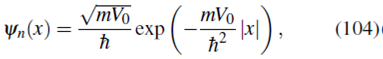Spanish (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
1 Introducción
En mecánica cuántica es posible abordar la mayoría de problemas a través de dos representaciones continuas: la representación de posición y la representación de momento. Sin embargo, es común que en los libros de textos y cursos tradicionales de mecánica cuántica 1 2 3 4 5) no se profundice en el estudio de la representación de momento lineal, suministrando únicamente una introducción formal y breve del tema. El hecho de que la ecuación de Schrödinger en la representación de momento se convierta en una ecuación integral, para la cual los estudiantes de pregrado pueden no tener las herramientas matemáticas suficientes para darle solución, en lugar de una típica ecuación diferencial como en la representación de coordenadas puede ser una de las razones por las que en los textos y cursos a nivel de pregrado se dedique mayor atención a esta última representación y se indique simplemente que la función de onda en el espacio de momento se calcula a través de la transformada de Fourier de la función en el espacio de coordenadas. Pero debe recalcarse, como lo sería la Guillaumín-Espafia et al. 6, que los operadores de posición y momento tienen roles simétricos en la teoría y por tanto, a nuestro parecer, el uso extendido de la representación de posición obedece a cuestiones pedagógicas.
Algunos autores han incursionado en la solución de problemas unidimensionales en la representación de momento. Por ejemplo, el potencial lineal, oscilador armónico, el átomo de Hidrógeno unidimensional y algunos pozos y barreras de potencial 6 7 8 9 pero en la mayoría, no se presenta una versión unificada en la que se resuleva el problema en ambas representaciones y además se verifique que tales soluciones están conectadas por la transformada de Fourier.
Comenzamos en la Sección 2 revisando las propiedades básicas de las representaciones de coordenadas y de momento, introduciendo primero la ecuación de Schrödinger en la notación de Dirac y luego definiendo las bases de posición y momento con las cuales se construyen las funciones de onda en cada representación y se establece su conexión mediante la transformada de Fourier. En la sección 3 se resuelve la ecuación de Schrödinger estacionaria en las representaciones de coordenadas y de momento, cuando el operador energía potencial es una función lineal, cuadrática (oscilador armónico) y tipo delta de Dirac. Además, verificamos que las funciones de onda obtenidas en cada representación están conectadas a través de la transformada de Fourier. Esperamos que este trabajo contribuya a que los estudiantes de pregrado en física comprendan que ambas soluciones contienen información de igual valor teórico y constituyen dos representaciones complementarias del mismo estado cuántico.
2 Teoría
En mecánica cuántica, la evolución temporal del estado de un sistema |Ф(t)) queda determinada por la ecuación de Schrödinger 1 2
donde ħ es la constante de Planck racionalizada y ˆH es el operador Hamiltoniano. A esta manera de analizar la dinámica del sistema se le conoce como imagen de Schrödinger de la mecánica cuántica.
El operador Hamiltoniano se puede construir en términos de los operadores posición ˆR y momento lineal ˆP como
donde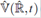 
es el operador energía potencial.
Cuando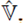 
, y por tanto 
, no depende del tiempo y el estado en el instante inicial t = to es | Ф (to)), la solución de (1) se puede escribir como
Además, el operador satisfará la ecuación de valores y estados propios
en la que n etiqueta cada valor y estado propio. La ecuación (4) es conocida con el nombre de ecuación de Schrödinger estacionaria o independiente del tiempo. Los valores propios de energía En son reales y el conjunto de estados {| y n )} constituye una base ortonormal y completa en la que expandimos | Ф (t 0 )) para encontrar | Ф (t)), solución de (1).
En este trabajo solucionamos la ecuación (4), en el caso unidimensional, considerando las dos representaciones continuas de posición y momento.
2.1 Representaciones de Posición y Momento
Si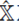 
y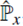 
son los operadores que representan aparatos de medida capaces de medir la posición y el momento lineal de una partícula en el eje x,
Donde x (p x ) es el valor propio de posición (momento) asociado al estado propio |x) (|p x )).
La experiencia muestra que la posición (momento) de la partícula puede ser cualquier valor real, por tanto los valores propios de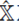
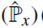forman un conjunto continuo. Así, el conjunto de estados propios {|x)} ({|p
x
)}) constituye una base continua ortonormal y completa.
donde δ(x - x') y δ (px - px) son deltas de Dirac.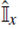 
y
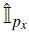son operadores identidad en cada base. Además,
2.2 Funciones de Onda
Un estado arbitrario |ψ› puede ser escrito como combinación lineal de los estados de la base de posición o de momento.
En la base de posición
donde a
se le llama función de onda, en la representación de posición, de la partícula que se encuentra en el estado |ψ›.
Similarmente, en la base de momento
donde a
se le llama función de onda, en la representación de momento lineal.
2.3 Relación entre las Funciones ψ(x) y Ф(p x )
Usando las ecuaciones (12), (7b) y (8)
Similarmente, usando (10), (7b) y (8) 1
En las cuales se nota que ψ(x) y Ф(p x ) están relacionadas a través de la transformada de Fourier.
2.4 Funciones de Operadores
Si
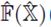y
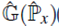son funciones de
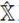
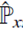, entonces en la base de posición
Donde f(x) es una función de variable real asociada a
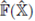
ĝ(x) es la transformada inversa de Fourier de la función de variable real g(px), asociada a
,
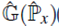De (15a) y (15b) se nota que, en la base de posición, el operador
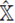se comporta como una variable real y como una función de
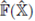esta variable
Además de (15c) se concluye que el operador
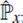actúa como un operador diferencial
En la base de momento
donde
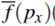es la tranformada de Fourier de f (x)
y g(px) está dada por
Ahora, a partir de (20a) se nota que, en la base de momento, el operador
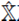actúa como un operador diferencial
El operador
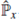se comporta como una variable real y
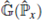como una función de dicha variable
3 Ejemplos
En esta sección, resolvemos la ecuación de Schrödinger en las representaciones de posición y de momento, es decir, encontramos las funciones de onda y los valores propios de energía en los siguientes casos.
Además, verificamos las ecuaciones (13) y (14) que permiten encontrar Ф ( p) a partir ψ(x) o visceversa.
3.1 Partícula en un Potencial Lineal
Consideremos una partícula de masa m sometida a un potencial
donde α es una constante positiva.
Representación de Posición
En este caso, según (16)
con lo que la ecuación de Schrödinger (25a) se puede escribir como
Reorganizando términos
cuya solución queda escrita en términos de las funciones de Ayri
Como Ai(x →∞⇢0 ) ! 0 y Bi(x →∞ ) →∞ la condición de frontera ψn(x→∞ ) →0 requiere que
F = 0. Por tanto
Usando la representación integral de la función de Airy 10, expresando la exponencial compleja en términos de funciones seno y coseno, usando las propiedades de paridad
Con podemos escribir
La constante D se halla con la condición de normalización 11
Escogiendo D real y positiva
Donde hemos usado
Por tanto (35) queda
Representación de Momento
Teniendo en cuenta (27), o reemplazando directamente (23), la ecuación de Schrödinger (26a) se puede escribir como
Reorganizando términos
La solución es de la forma
donde A es la constante de integración, que podemos encontrar a partir de la condición de normalización de la función de onda 11
escogiendo A real y positivo
Así, la función de onda (43) queda
Transformada de Fourier
Podemos encontrar la función de onda ψn(x) a partir de Фn( px) usando la transformada de Fourier (14)
Haciendo el cambio de variable
y definiendo
la ecuación (67) se puede escribir como
Expresando la exponencial compleja en términos de funciones seno y coseno, usando las propiedades de paridad y la representación integral de la función de Airy 10,
Por tanto la ecuación (50) queda
Para finalizar, usando las definiciones de α y ϐ se tiene
3.2 Oscilador Armónico
Consideremos una partícula de masa m y frecuencia angular ω sometida a un potencial
donde k = mω2 es una constante positiva.
Representación de Posición
En este caso, según (16)
con lo que la ecuación de Schrödinger (25a) se puede escribir como
Reorganizando términos
Siguiendo el procedimiento tradicional de los textos de Mecánica Cuántica 12,13,14 es conveniente adimensionar esta ecuación proponiendo x = α u, donde u es adimensional y α, que tiene unidades de distancia, está dado por
De manera que al reemplazar en (57) se tiene
Donde
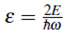es una cantidad dimensional.
La solución de (59) es
Donde H n (u) es un polinomio de Hermite de grado n(=0,1,2,…), se halla normalizando y además, se tiene la restricción ε-1=2n.
Escribiendo (60) en términos de x y normalizando
Representación de Momento
Teniendo en cuenta (27), o reemplazando directamente (23), la ecuación de Schrödinger (26a) se puede escribir como
Reorganizando términos
Para dimensionar, se hace el cambio de variable 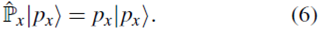con lo cual la ecuación (63) queda
La ecuación diferencial (64) tiene la misma estructura matemática de la ecuacin (59) por tanto la solución será
Regresando a la variable p x y normalizando
la cual coincide, como debe ser, con la ecuación (40) hallada al solucionar la ecuación de Schrödinger en la representación de coordenadas.
Transformada de Fourier
Podemos encontrar la función de onda ψn(x) a partir de Фn( px) usando la transformada de Fourier (14)
Para abreviar definamos 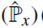con lo cual
Ahora, hacienda el cambio de la variable µ=ƴp x
Según Gradshteyn and Ryzhik,(15)
por tanto
Finalmente, remplazando ƴ y τ
donde i n es un factor de fase que no afecta la norma de la función de onda, por tanto podemos concluir que las funciones de onda (72) y (61) representan el mismo estado.
3.3 Potencial Delta de Dirac
Ilustramos el caso de un potencial tipo Delta de Dirac considerando los estados ligados de una partícula de masas m sometida a un potencial atractivo de la forma 12,3
Donde V o es una constante positiva.
Representación de Posición
Según (16), el potencial se puede escribir como
con lo cual la ecuación de Schrödinger estacionaria (25a) toma la forma
Reorganizando términos
Como estamos considerando estados ligados, escribimos E = -|E| y definimos 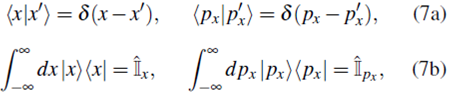con lo cual la ecuación (76) se transforma en
Para x < 0, δ (x) = 0 y la solución (77) es
Pero la condición de frontera cuando x -» - ∞ obliga a que A = 0, por tanto
Similarmente, para x > 0, δ(x) = 0 y (77) tiene como solución
La condición de frontera cuando
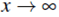exige que D = 0, por tanto
Para encontrar la energía y los valores de B y C, primero usamos la condición de continuidad de la función de onda en x = 0
que conduce a
Así, podemos agrupar(79)y(81)como
Como segundo paso consideramos la primera derivada de la función de onda. Aunque d ψ n (x) /dx no es continua en x = 0, la ecuación de Schrödinger (77) se puede integrar en un intervalo muy pequeño [-ε, +ε] alrededor de x = 0
Si usamos el hecho que en el intervalo [-ε, +ε] ψn(x) ≈ ψn(0) se obtiene
y la energía será
Entonces, reemplazando en (84)
Finalmente normalizamos y encontramos que
y por tanto,
Representación de Momento
La ecuación de Schrödinger (26a) se puede escribir como
Donde, usando (27)
Además, considerando estados ligados (E = -|E|) obtenemos
Para solucionar (93) se hace el cambio
Así que, a partir de (93)
Ahora, al reemplazar (95) en (94) y realizando la integración
Con lo cual
y la energía estará dada, como ya se había obtenido en (87), por
Reemplazando (97) en (95)
Al normalizar se encuentra
donde usamos la integral 17.6.8 de Spiegel 16. Por tanto, a partir de (99), la función de onda en la representación de momento queda de la forma
Transformada de Fourier
Partiendo de la función de onda (101) obtenemos ψn(x) usando la transformada de Fourier (14). Notemos que
por lo tanto obtenemos, como en (90 ), que la función de onda en representación de posición es
como en la ecuación (90).
4 Conclusiones
Hemos ilustrado el uso y conexión de las representaciones de coordenadas y de momentos en mecánica cuántica a través de tres ejemplos elementales. Esperamos que este trabajo permita comprender que ambas representaciones poseen el mismo estatus teórico y son dos aspectos complementarios con los que podemos describir el estado de un sistema cuántico
