1 Introducción
La propiedad χ (véase la Definición 3) juega un papel importante en geometría algebraica no conmutativa. Artin y Zhang en 2 describen algunas álgebras graduadas que satisfacen la condición χ y demuestran que una importante clase de álgebras que satisfacen χ son las álgebras regulares.
Gallego y Lezama en 4 definieron una clase especial de anillos de tipo polinomial, los cuales son llamados extensiones PBW torcidas. Varias propiedades de estas extensiones han sido ampliamente estudiadas (véase por ejemplo 5,6,7,9,11,12,13,14,15,16,17,19,21). Gran parte de los ejemplos, las propiedades y otros aspectos importantes de las extensiones PBW torcidas se encuentran compiladas en 3.
El primer autor en 18 definió las extensiones PBW torcidas graduadas como una generalización de las extensiones de Ore iteradas graduadas. Algunas propiedades de estas extensiones graduadas han sido estudiadas recientemente (véase por ejemplo 6,20).
Es natural preguntarnos qué condiciones deben cumplir las extensiones PBW torcidas graduadas para que satisfagan la propiedad χ. En este artículo mostramos que bajo ciertas condiciones para un anillo R, una extensión PBW torcida graduada de R satisface la propiedad χ. En especial, si R es un álgebra noetheriana N-graduada y A es una extensión PBW torcida cuasi-conmutativa graduada, entonces R satisface χ si y solo si A satisface χ. Las extensiones PBW torcidas cuasi-conmutativas graduadas también tienen la propiedad χ cuando el anillo de coeficientes R cumple alguna de las siguientes condiciones:
Si R es una PI-álgebra noetheriana.
Si R es un álgebra conmutativa noetheriana graduada.
Si R es un álgebra Artin-Schelter regular noetheriana.
También demostramos que las extensiones PBW torcidas graduadas de un álgebra conexa, finitamente presentada y Auslander-regular satisfacen χ.
Los principales resultados se encuentran en el Teorema 17, el Corolario 19, la Proposición 22 y la Proposición 26. Ilustramos estos resultados mediante algunos ejemplos.
2 Preliminares
En esta sección presentamos una serie de definiciones y propiedades que serán usadas posteriormente. Algunas de las definiciones y conceptos homológicos de la teoría de módulos, de la teoría de anillos y otros aspectos que utilizamos aquí, pueden encontrarse en 8.
Para lo que sigue del artículo fijamos la siguiente notación: 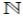 es el conjunto de los numeros naturales incluyendo el 0 y
es el conjunto de los numeros naturales incluyendo el 0 y 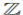 es el conjunto de los numeros enteros, todos los anillos son asociativos con identidad, los módulos son izquierdos,
es el conjunto de los numeros enteros, todos los anillos son asociativos con identidad, los módulos son izquierdos, 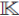 es un cuerpo, todas las álgebras son
es un cuerpo, todas las álgebras son 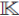 -álgebras,
-álgebras, 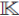 (x1,...,xn) es el álgebra libre en las variables X1,...,xn, R[x1; σ1,δ1] es una extensión de Ore del anillo R y R[x1 ; σ 1 ,δ
1
] • • • [xn; σ n, δ
n
] es una extensión de Ore iterada de R.
(x1,...,xn) es el álgebra libre en las variables X1,...,xn, R[x1; σ1,δ1] es una extensión de Ore del anillo R y R[x1 ; σ 1 ,δ
1
] • • • [xn; σ n, δ
n
] es una extensión de Ore iterada de R.
Un álgebra A es llamada 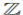 -graduada si tiene una descomposición en
-graduada si tiene una descomposición en 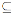 -espacios vectoriales A =
-espacios vectoriales A = 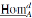 Pe
Pe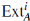 Ap tal que AiAj
Ap tal que AiAj 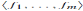 A
i+
j, para todo i, j є
A
i+
j, para todo i, j є 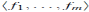 ; Ap se llama componente de grado p y un elemento de Ap es llamado homogéneo de grado p. Si Ap = 0 para p < 0, es decir, A =
; Ap se llama componente de grado p y un elemento de Ap es llamado homogéneo de grado p. Si Ap = 0 para p < 0, es decir, A =  pєNAp, se dice que A es un álgebra graduada positivamente o
pєNAp, se dice que A es un álgebra graduada positivamente o 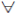 -graduada. Un álgebra
-graduada. Un álgebra 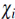 -graduada A =
-graduada A = 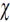 p>0Ap es llamada conexa si A0 =
p>0Ap es llamada conexa si A0 = 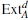 . Sean A un álgebra
. Sean A un álgebra  -graduada y M un A-módulo. Se dice que M es un módulo graduado si posee una familia de subespacios {Mp}pє
-graduada y M un A-módulo. Se dice que M es un módulo graduado si posee una familia de subespacios {Mp}pє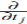 que satisface las siguientes condiciones:
que satisface las siguientes condiciones:
Si M es un módulo graduado, entonces dado un entero l, M(l) es el módulo graduado cuya componente homogénea de grado p es Mp+l. Sean M y N A-módulos graduados, un A-homomorfismo f : M - N es graduado si f (Mp) 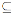 N
p
, para cada p є
N
p
, para cada p є 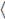 ;
;  (M, N) denota el conjunto de todos los A-homomorfismos h: M -› N tales que h(M
i
)
(M, N) denota el conjunto de todos los A-homomorfismos h: M -› N tales que h(M
i
) N
i+d
,
N
i+d
, 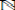 (M, N) =
(M, N) =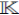 dG
dG
 (M,N) y
(M,N) y  (M,N) denota el correspondiente funtor derivado.
(M,N) denota el correspondiente funtor derivado.
Una identidad polinomial (PI) para un álgebra A es un polinomio no nulo f(x1,x2,...,x
n
) en un número finito de variables no conmutativas x1,x2,...,x
n
con coeficientes en 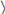 tal que f(α1, α 2,..., α n) = 0, para todo α 1, α 2,..., α n є A. Un álgebra para la cual existe una identidad poli-nomial se llama PI-álgebra.
tal que f(α1, α 2,..., α n) = 0, para todo α 1, α 2,..., α n є A. Un álgebra para la cual existe una identidad poli-nomial se llama PI-álgebra.
Ejemplo 1. Los siguientes son algunos ejemplos de PI-álgebras.
Las álgebras conmutativas, ya que f(x, y) = xy - yx es una identidad polinomial.
Las álgebras Booleanas, pues f (x) = x 2 - x es una identidad polinomial.
Cualquier cuerpo finito con n elementos, pues f( x) = x n - x es una identidad polinomial.
En general las álgebras libres 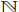 (x1,..., x
n
) con n > 2 no son PI-álgebras.
(x1,..., x
n
) con n > 2 no son PI-álgebras.
Una 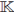 -álgebra A es finitamente generada como álgebra si existen elementos α1 , . . . , αn є A tal que el conjunto { α i1 α i2 • • • α im |1 ≤ ij ≤ n, m ≥ 1} U {1} genera a A como un
-álgebra A es finitamente generada como álgebra si existen elementos α1 , . . . , αn є A tal que el conjunto { α i1 α i2 • • • α im |1 ≤ ij ≤ n, m ≥ 1} U {1} genera a A como un 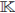 -espacio vectorial. Una K-álgebra A, N-graduada, conexa y finitamente generada se llama finitamente presentada, si existe un ideal homogéneo I =
-espacio vectorial. Una K-álgebra A, N-graduada, conexa y finitamente generada se llama finitamente presentada, si existe un ideal homogéneo I = 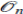 generado por finitos elementos homogéneos, tal que A =
generado por finitos elementos homogéneos, tal que A = 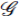 (x1,..., xn)/I.
(x1,..., xn)/I. 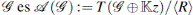 (x1,..., xn)/
(x1,..., xn)/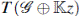 se llama una presentación de A con generadores x1 , . . . , xn y relaciones f1,..., fm.
se llama una presentación de A con generadores x1 , . . . , xn y relaciones f1,..., fm.
Sea M un A-módulo. Se dice que M es noetheriano si todos los submódulos de M son finitamente generados. El anillo (álgebra) A se llama noetheriano si A como A-módulo es noetheriano. Un álgebra graduada se llama noetheriana graduada a izquierda (derecha) si todo ideal graduado izquierdo (derecho) es finitamente generado.
Se define el grado de un A-módulo M como jA(M) := min{p | 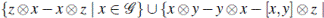 (M, A) = 0} o «> si no existe tal p. Notemos que j
A
(0) = °°. Cuando A es noetheriano, j
A
(M) < pd(M), donde pd(M) denota la dimensión proyectiva de M.
(M, A) = 0} o «> si no existe tal p. Notemos que j
A
(0) = °°. Cuando A es noetheriano, j
A
(M) < pd(M), donde pd(M) denota la dimensión proyectiva de M.
Definición 2 (10, Definición 2.1). Sea A un anillo noetheriano.
Definición 3 (2, Definición 3.7). Sea A un álgebra noetheriana N-graduada y M un A-módulo graduado. Se dice que A satisface xi(M) para un A-módulo M, si para todo d y para todo j < i, existe un entero n0 tal que ExtA (A/A>
n
, M) >
d
es un A-módulo finito, donde A>
n
= 0
m
>
n
A
m
y n > n0. Si A satisface 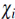 (M), para todo A-módulo finito M, se dice que A satisface
(M), para todo A-módulo finito M, se dice que A satisface 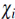 y si A satisface
y si A satisface 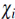 para todo i, se dice que A satisface
para todo i, se dice que A satisface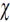 .
.
Definición 4 ((1), Página 171). Sea A = 
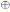 A1
A1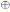
A2 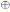 • • • un álgebra graduada finitamente presentada sobre
• • • un álgebra graduada finitamente presentada sobre 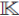 . El álgebra A es llamada Artin-Schelter regular si se tienen las siguientes propiedades:
. El álgebra A es llamada Artin-Schelter regular si se tienen las siguientes propiedades:
Sea R[x1; 1, 51] ••• [xn; σ n , ô n ] una extensión de Ore iterada de R. Si para 1 < i < n, σ i es el endomorfismo identidad entonces R[x1 ; σ 1, Ô1} ••• [xn; σ n, 8n] := R[x1 ; 81] ••• [xn; 8n] y se conoce como extensión de Ore iterada de tipo derivación. Si 8 i es la Gi-derivación nula, entonces la extensión de Ore iterada se denota por R[x1; σ 1] ••• [xn; σ n ] y se llama extensión de Ore iterada de tipo endomorfismo; en tal caso R[x1 ; σ 1] • • • [xn; σ n ] es un álgebra N-graduada.
Una clase especial de extensiones de Ore iteradas son los anillos de polinomios torcidos (véase 8). Un anillo de polinomios torcidos es una extensión de Ore iterada R[x1 ; σ 1, 81] • • • [xn; σ n , 8 n ] que satisface las siguientes propiedades:
σ i(xj)= xj, j < i;
δ i (x j ) = 0, j< i;
σ i σ 1 = σ 1 σ i , 1 ≤ i ≤ n;
δ i δ 1 = δ 1 δ i, 1 ≤ i ≤ n;
donde las últimas dos igualdades se entienden que están restringidas al anillo R. Como una consecuencia de las propiedades en la definición de un anillo de polinomios torcidos, tenemos que R[x1 ; σ 1, δ1] • • • [xn; σ n , δ n ] es un anillo de polinomios torcidos de R si y solo si
x i χ j = χ j x i , 1 < i, j < n,
σ i(R), δi(R) Ç R, 1 ≤ i ≤n.
Ejemplo 5 (4). Sea R = K[t1t
n
] y A
n
(K) := R[x1; δ
1] ••• [xn; δ
n
] con δj =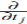 , para 1 ≤j ≤ n. An(
, para 1 ≤j ≤ n. An(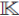 ) es una extensión de Ore iterada de tipo derivación y se conoce como álgebra de Weyl.
) es una extensión de Ore iterada de tipo derivación y se conoce como álgebra de Weyl.
Definición 6 (4, Definición 1). Sean R y A anillos, se dice que A es una extensión PBW torcida de R si se satisfacen las siguientes condiciones:
R /A.
Existen en A elementos x1 , . . . , xn tales que A es un R-módulo libre a izquierda, cuya base es el conjunto Mon(A) de los monomios estándar, Mon(A) := /| α := (α 1 ..., α n) є /n}. En tal caso se dice que A es un anillo de polinomios a izquierda sobre R con respecto a { x1 , . . . , x n } .
Para cada 1 ≤ i ≤n y r Є R - {0}, existe ci r Є R - {0} tal que
x i r - C i , r x i Є R.
Para todo 1 ≤ i, j ≤ n, existe c i , j Є R - {0} tal que
x j x i - c i , j xixj Є R + Rx 1 +…+ Rx n .
En tal caso, una extensión PBW torcida de R es denotada por A := σ (R)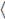 x1,..., x
n
x1,..., x
n
 .
.
Ejemplo 7. Todo anillo de polinomios torcidos es una extensión PBW torcida. En efecto, x i r - rx i = δi(r), x i x j - x j x i = 0.
La siguiente propiedad es muy importante en el estudio de las extensiones PBW torcidas y su demostración puede consultarse en [4, Proposición 3].
Proposición 8 (4, Proposición 3). Si A es una extensión PBW torcida de R entonces para cada 1 ≤ i ≤ n, existe un endomorfismo inyectivo de anillos σ i : R -› Ry una σ i -derivación δ i : R -› R, tal que
x i r = σ i (r)x i + δ i (r), (1)
para todo r Є R.
Dos subclases muy importantes de extensiones PBW torcidas son las siguientes.
Definición 9 (4, Definición 4). Sea A = σ (R) (x1,..., xn) una extensión PBW torcida de R.
A es cuasi-conmutativa si las condiciones (iii) y (iv) en la Definición 6 son reemplazadas por:
' Para cada 1 ≤ i ≤ n y r Є R - {0}, existe ci r Є R - {0} talque
x i r - c i,r x i .
' Para todo 1 ≤ i, j ≤ n, existe c iy j Є R - {0} tal que
x j x i - c i, j x i x j .
A es biyectiva si σ i es biyectiva para todo 1 ≤ i ≤ n y c i, j es invertible para cualquier 1 ≤ i ≤ j ≤ n.
Las extensiones de Ore y las extensiones de Ore iteradas (bajo algunas condiciones) son extensiones PBW torcidas. No todas las extensiones PBW torcidas son extensiones de Ore iteradas.
Ejemplo 10 (4). Cualquier extensión de Ore R[χ; Є, δ], con Є inyectivo, es una extensión PBW torcida. Si además δ = 0, entonces R[χ; σ] es cuasi-conmutativa. Una extensión de Ore iterada R[x1 ; σ 1, δ 1] • • • [xn; σ n , δ n ] es una extensión PBW torcidas si satisface las siguientes condiciones:
σ i es inyectiva para todo 1 ≤ i ≤ n.
Para todo r Є R, σ i (r), δ i (r) Є R con 1 ≤ i ≤ n.
Para i < j, σ j(x i ) = cx i + d con c, d Є R y c invertible a izquierda.
• Para i < j, δj(x i ) Є R + Rx 1 +…+ Rxn.
En particular un anillo de polinomios torcidos 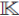 [t1,..., t
n
][x
1
; σ
1
, δ
1] • • • [xn; σ
n
, δ
n
] es una extensión PBW torcida si σ
i
es inyectiva para 1 ≤ i ≤ n y para todo p Є
[t1,..., t
n
][x
1
; σ
1
, δ
1] • • • [xn; σ
n
, δ
n
] es una extensión PBW torcida si σ
i
es inyectiva para 1 ≤ i ≤ n y para todo p Є 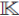 [t1,..., tn], σ i(p), δi(p) Є
[t1,..., tn], σ i(p), δi(p) Є 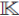 [t
1
,..., t
n
] con 1 ≤i ≤ n.
[t
1
,..., t
n
] con 1 ≤i ≤ n.
Si R es un anillo N-graduado entonces las extensiones de Ore iteradas de R se pueden dotar de una graduación. Sea A = R[x 1 ; σ 1 , δ 1] • • • [xn; σ n , δ n ] una extensión de Ore iterada de un anillo N-graduado R. Entonces A es llamada extensión de Ore iterada graduada si x1,..., x n tienen grado 1 en A, cada σ i es un automorfismo graduado de álgebras y cada δ i es una σ i -derivación graduada.
El primer autor definió en 18 las extensiones PBW torcidas graduadas como una generalización de las extensiones de Ore iteradas graduadas.
Proposición 11 (18, Proposición 2.7). Sea R = m
>
0
R
m
un álgebra
m
>
0
R
m
un álgebra -graduada y sea A = σ(R) (x1,...,xn) una extensión PBW torcida biyectiva de R que satisface las siguientes condiciones:
-graduada y sea A = σ(R) (x1,...,xn) una extensión PBW torcida biyectiva de R que satisface las siguientes condiciones:
σ i es un homomorfismo de anillos graduados y δ i : R(-1) -› R es una σ i -derivación graduada para cada 1 ≤ i ≤ n, donde σ i y δ i están definidas como en la Proposición 8.
x j x i - c i,j x i x j Є R2 + R1x1 + + R1xn y ci,j Є R 0.
Para p ≥ 0, sea A
p
el -espacio generado por el conjunto
-espacio generado por el conjunto
{r t x α 11 + l α | = p, r t Є R t yx α Є Mon(A)}.
Entonces A es un álgebra N-graduada con graduación
Definición 12 (18, Definición 2.6). Sea A = σ(R) (x1,...,xn) una extensión PBW torcida biyectiva de un álgebra N-graduada R = p>0
R
p
. Se dice que A es una extensión PBW torcida graduada si A satisface las condiciones (i) y (ii) de la Proposición 11.
p>0
R
p
. Se dice que A es una extensión PBW torcida graduada si A satisface las condiciones (i) y (ii) de la Proposición 11.
A continuación presentamos un resultado que usamos en la demostración del Teorema 17 y que muestra que toda extensión PBW torcida cuasi-conmutativa graduada es una extensión de Ore iterada graduada de tipo endomorfismo.
Proposición 13 (20, Proposición 2.7). Sea A = σ(R) (x1,...,xn) una extensión PBW torcida graduada. Si A es cuasi-conmutativa, entonces A es iso-morfa a una extensión de Ore iterada graduada de tipo endomorfismo R[z 1 ; Ө 1 ] • • • [z n ; d n ], donde 6 i es biyectiva, 6 i (r) = σ i (r) para r Є R, B 1 = σ 1 y
Ө j: R[z1 ; Ө 1] • • • [zj-1 ; Өj-1] - R[z1 ; Ө 1 ] • • • [zj-1 ; Өj-1]
es tal que Ө j(z i ) = c i, j z i (c i,j Є R0 como en (iv) de la Definición 6), 1 ≤ i ≤ j ≤ n.
Observación 14. La clase de extensiones de Ore iteradas graduadas es una subclase de las extensiones PBW torcidas graduadas (véase [18, Observación 2.11]).
La siguiente proposición es el análogo del teorema de la base de Hilbert para extensiones PBW torcidas graduadas.
Proposición 15 (20, Proposición 2.7-(i)). Sea A = σ(R)(x 1 ,...,xn) una extensión PBW torcida graduada. Si R es un álgebra noetheriana a derecha (izquierda) graduada, entonces cada extensión PBW torcida graduada de R es noetheriana a derecha (izquierda) graduada.
3 Propiedad χ
En esta sección presentamos algunos resultados de la condición χ en extensiones PBW torcidas graduadas. También damos otras propiedades que no presentamos en la sección anterior y que son necesarias para demostrar dichos resultados.
Un elemento a de un anillo R se llama normal si R α = α R.
Proposición 16 (2, Teorema 8.8). Sea A un álgebra noetheriana N-graduada con un elemento normal a de grado positivo. Entonces A satisface χ si y solo si A/( α) satisface χ, donde (α) es el ideal bilátero de A generado por α.
Teorema 17. Sean R =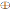 p
>
0
R
p
un álgebra noetheriana N-graduada y A = σ (R)(x
1
,..., xn) una extensión PBW torcida cuasi-conmutativa graduada. Entonces R satisface χ si y solo si A satisface χ.
p
>
0
R
p
un álgebra noetheriana N-graduada y A = σ (R)(x
1
,..., xn) una extensión PBW torcida cuasi-conmutativa graduada. Entonces R satisface χ si y solo si A satisface χ.
Proof. Por la Proposición 13 tenemos que A es isomorfa a una extensión de Ore iterada 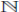 -graduada de tipo endomorfismo
-graduada de tipo endomorfismo
R[z1; Ө1] ••• [zn; Өn],
donde Ө i es biyectiva para cada i; z 1 , z 2, . . . , z n son elementos homogéneos de grado 1; Ө1 = σ 1 ; y para 1 ≤ j ≤ n,
Өj: R[z1 ; Ө1] • • • [zj-1 ; Өj-1] - R[z1 ; Ө1] • • • [zj-1 ; Өj-1] cumple las siguientes condiciones:
Además,
z1r = Ө1(r)z 1 = σ 1(r)z 1 Є Rz1
y como σ1 -1(r) = Ө1 -1 (r) Є R, entonces z1 Ө 1 - 1(r) Є z 1 R, pero
z101 -1(r) = σ 1(Ө1 - 1 (r))z 1 = σ 1 (σ1 - 1 (r))z 1 = rz 1 ,
es decir, rz
1 Є z
1
R. Por lo tanto, z
1 Є A
1 es un elemento normal no nulo de A1: = R[z1 ; Ө1]. Nótese que A1/ 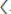 z1
z1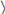 = R. Por la Proposición 16, A1= R[z
1; Ө
1
] satisface χ si y solo si A1/(z
1) = R satisface χ. Ahora, z
2 Є A
1 es un elemento normal no nulo de A2: =A1 [z2; Ө 2] = R[z
1
; Ө 1] fe; Ө 2] y A2/(z
2) = A1. Como R es noetheriana y N-graduada, R[z1; Ө 1] es noetheriana (Proposición 15) y N-graduada. Por la Proposición 16, A2= R[z1; Ө 1][z2; Ө 2] satisface χ si y solo si A2/(z2) = R[ z
1; Ө 1
] satisface χ. Finalmente, supongamos que
= R. Por la Proposición 16, A1= R[z
1; Ө
1
] satisface χ si y solo si A1/(z
1) = R satisface χ. Ahora, z
2 Є A
1 es un elemento normal no nulo de A2: =A1 [z2; Ө 2] = R[z
1
; Ө 1] fe; Ө 2] y A2/(z
2) = A1. Como R es noetheriana y N-graduada, R[z1; Ө 1] es noetheriana (Proposición 15) y N-graduada. Por la Proposición 16, A2= R[z1; Ө 1][z2; Ө 2] satisface χ si y solo si A2/(z2) = R[ z
1; Ө 1
] satisface χ. Finalmente, supongamos que
A (n-1) : = R[z1; Ө 1 ] ••• [zn-1; Ө n-1]
satisface χ. Notemos que zn Є A1 es un elemento normal no nulo de
A (n) : =A (n-1) [ zn; Ө n ] = R[z 1 ; Ө 1 ] ••• [zn-1; Ө n- 1][zn; Ө n] = A.
Como R es noetheriana y N-graduada, A (n-1) : = R[z 1 ; Ө 1] • • • [zn-1 ; Ө n-1] es noetheriana (Proposición 15) y N-graduada. Por la Proposición 16, A (n) = R[z1 ; Ө 1] • • • [zn-1 ; Ө n-1] [zn; Ө n] = A satisface χ si y solo si A (n) /(zn) = R[zV; Ө 1] • • • [zn-1; Ө n-1] satisface χ. Por transitividad tenemos que R satisface χ si y solo si A satisface χ.
El siguiente teorema lo usamos en la demostración del Corolario 19.
Teorema 18 (2, Teorema 5.1). Si R es una PI- álgebra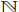 -graduada noetheriana, entonces R satisface χ.
-graduada noetheriana, entonces R satisface χ.
Corolario 19. Sea A = σ (R) (x1,..., xn) una extensión PBW torcida cuasi-conmutativa graduada.
Si R es una PI-álgebra noetheriana entonces A satisface χ.
Si R es un álgebra conmutativa noetheriana graduada entonces A satisface χ.
Proof. Sea A = σ (R)(x1,...,xn) una extensión PBW torcida cuasi-conmutativa graduada de un álgebra R. Por la Definición 12 tenemos que R es 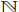 -graduada.
-graduada.
Si R es una PI-álgebra noetheriana entonces por el Teorema 18 tenemos que R satisface χ. Ahora, por el Teorema 17 tenemos que A satisface χ.
Si R es un álgebra conmutativa entonces por el Ejemplo 1 tenemos que R es una PI-álgebra. Como además R es noetheriana, entonces por el ítem (i) anterior tenemos que A satisface χ.
La propiedad Artin-Schelter regular de un álgebra R pasa a las extensiones PBW torcidas cuasi-conmutativas graduadas (véase (20)).
Proposición 20. Sea R un álgebra Artin-Schelter regular y sea A = σ (R) (x1,...,xn) una extensión PBW torcida cuasi-conmutativa graduada. Entonces A es Artin-Schelter regular.
Artin y Zhang en (2) demuestran que las álgebras Artin-Schelter regulares noetherianas satisfacen χ.
Proposición 21 ((2), Teorema 8.1). Sea A un álgebra Artin-Schelter regular noetheriana. Entonces A satisface la condición χ.
De las dos proposiciones anteriores obtenemos el siguiente resultado.
Proposición 22. Toda extensión PBW torcida cuasi-conmutativa graduada de un álgebra Artin-Schelter regular noetheriana satisface χ.
Proof. Sea A = σ (R)(x1,...,xn) una extensión PBW torcida cuasi-conmutativa graduada de un álgebra Artin-Schelter regular noetheriana R. Por la Proposición 20 tenemos que A es Artin-Schelter regular y por la Proposición 15 tenemos que A es noetheriana. Por lo tanto, aplicando la Proposición 21 concluimos que A satisface χ.
Usando los resultados anteriores, tenemos los siguientes ejemplos de extensiones PBW torcidas cuasi-conmutativas graduadas que satisfacen la condición χ.
Ejemplo 23 (Álgebra de operadores parciales lineales con q-dilatación). Para un elemento fijo q Є 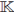 \ {0}, el álgebra de operadores parciales lineales con q-dilatación y coeficientes polinomiales es
\ {0}, el álgebra de operadores parciales lineales con q-dilatación y coeficientes polinomiales es 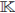 [t1,..., t
n
] [H
(q)
,..., H^], n > m, sujeto a las relaciones: t
j
t
i
= t
i
t
j
, 1 ≤ i ≤ j v n; H
i
-
(q)t
i
= qt
i
H
i
(q)
1 ≤ i ≤ m; H
j
(q)
t
i
= t
i
H
j
(q)
, i ‡ j; H
j
(q)
H
i
(q)
= H
i
(q)
H
j
(q)
, 1 ≤ i ≤ j v m. De acuerdo alas relaciones dadas anteriormente, tenemos que esta álgebra es una extensión PBW torcida cuasi-conmutativa graduada del álgebra
[t1,..., t
n
] [H
(q)
,..., H^], n > m, sujeto a las relaciones: t
j
t
i
= t
i
t
j
, 1 ≤ i ≤ j v n; H
i
-
(q)t
i
= qt
i
H
i
(q)
1 ≤ i ≤ m; H
j
(q)
t
i
= t
i
H
j
(q)
, i ‡ j; H
j
(q)
H
i
(q)
= H
i
(q)
H
j
(q)
, 1 ≤ i ≤ j v m. De acuerdo alas relaciones dadas anteriormente, tenemos que esta álgebra es una extensión PBW torcida cuasi-conmutativa graduada del álgebra 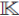 [t1,..., t
n
]. Como
[t1,..., t
n
]. Como 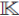 [t1,..., t
n
] es un álgebra conmutativa noetheriana entonces por el Corolario 19 (ii) tenemos que K[t1,..., tn] [H
1
(q)
,..., H
m
(q)
] satisface χ.
[t1,..., t
n
] es un álgebra conmutativa noetheriana entonces por el Corolario 19 (ii) tenemos que K[t1,..., tn] [H
1
(q)
,..., H
m
(q)
] satisface χ.
Ejemplo 24 (Análogo multiplicativo del álgebra de Weyl). Esta álgebra es denotada por 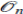 (λj
i
) y es generada por x1 , . . . , xn sujeta a las relaciones: x
j
x
i
= X
ji
x
i
x
j
, 1 ≤ i ≤ j ≤ n, λji Є
(λj
i
) y es generada por x1 , . . . , xn sujeta a las relaciones: x
j
x
i
= X
ji
x
i
x
j
, 1 ≤ i ≤ j ≤ n, λji Є 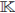 \ {0}. Entonces
\ {0}. Entonces 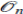 (λjt) es una extensión PBW torcida cuasi-conmutativa graduada de
(λjt) es una extensión PBW torcida cuasi-conmutativa graduada de 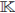 [x1 ]. Si n = 2, esta álgebra es llamada el plano cuántico. Nótese que
[x1 ]. Si n = 2, esta álgebra es llamada el plano cuántico. Nótese que 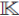 [x1] es un álgebra conmutativa noetheriana, así, por el Corolario 19 (ii) tenemos que
[x1] es un álgebra conmutativa noetheriana, así, por el Corolario 19 (ii) tenemos que 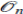 (λj
i
) satisface χ.
(λj
i
) satisface χ.
Usamos la siguiente proposición para la demostración de la Proposición 26.
Proposición 25 (20, Proposición 3.5). Sea A = σ(R)(x1,...,xn) una extensión PBW torcida graduada. Si R es un álgebra conexa, finitamente presentada y Auslander-regular, entonces A es Artin-Schelter regular.
Proposición 26. Toda extensión PBW torcida graduada de un álgebra conexa, finitamente presentada y Auslander-regular satisface χ.
Proof. Sea A = σ (R)(x1,...,xn) una extensión PBW torcida graduada de un álgebra R conexa, finitamente presentada y Auslander-regular. Por la Definición 2 tenemos que R es noetheriana y por la Proposición 15 concluimos que A es noetheriana. Ahora, por la Proposición 25 tenemos que A es Artin-Schelter regular. El resultado sigue entonces de la Proposición21.
Los siguientes dos ejemplos son extensiones PBW torcidas graduadas no cuasi-conmutativas que satisfacen χ.
Ejemplo 27. El plano de Jordan A es el álgebra libre generada por χ, y con la relación yx = xy+ x
2
, es decir, A = K(χ,y)/(yx - xy - x2). Por lo tanto, esta álgebra es una extensión PBW torcida de K[χ]. Para mayor información acerca del plano de Jordan, véase 5. Como 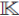 [χ] es noetheriana, finitamente presentada y Auslander-regular entonces por la Proposición 26 tenemos que el plano de Jordan satisface χ.
[χ] es noetheriana, finitamente presentada y Auslander-regular entonces por la Proposición 26 tenemos que el plano de Jordan satisface χ.
Ejemplo 28. Sea 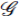 un álgebra de Lie de dimensión finita sobre
un álgebra de Lie de dimensión finita sobre 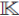 con base {x1,..., xn} y U (
con base {x1,..., xn} y U (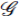 ) su álgebra envolvente. El álgebra envolvente homogeneizada de es
) su álgebra envolvente. El álgebra envolvente homogeneizada de es 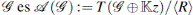 , donde
, donde 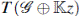 es el álgebra tensorial (libre), z es una nueva variable, y R es el subespacio generado por
es el álgebra tensorial (libre), z es una nueva variable, y R es el subespacio generado por 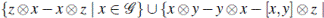
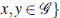 . Esta es un álgebra de Lie sobre el cuerpo de fracciones K(z). Por lo tanto
. Esta es un álgebra de Lie sobre el cuerpo de fracciones K(z). Por lo tanto  (
(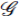 ) es una extensión PBW torcida graduada de K[z] (véase [18,Ejemplo 2.9]). Como
) es una extensión PBW torcida graduada de K[z] (véase [18,Ejemplo 2.9]). Como 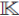 [z] es noetheriana, finitamente presentadas y Auslander-regular entonces por la Proposición 26 tenemos que el álgebra envolvente homogeneizada satisface χ
[z] es noetheriana, finitamente presentadas y Auslander-regular entonces por la Proposición 26 tenemos que el álgebra envolvente homogeneizada satisface χ