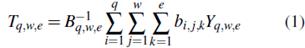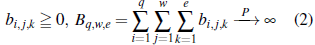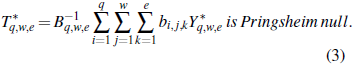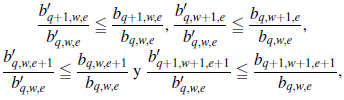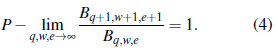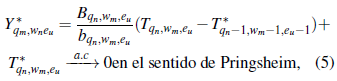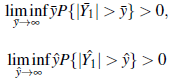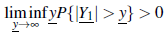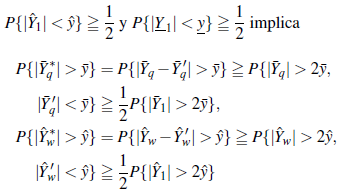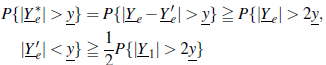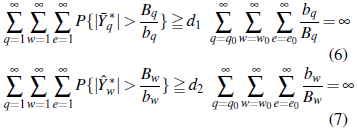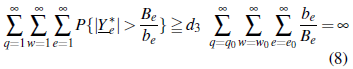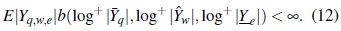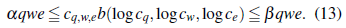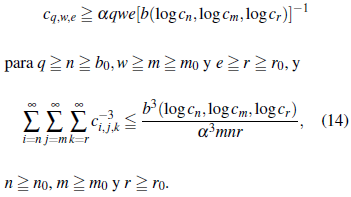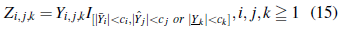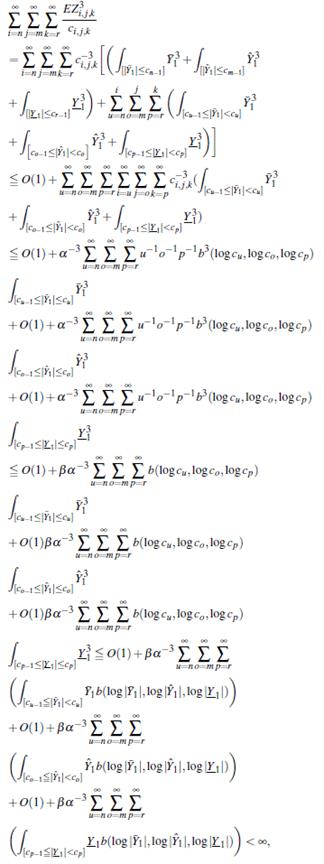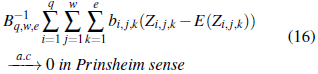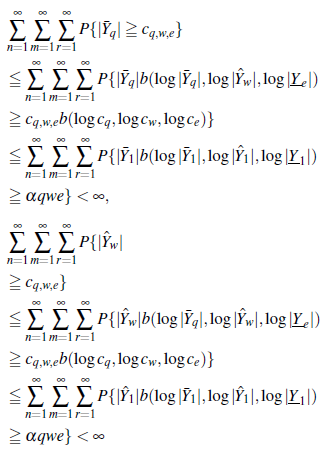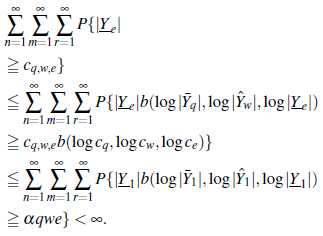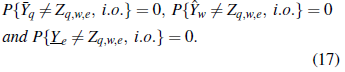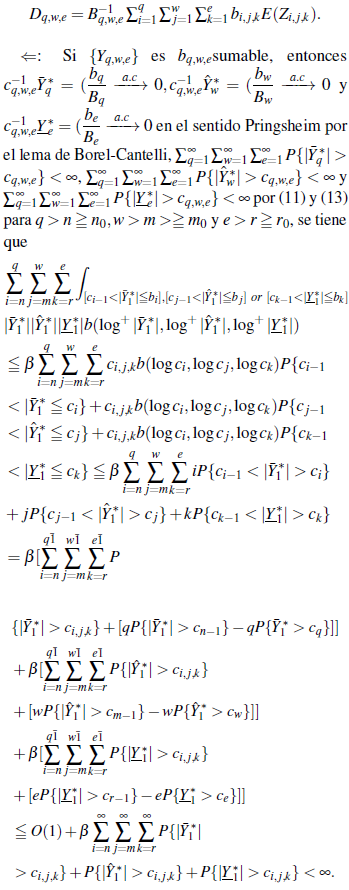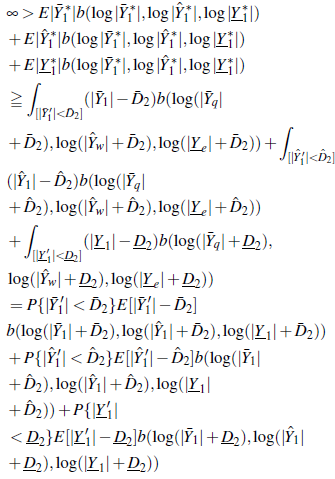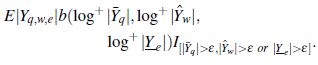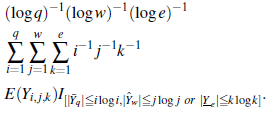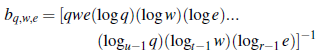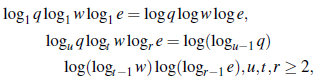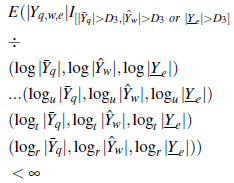1 Introducción y nociones preliminares

Las nociones de variables aleatorias independientes e idénticamente distribuidas {Y_q, q ≧ 1} con primer momento finito y métodos de sumabilidad aplicables a la secuencia de divergencia {Y _q } y una serie de Los teoremas de aproximación unidimensional fueron presentados por Chow y Teicher [³] en 1971. Luego, en 2021, Savas y Patterson [⁸] estudiaron estas nociones en variables aleatorias bidimensionales y mostraron algunos resultados interesantes. En este artículo, examinaremos variables aleatorias tridimensionales. Mediante el uso de estas variables demostramos que ninguna elección de {bq,w,e} y {Dq,w,e} hará que {Yq,w,e} sean independientes e idénticamente distribuidas con (masa 2^-q-w-e en el punto 2^q+^w+^e, q, w, e ≧ 1) para ser la distribución de Cauchy b _q,w,e -sumable. Para ello, comenzamos presentando las nociones de convergencia y divergencia de sucesiones triples en el sentio de Pringsheim.

Definición 1 ([⁷]). Una triple sucesión y = {y _q,w,e } tiene límit Pringsheim L denotado por P-limy = L dado un ε > 0 existe M ∈ ℕ tal que |y _q,w , _e - L| < | par cualquier q, w, e > M. Desribiremos y como P- convergent, y será denotado por y _q,w,e 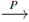L.

Definición 2 ([⁶]). Sea y = {y _q,w,e } una sucesión triple de números reales y para cada m, α _m = sup_m{y _q,w,e : q,w,e ≥ m}. El límite superior de Pringsheim y es definido de la siguiente manera:

1. If α _m = +∞ para cada m, entonces P-limsup y = +∞,

2. if α _m < ∞ para algún m, entonces P-lim sup y = inf _m { α _m } .

De igual manera, sea β _m = inf_m{y_q,_w,e: q, w, e ≥ m}. El límite inferior Pringsheim de y está definido de la siguiente manera:

1. Si β _m = - ∞ para cada m, entonces P-lim y =- ∞

2. Si β _m > ∞ para algún m, entonces P-limy = sup_m{ β _m }^.

Lema 1 ([²]). Si {B _m} es una sucesión de eventos y 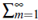P(B _m) < ∞ entonces P({B_m i-o}) = 0.

Observación 1. Sea {Y _q,w,e ,q, w,e ≥ 1} una sucesión triple factorizable independiente e idénticamente distribuida de variables aleatorias con E | Y _q,w,e | < ∞, y denotemos Y _q,w,e como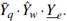

Definición 3. Se considerará una subclase de métodos de sumabilidad regulares y la preocupación se centrará en la convergencia casi segura (a.s) Pa cero de la sucesión triple transformada

donde

asegurando así la regularidad.

Observación 2. Si Tq ,w,e - Dq ,w,e 0 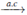0 en el sentido de Pringsheim para Dq,w,e, las variables aleatoria idependientes e idénticamente distribuidas {Yq,w,e} se llamarán bq,w,e-sumable con probabilidad uno o simplemente bwe-sumable.

Definición 4. Si Y*q,w,e = Yq,w,e, Y’q,w,e q,w,e ≧1 son simétricas Yq,w,e, i.e. {X’q,w,e = 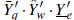} es idénticamente distribuida, y es independiente de {Yq,w,e} con la misma distribución, entonces b q,w,e -sumabilidad de {Y q,w,e} implica b q,w,e -sumabilidad de {Y ‘q,w,e} con desapración de centro i.e.,

Observación 3. Se puede demostrar que ninguna elección de {b q,w,e} y {D q,w,e} hará que las variables aleatorias independientes distribuidas de forma idéntica {Y q,w,e} con masa 2-q-w-e en el punto 2q+w+e, q, w, e ≧ 1 para ser la distribución de Cauchy b q,w,e-sumable.

2 Resultados

La idea principal de esta sección es presentar una comparación entre b q,w,e -sumable y b’ q,w,e -sumable. Si b q,w,e y b’ q,w,e son estrictamente positivos y

entonces bq,w,e-sumabilidad implica b’q,w,e -sumabilidad. Si {Y* q,w,e, q, w, e ≧ 1} es independiente e indenticamente distribuida y b’ q,w,e -sumable con D* q,w,e, entonces necesariamente

Si 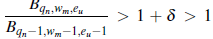para alguna triple sub-sucesión qn, wm, eu, m,n, u ≧ 1 de enteros positivos. Entonces, por (3) se tiene que

dado que 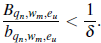No osbtante, una triple sucesión no degenerada e indenticamente distribuida de variables aleatorias no puede P-converger a.c a una constante finita, así, (2) se sigue.

Teorema 1. Sea {Y q,w,e} una viarab/e aleatoria independiente e ideníicamente disíribuida con /a distribución de Cauchy,

And

no se bq,w,e-sumable para cualquier {bq,w,e} que satisface (4).

Proof. Si {Yq,w,e} es bq,w,e-sumable, la simetría de la triple sucesión {Y*q,w,e} es bq,w,e-sumable con constantes de centrado que desaparecen, por lo tanto, por (4) se tiene P-lim 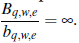. Tomando

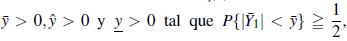
Y

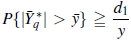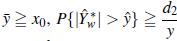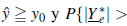
Por lo tanto, existen constantes positivas d1,d2,d3,x0,y0 y z0 con para para 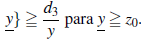Consecuentemente, si q0, w0 y e0 son enteros positivos tal que 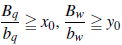y para

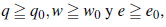
Y

por la propiedad factorable de {bq,w,e} y el teorema de Abel-Dini. Combinando (3) y (4), se tiene 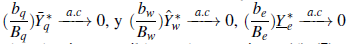el cual es incompatible con las ecuaciones (6), (7) y (8) por el lema de Borel-Cantelli. □

Definición 5. Una triple sucesión {bq,w,e} es totalmente creciente dado bq,w,e < bq+1w,e, bq,w,e < bq,w+1,e, bq,w,e < bq,w,e+1 y bq,w,e < bq+1,w+1,e+1.

De igual manera, se puede definir para sucesiones decrecientes.

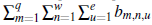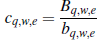Teorema 2. Si b(x,y,z) = b(x)b(y)b(z),x,y,z > 0 es positiva y totalmente decreciente y bq,w,e = bqbwbe = b(q) . b(w) . b(e), Bq,w,e = y donde

entonces. las variables aleatorias independientes e idénticamente distribuidas {Yq,w,e} son bq,w,e-sumable si y so/o si

Proof. ⇒: Dado que 0 < b(x,y, z) es totalmente no decreciente, y cq,w,e es totalmente no decreciente a o. Tomando m0, n0 y r0 tal que q ≥ n0, w ≧ m0 y e ≧ r0, implica que

Por lo tanto,

Consecuentemente, tenemos que

Combinando (13) y (14), y para n ≧ n0, m ≧ m0 y r ≧ r0, tenemos

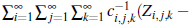
Por (12). Por lo tanto , 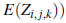P-convrgente casi seguramente , y así, por el Lema de Kronecker, se tiene que

Por (11) y (13), para n ≧ n ₀ , m≧ m ₀ y r≧ r ₀ , se tiene que

Y

Por lo tanto, por el lemma de Borel-Cantelli y dado que las variables aleatorias son factorables,

Combinadondo (16) y (17) {Y _q,w,e } es b _q,w,e - sumable coh centro constante

Por lo tanto,

lo cual implica(12)

Los siguientes dos colorarios son consecuencia directa de los teoremas anteriores, por lo tanto sus demostraciones son omitidas.

Corolario 1. Si {Y _q,w,e } es factorable con componentes 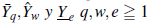son variables aleatorias independientes e idénticamente distribuidos, entonces

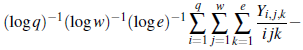
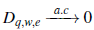en el sentido Pringsheim si y solo si,

Además D _q,w,e puede ser tomado como

Corolario 2. Si {Y _q,w,e } es factorab/e con componentes 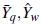and 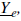, q,w,e ≧ 1 son vanables aleatorias independientes e identicamente distribuidos, y para algunos u, t, r ≥ 3

donde

entonces, {Y _q,w,e } es b _q,w,e -sumable, si y solo si, para lo suficientemente D₃ > 0,

3 Conclusión

La idea principal de este artículo, era tomar las nociones presentades de sumabilidad de variables aleatorias en una dimensión definidas por Chow y Teicher [³] y extendias a dos dimensiones por Savas y Patterson; y comprobar si estas mismas se satisfacían para una dimensión mayor, es decir, para una tercera dimensión. Los resultados presentados en este artículo, podría ser una base fundamental para comprobar si estas nociones se satisfacen en n-dimenciones. A su vez, estas nociones podrian ser extendidas para variables aleatorias neutrosóficas las cuales han sido estudiadas por [¹, ⁴, ⁵].