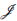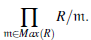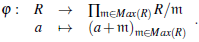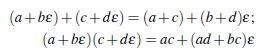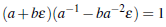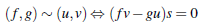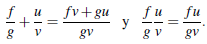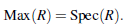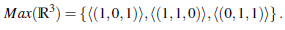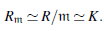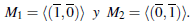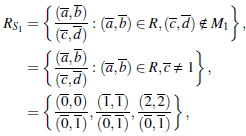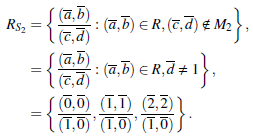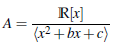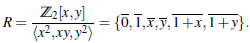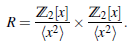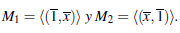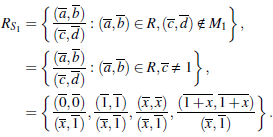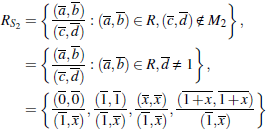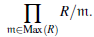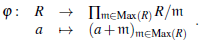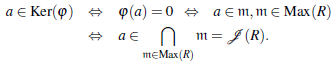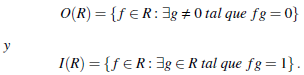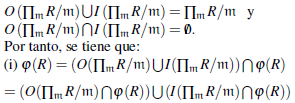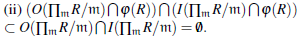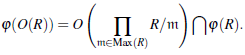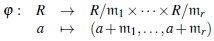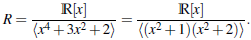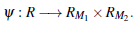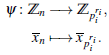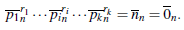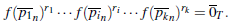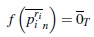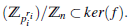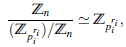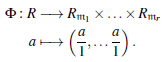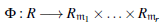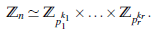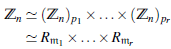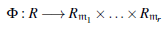1. Introducción
Sean R un anillo conmutativo con unidad, y p ≠ ⟨1⟩ un ideal de R. p es primo, si se cumple la siguiente condición: ab Єp implica que a Є p o b Є p; además un ideal m ≠ ⟨1⟩ de R es maximal si no existe ningún ideal а tal que m ⊂ а ⊂ ⟨1⟩.
El anillo R tiene asociado el espacio topológico
Spec(R) = {p: p es ideal primo de R}
llamado espectro primo de R y dotado de la topología de Zariski con base de abiertos {D( f )} fЄR , donde D( f ) = {p ∉ Spec(R) : f ∉ p}. El espectro primo de un anillo conmutativo relaciona dos areas de la matemática, el álgebra conmutativa y la topología.
El complemento de D(f) se llama variedad de f,
V(f ) = Spec(R) \ D(f ) = {p G Spec(R) : f g p}.
Si α es un ideal de A, entonces V(α) = ∩fЄα V(f) = {p Є Spec(R) : а ⊂ p}.
En particular, se tiene el espectro maximal de R dado por
Max(R) = {m : m es ideal maximal de R} ⊂ Spec(R).
Note que R/m es un cuerpo para todo m Є Max(R) y consideremos el producto de cuerpos
Por la propiedad universal del producto existe un homomorfismo de anillos
En general φ es no inyectiva pues K er (φ)=
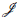 (R) donde
(R) donde
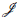 (R) =∩mЄMax(R) m es el radical de Jacobson de R.
(R) =∩mЄMax(R) m es el radical de Jacobson de R.
Cuando R es un dominio entero, R siempre está inmerso en el cuerpo de fracciones de R Note que si R es un anillo local, es decir R tiene un único ideal maximal m, entonces R no está necesariamente inmerso en el cuerpo de fracciones; por ejemplo el anillo local ℤ8 no está inmerso en su cuerpo de fracciones, ℤ2.
La inmersión de un anillo en un cuerpo es un tema de interés en algebra desde 1936 cuando Malcev publicara "On the immersion of an algebraic ring into a field" [9]. A partir de allí se han hecho estudios sobre la inmersión de un anillo en un anillo con division que es una estructura con menos condiciones que la de cuerpo [2, 8].
Nosotros queremos estudiar la inmersión de un anillo conmutativo con unidad, no local, R en el producto de cuerpos, donde los cuerpos son cocientes de R con sus ideales maximales. Además si el anillo R tiene un número finito de ideales maximales, tenemos que el homomorfismo canónico φ es un isomorfismo de anillos. Por otra parte, consideramos el caso donde R es un anillo total de fracciones con un número finito de ideales maximales y mostramos que el homomorfismo de R en el producto de sus localizados es inyectivo. Más aún, si R es de la forma ℤn, con n ≠ 0, o si R es un K-algebra finita con K un cuerpo tenemos que este homomorfismo de anillos es un isomorfismo. Nuestro interés por estos anillos está fundamentado en querer resolver el problema abierto de caracterizar la recta proyectiva sobre anillos, en particular, queremos caracterizar la recta proyectiva sobre anillos totales de fracciones. En este sentido, hemos estudiado las K-algebras finitas y el producto de cuerpos, pues ellos son anillos totales de fracciones [5, 6, 7].
2. Preliminares
En esta sección se incluyen resultados que hemos estudiado en [5, 6, 7], pero aquí se han incluido importantes ejemplos que harán mas fácil la lectora del artículo.
2.1. Anillos totales de fracciones
Definición 2.1 Un anillo R es un anillo total de fracciones si sus elementos son invertibles o divisores de cero.
Ejemplo 2.2 Un cuerpo es un anillo total de fracciones y un dominio entero que no es un cuerpo no es anillo fofa/ de fracciones.
Ejemplo 2.3 ℤn[x]/⟨x2⟩ con n ≠ 0, es un anillo total de fracciones. En efecto, considere R = ℤn[x]/ ⟨x2⟩ = ℤn [ε], donde ε2 = 0, con las operaciones suma y producto definidas por
para a + bε, c + dε Є R. Como ℤn es un anillo total de fracciones, tenemos dos afirmaciones:
1. (a + bε ) es divisor de cero si y so/o si a Є ℤn es divisor de cero. En efecto, para todo a + bε Є R divisor de cero, existe a'ε Є R tal que
(a + bε )(a'ε ) = 0
si y solo si para todo a Є ℤn, existe a' Є ℤn tal que aa' = 0.
2. (a + bε) es invertible si y so/o si a Єℤn es invertible. En efecto, para todo a + bε G R invertible, existe a-1 - ba-2ε Є R tal que
si y solo si para todo a Єℤn, existe a 1 Єℤn tal que aa-1 = 1 .
2.2. Producto directo de cuerpos
Sean I un conjunto arbitrario y {Ri} iЄ I una familia de cuerpos. Se llama R = al anillo producto con las operaciones suma y producto componente a componente. Sea П iЄI : R→R i la proyección i-ésima, es decir para f = (f (i))iЄI Є R, ϖ i(f)= f (i).
La siguiente proposition caracteriza los elementos de un producto de cuerpos.
Proposición 2.4 Sean R = П iЄI Ri y f= (f (i)) iЄI Є R. Entonces
1. f es invertible si y so/o si, para todo i Є I, Пi (f) = f (i) ≠ 0.
2. f es un divisor de cero si y so/o si existe i G1 tal que ϖ i (f ) = 0.
Demostración 1. Si para todo i Є I, f (i) ≠ 0, entonces para cada i Є I, tenemos que
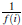 ≠
0. De esta forma, definimos el inverso de f como f
-1 = (
≠
0. De esta forma, definimos el inverso de f como f
-1 = (
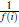 )
iЄI
Є R. El recíproco es inmediato.
)
iЄI
Є R. El recíproco es inmediato.
2. Si existe i Є I tal que f (i) = 0 entonces definimos g = (g(i)) iЄI Є R como g(i) = 1 y g(j) = 0 para todo j ≠ i. Luego, g ≠ 0 y f∙g = 0. El recíproco es inmediato.
2.2.1. Anillo de fracciones
Sean R un anillo y S un subconjunto multiplicativo de R, es decir, 1 Є S y si s, t Є S entonces st Є S. Se define en R x S la relation de equivalencia
para algún s Є S. En el conjunto RS = (R x S)/ ~, se denota a la clase de equivalencia de (f, g) como
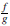 y se definen las operaciones suma y producto así,
y se definen las operaciones suma y producto así,
Estas operaciones están bien definidas y hacen de R
S un anillo conmutativo con unidad, donde el cero es
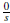 , para s Є S y la unidad es
, para s Є S y la unidad es
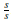 , para s Є S. Más aún, se tiene un homomorfismo canónico de anillos φ : R → R
S dado por φ (f) =
, para s Є S. Más aún, se tiene un homomorfismo canónico de anillos φ : R → R
S dado por φ (f) =
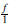 que en general no es inyectivo. El anillo R
S se llama anillo de fracciones o localización de R por S.
que en general no es inyectivo. El anillo R
S se llama anillo de fracciones o localización de R por S.
Sea R un producto de cuerpos, es decir, R = П iЄI R i , donde R i es un cuerpo. Por (Proposition 3.5, [7]), se tiene el isomorfismo entre el cuerpo R/m y el anillo de fracciones o localization R m, para todo m Є Max(R).
Por otra parte, como R es un producto de cuerpos, entonces
Ejemplo 2.5 Se considera R = ℝ3, entonces Spec(ℝ3) = Max(ℝ3) y
Proposición 2.6 (Coro/ario 3.7, [7]) Sean K un cuerpo finito, I un conjunto arbitrario y R = K1. Para todo m Є Max(R),
La prueba de la Proposición 2.6 es constructiva, para comprender mejor este resultado se presenta el siguiente ejemplo.
Ejemplo 2.7 Consideremos el cuerpo finito K = ℤ3 ye/ producto R = ℤ3 x ℤ3. Los idea/es maximales de R son
Puesto que M1 y M2 son idea/es primos, S1 = R \ M1 y S2 = R \ M2 son los conjuntos multiplicativos de R. El anillo de fracciones de R por S1 está dado por
y e/ anillo de fracciones de R por S2 es (a, b)
Por la propiedad universal de los anillos de fracciones, se definen los siguientes homomorfismos de anillos φ1:
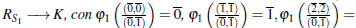
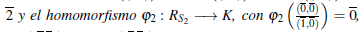
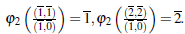 y Luego φ1 y φ1
son biyectivas y en consecuencia R
s1 ≃ K y R
s2 ≃ K. Además R/
y Luego φ1 y φ1
son biyectivas y en consecuencia R
s1 ≃ K y R
s2 ≃ K. Además R/
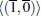 ≃ K y R
≃ K y R
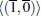 ≃ K como se indica en la Proposición 2.6.
≃ K como se indica en la Proposición 2.6.
2.3. K-álgebras finitas
Se dice que R es un K-álgebra finita si R es un algebra conmutativa con unidad y de dimension finita como K-espacio vectorial. Existen, salvo isomorfismos, tres algebras de dimensión 2 sobre ℝ, ℂ=
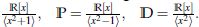
Esto es debido a que en una extensión de grado 2 de ℝ,
se pueden dar tres casos según x2 + bx + c tenga dos raíces imaginarias, dos raíces reales distintas o una raíz doble. Los conjuntos ℂ, ℙ, 𝔻 son, respectivamente, los números complejos, los números para complejos y los números duales. Observe que ℂ es un cuerpo, mientras que ℙ y 𝔻 no lo son pues ℙ tiene divisores de cero y 𝔻 tiene además elementos nilpotentes.
Por (Proposición 2.2, [5]), tenemos que un K-algebra finita se descompone en una suma directa de K-algebras finitas locales. Además, por (Proposición 4.2, [6]), un K-algebra finita es un anillo total de fracciones.
Lema 2.8 (Lema 2.3, [5]) Sea R = ⊕r i=1 R i un K-álgebra finita donde cada R i es un K-algebra finita local. Para i = 1,..., r sean m¡ el ideal maximal de R i. Entonces:
1. Max(R) = {M 1,...,M r} donde M i = Пr j =1m j con m j = R j, para todo j ≠ i y m i; = m i.
2. Para todo i = 1,..., r se tiene que R Mi ≃ R i.
Ejemplo 2.9 Considere el ℤ2 -álgebra
R tiene un único ideal maximal m = ⟨x, y⟩ con orden de m igual a 2.
Ejemplo 2.10 Considere el ℤ2-álgebra A = ℤ2[x]/⟨x2⟩ y el producto
Los ideales maximales de R son
Puesto que M1 y M2 también son ideales primos de R, S1 = R \ M1 y S2 = R \ M2 son conjuntos multiplcativos de R. El anillo de fracciones de R por S1 está dado por
Definimos φ1: RS1 →
A, donde φ1
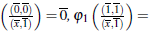
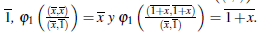
Analogamente, el anillo de fracciones de R por S2 esta dado por
De igual forma se define φ2: R
S2 → A, donde φ2
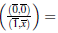
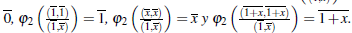
Por lo anterior RM1 ≃ RM2 ≃ ℤ2 [x]/ ⟨x2⟩, como se menciona en el Lema 2.8.
3. Inmersión de un anillo no local en un producto de cuerpos
Sea R un anillo y consideremos el producto de cuerpos
Por la propiedad universal del producto existe un homomorfismo de anillos
En general φ es no inyectiva pues Ker(p ) =
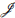 (R), donde
(R), donde
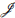 (R) es el radical de Jacobson de R. En efecto,
(R) es el radical de Jacobson de R. En efecto,
Así, si
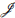 (R) = 0 entonces φ es un homomorfismo inyectivo.
(R) = 0 entonces φ es un homomorfismo inyectivo.
Proposición 3.1 Considere
Entonces,
1. φ (/(R)) = I(ПmЄMax(R) R/m) ∩ φ (R).
2. φ (a) Є O(ПmЄMax(R) R/m) ∩ φ (R), para todo a Є R, si y solo si existe m Є Max(R) tal que a Є m.
3. φ (O(R)) ⊂ (ПmЄMax(R) R/m) ∩ φ (R).
4. Si R es anillo total de facciones entonces φ (O(R)) = O (ПmЄMax(R) R/m) ∩ φ (R) Ademas, el recíproco se verifica si
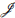 (R) = {0}.
(R) = {0}.
Demostracioón 1. Si a Є R es invertible entonces a ∉ m para todo m Є Max(R), luego a + m ≠ 0 en R/m para todo m, por tanto p (a) es invertible en ПmЄMax(R) R/m. Recíprocamente, sea b G /( ПmЄMax(R) R/m) H p (R), existe a G R tal que b = φ (a) y φ (a) es invertible en ПmЄMax(R) R/m entonces a + m ≠ 0 en R/m para todo m Є Max(R), por tanto a ∉ m para todo m, luego a es invertible y b Є φ (/(R)).
2. Inmediato porque un elemento de un producto de cuerpos es cero o divisor de cero si y solo si tiene una componente nula.
3. Un elemento que es cero o divisor de cero está contenido en algún maximal y por tanto aplicamos el ítem (2).
4. Sea Пm R/m =ПmЄMax(R) R/m, por la Proposición 2.4, Пm R/m es un anillo total de fracciones, entonces:
y
Además, por el ítem (1), φ (I(R)) = I (Пm R/m)∩ φ (R) y por el ítem (3), φ(O(R)) ⊂ 0(ПmR/m)∩ φ(R). ⇒: Por hipótesis, R es un anillo total de fracciones, entonces R = O(R) U /(R) y O(R) ∩I(R) = 0. En consecuencia,
⇐: Sea a Є R. Vamos a ver que R es anillo total de fracciones, para esto veUamos primero que si a ∉ /(R) entonces p(a) ∉ /(Пm R/m)∩ φ (R).
En efecto, si φ (a) Є I(Пm R/m)∩ φ (R) entonces, por el ítem (I), existe b Є R tal que φ (b) = φ (a) y b Є I(R), por tanto φ(b - a) = 0. Como φ es inyectiva ya que
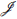 (R) = {0} entonces b = a y a Є I(R).
(R) = {0} entonces b = a y a Є I(R).
Ahora, si a ∉ I (R), entonces φ(a) ∉ I (ПmR/m) ∩ φ(R) pero φ (a) Є φ (R) luego, φ (a) ∉ I(Пm R/m). En consecuencia, φ (a) Є 0(Пm R/m) ∩ φ (R) = φ (0(R)). Luego, existe b Є O(R) tal que φ (a) = φ (b), esto es, φ (a - b) = 0. y como φ es inyectiva, a = b y a Є O(R). Así, R es un anillo total de fracciones.
Observación 3.2 El anillo de los enteros ℤ cumple que O(ℤ) = ∅ pues ℤ no tiene divisores de cero, además el conjunto O(ПmЄMax(R) R/m) ℤ/m) ∩ φ(ℤ) es infinito ya que los idea/es maximales de ℤ son de la forma m = ⟨ p⟩ con p numero primo.
Proposición 3.3 Sea R un anillo. Entonces, Max(R) = {m1,..., mr} y
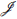 (R) = {0} si y solo si R = K1 x ∙ x Kr, donde Ki es un cuerpo para todo i = 1, ...∙r.
(R) = {0} si y solo si R = K1 x ∙ x Kr, donde Ki es un cuerpo para todo i = 1, ...∙r.
Demostración. Sea
Como
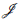 (R) = {0}, φ es inyectiva. Vamos a ver que φ es sobreyectiva para ello se debe probar que para todo (a1,∙ ∙ar) Є R
r existe a Є R con ai + m
i = a + m
i para todo i. En efecto, para todo i ≠ j, m
i + m
j = R, luego existe un residuo común, es decir, exite a Є R tal que a+ m
i = ai + m
i, para todo i.
(R) = {0}, φ es inyectiva. Vamos a ver que φ es sobreyectiva para ello se debe probar que para todo (a1,∙ ∙ar) Є R
r existe a Є R con ai + m
i = a + m
i para todo i. En efecto, para todo i ≠ j, m
i + m
j = R, luego existe un residuo común, es decir, exite a Є R tal que a+ m
i = ai + m
i, para todo i.
En consecuencia, φ es sobreyectiva y R es un producto de cuerpos.
Por otra parte, si R = K
1 x ∙ ∙ x K
r entonces, por (Proposición 2.5, [7]), Max(R) = {m1,..., mr} con m
i = {a Є R : a(i)= 0}. Luego,
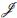 (R) = {0}.
(R) = {0}.
Ejemplo 3.4 Considere el anillo de las funciones continuas R =
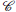 ([0,1],ℝ) y sea x Є [0,1]. En consecuencia, mx = {f Є R : f (x) = 0} es un ideal maximal, ∩xЄ[0,1] mx = {0} y como
([0,1],ℝ) y sea x Є [0,1]. En consecuencia, mx = {f Є R : f (x) = 0} es un ideal maximal, ∩xЄ[0,1] mx = {0} y como
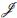 (R) ⊆ ∩xЄ[0,1]mx, entonces
(R) ⊆ ∩xЄ[0,1]mx, entonces
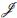 (R) = {0}. Pero R no es producto de cuerpos pues su espectro maximal tiene cardinalidad no finita.
(R) = {0}. Pero R no es producto de cuerpos pues su espectro maximal tiene cardinalidad no finita.
Ejemplo 3.5 Considere el ℝ-álgebra
Los ideales maximales de R son M
1 =⟨x2 + 1⟩ y M
2 =⟨x2 + 2⟩ Note que
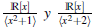 son cuerpos. Además,
son cuerpos. Además,
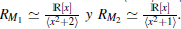 Tenemos un ejemplo de la Proposición 3.3, si se define el isomorfismo
Tenemos un ejemplo de la Proposición 3.3, si se define el isomorfismo
4. Inmersión de un anillo en su producto de localizados
En esta sección se demuestra que dado R un anillo total de fracciones con un número finito de ideales maximales, existe una inmersión de este en su producto de localizados. Para esto inicialmente probamos el Lema 4.1.
Consideremos el anillo ℤn de los residuos módulo n donde n = pr1 1...pn rn. Los ideales maximales en Z corresponden a los ideales maximales en ℤ que contienen al ideal generado por n, ⟨n⟩. Esto es, ⟨n⟩ с ⟨p⟩ ⊂ ℤ. Esto significa que p|n, así que los ideales maximales en ℤn son precisamente mi: = piℤn, donde i = 1,n. Ahora podemos enunciar el lema que nos lleva al objetivo de esta sección.
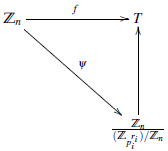
Lema 4.1 ([4], pag. 3) (ℤn)pi ≃ ℤpi ri, con n ≠ 0 y pri i |n, es decir, n = pri i b, para algún entero b.
Demostracion. Considere el homormorfismo canónico
Queremos probar que (ℤn) pi ≃ ℤpi ri, para esto, veamos que ψ satisface la propiedad universal de la localization. Es importante aclarar que estamos localizando respecto a S = ℤn/p i que consiste de todos lo elementos x̅n tales que pi no divide a x.
Si pi no divide a x, entonces x es invertible módulo pi ri, y de esto se concluye que ψ(x̅ n ) Є (ℤ pi ri )* para todo x̅ n G S.
Ahora supongamos que f : ℤn → T es un homorfismo de anillos tal que f (x̅ n) es invertible en T para todo x̅ n Є S. Por hipótesis, podemos considerar la identidad,
Aplicando f, se obtiene
Es decir,
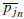 Є S para todo i ≠ j, así f (
Є S para todo i ≠ j, así f (
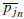 ) son invertibles en T y al multiplicar la última identidad por los inversos, obtenemos
) son invertibles en T y al multiplicar la última identidad por los inversos, obtenemos
y por lo tanto,
Esto implica que f se factoriza de modo único porel cociente de ℤn por (ℤ pi ri )/ℤn.
Por el Tercer teorema de isomorfismo, sabemos que
y se concluye que ψ satisface la propiedad universal de la localización (ℤn)pi .
Proposicion 4.2 Sean R un anillo total de fracciones y m1 , . . . , mr sus ideal es maximales, entonces
es un homorfismo inyectivo.
Demostracion. Si Ф(a) =(
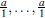 ) = (0,...,0) entonces
) = (0,...,0) entonces
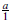 = 0 en cada Rmi. Luego existe b ∉ m
i para todo i = 1,..., r tal que ab = 0. Como R es un anillo total de fracciones, b no es divisor de cero. Luego a = 0, para todo i = 1, ,r.
= 0 en cada Rmi. Luego existe b ∉ m
i para todo i = 1,..., r tal que ab = 0. Como R es un anillo total de fracciones, b no es divisor de cero. Luego a = 0, para todo i = 1, ,r.
Proposición 4.3 Sean R = ℤn con n ≠ 0 y Max(R) = {m1,..., mr}.
Entonces,
es un isomorfismo.
Demostración. Puesto que n = p1 k1 pr kr entonces por el Teorema chino del resto,
Además, por el Lema 4.1, sabemos que (ℤn) pi ≃ ℤpi k1 para i = 1, ,r. Así,
donde Max(R) = {m1 = ⟨p 1⟩,..., m r = ⟨ p r ⟩}.
Proposicion 4.4 Sean R un K-algebra finita y Max(R) = {m1,...,mr}. Entonces,
es un isomorfismo.
Demostración. Como R es un K-álgebra finita, por (Proposición 2.2, [5]), R = ⊕r i=1 Ri donde cada Ri es un K-álgebra finita local y puesto que Max(R) = {m1,..., mr}, por el Lema 2.8, Rmi ≃ R', para todo i = 1,..., r. Así, Ф : R → Rm1 x ... x Rmr es un isomorfismo.
Ejemplo 4.5 Considere el ℤ2-álgebra
Los ideales maximales de A son m1 = ⟨x - 1⟩ y m2 = ⟨x +1⟩.
Entonces, A =
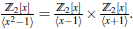 Note que Am1 ≃
Note que Am1 ≃
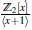 y Am2 ≃
y Am2 ≃
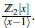 Así, tenemos el isomorfismo de la Proposición 4.4.
Así, tenemos el isomorfismo de la Proposición 4.4.
5. Conclusiones
Si R es un dominio entero, es conocido que R está inmerso en el cuerpo de fracciones de R. La inmersión de un anillo en un cuerpo o en un producto de cuerpos ha sido de mucho interés en algebra en los últimos anos. En este artículo nosotros consideramos R, un anillo conmutativo con unidad, no local, y logramos caracterizar cuando la inmersión es un isomorfismo.
El homomorfismo p de R en el producto directo de cuerpos cocientes está definido por la propiedad universal del producto y su núcleo es Kerφ =
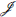 (R), donde
(R), donde
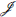 (R) es el radical de Jacobson de R. Si
(R) es el radical de Jacobson de R. Si
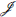 (R) = {0}, el homomorfismo φ es inyectivo en el caso infinito y en el caso finito probamos que φ es un isomorfismo. Además, logramos caracterizar la imagen de las unidades y divisores de cero de R a través de φ.
(R) = {0}, el homomorfismo φ es inyectivo en el caso infinito y en el caso finito probamos que φ es un isomorfismo. Además, logramos caracterizar la imagen de las unidades y divisores de cero de R a través de φ.
Por otra parte, cuando R es un anillo total de fracciones con un número finito de ideales maximales mostramos que el homomorfismo de R en el producto de sus localizados es inyectivo. Más aún, si R es de la forma ℤn, con n ≠ 0, vimos que el homomorfismo de anillos es un isomorfismo y tuvimos el mismo resultado si R es un K-álgebra finita con K un cuerpo.