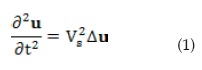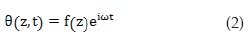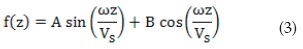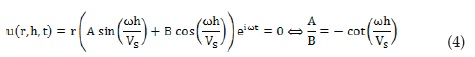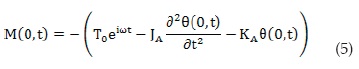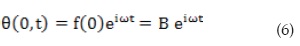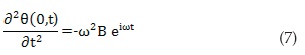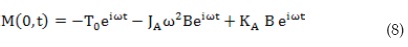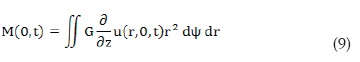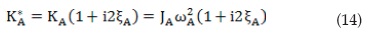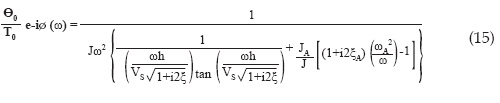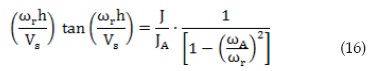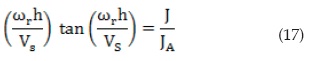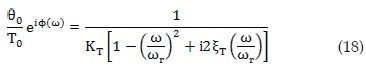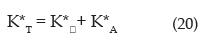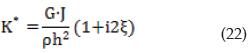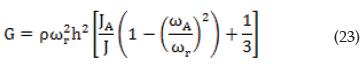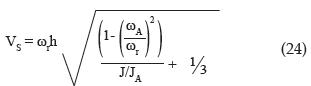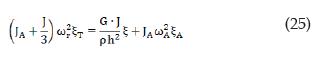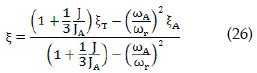Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería y Desarrollo
Print version ISSN 0122-3461
Ing. Desarro. vol.31 no.2 Barranquilla July/Dec. 2013
ARTÍCULO DE INVESTIGACIÓN / RESEARCH ARTICLE
Comparison between exact and approximated visco-elastic transfer functions for a resonant-column system
Comparación entre las funciones de transferencia viscoelástica exacta y aproximada de un sistema de columna resonante
Javier Camacho-Tauta*
Universidad Militar Nueva Granada (Colombia)
*Ingeniero civil, Universidad Militar Nueva Granada (Colombia). Magíster en Ingeniería Civil, Universidad de los Andes (Colombia) y Doctor en Ingeniería Civil, Universidad Técnica de Lisboa (Portugal). Profesor asociado de tiempo completo. Grupo de Investigación Geotecnia. Facultad de Ingeniería, Universidad Militar Nueva Granada. javier.camacho@unimilitar.edu.co
Correspondencia: Universidad Militar Nueva Granada, Carrera 11 n° 101-80 Edificio F, Bogotá (Colombia). Teléfono: +57(1) 6500000 Ext. 1291 Origen de subvenciones: Esta investigación forma parte de los proyectos de investigación ING-953 "Hacia la obtención de un modelo unificado de curvas de reducción del módulo" y PIC ING-905, financiados por la Universidad Militar Nueva Granada.
Fecha de recepción: 14 de septiembre de 2012
Fecha de aceptación: 13 de mayo de 2013
Abstract
The resonant column test is the standard method in the laboratory to obtain the dynamic properties of the soil. The state of dynamic equilibrium during the test can be represented by a viscoelastic model that is expressed by a transcendent equation in complex variables. It implies that the solution of the equation to find the shear modulus and damping ratio should use fairly sophisticated numerical techniques. This article presents and compares an approximate viscoelastic equation that allows obtaining an approximate value of the dynamic properties of the soil. Finally, a set of resonant-column test was performed in order to verify the proper performance of the proposed solution.
Keywords: Resonant-column, Shear-wave velocity, Soil stiffness, Visco-elasticity.
Resumen
El ensayo de columna resonante es el método de referencia en laboratorio para obtener las propiedades dinámicas del suelo. El estado de equilibrio dinámico durante el ensayo se puede representar mediante un modelo viscoelástico que se expresa mediante una ecuación trascendente en variable compleja. Lo anterior implica que se deben utilizar técnicas numéricas de cierta sofisticación para la resolución de la ecuación y así poder encontrar los valores del módulo de corte y de la relación de amortiguamiento. En el presente artículo se propone y compara una ecuación viscoelástica aproximada que permite obtener un valor cercano de las propiedades dinámicas del suelo. Finalmente, se llevó a cabo un conjunto de ensayos de columna resonante para verificar la exactitud de la solución propuesta.
Palabras clave: Columna resonante, Rigidez del suelo, Velocidad de la onda cortante, Viscoelasticidad.
1. INTRODUCTION
The resonant-column (RC) test is currently recognized as the reference laboratory method to evaluate dynamic properties of soils [1]. During this test, a cylindrical specimen of soil is subjected to a steady-state harmonic excitation, and the response of the system in terms of vibration is measured. The frequency of the input signal is shifted until resonance is achieved. Then, it is possible to compute the dynamic properties (i.e. modulus and damping ratio) of the soil as derived from the dynamic equilibrium of the specimen. Woods [2] traced back to the first application of the RC method made by the Japanese engineers Ishimoto and Ida in 1937. About twenty years later, Shannnon et ál. [3] revived the technique, which has been continuously improved over the years, until present.
The exact solution of the dynamic system makes use of the theory of wave propagation, since the specimen is idealized as a viscoelastic rod subjected to a forced vibration. The governing equation of motion establishes the proportionality between the resonant frequency and the shearwave velocity. Santos [4] derived an equation for a Drnevich-type RC apparatus. Following a similar procedure, Lai et ál. [5] derived an expression for a Stokoe-type RC apparatus. These exact viscoelastic solutions adopt the form of a transcendent and complex-value function, in which the shear modulus and the damping ratio should be solved simultaneously by a curve fitting method. This process is performed by an iterative procedure that needs an initial estimated value. Usually, the procedure only converges if such initial value is closely approximate to the actual value. Otherwise, the iterative process may not to converge or even reach illogical results.
Variables included in the viscoelastic model, such as the calibration factors and the physical and geometrical properties of the specimen could have different extents of influence on the computed values of the shear modulus and damping ratio. The influence of these factors is analysed in this paper.
The objective of the work is to propose an approximate solution of the RC system based on a single-degree-of-freedom (SDOF) representation of the system. Although the approximate equation is complex and transcendent as well the exact solution, it has fewer variables and usually converges faster. The approximate soil parameters obtained by the proposed equation could provide satisfactory results in most cases, or at least approximate results could serve as the initial values in the iterative procedure using the exact viscoelastic solution.
2. THEORETICAL BACKGROUND
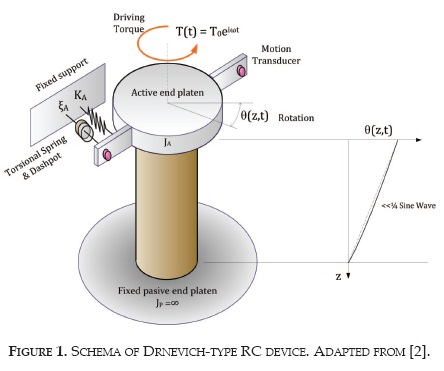
The two most common types of RC devices are known as the Stokoe and Drnevich [6]. In the first one, the top end of the specimen is in totally free condition, whereas in the second one, the top end of the specimen is partially restrained by a spring and a dashpot. In both cases, the top end of the specimen is firmly bonded to an active end mass with rotational mass inertia JA.
The top mass includes the driving motor used to apply torque to the cylinder. The inertial mass of the top end contributes to produce a nearly linear distribution of the rotation through the height [7]. The base of the specimen is firmly bonded to the pedestal and no rotation is allowed. The pedestal, in turn, is rigidly anchored, or at least, has a rotational mass inertia JP, 100 times greater than the rotational mass inertia of the soil specimen [1]. The soil specimen having an inertial rotational mass J, is forced to vibrate under a harmonic torque T(t) with amplitude T0 and arbitrary frequency ω. As a result of this external excitation, the specimen rotates an angle of twist ϴ, with a magnitude that depends on the time t, and the elevation z.
A schematic representation of the Drnevich-type RC device is presented in Figure 1. The top active platen is partially restrained by a spring with constant KA and a dashpot with constant damping ratio ξA. This feature produces a better distribution of the rotation angle and the system is able to apply up to medium shear strain levels.
The exact viscoelastic solution
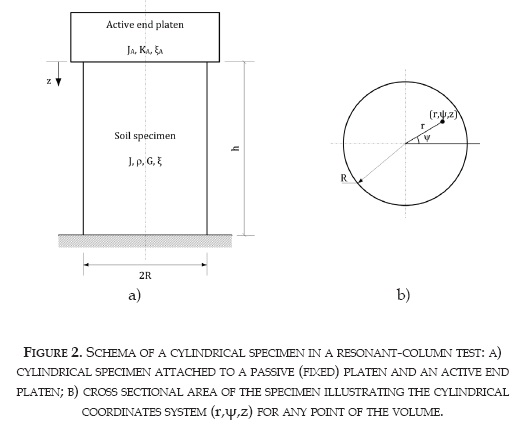
In the following derivation, it is assumed that the rod is a homogeneous, isotropic and elastic solid. Figure 2a shows a cylindrical specimenwith mass density ρ, mass polar moment of inertia J, shear modulus G and damping ratio ξ. The base of the cylinder is firmly attached to a fixed support and the top is attached to the active end platen.
The dynamical properties of the active platen JA, KA and ξA are known. Taking into account the geometrical shape of the components, it is advantageous the use of a cylindrical coordinate system specified by three independent components, namely: radius r; angular position ψ and height z. The components of the cylindrical coordinate system are illustrated in Figure 2b.
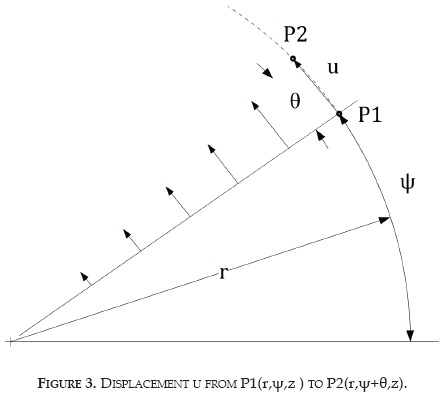
The phenomenon of propagation of shear waves in an isotropic homogeneous and elastic medium is represented by the wave equation expressed in Equation (1). The Equation describes the movement of a particle located at any position of the medium.
Where Δ is the Laplacian operator in cylindrical coordinates (r,ψ,z), u the displacement of a particle located at position (r,ψ,z), t the time and VS the shear-wave velocity. Figure 3 shows the displacement u of a point P1 located at coordinates (r,ψ,z).
The displacement component in direction ψ can be considered as u=r∙θ (z,t). The rotation angle θ depends on both z coordinate and time t according to:
Where ω is the angular frequency of the wave. For a harmonic wave, the solution of the partial differential Equation (1) implies that the function f(z) follows the forms of Equation (3):
The constants A and B depend on the boundary conditions of the specimen as follows:
I) Angular displacement at the fixed end at any time is equal to zero, u(r,h,t) = 0:
II) The top of the specimen (z=0) is attached to a rigid mass with mass moment of inertia JA and subject to an externally applied harmonic torque. Additionally, for a Drnevich apparatus, there is a link between the top mass and the structure, which can be represented by a spring with constant KA. The total external moment is thus a result of three forces: applied torque, inertial force of the top mass and spring force, as expressed by [4]:
The value of the rotation at the point z=0 is given by Equation (2):
and its second derivative:
Introducing Equations (6) and (7) in Equation (5):
Moreover, if self-weight is neglected, only shear stress is non-zero. The moment is computed by integration of the shear stress over the area of the cross-section, located at depth z=0:
Where G=ρVS 2. By integration, the torsional moment yields to:
Therefore, combining Equations (8) and (10), the equilibrium at z=0 is represented by:
By dividing both sides of the equation by the rotation angle at z=0, taking into account that J=0.5ρh}πR4 and after some arrangements, the rotationto-torque ratio is given by:
Until now, only elastic behaviour was admitted. However, the system is more realistic modelled if it is considered as slightly visco-elastic. This can be done by introducing the complex parameters VS* and KA*, using the Elastic/Visco-elastic correspondence principle [8]:
Whre wA is the resonant frequency of the apparatus without specimen (torsional resonant frequency of the active mass). On the other hand, torque and rotation have the same frequency and are generally out in phase. Thus, ωt can be substituted by the phase lag between signals. ϕ(ω). By introducing these two modifications, Equation (12) becomes:
Equation (15) is known as the transfer function of the RC system that relates the amplitude of the twist angle ϴ0, the amplitude of the torque T0, and the phase lag ϕ, between them for any angular frequency ω of the excitation signal.
A particular case of the function is when the system is vibrating at resonant frequency ωr, the response of the system tends to infinity for a zero material damping and zero apparatus damping, therefore Equation (15) becomes:
Equations (15) and (16) are equivalent to those derived by Santos [4] and are exact for a slightly visco-elastic material, which is valid for a soil under small-strain loading. If the apparatus does not have springs attached to the active end (i.e. Stokoe-type apparatus), the value of ωA becomes zero and Equation (16) takes the classical form as expressed by Richart et ál. [9]:
In the conventional procedure, the resonant frequency is experimentally measured by gradually shifting the excitation frequency ω of a sinusoidal torque T, until observe that T and ϴ at the top end are ϕ=π/2 out in phase.
Then, VS is directly computed from Equation (16) because h and J are measurable properties of the specimen, and JA and ωA are apparatus constants previously obtained by calibration. Once the VS is determined, Equation (15) serves to compute ξ because other variables are known by either direct measurement or previous calibration. Moreover, both material properties can be obtained simultaneously in Equation (15) since the relationship between them, through the complex shear-wave velocity expressed in Equation (13).
Since Equation (16) is transcendental (that is, the unknown variable cannot be isolated), it becomes necessary to solve it by an iterative process that needs an initial estimated value. Equation (15) on the other hand, is transcendental and complex, requiring a precise determination of the experimental data and solved by a curve fitting procedure involving complex-value data. The procedure only converges if the initial estimated value is closely approximate to the actual result.
The approximate viscoelastic solution
Soil properties have huge variations depending of many factors, even for a particular soil specimen. For this reason, the proper selection of initial values to find the dynamic soil parameters in Equation (15) allows the successful and fast convergence of the iterative process. The approximate solution presented in this section looks to provide the initial estimate values based on a single degree of freedom model (SDOF) [10]. A RC system can be approximately represented by a SDOF model [11].
Where ξT is the total damping of the system. Although it is a complex-value equation, it has fewer variables and usually converges faster than the exact solution expressed in Equation (15). According to Cascante [12] and Kumar and Clayton [13], Rayleigh’s method for torsional vibration provides an approximation for the mass polar-moment of inertia of this system and the associated shear stiffness KT:
The SDOF system is composed by two serial-connected elements: the soil specimen and the active end platen (Figure 4). For simplicity, this figure illustrates a system with an axial DOF, but the analysis is also valid for a rotational system.
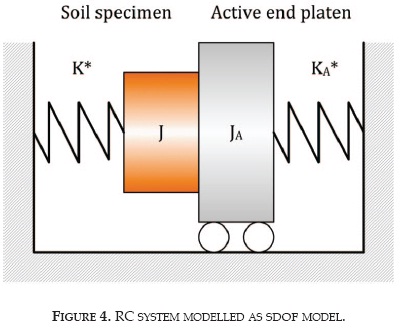
Since both springs are in series and subjected to the same twist angle, the total complex stiffness can be approximately expressed as:
Where:
KA* was defined by Equation (14) and the complex torsional stiffness of the soil specimen K*, can be computed from:
From the real part of Equation (20), the approximate value of the shear modulus is represented by:
while the approximate shear-wave velocity can be a function of measurable variables ω r, h, J/JA and ωA/ωr :
From the imaginary component of Equation (20):
By using Equation (23) and rearranging variables, Equation (26) enables to find an approximate value of the soil damping as function of measurable variables ξT, ξA, J/JA and ωA/ωr :
Comparison of viscoelastic equations
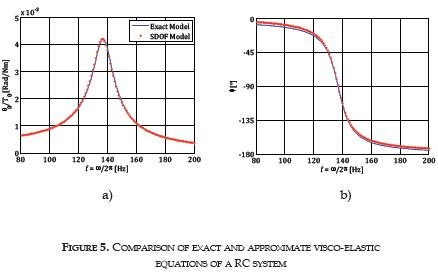
To illustrate the shape of exact and approximate visco-elastic equations, Figure 5 plots the absolute amplitude and phase angle for a resonant-column system for typical property values of a hypothetical soil specimen (G = 100 MPa, ξ = 5%, d = 0.07 m, h = 0.10 m, ρ = 1500 kg/m3) and calibration factors (JA = 0.003087 kg m2, ωA= 100 Rad/seg, ξA= 4.54%).
In the example, while the actual shear modulus is 100 MPa and the actual damping ratio is 5%, the estimations with the approximate solution are 99.97 MPa and 5%, respectively. These approximate results could be satisfactory in practice. Nevertheless, if a refinement is required, approximate results are optimum initial values of the curve fitting procedure to estimate the parameters by using the exact solution.
Factors influencing the viscoelastic solutions
Shear-wave velocity
At resonance, exact and approximate viscoelastic solutions provide a solution for the shear-wave velocity by Equations (16) and (24), respectively. Both equations depend on J/JA, ωA/ωr, ωr and h. In the exact solution, VS cannot be isolated and therefore the actual value should be obtained by numerical methods. In contrast, in the approximate solution VS is directly obtained.
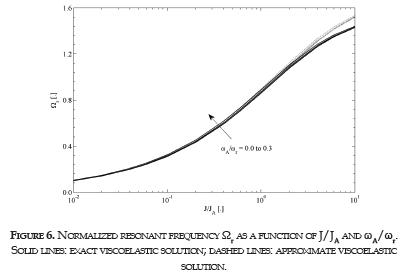
The normalized resonant frequency, Ωr describes the direct linear relationship between the resonant frequency and the shear-wave velocity for a specific soil specimen:
Figure 6 shows Ωr as a function of J/JA and ωA/ωr for the exact solution as well as for the approximate. Both solution exhibit a very well agreement between them for J/JA<0.5. This ratio is usually lower than 0.1 and consequently the approximate solution is a good substitute for the exact one. Regarding the influence of the apparatus resonant frequency, ωA/ωr is an adequate parameter to analyze it. From the figure, the higher the value of /ωis, the lower the estimation of VS. For instance, the value of Ωfor J/ωAr r JA=0.5 and ωA/ωr=0, differs only 1.7% from the respective value for J/JA=0.5 and ωA/ωr=0.2, which is a typical maximum ratio in most Drnevich-type apparatuses. It means that a deviation in the determination of ωA during calibration implies an insignificant error in the calculated value of the shear-wave velocity.
Finally, J/JA is an important ratio that must be accurately determined because it has strong influence on Ωr. J depends on the total mass and the diameter of the specimen. Both properties can be measured with sufficient precision with conventional instruments available in laboratory. On the other hand, JA is obtained by calibration. A method to measure this calibration factor as an alternative to the method described in the standard method [1] was proposed in [6]. Both methods allow stable measurements of JA.
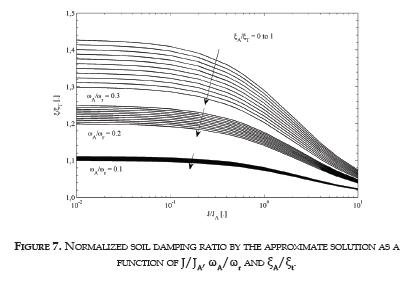
Damping ratio
Concerning the damping ratio, Equations (15) and (27) are used to compute the damping ratio by the exact and approximate viscoelastic solutions, respectively. The approximate solution provides a direct value of the damping ratio that depends on J/JA, ωA/ωr, ξA and ξT. Figure 7 presents the influence of each of these ratios. For convenience, ξ and ξA were normalized by ξT and the curves are grouped in three sets according to their respective value of ωA/ωr. For a Stokoe-type apparatus in which neither ωA nor ξA exist, the total damping of the system is only due to the soil and therefore ωA/ωr =0 and ξ/ξT =1 for any value of J/JA.
The three sets of curves correspond to increasing values of ωA/ωr. As this ratio increases, the effect of the apparatus damping ratio has more influence on ξ/ξT. This fact confirms the requisite of RC devices with small values of ωA and a careful determination of ξA. It is remarkable that ξ≥ξT because in this serial model ξT ≠ξ+ξA.
In the case of the exact solution, there is not a direct solution of the damping ratio, as can be verified in Equation (15). Thus, it is not possible to make a sensibility analysis as performed with Equation (27).
3. EXPERIMENTAL PROCEDURE
Equipment
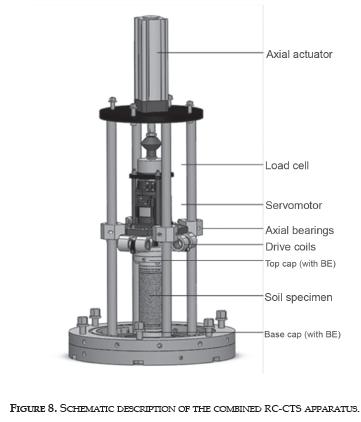
A Drnevich-type device capable of performing sequentially resonant-column (RC) and cyclic torsional shear (CTS) tests was designed and implemented in a triaxial stress system. In this device, it is possible to apply vibrations to the soil specimen ranging from 0.01 to 20 kHz. Figure 9 shows a schematic description of the apparatus with its main components.
The resonant-column subsystem is composed by four drive coils to produce the rotational vibration on the specimen. The input signal is generated by a function generator (Hameg HM8150, 12.5 MHz) and the current amplified by an amplifier (STP-890, 700 W). The vibration is measured by an accelerometer (Dytran, 3055B2) and the signal amplified by a signal conditioner (Dytran, 4119B). The Cyclic torsional subsystem is composed bya servomotor (Yaskawa, Sigma-5 200W, 1.96 Nm). The servomotor applies the torque and measures the resulting rotation with a precision of 10-5 rad.
Axial and volumetric deformations, as well as cell, back and pore pressure, and axial force are measured by electronic sensors and all the information is acquired by a data acquisition card (NI, CompactDAQ 9174). The information is automatically processed by a software in LabView [14]. The apparatus calibration factors were: JA = 0.003087 kg m², ωA= 114.98 Rad/seg, ξA = 4.54%
Tests
The initial water content of the commercial kaolinite was determined previously as well as the liquid and plastic limits. The material was disintegrated by the use of a hammer, passed through a sieve and lumps disintegrated again until total reduction of the material into powder. The powder was mixed with water in proportions to obtain a water content equivalent to 1.5 times the liquid limit of the clay. Then, the mixture was poured into a cylindrical mold, which rests on a bed of sand covered by filter paper. The set was placed in a water tank and the soil was gradually loaded.
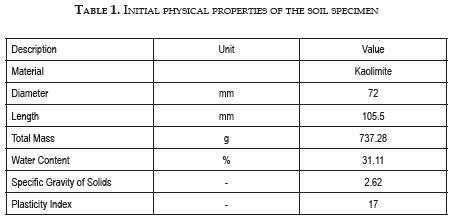
After the consolidation process, the specimen was extruded and cut. The specimen was weighted and its dimensions measured before the installation in the equipment. Filter papers were used to avoid solid migration into the porous stones. The latex membrane was placed by means of the membrane expansion tube and the top cap was carefully positioned on to the specimen. Once obtained full contact between top cap and specimen, the membrane was fixed to the top cap by means of two o-rings. Finally, the triaxial chamber was placed, filled with water and pressurized up to 20 kPa. Vertical load was adjusted accordingly to impose the isotropic stress. Table 1 shows the main initial physical properties of the soil specimen.
The specimen was confined and consolidated under 50 kPa of isotropic stress. Once the consolidation process was completed, the specimen was tested with the Non-Resonance (NR) method [15]. In this type of RC method, the system is excited with a continuous sine signal with fixed frequency, the vibratory response is measured by mean of the accelerometer, and the amplitude of the input signal is adjusted until the response reaches a desired level.
This procedure was repeated for different frequencies in a 25 Hz bandwidth around resonance. Next, the target vibration level was increased in order to impose a higher shear strain (a total of four strain levels between 2.5x10-6 and 2.5x10-5) and the NR method was re-started. Finally, the specimen was consolidated under a higher isotropic stress (100, 200 and 400 kPa), iterating the entire process along the shear strains and frequencies. The software is capable of performing this process for each stress state without operator intervention.
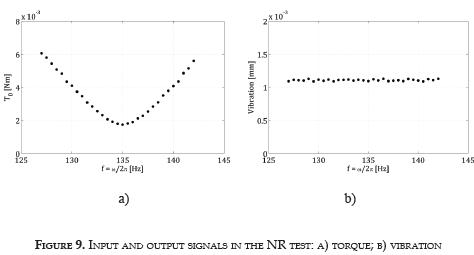
Plots of the torque (T0) and vibration (u0) amplitudes as a function of frequency for 200 kPa of isotropic effective stress of and 5x10-6 of shear strain are presented in Figure 9.
As the frequency approaches to resonance, reduces the torque needed
(Figure 9a) to impose the desired vibration (Figure 9b). The NR method ensures that the strain level is almost constant for every frequency. A total of sixteen pair of graphs similar to the one presented in Figure 9 were obtained by means of this laboratory methodology (four stress states and four shear strain levels).
All the information was processed by using both the exact visco-elastic model (Equation 15) and the SDOF model (Equation 18) by complex curve fitting in order to obtain the resonant frequency, the shear-wave velocity and the shear damping ratio.
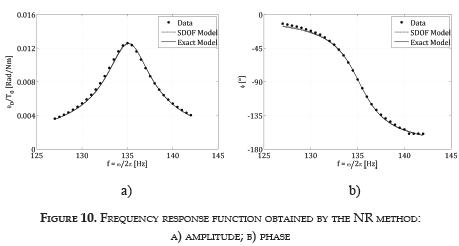
Figure 10 shows the frequency response function obtained by the NR test for the kaolinite specimen. In this figure, the representation of this complex function was separated in two parts: the amplitude and the phase angle function between the torque and the rotation. Exact and approximate visco-elastic solutions are also included in the figure, showing the high similarity between them.
4. RESULTS AND DISCUSION
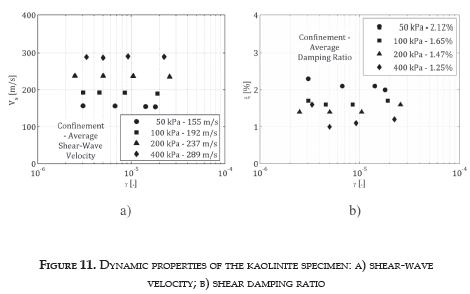
Figure 11 presents the shear-wave velocity and the associated damping ratio computed by means of the exact viscoelastic model. For each confinement, the shear-wave velocity (Figure 11a) is practically constant because the soil behavior is essentially elastic in these small-strain levels [16].
In addition, the shear-wave velocity increases as the confinement increases. The damping ratio (Figure 11b) oscillates between 1% and 2.3% being the lower values associated to high confinements, which agrees with Darendeli [17]. There is not a clear trend due to the small-strain range.
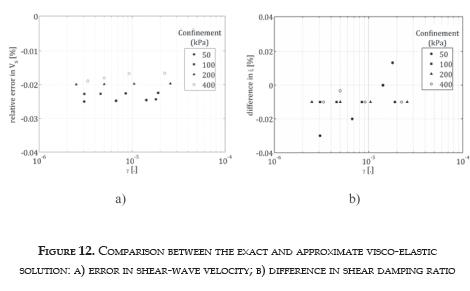
The SDOF model provided approximate values of the dynamic properties. Figure 12a shows the relative error in the computation of the shear-wave velocity by this method. In all the tests, the approximate solution was lower than the exact one and the error did not exceed -0.025%. It means that the difference between solutions is in average 0.05 m/s, which is irrelevant for practical purposes. According to the figure, the higher the confinement, the smaller the relative error. This effect could be attributed to the increase in the shear-wave velocity according to the confinement, which reduces mathematically the relative error.
Regarding the damping ratio, Figure 12b shows the difference between the approximate and the exact visco-elastic solutions. The difference was closely constant of -0.01% with the exception of tests done under 50 kPa in which this difference varies according to the shear strain. As in the shear-wave velocity, these differences are too small for practical purposes.
The experimental evidence presented allows to suggest that the approximate solution is sufficient to compute the dynamic soil properties. However, it is possible to add a final step to the fitting process by using the exact viscoelastic solution. In this additional iterative process, the initial value could be the approximate one found by the approximate solution.
The confinement range of the test program comprises the usual values applied in current practice. For this reason, it is reasonable to assume that other materials will exhibit similar agreement between solutions. Concerning the strain level, the method is valid for slightly visco-elastic materials, and therefore, the agreement between both solutions should decrease as the strain increases. However, the NR method used in this work has practical limitations in medium and high strains that makes not viable to extend this study beyond 5x10-5. There are other types of RC tests that can provide information beyond this strain level, but they have the following limitations: i) The conventional RC test only provides information on the resonant frequency, while the fitting process needs experimental data for a range of frequencies around resonance; ii) The RC test using a sine sweep as the input signal and processed by frequency domain methods [18] pro-vides frequency-dependant information (as presented in Figure 10), but the transfer function obtained by this method is not strain-constant (as presented in Figure 9b).
5. CONCLUSIONS
The resonant-column test is the standard laboratory method for obtaining the dynamic properties of soil. The test is based on the theory of wave propagation on a soil cylinder. The dynamic equilibrium can be characterized by an equation that represents the transfer function of the system composed by the apparatus and the soil specimen. This transfer function includes the calibration constants of the apparatus (resonant frequency, rotational mass inertia and damping ratio) and the complex stiffness of the soil.
An alternative representation of the system was presented by mean of a single-degree-of-freedom (SDOF) system. The advantage of this alternative relies on the ease of resolution, making possible that its result may be used directly or as an initial value in the iterative process of solving the exact equation. It was experimentally founded that the relative error in the shearwave velocity did not exceed 0.025% and the difference in the damping ratio was lower than 0.03%. For this reason, it is recommended to carry out a rough calculation using the SDOF model prior to the curve fitting by meansof the exact solution if the approximate one is considered insufficient.
The calibration of the apparatus is a very important process for guaranteeing the reliability of the results, especially in the Drnevich-type apparatus which has two additional parameters, compared with Stockoe-type equipment. In the first type of apparatus, a calibration error affects mainly the determination of the damping ratio. The shear-wave velocity is less distorted by calibration errors.
Acknowledgements
This paper is a result of the Research Projects ING-953 "Towards obtaining an unified model for modulus reduction curves" and PIC ING-905 funded by Nueva Granada Military University. The author acknowledges this financial support.
REFERENCES
[1] Standard Test Methods for Modulus and Damping of Ssoils by the Resonantcolumn Method, ASTM Int. Standard D 4015-1992. [ Links ]
[2] R. D. Woods, "Measurement of dynamic soil properties", in Earthquake Engineering and Soil Dynamics, Pasadena, CA, 1, 1978, pp. 91-178. [ Links ]
[3] W.L. Shannon et ál. "Dynamic triaxial test on sand", in First Panamerican Conference on Soil Mechanics and Foundation Engineering, Mexico City, 1959, pp. 476-86. [ Links ]
[4] J.A. Santos, "Soil characterization by dynamic and cyclic torsional shear test. Application to study of piles under static and dynamic horizontal loading", (in Portuguese), Ph.D. dissertation, Dept. Civil Eng., Technical Univ. of Lisbon, Lisbon, Portugal, 1999. [ Links ]
[5] C. G. Lai et ál., "Low-strain stiffness and material damping ratio coupling in soils", in Advanced Laboratory Stress-Strain Testing of Geomaterials, 2001, pp. 265-74. [ Links ]
[6] F. Tatsuoka and L. Silver, "New method for the calibration of the inertia of resonant column devices", ASTM Geotechnical Testing Journal, vol. 3, pp. 3034, 1980. [ Links ]
[7] Z. Khan et ál., "Evaluation of the first mode of vibration and base fixidity in Resonant-Column Testing", ASTM Geotechnical Testing Journal, vol. 31, no. 1, 2008. [ Links ]
[8] R.M. Christensen, Theory of Viscoelasticity - An Introduction, Academic Press, 1971. [ Links ]
[9] F. E. Richart, Vibrations of Soils and Foundations, Englewood Cliffs: Prentice-Hall, 1970. [ Links ]
[10] J. C. Santamarina and D. Fratta, Discrete Signals and Inverse Problems, West Sussex: John Wiley & Sons Ltd., 2005. [ Links ]
[11] Z. Khan et ál. "Measurement of frequency-dependent dynamic properties of soils using the resonant-column device", ASCE Journal of Geotechnical and Geoenvironmental Engineering, vol. 134, pp. 1319-26, 2008. [ Links ]
[12] G. Cascante, "Propagation of mechanical waves in particulate materials. Experimental micromechanics", Ph.D. dissertation, Univ. of Waterloo, Canada, 1996. [ Links ]
[13] J. Kumarand C. R. I. Clayton, "Effect of sample torsional stiffness on resonant column test results", Canadian Geotechnical Journal, vol. 44, pp. 221-30, 2007. [ Links ]
[14] National Instruments, LabView 2010 Professional Development System, 2010. [ Links ]
[15] G. J. Rix and J. Meng, "A non-resonance method for measuring dynamic soil properties", ASTM Geotechnical Testing Journal, vol. 28, pp. 1-8, 2005. [ Links ]
[16] M. V. Vucetic, "Cyclic threshold shear strain in soils", Journal of Geotechnical Engineering ASCE, vol. 120, no. 12, pp. 2208-2228, 1994. [ Links ]
[17] M. B. Darendeli, "Development of a new family of normalized modulus reduction and material damping curves", Ph.D. dissertation, The University of Texas, AU, 2001. [ Links ]
[18] J. F. Camacho-Tauta, "Evaluation of the small-strain stiffness of soil by non-conventional dynamic testing methods", Ph.D. dissertation, Technical University of Lisbon, Portugal, 2011. [ Links ]