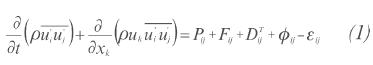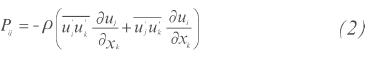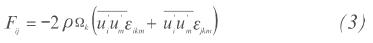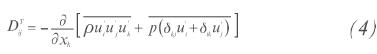Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
CT&F - Ciencia, Tecnología y Futuro
Print version ISSN 0122-5383On-line version ISSN 2382-4581
C.T.F Cienc. Tecnol. Futuro vol.4 no.4 Bucaramanga July/Dec. 2011
HYDRODYNAMIC COMPUTATIONAL EVALUATION IN SOLAR TUBULAR PHOTOBIOREACTORS BENDS
José-Luis Ramírez-Duque1* and Mabel-Angélica Ramos-Lucumi1*
1Universidad Autónoma de Occidente, Cali, Valle, Colombia
E-mail: joslurad@hotmail.com mabelramos@gmail.com
(Received Jun. 08, 2011; Accepted Nov. 02, 2011)
*To whom correspondence should be addressed
ABSTRACT
In this article, the hydrodynamic behavior of a single-phase flow in various solar collectors with diffe-rent cross sections (circular, octagonal, hexagonal and square), with same hydraulic diameter and longitudinal profile was analyzed. Secondary flow, pressure drop and shear stress were evaluated, because the photosynthetic efficiency and microalgae endurance depend on these properties. These parameters were reviewed at six different culture inlet rates in the collector (from 0,25 m/s to 0,5 m/s), emphasizing in the bends regions. A higher speed and agitation was pre-sent in the square solar collector, contrary to what happened to the circular one. Despite this, the circular solar collector remains the best option for the industrial implementation phase. However, the shear stress generated in the culture -as it passes through the 180° bend of the solar collector- affects the microalgae growth, as stated in the literature.
Keywords: Computational fluid dynamic, Microalgae, Microalgal biomass, Shear stress, Solar collector, Tubular photobioreactor.
RESUMEN
En este artículo se analizó el comportamiento hidrodinámico de un flujo monofásico en varios colectores solares, con diferentes perfiles transversales (circular, octagonal, hexagonal y cuadrado), de igual diámetro hidráulico y perfil longitudinal. Se evaluó el flujo secundario, las caídas de presión y el esfuerzo cortante del fluido, ya que de estos depende la eficiencia fotosintética y la vitalidad microalgal. Los anteriores parámetros se revisaron para seis diferentes velocidades de entrada del cultivo en el colector (entre 0,25 m/s a 0,5 m/s) enfatizándose en la región de los codos, donde se presenta una mayor velocidad y agitación en el colector solar cuadrado, contrario a lo que sucede con el circular. A pesar de esto, el colector solar circular continúa siendo la mejor opción en la etapa de implementación industrial. Sin embargo, el esfuerzo cortante que se genera en el cultivo, a medida que atraviesa el codo de 180° del colector solar, afecta el crecimiento de las microalgas, según lo estipulado en la literatura relacionada.
Palabras claves: Biomasa microalgal, Colectores solares, Dinámica de fluidos computacional, Esfuerzos cortantes, Microalgas, Fotobiorreactor tubular.
RESUMO
Neste artigo foi analisado o comportamento hidrodinâmico de um fluxo monofásico em vários coletores solares, com diferentes perfis transversais (circular, octogonal, hexagonal e quadrado), de igual diâmetro hidráulico e perfil longitudinal. Foi avaliado o fluxo secundário, as quedas de pressão e o esforço cortante do fluido, já que destes depende a eficiência fotossintética e a vitalidade microalgal. Os anteriores parâmetros foram revisados para seis diferentes velocidades de entrada do cultivo no coletor (entre 0,25 a 0,5 m/s) sendo enfatizado na região dos joelhos, onde é apresentada uma maior velocidade e agitação no coletor solar quadrado, contrário ao que acontece com o circular. Apesar disto, o coletor solar circular continua sendo a melhor opção na etapa de implantação industrial. Porém, o esforço cortante que é gerado no cultivo, a medida que atravessa o joelho de 180° do coletor solar, afeta o crescimento das microalgas, segundo o estipulado na literatura relacionada.
Palavras-chaves: Biomassa microalgal, Dinâmica de fluidos computacional, Esforços cortantes, Microalgas, Fotobio-rreator tubular.
1. INTRODUCTION
Since the fifties, multiple scientific studies have been carried out to obtain new energy sources from microalgae, with the purpose of replacing fossil fuels and causing less environmental impact (Dyer & Richardson, 1962; Ukeles, 1965). Microalgae also have a large amount of proteins, vitamins and minerals that can be used as raw material in the production of food supplements, organic fertilizers, pharmaceutical products and cosmetics for both human and animal consumption (Harun, Singh, Forde & Danquah, 2011; Mata, Martins & Caetano, 2010; Rawat, Ranjith-Kumar, Mutanda & Bux, 2011; Spolaore, Joannis-Cassan, Duran & Isambert, 2006).
Many countries have implemented the study of microalgae due to their great demand and their suitability as a food source that can compete with traditional agriculture, because their production does not require much water or fertile soil. Even when they are used as biofuels, they are competitive in comparison to those obtained from traditional oily or sweetened plant species as far as performance is concerned. This fact has a positive impact on human and animal food markets. Besides, they do not lead to price increases and other serious problems that traditional plants carry out (Rosello-Sastre, Csögör, Perner-Nochta, Fleck-Schneider & Posten, 2007).
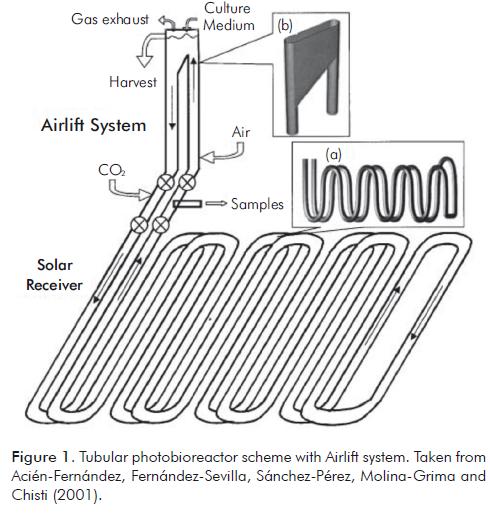
The cultivation of microalgae is found in open systems (ponds, wells, canals, etc) and close systems or photobioreactors (PBR). The latter are characterized by their ability to guarantee optimal conditions for the healthy grow and reproduction of microalgae and cyanobacteria, with the injection of nutrients -such as carbon dioxide, nitrogen and phosphorus- (sunlight or artificial lighting) and the elimination of waste produced by the photosynthesis process, typical of these organisms (Chen, Jiang, An & Yuan, 2009). Among the most widely used PBR's are the tubular photobioreactor (see Figure 1), the bubble column and flat panel photobioreactor. This study will analyze the section of the solar collector of a tubular photobioreactor (TPBR), where the culture medium is found and where the microalgae receive the photonic energy.
For the microalgae to receive the necessary photonic energy to carry out its photosynthetic process and provide a homogeneous concentration of nutrients that increase the production of biomass, it is necessary to make the mixing of the microalgae culture in the solar collectors of the TFBR. For this process, tools such as static mixers are commonly used (García & Haoulo, 2009; Leeuwner & Eksteen, 2008; Perner-Nochta & Posten, 2007). As an alternative to this mixture system, this work proposes the utilization of noncircular solar collectors. These, together with the curves in the collector, allow certain turbulence levels in the culture medium that could replace the static mixer in the collector of the TFBR, thus decreasing - in comparison to the traditional methods of agitation - the microalgae mortality rate, caused by the shear stress in this section of the TFBR (Camacho-Rubio, Acién-Fernández, Sánchez-Pérez, García-Camacho & Molina-Grima,1999; Schneiderbauer & Pirker, 2010).
Retaking research done on the flow in sections or curved ducts, Rowe (1970) revealed that the water flow presents the maximum increase in the secondary flow when it enters the 180º-curvature. Azzola, Humphrey, Iacovides & Launder (1986) noticed that the flow speed increases notably while crossing the curvature due to pressure associated with the main flow, which gene-rates the secondary flow in the duct. Khalid, Legrand & Rosant (1996) highlighted the curves influence in the speed profiles, which confirms that the resulting flow is explained by the coupling between the effects of the curves (acceleration and deceleration of the fl uid entering the curvature). Sudo, Sumida and Hibara (2000) showed that the high speed region is located in the 90°-section in a 180º elbow and this occurs thanks to the secondary fl ow and the turbulence level present in this area
The interest in the fl ows study in curved tubes stems from its wide range of applications in engineering (for example, hydraulic piping systems related to corro- sion) and the dynamics of biofl uids, such as the blood fl ow in the vascular system, where the distribution of speed, pressure, and shear stress can help to understand arterial disorders such as atherosclerosis (Santamarina, Weydahl, Siegel & Moore, 1998; Arada, Pires & Se- queira, 2007). Previous generalized studies have been conducted on the behavior of a fl uid in curved ducts. One such study by Zhang, Zhang and Jü (2001) found that in rectangular ducts, four types of secondary vortex coexist and they produce a variation of the secondary fl ow and the main axial fl ow in the duct (vortices due to centrifugal force, Coriolis force, centrifugal instabi- lity and Coriolis instability). Huttl and Friedrich (2000 and 2001) demonstrated that the amounts of fl ow were affected by the curvature of helical spiral pipe because the secondary fl ow induced by the curvature leads to an increase of the kinetic energy and a fl uctuation of the dissipation rate, while Ma, Shen, Zhang and Zhang (2006) discovered that the laminar fl ow rotation in the curve input region of a duct infl uences the fl ow structure and the friction factor. The secondary fl ow appears in the early stage of the development and then becomes the vortex structure. Yamamoto, Akita, Ikeuchi, & Kita, (1995) and Chang, Chiang and Chou (2010) worked in hexagonal ducts; the fi rst ones for establishing the destabilizing effect on the fl ow due to the torques gene- rated and the last ones have reported the infl uence of this profi le in the heat transfer and the pressure drop.
However, no advances have been recently published about the microalgae cultivation in a FBRT, which are focused on the collector curvature where the critical area is located and the infl uence of uncommon geometries is considered for the solar collector (square, hexagonal and octagonal) in the agitation of the cultivation. Taking into account the neutral buoyancy of the algae in the culture medium (Michels, van der Goot, Norsker & Wijffels, 2010), this article analyzes the development of a single phase fl ow -water- through horizontal ducts of different profi le (circular, octagonal, hexagonal and square) using the computational tool of Dynamic Fluids (CFD) called FLUENT 12.1.2, under the Reynolds stress model.
2. THEORETICAL FRAMEWORK
Turbulence Models
The turbulence models k-epsilon (k-ε) and Reynolds stress (RSM) are the most used models for establishing the behavior of this type of fl ow and are based on the continuity equations of average momentum (Bitog et al., 2011). The k-ε model is simple, numerically robust and easy convergence, but it is known to generate poor results for fl ow with high agitation or a large amount of vortices. Meanwhile, the RSM is more appropriate for this type of simulations although it require machines with more powerful computational characteristics and can present stability problems (Shalaby, Pachler, Wozniak, & Wozniak, 2005).
The Reynolds Stress Model (RSM) is a detailed proto- type of turbulence that provides better approximations to the true fl ow behavior (Alpma & Long, 2005; Fernández- Roque, Toledo-Velásquez &Vásquez-Flores, 2006). The RSM is used for calculating the Reynolds stress from the differential transport equations, represented in the Equation 1 (Alpma & Long, 2005; Fernández-Roque et al., 2006).
In Equation 1, the term on the left is known as the convection term, Cij; Pij, from which the stress produc- tion is deduced:
Fij represent the rotation:
The turbulent diffusion is indicated by DijT:
Φij symbolizes the correlation between the pressure and the deformation:
εij is the turbulence dissipation:
Shear Stress
The hydrodynamic forces present in a FBRT solar collector may cause high shear stress that affects the microalgae (Mazzuca-Sobezuk, García-Camacho, Molina-Grima & Chisti, 2006; Sánchez-Mirón, García- Camacho, Contreras-Gómez, Molina-Grima & Chisti, 2000), reducing its growth or causing its cellular death. However, this agitation movement in the cultivation is necessary for the microalgae to remain in suspension and for improve the light distribution (Michels et al., 2010). This shear stress, present in the solar collector, is directly related to the viscosity of the culture medium and the strain rate, as shown in Equation 7 (Mott, 2005).
Where τ is the Shear Stress, µ is the viscosity of the fluid; u is the fl uid speed and y is the coordinate perpen- dicular to the direction of fl ow.
3. METHODOLOGY
The present study aims at establishing a suitable methodology and a complete validation of the initial data to obtain an appropriate simulation of the culture medium in the solar collector of the FBRT. For this purpose, the main parameters are speed, agitation and shear stress present in the flow.
Geometry
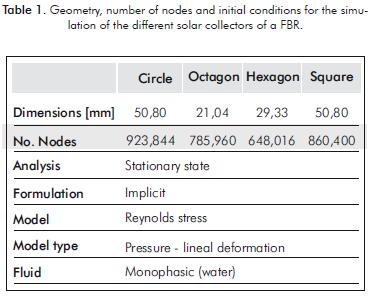
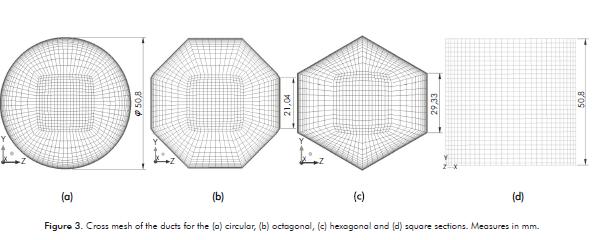
The hydraulic diameter, the curvature and the length of these pipes are the only factors that remain constant for the different profi les. Therefore, it is necessary to establish the general dimensions of each one of the studied profi les (see Figure 2). In the case of the circular duct, the hydraulic diameter corresponds to the diameter of the profi le. However, for the other confi gurations, the hydraulic diameter, Dh, is given by Equation 8 (Aparecido & Cotta, 1990) which relates the cross sectional area (A) with the wet perimeter (Pwet) of the duct. See Table 1.
Mesh Generation
The RSM equations are an adequate mathematical representation of the fl ows, even the turbulent ones.
However, the resolution of these equations for the calculation of the turbulent fl ow requires for a tempo- rary discretization and a fi ne mesh calculation. For this reason, the generation of the mesh is the initial step in the simulations CFD.
This work relies on a section of the solar collector of the FBR as a simulation object. The non-structured three dimensional mesh used in these sections of the ducts has more than 600 000 nodes totally (see Table 2) and was created with the software ICEM CFM (ANSYS 12.1). See Figure 3.
Initial Conditions And Simulation
The numerical simulation of the monophasic flow (water) in the ducts was performed by using the FLUENT software version 12.1.2. (Ansys Inc.). The workplace was a Dell™ Precision™ M6500 laptop computer with an Intel Core i7 quad-core processor of 1.6 GHz. The time of calculation of each one of the 24 simulations was two hours, approximately.
Due to the small size of the bubbles that are gene-rated by the injection of carbon dioxide in the horizontal solar collector, a homogeneous flow is assumed in this situation (Camacho-Rubio et al., 1999). The laminar flow was analyzed under a stationary state with implicit formulation through the Reynolds Stress Model (pressure - linear deformation), using different fluid inlet velocity in all the ducts (see Table 2) and a turbulence intensity of 10%. The condition at the entrance of the ducts is velocity. For the output, it is pressure equal to ΔP.
The fluids turbulence in these collectors is significantly affected by the walls. Therefore, the mesh dependence in this analysis also stems from the fact that the gradient near the walls should not be very big (Salim & Cheah, 2009).
In order to guarantee the validity of the obtained results, the parameters that affect the numerical resolution of the problem should be controlled. It is possible to act on the iterative process by defining the types of discretization, varying the relaxation factors and setting the finalization criteria of the iterations. (Aparecio & Cotta, 1990).
4. RESULTS AND DISCUSSION
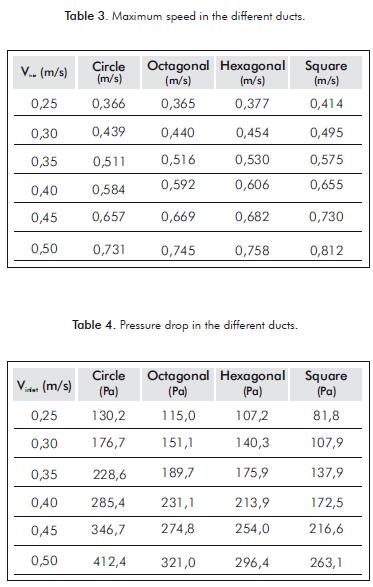
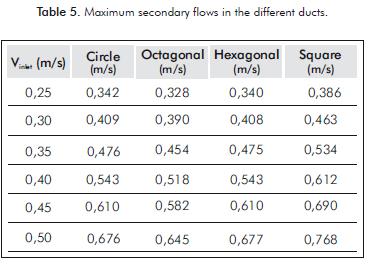
The main interests of this study are the changes in the speed, the pressure drop along the duct curvature and the development of the secondary flow according to the geometry. This is due to the dependence that these factors have on the losses produced by the fluid friction on the duct walls and also the dependence on the shear stress generated by the fluid on the algae, which can cause cellular damage. Tables 3, 4 and 5 show the maximum speeds reached by the fluid within the duct and the pressure at the entrance of the ducts (maximum pressure) and the maximum magnitude of the secondary flow, respectively.
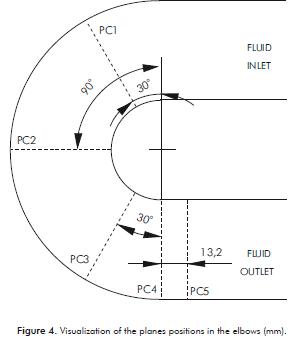
In order to identify the fluid behavior in the curvature of the solar collector for the different profiles, this elbows section has been fragmented in 5 parts. See Figure 4.
The acceptance of the obtained results can be exa-mined through diverse numerical studies or by comparison to the experimental data.
Speed
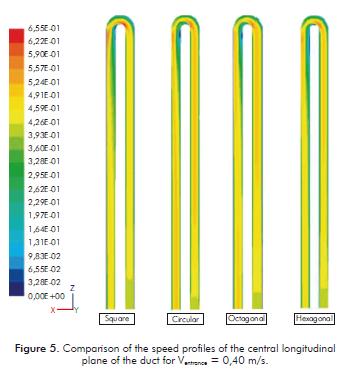
The flow speed makes it possible to predict the fluid behavior in the ducts and to establish the critical situations of the process. In this study, the speed development was completed before 0,5 m of the entrance of the fluid in the ducts, long before the elbow beginning, which makes it possible to establish the typical features of the fl uid when entering the curvature of the duct as is shown in Figure 5.
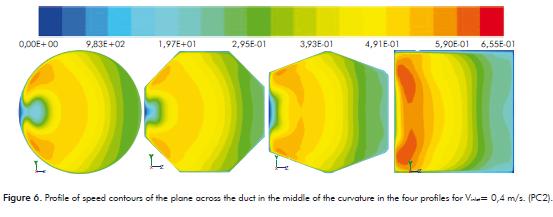
Figure 6 shows the speed contour profi le of the di- fferent types of solar collectors on a plane located in the center of the elbow curvature (PC2) when the fl uid en- trance speed in all the collectors is 0,4 m/s; while Figure 7 shows the speed vectors in fi ve different positions in the curvature (see Figure 4) when the fl uid entrance speed in all the collectors is 0,4 m/s. The right side of each image represents the internal zone of the curvature.
Secondary Flow
The resistance due of the friction of the ducts walls and the action of the centrifugal force produce a rotation in the fl uid movement known as secondary fl ow; this movement is perpendicular to the axis of the pipe and is opposed to the axial movement of the fl ow (Belt, Van't Westende, Portela, Mudde & Oliemans, 2004; Molina-Grima, Acién- Fernández, García-Camacho & Chisti, 1999).
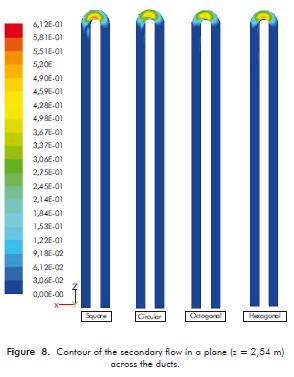
Figure 8 shows the secondary fl ow for each of the profi les when the water entrance speed is 0,4 m/s.
The secondary flow is related to the agitation of the fluid in the duct due to the rotation of the flow, which explains the behavior of the fluid in the curvature of the collector.
Shear Stress
Algae's tolerance to shear stress depends specifically on the species of microalgae. Chaetoceros muelleri, in particular, can endure 1,8 Pa without presenting changes in the growing process (Michels et al., 2010); the growth of the microalgae Spirulina platensis undergoes a change when affected by a shear stress higher than 0,3 Pa (Mitsuhashi, Hosaka, Tomonaga, Muramatsu, & Tanishita, 1995) but no significant cellular damage is produced. While, for the highly sensitive Protoceratium reticulatum microorganism, a damage threshold was observed at an average shear stress of approximately 0,16 mPa (García-Camacho et al., 2007); for Phaeodactylum tricornutum, a shear stress value of 7 Pa led to the highest growth rate caused by a balance between mass transfer limitations and shear damage (Contreras, García, Molina & Merchuk, 1998).
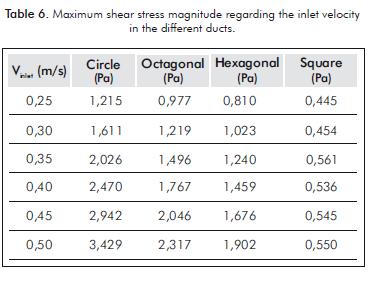
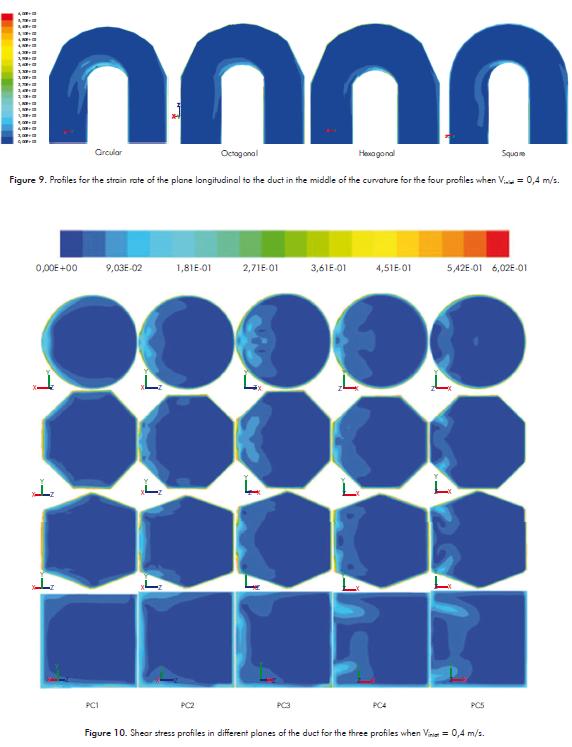
Table 6 shows the maximum shear stress that the flow reaches in each of the ducts. The shear stress is directly related to the fluid viscosity (Hämäläinen, 2001; Ugwu, Ogbonna & Tanaka, 2005; Wu & Merchuk, 2004), and is higher near to the walls of the ducts. Figure 10 illustrates this phenomenon in the collectors when the speed of entrance is 0,4 m/s.
5. CONCLUSIONS
-
According to the results, it is possible to establish a parameter of duct selection for transporting fluids such as the microalgae cultivation according to the axial and rotational movements that are required and the change of pressure. The square profile is the most critical case among the collectors, mainly in the curved zone. This guarantees the constant movement of the fluid and the diminution of the sealing effect of the algae in the collectors.
-
Since the pressure drop is affected by the fluid speed, it determines the direction and the movement of the flow in the duct. The secondary flow is generated from the high pressure region to the low pressure region (Yue, Dooley & Feng, 2008). This flow dissipates after the fluid leaves the elbow, as presented by Azzola et al. (1986) and Sudo et al. (2000) in their works. This situa-tion can be seen in Tables 4 and 5, in which the higher pressure drop occurs in the circular profile. Similarly, the highest secondary flow occurs in comparison to other profiles.
-
It should be noticed in Table 3 that the flow can reach a higher speed in the duct with a square profile than in the other ducts (Figure 5). This is due to the vortex intensity before initiating the curvature, since it is inversely related to the entrance speed of the flow into the elbow (Pruvost, Legrand & Legentilhomme, 2004). According to Figure 5, the flow is not totally developed in the square profile, contrary to what ha-ppens in the circular profile. When it enters the elbow, the fluid speed is higher in the internal section, which leads to a higher drop in speed at the exit of the internal section of the elbow, due to the vortices that originate here thanks to the change in speed within the elbow (Sudo et al., 2000).
-
The maximum shear stress that occurs in the flow should not exceed the maximum shear stress withstood by the cultivation, as the development and growth of the microalgae would be put at risk. Each type of algae tolerates a certain magnitude of shear stress, such as Chaetoceros muelleri, which can withstand 1,8 Pa without presenting changes in its growing process (Michels et al., 2010). Therefore, for microorganisms highly shear sensitive like the Protoceratium reticulatum, low speeds should be used for the entrance of the cultivation medium into the solar collector.
-
Although the solar collector with square profile presents the best features as far as shear stress and agitation are concerned, its weakness is its difficult manufacture. It is feasible to use a circular profile solar collector, which ensures low speed of the culture when it enters the collector, thus avoiding the presence of shear stress that are harmful to microalgae.
ACKNOWLEDGMENTS
The author of this work is grateful to the Research Direction at Universidad Autónoma de Occidente, for the funding of the project "Design of a Photo-Bioreactor Prototype for the Production of Biomass from Algae as a Cleaner Source of Energy in Valle del Cauca."
REFERENCES
Acién-Fernández, F. G., Fernández-Sevilla, J. M., Sánchez- Pérez, J. A., Molina-Grima, E. & Chisti, Y. (2001). Airlift-driven external-loop tubular photobioreactors for outdoor production of microalgae: assessment of design and performance. Chem. Eng. Scie., 56: 2721-2732. [ Links ]
Alpma, E. & Long, L. N. (2005). Separated turbulent flow simulations using a Reynolds stress model and unstructured meshes. 43rd. Aerospace Sciences Meeting & Exhibit. Reno, Nevada USA. [ Links ]
Aparecido, J. B. & Cotta R. M. (1990). Laminar flow inside hexagonal ducts. Computational Mechanics, 6 (2), 93-100. [ Links ]
Arada, N., Pires, M. & Sequeira, A. (2007). Viscosity effects on flows of generalized Newtonian fluids through curved pipes. Computers and Mathematics with Applications, 53: 625-646. [ Links ]
Azzola, J., Humphrey, J. A. C., Iacovides, H. & Launder, B. E. (1986). Developing turbulent flow in a U-bend of circular cross-section: measurement and computation. J. Fluids Eng., 108: 214-221. [ Links ]
Belt, R. J., Van't Westende, J. M. C., Portela, L. M., Mudde R. F. & Oliemans, R.V. A. (2004). Particle-driven secondary flow in turbulent horizontal pipe flows. 3rd. International symposium on two-phase flow modeling and experimentation. Pisa, Italia. [ Links ]
Bitog, J. P., Lee, I. B., Lee, C. G., Kim, K. S., Hwang, H. S., Hong, S. W., Seo, I. H., Kwon, K. S. & Mostafa, E. (2011). Application of computational fluid dynamics for modeling and designing photobioreactors for microalgae production: A review. J. Comp. Elec., 76 (2), 131-147. [ Links ]
Camacho-Rubio, F., Acién-Fernández, F. G., Sánchez-Pérez, J. A., García-Camacho, F. & Molina-Grima, E. (1999). Prediction of dissolved oxygen and carbon dioxide concentration profiles in tubular photobioreactors for microalgal culture. Biotechnology and Bioengineering, 62 (1), 71-86. [ Links ]
Chang, S. W., Chiang, K. F. & Chou, T. C. (2010). Heat transfer and pressure drop in hexagonal ducts with surface dimples. Experimental Thermal and Fluid Science, 34 (8), 1172-1181. [ Links ]
Chen, W. Y., Jiang, N., An, Y. R. & Yuan, Q. H. (2009). Study on numerical simulation of single-phase injection device flow flied. Second International Conference on Information and Computing Science, 358-361. Manchester, United Kingdom. [ Links ]
Contreras, A., García, F., Molina, E. & Merchuk, J. C. (1998). Interaction between CO2-mass transfer, light availability, and hydrodynamic stress in the growth of Phaeodactylum tricornutum in a concentric tube airlift photobioreactor. Biotechnol Bioeng, 60 (3), 317-325. [ Links ]
Dyer, D. L. & Richardson, D. E. (1962). Materials of construction in algal culture. Ap-pl. Microbial., 10: 129-131. [ Links ]
Fernández-Roque, T., Toledo-Velázquez, M. & Vázquez- Flores, J. F. (2006). Caída de presión debida a un flujo en torbellino. Científica, 10 (4), 159-165. [ Links ]
García, F. & Haoulo, M. (2009). Estudio experimental de patrones de flujo bifásico aire-agua en tuberías horizontales y ligeramente inclinadas. Información Tecnológica, 20 (3), 3-12. [ Links ]
García-Camacho, F., Gallardo-Rodríguez, J. J., Sánchez- Mirón, A., Cerón-García, M. C., Belarbi, E. H. & Molina-Grima, E. (2007). Determination of shear stress thresholds in toxic dinoflagellates cultured in shaken flasks Implications in bioprocess engineering. Process Biochemistry, 42: 1506-1515. [ Links ]
Hämäläinen, V. (2001). Implementing an explicit algebraic Reynolds stress model into the three-dimensional FINFLO flow solver. Report B-52. Finland: Helsinki University of Technology. [ Links ]
Harun, R., Singh, M. Forde, G. M. & Danquah, M. K. (2011). Bioprocess engineering of microalgae to produce a variety of consumer products. Renewable and Sustainable Energy Reviews, 14 (3), 1037-1047. [ Links ]
Huttl, T. J. & Friedrich, R. (2000). Influence of curvature and torsion on turbulent flow in helically coiled pipes. Int. J. Heat Fluid Flow, 21 (3), 345-353. [ Links ]
Huttl, T. J. & Friedrich, R. (2001). Direct numerical simulation of turbulent flows in curved and helically coiled pipes. Comput Fluids, 30 (5), 591-605. [ Links ]
Khalid, A., Legrand, J. & Rosant, J. M. (1996). Turbulent flow induced by an impeller in a closed toroidal loop. J. Fluids Eng.. 118 (4), 677-684. [ Links ]
Leeuwner, M. J. & Eksteen J. J. (2008). Computational fluid dynamic modeling of two phase flow in a hydrocyclone. J. South. Afri. Institute Min. and Metal., 108 (4), 231-236. [ Links ]
Ma, J. Shen, X. Zhang, M. & Zhang, B. (2006). Laminar developing flow in the entrance region of rotating curved pipes. J. Hydro Ser. B, 18 (4), 418-423. [ Links ]
Mata, T. M., Martins, A. A. & Caetano, N. S. (2010). Microalgae for biodiesel production and other applications: A review. Renewable and Sustainable Energy Reviews, 14 (1), 217-232. [ Links ]
Mazzuca-Sobezuk, T., García-Camacho, F., Molina-Grima, E. & Chisti, Y. (2006). Effects of agitation on the microalgae Phaeodactylum tricornutum and Porphyridium cruentum. Bioprocess Biosyst Eng., 28 (4), 243-250. [ Links ]
Michels, M., J. van der Goot, A., Norsker, N. H., Wijffels, R. H. (2010). Effects of shear stress on the microalgae Chaetoceros muelleri. Bioprocess Biosyst Eng., 33 (8), 921-927. [ Links ]
Mitsuhashi, S., Hosaka, K., Tomonaga, E., Muramatsu, H. & Tanishita, K. (1995). Effects of shear flow on photosynthesis in a dilute suspension of microalgae. Appl. Microbiol Biotechnol, 42 (5), 744-749. [ Links ]
Molina-Grima, E., Acién-Fernández, F. G., García-Camacho, F. & Chisti, Y. (1999). Photobioreactors: light regime, mass transfer, and scaleup. J. Biotech., 70 (1-3), 231-247. [ Links ]
Mott, R. L. (2005). Applied fluid mechanics. USA: Prentice Hall. [ Links ]
Perner-Nochta, I. & Posten, C. (2007). Simulations of light intensity variation in photobioreactors. J. Biotech.,131 (3), 276-285. [ Links ]
Pruvost, J., Legrand, J. & Legentilhomme, P. (2004). Numerical investigation of bend and torus flows, part I: effect of swirl motion on flow structure in U-bend. Chem. Eng. Scie., 59 (16) , 3345-3357. [ Links ]
Rawat, I., Ranjith-Kumar, R., Mutanda, T. & Bux, F. (2011). Dual role of microalgae: Phycoremediation of domestic wastewater and biomass production for sustainable biofuels production. Applied Energy, 88 (10), 3411-3424. [ Links ]
Rosello Sastre, R., Csögör, Z., Perner-Nochta, I., Fleck-Schneider, P. & Posten, C. (2007). Scale-down of microalgae cultivations in tubular photo-bioreactors-A conceptual approach. J. Biotec., 132 (2), 127-133. [ Links ]
Rowe, M. (1970). Measurements and computations of flow in pipe bends. J. Fluids Mech., 43 (4), 771-783. [ Links ]
Salim, S. M. & Cheah, S. C. (2009). Wall Y+ strategy for dea-ling with wall-bounded turbulent flows. Proceedings of the International Multi Conference of Engineers and Computer Scientists, 3 (2), 18-20. [ Links ]
Sánchez-Mirón, A., García-Camacho, F., Contreras-Gómez, A., Molina-Grima, E. & Chisti, Y. (2000). Bubble-column and airlift photobioreactors for algal culture. AIChE Journal, 46 (9), 1872-1887. [ Links ]
Santamarina, A., Weydahl, E., Siegel, J. M. & Moore, J. E. (1998). Computational analysis of flow in a curved tube model of the coronary arteries: effects of time-varying curvature. Annals of Biomedical Engineering, 26 (6), 944-954. [ Links ]
Schneiderbauer, S. & Pirker, S. (2010). Determination of open boundary conditions for computational fluid dynamics (CFD) from interior observations. Applied Mathematical Modelling, 35 (2), 763-780. [ Links ]
Shalaby, H., Pachler, K., Wozniak, K. & Wozniak, G. (2005). Comparative study of the continuous phase flow in a cyclone separator using different turbulence models. Int. J. Numer. Meth. Fluids, 48 (11), 1175-1197. [ Links ]
Spolaore, P., Joannis-Cassan, C., Durán, E. & Isambert, A. (2006). Commercial applications of microalgae. J. Bios. Bioen., 101 (6), 201-211. [ Links ]
Sudo, K., Sumida, M. & Hibara, H. (2000). Experimental investigation on turbulent flow through a circular-sectioned 180° bend. Experiments in Fluids, 28 (1), 51-57 [ Links ]
Ugwu, C. U., Ogbonna, J. C. & Tanaka, H. (2005). Characterization of light utilization and biomass yields of Chlorella sorokiniana in inclined outdoor tubular photobioreactors equipped with static mixers. Process Biochemistry, 40 (11), 3406-3411. [ Links ]
Ukeles, R. (1965). A simple method for the mass culture of marine algae. Limnology and Oceanography, 10 (3), 492-495. [ Links ]
Wu, X. & Merchuk, J. C. (2004). Simulation of algae growth in a bench scale internal loop airlift reactor. Chem. Eng. Scie., 59 (14), 2899-2912. [ Links ]
Yamamoto, K., Akita, T., Ikeuchi, H., & Kita, Y. (1995). Experimental study of the flow in a helical circular tube. Fluid Dyn Res., 16 (4), 237-249 [ Links ]
Yue, P.; Dooley, J. & Feng, J. J. (2008). A general criterion for viscoelastic secondary flow in pipes of noncircular cross section. J. Rheol., 52 (1), 315-332. [ Links ]
Zhang, J., Zhang, B. & Jü, J. (2001). Fluid flow in a rota-ting curved rectangular duct. Int. J. Heat Fluid Flow, 22: 563-592. [ Links ]
NOTATION