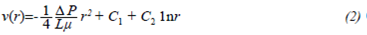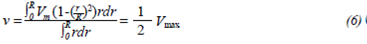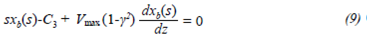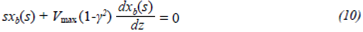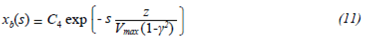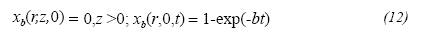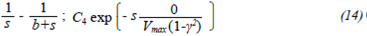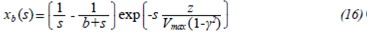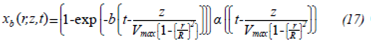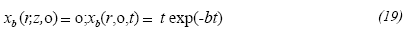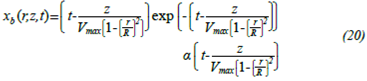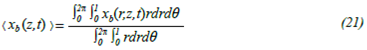1. Introduction
Although computational fluid dynamics (CFD) methods have been implemented to study both, velocity and concentration profiles, it is interesting to provide analytical solutions (Zhang, Xu, & Li, 2012; Xue-Yi, Zhang, & Zheng, 2014) to describe phenomena such as flow in rotor-stator mixers (Barailler, Heniche & Tanguy, 2006.), in helical coils (Trivedi & Vasudeva, 1975; Daskopoulos & Lenhoff, 1988), mixed convection in horizontal tubes (Chae & Chung, 2014) and free convection from horizontal cylinders (Chandra & Chhabra, 2012), all these under a laminar regime.
In the oil industry, heavy crude transport challenges are increasing due to the characteristics of the fluid produced, particularly with regards to its very high viscosity and compositional variation. One of the main problems is flocculation in crude oils as a result of pressure and temperature changes (Hosseini-Dastgerdi, Tabatabaei-Nejad, Sahraei & Nowroozi, 2015; Adams, 2014; (Zendehboudi et.al). In such cases, viscosity is modified through the injection of diluents or flow improvers. When these products are injected at a point in a flowing fluid, and there is no previous mechanical mixing (Gabrienko, Subramani, Martyanov, & Kazarian, 2014), the generally laminar flow regime inhibits homogenization and therefore molecular diffusion is the only mixing mechanism that takes place. The macroscopic action of the product will depend on the convective transport mechanism and the concentration profile that ensues. Concentration profiles are difficult to measure and an analytical solution is not usually found (Martínez-Palou et al. 2011; Centeno, Sánchez-Reyna & Ancheyta, 2015).
This paper proposes a mathematical model that describes the transient behavior of the concentration profile, taking into account the method used to inject a fluid into another fluid of similar characteristics of viscosity and density. The model was generated on the basis of the transient conservation equations of mass and momentum transport, considering that the dominant mechanism associated with the mass transport is convection. This paper presents an accurate solution to the partial differential equation system that enables a simplified application.
2. Experimental methodology
To develop the analytical model, the following assumptions are considered: i) the viscosity of fluid A in the pipe (main fluid) is constant and independent of the concentration of fluid B (injected fluid); ii) the flow is laminar; iii) only mass transport by convection is considered; iv) isothermal system; v) the injection of fluid B does not affect significantly the main flow of fluid A in the pipe, so the velocity profile in the pipe is a function of only the radial coordinate and it can be considered in steady state. Figure 1 shows a schematic of the design concept studied.
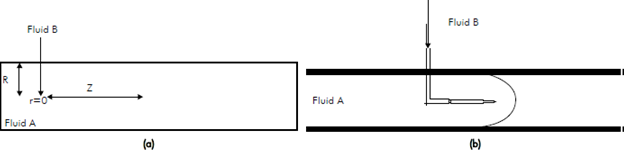
Figure 1 a) Injection analysis of B concentration/ depending on the type of injection b) Description of the system
Fluid A can represent a heavy crude oil and fluid B the injected product. Both fluids A and B, have the same physical properties, i.e. density and viscosity, and the same chemical composition. Although in this case the fluids do not undergo any physical change, this theoretical consideration allows a first approximation regarding the transient behavior of a two-fluid mixture, which can be complemented with further study.
Pipeline concentration profile in unsteady state.
Under the assumption that fluid B does not affect neither the fluid viscosity nor the velocity profile of fluid A, the latter can be determined from the following momentum (Bird, Steart, & Lightfoot) (2002):
where P is pressure, v is velocity, u is dynamic viscosity and r is the pipeline radius. The exact solution of differential equation (1) is:
C1 and C2 are constants, which are determined considering that:
The velocity profile results:
Defining 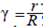 and knowing that V
max
=
and knowing that V
max
=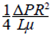 equation 4 can be rewritten as:
equation 4 can be rewritten as:
and the average velocity is given by:
Considering that the transport mechanism is only convection, the equation that describes the transient and axial variation of concentration of B in A, i.e. x b is given by:
Substituting equation 5 in 7:
To solve the differential partial equation 8, Laplace transform is applied, in such way that it is expressed as a differential equation:
Considering that x b (r,0) = 0, it leads to C3 = 0 and therefore:
The exact solution of equation 10 is given by:
where C 4 is determined depending on the injection mechanism analyzed.
The general model given by Equation 11 was solved for two types of injection of fluid B: a gradual injection and a pulsed-type input.
Experimental Setup
To obtain qualitative evidence of the flow phenomena previously described, the experimental apparatus shown schematically in Figure 1b was implemented. A glass tubing of 5 mm diameter and 4 m long allows visualization of a colored injected fluid into the main flow. The prescribed flow rate is lcm3/s which is provided by a constant head tank, and the outflow is at ambient pressure. The fluid used was glycerin with a viscosity of 1080cP. Experiments were performed three times to ensure repeatability under isothermal conditions of 20°C (ambient temperature) with the prescribed flow rate. After 5 minutes from startup (to ensure a steady state), the same glycerin (artificially black colored) is injected using a manual syringe with a 0.8 mm needle for 5 s to simulate a pulsed/gradual input. Images were recorded at regular time intervals with a 7 Mpixel digital camera. The colored "plume" advance is then compared with the theoretical transient evolution of concentration. Since chemical reaction or heat transfer/generation is absent (given the tube length and low fluid velocity, friction effects are negligible), adiabatic mixing of the two fluids is precluded in the analysis.
3. Results and discussion
The obtained model is based on the conservation of momentum and mass transport equations for multicomponent systems so that it is an ideal model where caloric effect is associated with the thermodynamic and viscosity friction process (and effects associated to the mixing) so that system temperature is uniform without heat transport.
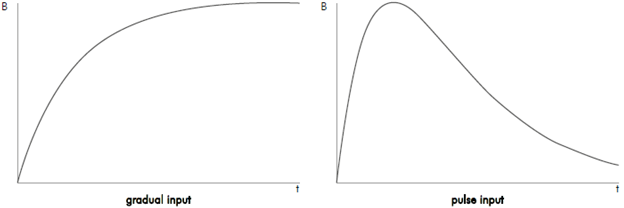
To study the effect of the injection dynamics of fluid B on the concentration profile, two cases are considered: a gradual injection of B and a pulsed-type input, as shown in Figure 3.
Determination of the concentration transient profile for gradual input of B
For this case, it is considered that:
Then:
Substituting equation 13 in equation 11:
So:
therefore:
and applying the inverse of Laplace transform:
Where a is the Heaviside function given by:
Temporal and spatial qualitative profiles of fluid B's concentration predicted by the model given by equation 18 are shown in Figures 4 and 5, considering R = 1, Z = 1 and b = 1
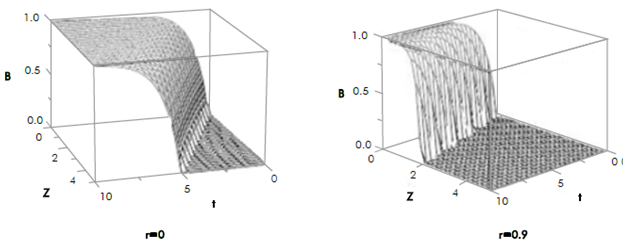
Figure 4 Qualitative profile of B concentration profile with respect to time t and distance z for r =0 (tube center) and r = 0.9 (near tube wall)
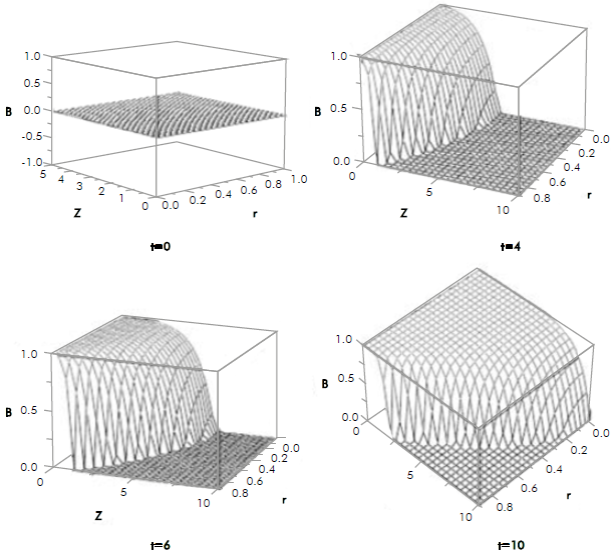
Figure 5 Qualitative profile of B concentration profile with respect to radius r and distance z for different times.
It can be observed that for each spatial point, the injection process is reproduced, in which the concentration gradually increases until it reaches a constant value. The concentration profile with respect to radius and axial distance for a specified time shows that the concentration decreases with increasing radius, as the velocity is very small near the tube wall and the assumed mechanism that drives the mass transport is convection.
Determination of the concentration profile of Bin time for a pulse input type
For this case it is considered that:
Following a similar method as in the previous case, the following equation is obtained:
Temporal and spatial qualitative profiles of B concentration predicted with the model given by equation 18 are shown on Figures 6 and 7, considering R = 1, Z = 1 and b = 1.
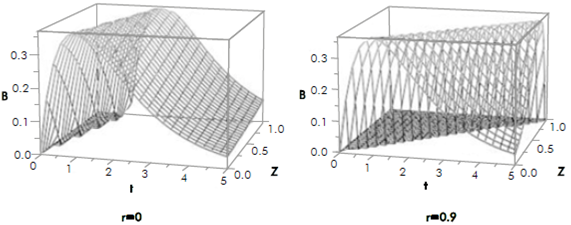
Figure 6 Qualitative profile of B concentration profile with respect to time t and distance z for r =0 (tube center) and r = 0.9 (near tube wall).
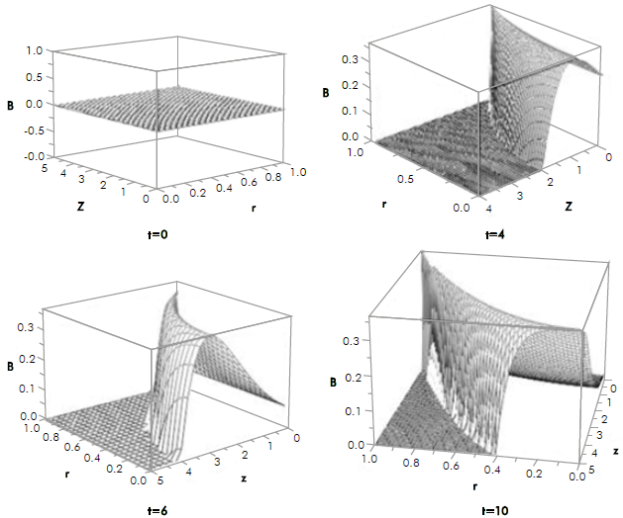
Figure 7 Qualitative profile of B concentration profile with respect to radius r and distance z for different times.
For this dynamic type of injection, the results show that the concentration has a profile that evolves strongly with time and distance from the injection point. For each spatial point and within a certain distance, the concentration increases over time, reaching a given value, from which it decreases to zero. That is, each point in space in the concentration profile qualitatively reproduces the time behavior of the injected fluid. For a given time, the behavior of the concentration profile shows a decrease in concentration with respect to the radius for higher values of z, while for lower values the profile is reversed and the concentration increases with the radius.
Behavior of average concentration
The average concentration with respect to the flow area is determined by:
The integration of equation 21 does not have an exact analytical solution, so it is necessary to apply a numerical solution method. The behavior predicted is shown in Figure 8. It is observed that at a given distance, the concentration of fluid B increases with the average flow velocity. The system tends to a steady state where the concentration is the same at all points for a gradual injection, while it tends to zero for a pulsed injection. In both cases the average concentration reflects the method of injection.
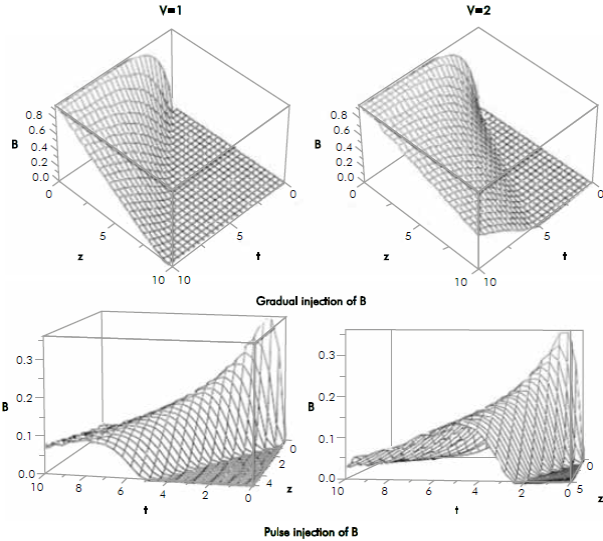
Figure 8 Qualitative average concentration profiles for two different average velocities and injection dynamics.
This behavior is explained as the transport mechanism is predominantly by convection.
Experimental Observations
Figure 9 shows pictures obtained during the test in a tube. It is observed qualitatively that the concentration profile evolution is mainly due to convective transport of the colored fluid. At the end of the test, a constant width "line" of the colored fluid spans a length of (4.5 - 6.5) cm.

Figure 9 Pictures taken after a. 1s, b. 2s, c.3s and d. 4s of the injection. e and f are pictures b/w pictures of the inner fluid tip.
Although axial transport is reported in previous studies (Trivedi & Vasudeva, 1975), the theoretical analysis presented describes this phenomenon in a simplified manner as compared to the solution presented by Zhang et al. 2012. The proposed model can be complemented for two liquids with different physical properties, to represent a more realistic additive injection problem, as presented in the oil industry or similar, but considering different physical properties, which is a matter of consideration for authors in further work.
4. Conclusions
A mathematical model for prediction of the spatial and transient concentration profile of an injected fluid as a function of the injection method is proposed. According to calculated theoretical results, the dynamics of the injection process is qualitatively reproduced at each spatial point, and the same occurs for the average concentration. Although in this paper only two cases are analyzed, it is possible to consider other injection methods, which must be studied when products are injected to decrease the precipitation of heavy fractions in a crude oil or to increase the stability of dispersed particles, where the effectiveness depends on the fluid injected concentration. It is necessary to point out that the present model is valid if the mechanism associated with mass transport is predominantly by convection, the main flow is laminar and the effect of the injected product on viscosity can be considered negligible.
An exact solution to the partial differential equations system is presented, which enables a simplified application. The present model can be improved to consider changes in viscosity due to the concentration of fluid B in fluid A, and thereby obtain and quantify a drag reducing effect. Initially, experiments with a high viscosity fluid show that radial diffusion is negligible as compared to convective transport. Future work can be applied in results like those presented by Abdulbari, Shabirin, & Abdurrahman, 2014, with polymers diluted in the same stream.