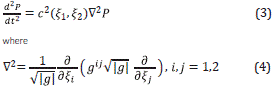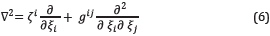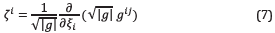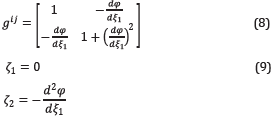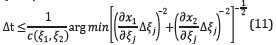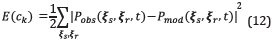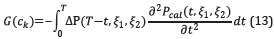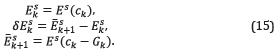1. INTRODUCTION
Artificial seismic waves are used to study the Earth's inner structure. These waves travel through the subfurface and their echoes are collected by sensors placed at the surface, known as geophones. This information is used to infer the properties of the subsurface such as velocity of propagation of seismic waves or density. Subfurface velocity models were traditionally obtained with first arrival travel time tomography, a technique that uses part of the recorded information, like early arrivals [1]. The advances of computational power in hardware and software enable current methods to consider the full information of the waveform to produce high-resolution properties maps; this is the case of FWI [2]- [5]. After applying this method, migration algorithms can find an accurate location of subsurface reflectors.
FWI is a data-fitting method that uses a rough velocity model of the subsurface and iteratively finds better estimates. The purpose is to iteratively reduce the squared error between the modeled seismogram (computed with the estimated velocity model) and the observed seismogram. FWI can be applied in time domain [3,4,6] or frequency domain [7]; each option implies advantages and disadvantages. The first scheme is more straightforward, faster and requires less memory. It is also sensitive to time sampling, requires more computational time, and may present cycle-skipping problems. On the other hand, in the frequency domain, only one or a few frequencies can be used for FWI. If all the frequencies are simultaneously inverted [7], this approach is equivalent to its time domain counterpart. There are several ways to update the estimate of the velocity model in each iteration, but one of the simplest is the gradient descent method. Furthermore, the strategy proposed by Plessix [8] can be used to compute the gradient via the ad-joint state method. We refer the reader to a comprehensive review for the FWI method written by J. Virieux and S. Operto [5].
Currently, FWI is an active research topic from a mathematical, computational and geophysical standpoint. Several drawbacks of this method still remain as open problems. Other issues are t the inconvenience of avoiding local minima, the sensitivity of the method to amplitude errors [5], and its computational efficiency-related complications. In addition, the problem of incorporating a curved topography into the method is also of great interest as good estimates of model parameters at the near surface are required. This is important in the oil industry because the extractive potential may be significant in onshore zones with complex geology that hide complicated structures. The traditional approach to handle topography is the datuming method [9], which adjusts the amplitudes of the computed wave-field so that the wave-fronts seem to be emitted from points in the curved surface of a complex topography. However, datuming introduces amplitude errors to which the FWI algorithm is very sensitive, leading to potentially inaccurate images of the Earth's subsurface.
Thus, we propose hereunder a method based on a previous work that used generalized meshes for seismic modeling [10]. This work used a general physical domain with curved upper surface and mapped it into a rectangular domain, where a uniform grid was used to propagate and retro-propagate wavefields. The same transformation domain was used to obtain imaging conditions. The general transformation consists of modifying the Laplacian operator by introducing space-dependent coefficients known as metric coefficients. Wave propagation in this domain is similar to that of a Riemannian space, where the metric is not Euclidean. Once the wave-fields and velocity models are computed in the transformed domain, these are translated back into the (curved) physical domain.
Reverse time migration in curved meshes [11] and FWI methods for rugged topography [12] have been proposed before. Unfortunately, their computational cost is greater than that of their Cartesian counterparts. The approaches proposed in the literature, although very clever, are rather unpractical as transformations drastically reduce the spatial step size, which results in limiting the time step size due to the Courant-Friedrichs-Lewy condition.
In this work, we introduce a type of transformation that preserves the spatial size and, therefore, the time step. Hence, the execution time of the algorithm is shorter compared to the same method using Cartesian coordinates. Experimental results show that our approach enables to perform FWI in domains with a general rugged surface. It also estimates satisfying velocity models even for the near-surface region, where obtaining good results is usually difficult.
2. THEORETICAL FRAME
The transformation that maps a rectangular domain with coordinates (ξ 1, ξ 2) (named computational domain) into the physical domain of coordinates (x 1, x 2) is
where φ(ξ 1)=φ(x1) is a smoothed function that represents the curved upper boundary of the physical domain. This transformation is depicted in Figure 1.
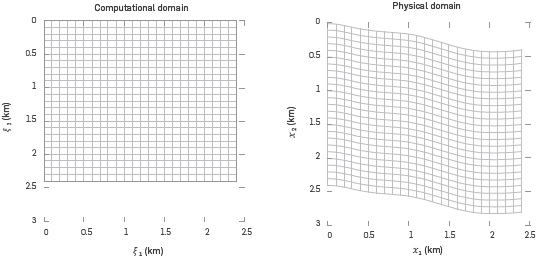
Figure 1 The straight lines of the rectangular domain are transformed into curved lines in the physical domain. For example, the horizontal line on top of the computational domain is mapped into the curved dark line in the physical domain, which represents the topographic profile.
Note from (1) that Δx1= Δξ 1 and from (2) that if we vary ξ 2 along a vertical line with ξ 1 =const, we have φ=const, which implies Δx2= Δξ 2, i.e., the step size in space is not affected by the transformation.
When the variables in (1) and (2) are changed, a new expression is found for the Laplacian operator by using the chain rule. The acoustic wave equation for the transformed domain is given by
Equation 4 gives the generalized Laplacian, where |g| is the absolute value of the determinant of the metric tensor g ij, given by
In order to re-write the wave equation, we need the contravariant representation of the metric tensor g ij =(g ij) -1 [13], and a sum over repeated indexes is implied. Note that c 2 is the square of the velocity vector, which is a scalar value and, therefore, it is not transformed. However, its arguments are transformed.
Expanding the Laplacian we can re-write Equation 4 in a more convenient way, as
Where
The elements ζ i are also geometric coefficients that are computed only once, as well as g ij . For our specific transformation, given in Equations 1 and 2, we have
(11) introduced a heuristic stability condition for this equation, given by
Now, Equation 3 can be numerically solved in the computational domain, i.e., in a rectangular domain, and the classic FWI algorithm can be implemented.
The purpose of the traditional FWI algorithm is to minimize the quadratic error given by
where ξs=(ξ 1s,ξ 2s=0) are the source positions, that according to Equation 2 corresponds to
x2= φ(ξ 1)=φ(x1), i.e., the mountain border, and the ξ r are the locations of the receivers. In Equation 11, P obs is the wave-field measured by the sensors (geophones in a real on-shore seismogram), and P mod is the modeled seismogram, obtained with the velocity model, c k, estimated at iteration k. The algorithm requires an initial velocity model c0, and it updates the estimate at each iteration by using the gradient descent direction. This is
where G(ck) is the gradient given by Plessix [8]:
In Equation 13, ΔP(T-t,ξ 1,ξ 2) is the retro-propagation of the residual field P mod - P obs . The parameter λ k is a step size that can be optimized by Liu, et. al. [14]
where
Once the FWI method retrieves the estimated velocity models, it can be mapped into the physical domain by using the transformation given in Equation 2.
3. EXPERIMENTAL DEVELOPMENT
We evaluate the performance of the FWI method in generalized coordinates using the Canadian Foothills model, a synthetic velocity model for a zone in British Columbia that shows several complex structures common in that region of Canada. The computational grid of the proposed experiment is 334x200, with ∆x1=∆x2=0.03 km. In every grid point, a receiver is located. The minimum offset is 0.03 km, and the maximum is 8 A km. We used seven point sources in shape of a Ricker wavelet, placed every 40 grid points starting in the grid point number 60. This FWI follows a multi-scale strategy where the sources have central frequencies of f1=5 Hz and f1=15 Hz. In the multi-scale strategy, the estimated velocity model obtained for the first frequency is then used as starting-point for the second frequency. For each wave-propagation, we use a sampling time of 1ms, a total acquisition time of 2.5 s, and the FWI included 200 iterations. The initial velocity model is shown In Figure 2a. The final estimated models for one and two frequencies are shown in Figures 2b and 2c, respectively. As the velocity model originally presents a flat bottom, the curved mesh must go beyond. Therefore, the missing area of the curved mesh Is filled with a constant velocity (6 Km/s) which does not negatively affect the results because those points are mainly immersed in the attenuation layer and do not imply a significant variation of velocities. Additionally, the topographic profile of the original model was smoothed before making any computation. The observed data was generated synthetically using the original model shown in Figure 2d.
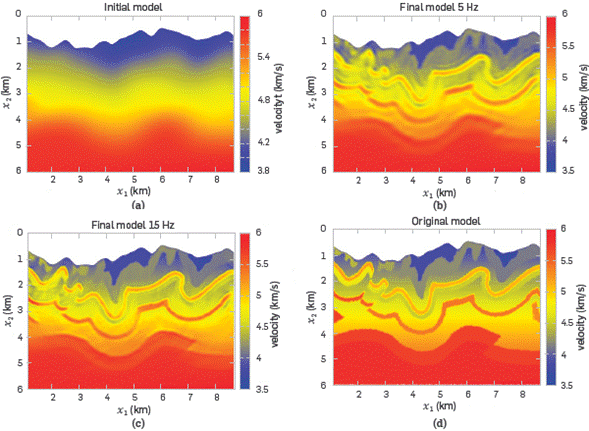
Figure 2 (a) The starting velocity model. (b) final velocity model for a source of 5 Hz. (c) final velocity model using a source of 15 Hz and taking the model in (b) as the starting model. (d) original model.
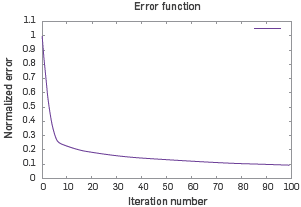
Figure 3 shows the convergence curve for the final result corresponding to Figure 2c. The residual decreases around 90%, when 100 iterations are performed. A quick decrease is observed for the first 10 iterations and then it flattens up. Figure 4 shows the difference between the inverted model and the original model. Small differences between the two models are observed, except at a few points near the borders of the model. It shows the percentage residual for the last stage in FWI. A difference of less than 10% is observed at the center of the model. Note that although the error bar is between -20% and +20%, these extremes are reached only in small spurious locations.
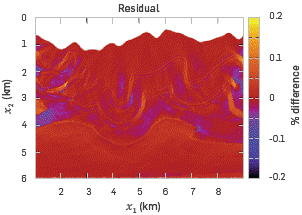
Figure 4 Percentage difference between final inverted model and the original model (Figure 2d). The color bar shows a scale between -20% and +20%.
CONCLUSIONS
The proposed transformation, in combination with the classical FWI algorithm, produces results with small errors as compared to the original synthetic model.
The curved grid used allows the FWI algorithm to map, in a clear way, the near-surface structures of the velocity model.
Other curved grids applied to simple velocity models were reported previously by other authors. Our method was applied to a complex model that exhibits imbricate geological structures and curved topography. The resulting velocity model shows good agreement with the original, within a small percentage difference.