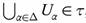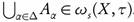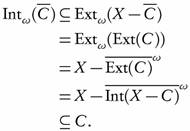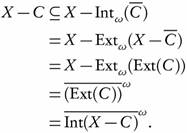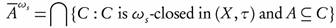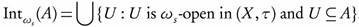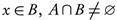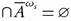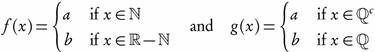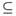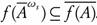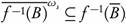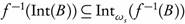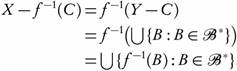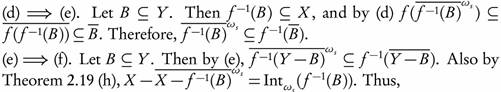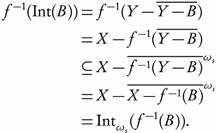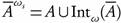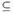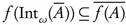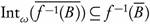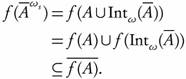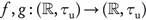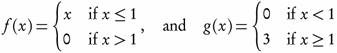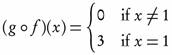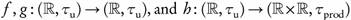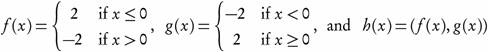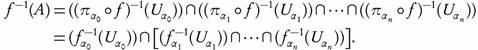Introduction
Let (X, τ) be a topological space and 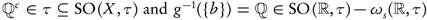 . We will denote the complement of A in X, the closure of A, the interior of A, the exterior of A, and the relative topology on A, by X - A,
. We will denote the complement of A in X, the closure of A, the interior of A, the exterior of A, and the relative topology on A, by X - A,  , Int(A), Ext(A), and τA, respectively. In 1963, Levine [7] defined semi-open sets as a class of sets containing the open sets as follows: A is semi-open if there exists an open set U such that
, Int(A), Ext(A), and τA, respectively. In 1963, Levine [7] defined semi-open sets as a class of sets containing the open sets as follows: A is semi-open if there exists an open set U such that 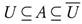 , this is equivalent to say that
, this is equivalent to say that 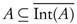 . Using semi-open sets he also generalized continuity by semi-continuity as follows: A function
. Using semi-open sets he also generalized continuity by semi-continuity as follows: A function 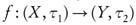 is semi-continuous if for all
is semi-continuous if for all 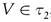 , the preimage
, the preimage 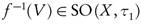 . The complement of a semi-open set is called semi-closed[5]. A point
. The complement of a semi-open set is called semi-closed[5]. A point 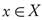 is called a condensation point [6] of A if for every
is called a condensation point [6] of A if for every 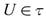 with
with 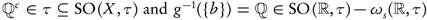 , the set
, the set 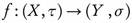 is uncountable. Hdeib [6] defined ω-closed sets and ω-open sets as follows: A is called ω-closed if it contains all its condensation points. The complement of an ω-closed set is called ω-open. The collection of all ω-open sets of a topological space (X, τ) will be denoted by τω. In [1], the author proved that (X, τω
) is a topological space and
is uncountable. Hdeib [6] defined ω-closed sets and ω-open sets as follows: A is called ω-closed if it contains all its condensation points. The complement of an ω-closed set is called ω-open. The collection of all ω-open sets of a topological space (X, τ) will be denoted by τω. In [1], the author proved that (X, τω
) is a topological space and 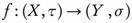 . Moreover, it was observed that A is ω-open if and only if for every x in A there is an open set U and a countable subset C such that
. Moreover, it was observed that A is ω-open if and only if for every x in A there is an open set U and a countable subset C such that 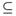 . The ω-closure of A in (X, τ), denoted by
. The ω-closure of A in (X, τ), denoted by 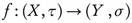 , is the smallest ω-closed set in (X, τ) that contains A (cf. [1]). The ω-interior of A in (X, τ), denoted by Int ω(A), is the largest ω-open set in (X, τ) contained in A. The ω-exterior of A in (X, τ), denoted by Ext ω(A), is defined to be Int ω(X - A). It is clear that the ω-closure (resp. ω-interior) of A in (X, τ) equals the closure (resp. interior) of A in (X, t ω). In 2002, Al-Zoubi and Al-Nashef [2] used ω-open sets to define semi ω-open sets as a weaker form of semi-open sets as follows: A is semi ω-open if there exists an ω-open set U such that
, is the smallest ω-closed set in (X, τ) that contains A (cf. [1]). The ω-interior of A in (X, τ), denoted by Int ω(A), is the largest ω-open set in (X, τ) contained in A. The ω-exterior of A in (X, τ), denoted by Ext ω(A), is defined to be Int ω(X - A). It is clear that the ω-closure (resp. ω-interior) of A in (X, τ) equals the closure (resp. interior) of A in (X, t ω). In 2002, Al-Zoubi and Al-Nashef [2] used ω-open sets to define semi ω-open sets as a weaker form of semi-open sets as follows: A is semi ω-open if there exists an ω-open set U such that 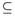 . The collection of all semi ω-open sets of a topological space (X, τ) will be denoted by SωO (X, τ). Al-Zoubi [4] used semi ω-open sets to introduce semi -continuous functions as a weaker form of -continuous functions as follows: A function
. The collection of all semi ω-open sets of a topological space (X, τ) will be denoted by SωO (X, τ). Al-Zoubi [4] used semi ω-open sets to introduce semi -continuous functions as a weaker form of -continuous functions as follows: A function 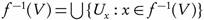 is semi ω-continuous [4] if for all
is semi ω-continuous [4] if for all 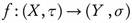 , the preimage
, the preimage 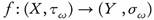 . This paper is devoted to define ωs-opennes as a property of sets that is strictly weaker than openness and stronger than semi-openness as follows: A is ωs-open if there exists an open set U such that
. This paper is devoted to define ωs-opennes as a property of sets that is strictly weaker than openness and stronger than semi-openness as follows: A is ωs-open if there exists an open set U such that 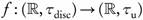 . We investigate this class of sets, and use it to study a new property of functions strictly between continuity and semi-continuity, and another new property of functions strictly between slight continuity and slight semi-continuity.
. We investigate this class of sets, and use it to study a new property of functions strictly between continuity and semi-continuity, and another new property of functions strictly between slight continuity and slight semi-continuity.
Throughout this paper R, N, Q, and Qc, will denote the set of real numbers, the set of natural numbers, the set of rational numbers, and the set of irrational numbers, respectively. For any non-empty set X we denote by τdisc the discrete topology on X. Finally, by τu we mean the usual topology on R.
The following sequence of theorems will be useful in the sequel:
Theorem 1.1 ([3]). Let (X, τ) be a topological space and 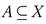 . Then
. Then
(a) If A is non-empty, then (τA)ω = (τω)A.
(b) (τω) ω = τω.
Theorem 1.2 ([2]). Let (X, τ) be a topological space. Then
(a) SO (X, τ)
SωO (X, τ), and SO (X, τ) ≠ SωO (X, τ) in general.
Theorem 1.3 ([1]). Let (X, τ) be a topological space. Then
(a) If (X, τ) is anti-locally countable, then
for all
, and Intω (A) = Int(A) for all ω-closed set A in (X, τ).
(b) If (X, τ) is locally countable, then τω is the discrete topology.
ωs -Open sets
Definition 2.1. Let A of be a subset of a topological space (X, τ). Then A is called ωs-open of (X, τ), if there exists 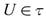 such that
such that 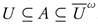 and A is called ωs-closed if X - A is ωs-open. The family of all ωs-open subsets of (X, τ) will be denoted by ωs(X, τ).
and A is called ωs-closed if X - A is ωs-open. The family of all ωs-open subsets of (X, τ) will be denoted by ωs(X, τ).
Theorem 2.2. Let (X, τ) be a topological space. Then τ 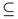 ω
s
(X, τ)
ω
s
(X, τ)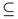 SO (X, τ).
SO (X, τ).
Proof. Let A ∈ τ Take U = A. Then U ∈ τ and 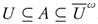 . This shows that A ∈ ωs (X, τ). It follows that
. This shows that A ∈ ωs (X, τ). It follows that 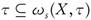 . Let A ∈ ωs (X, τ). Then there exists U ∈ t such that
. Let A ∈ ωs (X, τ). Then there exists U ∈ t such that 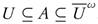 , but
, but 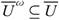 . Thus A ∈ SO (X, τ). This shows that
. Thus A ∈ SO (X, τ). This shows that 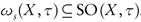 .
.
In the following example we will see that, in general, neither of the two inclusions in Theorem 2.2 are equalities:
Example 2.3. Consider (R, τ), where 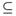 . It is not difficult to check that
. It is not difficult to check that 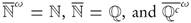 . Thus Q ∈ SO (X, τ) - ωs(X, τ) and R - N ∈ ωs(X, τ) - τ.
. Thus Q ∈ SO (X, τ) - ωs(X, τ) and R - N ∈ ωs(X, τ) - τ.
Theorem 2.4. Let (X, τ) be a topological space. Then
(a) If (X, τ) is anti-locally countable, then ωs(X, τ) = SO (X, τ).
(b) If (X, τ) is locally countable, then t = ωs(X, τ).
Proof. (a) By Theorem 2.2 it is sufficient to show that SO (X, τ) 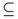 ω
s
(X, τ). Let A ∈ SO (X, τ). Then there exists U ∈ τ such that U
ω
s
(X, τ). Let A ∈ SO (X, τ). Then there exists U ∈ τ such that U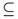 A
A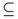 U. Since (X, τ) is anti-locally countable, then by Theorem 1.3 (a), U = U .It follows that A ∈ v, (X, τ).
U. Since (X, τ) is anti-locally countable, then by Theorem 1.3 (a), U = U .It follows that A ∈ v, (X, τ).
(b) By Theorem 2.2 it is sufficient to show that co s (X, τ) C τ. Let us take A ∈ co s (X, τ). Then there exists U ∈ t such that U C A C U . Since (X, τ) is locally countable, then by Theorem 1.3 (b), U ω = U. It follows that A = U and hence A ∈ t.
The following example shows that v-open sets and ω s-open sets are independent:
Example 2.5. Consider (R, τ) where 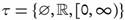 . It is not difficult to check that
. It is not difficult to check that 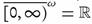 . Thus [-1, ∞) ∈ ωs(X, τ) - Tω and (0, ∞) ∈ Tω - ωs(X, Τ).
. Thus [-1, ∞) ∈ ωs(X, τ) - Tω and (0, ∞) ∈ Tω - ωs(X, Τ).
Theorem 2.6. A subset A of a topological space (X, T) is ωs -open if and only if 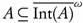 .
.
Proof. Necessity. Let A be ωs -open. Then there exists some U ∈ T such that 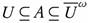 . Since U
. Since U 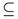 A, then U = Int(U)
A, then U = Int(U)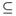 Int(A) and so
Int(A) and so 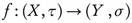 . Therefore, A
. Therefore, A 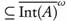 .
.
Sufficiency. Suppose that A 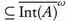 . Take U = Int(A). Then U ∈ T with
. Take U = Int(A). Then U ∈ T with 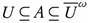 . It follows that A is ωs-open.
. It follows that A is ωs-open.
Theorem 2.7. Arbitrary unions of ωs-open sets in a topological space is ωs-open.
Proof. Let (X, τ) be a topological space and let 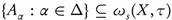 . For each
. For each 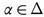 , there exists Uα ∈ τ such that
, there exists Uα ∈ τ such that 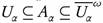 . So, we have
. So, we have
Corollary 2.8. If 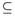 is a collection of ω
s
-closed subsets of a topological space (X, τ), then
is a collection of ω
s
-closed subsets of a topological space (X, τ), then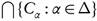 is ω
s
-closed.
is ω
s
-closed.
The following example shows that the intersection of two ω s-open sets need not to be ω s-open in general:
Example 2.9. Consider (R, τu). Let A = [0,1], B = [1,2]. By Theorem 1.3 (a), 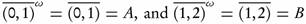 . Thus A, B ∈ ωs(X, τ), but
. Thus A, B ∈ ωs(X, τ), but 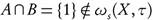 .
.
Theorem 2.10. For any topological space, the intersection of two ωs-open sets where one of them is open is also ωs-open.
Proof. Let (X, τ) be a topological space, A G t and B G ωs(X, τ). Choose a set U ∈ τ such that 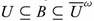 . Now we have
. Now we have 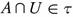 , and then
, and then 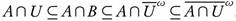 . This shows that,
. This shows that, 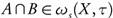 .
.
Corollary 2.11. For any topological space, the union of two ωs-closed sets where one of them is closed is also ωs-closed.
Theorem 2.12. Let (X, τ) be a topological space, B a non-empty subset of X and A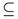 B. Then
B. Then
(a) If A ∈ ωs (X, τ), then A ∈ ωs (B, tB).
(b) If B ∈ τ and A ∈ ωs (B, τB), then A ∈ ωs (X, τ).
Proof. (a) Let A ∈ ωs(X, τ). Then there is U ∈ τ such that 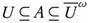 . Then
. Then 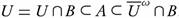 . Note that
. Note that 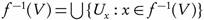 is the closure of U in (τω)B and by Theorem 1.1 (a), it is the closure of U in (τ
B
)
ω. This shows that A ∈ ω
s
(B, τ
B).
is the closure of U in (τω)B and by Theorem 1.1 (a), it is the closure of U in (τ
B
)
ω. This shows that A ∈ ω
s
(B, τ
B).
(b) Let B ∈ τ and A ∈ ms(B, τ
B). Since A ∈ ω
s
(B, τ
B), there is V ∈ τ
B such that V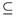 A
A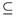 H where H is the closure of V in (B, (τ
B)m). Since B ∈ τ, then V ∈ τ. Also,
H where H is the closure of V in (B, (τ
B)m). Since B ∈ τ, then V ∈ τ. Also,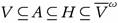 . Therefore, A ∈ ω
s
(X, τ).
. Therefore, A ∈ ω
s
(X, τ).
Theorem 2.13.
Let (X, τ) be a topological space. Let A
∈
ω
s
(X, τ) and suppose that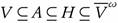 , then B ∈ ωs(X, τ).
, then B ∈ ωs(X, τ).
Proof. Since A ∈ ωs(X, τ), there exists U ∈ τ such that 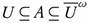 . Since
. Since 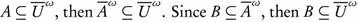 . Therefore, we have U ∈ τ and
. Therefore, we have U ∈ τ and 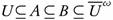 . This shows that B ∈ ωs(X, τ).
. This shows that B ∈ ωs(X, τ).
Theorem 2.14. For any topological space (X, τ) we have that SO (X, τω) = ωs(X, τω).
Proof. By Theorem 2.2, we have ωs(X, τω)//rSO (X, τω). Conversely, let A ∈ SO (X, tm), then there exists U ∈ τω such that U 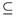 A
A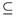 H, where H is the closure of U in (X, τ
ω
). By Theorem 1.1 (b), we have (τ
ω
)
ω
= τ
ω and so H = U .It follows that A
∈
co
s
(X, τ
ω
).
H, where H is the closure of U in (X, τ
ω
). By Theorem 1.1 (b), we have (τ
ω
)
ω
= τ
ω and so H = U .It follows that A
∈
co
s
(X, τ
ω
).
Theorem 2.15. For any topological space (X, τ) we have the relation τ = {Int(A): A ∈ ω s (X, τ)}.
Proof. It follows because from Theorem 2.2 we have τ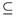 ω
s
(X, τ).
ω
s
(X, τ).
Theorem 2.16.
A subset C of a topological space (X, τ) is ω
s
-closed if and only if Int ω
(C)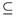 C.
C.
Proof. Necessity. Suppose that C is ω
s-closed in (X, τ). Then X
-
C is ω
s-closed and by Theorem 2.6, X
-
C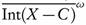 . So
. So
Sufficiency. Suppose that 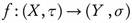 . Then
. Then
By Theorem 2.6 it follows that X - C is ωs-open, and hence C is ωs-closed.
Definition 2.17. Let (X, τ) be a topological space and let A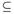 X.
X.
(a) The ωs-closure of A in (X, τ) is denoted by
and defined as follows:
(b) The co s-interior of A in (X, τ) is denoted by Int ωs (A) and defined as follows:
Remark 2.18. Let (X, τ) be a topological space and let A 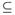 X. Then
X. Then
(c) Int ωs(A) is the largest ωs-open set in (X, τ) contained in A.
(d) A is ωs-open in (X, τ) if and only if A = Int ωs(A).
Theorem 2.19. Let 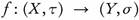 be an open function such that
be an open function such that 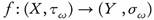 is continuous. Then for every
is continuous. Then for every 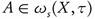 we have
we have 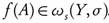 .
.
Proof. Let A ∈ ωs(X, α). Then there exists U ∈ τ such that 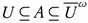 , and so
, and so 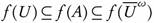 . Since
. Since 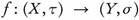 is open, then
is open, then 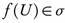 . Since
. Since 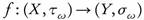 is continuous, then
is continuous, then 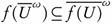 . It follows that
. It follows that 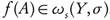 .
.
The condition “open function” cannot be dropped from Theorem 2.19 as shown by:
Example 2.20. Consider 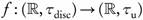 , where f (x) = 0 for all x ∈ R. Then it is obvious that
, where f (x) = 0 for all x ∈ R. Then it is obvious that 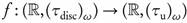 is continuous. On the other hand,
is continuous. On the other hand, 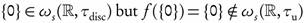 .
.
ωs-Continuous functions
Definition 3.1. A function 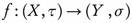 is called o
s-continuous, if for each V ∈ α, the preimage
is called o
s-continuous, if for each V ∈ α, the preimage 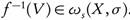 .
.
Theorem 3.2. The notions of continuity satisfy that
(a) Every continuous function is ωs-continuous.
(b) Every ωs-continuousfunction is semi-continuous.
Proof. Theorem 2.2. □
The following example will show that the converse of each of the two implications in Theorem 3.2 is not true in general:
Example 3.3. Let f, g: 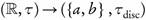 , with τ as in Example 2.3 and
, with τ as in Example 2.3 and
Since 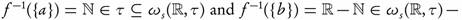 τ, then f is ωs continuous but not continuous. Also, Since
τ, then f is ωs continuous but not continuous. Also, Since 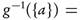
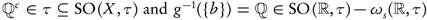 then f is semi-continuous but not ωs-continuous.
then f is semi-continuous but not ωs-continuous.
Theorem 3.4. Let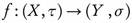 be a function.
be a function.
(a) If (X, τ) is locally countable, then f is continuous if and only if f is ωs -continuous.
(b) If (X, τ) is anti-locally countable, then f is ωs -continuous if and only if f is semi-continuous.
Proof. (a) It is a consequence of Theorems 2.4 (a) and 3.2 (a).
(b) It is a consequence of Theorems 2.4 (b) and 3.2 (b). □
Theorem 3.5.
A function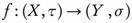 is ωs
-continuous if and only if for every x ∈ X and every open set V containing f (x) there exists U ∈ ωs
(X, τ)
such that x ∈ U and f (U)
is ωs
-continuous if and only if for every x ∈ X and every open set V containing f (x) there exists U ∈ ωs
(X, τ)
such that x ∈ U and f (U)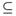 V.
V.
Proof. Necessity. Assume that 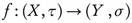 is ωs-continuous. Let us take V ∈ α with f (x) ∈ V. By ωs-continuity, f-1(V) ∈ ωs
(X, τ). Set U = f
-1
(V). Then U ∈ ωs
(X, τ) satisfies x ∈ U and f (U)
is ωs-continuous. Let us take V ∈ α with f (x) ∈ V. By ωs-continuity, f-1(V) ∈ ωs
(X, τ). Set U = f
-1
(V). Then U ∈ ωs
(X, τ) satisfies x ∈ U and f (U)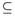 V.
V.
Sufficiency. Let V ∈ α. For each x ∈ f
-1( V) we have f (x) ∈ V, and thus there exists U
x
∈ ωs
(X, τ) such that x ∈ U
x, f (U
x
)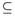 V, and x ∈ U
x
V, and x ∈ U
x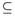 f-1(V). Thus
f-1(V). Thus 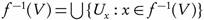 . Therefore, by Theorem 2.7, it follows f-1(V) ∈ ωs (X, τ). This shows that f is ωs-continuous.
. Therefore, by Theorem 2.7, it follows f-1(V) ∈ ωs (X, τ). This shows that f is ωs-continuous.
Theorem 3.6. Let 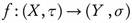 be a function. Then the following conditions are equivalent:
be a function. Then the following conditions are equivalent:
(a) The function f is o ¡-continuous.
(b) Inverse images of all members of a base B for a are in ωs (X, τ).
(c) Inverse images of all closed subsets of (Y, σ) are ωs -closed in (X, τ).
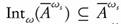 . Suppose
. Suppose 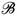 is a base for a such that f
-1(B) ∈ ωs
(X, τ) for every B ∈
is a base for a such that f
-1(B) ∈ ωs
(X, τ) for every B ∈ 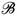 . Let C be a non-empty closed subset of (Y, σ). Then
. Let C be a non-empty closed subset of (Y, σ). Then 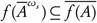 .
.
By assumption f-1(B) ∈ ωs(X, τ) for every 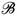 ∈
∈ 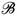 *, then by Theorem 2.7 we have X - f-1(C) ∈ ωs(X, τ), and hence f -1(C) is ωs-closed in (X, τ).
*, then by Theorem 2.7 we have X - f-1(C) ∈ ωs(X, τ), and hence f -1(C) is ωs-closed in (X, τ).
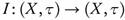 . Let A
. Let A 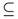 X. Then
X. Then  is closed in (Y, σ), and by (c)
is closed in (Y, σ), and by (c) 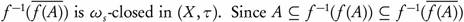 , and
, and 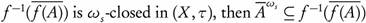 , and thus
, and thus 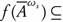
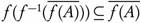 .
.
Lemma 3.7. Let (X, τ) be a topological space and let A 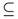 X. Then
X. Then
Proof. Since 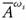 is ωs-closed, then by Theorem 2.15 Int">/
is ωs-closed, then by Theorem 2.15 Int">/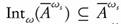 . Therefore,
. Therefore, 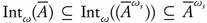 , and hence
, and hence 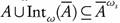 . To see that
. To see that 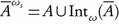 , it is sufficient to show that
, it is sufficient to show that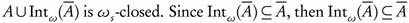 . Therefore,
. Therefore,
and by Theorem 2.15 it follows that 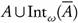 is ωs-closed. □
is ωs-closed. □
Theorem 3.8. Let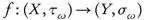 be a function. Then the following statements are equivalent:
be a function. Then the following statements are equivalent:
(a) f is ωs -continuous.
Proof.  . Suppose that f is ωs-continuous. Let A
. Suppose that f is ωs-continuous. Let A 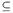 X. Then by Theorem 3.6 (d),
X. Then by Theorem 3.6 (d), 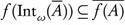 . Therefore, by Lemma 3.7 we have
. Therefore, by Lemma 3.7 we have 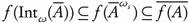 .
.
 . We will apply Theorem 3.6 (d). Let A
. We will apply Theorem 3.6 (d). Let A 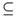 X. Then by (b), we have
X. Then by (b), we have 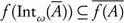 . Also, we have
. Also, we have 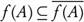 always. Therefore, by Lemma 3.7 we have
always. Therefore, by Lemma 3.7 we have
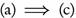 . Suppose that f is ωs-continuous. Let B
. Suppose that f is ωs-continuous. Let B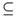 Y. Then by Theorem 3.6 (e),
Y. Then by Theorem 3.6 (e), 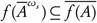 . Therefore, by Lemma 3.7 we have
. Therefore, by Lemma 3.7 we have 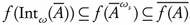 .
.
 . We will apply Theorem 3.6 (e). Let B
. We will apply Theorem 3.6 (e). Let B 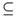 Y. Then by (c), we have
Y. Then by (c), we have  . Also, we have
. Also, we have 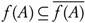 always. Therefore, by Lemma 3.7 we have
always. Therefore, by Lemma 3.7 we have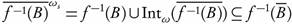 .
.
Theorem 3.9. If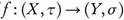 is ωs
-continuous and
is ωs
-continuous and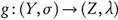 is continuous, then g o
is continuous, then g o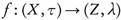 is a o ¡-continuous.
is a o ¡-continuous.
Proof. Let 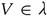 . Since g is continuous, then
. Since g is continuous, then 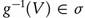 . Since f is ωs-continuous, then
. Since f is ωs-continuous, then 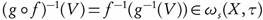 . □
. □
In general, the composition of two ωs-continuous functions does not need to be ωs-continuous as the following example clarifies:
Then
Since f and g are obviously semi-continuous and 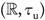 is anti-locally countable, then by Theorem 3.4 (b) f and g are ωs-continuous. On the other hand, since
is anti-locally countable, then by Theorem 3.4 (b) f and g are ωs-continuous. On the other hand, since 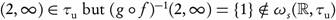 , then g o f is not ωs-continuous.
, then g o f is not ωs-continuous.
Theorem 3.11. Let  be a family offunctions. If the function
be a family offunctions. If the function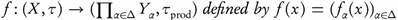 is ωs
-continuous, then f
α
is ωs
-continuous, for every α ∈ A.
is ωs
-continuous, then f
α
is ωs
-continuous, for every α ∈ A.
Proof. Suppose that f is ωs-continuous and let 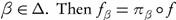 where
where 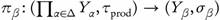 is the projection function on Yβ. Since Πβ is continuous, then by Theorem 3.9, f
β is ωs-continuous.
is the projection function on Yβ. Since Πβ is continuous, then by Theorem 3.9, f
β is ωs-continuous.
The following example will show that the converse of Theorem 3.11 is not true in general:
Since f and g are obviously semi-continuous, and 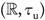 is anti-locally countable, then by Theorem 3.4 (b) f and g are ωs-continuous. On the other hand, since
is anti-locally countable, then by Theorem 3.4 (b) f and g are ωs-continuous. On the other hand, since 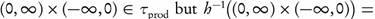
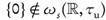 , then h is not ωs-continuous.
, then h is not ωs-continuous.
Theorem 3.13. Let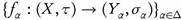 be a family of functions. If
be a family of functions. If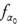 is ωs
-continuous for some
is ωs
-continuous for some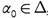 , and if fα is continuous for all
, and if fα is continuous for all 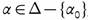 , then the function
, then the function 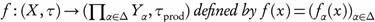 is ωs
-continuous.
is ωs
-continuous.
Proof. We will apply statement (b) of Theorem 3.6. Let A be a basic open set of 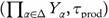 , without loss of generality we may assume that A =
, without loss of generality we may assume that A = 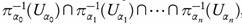 , where
, where 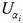 is a basic open set of
is a basic open set of 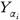 for all i = 0,1, ..., n. Then
for all i = 0,1, ..., n. Then
By assumption 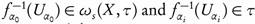 for all i = 0,1, ..., n. Thus
for all i = 0,1, ..., n. Thus 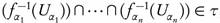 , and by Theorem 2.9, we have that
, and by Theorem 2.9, we have that 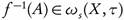 . It follows that f is ωs-continuous.
. It follows that f is ωs-continuous.
Corollary 3.14. Let 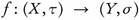 be a function and denote by
be a function and denote by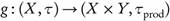 the graph function of f given by g (x) = (x, f (x)), for every x ∈ X. Then g is ωs
-continuous if and only iff is ωs
-continuous.
the graph function of f given by g (x) = (x, f (x)), for every x ∈ X. Then g is ωs
-continuous if and only iff is ωs
-continuous.
Proof. Necessity. Suppose that g is ωs-continuous. Then by Theorem 3.11, f is ωs-continuous.
Sufficiency. Suppose that f is ωs-continuous. Note that h(x) = (I(x), f (x)) where 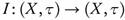 is the identity functions. Since the function I is continuous, then by Theorem 3.13, g is ωs-continuous.
is the identity functions. Since the function I is continuous, then by Theorem 3.13, g is ωs-continuous.