Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería y Universidad
Print version ISSN 0123-2126
Ing. Univ. vol.14 no.1 Bogotá Jan./June 2010
Cálculo de deformaciones elásticas en estructuras óptimas bidimensionales para diferentes ensamblajes*
Calculation of Elastic Deformations in Optimal Two-Dimensional Structures for a Number of Assembly Cases**
Cálculo de deformações elásticas em estruturas ótimas bidimensionais para diferentes montagens***
Diego Alexander Garzón-Alvarado*****
* Este artículo se deriva de un proyecto de investigación denominado Síntesis de mecanismos y optimización de estructuras, financiado por la Universidad Nacional de Colombia.
** This article results from the research project called Mechanism Synthesis and Structure Enhancement, financed by the Universidad Nacional de Colombia.
*** Este artigo deriva-se de um projeto de pesquisa denominado Síntese de mecanismos e otimizaçõo de estruturas, financiado pela Universidade Nacional da Colômbia.
**** Ingeniero Mecánico, Universidad Nacional de Colombia, Bogotá, Colombia. Estudiante de la Maestría en Ingeniería Mecánica, Universidad Nacional de Colombia. Docente de la Facultad de Ingeniería Mecánica, Universidad Santo Tomás, Bogotá, Colombia. Correo electrónico: cjcamachol@bt.unal.edu.co.
**** Ingeniero mecánico, Universidad Nacional de Colombia, Bogotá, Colombia. Máster en Ingeniería Mecánica, Universidad de los Andes, Bogotá, Colombia. Doctor en Mecánica Computacional, Universidad de Zaragoza, España. Profesor asociado del Departamento de Ingeniería Mecánica y Mecatrónica, Universidad Nacional de Colombia. Correo electrónico: dagarzona@bt.unal.edu.co.
Fecha de recepción: 8 de marzo de 2010. Fecha de aceptación para publicación: 21 de marzo de 2010.
Submitted on March 8, 2010. Accepted on March 21, 2010.
Data de recepçõo; 8 de março de 2010. Data de aceitaçõo para publicaçõo: 21 de março de 2010.
Resumen
En este trabajo se presenta un método para analizar las deformaciones elásticas y la rigidez de estructuras bidimensionales con diferentes configuraciones de unión entre sus elementos. Inicialmente se obtiene la estructura óptima mediante una optimización topológica y luego se desarrolla un método de análisis de diferentes tipos de uniones (articulación, unión flexible o unión rígida) entre los componentes de la estructura. Luego se desarrollan y validan dos ejemplos ampliamente referenciados en la literatura. Se ha determinado la versatilidad del método y la funcionalidad en el proceso de diseño y en la elección de la mejor opción de ensamble. Respecto a trabajos previos, este se constituye en un aporte al análisis de estructuras con diferentes configuraciones de interconexión de sus elementos, pues integra el diseño topológico y la elección de la mejor configuración para diferentes escenarios de relación ensamble-requerimientos de diseño.
Palabras clave: Acoplamientos flexibles, optimización estructural, diseño de estructuras.
Abstract
This paper presents a method to analyze elastic deformations and stiffness in two-dimensional structures with different assembly configurations among their elements. Initially, the optimal structure is obtained through topology optimization, and then a method to analyze different types of connections (hinge, flexible and rigid connections) in structural components is developed. Next, two widely documented examples are developed and validated. The versatility of the method and its functionality during both the design process and the selection of the best assembly option are determined. This work contributes to analyzing structures with different interconnection setups among their elements. Existing work is complemented through both the integration of topological design and the choice of the best setup features for a number of cases where assembly and design requirements are related.
Key words: Couplings, flexible, structural optimization, structural design.
Resumo
Neste trabalho apresenta-se um método para analisar as deformações elásticas e a rigidez de estruturas bidimensionais com diferentes configurações de uniõo entre seus elementos. Inicialmente obtêm-se a estrutura ótima mediante uma otimizaçõo topológica e depois se desenvolve um método de análise de diferentes tipos de uniões (articulaçõo, uniõo flexível ou uniõo rígida) entre os componentes da estrutura. Depois se desenvolvem e validam dois exemplos amplamente referenciados na literatura. Determinouse a versatilidade do método e a funcionalidade no processo de desenho e na seleçõo da melhor opçõo de montagem. Em comparaçõo com trabalhos anteriores, este se constitui como uma contribuiçõo à análise de estruturas com diferentes configurações de interconexõo de seus elementos, pois integra o desenho topológico e a seleçõo da melhor configuraçõo para diferentes cenários de relaçõo montagem-requerimentos de desenho.
Palavras-Chave: Acoplamentos flexíveis, otimizaçõo estrutural, desenho de estruturas.
Introducción
La mayoría de los productos mecánicos están constituidos por componentes relacionados e integrados (módulos) que deben cumplir con especificaciones de usuario para el correcto funcionamiento del ensamble final. En la actualidad, los requerimientos de diseño estructural se concentran tanto en desarrollar nuevos materiales y estructuras más resistentes y livianas como en solucionar problemas de producción (Boothroyd, 2001; Lyu, Lee y Saitou, 2004; Zuo et al., 2006; Booker, Swift y Brow, 2005; Cetin y Saitou, 2005). Por tal motivo, los ingenieros y diseñadores se encuentran con problemas más complejos y exigentes que necesitan la optimización estructural y la optimización de recursos.
En este camino se han desarrollado algoritmos para la optimización estructural de carrocerías automotrices (Yetis y Saitou, 2002; Lyu y Saitou, 2005a), la optimización de estructuras en voladizo (Takezawa et al., 2006) y el desarrollo óptimo de ensambles modulares para diferentes tipos de juntas de elementos estructurales (Cetin, 2003; Cetin y Saitou, 2006; Lyu y Saitou, 2006). El desarrollo de este tipo de problemas de diseño, y en general, de problemas que involucran gran cantidad de variables y procesos, ha llevado a usar métodos de análisis y diseño simultáneo, optimización multiobjetiva y combinatoria, entre otros.
Dentro de estos se encuentra el método de síntesis por descomposición de ensambles automotrices (Yetis y Saitou, 2002; Cetin, 2003; Lyu y Saitou, 2005b), que busca simplificar el análisis estructural en una estructura constituida por múltiples componentes. Este método incorpora procesos de optimización topológica estructural, análisis multicuerpo de la estructura y diseño de acuerdo con criterios de producción (Lyu, Lee y Saitou, 2004; Zuo et al., 2006; Cetin y Saitou, 2004 y 2005; Pavlovçiç et al., 2004).
A partir del enfoque de diseño de estructuras ensambladas, este trabajo propone un nuevo algoritmo para buscar el mejor ensamble de componentes entre las diferentes opciones de unión, a partir del directo barrido de una estructura topológicamente optimizada. Para ello se deben evaluar cada una de las uniones entre los elementos de una estructura (rígida, semirrígida y flexible) con el fin de hallar las subestructuras que al ensamblarse obtengan las características mecánicas de rigidez y flexibilidad que se desean en el diseño.
En este artículo se plantea inicialmente la metodología para calcular deformaciones elásticas en estructuras óptimas según sus características de ensamble. La definición de esta metodología de análisis se desarrolla en tres etapas: (1) descomposición en subsistemas, a partir de un resultado previo de optimización topológica estructural; (2) incorporación de los efectos estructurales por el empleo de conexiones flexibles, y (3) cálculo de las deformaciones elásticas por medio del método de elementos finitos. Por último, se aplica este algoritmo al estudio y solución de dos casos específicos de análisis estructural.
Los resultados muestran que para diferentes tipos de modularización de un ensamble se presenta variación en la rigidez y la estabilidad de la configuración estructural. De igual forma, los resultados demostraron la pertinencia de integrar la rigidez de las uniones entre componentes para hacer más exacto el análisis y planear los métodos de producción de los módulos de la estructura.
1. Materiales y métodos
1.1 Método para el análisis estructural de ensambles
El método propuesto consta de tres etapas secuenciales, las cuales son ilustradas en la Figura 1. En la primera etapa se determina la gráfica topológica estructural a partir de tres procesos: optimización topológica estructural, filtrado y esqueletización de la figura topológica y, por último, identificación de nodos y elementos.
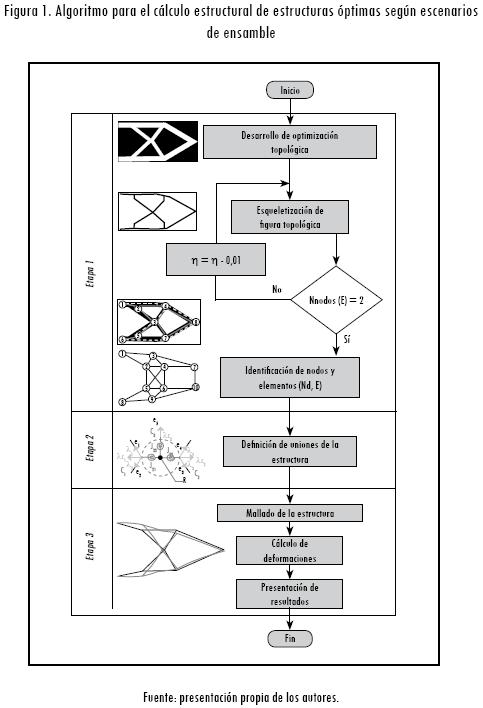
La segunda etapa define las condiciones de conectividad de la gráfica topológica de acuerdo con un escenario de ensamblaje. Por último, la tercera etapa emplea la estructura del método de elementos finitos, y para ello se desarrollan los procesos de mallado, cálculo de las deformaciones elásticas de la estructura y presentación final de resultados.
Este trabajo está enfocado en desarrollar un algoritmo para identificar nodos y elementos por medio del barrido directo de la estructura y la posterior utilización del modelo de Dhillon y O'Malley (1999), a fin de calcular la deformación de la estructura optimizada de acuerdo con diferentes escenarios de ensamblaje. A continuación se describen cada uno de los procesos desarrollados en la definición del algoritmo de análisis estructural planteado.
1.2 Desarrollo de la optimización topológica estructural
En esta etapa se realiza la optimización topológica estructural del problema de diseño. Para tal fin se han empleado dos software de optimización topológica: el código de optimización desarrollado por Bendsøe y Sigmund (2003) y la herramienta NDOPTI, la cual basa su trabajo en la optimización a través de autómatas celulares híbridos (HCA, por su sigla en inglés) (Tovar et al., 2006a y 2006b).
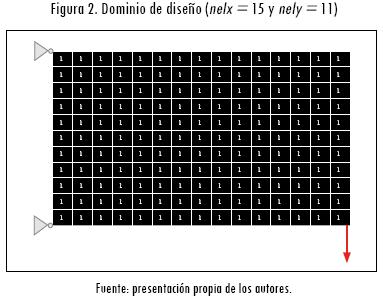
En cada una de estas técnicas, el dominio de diseño corresponde a una región rectangular continua que se discretiza por elementos finitos cuadriláteros bilineales (Hughes, 2000) y sometida a ciertas condiciones de carga y restricciones de desplazamiento. La relación de aspecto de esta región está dada por la relación entre el número de elementos en la dirección horizontal (nelx) y en la dirección vertical (nely) (Figura 2).
A partir de lo anterior, el problema de optimización topológica se formula como:


Donde u y F son los vectores de desplazamientos y fuerza globales, respectivamente; k es la matriz de rigidez global, ue y ke son el vector de desplazamientos y la matriz de rigidez por elemento, respectivamente; x es el vector de variables de diseño definido como el vector de densidades relativas; xmin es un vector de densidades relativas mínimas (diferente a cero para evitar singularidades); N(=nelx x nely) es el número de elementos usados en la discretización del dominio de diseño; p es la potencia de penalización (típicamente p = 3); V(x) y V0 son el volumen material y el volumen del dominio de diseño, respectivamente, y ƒ(volfrac) es la fracción de volumen prescrita (Sigmund, 2001).
Al solucionar este problema de optimización para diferentes condiciones de carga y restricciones de desplazamiento, se determina el vector óptimo x. Este vector, dentro de un espacio bidimensional, se puede definir a partir de nelx y nely como la matriz de distribución óptima de densidad X, donde X ∈ Rnelx x nely con:
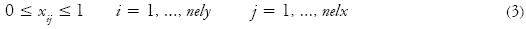
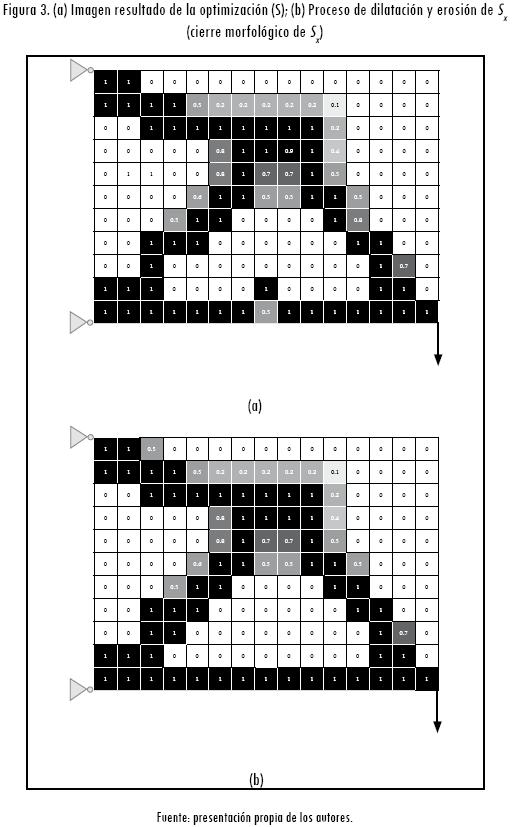
La imagen en escala de grises que representa la matriz X es llamada Sx (Figura 3a), donde cada pixel definido por el color blanco establece que xij = 0 e, inversamente, un pixel negro corresponde a xij = 0.
1.3 Filtrado y esqueletización de la figura topológica resultante
Este proceso de filtrado y esqueletización inicia con las operaciones morfológicas de dilatación y erosión de la imagen Sx —proceso llamado cierre morfológico (Russ, 2007)—. El cierre morfológico permite eliminar las discontinuidades existentes en la imagen Sx (Figura 3b). La imagen y la matriz de densidades resultantes de esta operación son Sx-cm y Xcm, respectivamente.
Posteriormente, se desarrolla un subproceso de filtrado, en el cual cada término de la matriz de densidades Xcm que sea mayor o igual a la constante de filtrado η es almacenado en la matriz Sfil y su valor correspondiente convertido a 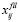 = 1. La imagen filtrada resultante corresponde a
= 1. La imagen filtrada resultante corresponde a 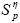 .
.
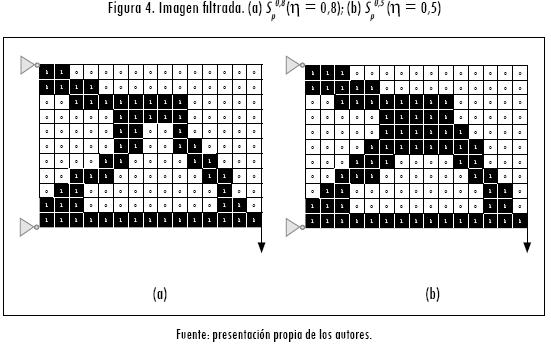
En la Figura 4 se pueden apreciar las imágenes filtradas para η = 0,8 y η = 0,5. Este subproceso de filtrado se plantea entonces como:

donde, Xfil corresponde a la matriz de distribución de densidades filtrada.
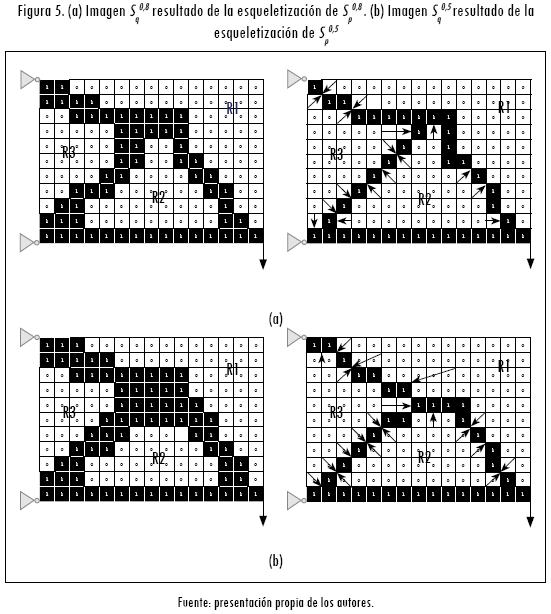
Posteriormente, se aplica el proceso de esqueletización, el cual, de forma iterativa, remueve pixeles en los bordes de cada una de las regiones de densidad nula (xij = 0) existentes en la imagen 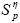 , hasta cuando al eliminar estos pixeles se pueda generar la mínima separación o unión de alguna de estas regiones. En la Figura 5, las imágenes filtradas
, hasta cuando al eliminar estos pixeles se pueda generar la mínima separación o unión de alguna de estas regiones. En la Figura 5, las imágenes filtradas 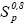 y
y 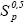 presentan tres regiones (R1, R2 y R3), de las cuales sus bordes son erosionados hasta que se garantiza que ninguna de ellas se ha divido o unido entre sí. El resultado final de este proceso se representa por medio de la imagen esqueletizada
presentan tres regiones (R1, R2 y R3), de las cuales sus bordes son erosionados hasta que se garantiza que ninguna de ellas se ha divido o unido entre sí. El resultado final de este proceso se representa por medio de la imagen esqueletizada 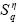 . Los procesos anteriores de dilatación, erosión y esqueletización se implementaron a partir del toolbox de procesamiento de imágenes existente en MATLAB®.
. Los procesos anteriores de dilatación, erosión y esqueletización se implementaron a partir del toolbox de procesamiento de imágenes existente en MATLAB®.
1.4 Identificación final de nodos y elementos
El proceso de identificación de nodos y elementos se lleva a cabo a partir de tres subprocesos: barrido de la imagen, evaluación de η y colapso de nodos. En el primer subproceso hay un barrido por cada uno de los pixeles del esqueleto 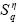 y se identifican los diferentes nodos de unión Ndi que durante el barrido generan ramificación o cambios de dirección iguales a 90 grados. En la Figura 6 se muestran algunos de los nodos básicos característicos, los cuales pueden variar de orientación dentro de la imagen
y se identifican los diferentes nodos de unión Ndi que durante el barrido generan ramificación o cambios de dirección iguales a 90 grados. En la Figura 6 se muestran algunos de los nodos básicos característicos, los cuales pueden variar de orientación dentro de la imagen 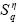 .
.
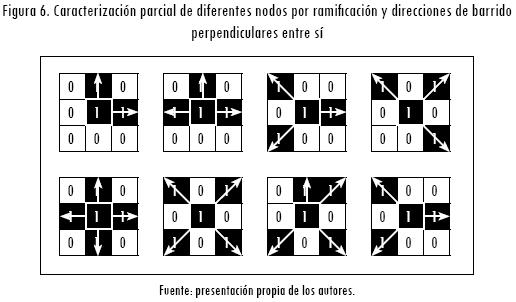
Durante el barrido de Sq, de igual forma se identifican los elementos estructurales (E) que unen los diferentes nodos Nd y que se relacionan de acuerdo con las ramificaciones encontradas. Si el número total de elementos obtenidos en la estructura corresponde a NelS, entonces:

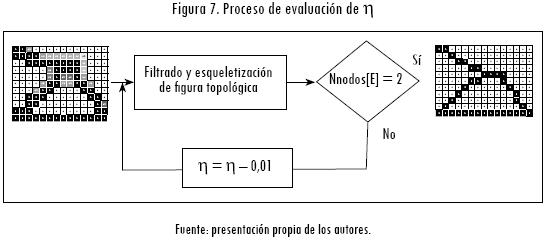
En el segundo subproceso (Figura 7), la imagen 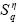 es evaluada por medio de la función Nnodosi, la cual determina la cantidad de nodos de cada i-ésimo elemento estructural (ei) y busca garantizar que cada elemento estructural que se vaya a identificar tenga asignados únicamente dos nodos dentro de la estructura (un nodo por cada extremo). Cuando en esta función algún elemento presenta un valor diferente de dos, la constante de filtrado η es reducida hasta que se garantiza la apropiada asignación de nodos y elementos.
es evaluada por medio de la función Nnodosi, la cual determina la cantidad de nodos de cada i-ésimo elemento estructural (ei) y busca garantizar que cada elemento estructural que se vaya a identificar tenga asignados únicamente dos nodos dentro de la estructura (un nodo por cada extremo). Cuando en esta función algún elemento presenta un valor diferente de dos, la constante de filtrado η es reducida hasta que se garantiza la apropiada asignación de nodos y elementos.
Por otro lado, el subproceso de colapso de nodos busca una mayor aproximación a la imagen resultante obtenida de la optimización topológica (Sx) y a las condiciones iniciales del problema de diseño planteado (ubicación de cargas y apoyos). Para tal fin se desarrolla inicialmente el colapso por parte de ciertos nodos Ndi hacia los nodos de frontera Ndbdy. Estos últimos definen las coordenadas donde se aplican las cargas externas y se ubican las restricciones de desplazamiento planteadas en el problema que se está analizando.
Este colapso se realiza para todos los Ndi que se encuentran a una distancia menor a un porcentaje Cbdy de la máxima dimensión del espacio de diseño estudiado (nelx o nely) (Figura 8a). Este subproceso se define como:
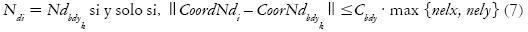
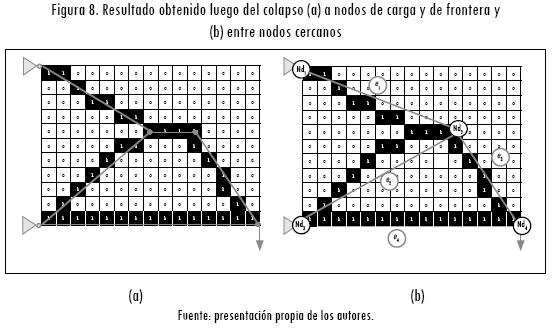
De forma similar, los nodos Ndi que se encuentran muy cercanos entre sí se colapsan a un único nodo común si su distancia es menor a un porcentaje Cproximidad de la máxima distancia existente entre los Ndi (Figura 8b). Este proceso de colapso se encuentra definido como:
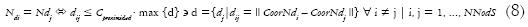
Al analizar un problema particular de diseño se determina, por medio de un análisis de sensibilidad, los valores Cbdy y Cproximidad para los cuales se obtiene la estructura con mayor aproximación tanto a la gráfica Sx como a las condiciones iniciales del problema planteado. En este análisis de sensibilidad se evalúa, adicionalmente, el comportamiento de la estructura a través de su flexibilidad (C) para diferentes valores de Cbdy y Cproximidad. El cálculo de la flexibilidad de la estructura se trata posteriormente.
Al final de este proceso de identificación se obtienen el conjunto de nodos (Nd) y el conjunto de elementos estructurales (E) que representan la estructura optimizada para su posterior análisis de ensamblaje. De igual forma, el estado de conectividad inicial de la estructura es definido y expresado como la matriz binaria Jo, donde cada término Joij igual a uno representa la existencia de la unión entre el elemento ei y el elemento ej.
1.5 Definición de uniones y escenarios de ensamblaje de la estructura
A continuación se requiere analizar las conexiones existentes entre elementos, de tal forma que se incorpore la flexibilidad de las uniones en el análisis de la estructura. En este tipo de conexiones, llamadas uniones semirrígidas o uniones flexibles, la rigidez de la unión depende tanto de los parámetros geométricos de los elementos que se van a unir como del momento que se transfiere en la unión (Dhillon y O'Malley, 1999). Por tal razón, el comportamiento de estas conexiones se modela como resortes de torsión y se caracteriza por las respectivas constantes de rigidez torsional.
Por lo anterior, para analizar un determinado escenario o configuración de ensamblaje en una estructura se debe tener en cuenta: (a) la caracterización de la conectividad existente entre los diferentes elementos de la estructura original, representada por medio de la gráfica topológica base 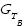 ; (b) la verificación de las variables y restricciones de ensamblaje, y (c) la definición de las constantes de rigidez torsional que permitan caracterizar el tipo de unión.
; (b) la verificación de las variables y restricciones de ensamblaje, y (c) la definición de las constantes de rigidez torsional que permitan caracterizar el tipo de unión.
1.5.1 Caracterización de la conectividad por medio de grafica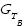
La definición de la grafica topológica base 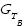 se realiza a partir del conjunto de nodos (Nd) del conjunto de elementos estructurales (E), identificados en la etapa anterior, y de la matriz binaria de conectividades J0. En esta gráfica topológica
se realiza a partir del conjunto de nodos (Nd) del conjunto de elementos estructurales (E), identificados en la etapa anterior, y de la matriz binaria de conectividades J0. En esta gráfica topológica 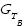 (Nd, E, J0), los nodos corresponden a los elementos de la estructura, mientras que las líneas especifican la existencia de la conexión entre dichos elementos (Figura 9). Con la definición de
(Nd, E, J0), los nodos corresponden a los elementos de la estructura, mientras que las líneas especifican la existencia de la conexión entre dichos elementos (Figura 9). Con la definición de 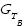 culmina la primera etapa del método propuesto.
culmina la primera etapa del método propuesto.
1.5.2 Verificación de las variables y restricciones de ensamblaje
A partir de este proceso de verificación se inicia con la segunda etapa del proceso de análisis estructural de ensambles propuesto (Figura 1) y donde las variables y restricciones de ensamblaje corresponden a: variable de conectividad, restricción de cobertura y restricción de conectividad.
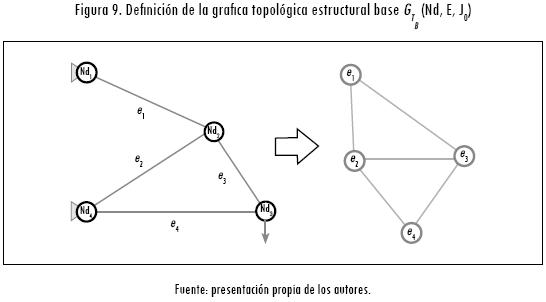
En cuanto a la variable de conectividad: y, se debe tener en cuenta que una estructura ensamblada está compuesta por elementos multicuerpo, los cuales corresponden a conjuntos estructurales conformados por uno o varios elementos ei, unidos o conectados entre sí, y los cuales son llamados componentes de la estructura ensamblada (Ci). En la Figura 10 se presentan ejemplos sobre la especificación de componentes dentro de una disposición de ensamble para una estructura determinada.
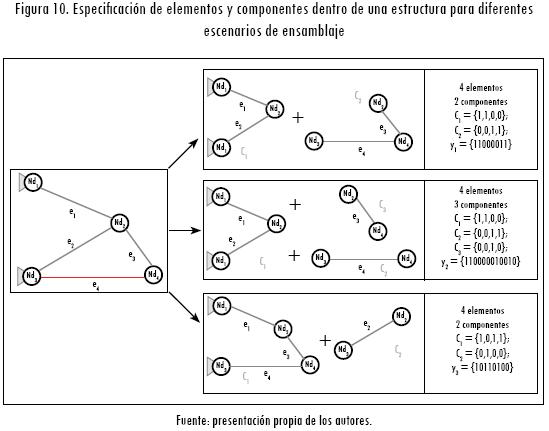
Por lo anterior para determinar la conectividad de una estructura ensamblada (o escenario de ensamblaje de una estructura) se establece la variable de conectividad y, que configura los diferentes componentes (Ci) de la estructura a través del siguiente vector binario:
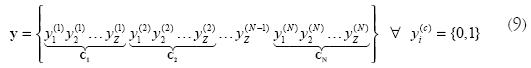
Con N que es el número de componentes de la estructura, y Z, el número de elementos de la estructura. De tal forma que, 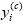 = 1 si el elemento i hace parte del componente c. En los ejemplos planteados en la Figura 16 se presentan tres escenarios posibles de ensamble, donde cada uno establece condiciones diferentes de conectividad de la estructura (y1, +y2 y y3).
= 1 si el elemento i hace parte del componente c. En los ejemplos planteados en la Figura 16 se presentan tres escenarios posibles de ensamble, donde cada uno establece condiciones diferentes de conectividad de la estructura (y1, +y2 y y3).
Para la configuración del cualquier escenario posible de ensamblaje de componentes de la estructura, esta variable y debe cumplir con las restricciones de cobertura y conectividad señaladas en la Figura 10. Respecto a la restricción de cobertura, esta restricción a la variable y busca garantizar que:
- Todos y cada uno de los elementos que componen la gráfica topológica
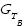 (Nd, E, J0) hagan parte de algún componente (Ci) definido por y (cobertura de todos los elementos).
(Nd, E, J0) hagan parte de algún componente (Ci) definido por y (cobertura de todos los elementos). - Cada uno de los elementos no pueden ser parte a la vez de múltiples componentes, lo cual permite que cada componente sea conformado por mínimo un elemento de la estructura (cobertura de todos los componentes). Esta restricción se establece entonces como:

Por último, está la restricción de conectividad. A partir de la gráfica topológica 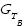 (Nd, E, J0) se establece que un componente solamente puede estar conformado por elementos (ei), cuyas conexiones estén incluidas dentro del conjunto J0. Adicionalmente, se debe cumplir que las conexiones entre diferentes componentes sólo son permitidas entre elementos de dichos componentes, donde la conexión también está incluida en J0.
(Nd, E, J0) se establece que un componente solamente puede estar conformado por elementos (ei), cuyas conexiones estén incluidas dentro del conjunto J0. Adicionalmente, se debe cumplir que las conexiones entre diferentes componentes sólo son permitidas entre elementos de dichos componentes, donde la conexión también está incluida en J0.
1.5.3 Definición de constantes de rigidez de las uniones existentes
A partir de 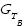 y la definición de las variables y restricciones de ensamblaje, se establece la variable J, que caracteriza las constantes de rigidez torsional de las conexiones existentes. Esta variable J permite incorporar los efectos generados en la rigidez y el estado deformacional, por la existencia de uniones flexibles dentro de la estructura ensamblada.
y la definición de las variables y restricciones de ensamblaje, se establece la variable J, que caracteriza las constantes de rigidez torsional de las conexiones existentes. Esta variable J permite incorporar los efectos generados en la rigidez y el estado deformacional, por la existencia de uniones flexibles dentro de la estructura ensamblada.
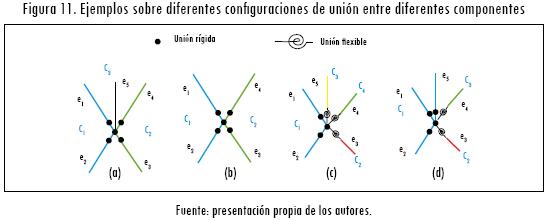
Para definir esta variable previamente se desarrolla un proceso de expansión de los nodos que unen dos o más componentes. Con ello se busca diferenciar en los nodos de conexión la flexibilidad generada por cada componente en la unión. En las figuras 11a y 11b se puede apreciar que sin expansión, para ciertas configuraciones de ensamblaje, no es posible incorporar la flexibilidad que cada componente induce a la estructura. Al contrario, en las figuras figuras 11c y 11d se muestra que en otros casos la expansión no es necesaria, ya que es suficiente con incorporar la flexibilidad en los elementos que componen los componentes.
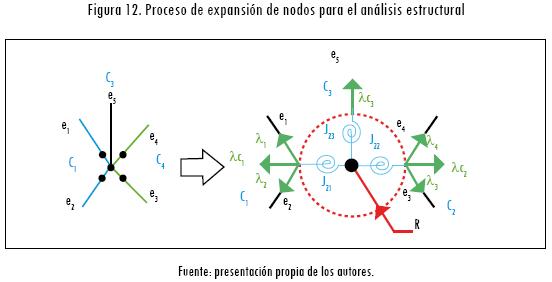
En las uniones expandidas se traslada la ubicación de estos nodos desde el centro de la unión a una distancia R. En la Figura 12 se puede apreciar un ejemplo para la unión U2, conformada por cinco elementos (e1, e2, e3, e4 y e5) y tres componentes (C1, C2 y C3).
La expansión de los nodos se lleva a cabo de acuerdo con la restricción de expansión, definida como:
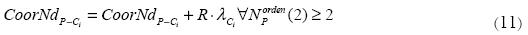
Donde 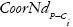 son las coordenadas de nodo P que se va a expandir del componente Ci; R es el radio de expansión;
son las coordenadas de nodo P que se va a expandir del componente Ci; R es el radio de expansión; 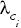 es la dirección de desplazamiento del i-ésimo componente determinado por medio del vector unitario resultante de la suma de los vectores unitarios de cada uno de los elementos (e) que conforman dicho componente;
es la dirección de desplazamiento del i-ésimo componente determinado por medio del vector unitario resultante de la suma de los vectores unitarios de cada uno de los elementos (e) que conforman dicho componente; 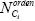 es una función que ordena de mayor a menor la cantidad de elementos por componente existentes en cada nodo que une dos o más componentes de la estructura ensamblada. Cuando en esta función el segundo mayor término del conjunto ordenado posee más de dos elementos o miembros, se desarrolla la expansión del nodo respectivo.
es una función que ordena de mayor a menor la cantidad de elementos por componente existentes en cada nodo que une dos o más componentes de la estructura ensamblada. Cuando en esta función el segundo mayor término del conjunto ordenado posee más de dos elementos o miembros, se desarrolla la expansión del nodo respectivo.
A partir de este proceso de expansión, se define la variable J, la cual, como se presentó, configura las constantes de rigidez de las uniones entre los componentes existentes en la estructura. Esta variable se expresa como la matriz J, en la cual:

Con Jij como constante de rigidez torsional en la unión i del componente J [Nm/rad].
El valor de Jij corresponderá a valores muy cercanos a cero si la unión se comporta como una articulación (diferente a cero para evitar singularidades), e infinito (∞) si la conexión se comporta como una unión perfectamente rígida. En la Figura 12 se puede observar que la unión estructural dos, luego de la expansión, se encuentra definida por las constantes J21, J22, J23. Para la descomposición de una estructura en subconjuntos o componentes, en este artículo las constantes de rigidez torsional de las diferentes uniones de la estructura se determinan de acuerdo con una librería preestablecida en la herramienta desarrollada.
1.6 Análisis por elementos finitos de la estructura
El análisis por elementos finitos (FEM, por su sigla en inglés) a la estructura permite verificar la deformación de los elementos de la estructura (componentes y uniones) de acuerdo con las condiciones iniciales impuestas en el problema. Este análisis se realiza a partir de los resultados obtenidos en las etapas anteriores.
Para determinar los desplazamientos generados en la estructura bidimensional, incorporando la flexibilidad de las uniones, cada uno de los elementos que la constituyen se definen como elementos tipo viga con conexiones semirrígidas en sus extremos (Figura 13).
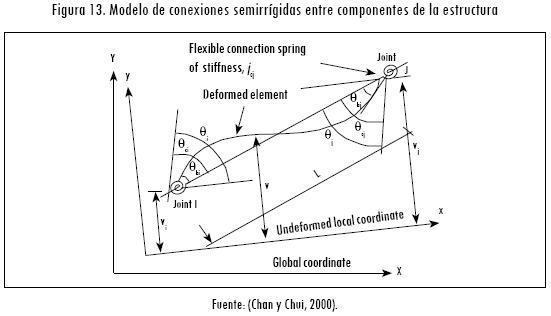
Este tipo de conexiones se representa por un resorte de torsión en cada uno de los extremos y se caracterizan por sus correspondientes constantes de rigidez Jci y Jcj. Donde,

La influencia de la flexibilidad de las conexiones es incorporada al análisis estructural, a través de la matriz de rigidez, en coordenadas globales de cada uno de los elementos o miembros de la estructura [k]. Estos términos de esta matriz son presentados por Hayalioglu y Degertekin (2005), derivados del trabajo de Dhillon y O'Malley (1999). En el presente trabajo, las propiedades geométricas y mecánicas de cada uno de los elementos —área transversal (A), inercia (I), módulo de elasticidad (E)— se consideraron constantes en toda la estructura. Con lo anterior, y junto con la discretización o mallado de la estructura (según su tamaño o cantidad de elementos), y de acuerdo con la matriz de rigidez [k] de cada elemento, se construye y ensambla la matriz de rigidez global de la estructura (kG). Posteriormente, según la condiciones de carga (vector F) y las restricciones de desplazamiento, se calcula el vector de desplazamientos nodales existentes (U) en la estructura. De igual forma en la estructura se determina su flexibilidad por medio de la relación:

Esta relación permite evaluar los valores de Cbdy y Cproximidad para el análisis de sensibilidad de las estructuras identificadas. Los resultados obtenidos en esta etapa se muestran a través de la gráfica de la estructura deformada.
2. Casos de estudio
En esta sección se emplea el método planteado para el estudio de dos tipos de estructuras, las cuales han sido ampliamente documentadas en estudios de optimización topológica estructural (Yetis y Saitou, 2002; Bendsøe y Sigmund, 2003).
2.1 Resultados preliminares
En la Figura 14 se pueden apreciar los dos casos planteados para su solución por medio de optimización topológica. En el caso I, el elemento continuo se encuentra en voladizo apoyado por dos articulaciones en el extremo izquierdo y con una carga concentrada vertical hacia abajo de 1.000 newtons (N), tal como se muestra en la Figura 14a. Para el caso II (Figura 14b), este mismo elemento se encuentra simplemente apoyado con una carga vertical de 1.000 N, ubicada en la mitad entre los apoyos. En ambos casos nelx = 80 y nely = 40.
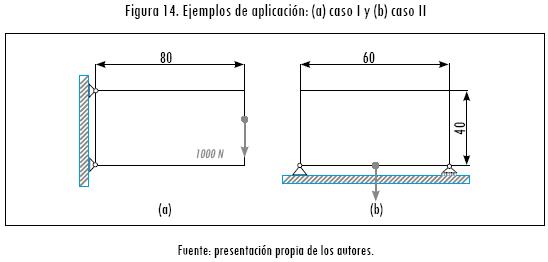
Inicialmente, se desarrolla la optimización topológica para los casos I y II y se obtienen como resultado las imágenes presentadas en las figuras 15a y 15b, respectivamente. Luego estas imágenes se transforman por medio del proceso de cierre morfológico a las imágenes mostradas en las figuras 15c y 15d. En este paso se puede apreciar cómo el proceso de cierre morfológico modifica para cada caso de estudio los contornos existentes en la imagen.
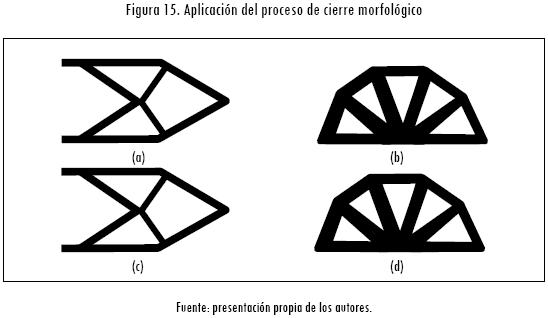
Posteriormente, a través del proceso de evaluación de η (Figura 7), se determina para el caso I y el caso II que las respectivas constantes de filtrado son η = 0,76 y η = 1. Como resultado se obtienen las graficas 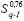 y
y 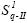 (Figura 16). A continuación se desarrolla el proceso de barrido, identificando de los diferentes nodos (Nd) y elementos (E) que conforman la estructura requerida para analizar los escenarios de ensamblaje.
(Figura 16). A continuación se desarrolla el proceso de barrido, identificando de los diferentes nodos (Nd) y elementos (E) que conforman la estructura requerida para analizar los escenarios de ensamblaje.
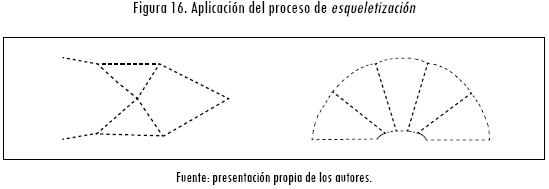
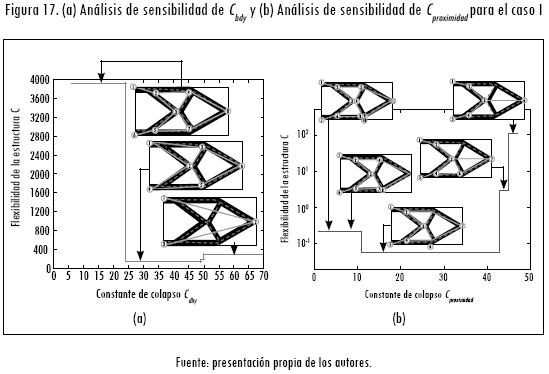
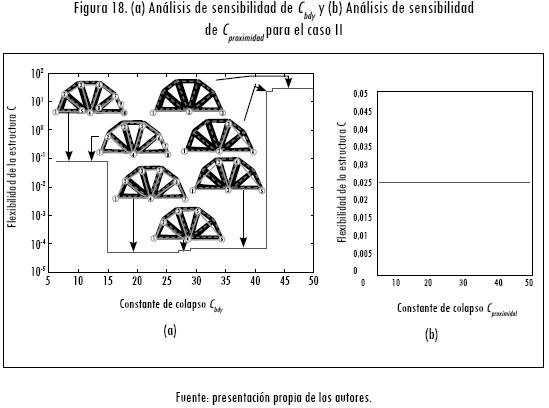
Para identificar estos nodos y elementos se determinó, a partir del análisis de sensibilidad (figuras 17a, 17b, 18a y 18b), como constante de colapso a nodos de frontera Cbdy = 0,15; mientras que la constante entre nodos cercanos o de proximidad se estableció como Cproximidad = 0,15. En cada uno de los análisis de sensibilidad se determina la flexibilidad de la estructura y se analiza la semejanza de la estructura respecto a la imagen obtenida en el proceso de optimización topológica. En la Figura 18b se puede observar que para el caso II la variación de la constante Cproximidad no incide en los resultados obtenidos.
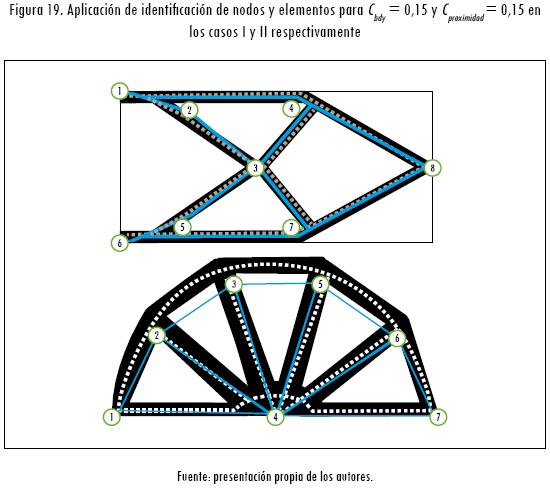
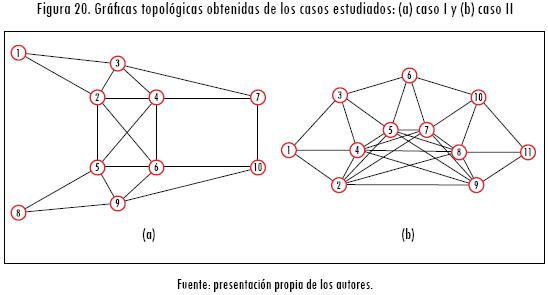
Igualmente, en esta etapa se determina la matriz de conectividades de la estructura base J0. El resultado final corresponde a las estructuras mostradas en la Figura 19. A partir de estos resultados se construyen las respectivas gráficas topológicas estructurales base 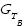 (Nd, E, J0), las cuales se pueden observar en la Figura 20. Para el caso I, en la gráfica topológica (Figura 20a) se presentan 10 nodos identificados de 1~10, que representan los miembros básicos de la estructura. Las líneas en esta gráfica representan las uniones o conexiones potenciales que pueden existir entre los miembros básicos de la estructura identificada para cada caso en estudio.
(Nd, E, J0), las cuales se pueden observar en la Figura 20. Para el caso I, en la gráfica topológica (Figura 20a) se presentan 10 nodos identificados de 1~10, que representan los miembros básicos de la estructura. Las líneas en esta gráfica representan las uniones o conexiones potenciales que pueden existir entre los miembros básicos de la estructura identificada para cada caso en estudio.
2.2 Resultados para diferentes condiciones de ensamblaje
Para calcular las deformaciones en los dos casos de estudio se establecieron los siguientes escenarios de ensamblaje: (a) estructura tipo marco con uniones rígidas, (b) estructura tipo armadura con uniones completamente articuladas y (c) estructura con uniones semirrígidas o flexibles. Para los dos casos de estudio, y de acuerdo con los escenarios (a) y (b), se calculó la deformación en la estructura por medio de la aplicación desarrollada en este trabajo; posteriormente, se validaron los resultados alcanzados por medio de un software comercial de elementos finitos.
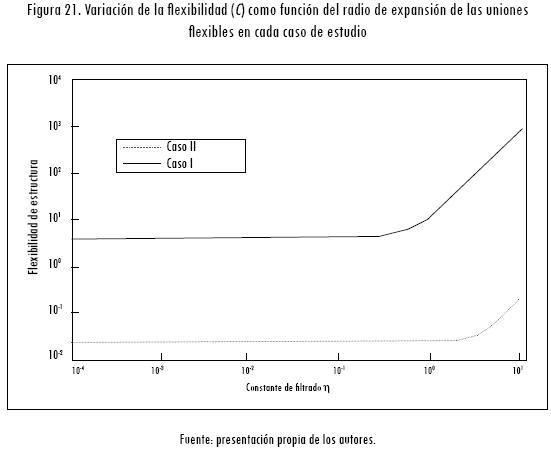
En la aplicación de la herramienta se analizaron los resultados sin expansión de los nodos de conexión y con estos, según lo tratado anteriormente. Para aquellos nodos donde se requiere la expansión, el radio de expansión es R = 1x10-4 m. La sensibilidad de los resultados por la variación R para cada caso de estudio en un escenario de ensamblaje (Figura 21) muestra que para valores muy pequeños la flexibilidad de la estructura no se ve afectada; al contrario, muestra un comportamiento análogo a lo presentado por Lee y Nicolaidis (1992) en su estudio de uniones bidimensionales flexibles:
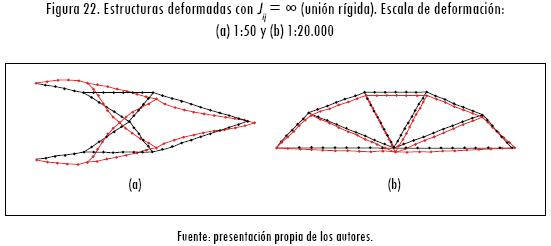
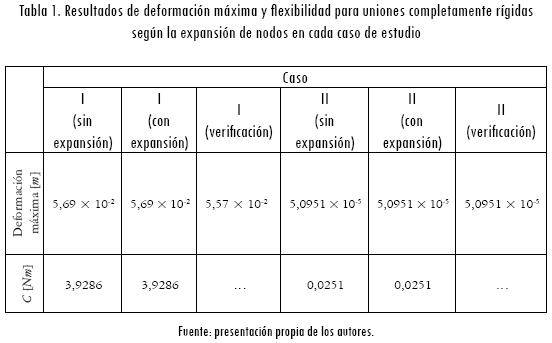
a) Estructuras con uniones completamente rígidas. En este escenario las estructuras presentan constantes de rigidez torsional en las uniones Jij = ∞ y para tal fin se obtienen los siguientes resultados (figuras 22a y 22b; Tabla 1).
b) Estructuras con uniones articuladas: en este escenario se puede evidenciar que para el caso I no se pueden calcular las deformaciones de la estructura, ya que se hace inestable internamente bajo estas condiciones (Tabla 2). La rigidez torsional de las uniones articuladas corresponde a Jij = 1.
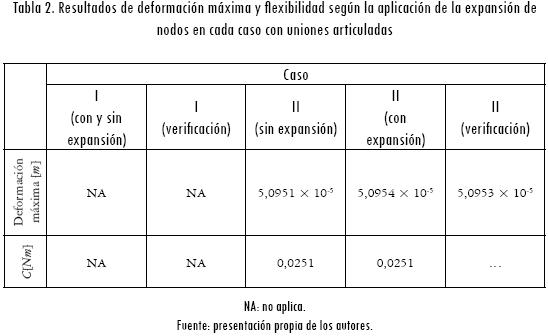
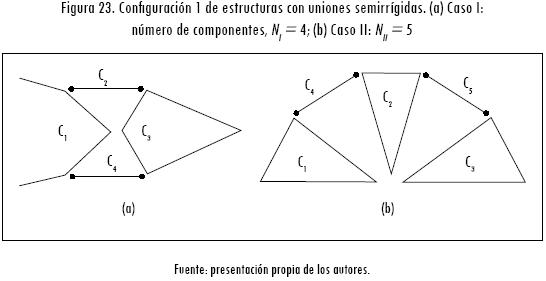
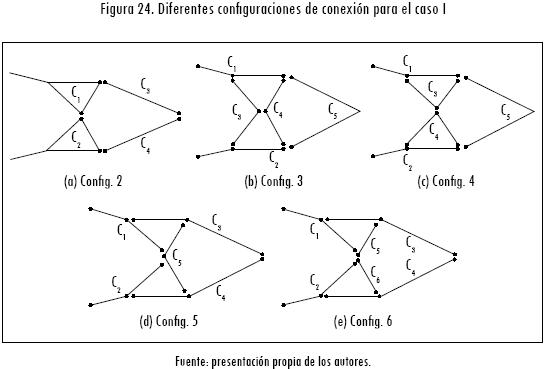
c) Estructuras con uniones semirrígidas: al establecer en las uniones conexiones semirrígidas para una condición de ensamblaje, la flexibilidad y las deformaciones de sistema varían y permiten el análisis de estructuras inestables tipo armadura. Los resultados siguientes se establecieron para valores Jij = {1;6,5;7,5;25.000}. Aquellos valores pequeños son establecidos con el fin de minimizar los errores producidos por las singularidades existentes en la matriz de rigidez global. En las figuras 23 y 24 se pueden apreciar las diferentes configuraciones analizadas para este tipo de conexiones flexibles o semirrígidas. Para la configuración 2 se desarrolló el análisis para dos valores Jij = {6,5; 25.000} con el fin verificar la estabilidad de la estructura en condiciones diferentes de flexibilidad en las conexiones existentes.
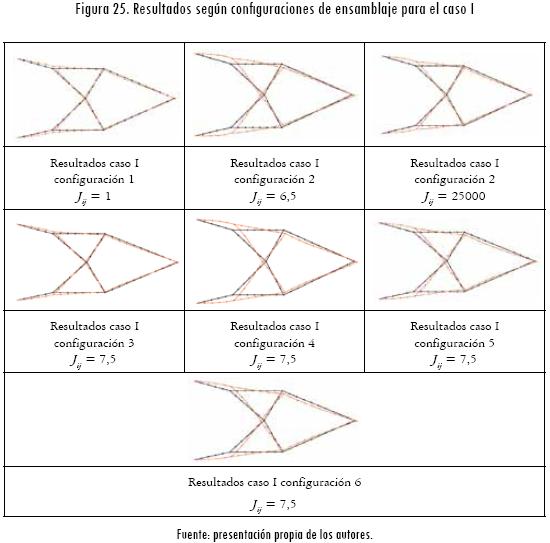
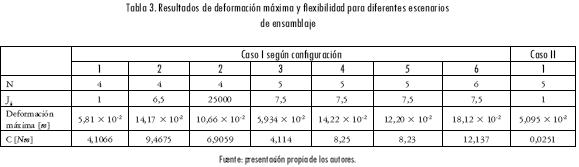
Los resultados mostrados en la Figura 25 y condensados en la Tabla 3 permiten evidenciar que para el caso I, con las configuraciones de ensamblaje 1 y 3, se obtienen resultados en la flexibilidad y deformación máxima cercanos a los alcanzados con la estructura fabricada completamente rígida (Figura 22). Sin embargo, al comparar estos tres escenarios de ensamblaje, la configuración 3 garantiza —según el diseño para la manufactura y ensamble (DFMA, por su sigla en inglés) (Boothroyd, 2001)— menor costo de fabricación y mayor capacidad de ensamblaje, ya que permitirá la modularización de los componentes, la reducción del área de trabajo y mayor manipulación de la estructura al momento de ser fabricada o ensamblada.
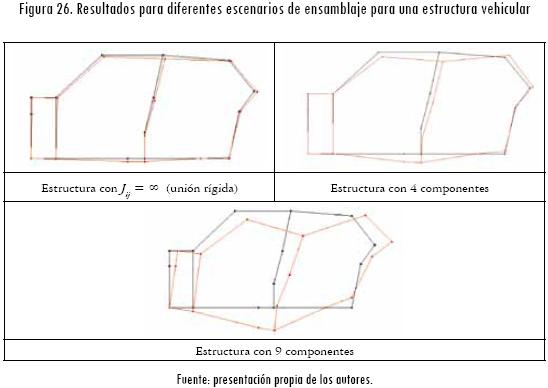
El empleo de uniones semirrígidas permite, de igual forma, garantizar condiciones de diseño, las cuales requieren cierta flexibilidad en la estructura para ser cumplidas, tal como lo plantean Lyu y Saitou (2003), en el análisis de una estructura vehicular. En este tipo de estructura es necesario controlar las dimensiones de la puerta del conductor, de tal forma que garantice su funcionamiento al momento de presentarse cualquier deformación de la estructura. Empleando la información presentada por Chang (1974), se analizó este tipo de estructura para diferentes configuraciones de ensamblaje y se obtuvieron los resultados mostrados en la Figura 26, los cuales muestran ser análogos a los obtenidos por Lyu y Saitou (2003).
3. Conclusiones
El desarrollo de una herramienta para calcular la deformación de estructuras óptimas ensambladas requiere estudiar uniones flexibles que permitan diferenciar los estados de conexión entre diferentes escenarios de diseño y, de esta forma, evidenciar las variaciones en la rigidez y la estabilidad de las estructuras óptimas que serán ensambladas.
La verificación de los resultados alcanzados, a través de la empleo de una herramienta comercial, permite demostrar la exactitud y precisión del modelo planteado con respecto a los métodos tradiciones de análisis de armaduras (truss) y marcos (frame) bidimensionales.
Los resultados muestran que con el barrido directo de la imagen resultante de la optimización topológica (reconocimiento de líneas y nodos) se obtienen los nodos de unión de la estructura óptima y así se proporciona la base para definir y comparar los estados posibles de unión entre los diferentes componentes de la estructura ensamblada cuando las especificaciones de diseño y manufactura lo requieran.
De igual forma, este barrido directo de la imagen permite manipular los resultados de la optimización topológica y constituye un trabajo preliminar para analizar problemas tridimensionales, los cuales no son desarrollados con los métodos de procesamiento de imágenes presentados en trabajos anteriores.
Dentro del diseño conceptual de un producto sometido bajo ciertas condiciones de carga y con restricciones de desplazamiento, se pueden complementar los resultados obtenidos a través de la optimización topológica estructural con el análisis por elementos finitos de los posibles estados de unión de la estructura, para determinar de manera cuantitativa cuál será el mejor escenario de ensamble que garantiza la mayor resistencia y la mayor facilidad de producción de dicho producto. Este trabajo, de forma similar, permite incorporar los conceptos de diseño para la manufactura y el ensamblaje, que han demostrado su versatilidad y aplicabilidad en el desarrollo de nuevos y mejores productos.
Referencias
BENDSØE, M. P. y SIGMUND, O. Topology optimization: theory, methods, and applications. Berlin: Springer, 2003. [ Links ]
BOOKER, J. D.; SWIFT, K. G. y BROWN, N. J. Designing for assembly quality: strategies, guidelines and techniques. Journal of Engineering Design, 2005, vol. 16, núm. 3, pp. 279-295. [ Links ]
BOOTHROYD, G. Product design for manufacture and assembly. 2a ed. New York: Marcel Dekker Incorporated, 2001. [ Links ]
CETIN, O. L. Decomposition-based assembly synthesis of family of structures. Tesis de Doctorado. University of Michigan, Department of Mechanical Engineering, 2003. [ Links ]
—. y SAITOU, K. Decomposition-based assembly synthesis for maximum structural strength and modularity. Journal of Mechanical Design, 2004, vol. 126, núm. 2, pp. 244-253. [ Links ]
—. Decomposition-based assembly synthesis of multiple estructures for minimum manufacturing cost. Journal of Mechanical Design, 2005, vol. 127, núm. 4, pp. 572-579. [ Links ]
CHAN, S. L. y CHUI, P. P. T. Non-linear static and cyclic analysis of steel frames with semi-rigid connections. New York: Elsevier, 2000. [ Links ]
CHANG, D. C. Effects of flexible connections on body structural response. s. l.: SAE Transactions, 1974. [ Links ]
DHILLON, B. y O'MALLEY, J. Interactive design of semirigid steel frames. Journal of Structural Engineering, 1999, vol. 125, núm. 5, pp. 556-564. [ Links ]
HAYALIOGLU, M. y DEGERTEKIN, S. Minimum cost design of steel frames with semirigid connections and column bases via genetic optimization. Computers & Structures, 2005, vol. 83, núm. 21-22, pp. 1849-1863. [ Links ]
HUGHES, T. J. R. The finite element method: linear and dynamic element analysis. s. l.: Dover, 2000. [ Links ]
LEE, K. y NICOLAIDIS, E. A two dimensional model for joints in vehicle structures. Computer & Structures, 1992, vol. 45, núm. 4, pp. 775-784. [ Links ]
LYU, N. y SAITOU, K. Decomposition-based assembly synthesis of a three dimensional bodyin-white model for structural stiffness. Journal of Mechanical Design, 2005a, vol. 127, núm. 1, pp. 34-48. [ Links ]
—. Decomposition-based assembly synthesis for structural stiffness. Journal of Mechanical Design, 2003, vol. 125, pp. 452-463. [ Links ]
—. Decomposition-based assembly synthesis of space frame structures using joint library. Journal of Mechanical Design, 2006, vol. 128, núm. 1, pp. 57-65. [ Links ]
—. Topology optimization of multicomponent beam structure via decomposition-based assembly synthesis. Journal of Mechanical Design, 2005b, vol. 127, núm. 2, pp. 170-183. [ Links ]
LYU, N.; LEE, B. y SAITOU, K. Assembly synthesis for stiffness, dimensional adjustability and manufacturability. The Fourth International Conference on Engineering Computational Technology, Lisboa, Portugal, 7-9 de septiembre de 2004. [ Links ]
PAVLOVÇIÇ, L. et al. Cost function analysis in the structural optimization of steel frame. Structural and Multidisciplinary Optimization, 2004, vol. 28, núm. 4, pp. 286-295. [ Links ]
RUSS, J. C. The image processing handbook. 5a ed. Boca Ratón: CRC Press, 2007. [ Links ]
SIGMUND, O. A 99 line topology optimization code written in MATLAB. Structural and Multidisciplinary Optimization, 2001, vol. 21, núm. 2, pp. 120-127. [ Links ]
TAKEZAWA, A. et al. Structural optimization based on topology optimization techniques using frame elements considering cross-sectional properties. Structural and Multidisciplinary Optimization, 2006, vol. 34, núm. 1, pp. 41-60. [ Links ]
TOVAR, A. et al. Optimización topológica con restricciones de masa, desplazamiento y esfuerzo utilizando el método de los autómatas celulares híbridos. Tercer Congreso Internacional de Ingeniería Mecánica y Primero de Ingeniería Mecatrónica, Bogotá, Colombia, 20-22 de septiembre de 2006a. [ Links ]
—. Topology optimization using a hybrid cellular automaton method with local control rules. Journal of Mechanical Design, 2006b, vol. 128, núm. 6, pp. 1205- 1216. [ Links ]
YETIS, A. y SAITOU, K. Decomposition-based assembly synthesis based on structural considerations. Journal of Mechanical Design, 2002, vol. 124, núm. 4, pp. 593-601. [ Links ]
ZUO, K. T. et al. Manufacturing-and machining-based topology optimization. International Journal of advanced Manufacturing Technology, 2006, vol. 27, núm. 5-6, pp. 531-536. [ Links ]














