Acerca de la formación de patrones de Turing bajo consideraciones probabilistas¹

On Turing Pattern Formation under Stochastic Considerations²

Sobre a formação de padrões de Turing em considerações probabilistas³

Diego Garzón-Alvarado⁴
Angélica Ramírez-Martínez⁵
Carlos Duque-Daza⁶   

¹Este artículo se deriva de un proyecto de investigación denominado Simulación computacional en ingeniería mecánica y biomédica, patrocinado por la Dirección de Investigación de Bogotá (DIB) de la Universidad Nacional de Colombia y desarrollado por el Grupo de Modelado y Métodos Numéricos en Ingeniería (GNUM). Universidad Nacional de Colombia y Universidad Central de Colombia, Bogotá, Colombia.
²Submitted on: February 25, 2011. Accepted on: March 27, 2012. This article is derived from the research project Computational Simulation in Mechanic and Biomedic Engineering, sponsored by Universidad Nacional de Colombia, Direction of Research - Bogota, and developed by the research group Modelling and Numerical Methods in Engineering, GNUM. UniversidadNacional de Colombia and Universidad Central de fo/omi/a.Bogota, Colombia.
³Data de recebimento: 25 de fevereiro de 2011. Data de aceite: 27 de março de 2012. Este artigo deriva se de um projeto de pesquisa denominado Simulação computacional em engenharia mecânica e biomédica, patrocinado pela Direção de Pesquisa de Bogotá (DIB) da Universidade Nacional de Colômbia e desenvolvido pelo Grupo de Modelado e Métodos Numéricos em Engenharia (GNUM). Universidade Nacional de Colômbia e Universidade Central de Colômbia, Bogotá, Colômbia.
⁴Ingeniero mecánico, Universidad Nacional de Colombia, Bogotá, Colombia. Magíster en Ingeniería Mecánica, Universidad de los Andes, Bogotá, Colombia. Doctorado en Mecánica Computacional, Universidad de Zaragoza, España. Profesor asociado, Departamento de Ingeniería Mecánica y Mecatrónica, Universidad Nacional de Colombia. Correo electrónico: dagarzona@bt.unal.edu.co.
⁵Ingeniera mecánica, Universidad Nacional de Colombia, Bogotá, Colombia. Magíster y doctorada en ingeniera biomédica, Universidad de Zaragoza, España. Profesora, Departamento de Ingeniería Mecánica, Fundación Universidad Central, Bogotá, Colombia. Correo electrónico: aramirezm3@ucentral.edu.co.
⁶Ingeniero mecánico, Universidad Nacional de Colombia, Bogotá, Colombia. Magíster en Ingeniería Mecánica, Universidad de los Andes, Bogotá, Colombia. Doctorado en Ingeniería Mecánica, Universidad de Warwick, Inglaterra. Profesor asociado, Departamento de Ingeniería Mecánica y Mecatrónica, Universidad Nacional de Colombia. Correo electrónico: caduqued@bt.unal.edu.co.

Fecha de recepción: 25 de febrero de 2011. Fecha de aceptación: 27 de marzo de 2012.

Resumen

Este artículo presentan varios ensayos numéricos sobre las ecuaciones de reacción-difusión en el espacio de Turing, bajo el mecanismo de reacción de Schnakenberg. El objetivo es obtener los patrones de cada coeficiente de la expansión en polinomios de caos. Los ensayos se realizan en 2D sobre cuadrados unitarios, a los cuales se les imponen condiciones iniciales aleatorias y condiciones de Neumann nulas sobre el contorno. Los parámetros que definen el comportamiento de las ecuaciones se modelan como campos estocásticos; específicamente, se utilizan la difusión y los parámetros reactivos como valores de tipo aleatorio. Por lo tanto, se combina el método estándar de elementos finitos con Newton-Raphson con el método de los elementos finitos estocásticos espectrales. Los parámetros de cada ecuación se describen mediante la expansión de Karhunen-Loéve, mientras que la incógnita se representa mediante la expansión de los polinomios de caos. Los resultados muestran la versatilidad del método para solucionar diferentes problemas físicos. Además, se logra la descripción estadística de la solución. Para los coeficientes estocásticos de la incógnita, los resultados muestran patrones complejos que mezclan bandas y puntos, los cuales no se pueden predecir desde la dinámica del sistema.

Palabras clave: Elementos finitos estocásticos, reacción-difusión, patrones de Turing, mecanismo de reacción de Schnakenberg.

Abstract

In this paper we present several numerical tests on reaction-diffusion equations in the space of Turing, under the Schnakenberg reaction mechanism. The objectivge is to obtain the patterns of each coefficient of expansion in chaos polynomials. The tests were performed on 2D unit square, to which random initial conditions and Neumann zero conditions on the boundary were imposed.The parameters that define the behavior of the equations, more specifically the diffusion and reactive parameters, are modeled as stochastic fields.Thus, the standard method of finite element with Newton-Raphson was combined with the spectral stochastic finite element method. The parameters of each equation are described by Karhunen-Loeve expansion, while the unknown is represented by the expansion of the polynomials of chaos. The results show the versatility of the method to solve different physical problems. Furthermore, it achieves statistical description of the solution. The results for the unknown stochastic coefficients, show complex patterns that mix bands and points which can not be predicted from the dynamics of the system.

Key words: Stochastic finite elements, reaction-diffusion Turing patterns, Schnakenberg reaction mechanism.

Resumo

Este artigo apresenta vários testes numéricos sobre equações de reação-difusão no espaço de Turing no âmbito do mecanismo de reação Schnakenberg. O objetivo é a obtenção de padrões de cada coeficiente de expansão em polinómios de caos. Os ensaios foram realizados em 2D sobre quadrados unitários, aos que são impostas condições iniciais aleatórias e condições de Neumann nulas no contorno. Os parâmetros que definem o comportamento das equações são modelados como campos estocásticos, especificamente utilizando difusão e parâmetros reagentes como valores de tipo aleatório. Por conseguinte, combina-se o método padrão de elementos finitos com Newton-Raphson com o método de elementos finitos es-tocásticos espectrais. Os parâmetros de cada equação são descritos mediante a expansão de Karhunen-Loève, ao passo que a incógnita é representada pela expansão dos polinómios de caos. Os resultados mostram a versatilidade do método para resolver variados problemas físicos. Além disso, consegue-se a descrição estatística da solução. Para os coeficientes estocásticos da incógnita, os resultados mostram padrões complexos que misturam bandas e pontos, o que não pode ser predito a partir da dinâmica do sistema.

Palavras-chave: Elementos finitos estocásticos, reação-difusão, padrões de Turing, mecanismo de reação de Schnakenberg.

Introducción

Muchos problemas de la física, la química, la economía, la biología, la bio-ingeniería e, incluso, la ecología, entre otros campos, pueden ser modelados balanceando tres fenómenos: la difusión, la convección y la reacción (Babuska, et al., 1995; Garzón, et al., 2009; Ferreira, et al., 2002; Chaplain, et al., 2001; Madzvamuse, 2002; Kondo y Asai, 1995; Crauste, et al., 2008; Rossi, et al., 2008; Rothschild y Ault, 1996; Nozakura y Keuchi, 1984; Smith, 2000; Richter, 2008; Ferragut, et al., 2007). Dicho balance se plantea en la ecuación diferencial de reacción-convección-difusión (1), y se complementa con las condiciones de contorno descritas en (2), (3) y (4).

Donde k ≥ 0 es el coeficiente difusivo, X ∈ R denota el vector posición en el domino, u es el campo de velocidad asociado al proceso convectivo, s es el coeficiente fuente (s > 0 significa producción y s < 0 significa disipación), f(x) es la función de generación, ^g(x) es la función que define el valor del campo escalar <p sobre la frontera y h(x) es la función que define el valor del flujo sobre la frontera r_r

Estas ecuaciones de reacción-advección-difusión (1) y otros modelos más complejos, donde intervienen más especies o reactantes, tienen la habilidad de crear patrones espacio-temporales. Un caso particular de estos patrones son las inestabilidades de Turing (Garzón, 2007; Madzvamuse, et al., 2003), que se caracterizan por la aparición de distribuciones de especies (patrones) estables en el tiempo e inestables en el espacio. Dada su especial respuesta, este tipo de modelos matemáticos han inspirado modelos para el estudio de problemas en muy diversos campos, como la dinámica de fluidos (Hirayama y Takaki, 1988), la transferencia de calor (Ardes, et al., 1997; Lir y Lin, 2001), la física de semiconductores (Balkarei, et al., 1988), la ingeniería de materiales (Krinsky, 1984), la química (Zhang y Liu, 2009), la biología (Garzón, 2007; Crauste, et al., 2008; Rossi, et al., 2008; Frederik y Maine, 2003), la dinámica de poblaciones (Yi, et al., 2009; Baurmanna, et al., 2007; Rothschild y Ault, 1996), la astrofísica (Nozakura y Ikeuchi, 1984), la ingeniería biomédica (Madzvamuse, 2002; García-Aznar, et al., 2007; Ferreira, et al., 2002) y las matemáticas financieras.

El análisis de estos sistemas de reacción-difusión (RD), que presentan inestabilidad de Turing, se ha desarrollado tradicionalmente desde dos marcos de trabajo: mediante análisis matemático (Mei, 2000) y mediante simulación numérica (Garzón, 2007; Madzvamuse, 2003; Madzvamuse, 2000).

Desde el punto de vista analítico, los esfuerzos por entender el comportamiento de los sistemas de RD se han centrado en el estudio de la relación entre las bifurcaciones del espacio de parámetros y la formación de patrones. Desde esta perspectiva, se han estudiado los sistemas de RD mediante comparaciones de sub- y supersoluciones, teoría de grado, índice de Conley, teoría de puntos críticos y perturbaciones singulares para varios tipos de máximos principales (Mei, 2000). Estos métodos han sido efectivos para el análisis de soluciones estacionarias y ondas viajeras. También se han estudiado escenarios de bifurcaciones complejas en sistemas de RD aplicando métodos de teoría de grupo para problemas con simetrías. Los esfuerzos en esta área del análisis matemático y, específicamente, de la dinámica de sistemas han permitido construir un gran conocimiento, el cual se ha comprobado y ampliado con el uso de la simulación numérica.

El objetivo de este artículo —siguiendo el estudio sobre los patrones de Turing y la inclusión de parámetros probabilistas— es solucionar computa-cionalmente y de forma simultánea las ecuaciones de RD en 2D. Se utiliza el modelo de reacción de Schnakenberg, cuyos parámetros cinéticos y difusivos se encuentran en el espacio de Turing y, se les asigna un comportamiento estocástico. Para ello, se soluciona el sistema de ecuaciones de RD mediante un planteamiento conjunto de tres métodos: el de los elementos finitos, el de Newton-Raphson (Garzón, 2007) y el de los elementos finitos estocásticos espectrales. Se desarrollan varios ejemplos numéricos que permiten observar el efecto de los patrones sobre los coeficientes de la expansión del polinomio de caos. En este sentido, se busca estudiar la influencia de los campos estocásticos en la formación de patrones de Turing y obtener los patrones de cada coeficiente de la expansión en polinomios de caos. Se demuestra la versatilidad del método para solucionar problemas físicos que contienen incertidumbre. Además, se logra la descripción estadística de la solución.

Por su parte, los resultados muestran patrones complejos que mezclan bandas y puntos que llegan a la condición estable en aquellos coeficientes que pertenecen al polinomio de caos. Los patrones revelan la incertidumbre en los coeficientes estocásticos que depende de la dinámica de la difusión y la reacción.

1. Materiales y métodos

1.1. Modelo de reacción-difusión (RD): condiciones de inestabilidad de Turing Siguiendo el modelo reactivo de Schnakenberg (Garzón, 2007; Madzvamuse, et al., 2003), el sistema de ecuaciones diferenciales de RD en (1) (sin convección), puede escribirse como (5):

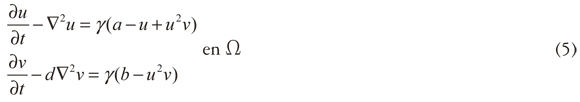
Donde u, v son las especies químicas, V²u y dV²v son los términos difusivos, d es la relación entre los coeficientes difusivos de cada especie, γ es una constante adimensional, a y b son parámetros del modelo y f (u,v) = (a — u + u²v) y g(u,v) = (b—u²v) son las funciones de reacción de Schnakenberg.

La solución de este sistema de ecuaciones conducirá a una distribución de concentraciones espacialmente inestables o patrones de Turing, si se cumplen determinadas condiciones, las cuales, para el caso de un modelo de RD, están dadas por las desigualdades descritas en (6):

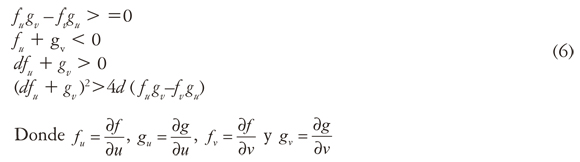
Haciendo uso del análisis de estabilidad lineal (Garzón, 2007; Madzvamuse, et al., 2003; Madzvamuse, 2000), se pueden calcular los valores de los parámetros adimensionales d y y, requeridos para la formación de patrones de Turing bajo el modelo de RD. Estos patrones pueden ser identificados por los correspondientes números de onda, como los que se mencionan (Madzvamuse, 2000).

1.2 Método de los elementos finitos espectrales

En el caso en que los parámetros de las ecuaciones se pueden representar como campos aleatorios, la ecuación de residuos se convierte en (7):

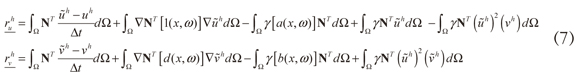
Donde los parámetros del modelo (1, d, a y b) dependen del espacio y tienen naturaleza aleatoria, la cual está indicada por el argumento C0. En los siguientes apartados, se muestra la metodología para resolver el problema con elementos finitos estocásticos.

1.3. Expansión de Karhunen-Loève

La expansión de Karhunen-Loève de un proceso estocástico, por ejemplo d(x,C0), se basa en la expansión espectral de su función de covarianza R_EE (x₁,x₂), donde x₁ y x₂ denotan las coordenadas espaciales y C0 denota la aleatoriedad. Por definición, la función de covarianza es simétrica y definida positiva; por lo tanto, las autofunciones son mutuamente ortogonales y los autovalores son reales. De esta forma, el conjunto de autofunciones y autovalores que permiten obtener la representación de d(x,C0) toman la forma (8):

Donde d (x) es el valor promedio del proceso estocástico, en este caso, del coeficiente de difusión de la segunda ecuación de (16) —este valor medio debe cumplir las restricciones de Turing dadas en (6)—; los términos j(C0)} forman un conjunto ortogonal de variables aleatorias; es el conjunto de autovalores, y {d(x)} es el conjunto de autofunciones de la función de covarianza.

En el caso de los coeficientes cinéticos de reacción a y b, se puede hacer una expansión para cada una, así (9):

Las funciones 1 (x), d_jd(x), a_ja y b_jb (x) corresponden a las autofunciones de la función de covarianza de la variable de campo. Igualmente, los valores λ¹_j1, λ^d_jd. y λ^a_ja λ^b_jb son los autovalores. De esta forma, cada conjunto de autofunciones y autovalores, conforman el denominado autopar.

Por lo tanto, se obtiene:

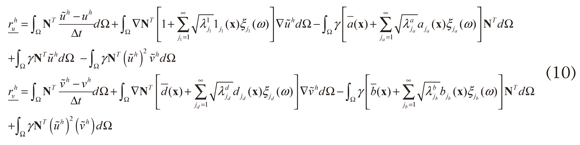
1.4 Aspectos computacionales y condiciones de contorno e iniciales

Con el fin de evaluar la solución del problema de patrones de Turing con elementos finitos estocásticos, se analizaron tres ejemplos con diferentes modos de onda. Los problemas fueron implementados en lenguaje Fortran y solucionados para una malla de 2500 elementos y 2601 nodos, como se muestra en la figura 1. Los elementos utilizados son cuadriláteros con funciones de forma bilineales.

Las condiciones iniciales se imponen a la variable determinista mediante una pequeña perturbación del 10% alrededor de su condición estable; esto es, alrededor de 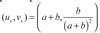(Madzvamuse, 2000). Para las variables estocásticas, las condiciones iniciales son nulas. De igual forma, las condiciones de Neumann (naturales) son nulas para todas las variables de cada ejemplo en la frontera del dominio mostrado en la figura 1.

2. Experimentación numérica

En el ejemplo se utilizaron los siguientes valores promedio de los parámetros del sistema (5): a₀ = a = 0,1, b₀ = b = 0,9, d₀ = d = 10 y J = 29. Para el caso estocástico se hicieron tres pruebas numéricas, con diferentes valores de M , M_¿, M_a y M , y P Adicionalmente se utilizó C₀=10^-2, |a| = 0,5, b = b₂ = 0,25. El tamaño del paso temporal (adimensional) es t = 0,01. En cada caso solo se presentan los resultados cuando se alcanza la estabilidad en el tiempo.

En el primer caso se utilizaron los siguientes límites para el truncamiento de las series dadas por Madzvamuse (2002): M₁ = 2, M_d = 2, M_a = 2 y M_b = 2, y P = 2. Por lo tanto, se tiene α₁ = 2,1537, α₂ = 4,5779.

Los resultados se muestran en la figura 2. La fila a) muestra los resultados para la variables u₀, u y u , ordenados por columnas, respectivamente. De la misma forma se observan, en la fila b), los resultados para v₀, v₁ y v₂

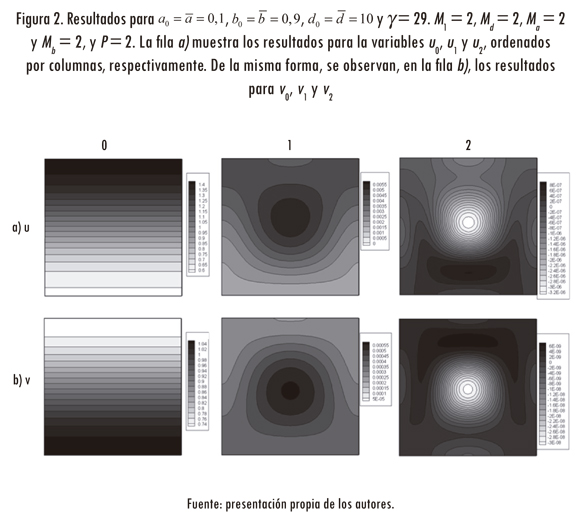
En este ejemplo, la expansión de los polinomios de caos lleva tan solo tres términos (el primero de ellos, determinista). De igual forma, se utilizan tres términos para representar la difusión y los parámetros de reacción. En la columna 0 de la figura 2 se observa la formación de un patrón con modo de onda 1-0 (Madzvamuse, 2000). Para u₀ se observa un patrón con alta concentración en la parte superior, y para el inhibidor v₀, en la parte inferior. En la columna 1 se muestra la formación de un punto de alta concentración. En u₁ se observa un gradiente en la parte inferior. En la parte superior del dominio se forma un punto. Comparando las dos primeras columnas, se observa que en la zona del punto (de u₁) se presenta el mayor gradiente de la variable determinista (u₀). Además, nótese que los valores para u₁ disminuyen en el contorno debido a que se tiene una condición de flujo nulo (para la variable u₀). Para v se observa exactamente el mismo comportamiento de u₁, pero con el punto en la parte inferior. En la columna 2 se observan los resultados para u₂. En la parte inferior de u₂ se muestra una región de alta concentración que indica el mayor gradiente de u₁. En la zona central superior se muestra un punto de mínima concentración ubicado en el mismo sitio que para u₁.

En el segundo caso se utilizaron los siguientes valores de truncamiento de las series dadas en Madzvamuse (2002): M = 4, M_d = 4, M_a = 4 y M_b = 4, y P = 4. Y de nuevo, se tiene α₁ = 2,1537, α₂ = 4,5779, α₃ = 7,2868, α₄ = 10,1732.

Los resultados se muestran en la figura 3. La fila a) muestra los resultados para las variables u₀, u₁, u₂, u₃ y u₄, ordenados por columnas, respectivamente. De la misma forma se observan, en la fila b), los resultados para v₀, v₁ , v₂, v₃ y v₄.

En este ejemplo, la expansión de los polinomios de caos y de Karhunen-Loève lleva un mayor número de términos que en el caso anterior. En la columna 0 de la figura 3, se observa la formación de un patrón con modo de onda 1-0, pero esta vez el gradiente está rotado 90°, por lo tanto, la orientación del patrón es horizontal. En la columna 1 se puede ver la formación de un punto en el dominio. En u₁ se observa un gradiente en la parte izquierda. En la derecha del dominio se forma un punto similar al ejemplo anterior. Para v se observa exactamente el mismo comportamiento de u pero en dirección contraria. En la columna 2 se observan los resultados para u₂. Se nota la formación de estructuras de mayor número de onda (Garzón, 2007; Madzvamuse, 2000). También se observa la formación de dos máximos en la esquinas de la derecha del dominio. En la fila b), para la variable v se nota el mismo patrón, pero con sus máximos en la parte izquierda. En las columnas 3 y 4, la fila a) muestran los resultados para u₃ y u₄, respectivamente. De nuevo se notan estructuras de mayor número de onda que las anteriores (Madzvamuse, 2000), con máximos dirigidos hacia la zona derecha. En la fila b) de estas mismas columnas se puede observar el máximo en la parte izquierda del dominio. Nótese que en la figura 3 conforme se observa de izquierda a derecha, crece el número de onda. Además, se puede observar que los máximos de las columnas 3 y 4 se presentan hacia la zona de mayor concentración de la variable determinista de la columna 0.

En el tercer caso (figura 4) se utilizaron los siguientes valores de truncamiento de las series dadas en Madzvamuse (2002): M₁ = 4, M_d = 4, M_a = 0 y M_b = 0 y P = 4. En este caso, la incertidumbre se presenta sobre los parámetros difusivos; por lo tanto, son estos parámetros los que se representan por una expansión de Karhunen-Loève. En el caso de los coeficientes reactivos, estos se consideran totalmente deterministas. Los resultados se muestran en la figura 4. El orden para mostrar las figuras es igual que para los casos anteriores.

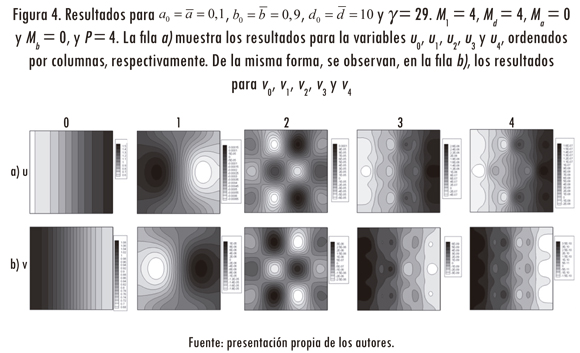
En la figura 4 se observa que el patrón determinista (columna 0) es similar al anteriormente descrito, cuyo gradiente está rotado 90°; por lo tanto, la orientación del patrón es horizontal. En la columna 1 se puede ver la formación de dos puntos. En u₁ se observa un gradiente en la parte central. En la izquierda y derecha del dominio se forman dos puntos que determinan un máximo y un mínimo, respectivamente. Nótese que el patrón tiene simetría en x y antisimetría en y. En las columnas 2, 3 y 4 se presentan patrones con puntos y bandas, con mayor número de onda. En las figuras 3 y 4, los patrones exhiben un comportamiento poco definido. En la fila a) de las columnas 3 y 4 la mayor concentración se presenta en el lado derecho, igual que en el caso determinista. Por el contrario, en la fila b) la mayor concentración está del lado izquierdo.

3. Discusión y conclusiones

En este artículo se utilizó el método de los elementos finitos estocásticos espectrales para solucionar un sistema de ecuaciones de RD de carácter no lineal. Para estudiar la versatilidad del método se desarrollaron tres ejemplos de RD, con un sistema reactivo de tipo Schnakenberg, cuyos parámetros tienen un comportamiento probabilista. El sistema no lineal se ha resuelto mediante el método de Newton-Raphson. Los parámetros deterministas del modelo cumplen las restricciones del espacio de Turing; por lo tanto, los patrones que se obtienen en la solución, específicamente para la variable determinista, exhiben inestabilidades espaciales, denominadas "de Turing".

Una limitación del modelo numérico aquí desarrollado es el empleo de la misma función de covarianza, de las funciones de correlación y de los valores de longitud de correlación para todos los parámetros estocásticos. En futuros trabajos se desarrollarán ejemplos con otros valores de la longitud de correlación y diferentes funciones. Por otra parte, no se llevó a cabo el análisis de sensibilidad de la malla en conjunto con los parámetros estocásticos; este tipo de trabajo se desarrollará en futuros artículos.

En conclusión, el método de los elementos finitos estocásticos espectrales con aplicación a la ecuación de reacción-difusión permite incluir los parámetros reactivos y difusivos dependientes del espacio y de la aleatoriedad. La dinámica de los patrones de los coeficientes del polinomio de caos está bajo la influencia del número de términos utilizados en cada parámetro de la ecuación. En general, la localización de la incertidumbre depende de la expansión de Karhunen-Loève para el término reactivo y el difusivo. El término reactivo introduce, de forma independiente del patrón de Turing, un alto componente de incertidumbre en comparación con el término difusivo.

Referencias

ARDES, M.; BUSSE, F. y WICHT, J. Thermal convection in rotating spherical shells. Physics of the Earth and Planetary Interiors. 1997, vol. 99, pp. 55-67.         [ Links ]

BABUSKA, I.; IHLENBURG, F.; PAIK, E. et al. A generalized finite element method for solving the Helmholtz equation in two dimensions with minimal pollution. Computer Methods in Applied Mechanics and Engineering. 1995, vol. 128, pp. 325-359.         [ Links ]

BALKAREI, Y; GRIGORYANTS, A. y RHZANOV, Y et al. Regenerative oscillations, spatial-temporal single pulses and static inhomogeneous structures in optically bitable semiconductors. Optics Communications. 1988, vol. 66, pp. 161-166.         [ Links ]

BAURMANNA, M.; GROSS, T. y FEUDEL, U. Instabilities in spatially extended predator-prey systems: Spatio-temporal patterns in the neighborhood of Turing-Hopf bifurcations. Journal of Theoretical Biology. 2007, vol. 245, pp. 220-229.         [ Links ]

CHAPLAIN, M.; GANESH, M. y GRAHAM, I. Spatio-temporal pattern formation on spherical surfaces: Numerical simulation and application to solid tumor growth. Journal of Mathematical Biology. 2001, vol. 42, núm. 5, pp. 387-423.         [ Links ]

CRAUSTE, F. ; LHASSAN, M. y KACHA, A. A delay reaction-diffusion model of the dynamics of botulinum in fish. Mathematical Biosciences. 2008, vol. 216, pp. 17-29.         [ Links ]

FERRAGUT, L.; ASENSIO, M. y MONEDERO, S. A numerical method for solving convection-reaction-diffusion multivalued equations in fire spread modelling. Advances in Engineering Software. 2007, vol. 38, pp. 366-371.         [ Links ]

FERREIRA, S.; MARTINS, M. y VILELA, M. Reaction-diffusion model for the growth of avascular tumor. Physical Review. 2002, vol. 65, num. 2, pp. 1-8.         [ Links ]

FREDERIK, H.; MAINI, P; MADZVAMUSE, A. et al. Pigmentation pattern formation in butterflies: experiments and models. C. R. Biologies. 2003, vol. 326, pp. 717-727.         [ Links ]

GARCÍA-AZNAR, J.; KUIPER, J. y GÓMEZ-BENITO, M. et al. Computational simulation of fracture healing: Influence of interfragmentary movement on the callus growth. Journal of Biomechanics. 2007, vol. 40, num. 7, pp. 1467-1476.         [ Links ]

GARZÓN, D. "Simulación de procesos de reacción-difusión: Aplicación a la morfogénesis del tejido óseo". Tesis doctoral. Universidad de Zaragoza. 2007.         [ Links ]

GARZÓN-ALVARADO, D.; GARCÍA-AZNAR, J. y DOBLARÉ M. Appearance and location of secondary ossification centres may be explained by a reaction-diffusion mechanism. Computers in Biology and Medicine. 2009, vol. 39, pp. 554-561.         [ Links ]

HIRAYAMA, O. y TAKAKI, R. Thermal convection of a fluid with temperature-dependent viscosity. Fluid Dynamics Research. 1988, vol. 12, num. 1, pp. 35-47.         [ Links ]

KONDO, S. y ASAI, R. A reaction-diffusion wave on the skin of the marine anglefish, Pomacanthus. Nature. 1995, vol. 376, pp. 765-768.         [ Links ]

KRINSKY V I. Self-organization: Auto-waves and structures far from equilibrium. Berlín: Editorial Springer, 1984.         [ Links ]

LIR, J. y LIN, T. Visualization of roll patterns in Rayleigh-Bénard convection of air in rectangular shallow cavity. International Journal of Heat and Mass Transfer. 2001, vol. 44, pp. 2889-2902.         [ Links ]

MADZVAMUSE, A. A numerical approach to the study of spatial pattern formation. Tesis doctoral. Oxford University. UK. 2000.         [ Links ]

MADZVAMUSE, A. A Numerical approach to the study of spatial pattern formation in the ligaments of arcoid bivalves. Bulletin of Mathematical Biology. 2002, vol. 64, pp. 501-530.         [ Links ]

MADZVAMUSE, A.; WATHEN, A. y MAINI, P. A moving grid finite element method applied to a model biological pattern generator. Journal of Computational Physics. 2003, vol. 190, pp. 478-500.         [ Links ]

MEI, Z. Numerical bifurcation analysis for reaction-diffusion equations. Berlín: Springer Verlag, 2000.         [ Links ]

NOZAKURA, T. y IKEUCHI, S. Formation of dissipative structures in galaxies. Astrophys Journal. 1984, vol. 279, pp. 40-52.         [ Links ]

RICHTER, O. Modelling dispersal of populations and genetic information by finite element methods. Environmental Modelling & Software. 2008, vol. 23, num. 2, pp. 206-214.         [ Links ]

ROSSI, E; RISTORI, S. y RUSTICI, M. et al. Dynamics of pattern formation in biomimetic systems. Journal of Theoretical Biology. 2008, vol. 255, pp. 404-412.         [ Links ]

ROTHSCHILD, B. y AULT, J. Population-dynamic instability as a cause of patch structure. Ecological Modelling. 1996, vol. 93, pp. 237-239.         [ Links ]

SMITH, R. Optimal and near-optimal advection-diffusion finite-difference schemes iii. Black-Scholes equation. Mathematical, Physical and Engineering Sciences. 2000, vol. 456, pp. 1019-1028.         [ Links ]

YI, F.; WEI, J. y SHI, J. Bifurcation and spatio-temporal patterns in a homogeneous diffusive predator-prey system. Journal of Differential Equations. 2009, vol. 246, num. 5, pp. 1944-1977.         [ Links ]

ZHANG, L. y LIU, S. Stability and pattern formation in a coupled arbitrary order of autocatalysis system. Applied Mathematical Modelling. 2009, vol. 33, pp. 884-896.         [ Links ]