Theories of Mechanically Induced Tissue Differentiation and Adaptation in the Musculoskeletal System¹

Teorías de diferenciación y adaptación mecánicamente inducida en el sistema músculo-esquelético²

Daniel R. Suarez³

¹Review article. Submitted on: December 10^th, 2014. Accepted on: August 14^th, 2015.
²Artículo de revisión. Fecha de recepción: 10 de diciembre de 2014. Fecha de aceptación: 14 de agosto de 2015.
³Mechanical Engineer and MSc in Mechanical Engineering, Universidad de los Andes, Colombia. Ir./M.Sc. Biomedical Engineering, Delft University of Technology. PhD Delft University of Technology. Associate professor, Departamento de Ingeniería Industrial, Pontificia Universidad Javeriana, Bogotá, Colombia. E-mail: d-suarez@javeriana.edu.co.

How to cite this article:

D. R. Suarez. "Theories of mechanically induced tissue differentiation and adaptation in the musculoskeletal system," Ing. Univ., vol. 20, no. 1, pp. 21-40, 2016. http://dx.doi.org/10.11144/Javeriana.iyu20-1.tmit

Abstract

It is well known that the mechanical environment affects biological tissues. The importance of theories and models that aim at explaining the role of the mechanical stimuli in process such as differentiation and adaptation of tissues is highlighted because if those theories can explain the tissue's response to mechanical loading and to its environment, it becomes possible to predict the consequences of mechanical stimuli on growth, adaptation and aging of tissues. This review aims to present an overview of the various theories and models on tissue differentiation and adaptation, and their mathematical implementation. Although current models are numerically well defined and are able to resemble the tissue differentiation and adaptation processes, they are limited by (1) the fact that some of their input parameters are likely to be site-and species-dependent, and (2) their verification is done by data that may make the model results redundant. However, some theories do have predictive power despite the limitations of generalization. It seems to be a matter of time until new experiments and models appear with predictive power and where rigorous verification can be performed.

Keywords : computational biology; mechanobiology; finite element; tissue growth; tissue differentiation; skeletal regeneration

Resumen

Se ha aceptado ampliamente que el ambiente mecánico afecta los tejidos bilógicos. La importancia de teorías y modelos que buscan explicar el rol de los estímulos mecánicos en procesos como la diferenciación y adaptación de tejidos radica en que si pueden explicar la respuesta de un tejido a su ambiente alrededor, es posible predecir las consecuencias de estímulos mecánicos en procesos como el crecimiento, la adaptación y el envejecimiento de tejidos. Este trabajo resume teorías y modelos de diferenciación y adaptación de tejidos y su implementación matemática. Aunque los modelos actuales están numéricamente bien definidos y son capaces de emular los procesos de diferenciación y adaptación, están limitados a causa de 1) la naturaleza de sus parámetros, que son muy probablemente dependientes de la especie y lugar de análisis, y 2) los datos que usualmente son empleados para su verificación, ya que podrían llegar a hacer redundantes los resultados del modelo. A pesar de estas limitaciones que impactan en la generalización de resultados, las teorías y modelos actuales tienen el poder predictivo necesario para el estudio general de los procesos de diferenciación y adaptación de tejidos. Es cuestión de tiempo, la llegada de nuevos modelos y experimentos que permitan una mayor generalización y verificación.

Palabras clave : biología computacional; mecanobiología; elementos finitos; diferenciación de tejidos

Introduction

It is well known that the mechanical environment affects biological tissues, in which mechanical loads activate or inhibit processes involving the genesis, adaptation, and aging of tissues [1]. This is especially important for tissues that have a primary biomechanical function such as musculoskeletal or cardiovascular tissues; however, biomechanical and mechanobiological factors appear to be critical for regulating cell behavior, and tissue maintenance and transformation in virtually all other tissues of the body [2].

The study of tissue differentiation and adaptation to their mechanical environment is challenging. These processes are complex, involving so many variables that physical experimentation is often either time consuming, expensive, or impossible [3]. For instance, forces applied to tissue might be of different type or nature: internal quasi-static forces caused by tissue growth; external forces imposed on the organism; and intermittent joint forces caused by muscle contractions [4]. As a result of the mechanical environment created by all those forces, time-dependent, spatially complex patterns of internal tissue stresses and strains are created in all tissues [4].

Since the 19^th century, several theories and models have been proposed to explain the role of mechanical stimuli on biological processes [5]-[13]. In the last decades, the increasing computational power has allowed the implementation and simulation of many of the proposed theories and models of tissue differentiation and adaptation. In mechanobiology, a field that describes the mechanisms by which mechanical loads regulate biological processes, computational models have been developed to complement lab experiments in order to propose and test rules that may govern the effects of mechanical loading on cells and tissues [14].

The importance of such theories and models is highlighted because if those theories can explain the tissues' response to mechanical loading, it becomes possible to predict the consequences of mechanical stimuli on growth, adaptation, and aging. Additionally, it is now clear that mechanobiological interactions between cells and their underlying substrate can critically influence cell behavior and the resulting tissue, even in tissues and organs without a predominant biomechanical role [2],[15]. Currently, models of tissue differentiation and adaptation gain importance due to the studies on functional tissue engineering, in which the effects of biomechanical factors on native and repair tissues, and the development and application of computational models of tissue growth and remodeling are among its priorities [15].

Several works have reviewed the processes of tissue differentiation and adaptation in musculoskeletal tissues from different perspectives [16]-[18]. However, to the knowledge of the author, the literature that reviews their mathematical fundamentals and implementation is scarce. For example [19], this review aims to present an overview of the various theories on tissue differentiation and adaptation, their mathematical implementation, and a discussion and possible future steps in this research area.

1. Theories of Tissue Differentiation

1.1. Classic Theories

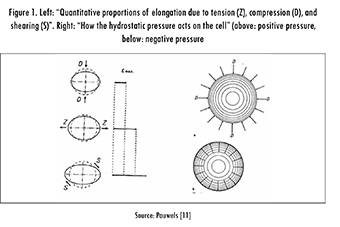
In the late 19^th century, W. Roux (1981) suggested a relationship between mechanical stimuli and tissue differentiation [5]. His thesis, the "Theory of Functional Adaptation," was that cells are in constant competition among themselves for their own "functional stimulus" and, eventually, this competition determines the final tissue phenotype. The "functional" stimuli were defined as compression for the formation and maintenance of bone, tension for connective tissue, and a combination of both with shear for cartilage. Like Roux, F. Pauwels based his theory almost exclusively on clinical observations and simple experiments [11]. However, he introduced basic concepts of stress and strain to the description of the problem. In his theory, he identified the mechanical stimuli that are "felt" by the cells as elongation and hydrostatic pressure (Figure 1).

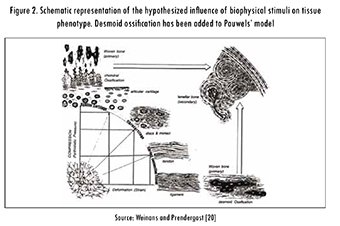
Pauwels proposed elongation as the stimulus for the formation of connective tissue and hydrostatic pressure as the stimulus for the formation of cartilage. In this theory, bone formation does not have a specific stimulus and only occurs by calcification of the cartilage when "the cell is protected from all direct mechanical stresses" and under the influence of hydrostatic pressure, see Figure 2. With the consideration of elongation and hydrostatic pressure as stimuli, Pauwels effectively described the tissue differentiation process in terms of mechanical invariants, i.e., magnitudes independent of the coordinate system.

1.2. Interfragmentary Strain Theory

Considering that strain tolerance is higher for granulation tissue, moderate for cartilage, and lower for bone tissue, Perren and Cordey [6] proposed that at the beginning of the fracture-healing process, when motion and strain are high, the first tissue that appears is granulation tissue since it is the only one able to withstand this mechanical environment. Once the granulation tissue stiffens the mechanical environment, the formation of cartilage can begin. Finally, with the presence of cartilage inside the gap, the mechanical environment becomes more suitable for bone generation. Perren and Cordey defined the concept of Interfragmentary Strain (IFS) for fractures as:

where L is the length of the "fracture" gap and ΔL is the change in length caused by loading. Both terms are defined in the axial direction of the bone. The IFS is a measurement of stretch capacity that can be related to adequate environments for specific tissues.

1.3. Consideration of the Load History

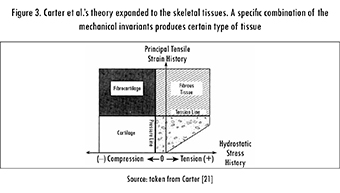
Carter et al. were the first to explicitly interpret Pauwels' theory in terms of well-defined mechanical magnitudes and to include loading history in the analysis. They associated elongation with either octahedral shear strain or octahedral shear stress, and hydrostatic pressure with either hydrostatic stress or volumetric strain [21]. The hypothesis of Carter et al. involves these invariants with their load history, assuming that the variation in time of the mechanical loading is the triggering factor that stimulates tissue differentiation. Finally, Carter et al. proposed the use of an index that measures the load history of the suggested invariants. This index, initially considered only for osteogenesis, was called the Osteogenic Index (OI) [7]; however, a similar combination of hydrostatic stress and octahedral shear stress histories could be used for other tissues, see Figure 3.

1.4. The Fluid Flow as Stimulus

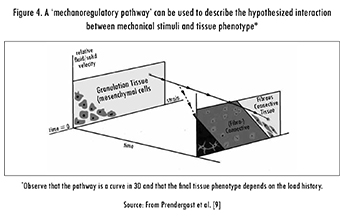
Considering that there is evidence showing the importance of fluid flow at the cellular level [22], Prendergast et al. described how fluid flow can amplify cellular deformation [9], [23] and thus proposed the use of the relative velocity between the phases as a stimulus for tissue differentiation. The biphasic theory developed by Mow [24] was used to determine the substrate strain as well as the relative velocity between the phases.

Prendergast et al.'s theory affirms that the mechanical environment, in terms of the substrate strain and the relative fluid velocity, is the relevant factor in tissue differentiation. Finally, they hypothesized that changes in the mechanical environment are systematic and, consequently, that the mechanical stimuli could stimulate the replacement of one cell population by another. This means that the stimuli are not only the key factor for the generation of tissues, but are also important for the constant adaptation of tissues [9]. This theory is illustrated in Figure 4.

1.5. A Simple Quantitative Theory

Claes and Heigele [8] followed the main idea of Pauwels and Carter et al. in considering that the most important mechanical stimuli are strain and hydrostatic pressure. However, they included clinical information on ossification paths, which may guide the fracture-healing process. Their hypothesis was that "new bone formation in fracture healing occurs primarily along fronts of existing bone or calcified tissue and that the type of bone healing [...] depends on the local strain and stress magnitudes". They used a finite analysis model to estimate the local magnitudes of strain and stress in callus tissues and along different ossification paths, which were obtained from histological images of a previous in vivo experiment.

The analysis performed by Claes and Heigele was a visual comparison of the typical locations of intramembranous bone formation and endochondral ossifications with the calculated strain and hydrostatic pressure. This analysis allowed them to state the quantitative relationships between mechanical stimuli and tissue differentiation shown in Figure 5. These relationships, determined by the mechanical stimuli, define specific areas in the figure that correspond to endochondral versus intramembranous ossification.

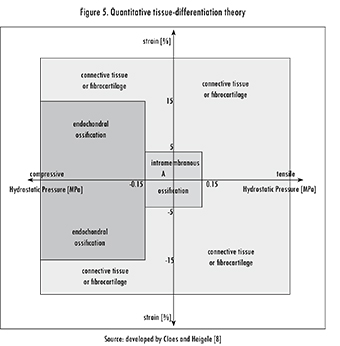
1.6. The Strain as Unique Mechanic Factor in Tissue Differentiation

In 2005, Duda et al. [25] presented a model of osteochondral defect healing that is based on the hypothesis that the strain of the tissue, expressed as the minimum principal strain, is a main stimulus for tissue differentiation. However, Duda et al. did not consider local stress as an additional stimulus, as Claes and Heigele did. Despite the simplicity of the model, it showed good qualitative and quantitative agreement with the histological findings.

1.7. Other Factors Different than Mechanical Loading

Biochemical signaling, cellular mechanisms, and local vascularization also play important roles in tissue differentiation and adaptation. Therefore, recent works have developed algorithms that emulate the effects of those factors, sometimes including them in the models of mechanically induced adaptation, in the search for a more comprehensive representation of the differentiation and adaptation processes.

Bailon-Plaza and Van der Meulen [26] proposed an early mathematical framework in which the effect of growth factors, as biochemical signals, was included in the process of bone healing. This model was later extended to include mechanically induced adaptation [27]. Isaksson et al. [10] and Moore et al. [28] also combined biological and mechanical factors in a mechanistic model of bone healing. They accounted for cell activities such as migration, proliferation, differentiation, and apoptosis. Quantification of the model constants, which mainly dictate the rates of various processes, was seen as a problem because they likely depend on the conditions of the subject (e.g., species, gender, clinical status, age, etc.).

Additionally, vascularization plays an important role in tissue generation and maintenance. To test how this factor may influence bone healing, Geris et al. [29] include the possibility of angiogenesis in the model previously developed by Bailon-Plaza and Van der Meulen [26]. This was done by describing the angiogenesis as a process involving endothelial cells, a vascular matrix, and a generic angiogenic growth factor produced by osteoblasts and hypertrophic chondrocytes.

2. Mathematical Implementation

The first implementations of the theories of tissue differentiation and adaptation used static mechanical models to determine the general stress state during a specific moment of the biological process. Currently, the models for the various theories have improved through the use of finite element analysis within an iterative algorithm that allows the study of the complete development of the process. Recent studies have commonly included dynamic variation of material properties, cell distribution, and mechanical loading.

All the algorithms used have similar outlines (see Figure 6). First, there is an initial step in which the characteristics of the tissue are established (i.e., geometry and material properties). Second, the tissue is mechanically loaded and biophysical stimuli are determined (e.g., stresses, strains, flow velocities). Third, the phenotype for each point in the geometry is updated based on a numerical approximation of a chosen theory. Fourth, if the migration of pluripotent cells is considered, a new cell distribution within the tissue is obtained using, for instance, diffusion analysis. Fifth, the material properties are updated, and a new iteration, corresponding to a new time point, can be started. Convergence of the numerical procedures is often evaluated in terms of the mechanical properties; that is, if the change in mechanical properties is lower than a certain limit, the algorithm converges.

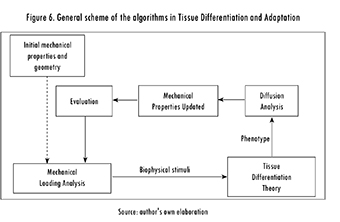
In a numerical description of the tissue differentiation and adaptation processes, it is possible to identify the following three different parts or (sub-) models:

• A mechanical (sub-) model, which calculates the mechanical state of the tissue: stress/strain, flow velocities, and pressures.
• A diffusion (sub-) model, which estimates the motion of cells and bio-signals due to concentration gradients.
• A reaction (sub-) model, which predicts the change in the phenotype of the tissue cells as a result of the mechanical state of the tissue and the concentration of bio-factors. These are the numerical implementations of the previously described theories.

Brief descriptions of each model and their numerical implementations are presented below.

2.1. Mechanical Models

Determining the mechanical state of a tissue requires a proper description of the tissue as a material. Frequently, the tissues in the previously described theories are modeled as single-phase elastic and biphasic materials. The choice between these two material descriptions relies on the loading and boundary conditions as well as on the level of consideration of the model. In general terms, a single-phase elastic model is usually appropriate when strain rates are higher than 0.1 or 0.01 Hz, when the boundary conditions constrain free fluid flow from and to the tissue (low permeability), or when the consideration level is larger than the tissue level. Otherwise, a biphasic description should be used [30]. C

2.1.1. Single-Phase Elastic Model

Considering isotropy and linear elasticity (Hooke's law), the equations that relate stress and strain are as follows:

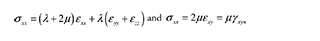
where λ and μ are the Lamé constants, defined as

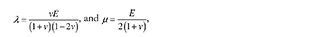
with E as the Young's modulus and υ as the Poisson ratio. The stiffness relation can be written as follows:

with D^e as the elastic stiffness matrix.

Finally, invariants such as the hydrostatic stress (σ_d) and octahedral shear stress (σ_s), parameters for the other (sub-) models (diffusion and reactive models), are calculated as follows:

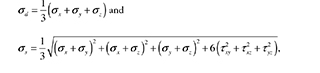
2.1.2. Biphasic Approach

A more accurate material description is given by the biphasic theory or by poro-elasticity. When incompressibility is assumed, the mathematical implementations and solutions of these techniques are equivalent [31], [32], and both approaches estimate the stress state of the phases as follows [33]:

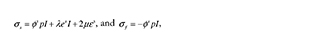
where σ_∫ is solid stress,σ_ƒ is fluid stress, e and ε are dilatational strain and total strain, respectively; p is apparent pressure, θ is the volume fraction, and λ and μ are the Lamé constants.

2.2. Diffusion Model [34]

Differentiation and adaptation of tissues are influenced by the local concentration of cells and bio-signals (e.g., growth factors). Motion of both, cells and bio-signals, can be modeled as following a diffusion process. However, this diffusion process can have either of two approaches: the chemical pattern approach and the mechanochemical approach. On the one hand, in the chemical pattern approach, pattern formation and morphogenesis take place sequentially. Morphogenesis, i.e., formation of the structure, is essentially a slave process that is determined once the chemical pattern has been solved. On the other hand, in the mecha-nochemical approach, pattern formation and morphogenesis are considered to go on simultaneously as a single process, which may be closer to reality.

The diffusion model that uses the mechanochemical approach consists of three governing equations: The conservation equation for the cell population density, the mechanical balance of the forces between the cells and the extracellular matrix (ECM), and the conservation law governing the ECM. Without minor details, the equations are written as follows:

2.2.1. Cell Conservation Equation

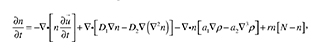
where the terms from left to right in the right side of the equation are related to cell convection, diffusion, haptotaxis, and mitosis, respectively; D₁, D₂, a₁, a₂, r, and N are positive parameters. The vector u is the displacement of ECM, and n and p are the number of cells and density of the ECM, respectively.

2.2.2. Cell-Matrix Mechanical Interaction Equation

where F is the external force acting on the matrix and σ is the stress tensor. However, the stress tensor has contributions from the ECM and the cells, such that:

σ = σ_ECM + σ_CELLS '

where σ_ECM as a linear viscoelastic material, can be written in terms of the viscous and elastic components as:

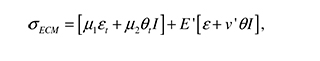
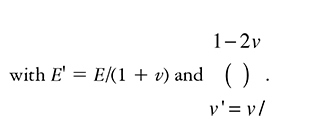
The subscript t denotes partial differentiation, I is the unit tensor, and μ and μ₂ are the shear and bulk viscosities of the ECM. ε is the strain tensor, defined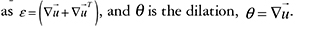

On the other hand, the stress due to the cell traction, σ _CELLS, is:

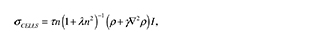
where τ is the traction force generated by the cell, λ is a measure of how the force is reduced because of neighboring cells, and γ is a measure of the nonlocal long-range cell-ECM interactions. Finally, to complete the description of the terms in the cell matrix:

where s > 0 is an elastic parameter characterizing the substrate attachments.

2.2.3 Matrix conservation equation

The conservation equation for the matrix material, ρ(r,t), is

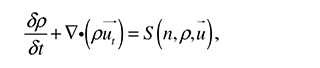
where matrix flux is considered due to convection and S(n,ρ,u) is the rate of secretion of matrix by the cells.

2.3. Reaction (Sub-) Model

The theories described in the first section can be written as numerical algorithms to be included, along with the mechanical and diffusion (sub-) models, in a model of tissue development and adaptation. Various authors highlighted above, among others, have implemented their theories using different mechanical stimuli, mechanical thresholds, or the methods of modeling the tissue. The mathematical implementations are described briefly in this section.

2.3.1. The Osteogenic Index

Carter et al.'s theory is qualitative, and no specific relationships between the stimuli have been proposed to define the regions shown in Figure 9. However, to achieve physiologic ossification patterns in their models, Carter et al. define an Osteogenic Index as:

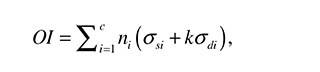
where η_i is the number of cycle repetitions for each load case, c is the number of load cases, and κ is an experimental constant. σ_d and σ_s are the magnitudes of the stimuli considered by the authors, i.e., hydrostatic stress and octahedral shear stress.

The mechanical stimuli can be calculated for each load case as:

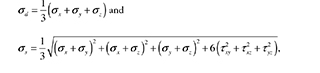
where the stress terms, σ and τ_ij , are expressed in an orthogonal base (x, y, z). Cartilage growth and ossification processes are accelerated in presence of high values of OI and delayed or avoided in areas of low OI values [35]. In the case of articular cartilage development (loaded with a cyclic stimulus), the proposed equation is modified to:

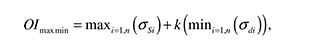
where a cyclic load condition has been discretized in n consecutive loading cases. For each point of the material one IO_maxmin can be found using the maximum shear stress and the minimum value of hydrostatic stress during the entire cycle load [35]. The value of constant k must be previously calculated for each specific case (specific geometry, specific load conditions). This parameter is calculated by iteration until the plot of the OI matches the documented ossification patterns. Finally, matching plots of strain and hydrostatic stresses with histological images allows the determination of levels of pressure and strain for each phenotype.

The various models of Carter et al. have used an elastic material model to represent the tissue, in a single-phase approach. This is held by the authors with the premise that the solution is sufficient to describe the ossification patterns, while other problems, such as the behavior of the cartilage, must be handled with biphasic theory [36].

2.3.2. Biphasic Implementation

When authors want to consider the relative flow as a stimulus for tissue differentiation, they must apply a biphasic theory. In the constitutive equations it is possible to relate the boundary conditions with the internal mechanical loads such as substrate strain, poro-pressure and/or relative velocity among phases, and the material properties of the tissue. Huiskes et al. [37] proposed some rules for tissue differentiation using the biphasic approach that were later refined by Lacroix et al. [38], and Kelly and Prendergast [39] as follows:

where γ is the substrate (distortional) strain, ν is the relative fluid velocity, and a and b are experimental constants. The values of a ( = 0.0375) and b ( = 3 ptm/s) were calculated by Huiskes et al. from experiments conducted in dogs by S0bolle [40]. However, these values should be used cautiously because these constants are likely site- and species-dependent.

3. Discussion and Future Steps

The first theories of tissue differentiation and adaptation were based on simple experiments and clinical experiences. Later, similar hypotheses included mechanical variables in the description of the process. The implementations of mechanical variables and computational power have allowed not only the description, but also the prediction of events. Currently, models include other variables and parameters such as biosignaling and vascularization to increase their prediction capacity. Although the nature of these recently-included variables is distinct from the mechanical state of the tissue, they are influenced by the mechanical environment of the tissue and its function by being subject.

However, although it is accepted that mechanical function can influence the shape and structure of skeletal tissues, as well as the regulation of their development, it is still not totally clear how these processes are accomplished and how different inducing factors work together. Experimental verification of the different theories is out of the scope of this review. Nevertheless, verification is always an essential part of modeling, and the theories presented here have an important setback: their models often need input data that obviates the need for the models in the first place [41].

In general, tissue regulation includes two biological processes: an initial tissue differentiation and a subsequent tissue adaptation. The boundary between these processes is not well defined. To study both process using a single theory or model would require a common definition of change-inducing factors. However, the specific weights of those common change-inducing factors on the overall process are likely to change over time and based on tissue maturity, making it difficult to achieve a unified theory of tissue regulation.

The different quantitative relationships in the reaction models have been widely tested using computer models [29], [39]. However, conclusions from those works are always limited by the fact that many of the parameters have been defined based on specific experiments. This imposes a limitation because the value of such parameters is very likely to be site- and species-dependent [42], [43]. Moreover, the data needed to validate mechanoregulation theories often provide the same insight as the models, making the models less useful in certain cases of basic research [41]. However, some theories do have predictive power despite the limitations of generalization. It seems to be a matter of time until new experiments and models appear with predictive power and where rigorous verification can be performed [44].

Current theories and models are proper steps toward a final model that remains elusive. In general, numerical models force us to describe every detail of a theory in a quantitative way and, at the same time, allow us to make predictions instead of merely describing the process. However, the need for new experiments to evaluate the different tissue differentiation theories is evident. Testing of more and more complex research hypotheses is encouraged by the new and more powerful computational resources, but the original theories still require definitive validation or verification.

References

[I] D. R. Carter, M. C. van der Meulen, and G. S. Beaupre, "Mechanical factors in bone growth and development," Bone, vol. 18, pp. 5S-10S, Jan, 1996.         [ Links ]

[2] D. E. Ingber, "Mechanobiology and diseases of mechanotransduction," Ann. Med., vol. 35, pp. 564-577, 2003.         [ Links ]

[3] H. Isaksson, "Recent advances in mechanobiological modeling of bone regeneration," Mech. Res. Commun., vol. 42, pp. 22-31, 2012.         [ Links ]

[4] D. R. Carter and G. S. Beaupré, Skeletal Function and Form: Mechanobiology of Skeletal Development, Aging, and Regeneration. Cambridge University Press, 2007.         [ Links ]

[5] W Roux, "Der zuchtende Kampf der Teile, oder die 'Teilau-slese' im Organismus (Theorie der "funktionellen Anpassung")," Wilhelm Engelmann, Leipzig, 1891.         [ Links ]

[6] S. Perren and J. Cordey, "The concept of interfragmentary strain," Current Concepts of Internal Fixation of Fractures, pp. 63-77, 1980.         [ Links ]

[7] D. R. Carter, "Mechanical loading history and skeletal biology," J. Biomech., vol. 20, pp. 1095-1109, 1987.         [ Links ]

[8] L. Claes and C. Heigele, "Magnitudes of local stress and strain along bony surfaces predict the course and type of fracture healing,"J. Biomech., vol. 32, pp. 255-266, 1999.         [ Links ]

[9] P. Prendergast, R. Huiskes, and K. Soballe, "Biophysical stimuli on cells during tissue differentiation at implant interfaces,"J. Biomech., vol. 30, pp. 539-548, 1997.         [ Links ]

[10] H. Isaksson, C. C. van Donkelaar, R. Huiskes, and K. Ito, "A mechano-regulatory bone-healing model incorporating cell-phenotype specific activity,"J. Theor. Biol., vol. 252, pp. 230-246, 2008.         [ Links ]

[11] F. Pauwels, "GrundriB einer Biomechanik der Frakturheilung. Verh dtsch orthop Ges 34. KongreB 62-108," Ges Abh Springer, Berlin, 1980.         [ Links ]

[12] H. M. Frost, The Laws of Bone Structure. CC Thomas, 1964.         [ Links ]

[13] C. H. Turner, "Homeostatic control of bone structure: an application of feedback theory," Bone, vol. 12, pp. 203-217, 1991.         [ Links ]

[14] M. C. van der Meulen and R. Huiskes, "Why mechanobiology?: A survey article," J. Biomech., vol. 35, pp. 401-414, 2002.         [ Links ]

[15] F. Guilak, D. L. Butler, S. A. Goldstein, and F. P. Baaijens, "Biomechanics and mechano-biology in functional tissue engineering,"J. Biomech., vol. 47, pp. 1933-1940, 2014.         [ Links ]

[16] A. Carlier, L. Geris, J. Lammens, and H. Van Oosterwyck, "Bringing computational models of bone regeneration to the clinic," Wiley Interdisciplinary Reviews: Systems Biology and Medicine, 2015.         [ Links ]

[17] D. C. Betts and R. Müller, "Mechanical Regulation of Bone Regeneration: Theories, Models, and Experiments," Frontiers in Endocrinology, vol. 5, 2014.         [ Links ]

[18] L. Geris, J. Vander Sloten, and H. Van Oosterwyck, "In silico biology of bone modelling and remodelling: regeneration," Philos. Trans. A. Math. Phys. Eng. Sci., vol. 367, pp. 2031-2053, May 28, 2009.         [ Links ]

[19] R. Hart, "Bone modeling and remodeling: Theories and computation," in Bone Mechanics Handbook, second edition ed., S. C. Cowin, Ed. Boca Raton: CRC Press, 2001, pp. (31) 1.         [ Links ]

[20] H. Weinans and P. Prendergast, "Tissue adaptation as a dynamical process far from equilibrium," Bone, vol. 19, pp. 143-149, 1996.         [ Links ]

[21] D. R. Carter, G. S. Beaupré, N. J. Giori and J. A. Helms, "Mechanobiology of skeletal regeneration," Clin. Orthop., vol. 355, pp. S41-S55, 1998.         [ Links ]

[22] I. Owan, D. B. Burr, C. H. Turner, J. Qiu, Y Tu, J. E. Onyia, and R. L. Duncan, "Mechanotransduction in bone: osteoblasts are more responsive to fluid forces than mechanical strain," Am. J. Physiol.-Cell Ph., vol. 273, pp. C810-C815,         [ Links ] 1997.

[23] P Prendergast, "Computational mechanobiology," in Computational Bioengineering: Current Trends and Applications. s. p.: Imperial College Press, 2004, pp. 117-133.         [ Links ]

[24] V. Mow, "Biphasic creep and stress relaxation of articular cartilage in compression," J.Biomech. Eng., vol. 102, pp. 73-84, 1980.         [ Links ]

[25] G. N. Duda, Z. M. Maldonado, P Klein, M. O. Heller, J. Burns. and H. Bail, "On the influence of mechanical conditions in osteochondral defect healing," J. Biomech., vol. 38, pp. 843-851, 2005.         [ Links ]

[26] A. Bailon-Plaza and M. C. Van Der Meulen, "A mathematical framework to study the effects of growth factor influences on fracture healing,"J. Theor. Biol., vol. 212, pp. 191-209, 2001.         [ Links ]

[27] A. Bailon-Plaza and M. van der Meulen, "Beneficial effects of moderate, early loading and adverse effects of delayed or excessive loading on bone healing,"J. Biomech., vol. 36, pp. 1069-1077, 2003.         [ Links ]

[28] S. R. Moore, G. M. Saidel, U. Knothe and M. L. K. Tate, "Mechanistic, mathematical model to predict the dynamics of tissue genesis in bone defects via mechanical feedback and mediation of biochemical factors," PLoS Computational Biology, vol. 10, pp. e1003604, 2014.         [ Links ]

[29] L. Geris, A. Gerisch, J. V. Sloten, R. Weiner, and H. V. Oosterwyck, "Angiogenesis in bone fracture healing: a bioregulatory model,"J. Theor. Biol., vol. 251, pp. 137-158, 2008.         [ Links ]

[30] E. Loboa, T. Wren, G. Beaupre and D. Carter, "Mechanobiology of soft skeletal tissue differentiation-a computational approach of a fiber-reinforced poroelastic model based on homogeneous and isotropic simplifications," Biomechanics and Modeling in Mechanobiology, vol. 2, pp. 83-96, 2003.         [ Links ]

[31] M. Levenston, E. Frank and A. Grodzinsky, "Variationally derived 3-field finite element formulations for quasistatic poroelastic analysis of hydrated biological tissues," Comput. Methods Appl. Mech. Eng., vol. 156, pp. 231-246, 1998.         [ Links ]

[32] B. R. Simon, "Multiphase poroelastic finite element models for soft tissue structure," Appl. Mech. Rev., vol. 45, 1992.         [ Links ]

[33] P. Prendergast and M. Van der Meulen, "Mechanics of bone regeneration," in Bone Mechanics Handbook. Boca Raton: CRC Press, 2001, pp. 32-31.         [ Links ]

[34] J. D. Murray, "Mechanical models for generating pattern and form in development", Mathematical Biology, 1993.         [ Links ]

[35] D. R. Carter and G. S. Beaupré, Skeletal Function and Form: Mechanobiology of Skeletal Development, Aging, and Regeneration. Cambridge: Cambridge University Press, 2001.         [ Links ]

[36] D. R. Carter, G. S. Beaupré, M. Wong, R. L. Smith, T. P. Andriacchi, and D. J. Schurman, "The mechanobiology of articular cartilage development and degeneration," Clin. Orthop., vol. 427, pp. S69-S77, 2004.         [ Links ]

[37] R. Huiskes, W Van Driel, P Prendergast, and K. Soballe, "A biomechanical regulatory model for periprosthetic fibrous-tissue differentiation," J. Mater. Sci. Mater. Med., vol. 8, pp. 785-788, 1997.         [ Links ]

[38] D. Lacroix, P Prendergast, G. Li, and D. Marsh, "Biomechanical model to simulate tissue differentiation and bone regeneration: application to fracture healing," Medical and Biological Engineering and Computing, vol. 40, pp. 14-21, 2002.         [ Links ]

[39] D. Kelly and P J. Prendergast, "Mechano-regulation of stem cell differentiation and tissue regeneration in osteochondral defects,"J. Biomech., vol. 38, pp. 1413-1422, 2005.         [ Links ]

[40] K. Soballe, "Hydroxyapatite ceramic coating for bone implant fixation: mechanical and histological studies in dogs," Acta Orthopaedica, vol. 64, pp. 1-58, 1993.         [ Links ]

[41] C. R. Jacobs and D. J. Kelly, "Cell mechanics: The role of simulation," in Advances on Modeling in Tissue Engineering. New York: Springer, 2011, pp. 1-14.         [ Links ]

[42] D. R. Carter, "Mechanical loading histories and cortical bone remodeling," Calcif. Tissue Int., vol. 36, pp. S19-S24, 1984.         [ Links ]

[43] J. E. Bertram and S. M. Swartz, "The 'Law of Bone Transformation': A Case of Crying Wolff?" Biol Rev, vol. 66, pp. 245-273, 1991.         [ Links ]

[44] H. Khayyeri, H. Isaksson and P J. Prendergast, "Corroboration of computational models for mechanoregulated stem cell differentiation," Comput. Methods Biomech. Biomed. Engin., vol. 18, pp. 15-23, 01/02; 2014/11, 2015.         [ Links ]