Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería y competitividad
Print version ISSN 0123-3033
Ing. compet. vol.16 no.1 Cali Jan./June 2014
Análisis cinemático de un miembro inferior para determinar el centro de rotación en el plano sagital
Kinematic analysis of a lower limb to determine the center of rotation of the knee at the sagittal plane
Héctor A. Tinoco
Autonomous University of Manizales. Faculty of Engineering, Department of Mechanical and Production Engineering, Manizales, Colombia
E-mail: htinoco@autonoma.edu.co
Andrés J. Arias-Moreno
Autonomous University of Manizales. Faculty of Engineering, Department of Mechanical and Production Engineering, Manizales, Colombia
E-mail: empiducan@gmail.com
Eje temático: Ingeniería biomédica / Biomedical engineering
Recibido: 7 de noviembre de 2012
Aceptado: 4 de octubre de 2013
Resumen
En esta investigación se establece una metodología que permite describir el movimiento de miembros inferiores usando cadenas cinemáticas cerradas. Este análisis es realizado con el objetivo de determinar la posición del centro de rotación (CR) de la rodilla localizado en el plano sagital. Un paciente sano y sin antecedentes patológicos realizó pruebas de flexión-extensión con uno de sus miembros inferiores. Cuando el paciente realizo el movimiento articular (la flexo-extensión) un dispositivo de video y un programa (World In motion v4.0) determinan la posición de cuatro marcadores pasivos ubicados en el miembro inferior. Los datos obtenidos de los marcadores son utilizados en un modelo propuesto que permite localizar la posición del CR de la rodilla. En este estudio se concluye que el CR de la rodilla presenta movimiento relativo respecto a un punto fijo marcado en un miembro inferior. Los resultados comprueban que el CR de la rodilla delimitado en el plano sagital no presenta comportamiento de una junta completa (junta con un grado de libertad) como ha sido presentado en otros estudios.
Palabras clave: análisis cinemático, centro de rotación (CR), flexión-extensión.
Abstract
A methodology is established in this research which permits to describe the movement of a lower limb using closed kinematic chains. This analysis is developed with the aim to determine the location of the center of rotation (CR) of the knee joint in the sagittal plane. Flexion-extension tests were carried out on one of the lower limbs of a healthy patient without pathological antecedents. When the patient does articular movement (flexion-extension), a video equipment and a software determine the position of four passive markers installed on the lower limb. The information obtained from the markers is applied to the proposed model which allows to locate the center of rotation of the knee joint. Hence it was concluded that the CR of the knee joint undergoes a relative movement with respect to the fixed point marked on the lower limb. The results prove that the knee joint established in the sagittal plane does not show the behavior of a complete joint (a joint with one degree of freedom) as it has been described in other studies.
Keywords: center of rotation, flexion-extension, kinematic analysis, knee.
1. Introduction
As it was described by Vera (1999), normal human locomotion is a set of rhythmic and alternating movements of the extremities, which determines the forward movement of the body´s center of mass. In the field of human locomotion, there are described different types of articular movement performed by the joints in the extremities. The knee joint is the widest articulation and maybe the most complex one in the body (Proubasta et al., 1997). This joint is a biarticular structure composed of the tibiofemoral and femoropatellar articulation. The knee joint can support high forces and moments since this articulation consists of femur and tibia, which are located between the two longest lever arms in the body. Adetailed description of the knee joint physiology can be found in Bronzino et al. (2003). A balance between stability and mobility is needed that knee joint works normally and this depends on the interaction of the ligaments and interaction of contact surfaces and muscles that enclose the knee joint (Koo et al., 2008). The movement of a knee joint occurs simultaneously in three planes, but the whole movement of the joint can be observed only at the sagittal plane. The movement of the joint at the sagittal plane may be limited if the articulation is restricted to a movement in a two-dimensional plane (see Nordin et al., 2004; Zuppinger, 2004). A two-dimensional approximation of the movement of the knee joint may be established from the kinematic relations similar to those of a planar mechanism (see Abdel-Rahman et al., 1993). However, significant progress has been made analyzing the kinematics of the knee joint in all the planes, as it is described by Freeman et al. (2005). Nevertheless, different analyses have been made to explain the movement of the knee joint (Gerber et al., 1983; Moeinzadeh et al., 1983; Haher et al., 1992; Hemmerich et al., 2008) with the aim to describe its kinematics in all the planes (van den Bogert et al., 2008; Anderst et al., 2010.).
The movement in the knee joint is produced by resultant forces generated by various muscle groups located in each kinematic plane. These forces may be represented by a unique resultant force which includes most of the muscle forces that act in the knee joint. In the tibiofemoral joint, the forces generate a máximum spatial movement in which the rotatory amplitudes are admisibles. As a result, kinematic approximations of the tibiofemoral joint may be delimited in the sagittal plane. Williams et al. (1991) proposed a mathematical model of the knee joint movement in the sagittal plane. The cruciate ligaments were considered as a four bar linkage. This model establishes an equation system for obtaining 11 kinematic parameters. The results depicted the slippage and rotation effects which form the complex movement of the surfaces articulated in the lateral condyle.
In the sagittal plane, there is observed that the movement of the knee joint from extension to the complete flexion produces a rotation between 0° and 140°, approximately. In the transversal plane, the movement is influenced by the position of the joint in the sagittal plane. When the knee joint is completely extended, the rotation is almost fully restricted by the impact of femoral and tibial condyles, this happens because the medial femoral condyle is longer than the lateral condyle. The muscles and ligaments also show restrictions to the knee joint movement, this phenomenon was studied by Moeinzadeh (1983). A dynamic model of tibiofemoral joint which incorporates the restrictions of ligaments in femur and tibia was described by Wongchaisuwat (1984). Goodfellow (1978) showed some methods for analyzing the mechanics of the knee joint, among others, for example: uniplanar or sagittal methods, triplanar method and instant center of rotation (ICR) method or the Reuleaux (1875) technique. Recent studies on articular determination were also carried out by Favre et al. (2008, 2009).
A Reuleaux (1875) technique is used in this research to relate the knee joint by means of kinetic chains with fixed points established on the lower limb. Inertial effects of the lower limb are not considered in this studysince this research is based on the kinematics of the lower extremity. This means that the lower limb is analogous to two rigid and articulated bodies (a thigh and a shank with movement of the joint in the sagittal plane). The main objective of this study is to estimate the position of the center of rotation of the knee joint by experimental measurements and to show that it is not a complete joint at the sagittal plane. The suggested model may be classified within the sagittal methods.
2. Methodology
2.1 Kinematic analysis
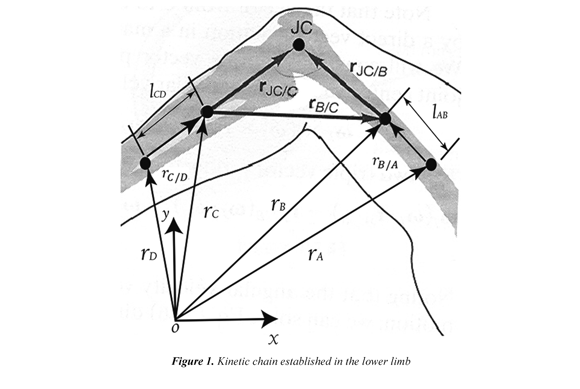
To describe the movement of the lower limb and to carry out a kinematic analysis of it, a theoretical model should be proposed. Let´s consider that the kinematic information of four points that belongs to the lower limb are known. So, Figure 1 shows a lower limb marked with four fixed points (A, B, C, D) and a point that belongs to the knee joint (JC). The points A, B, C and D are referred with regard to a fixed coordinate system O. The union between these points is represented by vectors in the following form: relative position vector rB/A (points A and B), relative position vector rC/D (points C and D), relative position vector rJC/B (points B and JC), relative position vector rJC/C (points C and JC), relative position vector rB/C (points B and C), rA (position of point A with regard to the fixed frame of reference O), rB (position of point B with regard to the fixed frame of reference O), rC (position of point C with regard to the fixed frame of reference O), rD (position of point D with regard to the fixed frame of reference O), l (magnitude of the vector rABB/A and l(magnitude of the vector rCD).
The thigh and shank are considered rigid bodies which move in the sagittal plane coincident with the plane ![]() x-y. Therefore, the connection of vectors established in the limb is also defined in the sagittal plane. For the vectors shown in Figure 1, the relative velocity ṙB/A of the thigh in any point in time t,∀ t∈R, may be defined as:
x-y. Therefore, the connection of vectors established in the limb is also defined in the sagittal plane. For the vectors shown in Figure 1, the relative velocity ṙB/A of the thigh in any point in time t,∀ t∈R, may be defined as:
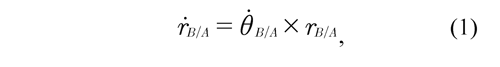
where θ is the angular velocity of the vector where θBA is the angular velocity of the vector rB/A. Eq. (1) may be rewritten as:
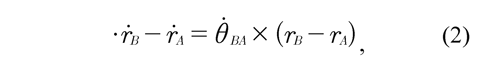
where ṙB is absolute velocity of the point B, ṙA is absolute velocity of the point A. In the same way as Eq. (1) is defined, also the relative velocity ṙC/Dcorresponding to the velocity of the shank can be expressed. For any point in time t, the velocity ṙC/Dis given by:

![]() where θCD is angular velocity of the shank. In
where θCD is angular velocity of the shank. In ![]() the same way as Eq. (1), also Eq. (3) may be
the same way as Eq. (1), also Eq. (3) may be ![]() determined as:
determined as:
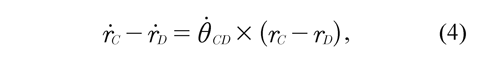
where ṙC is absolute velocity of the point C, ṙD is absolute velocity of the point D.
Angular velocity of the knee joint θJ is defined as relative angular velocity between the angular velocity of the thigh θBA and the angular velocity of the shank θCD, such that:
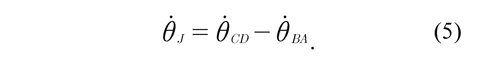
In this case, the flexion may be considered positive and the extension negative. The velocity of the joint (JC) ṙJC is determined by means of the relative velocity between the points JC and B that correspond to the thigh, then the velocity of the joint (JC) is obtained as:
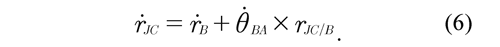
Similarly, the velocity of the joint (JC) ṙJC is determined by means of the relative velocity between the points JC and C that correspond to the shank, then the velocity of the joint (JC) is obtained as:
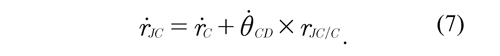
By equating Eq. (6) with Eq. (7), it is obtained that:
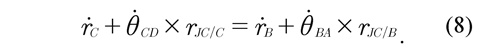
The points B, C and JC are related among each other in the following way:
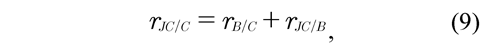
by replacing Eq. (9) into Eq. (8) and organizing Eq. (8), it is obtained that:
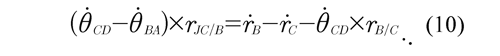
It can be observed that all the vectors on the right side of Eq. (10) are known, therefore the angular velocity of the center of the joint θJ is determined by substituting Eq. (5) into Eq. (10) and into the relative velocity (ṙB/C = ṙB -ṙC) between the points B and C, such that:
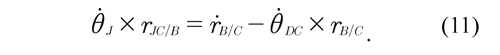
Multiplying Eq. (11) by the vector θJ , it is obtained that:

Applying the properties of the vector triple product of Eq. (12), this equation may be rewritten in the following form:
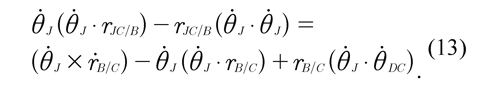
The angular velocity θ ̇_J is perpendicular to the vectors that are located in the sagittal plane, consequently io J (θ. J θj (θj . rB/C) = 0. Relative position rJC/B of the center of the joint seen from B to JC may be determined from Eq. (13) as:
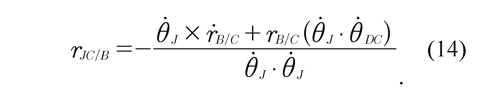
Eq. (14) represents the vector or the position of the center of the joint with regard to the point B located on the thigh.
2.2 Polynomial approximation
A set of N +1 data represented in Cartesian coordinate system may be adjusted or approximated by means of a polynomial of grade N. Then, for the obtained N +1 data {(x0, y0 ), (x1, y1 ) ... ,(xN, yN )}, a polynomial of grade N with N+1 coefficients is defined such that:
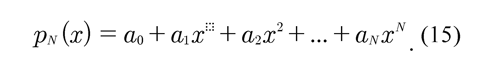
Each ordered pair (xN,yN ) is replaced in Eq. (15) and a system of linear equations is established with the aim to determine the coefficients of this polynomial. Yang . (2005) described this procedure which is applied in this study in the following form:
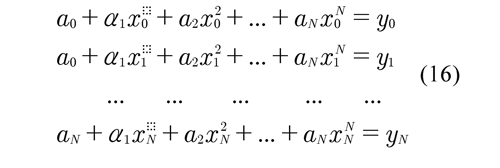
For determining the coefficients {a0, a1, a2, a3,... ,aN } from Eq. (16), it is established that:
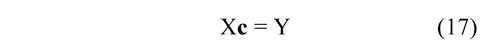
Solving for c from Eq. (17), the following is obtained:
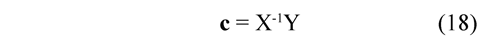
where X is the matrix of all the ordered pairs x, c is the coefficients vector and Y is the vector of ordered pairs y. The coefficients c are determined for positions obtained from each marker. For the determined polynomials, the derivative may be obtained numerically by means of an inclination established between two points in time ti and ti+1 that pertain to each function of position Xn(t),∀ n = 1,2,3 y 4. The derivative approximated from Xn (t), when ∆t → 0, is defined by:
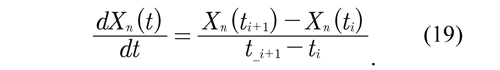
The lineal velocity of the points marked on the lower limb (points A, B, C and D) may be obtained from Eq. (19). The derivative proposed in Eq. (19) is a numerical approximation that works well if the data not present perturbations of high frequency, this is not the case of this study. But when the first derivative is applied to the set of data (xN, yN ), this is reduced to N - 1 data and the reduction will not affect the analysis because these are obtained in low frequency.
2.3 Experimental method
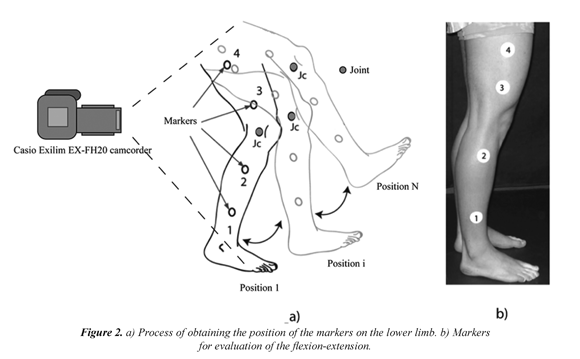
Figure 2 shows the methodology established for obtaining the position of four passive markers attached to the lower limb of a male patient of the age of 23 years, healthy and without any motional pathological antecedents which might affect the testing. The procedure for detection of the movement of lower limb was established in the following form: in the right lower limb, markers 1 and 2 were placed on the right shank and markers 3 and 4 on the right thigh (Figure 3) with a fixed relative position and a distance between markers 1 and 2 corresponding to d12 = 193 mm and a distance between markers 3 and 4 corresponding to d34 = 118 mm. The position of the markers is caught by a digital video device (Casio Exilim EXFH20 camcorder) which provides the information on the movement in a commercial video format, this information is read by World In Motion v4 (2007) software. The software World In Motion v4 (2007) allows for determining, in a discrete form, the position of the passive markers when low frequency movements are carried out, and at the same time, it corrects the camera´s perspective of projection adjusting a projection plane to the plane of position measures.
For evaluation of the characteristic movements of the four markers (see Figure 3), the patient was positioned in such a way that the flexion-extension exercise was done without kinematic restrictions in sagittal plane however a guideline was put in place to ensure a standard initial stance for the exercise. This was done with the aim to avoid indiscriminate movements in lateral and transversal plane as the movement of sagittal plane should be projected into the plane of the camera during the flexionextension. The above mentioned exercise was carried out taking into account the considerations and parameters done by Kankaanpa et al. (1998), Roy et al. (2003) and Bronzino et al. (2003). Since, the flexion-extension is not a simple movement of the joint around a transversal axis neither it is a simple movement done in one single plane. When the patient performed the exercise for kinematic evaluation, the video capturing was programmed at 3.3330s as the sequence of the patient´s movement was done in a shorter time interval.
Data on the position of the markers estimated from World In Motion v4 (2007) were exported to MatLAB for kinematic analysis. Numerical derivation functions were applied to estimate, by means of interpolation, the velocities of the markers located on the analyzed lower limb (see section 2.2). Eq. (14) including all the estimated kinematic information is shown in section 2.1 and it is used to determine relative position of the rotary knee joint in the sagittal plane.
3. Results and discussion
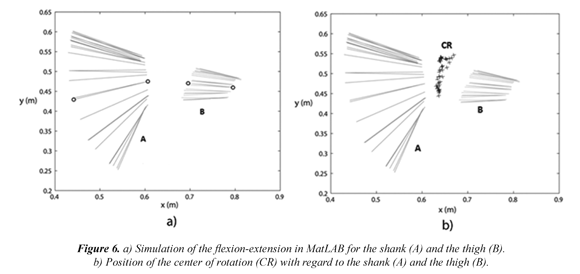
Figure 6a shows the position coordinates obtained from markers 1, 2, 3 and 4 as rigid links; these coordinates are simulated and coupled with in the following way: marker 1 and 2 (link 1) and marker 3 and 4 (link 2). The simulation is carried out for different time increments (∆t = 0,067 s) during all the patient´s exercise which consisted in the simultaneous movement of the shank and thigh until the complete extension of the right lower limb. In Figure 6a, it can be observed that the link 1 presents a wider movement than the link 2. It is caused because of the fact that link 1 represents the shank which is flexed towards the thigh and therefore it presents higher mobility. The movement of the link 2 consists of the translation and slight rotation since this link (thigh) is restricted by the support (chair) used during the performance of this exercise. No noise or perturbations were observed in the results of this simulation due to the relatively low velocity of the exercise (flexion -extension) which contributes to the fact that the obtained measurements are of low frequency.
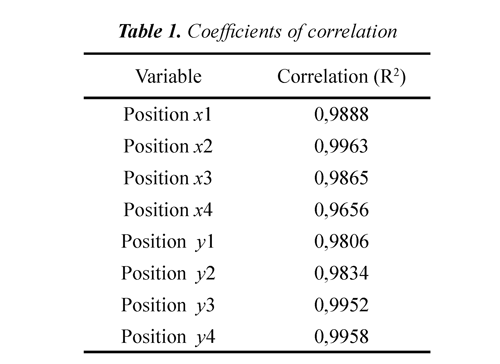
The coordinates of the markers´ displacement are approximated by a polynomial of grade N - 1 for a set of N determined data (see Eq. (16), Eq. (17) and Eq. (18)). Table 1 shows the coefficients of correlation for every approximation done for each coordinate x and y corresponding to the markers 1, 2, 3 and 4. An interpolation process was implemented because the time intervals between two consequent images were 0.067s. Within this time interval, the information about the position of the center of rotation of the knee joint might be lost, however the implemented process of interpolation allowed to obtain more reliable results. The results listed in Table 1 show that the obtained coefficients of correlation indicate high reliability with the obtained approximations since the values of R2 are very close to 1.
3.1 Results for position
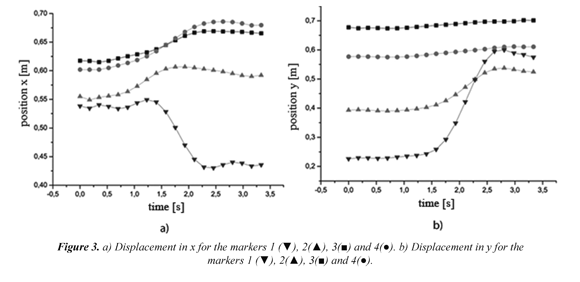
The displacement of the four markers in directions x and y with regard to a fixed coordinate system O may be observed in Figures 3a and 3b. This coordinate system was established by an experimental measurement. First, a scene where the patient did the exercise was delimited with the aim to establish the reference axes x and y. Then the reference limits were calibrated by the camera obtaining in this way a mobility plane of the patient.
Figure 3a shows the displacement of each marker in x (1, 2, 3 and 4). In this figure, it can be observed that the markers located on the thigh (3 and 4) did not evince big displacements. On the other hand, the markers 1 and 2 located on the shank showed greater displacements than markers 3 and 4, especially the marker 1 recorded bigger movement in this direction. It is consistent that the marker 1 evince greater displacement as the lower point on the shank is the one which does biggest movement. Figure 3b shows the displacements of the markers 1, 2, 3 and 4 in y. The markers 3 and 4 did not evince big mobility in the axis y because the patient did the exercise while sitting and the thigh was restricted by the platform of the stance. However, the markers located on the shank (1 and 2) recorded great mobility, especially the marker 1.
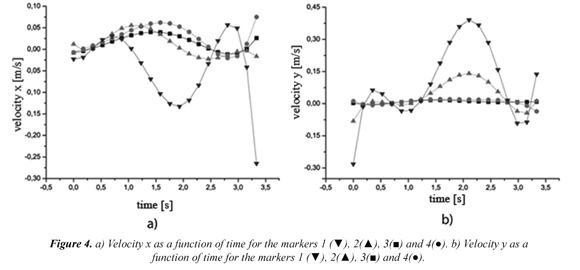
3.2 Results for velocity
Figures 4a and 4b show numerically calculated velocities of each marker in directions x and y. The velocity of the markers is obtained by the numerical derivative of the polynomials determined from the position. The numerical derivative was solved by means of Eq. (19) and applying an incremental algorithm written in MatLAB. It is important to mention that the process of differentiation was carried out on the polynomials determined from the position of each marker and therefore the noise generated during the differentiation process was controlled by means of the intervals evaluated by the polynomials.
Figure 4a shows the velocity component in x for each marker. All the markers experienced velocities with different amplitudes, this effect takes place because the patient not only turned the lower part of the shank, but at the same time, he also moved the thigh to perform the rotation of the lower part. The marker 1 underwent higher velocity amplitude in x due to its location on the lower part of the shank.
Figure 4b shows the velocity component in y for each marker. The markers 3 and 4 in fact evince zero velocity because the thigh is restricted in its movement by the supporting platform on which the patient was sitting. The markers 1 and 2 recorded higher velocity magnitudes caused by the movement of the lower shank at the moment of performing the flexion.
3.3 Determination of the knee joint position
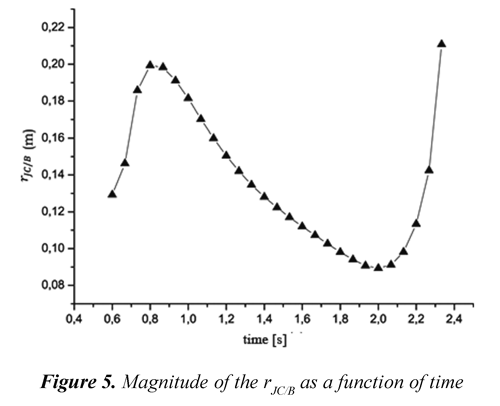
The results obtained in figures 3 and 4 are used in eq. (14). this equation represents the magnitude of the vector RJC/B established from the point b to the point jc (the distance from the point b to the center of rotation of the knee joint). the obtained data are shown in figure 5. in this figure, there can be observed the change in magnitude of the vector determined on the basis of an experimental rJC/B data and included in the proposed model (see eq. (14)).
The magnitude of the center of rotation of the knee joint increases in the interval t ∈ 0.6,0.8 s and becomes to decrease in t ∈ 0.8,2 s. it can be observed that the magnitude of the vector rJC/Bshows a maximum change of 12 mm with respect to the marker b. the values of the magnitude of change in every point in time, therefore the rJC/B magnitude to the center of rotation is not constant with regard to the point b. this result shows that the knee joint does not act as a simple rotary joint (a joint with one degree of freedom) as it was mentioned by koo et al. (2008); hemmerich et al. (2008) and favre et al. (2008), because the joint located in the knee evinces more complex movements which are a combination of translation and rotation when the articulation is moving.
The data shown in Figure 5 may be affected by the experimental measurement, however the results obtained by the proposed model do not show big deviations with regard to the reference point established on the thigh (rJC/B, see Figure 1). The influence of small errors on the results is detected in the measurement plane of (sagittal plane) shown in Figure 6b. The errors produced in the measurement are caused because the patient possibly did small movements perpendicular to the sagittal plane when he was performing the flexion-extension exercise. The position of the center of rotation through the x -y space may be observed in Figure 6b. In this figure, the CR is being moved 15 cm approximately in y because the patient starts to turn the entire lower limb and makes the center of rotation moves linearly in y. On the other hand, the coordinate x has only been moved 12 cm, approximately.
The displacements of 15 and 12 cm can be observed when the patient carries out the flexion-extension exercise with his lower limb. The changes in the position of the CR indicate a composed movement. It can also be observed in Figure 6b that the obtained points do not generate a defined contour since some errors as small movements were produced in other planes.
4. Conclusions
It is possible to determine the kinematics and the position of the rotary knee joint from the results obtained for the position and velocity of the markers located on the lower limb. In the measurement plane parallel to the system of measurement (sagittal plane), the results showed that the rotary knee joint evinces mobility between a fixed marker located on the thigh and the rotary joint estimated from the magnitude rJC/B, which is not constant. The results determined in this study indicate that the rotary knee joint is not a simple joint (a joint with one degree of freedom) since the articulation undergoes sliding and rolling movements.
The position of the obtained CR is coherent with the kinematics of the lower limb as it is found in a feasible region and not in regions out of the projections for the shank and the thigh. It is important to point out that this study does not analyze the position reliability in a quantitative form since there is no parameter for comparison. The strategy of establishing a relation between a lower limb of a disabled patient by means of a kinetic chain may be an option for analyzing the kinematics of a healthy lower limb. This is proposed with the aim to simulate a behavior of the articulations in amputated limbs.
For a plane study, the experimental measurement system adds errors to the results given that the information on the movement in the plane perpendicular to the sagittal plane is not caught by the video camera. This study may be extended to a two-plane system with the aim to determine the movement of the joint in three dimensions. It also may be adapted to the studies on the walk analysis as a supporting tool for identification of natural displacement gestures with such objectives as to identify movement pathologies or to improve the design of a knee immobilizer and an artificial limb.
5. Acknowledgements
The authors would like to thank to the biomedical engineers Carolina Bustos Cortes and JulianaAndrea Cárdenas Álvarez for their experimental collaboration on this study.
6. References
Abdel-Rahman, E.,& Hefzy M.S. (1993). A twodimensional dynamic anatomical model of the human knee joint. Journal of Biomechanical Engineering , 115, 357-365. [ Links ]
Anderst, W.,& Tashman, S. (2010). Using relative velocity vectors to reveal axial rotation about the medial and lateral compartment of the knee. Journal of Biomechanics , 43, 994-997. [ Links ]
Bronzino, J.D., & Schneck, D.J. (2003). Biomechanics Principles and Applications. CRC Press. [ Links ]
Favre J., Jolles, B.M., Aissaoui, R., & Aminian, K. (2008). Ambulatory measurement of 3D knee joint angle. Journal of Biomechanics , 41, 1029- 1035. [ Links ]
Favre, J., Aissaoui, R., Jolles, B.M., deGuise, J.A., & Aminian, K. (2009). Functional calibration procedure for 3D knee joint angle description using inertial sensors. Journal of Biomechanics , 42 (14), 2330-2335. [ Links ]
Freeman, M.A.R.,& Pinskerova, V. (2005). The movement of the normal tibio-femoral joint. Journal of Biomechanics , 38, 197-208. [ Links ]
Gerber, C. & Matter. P. (1983). Biomechanical analysis of the knee after rupture of the Anterior Cruciate Ligament and its primary repair. Journal of Bone and Joint Surgery , 6B, 391-399. [ Links ]
Goodfellow, J., & O'Connor, J. (1978). The mechanics of the knee and prosthetic design. Journal Bone Joint Surgery , 60, 358-69. [ Links ]
Haher, T.R., O'Brien, M., Felmly, W.T., Welin, D., Perrrier, G., Choueka, J., Devin, V., & Vassiliou, A., Chow, G. (1992). Instantaneous axis of rotation as a function of the three columns of the spine. Spine , 17, 149-154. [ Links ]
Hemmerich, A., van der Merwe, W., & Vaughan, C.L. (2008). Measuring three-dimensional knee kinematics under torsional loading. Journal of Biomechanics , 42(2), 183-186. [ Links ]
Kankaanpa, M., Taimela, S., Laaksonen, D., Hanninen, O., & Airaksinen, O. (1998). Back and hip extensor fatigability in chronic low back pain patients and controls. Archives of Physical Medicine and Rehabilitation , 79 (4), 412-7. [ Links ]
Koo, S., & Andriacchi, T.P. (2008). The knee joint center of rotation is predominantly on the lateral side during normal walking. Journal of Biomechanics , 41, 1269-1273. [ Links ]
MATLAB. (1992). User's Guide. The MathWorks Inc. Natick (MA) 01760. [ Links ]
Moeinzadeh, M.H., Engin, A.E.,& Akkas, N. (1983). Two-dimensional dynamic modeling of human knee joint. Journal of Biomechanics , 16, 253-264. [ Links ]
Muller, W. (1983). The knee: form, function and ligament reconstruction. Berlin: Springer-Verlag. [ Links ]
Nordin, M., & Frankel, V.H. (2004). Biomecánica Básica del Sistema Músculo Esquelético. México D.F.: McGraw-Hill. [ Links ]
Proubasta, I., Gil Mur, J., & Planall, J. (1997). Fundamentos de biomecánica y biomateriales. Madrid, España: Ergon S.A. [ Links ]
Releaux, F. (1975). The Kinematics of Machinery: Outline of a Theory of Machines (trans. A. M. W. Kennedy). New York: Dover. [ Links ]
Roy, A.L., Keller, T.S., & Colloca, C.J. (2003). Posture-dependent trunk extensor EMG activity during maximum isometrics exertions in normal male and female subjects. Journal of Electromyography Kinesiology , 13, 469-76. [ Links ]
van den Bogert, A. J., Reinschmidt, C., & Lundberg, A. (2008). Helical axes of skeletal knee joint motion during running. Journal of Biomechanics , 41 (8), 1632-1638. [ Links ]
Vera, P. (1999). Biomecánica de la marcha humana normal y patológica. Valencia, España: editorial IBV. [ Links ]
Williams, P. F., Peura, G. D., & Hoffman, A. H. (1991). A model of knee motion in the sagittal plane. In Bioengineering Conference, 1991., Proceedings of the 1991 IEEE Seventeenth Annual Northeast (pp. 273-274). [ Links ]
Wongchaisuwat, C., Hemami, H., & Buchner, H.J. (1984). Control of sliding and rolling at natural joints. Journal of Biomechanics Engineering , 106, 368-375. [ Links ]
World In Motion v4 (2007). User's Guide, Physics Curriculum & Instruction Video Analysis Software. [ Links ]
Yang, Y., Cao, W., Chung, T.S.,& Morris, J. (2005). Applied Numerical Methods Using MATLAB. New York: John Wiley & Sons. [ Links ]
Zuppinger, H. (1904). Die aktive Flexion im unbelasten Kniegelenk. Wiesbaden, Germany: Bergamann. [ Links ]

Revista Ingeniería y Competitividad por Universidad del Valle se encuentra bajo una licencia Creative Commons Reconocimiento - Debe reconocer adecuadamente la autoría, proporcionar un enlace a la licencia e indicar si se han realizado cambios. Puede hacerlo de cualquier manera razonable, pero no de una manera que sugiera que tiene el apoyo del licenciador o lo recibe por el uso que hace.