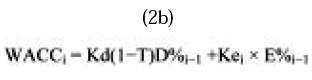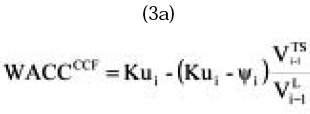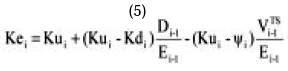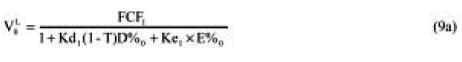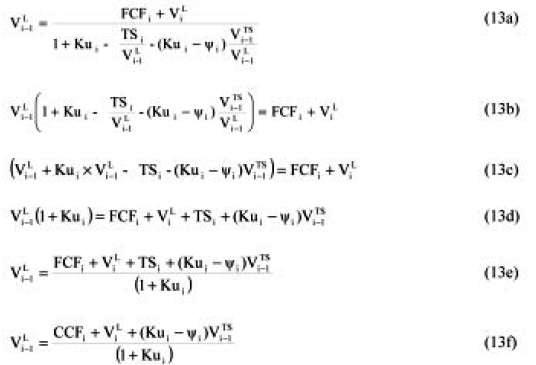Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Estudios Gerenciales
Print version ISSN 0123-5923
estud.gerenc. vol.22 no.98 Cali Jan./Mar. 2006
THERE EXISTS CIRCULARITY BETWEEN WACC AND VALUE? ANOTHER SOLUTION.
Ignacio VélezPareja1, Julián BenavidesFranco2
1Politécnico Grancolombiano Bogotá, Colombia ivelez@poligran.edu.co
2ICESI Cali, Colombia jbenavid@icesi.edu.co
Fecha de recepción: 21102005 Fecha de aceptación: 12112005
ABSTRACT
Although we know there exists a simple approach to solve the circularity between value and the discount rate, known as the Adjusted Present Value proposed by Myers, 1974, it seems that practitioners still rely on the traditional Weighted Average Cost of Capital, WACC approach of weighting the cost of debt, Kd and the cost of equity, Ke and discounting the Free Cash Flow, FCF. We show how to solve circularity when calculating value with the free cash flow, FCF and the WACC. As a result of the solution we arrive at a known solution when we assume the discount rate of the taxsavings as Ke, the cost of unlevered equity: the capital cash flow, CCF discounted at Ku. When assuming Kd as the discount rate for the tax savings, we find an expression for calculating value that does not implies circularity. We do this for a single period and for N periods.
KEY WORDS
Firm valuation, cost of capital, cash flows, free cash flow, capital cash flow, WACC, circularity
JEL CLASSIFICATION M21, M40, M46, M41, G12, G31, J33
INTRODUCTION
Although we know there exists a simple approach to solve the circularity between value and the discount rate, known as the Adjusted Present Value proposed by Myers, 1974, it seems that practitioners still rely on the traditional Weighted Average Cost of Capital, WACC approach of weighting the cost of debt, Kd and the cost of equity, Ke and discounting the Free Cash Flow, FCF. We show how to solve circularity when calculating value with the free cash flow, FCF and the WACC. As a result of the solution we arrive at a known solution when we assume the discount rate of the tax savings as Ke, the cost of unlevered equity: the capital cash flow, CCF discounted at Ku. When assuming Kd as the discount rate for the tax savings, we find an expression for calculating value that does not implies circularity. We do this for a single period and for N periods.
The typical solution for solving the circularity between value and WACC is to activate the option for iteration in a modern spreadsheet (VélezPareja and Tham, 2000
Tham and VélezPareja, 2004, and VélezPareja and Tham, 2005). However, this approach seems to be not easy to apply. We have examined the analytical solution of this problem and found what is known well before: when discounting with the proper discount rate the CCF will give identical answer to the calculation of value with the FCF discounted at the weighted average cost of capital, WACC.
THE PRACTICAL SOLUTION OF CIRCULARITY
The solution of circularity is very simple. This problem can be easily solved: in the Excel spreadsheet select Tools, then select Options, and there, select the tab Calculate and tick the option Iterations. Done this, the formulas for WACC and Ke, (the cost of the levered equity), that imply circularity, can be constructed. (See, VélezPareja and Tham, 2000 and 2005, Tham and VélezPareja, 2004). The analytical solution is simple as well.
AN ANALYTICAL SOLUTION FOR CIRCULARITY
Modigliani and Miller (1958 and 1963), in illuminating and seminal works defined the relationship between cash flows and values. These are the free cash flow, FCF, the cash flow1 to debt, CFD, the cash flow to equity, CFE, the tax savings, TS and the capital cash flow1 and their corresponding values. These relationships are:
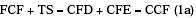
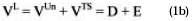
Where VL is the levered value of the firm, VUn is the unlevered value of the firm, VTS is the value of TS, D is the market value of debt and E is the market value of equity.
In Taggart, 1991, Tham and Velez Pareja, 2002 and 2004, VélezPareja and BurbanoPérez, 2003 and 2005 it is shown the general formulation for the WACC and the Ke, as follows
- The general expression for the WACC for the free cash flow, FCF, is
A particular and special case of (2a) is the traditional expression for WACC:
- For discounting the Capital Cash Flow CCF, (CFD + CFE = FCF + TS), we use the general formulation for WACCCCF
Depending on the assumption for the discount rate for the tax savings Ψ, we have the WACC for the CCF as follows:
For Ψ = Kd, the cost of debt

For Ψ = Ku
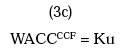
-
If we use CFE we should discount it with (in this case we have to add the value o debt to obtain the total value)
Single periodo
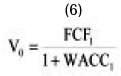
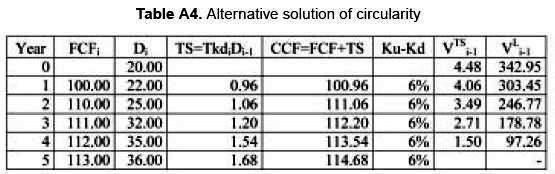
We have for a single period:
Where Ψ is the discount rate for the TS and Ku is the unlevered cost of equity.
USING A GENERAL EXPRESSION FOR WACC
If we replace equation 2a into equation (6) we find:

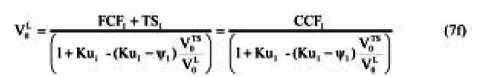
This expression is just (see equation (3a))
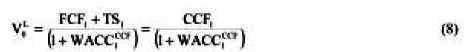
USING THE TRADITIONAL AND SPECIAL EXPRESSION FOR WACC
If we replace (2b) in (6) and replace Ke for its general expression (5) we have
Replacing Ke in (9a) with (5) we have

Simplifying,
Again, this expression is the value of the CCF and the discount rate is (3). In both cases we find circularity again. In order to solve it we depart from (9h)

And with the circularity fully solved we have for each case, for ψ = Kd
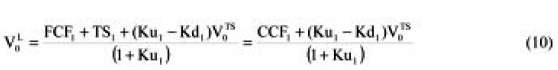
This means that when solving the circularity and assuming ψ = Kd we need to "adjust" the CCF by (Ku1Kd1) V0 TS.
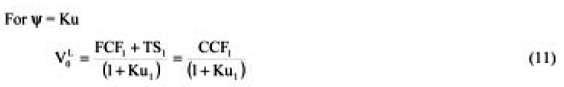
Observe the clean, neat and easy formulation when we assume ψ = Ku
THE NPERIOD CASE
There is a recursive equation to calculate the present value of a cash flow for any discount rate:
Replacing (2a) into (12) we have,
When ψ =Ku

And this is the recursive equation to calculate the present value of a cash flow (in this case with the CCF and Ku as discount rate).
When ψ =Kd
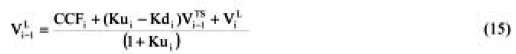
This is the same equation as before using the recursive equation to calculate the present value of a cash flow, in this case, the "Adjusted" CCF.
CONCLUDING REMARKS
We have shown that circularity can be solved analytically. The interesting finding is that when solving for circularity we arrive at a well know result: the discounting of the capital cash flow, CCF.
When we assume that the discount rate for the tax savings is Ku, the cost of unlevered equity, the solution is very simple: discount it with Ku. If we assume that the discount rate is Kd, then we have either to adjust the CCF with an amount function of the value of the tax savings, or we use the traditional expression for the CCF and discount it with Ku adjusted with some percent that is function of the value of the tax savings.
APPENDIX
AN EXAMPLE
Assume the following input data:
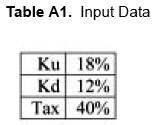
And the following FCF and debt, D
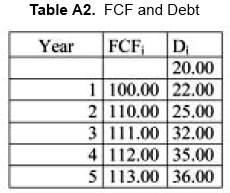
From this information we can calculate TS
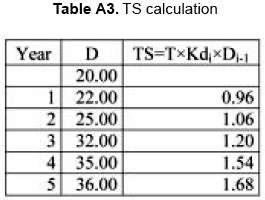
PROPOSED APPROACH
Using (13f) and assuming Ψ = Kd
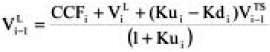
We have
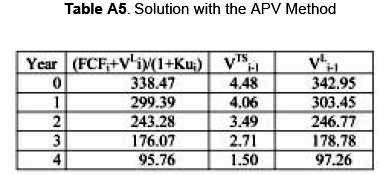
THE APV METHOD
Using the Adjusted Present Value, APV we have
PRACTICAL SOLUTION OF CIRCULARITY
Finally using the practical solution for perpetuity we have Temporal solution for WACC = 0%
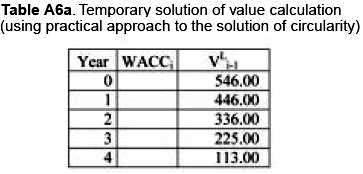
Observe that this is not the final solution because we are using WACC = 0%. Now, introducing the general formulation (2a) for WACCFCF and solving the circularity, we have
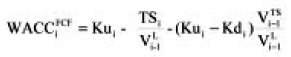
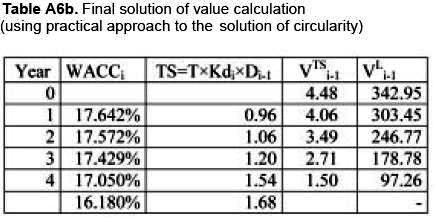
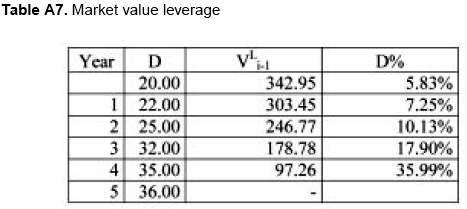
As can be seen, the circularity can be solved not only with the practical method, but using formulation (13f).
Observe as well that we do not need to set any target leverage. The approach allows for non constant leverage that is the usual situation in reality.
Note: The paper can be accesed at the SSRN (Social Science Research Network) www.ssrn.com
FOOTNOTES
1.The Capital Cash Flow, CCF, is the essence of the original Modigliani and Miller proposal in 1958; however, it was popularized by Ruback, 2000.
REFERENCES
1. Modigliani, F. & Miller M. H.(1958). The Cost of Capital, Corporation Taxes and the Theory of Investment, The American Economic Review. XLVIII, 261297. [ Links ]
2. Modigliani, F. & Miller, M. (1959). The Cost of Capital, Corporation Finance, and the Theory of Investment: Reply. The American Economic Review. XLIX,524527. [ Links ]
3. Modigliani, F. & Miller, M. H. (1963). Corporate Income Taxes and the Cost of Capital: A Correction. The American Economic Review. LIII, 433443. [ Links ]
4. Myers, S. C. (1974). Interactions of Corporate Financing and Investment Decisions: Implications for Capital Budgeting. Journal of Finance. 29, 125. [ Links ]
5. Taggart, Jr. & Robert A. (1991). Consistent Valuation Cost of Capital Expressions with Corporate and Personal Taxes. Financial Management, Autumn,820. [ Links ]
6. Tham, J. & VélezPareja, I. (2002). An Embarrassment of Riches: Winning Ways to Value with the WACC. Working Paper en SSRN, Social Science Research Network, http://papers.ssrn.com/sol3/ papers.cfm?abstract_id=352180. [ Links ]
7. Tham, J. & VélezPareja, I. (2004). Principles of Cash Flow Valuation. An Integrated Market Approach. S.L: Academic Press. [ Links ]
8. VélezPareja, I. & Tham, J. (2000). A Note on the Weighted Average Cost of Capital WACC. Social Science Research Network. [ Links ]
9. VélezPareja, I. & Burbano Pérez, A. (2003, November 9th). A Practical Guide for Consistency in Valuation: Cash Flows, Terminal Value and Cost of Capital (9th november 2003). http://ssrn.com/abstract=466721 [ Links ]
10. VélezPareja, I. & BurbanoPérez, A. (2005). Consistency in Valuation: A Practical Guide. SSRN http://papers.ssrn.com/sol3/papers.cfm?abstract_id=758664 [ Links ]
11. VélezPareja, I. & Tham, J. (2005). Proper Solution of Circularity in the Interactions of Corporate Financing and Investment Decisions: A Reply to the Financing Present Value Approach. Working Paper en SSRN: Social Science Research Network.Forthcoming in Management Research News 28 (7).2005 en http://papers.ssrn.com/sol3/papers.cfm?abstract_id=653222.. [ Links ]