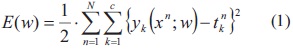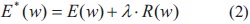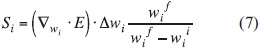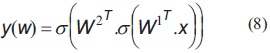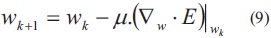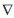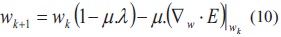Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Tecnura
Print version ISSN 0123-921X
Tecnura vol.16 no.33 Bogotá July/Sept. 2012
Selección eficiente de arquitecturas neuronales empleando técnicas destructivas y de regularización
An efficient selection of neural-network architectures using pruning and regularization techniques
Andrés Eduardo Gaona Barrera1, Dora María Ballesteros Larrotta2
1 Ingeniero Electrónico, magister en Ingeniería. Docente de la Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. Contacto: aegaona@udistrital.Qau.co
2 Ingeniera Electrónica, magister en Ingeniería Electrónica y de Computadores. Docente de la Universidad Militar Nueva Granada. Bogotá, Colombia. Contacto: dora.ballesteros@unimilitar.edu.co
Fecha de recepción: 31 de agosto de 2011 Fecha de aceptación: 14 de febrero de 2012
Resumen
Este artículo presenta una comparación detallada tanto a nivel teórico como práctico de redes neuronales ontogenéticas obtenidas a partir de algoritmos destructivos y de regularización. Inicialmente, se desarrolla el concepto de función de error regularizada y las diferentes formas de modificar esta función (weight decay (WD), eliminación de pesos, penalización de Chauvin y suavización de pesos). Luego, se muestran los algoritmos destructivos más representativos prestando especial atención en el OBD (Optimal Brain Damage). Para mostrar la forma de aplicación y funcionamiento de las técnicas destructivas y regularización se seleccionan los algoritmos de WD y OBD en el problema de la función XOR, cuyo resultado óptimo es conocido y que es posible visualizar de forma gráfica fácilmente. Para realizar comparaciones efectivas entre las técnicas, se programa el algoritmo de back-propagation en su forma básica y se realizan modificaciones del mismo para aplicar WD y hallar la matriz Hessiana en OBD. Los resultados muestran las bondades de WD en cuanto a velocidad de ejecución pero no de eliminación estricta de pesos, mientras OBD disminuye la complejidad de la arquitectura de la red neuronal pero su costo computacional es elevado.
Palabras clave: algoritmo back-propagation, redes neuronales, regularización, técnicas destructivas.
Abstract
This article shows a detailed comparison of both theoretical and practical Ontogenetic Neural Networks obtained through pruning and regularization algorithms. We initially deal with the concept of a regularized error function and the different ways to modify such a function (weight decay (WD), soft weight sharing, and Chauvin penalty). Then some of the most representative pruning algorithms are considered, particularly the OBD (Optimal Brain Damage) algorithm. We select OBD and WD within the problem of the XOR function with the purpose of analyzing pruning techniques and regularization algorithms. The basic back-propagation algorithm is used in both WD and the inverse Hessian matrix in OBD. According to the results, WD is faster than OBD, but it deletes a smaller number of weights. Additionally, OBD reduces the complexity of the neural-network architecture, but its computational cost is still high.
Key words: algorithm back-propagation, neural networks, regularization, pruning techniques.
1. Introducción
Uno de los inconvenientes cuando se desean modelar sistemas neuronales, ya sea de regresión o clasificación, es que se desconoce la estructura de la red que se adapte de una buena manera o de forma óptima al problema objeto de estudio [1]. Es difícil establecer la cantidad de capas, neuronas, conexiones o funciones de activación de forma automática y, generalmente, la forma de hacerlo viene de la experiencia del diseñador de la red neuronal o a través de múltiples pruebas en las que se varía alguno de los factores que afectan la arquitectura, pero sin lograr un control efectivo de la solución.
De forma a priori se puede plantear un modelo de gran tamaño (varias capas o neuronas) que lleve a una solución con error de aproximación cercano o igual a cero, pero que ocasiona que la red no pueda generalizar ante datos nuevos o desconocidos, esto último es el objetivo en la mayoría de problemas que usan redes neuronales. A estas soluciones se les denomina sobreajustadas (en inglés overfitting) y deben evitarse porque su capacidad de generalización es limitada [1], [2].
Modelos reducidos o con unas pocas neuronas provocan que la solución no represente el problema considerado, afectando tanto el error de aproximación como la generalización de la red neuronal. Luego, existe un compromiso entre la cantidad de parámetros y el desempeño del modelo, y esto es lo que se conoce como el dilema de la plasticidad-estabilidad [2].
Estudios teóricos demuestran que cuando se poseen dos o más modelos con desempeño similar debe elegirse aquel más simple, donde la métrica para medir la complejidad en redes neuronales es su dimensión VC [2]. Una manera práctica de realizar la selección es a través del número de neuronas o capas de la red, recordando que las redes neuronales con una capa oculta puede ser aproximadores universales.
Actualmente, se conocen modelos que intentan resolver el inconveniente de la arquitectura de la red a través de técnicas de optimización, heurísticas o algoritmos, en los cuales va aumentando o disminuyendo la cantidad de neuronas siempre monitoreando su desempeño, comúnmente a través del error entre el valor deseado y la salida del modelo [3]. Todas estas técnicas se han enmarcado en un tipo de redes neuronales denominadas ontogenéticas que intersectan los planos ontogenético y epigenético en el modelo POE (del inglés Phylogeny, Ontogeny y Epigenesis) [4], [5].
En este documento se muestra, a través de un ejemplo de clasificación de una función lógica, el concepto de adaptabilidad de la arquitectura en una red neuronal por medio de una técnica de pruning y una de regularización de la función de error. La organización del documento presenta, en la segunda sección, una visión global sobre las redes neuronales ontogenéticas particularizando en los métodos destructivos y regularización de la función de error. La tercera sección plantea el problema de clasificación y la cuarta sección muestra la obtención de varias soluciones usando las técnicas anteriormente mencionadas. Finaliza con un análisis de los resultados alcanzados y se concluye sobre la aplicación de las técnicas Weight decay y Optimal Brain Surgeon.
2. Marco teórico
Las redes neuronales ontogenéticas surgen como medio de respuesta a la evolución en la fase de entrenamiento o de ajuste de un modelo basado en redes neuronales [5]. Su nombre se puede atribuir al modelo POE, el cual intenta clasificar los sistemas bio-inspirados de acuerdo a analogías con la organización de la naturaleza en tres ejes diferenciados: filogenético, ontogenético y epigenético. De acuerdo con modelo POE, los sistemas conexionistas, como las redes neuronales, se encuentran enmarcados dentro del eje epigenético y a la evolución de una estructura particular sin interacción con el ambiente pertenece al eje ontogénico.
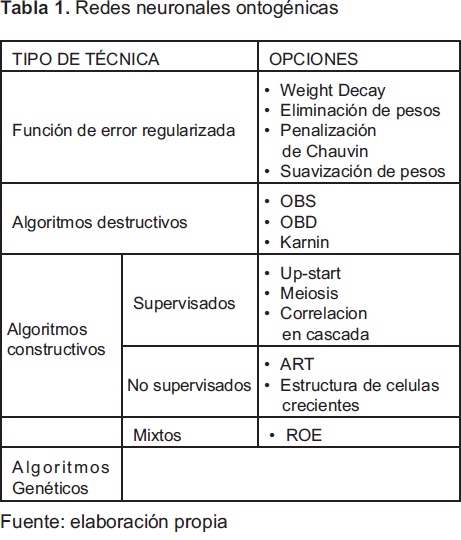
Las interacciones arquitectura-entrenamiento que proporcionan el modelo neuronal, son las que en realidad brindan la base ontogenética y un ejemplo de la intersección entre el eje filogenético y ontogenético que extienden el modelo POE original. Es de resaltar que en la clasificación realizada no sólo se encuentra los algoritmos genéticos para asegurar dicha intersección o dar las características ontogenéticas [6], [7], la estructura de la red se puede modificar a través de otros algoritmos de tipo analítico o heurístico como los presentados en la tabla 1 [2], [3], [6], [8].
Las redes neuronales ontogénicas pueden verse como un esquema de implementación de redes neuronales, en las cuales se intenta proporcionar a la arquitectura de la red, la sencillez necesaria para evitar el sobreajuste, usando procedimientos en los cuales se genera una interacción más fuerte entre la topología y el entrenamiento básico en el cual se encuentran los pesos de la red.
2.1 Métodos con función de error regularizada
Bajo el esquema de MLP, el algoritmo de back-propagation (BP) ha sido ampliamente estudiado y aplicado a problemas reales para encontrar los pesos o parámetros libres del modelo [1], [2], debido a su simplicidad en la obtención de los pesos de la red neuronal. El algoritmo BP proporciona una manera de resolver un problema de optimización no lineal irrestricto, en el cual la función objetivo es cuadrática y esta hace referencia al error cuadrático medio en función de los pesos w del MLP, tal como se muestra en la ecuación (1).
Donde:
El superíndice n indica la evaluación en un dato particular, donde N representa la cantidad de datos de entrenamiento y el subíndice k el número de salidas de la red y c el número total de salidas de la red.
Al observar la ecuación (1), esta proporciona una distancia euclidiana entre las diferencias entre el vector de etiquetas y la salida de la red, pero no considera la complejidad del modelo. La función de error mostrada en la ecuación (1), puede modificarse introduciendo un término de penalización del error ligado directamente con los pesos de la red; R(w), lo que implica que, de esta manera, la complejidad se considera a causa de que el error se incrementaría entre más neuronas o pesos posea la red, controlando de esta manera el sobreajuste [2].
Donde:
E (w): error total o modificado
E(w): error convencional dado por ecuación (1)
R(w): término de regularización que mide la complejidad del modelo
l: constante que determina la influencia del término R(w) en la respuesta.
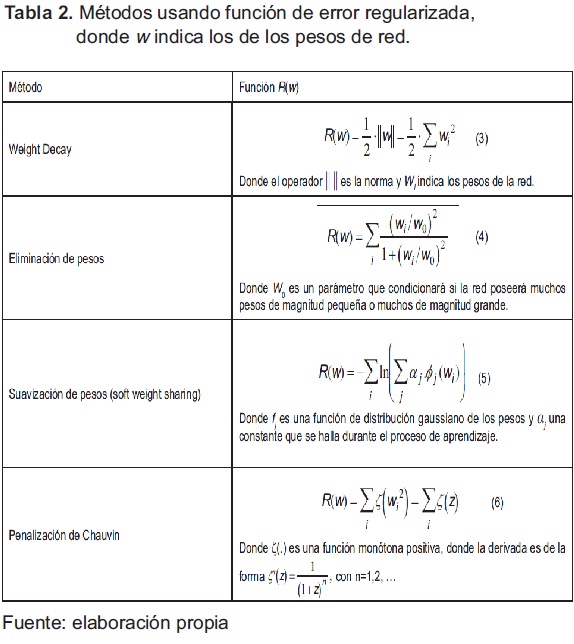
En la tabla 2 se presentan tres métodos que se pueden enmarcar dentro de la categoría de redes ontogénicas con función de error regularizada, en la cual se presenta la función que los describe según la ecuación (2) [3], [6] - [10].
Los métodos presentados en la tabla 2 poseen la característica que hacen que el algoritmo BP no se modifique de manera significativa, ya que en su versión original, que usa el método de descenso de gradiente, hay únicamente que incluir la función de error cuando se realiza la propagación hacia atrás (backward).
2.2. Algoritmos destructivos (Pruning)
Estos métodos parten de un MLP de un tamaño "grande" (solución sobreajustada) con un desempeño adecuado para el problema que se este trabajando, para luego eliminar aquellos pesos que aportan en menor medida a la solución [11] - [14]. La eliminación es selectiva y se hace considerando en general un parámetro denominado Saliency, que determina el aporte de dicho peso a la salida de la red, esto a partir de información de la primera o segunda derivada de la función de error. A continuación se muestran los métodos de pruning más relevantes: optimal brain surgeon, optimal brain damage y el método de Karnin.
Optimal Brain Damage (OBD): es un método de segundo orden debido a que emplea la segunda derivada de la función de error de la red con respecto a los pesos; es decir, es necesario el cálculo de la matriz Hessiana. Cuando la red posee una cantidad de pesos considerable el cálculo de la matriz se torna inviable, por lo tanto, se aproxima la matriz a una matriz diagonal, esto hace que la eliminación no sea tan precisa al considerar sólo la diagonal principal de la Hessiana [11].
Optimal Brain Surgeon (OBS): es otro método de segundo orden en el cual se resuelve el inconveniente de OBD de reentrenar la red por cada iteración del algoritmo. OBS calcula una aproximación de la matriz Hessiana inversa que se obtiene on-line, esta propuesta se encuentra reportada en [11]. La figura 1 resume el algoritmo OBS.
Método de Karnin: es un método de primer orden para el cual es necesario el gradiente de la función de error con respecto a los pesos para encontrar un parámetro denominado sensibilidad, que determina el peso a eliminar en la red [11], [12]. La sensibilidad se define como:
Donde 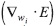 y
y 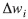 se estiman sobre el conjunto de entrenamiento y
se estiman sobre el conjunto de entrenamiento y 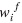 son los pesos en la iteración actual y
son los pesos en la iteración actual y 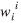 es el peso a eliminar.
es el peso a eliminar.
3. Metodología
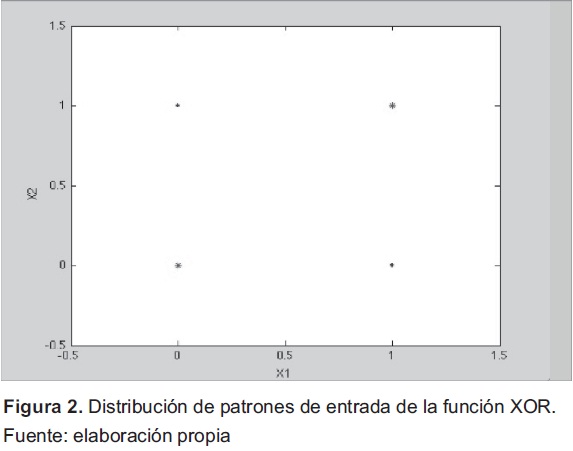
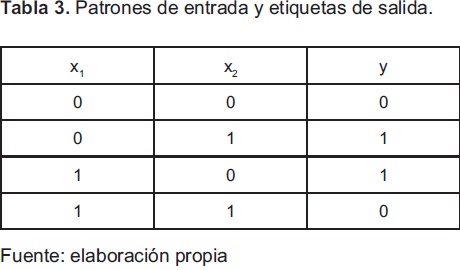
Para ilustrar los procedimientos usados por algunas de las redes ontogenéticas, se propone la ilustración de los procedimientos usados en tres de ellas, a través de un ejemplo típico de clasificación que se muestra en la figura 2. Este caso de estudio posee un espacio de entrada de dos dimensiones y las etiquetas de salida corresponden a los círculos azules (clase 1) y las estrellas rojas (clase 2). Los patrones de entrada para x1 y x2 y las etiquetas de salida y se observan en la tabla 3.
En general, este problema permite la implementación de la función lógica XOR utilizando un MLP, debido a que la distribución de los puntos no permite una clasificación correcta con un solo perceptrón. De forma a priori se conoce que son necesarias dos capas en el MLP y tres neuronas para resolver el problema, dos en la capa oculta y una neurona en la capa de salida.
Conociendo la solución al problema, se procede resolverlo por tres caminos diferentes: el algoritmo tradicional de Back-propagation, weight decay y OBS. Lo anterior permite realizar comparaciones sobre la efectividad en la solución del problema, complejidad del algoritmo y el modelo de red obtenido por cada uno de ellos.
El orden seguido para encontrar las tres soluciones es similar para los tres casos objeto estudio y consiste en: programación del algoritmo, descripción y explicación de los procedimientos, verificación de solución al problema de la XOR y de arquitectura obtenida. Finalmente, se realiza una comparación de los resultados alcanzados con cada uno de lo algoritmos, considerando como métricas de desempeño el error de la aproximación, dificultad de entrenamiento, complejidad y grado de optimización de la arquitectura.
Por simplicidad, los resultados son visualizados en un plano para poder explicar los procedimientos empleados de forma más sencilla. Los algoritmos y algunos de los resultados obtenidos pueden extenderse a problemas de mayor dimensión o con superficies de error más complejas.
4. Resultados
4.1 Solución preliminar
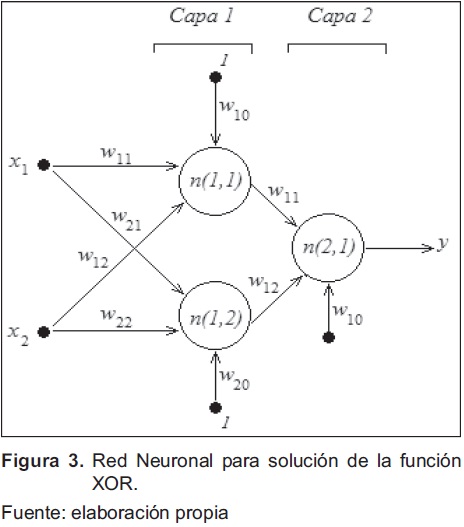
Para resolver el problema propuesto en la anterior sección, se desarrolla el algoritmo de Back-Propagation original [1], [2], [7]. La arquitectura del MLP está compuesta por dos capas; la de salida y una oculta; por ende, para obtener el modelo es necesario estimar seis pesos para las neuronas ocultas y tres para las neuronas de salida, los cuales se presentan en la figura 3. El modelo del MLP implementa la función dada por la ecuación (8), donde W1 corresponde a los pesos de la capa oculta y W2 los pesos de la capa de salida.
Donde:
σ(.): función de actividad sigmoidal.
W2 y W1: matrices de pesos de la capa de salida de la capa de entrada respectivamente.El método de optimización empleado es el de descenso de gradiente con tasa fija pero se resalta que la forma de realizar el algoritmo es a través de funciones, lo que permitiría migrar a otro forma de solución basada en gradiente conjugado, método de newton, Lenverq-Marquard. La actualización de los pesos está dada por la ecuación (9).
Donde:
E: función de error dado por la ecuación (1).
µ: tasa de aprendizaje.
El criterio de convergencia del algoritmo se da a través de dos procedimientos: el primero por número máximo de iteraciones las cuales se fijan en 10000 y el segundo fijando el error máximo entre iteraciones: 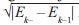 , donde la iteración está dada por k. El error se calcula usando la ecuación (1), con los patrones de entrada emulando el cálculo con un conjunto de validación en un problema con mayor cantidad de datos en donde se realice validación cruzada.
, donde la iteración está dada por k. El error se calcula usando la ecuación (1), con los patrones de entrada emulando el cálculo con un conjunto de validación en un problema con mayor cantidad de datos en donde se realice validación cruzada.
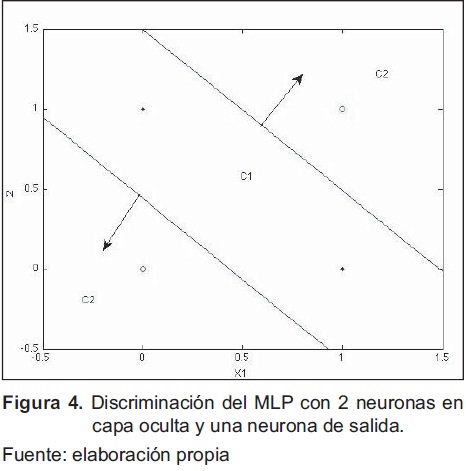
Después de ejecutar y obtener varias soluciones al MLP de manera satisfactoria (depende del valor semilla establecido para los pesos y la manera como se presenten las entradas en el entrenamiento), una solución al problema de clasificación se muestra en la figura 4., en la que se observan los discriminadores lineales dados por las neuronas de la capa oculta en el espacio de entrada x2 vs. x1 para cada una de las clases. Esta solución se obtiene para una tasa de aprendizaje m=0.7, luego de 9943 iteraciones y un error de 0.0114.
Los pesos encontrados por el algoritmo BP desarrollado y ejecutado son:
4.2 Aplicación usando Weight Decay
Es elegido el método de Weight Decay debido a que la derivada de la función R(w) con respecto a los pesos utilizada para la actualización en el algoritmo de BP es de fácil inclusión en la función de error [7], [8].
El método consiste en entrenar un MLP de un tamaño razonable, en el caso de estudio con una cantidad mayor a dos neuronas en la capa oculta, de tal manera que el método intente disminuir la cantidad de conexiones o neuronas de la red. A continuación se muestra el procedimiento seguido:
- Elegir una red "grande" que resuelva el problema.
- Entrenar usando el BP tradicional; este modelo sobre-ajustaría la solución.
- Con la misma red elegida entrenar usando Weight Decay.
- Establecer un criterio que elimine aquellas neuronas no relevantes.
- Obtener el modelo solución final.
El paso (b) puede eliminarse, en el presente documento se realiza para poder efectuar comparaciones efectivas del procedimiento, el cual se muestra para un caso:
-
Un solución sobreajustada al problema de la sección 4.1 estaría dada por cualquier MLP con una cantidad superior a dos neuronas en la capa oculta. Para mostrar el efecto de Weight Decay se elige una red con cuatro neuronas en la capa oculta y una neurona en la capa de salida debido a que tendrían que calcularse 17 pesos, que corresponden a casi el doble del modelo presentado en la sección 4.1.
-
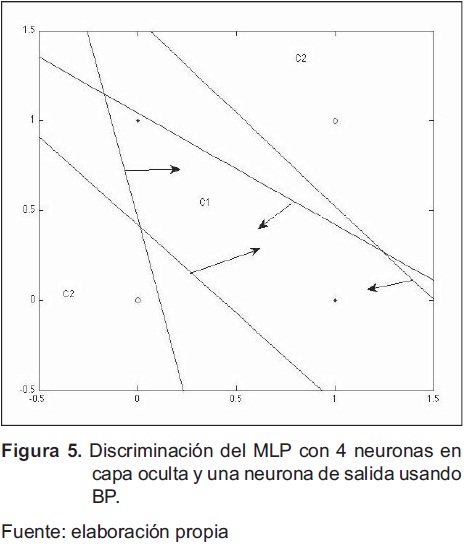
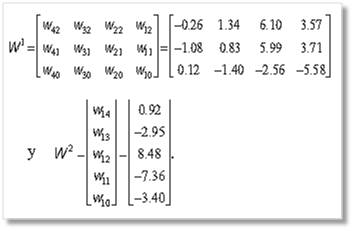
Con el algoritmo BP básico se soluciona el problema de estudio, cuyo resultado gráfico se presenta en la figura 5 y los pesos obtenidos se muestran a continuación:
Al comparar las regiones de clasificación de la figura 4 con la de la figura 5., claramente se ve que con más neuronas la región es más compleja, ya que es el resultado de la intersección de cuatro rectas (perceptrones) que determinan la clase Cl.
-
Con el mismo valor de pesos y tasa de convergencia usado en el numeral b., se entrena la red usando Weight Decay cuya actualización de los pesos por iteración esta dada por la ecuación (10).
-
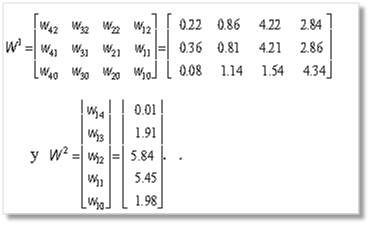
Al observar los pesos resultantes de aplicar Weight Decay, no existen pesos que sean cero, que es lo que se esperaría del algoritmo. Ignorando la contribución de los pesos bias (última fila tanto para W2 como para W1), sí existe una diferencia en la magnitud absoluta entre los pesos asociados a la neurona 1 (columna 1 de W1) y la neurona 2 (columna 2 de W1) con las otras dos neuronas de casi tres o más veces. Por lo tanto, esto indicaría que las neuronas 1 y 2 no contribuyen en gran medida a la región de salida del clasificador y su eliminación puede no incrementar significativamente el error.
-
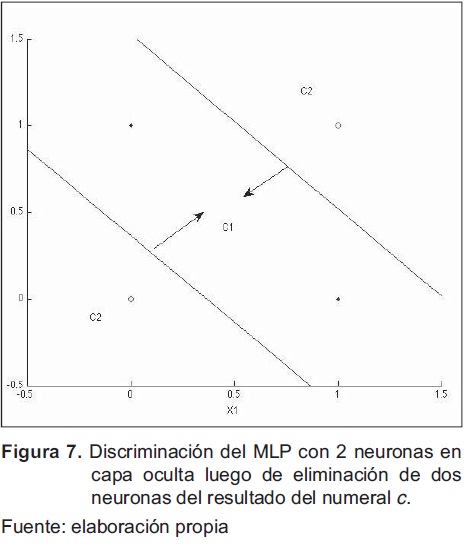
Al eliminar la neurona 1 y dos de acuerdo en las observaciones del numeral d., la región de clasificación se muestra en la figura 7, la cual es similar a la presentada en la figura 4.
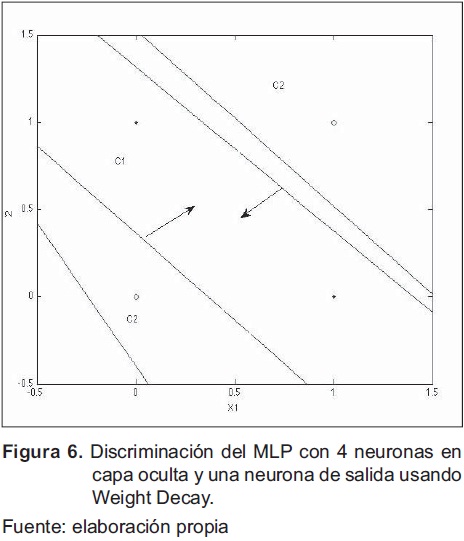
El valor de l se determina heurísticamente mediante múltiples corridas del algoritmo, el valor encontrado fue de 0.0005. Luego de 4401 iteraciones y un error de 0.054, el resultado gráfico de la clasificación se presenta en la figura 6 y los pesos obtenidos se muestran a continuación:
4.3 Aplicación usando OBS
Para mostrar la forma como se aplican y se obtienen los modelos neuronales a través de métodos de pruning, se selecciona el algoritmo OBS, ilustrado en la figura 1, debido a que en las referencias consultadas [11] y [12], estos muestran sus bondades al no tener que realizar múltiples entrenamientos de la red (únicamente es necesario entrenar una vez para obtener una solución inicial) y la eliminación de pesos es más precisa comparada con otros métodos de esta clase, al considerar la segunda y primera derivadas para el cálculo del saliency asociado a los pesos de la red.
El algoritmo OBS se desarrolla de acuerdo a la propuesta mostrada en [11] para solucionar el problema planteado en la sección 3.1, este algoritmo puede extenderse a modelos con mayor cantidad de entradas o neuronas en la capa oculta. El cálculo del error por iteración se realiza con los datos presentados en la tabla 3, emulando un problema en el cual se pueda realizar una validación cruzada y el criterio de convergencia del algoritmo sea el error de validación.
El entrenamiento necesario para OBS se realiza con una red de dos capas; cuatro en la oculta y una neurona en la de salida, razón por la cual se aceptan e integran los resultados obtenidos tanto en la sección 4.1 como en la 4.2.
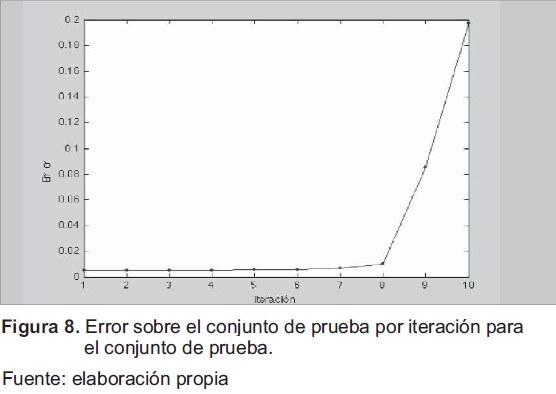
Entrenamiento con BP, la figura 8 muestra el comportamiento del error sobre el conjunto de prueba y el resultado después de eliminar 10 pesos, en ella se observa que durante las primeras ocho iteraciones el error varía levemente. Pero después de eliminar el peso 9 y 10, el error se dispara, por lo cual no resulta conveniente la eliminación de dichos pesos.
De acuerdo a la figura 8, cualquiera de los modelos parciales obtenidos desde la iteración 1 a 8 puede resolver adecuadamente el problema, pero por su simplicidad y menor número de conexiones, el elegido es el modelo resultante de iteración 8. Los pesos asociados a este modelo se muestran a continuación:
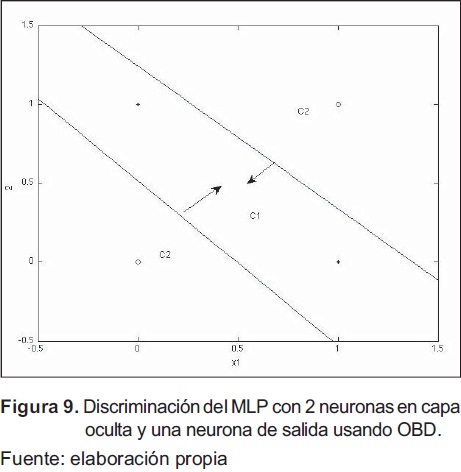
Al observar los valores para los pesos de las capas del MLP (W 2 y W 1) y la clasificación obtenida mostrada en la figura 9, se nota que el resultado es de dos neuronas en la capa oculta, a pesar que la arquitectura inicial era de cuatro neuronas. El error sobre los datos es igual a 0.012 con la eliminación de dos neuronas (8 conexiones).
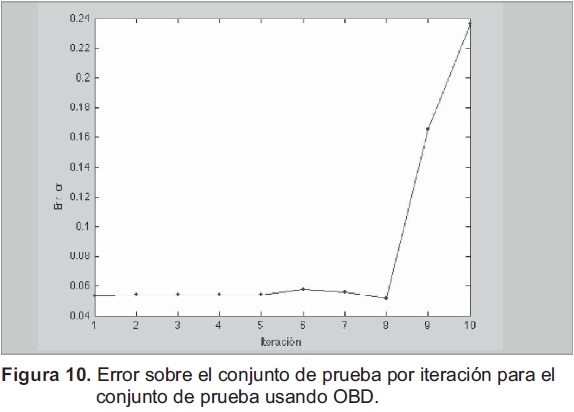
Entrenamiento con Weight Decay, con los resultados del entrenamiento con Weight Decay se aplica el algoritmo OBD cuyos resultados fueron un error de 0.0521, con la eliminación de dos neuronas (8 conexiones), en ocho iteraciones. El comportamiento del error se presenta en la figura 10, en donde se ve hasta la iteración 8 el error permanece constante y es bajo (inferior a 0.06)), luego se incremente notablemente para la iteración 9 y 10.
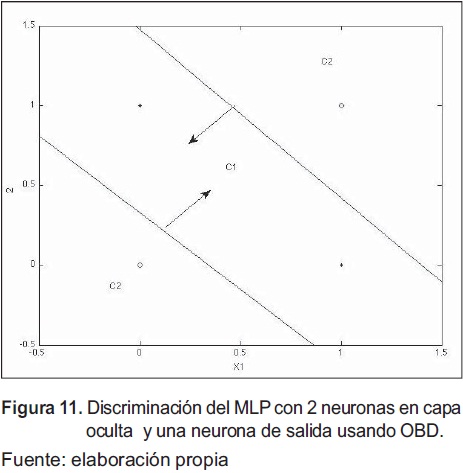
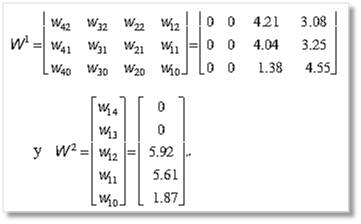
El modelo resultante para cada uno de los pesos se muestra a continuación y en la figura 11, el clasificador.
5. Análisis de resultados
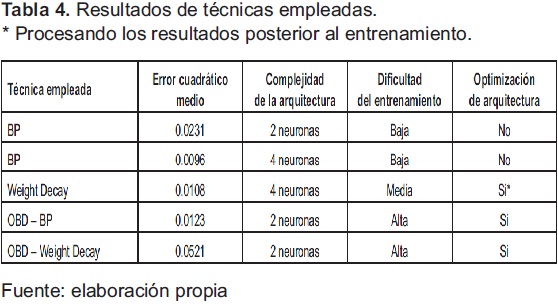
Para realizar una evaluación lo más objetiva posible de los resultados se plantea la tabla 4, en la cual se establecen cuatro criterios a considerar: error cuadrático medio, complejidad del modelo final, optimización de arquitectura y dificultad de entrenamiento.
La dificultad del entrenamiento en los algoritmos que son capaces de optimizar la arquitectura de un MLP es superior en operaciones y tiempo de procesamiento que el algoritmo BP tradicional. Siendo el algoritmo Weight Decay más simple que OBD pero requiere una eliminación de los pesos luego del entrenamiento, lo que supone la inserción de alguna métrica o umbral que permita eliminar conexiones de la red.
Hay que aclarar que, por el problema elegido, no se generaron datos de validación, lo cual hace que los modelos sobreajustados (utilizan cuatro neuronas) posean mejor error cuadrático medio, por lo tanto, no se pueden comparar con los modelos basados en dos neuronas. Pero para lo resultados con los modelos de dos neuronas mostrados en la tabla 4, el mejor error lo posee la técnica de Weight Decay por encima de OBS. A través de ejecuciones múltiples del algoritmo OBD se establece que esta mejora el error cuadrático medio, dependiendo de la calidad del entrenamiento inicial.
6. Conclusiones
Es posible optimizar la arquitectura de una red neuronal basada en perceptrones utilizando técnicas que se clasifican dentro de las redes ontogénicas. Dentro de los métodos estudiados se observa que son efectivos aquellos que modifican el problema de optimización; específicamente la función de error, a través de la inclusión de una función de costo que considera la complejidad del modelo. Mientras que con las técnicas de pruning se modifica la arquitectura de una red compleja a través de una eliminación especializada de pesos. Ambas técnicas mostraron ser efectivas para el problema de la función XOR debido a que pudieron converger a la solución más simple que usa dos neuronas en la capa oculta y una en la neurona de salida.
Debido a que uno de los problemas que posee un diseñador de sistemas bioinspirados, basados en redes neuronales, es que no conoce la arquitectura de la red de forma a priori y generalmente esta elección se realiza de forma heurística, resultan convenientes las redes ontogénicas, ya que estas pueden optimizar la arquitectura, tanto para problemas complejos como simples, intentando mejorar la capacidad de generalización del modelo.
OBD posee la dificultad de ser un algoritmo lento ante problemas con dimensiones altas, ya que se debe calcular la matriz Hessiana que con lleva a múltiples operaciones, siendo el tamaño de la Hessiana directamente proporcional a los pesos del modelo. El algoritmo propuesto por Hassibi posee la particularidad que calcula online la inversa de la matriz Hessiana, lo que agiliza el tiempo por iteración del algoritmo.
Las técnicas estudiadas, Weigh Decay y OBD, resultan difíciles de implementar en hardware por sus tasas de procesamiento y operaciones. Weight Decay resuelve un problema de optimización usando descenso de gradiente, lo que sería lento a nivel hardware mientras OBD requiere operaciones matriciales de gran complejidad en redes de tamaño considerable.
Como trabajo futuro puede establecerse un set de pruebas para las estructuras de redes ontogénicas presentadas en la tabla 1, con el ánimo de brindar las características principales de cada una de ellas en problemas prácticos.
7. Financiamiento
Este trabajo se desarrolla como parte del proyecto "Evaluación de arquitecturas neuronales para implementación hardware" de la Universidad Distrital Francisco José de Caldas.
Referencias
[1] C.M. Bishop, Neural Networks for Pattern Recognition, Oxford: Oxford University Press, 1995. [ Links ]
[2] S. Haykin, Neural Networks: A Comprehensive Foundation, Prentice Hall, 1998. [ Links ]
[3] M. Gupta, L. Jin, and N. Homma, "Static and Dynamic Neural Networks", in John Wiley & Sons, Inc, Hoboken, New Jersey, 2003. [ Links ]
[4] M. Sipper, E. Sánchez, D. Mange, M. Tomassini, Andrés Pérez-Uribe, and Andre Stauffer:, "A Phylogenetic, Ontogenetic, and Epigenetic View of Bio-Inspired Hardware Systems", IEEE Transactions On Evolutionary Computation, Vol, No. 1, 1997. [ Links ]
[5] E. Fiesler, "Comparative bibliography of ontogenic neural networks", in Proceedings of the Internacional Conference on Artificial Neural Networks, 1994. [ Links ]
[6] Y. Jin, T. Okabe and B. Sendhoff, "Neural Network Regularization and Ensembling Using Multi-objective Evolutionary Algorithms", in Proceedings of 2004 Congress Evolutionary Computation, 2004. [ Links ]
[7] Y. Li, Y. Fu, H. Li and S.W. Zhang, "The improved training algorithm of back propagation neural network with self adaptive Learning Rate", in Proceedings 2009 International Conference on Computational Intelligence and Natural Computing, 2009. [ Links ]
[8] S. Xu, L. Chen, "A novel approach for determining the optimal number of hidden layer neurons for FNN's and its Application in Data Mining", in Proceedings 5th. International Conference on Information Tecnhology and Applications, 2008. [ Links ]
[9] H. Wang, F Ji, G. Wei, C. Leung, and P Sum, "Regularization Parameter Selection for Faulty Neural Networks", in International Journal of Intelligent Systems and Technologies, 2009. [ Links ]
[10] J. Larsen, L.K. Hansen, C. Svarer and M. Ohlsson, "Design And Regularization Of Neural Networks: The Optimal Use Of A Validation Set", in VI. Proceedings of the 1996 IEEE Signal Processing Society Workshop, 1996. [ Links ]
[11] B Hassibi and D G. Stork, "Second Order Derivatives for Network Pruning: Optimal Brain Surgeon," in S J Hanson et al. (Eds.), Proceedings of the 1992 Conference Advances in Neural Information Processing Systems, Morgan Kaufmann Publishers, 1993. [ Links ]
[12] E. Karnin, "A simple procedure for pruning back-propagation trained neural networks", Transactions on Neural Networks, 1990. [ Links ]
[13] Y. Goh and E. Tan, "Pruning neural networks during training by backpropagation", in Proceedings of IEEE Region 10's Ninth Annual International Conference, 1994. [ Links ]
[14] G. Corani, "Air quality prediction in Milan: feed-forward neural networks, pruned neural networks and lazy learning", Ecológical Modellin, pp. 513-529, 2005. [ Links ]