Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Tecnura
versão impressa ISSN 0123-921X
Tecnura vol.17 no.37 Bogotá jul./set. 2013
Caracterización de flujos de datos usando algoritmos de agrupamiento
Characterizing data stream using clustering algorithms
Fabián Andrés Giraldo1, Elizabeth León2, Jonatan Gómez3
1Ingeniero de Sistemas. Estudiante de Maestría en Ingeniería de Sistemas y Computación de la Universidad Nacional de Colombia. Bogotá, Colombia. Contacto: fagiraldo@unal.edu.co.
2Ingeniero de Sistemas, Doctor en Computer Science. Docente de la Universidad Nacional de Colombia. Bogotá, Colombia. Contacto: eleonguz@unal.edu.co.
3Ingeniero de Sistemas, Doctor en Matemáticas con énfasis en Computer Science. Docente de la Universidad Nacional de Colombia. Bogotá, Colombia. Contacto: jgomezpe@unal.edu.co.
Fecha de recepción: 30 de mayo de 2012 Fecha de aceptación: 12 de febrero de 2013
Resumen
El artículo tiene como objetivo presentar una introducción al proceso de minería de flujos de datos usando técnicas de agrupamiento, observando las limitaciones de las técnicas tradicionales y explicando las diferentes aproximaciones existentes en la literatura.
Las principales tendencias en los diferentes algoritmos indican que la mayoría de ellos separan el proceso en dos fases: una fase online en la cual se realiza una sumarización de los datos del flujo adicional a la aplicación de funciones de decadencia para olvidar datos, y una fase ffiine, en la cual se ve la aplicación de técnicas de agrupamiento tradicionales para la obtención de los clúster solicitados por los usuarios. El resultado final del artículo es la selección de las características deseables de un algoritmo, basado en los sustentos teóricos de cada uno de los trabajos expuestos.
Palabras clave: agrupamiento, flujos de datos, minería de datos.
Abstract
This paper presents introductory materials to datastream mining processes using clustering techniques. The limitations of traditional techniques are observed and the various approaches found in the literature are explained. The major trends in the different algorithms indicate that most applications separate the process into two phases; namely an online phase, which makes a data stream summarization in addition to the application of decay functions regardless of the data, and an offine phase, which is the application of traditional clustering techniques in order to obtain the cluster requested by users.
The net result of this paper is a selection of desirable characteristics of an algorithm, based on the theoretical underpinnings of each of the works analyzed.
Key words: clustering methods, data stream, data mining.1. Introducción
El rápido desarrollo de las tecnologías de información (TI) ha influenciado cambios fundamentales en muchos procesos de la ciencia y la industria. Los sistemas para capturar, almacenar y gestionar datos han evolucionado de sistemas de procesamiento de archivos primitivos a sofisticados y poderosos sistemas de bases de datos. La enorme cantidad de datos ha excedido la capacidad humana de comprensión y, por tanto, se ha hecho necesario tener técnicas avanzadas para analizar, comprender y explorar dichos datos.
Con el fin de analizar los datos y descubrir conocimiento sobre ellos, la minería de datos emerge como un campo de investigación interdisciplinario de áreas como bases de datos, inteligencia artificial, aprendizaje de máquina, estadística, entre otros. Muchos algoritmos de minería de datos han sido planteados en la literatura; sin embargo, el agrupamiento (clústering) ha recibido mucha atención dado que puede ser utilizado en numerosas aplicaciones tales como segmentación de clientes, marketing, etc.
El agrupamiento es una técnica de aprendizaje no supervisada que a partir de un conjunto de n datos no etiquetados trata de clasificarlos en uno o más grupos de objetos similares, donde la similitud entre los objetos es frecuentemente definida utilizando alguna medida de distancia (euclidiana, coseno, Manhattan, etc.) o función objetivo. En términos generales, el algoritmo trata de maximizar la similitud inter-clúster (los objetos asignados al mismo clúster son altamente similares) y minimizar la similitud intra-clúster (objetos en diferentes clúster tienen baja similitud entre ellos) [1]. Diferentes métodos han sido considerados para realizar procesos de agrupación, entre ellos se encuentranlos métodos particionales, los cuales dividen un conjunto de datos en "k" subconjuntos no superpuestos. Entre los principales algoritmos se pueden mencionar: k-means [2], k-medoids [3], entre otros.
Los principales problemas de los algoritmos anteriores radican enque se debe conocer con anterioridad el valor de k y adicionalmente presentan inconvenientes en la identificación de grupos con formas irregulares y son sensibles al ruido. Para solucionar lo anterior, aparecen algoritmos basados en densidad que tratan de buscar regiones cuya densidad supera cierto umbral para conformar grupos candidatos. Ejemplo de ello son algoritmos como DBSCAN [4], OPTICS [5], HOP [6],DENCLUE [7], etc.
Otros métodos comúnmente considerados son los jerárquicos, los cuales a su vez se pueden dividir en: los aglomerativos (de abajo hacia arriba), en los cuales se empieza con cada punto del conjunto de datos formando un clúster y en cada paso se unen los puntos más cercanos basados en un medida de proximidad (MIN, MAX, GroupAverage), y los divisivos (de arriba hacia abajo), en los cuales se comienza con un único clúster y en cada paso, el algoritmo lo divide hasta llegar a clúster de puntos individuales. Entre los algoritmos jerárquicos representativos están BIRCH [8], CURE [9] y CHAMELEON [10].
Otros métodos propuestos son basados en procesos bioinspirados y físicos. Entre los basados en procesos bioinspirados se pueden considerarlas bandadas de pájaros en las cuales agentes individuales (pájaros) a partir de reglas de interacción local (alineamiento, separación, cohesión, similitud) generan comportamientos emergentes (clúster) [11], [12], [13].
Nasraoui et ál, proponen UNC (Unsupervised Niche Clustering), el cual es una aproximación al problema de agrupamiento usando una técnica conocida como nicho genético (Genetic Niching), la cual es robusta al ruido y tiene la capacidad de determinar el número de clúster automáticamente [14]. Basado en UNC, León et ál presentan un nuevo algoritmo de agrupamiento usando algoritmos genéticos que tienen la capacidad de realizar procesos de autoadaptación de los operadores genéticos, elemento que en UNC es estático y debe ser configurado dependiendo de la características del conjunto de datos, elemento que en muchos casos puede ser tedioso. Dicho algoritmo es denominado ECSAGO (Evolutionary Clustering with Self Adaptive Gene-tic Operators) [15].
En los métodos inspirados en procesos físicos se encuentra la técnica de agrupación basada en teoría gravitacional. Dicha técnica es utilizada para realizar procesos de agrupamiento simulando un sistema de gravitación universal, considerando cada dato como una partícula expuesta a campos gravitatorios. Una unidad de masa es asociada a cada punto y los puntos son movidos hacia el centro del clúster debido a los campos gravitacionales [16], [17], [18].
Posteriormente, con el fin de trabajar con grandes volúmenes de datos, Gómez et ál. Presentan una versión incremental del algoritmo de agrupamiento basado en la ley de gravitación. El funcionamiento es similar al anterior, sin embargo cuando finaliza la simulación, un conjunto de prototipos es generado. Cada prototipo tiene asociada una unidad de masa que es proporcional al número de partículas en cada sub-clúster y será usada como partículas adicionales cuando nuevos datos arriben para ser agrupados [19].
Es importante mencionar que todos los métodos anteriormente descritos usan conjuntos de datos que son considerados estáticos y completos, es decir, el conjunto de datos de entrenamiento está disponible para el algoritmo. Esta suposición permite que los algoritmos puedan realizar accesos aleatorios sobre los datos y procesar los objetos múltiples veces durante la ejecución.
Hoy en día muchas aplicaciones producen grandes volúmenes de información en intervalos de tiempo muy corto (flujos de datos), ejemplo de ellos son: datos de sensores, web clickStream, flujo de transacciones de tarjetas de crédito, log de eventos en redes, mercado de valores, etc.
Lo anterior causa limitantes en la capacidad de almacenamiento y tiempo de procesamiento. A pesar de estas características, la necesidad de caracterizar los datos sigue vigente,se requieren algoritmos de aprendizaje que actúen en entornos dinámicos donde los datos se recojan a través del tiempo.
Dada la naturaleza de un flujo de datos, las siguientes restricciones y exigencias emergen: la cantidad de datos debe ser considerada infinita, el tiempo para procesar un solo objeto es limitado, la memoria es limitada, existe evolución en la distribución de los datos, existen datos que son ruido, existen cambios en la tasa de entrada de datos [20].
Adicional a los requerimientos de flujos de datos, también aparecen requerimientos para los procesos de agrupamiento, entre los cuales se pueden mencionar: no existen supuestos válidos del número de clúster, se deben descubrir clúster con formas arbitrarias, se debe realizar un proceso de gestión de datos atípicos. En definitiva, se requieren funcionalidades adicionales para identificar y explorar grupos en diferentes porciones del flujo [21].
El presente artículo tiene como objetivo mostrar las diferentes aproximaciones que existen en la literatura para realizar procesos de caracterización de flujos de datos basados en técnicas de agrupación y adicionalmente, indicar las características deseables que deben tener nuevos algoritmos basados en los sustentos teóricos de cada una de las propuestas planteadas.
El artículo está organizado de la siguiente forma: en la sección 2 se presenta una definición de flujo de datos y las diferentes técnicas que pueden ser aplicadas. En la sección 3 se muestran los diferentes algoritmos existentes para minar flujos de datos usando algoritmos de agrupamiento. Las características deseables de un algoritmo de caracterización de flujo de datos basado en los sustentos teóricos de algoritmos existentes se exponen en la sección 4. Por último, se presentan las conclusiones.
2. Flujo De Datos
Un flujo de datos consiste en una secuencia continua de datos 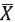 1 ...
1 ...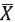 k... Potencialmente infinitos llegando en instantes de tiempo T1,..,Tk … Donde cada punto
k... Potencialmente infinitos llegando en instantes de tiempo T1,..,Tk … Donde cada punto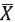 i de la secuencia es un registro multidimensional que contiene d dimensiones, denotado por
i de la secuencia es un registro multidimensional que contiene d dimensiones, denotado por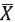 i= ( xi1,...,xid). Diversas técnicas para caracterizar flujos de datos se han aplicado, entre ellas se encuentra: modelos de clasificación, reglas de asociación, agrupamiento, entre otras[22].
i= ( xi1,...,xid). Diversas técnicas para caracterizar flujos de datos se han aplicado, entre ellas se encuentra: modelos de clasificación, reglas de asociación, agrupamiento, entre otras[22].
Para los modelos de clasificación se puede encontrar el algoritmo VFDT (Very Fast Decision Trees) el cual es una implementación de la técnica Hoeffding Tree. VFDT es un algoritmo incremental de inducción de árboles de decisión propuesto por Domingos et ál., que tiene la capacidad de aprender sobre flujos masivos de datos [23]. En el caso de minado de ítems frecuentes se encuentra CPS-tree (Compact Pattern Streamtree) que permite descubrir patrones frecuentes recientes sobre flujos de datos de alta velocidad [24].
Dado que el interés principal del presente artículo es la caracterización de flujos de datos usando técnicas de agrupamiento, a continuación se presentan las diversas aproximaciones existentes en la literatura.
3. Agrupamiento de flujos de Datos
Sea U={1,…,n}el universo de objetos a ser clusterizados, sea Ut=  U el conjunto de todos los objetos presentes en el instante de tiempo t y sea U≤j = el conjunto de todos los objetos presentes Uj'≤j Ut' hasta el instante t incluyendo el flujo de datos que arriban en t. El algoritmo de agrupamiento debe en cada instante de tiempo t producir una agrupación Ct de U≤j. Es importante indicar que Ct podría incluir objetos que han sido obtenidos en el pasado que no son parte del flujo actual. La calidad de Ct se determina basado en qué tan bien representa los datos presentes en el instante : ≤t [25].
U el conjunto de todos los objetos presentes en el instante de tiempo t y sea U≤j = el conjunto de todos los objetos presentes Uj'≤j Ut' hasta el instante t incluyendo el flujo de datos que arriban en t. El algoritmo de agrupamiento debe en cada instante de tiempo t producir una agrupación Ct de U≤j. Es importante indicar que Ct podría incluir objetos que han sido obtenidos en el pasado que no son parte del flujo actual. La calidad de Ct se determina basado en qué tan bien representa los datos presentes en el instante : ≤t [25].
Existen diversos algoritmos en la literatura que han sido utilizados para realizar procesos de agrupamiento, tales como los algoritmos clásicos, los cuales pueden ser clasificados en varios tipos como: algoritmos particionales, algoritmos basados en densidad, algoritmos basados en grillas, algoritmos basados en modelos, algoritmosbioinspirados, entre otros. A continuación se presentan los trabajos más relevantes en cada uno de ellos.
3.1 Algoritmos particionales
Guha et ál. desarrollan STREAM, el cual es un algoritmo que asume que los datos arriban en trozos X1,…,Xn, donde cada trozo Xi es un conjunto de puntos que pueden ser cargados en memoria principal. El algoritmo funciona de la siguiente manera: se realiza el proceso de agrupamiento al ith trozo Xi usando LSEARCH [26] y se asignaa cada mediana (centro) resultante un peso igual a la suma de los pesos de los miembros de Xi. Posteriormente se depura la memoria solo dejando los k centros ponderados. Si posteriormente se aplica LSEARCH a los pesos ponderados X1,…,Xi de cada uno de los trozos, se obtiene un conjunto de centros (ponderados) para el flujo completo.
Posteriormente, Babcock et ál. expanden STREAM a ventanas deslizantes resolviendo el problema para los N puntos más recientes del flujo [29].
A partir del trabajo anterior, Ackermann et ál. desarrollan StreamKM++, el cual es un algoritmo que busca obtener un subconjunto de puntos (coreSet) que representen el conjunto de datos original [30]. A partir de este coreSet, posteriormente es ejecutado el algoritmo k-mean++ para obtener los k grupos especificados por el usuario [31].
Para la obtención de los coreSet hacen uso de una estructura de datos denominada coreSetTree. Un coreSetTree T para un conjunto de puntos P es un árbol binario que es asociado con un clúster jerárquico divisivo para P. Se empieza con un único clúster que contiene el conjunto de puntos de P y sucesivamente se particionan clúster existentes en dos sub-clúster de tal manera que los puntos en los subgrupos estén lo más distante posible. El proceso de división es repetido hasta que el número de clúster corresponde al número deseado.
Aggarwal et ál. retoman las ideas de BIRCH, específicamente extienden el concepto de CF (Cluster Feature) y proponen el algoritmo CluStream para caracterizar flujos de datos. Este algoritmo separa el proceso de agrupamiento en dos componentes: online o micro-clúster (proceso eficiente para almacenar estadísticas de resumen apropiadas para un flujo de dato) y el componente ffiine o macro-clúster (usar las estadísticas resumen junto con otros parámetros especificados por el usuario -horizonte de tiempo-con el fin de proporcionar al usuario una rápida compresión de los grupos siempre que sea necesario).
El funcionamiento del algoritmo es sencillo: en la fase de inicialización se crean q micro-clúster iniciales usando un proceso ffiine al inicio, por tanto se deben almacenar los primeros InitN puntos en el discoy aplicar el algoritmo K-means para crear q cluster. En resumen, el componente online mantiene información resumen en una estructura CF basado en una ventana de tiempo piramidal y el componente ffiine analiza los flujos de datos sobre diferentes horizontes de tiempo usando la información resumen que es mantenida por el componente online [32].
Aggarwal et ál., proponen HPStream, el cual es un algoritmo cuyo esquema general de funcionamiento es similar al propuesto en el algoritmo CluStream; sin embargo, se tienen en cuenta los siguientes elementos: al inicio del proceso de agrupamiento de un flujo de datos se ejecuta un proceso de normalización con el fin de sopesar las diferentes dimensiones correctamente. El objetivo es equiparar la desviación estándar a lo largo de cada dimensión.
Otro de los elementos que varían con respecto a CluStream es que cuando se seleccionan los grupos iniciales usando K-mean, almacenan para cada clúster dos elementos adicionales: el peso del grupo, que está determinado por una función de decadencia, que es actualizada cada vez que se adicionan nuevos elementos al grupo (dicho parámetro es utilizado en el momento de eliminar grupos existentes dada la conformación de uno nuevo). El otro elemento que le adicionan a los grupos es que determinan los atributos que son representativos para realizar el cálculo de la distancia, entre los nuevos puntos y el centroide. Es decir, para cada grupo, solo las dimensiones que son relevantes son utilizadas en el cálculo de la distancia. Es importante indicar que los parámetros utilizados para realizar el proceso de normalización y las dimensiones que son relevantes para las medidas de distancia son actualizados cada ciertos periodos [33].
Zhou presenta SWClustering, el cual hace una extensión de CluStream para trabajar sobre ventanas deslizantes. Para tal fin introduce una estructura de datos denominada Exponential Histogram of Cluster Features (EHCF), la cual está conformada por el CF de cluStream y una estructura denominada histograma exponencial, la cual permite almacenar información de los datos más recientes [34].
Adicionalmente, en la fase ffiine hace uso de un algoritmo K-mean con peso, con el fin de obtener los grupos finales solicitados por el usuario. Un importante elemento a mencionar es que dicho algoritmo tiene buenos resultados cuando el flujo de datos está conformado por grupos esféricos.
Basados en los trabajos de CluStream, Zhu et ál. Proponen ACluStream, el cual resuelve parcialmente el problema de Clustream para trabajar con grupos de formas arbitrarias. Para tal fin introduce el concepto de agrupación de bloques basados en esquemas de densidad absoluta. Los resultados indican que mejoran el rendimiento con respecto a CluStream [35].
Los algoritmos anteriormente descritos son técnicas particionales que principalmente usan el algoritmo K-mean, el cual tiene ciertas limitaciones para descubrir grupos con formas arbitrarias y hacer frente a la natural dinámica de los datos. En general funcionan bien solo cuando son aplicados a flujos de datos esféricos.
Por tanto, nuevos algoritmos basados en densidad han sido propuestos en la literatura, los cuales tienen una serie de ventajas, a saber: pueden identificar grupos de formas arbitrarias y tienen la capacidad de lidiar con ruido.
3.2 Algoritmos basados en densidad
DenStream es un algoritmo basado en densidad propuesto por Cao et ál. Dicho algoritmo considera el problema de agrupamiento de un flujo de datos como un modelo de ventanas amortiguadas, en el cual el peso de cada punto decrece exponencialmente con el tiempo t vía una función de decadencia. La función de decadencia exponencial es ampliamente usada en aplicaciones dependientes del tiempo donde es deseable descontar gradualmente la historia del comportamiento pasado. Utiliza tres conceptos importantes como base para su funcionamiento: core-micro-clúster, potencial c-micro-clúster y outliers-micro-clúster, entre los cuales la diferencia radica en el peso que tiene en cuenta una función de decadencia y el radio de los microclúster. El funcionamiento del algoritmo de agrupamiento puede ser dividido en dos partes: una parte online de mantenimiento de micro-clúster, y una parte ffiine para generar los clúster finales, basados en la petición de los usuarios.
Para el mantenimiento de micro-cluster, en orden para descubrir los clúster en flujos de datos que evolucionan en el tiempo, DenStream mantiene un grupo de p-micro-cluster y o-micro-cluster de una forma online. En el proceso de inicialización se toman initN puntos y una variación del algoritmo basado en densidad DBSCAN es aplicado para detectar p-microclúster u o-microclúster basado en el peso y el radio. Cada p-microclúster se considera como un punto virtual situado en el centro con peso w. En la fase de actualización, cuando un nuevo punto llega en busca del p-micro-cluster cuya distancia sea menor que un umbral especificado, en caso de encontrarlo es absorbido y las estadísticas calculadas. En caso contrario, se busca en los omicroclúster y en caso de ser absorbidos se verifica que pueden convertirse en p-microclúster. Cuando los p-microclúster no absorben nuevos puntos, la función de decadencia va haciendo que se convierta en o-micro-cluster y en un momento determinado podrían llegar a desaparecer.
En el componente ffiine, cuando un requerimiento de agrupación se especifica, DBSCAN es usado para generar los grupos finales teniendo en cuenta los pmicro-clúster existentes en memoria principal [36].
El principal problema de este algoritmo es que cuando llega un nuevo punto se debe buscar la distancia mínima con todos los p-micro-clúster y en muchos casos con los o-micro-clúster, siendo esto altamente costoso en tiempo de ejecución.
Ren et ál., proponen SDStream, el cual es una extensión de SWClustering para identificar grupos con formas irregulares. SDStreames un método para descubrir grupos de formas arbitrarias enflujos de datos basados en ventanas deslizantes (realizar análisis sobre los datos más recientes). El funcionamiento de SDStream es similar a DenStream, sin embargo, tiene en consideración las siguientes modificaciones: los p-micro-clúster y o-micro-clúster son almacenados en memoria principal en una estructura denominada Exponential Histogram of Cluster Feature (EHCF), la cual es usada para trabajar el problema de flujos de datos basado en densidades bajo el esquema de ventanas deslizantes. Dicha estructura está conformada por un Temporal Cluster Feature (TCF), estructura similar a los CF utilizados en CluStream que además es mantenida incrementalmente a medida que nuevos puntos arriban [37].
Una variación de los algoritmos basados en densidades es el agrupamiento basado en grid. Es un método eficiente para conjuntos de datos de alta dimensionalidad y no está limitado a las restricciones esféricas de otros algoritmos. El funcionamiento básico se puede resumir en: divide cada atributo en intervalos de igual distancia, basado en dichas divisiones se particiona el espacio d-dimensional en grillas de igual tamaño, donde el centroide de la grilla actúa como representante de cada una de ellas. El proceso de ejecución del algoritmo consiste en asignar puntos a cada grilla dada una función de mapeo, al final del proceso a cada grilla se le asigna un peso de acuerdo al número de puntos que caen en ellas y se unen grillas densas para conformar los respectivos grupos.
3.3 Algoritmos basados en densidad
DStream es un algoritmo basado en grillas que retoma las ideas de DenStream, es decir, usa un componente online y un componente ffiine. En el componente online mapea los puntos de entrada a una grilla conformada por celdas. Cada celda de la grilla tiene asociada una medida de densidad que es igual a la suma de puntos mapeados a la celda. Adicionalmente, las densidades de las celdas constantemente están siendo amortiguadas con el tiempo de forma exponencial con un factor de decaimiento de entrada [38].
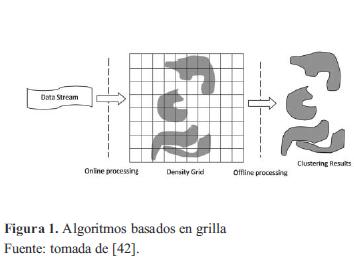
El componente ffiine une las celdas densas vecinas en grupos usando algoritmo de agrupamiento general basado en grillas, tales como: STING [39], WaveCluster [40] y CLIQUE [41]. Las celdas densas son diferenciadas de las dispersas mediante una función umbral de densidad que depende de un parámetro de entrada estático definido, el factor de decaimiento y el número total de celdas en la grilla. Un ejemplo puede ser visualizado en la figura 1.
El algoritmo DStream puede ser descrito de la siguiente forma: el componente online lee nuevos datos, mapea cada entrada en una malla de densidades y actualiza el vector de características, el cual registra información resumen de la grilla. Con el fin de eliminar Outlier, DStream periódicamente detecta celdas que representa outlier basadas en la función de decadencia.
Wan et ál. Proponen el algoritmo MRStream cuyo funcionamiento es equivalente a DStream, variando la fase ffiine, lo que permite producir grupos de diferentes resoluciones [42].
Uno de los principales problemas en los algoritmos basados en grillas es la elección de parámetros, como lo indica Magdy et ál., lo que causa que muchos puntos sean considerados ruido o que algunas regiones sean consideradas no densas. Adicionalmente, en los experimentos que se presentan no se tiene en cuenta la sensibilidad de los parámetros en el análisis de los resultados. Para resolver dichos inconvenientes se propone MDStream, en dicho algoritmo se tienen en cuenta medidas como Neighborhood Range y Relative Density Relatedness Measures, elementos que generalmente en los algoritmos tradicionales son fijos [43].
Tu et ál., realizan una mejora de DStream, para tal caso introducen el concepto atracción de celdas del grid, lo cual muestra en qué medida una celda vecina se acerca más a otra. El procedimiento de Clúster es igual que DStream, la única diferencia es que antes de unir dos celdas de un grid chequean la atracción entre ellas. Si la atracción es más alta que un umbral, luego las celdas están altamente correlacionadas y por tanto pueden ser unidas [44].
Luo et ál, proponen un algoritmo de agrupamiento basado en grid y PSO (Particle Swarmoptimization), el algoritmo se basa en la estructura de dos capas de CluStream. El funcionamiento de algoritmo es similar a DStream, sin embargo en el componente ffiine se usa PSO para obtener más precisión en la conformación de los grupos [45].
Hongyan et ál, proponen una mejora a DStream usando técnicas de computación de DNA para agrupar datos en el componente ffiine [46]. Ren et ál. Proponen un algoritmo de agrupamiento sobre flujo de datos basado en grillas para datos de altas dimensiones, denominado PKStream. Los algoritmos de grillas existentes no pueden manejar grandes dimensiones eficientemente, dada la cantidad de memoria de la grilla a gestionar. PKStream es un algoritmo basado en grillas y Pks-Tree permite un almacenamiento e indexamiento de las celdas en la grilla de forma eficiente. Cuando hay muchas dimensiones en los algoritmos tradicionales basados en grillas existen muchas celdas vacías, dado que se almacenan todas las celdas, y existe un alto consumo de memoria. Si solo se guardaran las celdas no vacías el algoritmo perdería la relación entre ellas.
A diferencia de DStream, PKStream en la fase online, mapea los datos a la estructura Pks-Tree en todos los niveles y en la fase ffiine ejecuta un algoritmo para obtener los grupos finales recorriendo la estructura Pks-tree. Celdas que no reciban datos periódicamente son eliminadas [47].
Otros algoritmos que conservan el principio de funcionamiento de PkStreamhan sido propuestos. Sun et ál. Proponen un algoritmo similar a PkStreamque en vez de usar Pks-tree, usa una estructura denominada CDS-Tree, con el fin de almacenar solo las celdas no vacías de las grillas. Un elemento interesante es que usan una medida para el sesgo de los datos denominada DSF (Data Skew Factor), la cual es usada para ajustar automáticamente la granularidad de las particiones de la grilla de acuerdo al cambio de los datos [48].
Lininget ál. Proponen GHStream, el cual, como PkStream, usa en el componente online una estructura de datos denominada HDG-Tree, con el fin de gestionar eficientemente la memoria [49].
La velocidad de procesamiento de los algoritmos basados en grid está altamente correlacionada con el número celdas de la grilla, el cual es determinado por el número de intervalos en que se dividen los atributos.
De los algoritmos anteriores se puede deducir que la estrategia de partición es crucial para los métodos basados en grid. Un método tradicional basado en clúster puede ser visto con una cuantificación uniforme de cada dimensión, lo cual causa que se ignore el hecho de que cada punto puede ser distribuido diferente en cada dimensión, así que la cuantificación de resultados no es satisfactoria cuando aplica a flujos dinámicos de alta dimensión.
Adicionalmente, la función de mapeo tiene en cuenta el centroide de cada celda para hacer la asignación. Con base en lo anterior,Wang et ál. Proponen CluRDP, algoritmo en el cual el flujo de datos es representado por puntos representativos [50]. Primero se hace una cuantificación en cada dimensión separadamente para obtener un conjunto de puntos representativos de cada dimensión y usar esos puntos representativos de cada dimensión para representar puntos en el flujo de datos. Los puntos representativos de cada dimensión son actualizados continuamente. Basado en las estadísticas almacenadas en los puntos representativos para cada dimensión, se introduce un método para descartar datos históricos a nivel de atributo. Adicionalmente, a diferencia de los anteriores métodos no se usa el centro de la grilla para realizar la asignación de los puntos; en este caso, dado que en el método se pueden cuantificar los puntos en cada dimensión, se utiliza la generalización de los puntos representativos de cada dimensión para sustituir los puntos centrales en cada intervalo en cada dimensión. Esto asegura una mejor calidad en la asignación.
Otro de los métodos que ha recibido atención es el denominado clúster basado en modelos, el cual permite dividir un conjunto de observaciones multivariadas en grupos/clases para maximizar una función de verosimilitud.
3.4 Algoritmos basados en modelos
Laiet ál. Presentan SVStream, un algoritmo para agrupación de flujos de datos basado en vectores de soporte para agrupamiento (SVC)[51]. En el algoritmo propuesto, los datos del flujo son mapeados a otro espacio vía una función kernel (gaussiano), los vectores de soporte son usados como información resumen de los elementos históricos para construir los límites de los grupos con formas arbitrarias.
Comparado con el algoritmo original de agrupamiento basado en vectores de soporte, uno de los mayores cambios para la extensión de los SVC a flujos de datos fue hacer el mantenimiento de los vectores de soporte para que se adapten a cambios graduales y drásticos en el flujo de datos. Para tal fin, proponen una representación multiesfera, donde múltiples esferas son mantenidas dinámicamente en un conjunto de esferas. Cada esfera describe los respectivos datos del flujo. Cuando un nuevo punto ingresa al flujo, si un cambio grande ocurre, una nueva esfera es creada, solo las esferas existentes son actualizadas teniendo en cuenta los nuevos elementos entrantes. Los datos de los nuevos flujos son asignados a un clúster de acuerdo a los límites construidos por el conjunto de esferas. Es importante indicar que se trata de una transformación no-lineal del espacio de entrada en un espacio de características gaussiano vía una función kernel [52].
3.5 Algoritmos bioinspirados
Forestiero et ál. Proponen FlockStream, el cual es una extensión del algoritmo basado en boid especificado en un apartado anterior. FlockStream es un método de agrupamiento de flujos de datos basado en densidad que emplea un sistema multiagente usando un esquema descentralizado bottom-up con una estrategia de autoorganización fundamentada en grupos similares. Cada punto es asociado con un agente, los agentes son desplegados en un espacio 2D, llamado espacio virtual, y trabajan simultáneamente aplicando una estrategia heurística basada en un modelo bioinspirado conocido como modelo de enjambres. Los agentes se mueven en un espacio por un tiempo fijado y cuando encuentran otros agentes en un radio de visibilidad predefinido pueden decidir si forman un enjambre (Micro-cluster), si ellos son similares. Sin embargo, la participación de un agente en un grupo no es definitiva, ya que si durante la exploración del espacio un agente más similar es encontrado, el enjambre actual puede ser borrado (deshecho) y el agente puede unirse al enjambre de losagentes más cercanos. Es importante indicar que el movimiento de los agentes en el espacio 2D no es aleatorio, está guiado por una función de similitud que agrega a los agentes a los vecinos más próximos [53].
FlockStream introduce dos novedades principales: en primer lugar, sustituye la búsqueda exhaustiva del vecino más cercano a un punto, necesario para asignar el punto a un adecuado microclúster, por un método de búsqueda local estocástico que trabaja en paralelo. En segundo lugar, puesto que los enjambres de agentes pueden unirse a otro enjambre de grupos similares, el régimen de dos fases anteriormente utilizadas en agrupamiento de flujos de datos se sustituye por una única fase. Esto significa que los resultados de la agrupación siempre están disponibles.
4. Características deseables en Un algoritmo de agrupamiento Basado en flujo de datos
Un algoritmo de agrupamiento debe cumplir con los requerimientos de los flujos de datos: poder descubrir clúster con formas arbitrarias, eliminar supuestos de número de clúster y tener las propiedades para la detección de valores atípicos.
Teniendo como base los resultados obtenidos por los algoritmos anteriores, se plantea una serie de elementos que se deben tener en cuenta:
- Realizar un proceso de normalización de los datos similar a como lo realiza HPStream, antes de procesar los datos del flujo, esto con el fin de sopesar las diferentes dimensiones correctamente. El objetivo es equiparar la desviación estándar a lo largo de cada dimensión.
- Separar el proceso de agrupamiento en dos fases, en la fase online realizar un proceso de sumarización y utilizar una estructura de almacenamiento de información similar a la utilizada por DenStream, la cual tiene en cuenta la aplicación de una función de decadencia sobre los datos con el fin de olvidar datos históricos que no se actualizan constantemente. Sin embargo, es necesario en el proceso de sumarización identificar los puntos representativos del grupo, de tal forma que no pierdan su dinámica. En la fase ffiine, aplicar algoritmos basados en densidad que tengan la capacidad de identificar grupos con formas arbitrarias.
- Si los datos del flujo tienen alta dimensionalidad, buscar identificar las dimensiones que son relevantes para el cálculo de la distancia, con el fin de agilizar el proceso de asignación de grupos a nuevos puntos.
- En un algoritmo de agrupamiento de flujos de datos, se debe tener en cuenta el planteamiento de MDStream, que indica que se debe realizar una adecuada elección de parámetros en los algoritmos basados en densidad, dado que se puede causar que muchos puntos sean considerados ruido o que algunas regiones sean consideradas no densas. Por tanto, se deben definir métricas que puedan variar a los largo de la ejecución, un ejemplo de ello es la función de densidad relativa. Adicionalmente, en los experimentos se debe tener en cuenta la sensibilidad de los parámetros en el análisis de los resultados. Lo anterior permitirá al usuario identificar si los resultados tienen una buena precisión.
- Tal como lo realiza FlockStream, se debe buscar sustituir la búsqueda exhaustiva del vecino más cercano a un punto necesario para asignar el punto a un adecuado micro-clúster por un método de búsqueda local, con el fin de agilizar el proceso de asignación del dato al grupo más cercano. Adicionalmente, se debe permitir que si en el proceso de ejecución un punto encuentra un grupo con más similitud a una asignación anterior, debe ser posible cambiarlo.
5. Conclusiones
A partir de las diversas aproximaciones presentadas para realizar el proceso de agrupamiento de flujos de datos, se pueden extraer las siguientes conclusiones.
A pesar de que existen diversas aproximaciones para realizar el proceso de agrupamiento en flujos de datos, CluStream se puede considerar el padre de todos algoritmos, dado que es el primero que estructura el proceso en dos fases: una fase online en la cual se realiza un proceso de sumarización de los puntos del flujo y se almacena en una estructura que facilite cálculos posteriores, y una ffiine en la cual se extraen los grupos de acuerdo a las necesidades del usuario empleando un algoritmo de agrupamiento clásico.
Los algoritmos basados en densidad son lo que según los estudios producen los mejores resultados, dado que tienen en consideración grupos de formas arbitrarias y adicionalmente tienen la capacidad de adaptarse a la dinámica del flujo y a la presencia de ruido.
Dados los estudios presentes en la literatura y los algoritmos clásicos de agrupación, es importante profundizar en el estudio de los algoritmos jerárquicos aglomerativos en flujos de datos, puesto que durante el proceso de ejecución en cada instante t del flujo se pueden realizar procesos de sumarización en línea y los puntos representativos obtenidos como resultado pueden estar presentes en diversas regiones de un grupo, lo cual permite representar mejor su dinámica. Elemento que no se puede garantizar en algoritmos particionales y basados en densidad.
La mayoría de estudios para realizar procesos de agrupamiento de flujos de datos se basan en algoritmos clásicos de agrupación. Es importante explorar algoritmos basados en procesos físicos y biológicos, dado que presentan esquemas de búsqueda local en procesos de mantenimiento online del flujo de datos, lo cual permite disminuir el número de comparaciones requeridas para realizar una asignación de un punto a un grupo. Por tanto, se puede lograr una disminución de tiempo significativo.
6. Financiamiento
Este proyecto fue financiado por Colciencias y la Universidad Nacional de Colombia según resolución No. 110152128885, cuyo objetivo es la caracterización de grandes flujos de datos mediante técnicas de agrupación.
Referencias
[1] P. Tan, M. Steinbach and V. Kumar, Introduction to Data Mining, USA: Addison-Wesley Longman Publishing Co., Inc. 2005. [ Links ]
[2] T. Kanungo, N. Netanyahu and A. Wu, "An Efficient k-Means Clustering Algorithm: Analysis and Implementation", IEEE Transactions on Pattern Analysis and Machine Intelligence, USA, 2002. [ Links ]
[3] T. Velmurugan and T. Santhanam, "A comparative analysis between K-Medoids and Fuzzy c-means clustering algorithm for statistically distributed data point", Journal of theorical and applied information technology, vol.27,no. 1, Mayo, 2011. [ Links ]
[4] M. Ester, H. Kriegel, J. Sander and X. Xu, "A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise". Proc. 2nd Int. Conf. On Knowledge Discovery and Data Mining, Portland, Oregon: AAAI Press, 1996. [ Links ]
[5] M. Ankerst, M. Breunig, H. Kriegel and J. Sander, "OPTICS: ordering points to identify the clustering structure", Proceedings of the 1999 ACM SIGMOD International Conference on Management of Data, Philadelphia, USA, 1999. [ Links ]
[6] D. Eisenstein and P. Hut. "Hop: A New Group Finding Algorithm for N-body Simulations", Astrophysics Journal, vol. 498, no. 1, pp. 137-142, 1998. [ Links ]
[7] A. Hinneburg and D. Keim, "An Efficient Approach to Clustering in Large Multimedia Databases with Noise", In International Conference on Knowledge Discovery and Data Mining (KDD'98), pp. 58-65, Aug. 1998. [ Links ]
[8] T. Zhang, R. Ramakrishnan and M. Livny. "BIRCH: an Efficient Data Clustering Method for Very Large Databases". In International Conference Management of Data (SIGMOD' 96), pp. 103-114, Jun. 1996. [ Links ]
[9] S. Guha, R. Rastogi and K. Shim, "CURE: An Efficient Clustering Algorithm for Large Databases". In International Conference Management of Data SIGMOD'98), pp. 73-84, Jun. 1998. [ Links ]
[10] G. Karypis, E. Han and V. Kumar. "CHAMELEON: A Hierarchical Clustering Algorithm Using Dynamic Modeling". Computer, vol. 32, no.8, pp. 68-75, 1999. [ Links ]
[11] F. Picarougne, H. Azzag, G. Venturini and C. Guinot, "A New Approach of Data Clustering Using a Flock of Agents". Evolutionary Computation 2007 by the Massachusetts Institute of Technology, Cambridge, USA,2007. [ Links ]
[12] X. Cui, J. Gao and T. Potok, "A focking based algorithm for document clustering analysis", Journal of Systems Architecture, vol. 52,505-515, 2006. [ Links ]
[13] X. Cui and T. Potok, "A Distributed Agent Implementation of Multiple Species Flocking Model for Document Partitioning Clustering", Berlin - Heidelberg: Springer-Verlag, 2006. [ Links ]
[14] O. Nasraoui and R. Krishnapuram, "A novel approach to unsupervised robust clustering using genetic niching", In In Proceedings of the Ninth IEEE International Conference on Fuzzy Systems, pp.170-175, Sichuan, China, 2000. [ Links ]
[15] E. Leon, O. Nasraou and J. Gomez, "ECSAGO: Evolutionary Clustering with Self Adaptive Genetic Operators", 2006 IEEE Congress on Evolutionary Computation, Vancouver, Canada, 2006. [ Links ]
[16] S. Kundu, "Gravitational clustering: a new approach based on the spatial distribution of the point", Pattern recognition, no. 32, pp. 1149-1160, 1999. [ Links ]
[17] W. Wright. "Gravitational clustering", Pattern recognition, no. 9, pp. 151-166, 1977. [ Links ]
[18] J. Gómez and E. León, "Parameterless Randomized Gravitational Clustering", Advances in Artificial Intelligence, 2012. [ Links ]
[19] J. Gomez, J. Pena-Kaltekis, N. Romero and E. Leon, "INCRAIN: An Incremental Approach for the Gravitational Clustering", Lecture Notes in Computer Science MICAI 2007: Advances in Artificial Intelligence, Heidelberg: Springer Verlag, 2007. [ Links ]
[20] J. Gama, "Knowledge Discovery from Data Streams", Chapman & Hall/CRC Data Mining and Knowledge Discovery Series, USA: CRC Press Inc,, 2005. [ Links ]
[21] P. Kranen, "Anytime Algorithms for Stream Data Mining", Diese Dissertation, RWTH Aachen University, 2011. [ Links ]
[22] M. Hahsler, "Mining Massive Data Streams", Computer Science and Engineering, Southern Methodist University, Texas, USA, 2012. [ Links ]
[23] P. Domingos and G. Hulten, "Mining high speed data streams", Proceedings of the sixth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Boston, USA, 2000. [ Links ]
[24] S. K. Tanbeer, C. F. Ahmed, B. S. Jeong, and Y. K. Lee, "Sliding window-based frequent pattern mining over data streams", Information Sciences, vol. 179, no. 22, 2009, pp. 3843-3865. [ Links ]
[25] D. Chakrabarti, R. Kumar and A. Tomkins, "Evolutionary Clustering", KDD'06, Philadelphia, USA, 2006. [ Links ]
[26] B. Zhang, G. Kleyner and M. Hsu, A Local Search Approach to K-Clustering, HP Laboratories, Palo Alto, USA,1999. [ Links ]
[27] S. Guha, N. Mishra, R. Motwani and L. O'Callaghan. "Clustering Data Streams", In Proc. IEEE FOCS Conference, pp. 359-366, USA, 2000, [ Links ].
[28] S. Guha, A. Meyerson, N. Mishra and R. Motwani. "Clustering Data Streams: Theory and Practice", TKDE special issue on clustering, vol. 15, 2003, pp. 515-528. [ Links ]
[29] B. Babcock, M. Datar, R. Motwani and L. O'Callaghan. "Maintaining Variance and k-Medians over Data Stream Win-dows". Proc. Of PODS 2003, San Diego, California, 2003, pp. 234-243. [ Links ]
[30] M. Ackermann, C. Lammersen, M. Martens, C. Raupach, C. Sohler and K. Swierkot, "StreamKM++: A Clustering Algorithm for Data Streams", In Proceedings of the 12th Workshop on Algorithm Engineering and Experiments (ALENEX '10), pp. 173-187, Society for Industrial and Applied Mathematics, 2010. [ Links ]
[31] D. Arthur and S. Vassilvitskii. "k-means++: the advantages of careful seeding", Proc. 18th ACM-SIAM Sympos. Discrete Algorithms, pp. 1027-1035, Texas, USA, 2007. [ Links ]
[32] C. Aggarwal, J. Han, J. Wang and P. Yu, "A Framework for Clustering Evolving Data Streams", Proceedings of the 29th VLDB Conference, Berlin, Germany, 2003. [ Links ]
[33] C. Aggarwal, J. Han, J. Wang and P. Yu, "A framework for projected clustering of high dimensional data stream", Proceedings of International Conference on Very Large Data Bases (VLDB'04), pp. 852-863, Toronto, Canada, 2004. [ Links ]
[34] Z. Aoying, C. Feng, Q. Weining and J. Cheqing, "Tracking clusters in evolving data streams over sliding windows", Knowledge and Information System, vol.15, no.2, pp.181-214. [ Links ]
[35] W. Zhu, J. Yin and Y. Xie, "Arbitrary shape cluster algorithm for data Stream", Journal of Software, vol. 17, no. 3, 2006. [ Links ]
[36] C. Feng, E. Martin, W. Qian and A. Zhou, "Density-Based Clustering over an Evolving Data Stream with Noise", 2006 SIAM Conference on Data Mining, Maryland, USA, 2006. [ Links ]
[37] J. Ren and R. Ma, "Density-Based Data Streams Clustering over Sliding Windows", Fuzzy Systems and Knowledge Discovery, 2009.FSKD '09. Sixth International Conference on, vol.5, pp.248-252, 14-16 Aug. 2009. [ Links ]
[38] C. Jia, C. Tan and A. Yong, "A grid and density-based clustering algorithm for processing data stream", in Proceedings of the Second International Conference on Genetic and Evolutionary Computing. Washington, DC, USA: IEEE Computer Society, 2008, pp. 517-521. [ Links ]
[39] W. Wang, J. Yang and R. R. Muntz. "STING: A Statistical Information Grid Approach to Spatial Data Mining". In 23rd International Conference on Very Large Data Bases (VLDB'97), pp.186-195, 1997. [ Links ] [ Links ] 1998.
[41] R. Agrawal, J. Gehrke, D. Gunopulos and P. Raghavan. "Automatic Subspace Clustering of High Dimensional Data for Data Mining Applications". In International Conference Management of Data (SIGMOD'98), pp. 94-105, Jun. 1998. [ Links ]
[42] L. Wan, W. K. Ng, X. H. Dang, P. S. Yu and K. Zhang. "Density-based clustering of data streams at multiple resolutions", ACM Transactions on Knowledge Discovery from Data, vol. 3, no. 3, pp.1-28, 2009. [ Links ]
[43] A. Magdy, N. Yousri and N. El-Makky, "Discovering Clusters with Arbitrary Shapes and Densities in Data Streams", Machine Learning and Applications, Fourth International Conference on, pp. 279-282, 2011 10th International Conference on Machine Learning and Applications and Workshops, 2011. [ Links ]
[44] L. Tu and Y. Chen, "Stream data clustering based on grid density and attraction",ACM Transactions on Knowledge Discovery Data, vol. 3, no. 3, pp. 1-27, 2009. [ Links ]
[45] K. Luo and L. Wang, "Data Streams Clustering Algorithm Based on Grid and Particle Swarm Optimization", 2009. [ Links ]
[46] Z. Hongyan and L. Xiyu, "A Data Streams Clustering Algorithm Using DNA Computing Techniques Based on Mobile Agent", Pervasive Computing (JCPC), 2009 Joint Conferences on, 2009. [ Links ]
[47] C. H. Ren and BinleiCai, "Clustering over data streams based on grid density and index tree", Journal of Convergence Information Technology, vol. 6, pp. 83-93, 2011. [ Links ]
[48] G. Yu, Y. Bao, F. Zhao and D. Wang, "CDS-Tree: an effective index for clustering arbitrary shapes in data streams", Research Issues in Data Engineering: Stream Data Mining and Applications, 2005. RIDE-SDMA 2005. 15th International Workshop on, 2005 [ Links ]
[49] L. Lining and Y. Xia, "HDG-Tree: A Structure for Clustering High-dimensional Data Streams", Intelligent Information Technology Application, 2009. IITA 2009. Third International Symposium on, 2009 [ Links ]
[50] X. Wang and H. Shen, "Clustering High Dimensional Data Streams with Representative Points", 2009 Sixth International Conference on Fuzzy Systems and Knowledge Discovery, 2009. [ Links ]
[51] A. Ben-Hur, D. Horn, H. Siegelmann and V. Vapnik, "Support Vector Clustering", Journal of Machine Learning Research, vol. 2,pp.125-137, 2001. [ Links ]
[52] J. Lai, D. Huang and W. Zheng, "SVStream: A Support Vector Based Algorithm for Clustering Data Streams", Knowledge and Data Engineering, IEEE Transactions on, New Jersey, USA, 2011. [ Links ]
[53] A. Forestiero, C. Pizzuti and G. Spezzano, "Flock Stream: a Bio-inspired Algorithm for Clustering Evolving Data Streams", 21st IEEE International Conference on Tools with Artificial Intelligence, 2009. [ Links ]