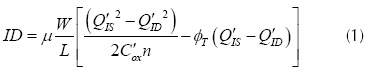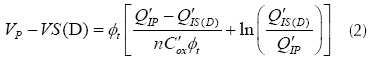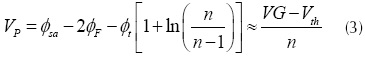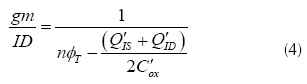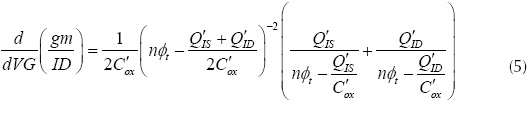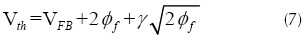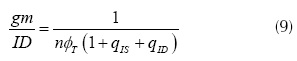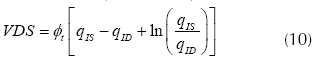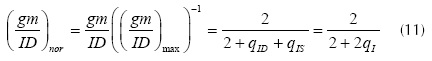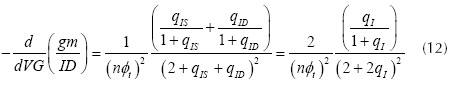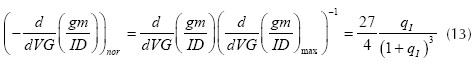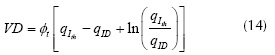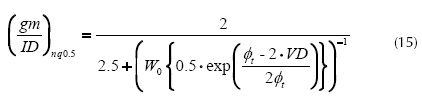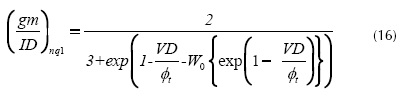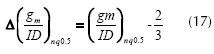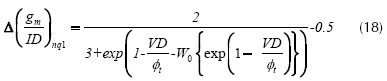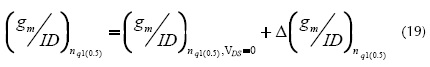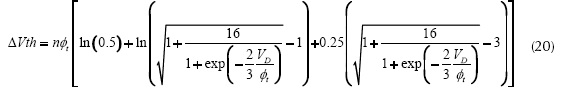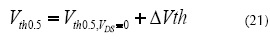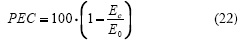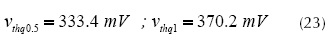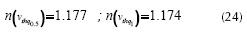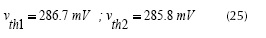Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Tecnura
versão impressa ISSN 0123-921X
Tecnura vol.21 no.52 Bogotá jan./abr. 2017
https://doi.org/10.14483/udistrital.jour.tecnura.2017.2.a02
DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2017.2.a02
Comparative analysis of threshold voltage extraction techniques based in the MOSFET gm/ID characteristic
Comparación de las técnicas de extracción del voltaje de umbral basadas en la característica gm/ID del MOSFET
Arturo Fajardo Jaimes1
1 Ingeniero electrónico, magíster en Electrónica. Profesor Asistente Pontificia Universidad Javeriana. Bogotá, Colombia. Contacto: fajardoa@javeriana.edu.co
Fecha de recepción: 4 de febrero de 2016 Fecha de aceptación: 15 de febrero de 2017
Cómo citar: Fajardo J., A. (2017). Comparación de las técnicas de extracción del voltaje de umbral basadas en la característica gm/ID del MOSFET. Revista Tecnura, 21(52), 32-44. doi: 10.14483/udistrital.jour.tecnura.2017.2.a02
Abstract
Context: In advanced ultralow-power devices, it is necessary to use the accuracy extraction procedures of the MOSFET threshold voltage to fully characterize the devices. These procedures are based in the measurement of the Tran-conductance efficiency (gm/ID) and its first derivative in function of the voltage gate source (d(gm/ID)/dVGS). In order to increase their independency respect to the non-zero drain source voltage (VDS ≠0) it is used a process to correct the error. Theoretically, VDS should be 0 V; however, the VDS is grater than 10 mV in the experimental setup in order to avoid electrical noise, but less than a certain maximum value for allowing the MOSFET operation in the linear region of the weak inversion.
Objective: To compare the extraction procedure proposed by (MC Schneider et al., 2006) and the method proposed by (Rudenko et al., 2011) with a generic, controlled and coherent test scenario.
Method: This paper proposes a test scenario based on the Advanced Compact MOSFET model (ACM) of a long channel MOSFET made in a standard 0.35 mm CMOS process, implemented numerically in MATLABâ. The concept of Power Error Correction (PEC) was used to compare the two processes numerically; it quantifies the sensitivity of the extraction process to the effect by the non-zero voltage value of the VDS in the experimental setup (i.e., NZ-DS effect).
Results: The error correction procedure proposed by (Siebel et al., 2012, Schneider et al., 2006) estimates the NZ-DS effect better than the procedure proposed by (Rudenko et al., 2011), considering the average, maximum and minimum PEC obtained for both extraction methodologies for a long channel MOSFET fabricated in a standard CMOS process of 0.35 μm, when the VDS is less than 50 mV.
Conclusions: The Vth extraction procedure proposed by (MC Schneider et al., 2006) is more robust than the method proposed by (Rudenko et al., 2011) regarding the NZ-DS effect.
Keywords: Threshold Voltage Extraction, MOSFET Modeling, Gm/ID transconductance efficiency.
Resumen
Contexto: En los dispositivos de ultrabaja potencia son necesarios procedimientos precisos de extracción de voltaje de umbral del MOSFET. Estos se basan en la medición de la eficiencia de la transconductancia (gm/ID) y su primera derivada respecto al voltaje puerta-fuente (d(gm/ID)/ dVGS). Para aumentar en algunas decenas de mV la precisión del voltaje de umbral extraído, se recurre a un proceso de corrección de errores que disminuye la influencia del voltaje dreno-fuente (VDS) que teóricamente debería ser 0 V. Típicamente, en el montaje experimental, el VDS es mayor a 10 mV con el fin de evitar el ruido eléctrico, pero menor a un cierto valor máximo con el fin de permitir que el MOSFET siempre opere en su región lineal.
Objetivo: Comparar el procedimiento de extracción propuesto por Schneider et al. (2006) y el método propuesto por Rudenko et al. (2011) con un escenario de prueba genérico, controlado y coherente.
Método: Se implementó un escenario de prueba en el softwareMatlab® para un MOSFET de canal largo fabricado en un proceso estándar CMOS de 0,35 mm, usando el modelo Advanced Compact MOSFET (ACM). Para comparar los dos procesos de extracción se tomó el concepto de potencia de corrección del error (PEC), el valor de este cuantifica la sensibilidad del proceso de extracción con respecto al valor no 0V del VDS usado experimentalmente (i.e., efecto NZ-DS).
Resultados: Considerando el promedio, el máximo y el mínimo PEC obtenido para ambas metodologías de extracción, el procedimiento de corrección de errores propuesto en Siebel, Schneider y Galup (2012) y Schneider et al. (2006) estima el efecto NZ-DS mejor que el procedimiento propuesto en Rudenko et al. (2011) para un MOSFET de canal largo fabricado en un proceso estándar CMOS de 0,35 μm, cuando el VDS es inferior a 50 mV.
Conclusiones: El procedimiento de extracción de Vth propuesto por Schneider et al. (2006) es más robusto que el sugerido en Rudenko et al. (2011) con respecto al efecto NZ-DS.
Palabras clave: extracción del voltaje de umbral, modelamiento de MOSFET, eficiencia transconductancia Gm/ID.
INTRODUCTION
Power consumption awareness began in the nineties. Nowadays, every circuit has to face the power consumption issue in both portable devices (e.g., for increasing the battery life) and high-end circuits (e.g., for avoiding packages and reliability issues). The advances in the solid-state devices had a direct impact in the efficiency and the cost of the electronic equipment (Sarmiento 2004); in particular, high-efficient systems such as inverters (Fajardo et al. 2014) and power supplies (Hernández et al. 2012) have been explored using high-frequency power MOSFET (i.e., Metal-Oxide-Semiconductor Field-Effect Transistor). Considering the micro-scale electronic systems, the power consumption has had a big reduction since the first integrate circuit; furthermore, the power reduction started with the invention of the complementary metal-oxide-semiconductor (CMOS) technology that allows the reduction of the static power consumption. The designing of integrate circuits using ultra-low power techniques, such as supply voltage reduction, sub threshold operation, and Biasing MOSFETs at very low current are not rare nowadays. Consequently, there have been dedicated proposed models for modeling the MOSFET in all its operation regions, including weak, moderate and strong inversion (Schneider et al. 2010).
The estimation of the MOSFET threshold voltage (Vth) is critical to model the complementary metal-oxide-semiconductor (CMOS) circuits, particularly on the design of ultra-low-power devices (Rudenko et al. 2011), (Siebel et al. 2012). The Vth is basically the gate source voltage (VGS) level necessary in the MOSFET to start working in Strong Inversion (SI). To identify a hard threshold in the drain current (ID) vs. gate source voltage (VGS) characteristic is difficult, because the continuous nature of the involved physical phenomena. Therefore, many researches have proposed Vth definitions and extraction procedures (Siebel et al. 2012). The extraction procedures generally use the ID vs. VGS characteristic of the MOSFET (Ortiz-Conde et al. 2002). Furthermore, most of them use only one regime of operation (i.e., ID-VG methods), the SI region or the Weak Inversion (WI) region in both its linear and saturation operation. However, the Vth extracted data using these approaches is inaccurate because the Vth occurs in the transition region between WI and SI (Schneider et al. 2010).
Recently, new physic-based Vth definitions have been proposed because of the introduction of charge-based models (Schneider et al. 2010). In addition, accurate extraction methods based in the measurement of the transconductance efficiency (gm/ID) and the transconductance efficiency change (d(gm/ID)/dVG) have been proposed by (Siebel et al. 2012, Schneider et al. 2006). Parasitic effects (such as drain or source series resistances and channel mobility degradation) tend to have less influence in these extraction techniques. Furthermore, they are less sensitive to short channel effects such as velocity saturation. However, these charge-based definition and extraction methods can be used for finding the conventional Vth value used in the potential-based models. The charge-based definition of the Vth involves a physically impossible extraction setup because both the gm/ID and the d(gm/ID)/dVG characteristics must be measured with the MOSFET operating at zero drain source voltage (VDS=0). However, the MOSFET in the real setup operates in its linear region with a very low voltage for decreasing the parasitic effects, but it is high enough to sense the ID (Schneider et al. 2010). All of these techniques propose a correction methodology in order to reduce the non-zero drain-to-source (NZ-DS) effect present on the Vth extraction methods, but a direct comparison of these methodologies based in the reported results is too difficult or even impossible to do. Recently, (Fajardo et al. 2013) proposed the power error correction (PEC) of NZ-DS effect concept to analyze the error correction in these methodologies of Vth extraction.
The fundamental purpose of this paper is to compare the accuracy of the gm/ID method proposed by (Schneider et al. 2006) and the d(gm/ID)/dVG method proposed by (Rudenko et al. 2011), using the power error correction (PEC) concept proposed by (Fajardo et al. 2013). Additionally, this paper develops a comprehensible presentation of the NZ-DS effect using analytical models, and implements a generic, controlled and consistent test scenario in MATLAB® for a long channel MOSFET made in a 0.35 mm CMOS standard process using the Advanced Compact MOSFET (ACM) model.
METHODOLOGY
Advanced Compact MOSFET (ACM) Model.
The ACM model represents the device behavior in all regimes of operation using an analytical equation set (Schneider et al. 2006). The following are the ACM equations explored in this paper (Equations (1) to (5)).
Where, µ is the mobility of the carriers in the semiconductor substrate, C'ox is the oxide capacitance per unit area, L and W are the channel length and the channel width of the MOSFET respectively, Q'ID is the drain inversion charge density, Q'IS is the source inversion charge density, Q'IP is the pinch-off charge density, VP is the channel pinch-off voltage, φF is the Fermi potential, φsa is the surface potential, VS is the source bulk voltage, VD is the drain bulk voltage, VG is the gate bulk voltage, n is the slope factor, and φt is the thermal voltage given equation (6) as follows.
Where q is the elemental electron charge, k is the Boltzmann constant, and T the absolute temperature. A script was implemented for solving the equations (1) to (5), assuming that the MOSFET was in non-saturated operation in the WI region. Furthermore, the test scenario considered a long channel NMOS transistor (W/L=32mm/3.2mm) at a temperature of 27°C, and the technological parameters of the standard 0.35 mm CMOS process (i.e., acceptor doping concentration NA= 6x1016 cm-3, oxide thickness tox=7.8 nm, low field mobility m0 = 0.36238 m2/V.s, and flat band voltage VFB=0.8 V). (Schneider et al. 2010) presents an analytic expression for the equilibrium threshold voltage (Vth); this expression allows the Vth calculus from technological parameters, as shown in (7).
Where, γ is the so-called body-effect factor.
Threshold voltage (Vth) definitions
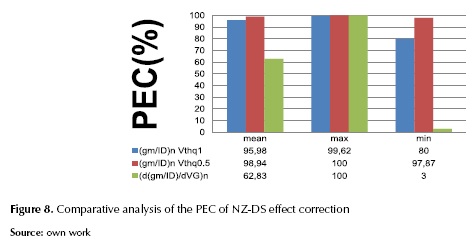
The Vth concept is directly related to the physical phenomenon that prevails in the current flow when the MOSFET goes from WI to SI. The Vth in the surface potential based models (Tsividis et al. 1999) is the VGS that produces a surface potential equal to twice the Fermi potential ( ). On the other hand, in the charge-based models (i.e., EKV, ACM), the Vth is the VG value associated to the threshold inversion charge density (Q'th). Addicionally, both Vth values are related by the analytic expressions (Siebel et al. 2012) summarized in table 1.
). On the other hand, in the charge-based models (i.e., EKV, ACM), the Vth is the VG value associated to the threshold inversion charge density (Q'th). Addicionally, both Vth values are related by the analytic expressions (Siebel et al. 2012) summarized in table 1.
The Vth extraction is generally based in the gm/ID extraction (Siebel et al. 2012, Schneider et al. 2006) in advanced ultra-low power applications. In order to understand this methodology we must discuss the gm/ID and the (d(gm/ID)/dVG) concepts using the charge-based model framework. The gm/ID is a quality factor of how much transconductance (gm) is produced for a given unit of bias current (Binkley 2007). The gm/ID in the bipolar transistor device is maintained at a constant high value over multiple tens of collector current. Unfortunately, the MOSFET device gm/ID is maximum in the WI region (always less than the gm/ID of the bipolar transistor), and drops significantly when operating in the SI region (Schneider et al. 2010). The gm/ID behavior (i.e., high for MI and low for SI and soft in the transition) allows defining directly the Vth from a specific inversion charge using the ACM model.
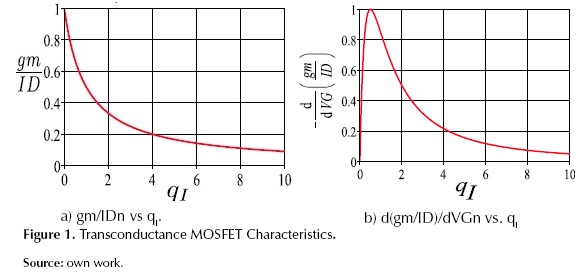
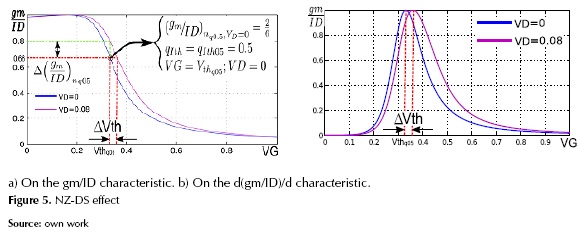
Defining the normalized inversion charge (qI) by equations (8) and (4), we expressed the gm/ID as a function of the normalized charges in the MOS channel in equation (9). Also, using equations (8) and (2) we found the VDS as a function of the channel charges in equation (10). The normalized gm/ID (gm/IDn) can be calculated using equation (11), this expression was found using equations (10) and (9), and assuming VDS=0 (i.e., MOS capacitor analysis qI= qID =qIS). As shown in figure 1(a), the gm/IDn characteristic is monolithical and without discontinuities. Therefore, the relative to the peak drop (RPD) can be used as a metric if we choose a RPD of 50% as the transition point between WI and SI, the related inversion charge would be qI=1.
Where qIS is the normalized source inversion charge, and qID is the normalized drain inversion charge. Another possible approach is to analyze the d(gm/ID)/dVG MOSFET characteristic: this characteristic may be interpreted like the d(gm/ID)/dVG for a given gate voltage change. The d(gm/ID)/dVG and its normalized value (d(gm/ID)/dVG) were found as a function of the normalized channel charges, following a similar procedure to the gm/ID characteristic. These are given by equations (12) and (13).
The gm/IDn and the d(gm/ID)/dVG are plotted in figure 1. As shown in figure 1(b), d(gm/ID)/dVGn has a maximum value between WI and SI (i.e., high and low values of qI); therefore, this maximum is chosen as a threshold between WI and SI operation. On the other hand, gm/IDn (figure 1(a)) does not have any particular characteristic in the transition.
The common charge-based definition of Vth is qIth=qIth0.5=0.5 or qIth=qIth1=1. If we use the qIth1 definition, the Vth is the voltage that produces the same drift and diffusion components of the drain current. On the contrary, if qIth0.5 is used for defining the Vth, it represents the voltage that produces the maximum value of the d(gm/ID)/dVG characteristic. The table 1 shows the Vth definitions, the used notation, the gm/ID RPD, the value of the qI at Vth, and the voltage difference between the classical and the charge Vth definitions.
Transconductance efficiency (gm/ID) methods used for Vth extraction
Some error source in gm/ID and d(gm/ID)/dVG extraction process
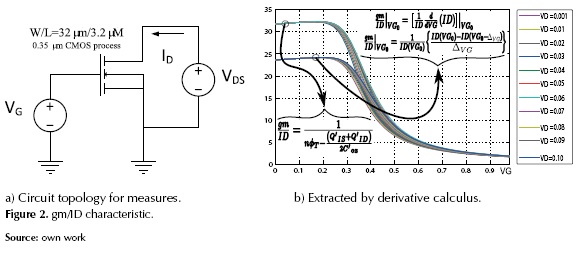
The test setup used for the Vth extraction process (applying the gm/ID methods) is shown in figure 2(a). The VDS was replaced from 10mV to 50mV for any VDS value the gm/ID, and the d(gm/ID)/dVG characteristics were extracted as functions of the gate voltage. Additionally to the usual error involved in any empirical measurement, the error introduced by the numerical derivatives calculus of the gm/ID, the d(gm/ID)/dVG characteristics, and the NZ-DS effect must be considered in this experimental setup. To show error influence, some normalized gm/ID curve samples (for several ID values) were calculated using the charge based expressions of the ACM model (equations (1) to (5)); then these curve samples were evaluated using the numerically derivatives of the correspondent drain current samples. The resulting curves were plotted in figure 2(b) where it is possible to see the impact of the numerical error especially for low values of the gate voltage (low measured current).
This work calculates the gm/ID and d(gm/ID)/dVG characteristics using the charge-based expressions which are the equations (4) and (5), so the error generated by the numerical calculus of these characteristics is not present. Furthermore, this controlled environment permits to evaluate in an easy way the PEC for the NZ-DS effect on the accuracy Vth extraction for advanced ultra-low power devices proposed by (Siebel et al. 2012, Schneider et al. 2006) because it is the only error source present in the extraction methodology.
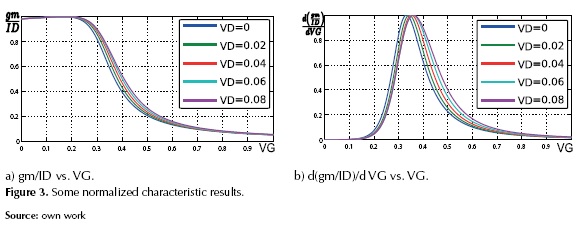
In order to analyze the NZ-DS effect, figure 3 presents the gm/ID and d(gm/ID)/dVG characteristics calculated with the charge-based expressions. In figure 3(a) it is clear that the NZ-DS effect is increased by the VDS growth, therefore the Vth extracted using the operational definition (RPD of 50% or 75%) increases too. Secondly, figure 3(b) makes it clear that the NZ-DS effect is the variation of the d(gm/ID)/dVG maximum point. In conclusion, the NZ-DS effect increases the extracted Vth; this effect must be corrected in order to have better accuracy of the extraction procedures in some mV.
The Vth extraction procedures based in the gm/ID characteristic.
When the VG=Vth and VS=0 (because our circuit topology qIS= qth), and using equation (8), we can rewrite equation (10) as equation (16).
Then, we found the gm/ID value related to the Vth charge condition as a function of the VD. Furthermore, we found the analytical expressions of the normalized gm/ID (i.e., gm/IDn) as a function of the VD using the common charge-based definitions of Vth (i.e., qIth=qIth0.5=0.5 and qIth=qIth1=1) and equations (11) and (14). These founded expressions are given by equations (15) and (16).
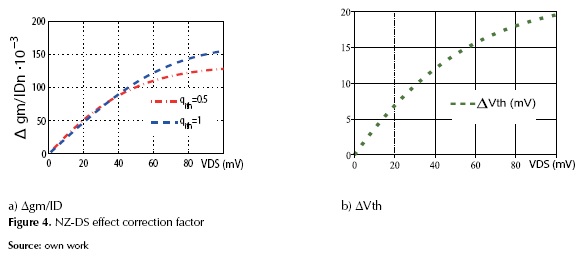
Where the gm/IDnq0.5 and gm/IDnq1 are the gm/IDn values related to the VGS (or VG) that creates a superficial inversion charge density of qIth1*Q'IP and qIth0.5*Q'IP respectively; W0 {*} is the Lambert function (Corless et al. 1996). This expression can be simplified for very low values of VDS as gm/IDnq0.5 = 2/3 or gm/IDnq1=0.5. Therefore, the extraction procedures consist of determining the gate voltage (i.e., Vthq0.5 or Vthq1) at which the gm/IDn vs. VGS characteristic is equal to 50% or 66.66%. Then it is necessary to correct the NZ-DS effect of the extracted value. (Siebel et al. 2012, Schneider et al. 2006) reports a closed expression for calculating the incremental error present in the gm/ID characteristic ∆(gm/ID), these errors for qIth0.5 and qIth1 are given by equations (17) and (18).
We used the incremental error in the gm/IDn and then extract the Vth (Vthq0.5 or Vthq1) by simply determining the VGS at which the gm/IDn characteristics are equal to the ideal condition plus the incremental error (equation (19)).
Figure 4(a) shows the ∆(gm/ID) behavior for low values of VDS, and figure 5(a) illustrates all the extracting process. On the other hand, (Rudenko et al. 2011) proposes for Vthq0.5 an error correction based in the incremental error ∆Vth, given by equation (20).
∆vg is shown in figure 4 (b). The error less Vthq0.5 is equal to the ideal condition plus the incremental error (equation (21)).
Where we extracted the Vthq0.5 from the gm/IDn characteristic (RPD 66.66%) or from d(gm/ID)/dVG characteristic (Vth=VGS where d(gm/ID)/dVG is maximum), then we estimate the error with equation (20) and determine the Vthq0.5 using equation (21). Figure 5(b) illustrates all the extracting processes for the d(gm/ID)/dVG characteristic.
Power Error Correction in Vth extraction gm/ID Methods
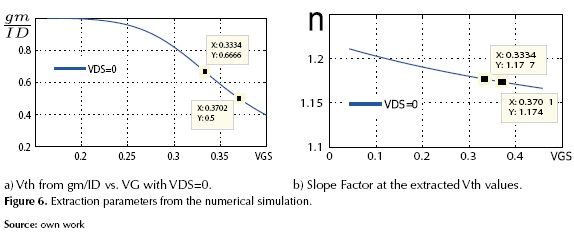
(Fajardo et al. 2013) defines the PEC with the following equation (22).
Where EC is the error of the extracted Vth for a VDS sweep from 0 mV to Vmax using the correction factor of the method, and E0 is the mean of the extracted Vth for the same VDS sweep without using the correction factor. The Vmax value is a technology value for a particular analyzed device; particularly for the long channel NMOS transistor studied in this paper, this value was set to 50 mV.
RESULTS
Consistency Analysis of the simulation results and the extraction methods.
First, we extracted the Vth from the simulation data using the charge-based expressions (figure 6(a)). The extracted values were sumarized in equation (23).
Where 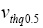 and
and 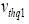 are the Vth extracted values using the charge-based definition qIth=qIth0.5=0.5 and qIth=qIth1=1, respectively. Second, we extracted the value of the slope factor (n) for these MOSFET operation points using the simulation data (figure 6(b)), and the extracted values were sumarized in equation (24).
are the Vth extracted values using the charge-based definition qIth=qIth0.5=0.5 and qIth=qIth1=1, respectively. Second, we extracted the value of the slope factor (n) for these MOSFET operation points using the simulation data (figure 6(b)), and the extracted values were sumarized in equation (24).
We estimated the classical Vth (the Vth used in the potential-based models) of this process from the values in equations (23) and (24) and using the relationship beetween the classical definition and the charge-based definition of Vth, summarized in table 1. Equation (25) shows the results.
Where vth1 and vth2 are the estimated values of the classical Vth and were based on qIth0.5 and qIth1 respectively.
Finally, we calculated the Vth of this process using equation (7). The resulting value was 283.6 mV. As we expected, the extracted and calculated values of the Vth were almost the same (the error was less than 3mV); therefore, it is possible to affirm that the test scenario for a long channel MOSFET implemented in MATLAB® is consistent.
Vth Results using gm/ID method
Using the generic, controlled and consistent test scenario for the long channel MOSFET fabricated in a 0.35 mm CMOS standard process, we obtained from both gm/ID and d(gm/ID)/dVG the Vthq data with and without correction for a parametric sweep of the VDS from 0.1mV to 50mV. Figure 7 presents the Vth extracted from the charge-based expressions (with and without NZ-DS effect). The PEC was calculated for the analyzed methodologies using equation (22), and the results were summarized in figure 7. If we consider all the analyzed VDS range (100mV-50mV), the error correction procedure proposed by (Siebel et al. 2012, Schneider et al. 2006) estimates the NZ-DS effect better than the procedure proposed by (Rudenko et al. 2011) in the case of a long channel MOSFET fabricated in a 0.35 mm CMOS standard process, but in the range near the typical voltage used in an experimental setup (VDS=10mV-20mV) the PEC of both methodologies is similar.
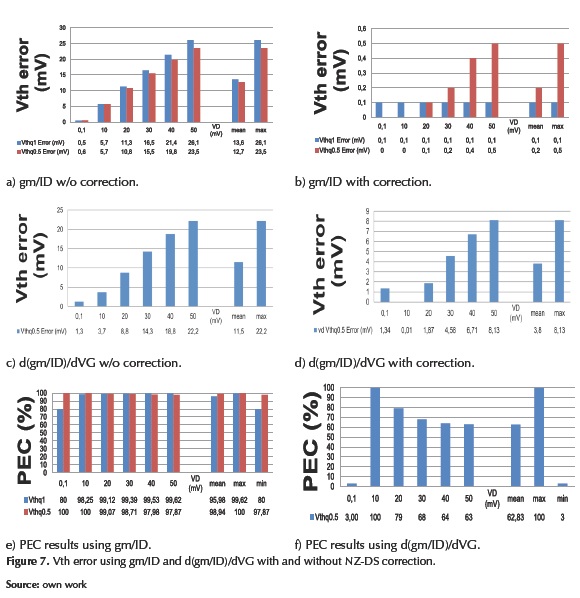
Comparative analysis of the PEC.
Figure 8 presents the mean, the maximum, and the minimum PEC achieved for each methodology in order to compare the two analyzed Vth extraction methodologies. Considering this figure, the error correction procedure proposed by (Siebel et al. 2012, Schneider et al. 2006) estimates the NZ-DS effect better than the procedure proposed by (Rudenko et al. 2011) for a long channel MOSFET fabricated in a 0.35 mm CMOS standard process when the VDS is less than 50mV. This methodology permits PEC always better than 80%; therefore, the correction procedure proposed by (Siebel et al. 2012, Schneider et al. 2006) is more robust and reliable than the procedure proposed by (Rudenko et al. 2011).
CONCLUSIONS
This paper compares the common extractions techniques proposed by (Rudenko et al. 2011, Siebel et al. 2012) in presence of non-zero drain source voltage (NZ-DS) effect, using the PEC concept proposed by (Fajardo et al. 2013) and a generic, controlled and consistent test scenario for a long channel MOSFET fabricated in a 0.35 mm CMOS standard process. In all the device operation on the linear region, the error correction procedure proposed by (Siebel et al. 2012, Schneider et al. 2006) estimates the NZ-DS effect better than the procedure proposed by (Rudenko et al. 2011), but in the typical voltage used in an experimental setup both methodologies are similar.
ACKNOWLEDGEMENTS
This work was partially supported by COLCIENCIAS, and the Pontificia Universidad Javeriana. Also, the author would like to thank all the students of the Radio Frequency Integrated Circuits Group (GRF-UFSC) for the important discussions.
REFERENCES
Binkley, D.M. (2008). Tradeoffs and Optimization in Analog CMOS Design. Chicheste: John Wiley & Sons -Interscienc. [ Links ]
Corless, R.M. et al. (1996). On the LambertW Function. Advances in Computational Mathematics, 5(1), 329-359. [ Links ]
Fajardo, A. & Montoro, C.G. (2013). Correction of the Errors due to the Non Zero Drain-to-Source Voltage in the gm/ID Based Vth Extraction Methods. Proceedings of the MICROELECTRONICS STUDENTS FORUM (SFORUM in Curitiba,Brazil) http://www.lbd.dcc.ufmg.br/colecoes/sforum/2013/004.pdf [ Links ]
Fajardo, A.F, et al. (2014). Modelado e implementación de un manejador eléctrico para un motor de inducción trifásico. Revista Tecnura, 18(39), 94-109. [ Links ]
Hernández, L.F.; Gomez, D.R. & Hernández, O.M. (2012). Rectificador monofásico con corrección del factor de potencia usando un convertidor Boost. Revista Tecnura, 16(33), 23-34. [ Links ]
Martínez, F.H. (2004). Estudio de eficiencia en los MOSFET e IGBT para su utilización en convertidores de potencia conmutados. Revista Tecnura, 15, 85-96. [ Links ]
Ortiz-Conde, A., et al. (2002). A Review of Recent MOSFET Threshold Voltage Extraction Methods. Microelectronics Reliability, 42(4), 583-596. [ Links ]
Rudenko, T. et al. (2011). On the MOSFET Threshold Voltage Extraction by Transconductance and Transconductance-to-Current Ratio Change Methods: Part I effect of Gate-Voltage-Dependent Mobility. IEEE Transactions on Electron Devices, 58(12), 4172-4179. [ Links ]
Schneider, M.C. & Galup-Montoro, C. (2010). CMOS Analog Design using all-Region MOSFET Modeling. Cambridge: Cambridge University Press. [ Links ]
Schneider, M.C.; Galup-Montoro, C.; Machado, M.B. & Cunha, A.I.A. (2006). Interrelations between Threshold Voltage Definitions and Extraction Methods. Technical Proceedings of the 2006 NSTI Nanotechnology Conference and Trade Show Volume 3, 868-871. http://www.nsti.org/procs/Nanotech2006v3/7/W56.11 [ Links ]
Siebel, O.F.; Schneider, M.C. & Galup-Montoro, C. (2012). MOSFET Threshold Voltage: Definition, Extraction, and some Applications. Microelectronics Journal, 43(5), 329-336. [ Links ]
Tsividis, Y. & McAndrew, C. (1999). Operation and Modeling of the MOS Transistor. New York: Oxford University Press. [ Links ]