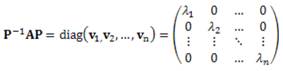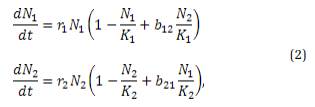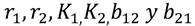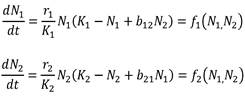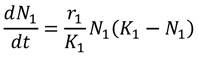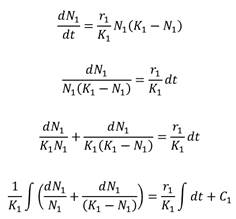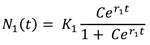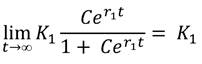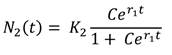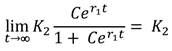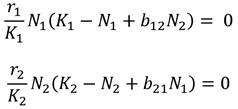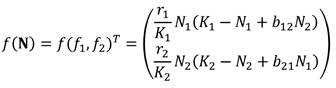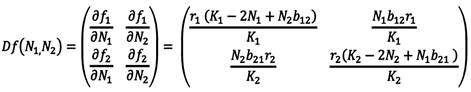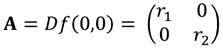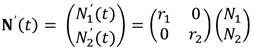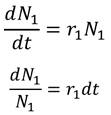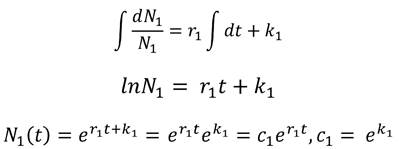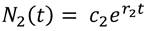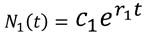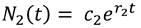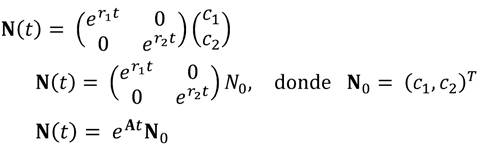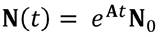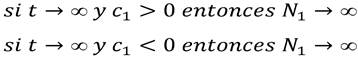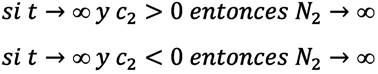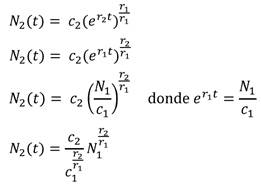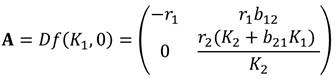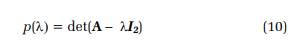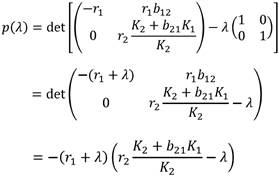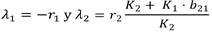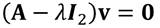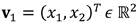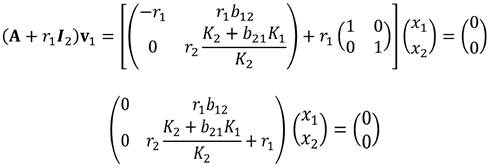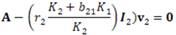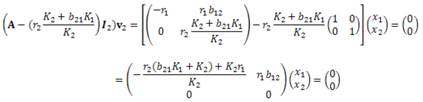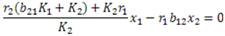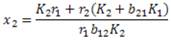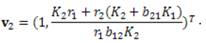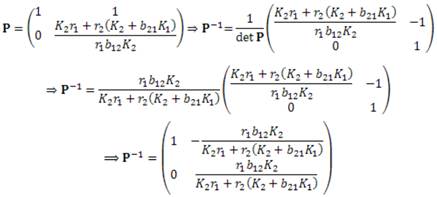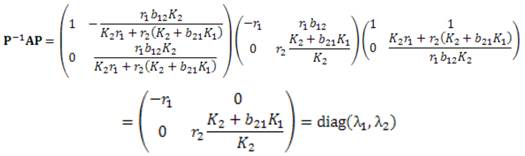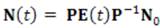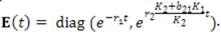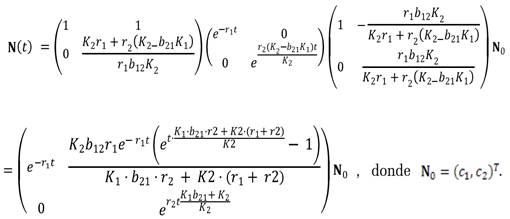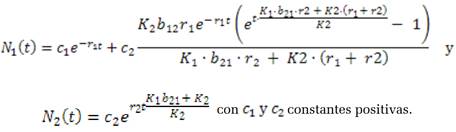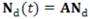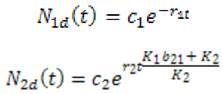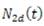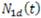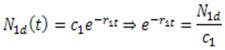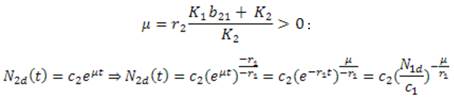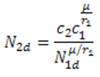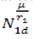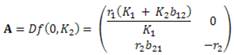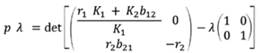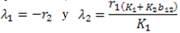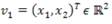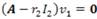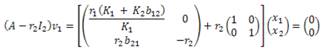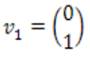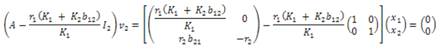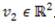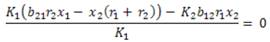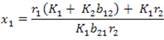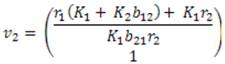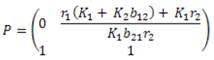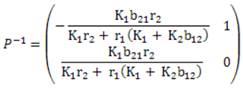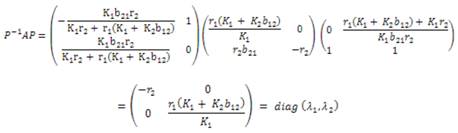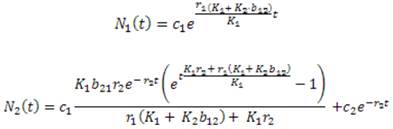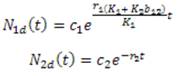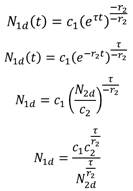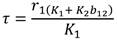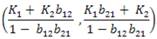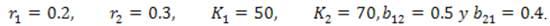Spanish (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
I. BIOECONOMÍA Y SU CONTRIBUCIÓN AL DESARROLLO
La actual crisis de mercado ha evidenciado como uno de los problemas fundamentales de las ciencias económicas ha sido su baja capacidad de interacción con ciencias como las naturales, las sociales o las físicas; centrando sus esfuerzos en el análisis de mercados y desconociendo la existencia de relaciones biológicas que se pueden generar en los entornos, bajo modelos holísticos y sistémicos.
Sobre este tema Nicholas Georgescu-Roegen (1994: 314), conocido como el padre de la bioeconomía y que basó sus supuestos en las leyes de la termodinámica y los análisis de Lotka, Schumpeter, entre otros teóricos, refiere la importancia de incorporar las leyes de la naturaleza en las teorías económicas así:
“Mi propia razón para afirmar que la economía debe ser una rama de la biología interpretada de forma amplia, descansa en el nivel más elemental de la cuestión. Somos una de las especies biológicas de este planeta, y como tal estamos sometidos a todas las leyes que gobiernan la existencia de la vida terrestre. Efectivamente somos una especie única, pero no porque hayamos obtenido el control total de los recursos de nuestra existencia. (…) la única característica que diferencia a la humanidad de todas las otras especies (…) es que somos la única especie que en su evolución ha violado los límites biológicos”.
De esa forma, los actuales esquemas de planeación y toma de política económica han fallado pues tratan de buscar el desarrollo en recetas económicas que desconocen particularidades y propenden por mejorar los indicadores de competitividad de los países en “vía de desarrollo”, pero que no funcionan pues desconocen los temas de “territorialidad” y “biodiversidad”.
En concordancia con lo anterior, el endogenismo se constituye en una alternativa de trabajo en búsqueda de bienestar social, pues su análisis discrepa de la teoría económica convencional y propone la formulación de modos de desarrollo propios, bajo conceptos de heterogeneidad, diversidad y complementariedad entre las diferentes áreas de estudio y la economía, de esta manera, se pueden generar interacciones positivas entre los ciclos artificiales del mercado y los procesos de consumo de recursos naturales y consumo de energía, es decir, posibilita dinámicas bioeconómicas.
En general, la bioeconomía juega un papel fundamental pues se define como:
“una economía que utiliza recursos biológicos a partir de la tierra y los océanos, así como desechos, como aportes para alimentos y alimentos para animales de producción, producción industrial y de energía… (Lo cual) también incluye el uso de bio-procesos para industrias sostenibles. Los bio-desechos, por ejemplo, tienen un importante potencial como alternativa a los fertilizantes químicos o para su conversión en bioenergía” (Comisión Europea, 2012).
Por lo anterior, la bioeconomía, como herramienta de interacción de las ciencias sociales, ciencias naturales, ciencias políticas, ciencias económicas, etc., permitiría generar un adecuado desarrollo territorial, cambiando el actual concepto de bienestar y negando los postulados antropocéntricos y antropomórficos que miran la naturaleza como inferior y desconocen las relaciones de dependencia o “mutualismo” en el ser humano y que por el contrario han fundamentado el modelo “presa-depredador”, que en palabras de Georgescu-Roegan (1996), derivan en una alta entropía. Por ello, la bioeconomía se convierte en un camino para reducir la desigualdad, la violencia, el racismo, y consumismo, sin dejar de lado la tecnificación, pero respectando los ecosistemas, es decir, posibilitando un “biodesarrollo”.
Finalmente, vale la pena aclararle al lector que los modelos bioeconómicos no representan una propuesta de modelos de desarrollo alternativos de tipo “super-fuerte” (Gudynas, 2011:83); sin embargo, se consideran modelos alternativos “dentro de la ideología del progreso y la modernidad” (Gudynas, 2011a: 47).
II. MUTUALISMO EN EL MODELO DE LOTKA-VOLTERRA
Antes de iniciar con el análisis formal de este modelo, es necesario resaltar que la teoría que fundamenta esta propuesta nace en los años 30, donde Alfred J. Lotka en 1930 y Vito Volterra en 1931, trabajando en forma independiente, pero con pensamientos similares desarrollan su trabajo más importante sobre dinámica poblacional, la cual propone tres principales tipos de interacción:
Si la tasa de crecimiento de una población N1 decrece y la otra población N2 se incrementa, éstas están en una situación de depredador-presa.
Cuando dos especies compiten por los recursos como alimento, agua, luz y espacio en un ecosistema, se presenta una interacción de competencia. Esto es, la tasa de crecimiento de dichas especies representa un decrecimiento de su población.
Si para cada población la tasa de crecimiento aumenta, entonces la interacción es de mutualismo o simbiosis.
Así, el modelo de Lotka-Volterra supone la existencia de tres formas de interacción poblacional: depredación, competencia, y mutualismo, donde el objetivo de este estudio será la aplicación del modelo mutualista mediante procedimientos matemáticos con el fin de: a) plantear formalmente que las interacciones mutualistas son posibles en un territorio. b) esbozar una alternativa de biodesarrollo sin desconocer la necesidad de dinámicas económicas, y c) fortalecer el conocimiento que hasta el momento existe sobre la bioeconomía y los modelos bioeconómicos discretos.
De este modo, conceptualmente se puede decir que el mutualismo es una interacción biológica entre dos o más especies, en donde todos se benefician y mejoran su aptitud biológica, jugando un papel fundamental en la supervivencia y conservación de las poblaciones, a modo de ejemplo se puede establecer como producto de la relación mutualista, la dispersión de plantas y semillas donde juegan un papel fundamental las aves, insectos y otras especies, y a nivel económico de un modo muy simple y básico se presenta la necesidad imperante de convivencia entre los compradores y vendedores, empleador y empleados, etc.; sin embargo, el análisis puede ir más lejos si se intenta comprender el modelo de equilibrio de Cournot, el modelo de equilibrio de Bertrand, la teoría de juegos, o las interacciones bioeconómicas resultado de las sinergias entre el ser humano y la naturaleza, como por ejemplo, el modelo dinámico Gordon-Schaefer.
Así, se procederá a desarrollar el análisis matemático del modelo, no sin antes establecer que el artículo no busca generar demostraciones sobre el mutualismo, pues el desarrollo de procedimientos matemáticos anula la prueba de hipótesis sobre la utilidad del modelo y por el contrario, trabaja intrínsecamente con la afirmación de que el mutualismo es la forma adecuada de lograr la sostenibilidad y sustentabilidad del mundo actual.
III. ANÁLISIS MATEMÁTICO MODELO DE LOTKA-VOLTERRA
1. Conceptos generales
A continuación se presentarán algunas definiciones y teoremas básicos de álgebra lineal utilizados para describir el mutualismo económico.
Definición 1.1. Se dice que x = pεRn es un punto de equilibrio del problema de valor inicial P.V.I x' = Ax , si x = p es una solución constante del P.V.I
Definición 1.2. Sea A una matriz cuadrada de orden n × n. Un escalar λ es un valor propio de A si existe en Rn un vector columna v distinto de cero, tal que Av = λv. Entonces v es un vector propio de A correspondiente al valor propio λ.
Definición 1.3. Una matriz cuadrada de orden n × n se llama diagonal si todos los registros que no están en la diagonal principal son cero.
Teorema 1.4. Si los valores propios de λ1, λ2, …, λn de una matriz Anxn son reales y distintos, entonces cualquier conjunto de vectores propios {v1, v2, ... vn} forman una base para Rn . La matriz P = {v1, v2, ... vn} es invertible y
Además la solución del P.V.I para el sistema
con x ∈ Rn A ∈ Rnxn viene dada por la expresión: x(t) = PE(t)P-1C, donde la matriz E (t) corresponde a E (t) = diag(eO1t eO2t, ... eOnt), denota el tiempo en cualquier
instante.
2. Modelo Propuesto
Como primer paso en la producción de un modelo mutualista se consideraran dos poblaciones N1 (Seres humanos) y N2 (Ambiente), se debe considerar el siguiente sistema.
Con
constantes positivas, donde r es la tasa intrínseca de crecimiento de cada especie y K es la capacidad de carga dada por el número de individuos que soporta un ecosistema1, b12 y b21 miden el efecto de competitividad2 de N2 sobre N1 y N1 sobre N2 respectivamente.
Cualquiera de las expresiones en el sistema (2), se reduce al modelo de crecimiento logístico, en ausencia de una de las especies, ya sea N1 ó N2 ; como se verá en el próximo apartado; mientras el factor N1N2 se introduce de forma positiva para representar que la interacción entre los entes mutualistas, conlleva su correspondiente beneficio.
3. Análisis del Modelo
Se prueba fácilmente que el sistema (2) equivale al sistema (3), en efecto,
(3)
Si N 1 denota el número de la especie I y N 2 denota la cantidad de la especie II, entonces se puede observar que en ausencia de la especie II (es decir N 2 = 0), se tiene que
(4)
Se analizará la E.D. (4). Para ello se utilizará el método de variables separables y posteriormente fracciones parciales, para encontrar la solución general. En efecto,
Realizando los procesos algebraicos necesarios se concluye que la solución de (4) es
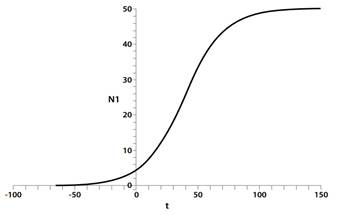
Ahora, el límite de la población N 1 cuando t crece indefinidamente, (t→∞) es
Por lo tanto, la especie I en ausencia de la especie II crece de forma logística y tiende a la población de estado estable3K 1 , como se ve en la figura 1. Realizando un análisis similar para la especie II que crece en ausencia de la especie I, se tiene que
4. Tipos de puntos críticos, estabilidad
Para determinar los puntos de equilibrio de (3), se encuentra la solución de las ecuaciones f 1 (N 1 , N 2 ) = 0 y f 2 (N 1 , N 2 ) = 0, es decir, se resuelven las siguientes ecuaciones:
Si N1 = 0 y N2 = 0, entonces f1 ( N1, N2 ) = 0 y f2 ( N1, N2 ) = 0, luego el punto (0,0) es un punto crítico de (3).
Si N1 = K1 y N2 = 0, entonces f1 ( N1, N2 ) = 0 y f2 ( N1, N2 ) = 0, entonces el punto ( K1 ,0) es un punto equilibrio del sistema (3).
Si N2 = K2 y N1 = 0, entonces f1 ( N1, N2 ) = 0 y f2 ( N1, N2 ) = 0, así el punto (0, K2 ) es un punto crítico de (3).
• Si
y
, contempla otro punto crítico, pero omitiremos las soluciones matemáticas alrededor de éste por la extensión de las operaciones.
Ahora, se encontrará el jacobiano de la siguiente función
Para ello se calculan las primeras derivadas parciales de las funciones f1 y f2. Se denota la matriz jacobiana de la función f en el punto (N1,N2) con la expresión
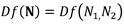y se define como:
La matriz jacobiana en el punto crítico (0,0) corresponde a
Dado que la matriz jacobiana es diagonal, se tiene el siguiente sistema no acoplado.
Donde N = (N1,N2)T. Es decir,
De aquí se tiene N'1 (t) = r1N1 y N'2 (t) = r2N. De la primera expresión,
De manera análoga se tiene que,
Luego, la solución general de (5), donde C1 Y C2 son números reales positivos es
(6)
(7)
En forma matricial la solución puede expresarse
Por lo tanto, la solución general de (5) es
(8)
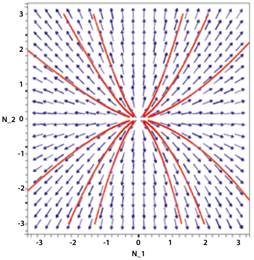
4.1. Retrato de fase y estabilidad delsistema (3)en el punto (0,0)
De las ecuaciones 6 y 7 se tiene:
además, para cuando c1 ≠ 0 y c2 ≠0 se tiene que
Puesto que los valores propios de A son λ1 = r1 > 0 y λ2 r2 > 0, entonces (0,0) es un punto fuente, además para r1 r2 , N2 es función lineal de N1 , y así el punto será un nodo propio inestable, mientras que si r2 ≠ r1 , las curvas solución tendrán un aspecto de ramas de parábola (Ver figura 2) y por lo tanto en general, el nodo es impropio e inestable, pero sus interacciones positivas cercanas muestran que la interacción es mutualista y depende de la tasa intrínseca de crecimiento, la capacidad de carga, y el nivel de competitividad o cooperación4.
Por su parte la matriz jacobiana para el punto crítico ( K1 ,0) es
Para el punto crítico se tiene el siguiente sistema acoplado:
Puesto que la matriz A no es diagonal, para resolver este sistema se debe calcular valores y vectores propios de la matriz A y diagonalizar la matriz para encontrar la solución del sistema.
a) Valores propios de A:
Sea λ un valor propio de la matriz A, en cuyo caso el polinomio caracterizado de A es
Donde I2 es la matriz idéntica de tamaño 2 × 2. Entonces,
Para determinar los valores propios de A, se encuentran las raíces de la ecuación (10). En este caso se obtiene
b) Vectores propios de A:
Para encontrar los vectores propios de la matriz A, se debe resolver el siguiente sistema
(11)
Donde v es un vector propio asociado al valor propio λ.
Sea
un vector propio de la matriz A asociado al valor λ1 = r1 , por (11), (A + r1I2 )v1 = 0, luego se tiene que
De aquí se tiene x2 = 0. Luego un vector propio es v1 = (1,0)T. Para el vector v2 ε R2 asociado al valor propio
se desarrolla
Entonces,
Luego,
, si x1 =1, entonces
de aquí se sigue que
Ahora la matriz P = (v 1 v 2 ) es
Por teorema (1.4) se tiene
Ahora, por teorema (1.4) la solución general en forma matricial viene dada por la expresión
donde.
Entonces se tiene que
Por componentes, la solución general es
4.1 Retrato de fase y estabilidad del sistema en el punto (K1, 0)
La solución para el sistema lineal asociado
en el punto (K 1 , 0), es
Desparametrizando, colocando
en función de
, estas ecuaciones se tiene
Ahora, hacemos lo correspondiente con N2d donde se ha cambiado
Así:
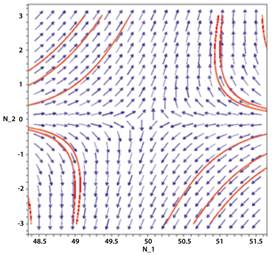
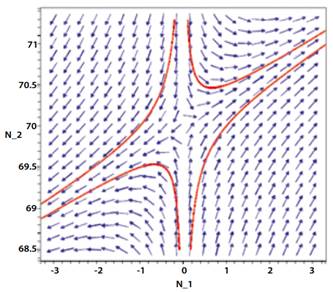
Se evidencia así la aparición de la familia de hipérbolas alrededor de este punto en el retrato de fase, puesto que N 2d es inversamente proporcional a
En la figura 3 se observa que las curvas en el diagrama de fase, son hipérbolas entorno del punto (K 1, 0), ahora dado que los valores propios de la matriz A tienen parte real positiva y parte real negativa, se deduce que le punto de equilibrio (K 1, 0) es un punto silla inestable del sistema (9), pero al igual que en la figura 2, se observan interacciones mutualistas que dependerán de la tasa intrínseca de crecimiento, la capacidad de carga, y el nivel de competitividad o cooperación, resumidas en el factor
que por ser positivo asegura el crecimiento de las dos especies.
En el punto crítico (0, K 2), la matriz jacobiana es la siguiente:
Dado que la matriz A no es diagonal, se tiene un sistema acoplado. Se procede de manera similar al análisis del punto crítico (K 1, 0) para encontrar la solución general del sistema (9).
a) Valores propios de A:
Sea O un valor propio de la matriz A. se tiene que:
Luego de hacer las correspondientes operaciones (como anteriormente se había visto) se encuentran los valores propios
b) Vectores propios de A:
Sea
un vector propio de la matriz A asociado al valor
por (11),
luego se tiene que
De este sistema se obtiene el vector propio asociado al valor propio λ 1 :
Para el valor propio λ2, se desarrolla el sistema:
Donde
Se obtiene la ecuación:
que para x 2 =1, se tiene que
Entonces el vector propio asociado al valor propio λ 2 corresponde a
Ahora, por el teorema (1.4) la matriz P = (v 1 v 2 ) es invertible y su inversa se encuentra aplicando la proposición (1.2). Entonces
De donde
Por otro lado, aplicando el teorema (1.4) se tiene
Ahora la solución matricial
Por medio de componentes, la solución es
Con
4.3 Retrato Fase y Estabilidad del sistema en (0, K 2 )
La solución para el sistema lineal asociado en el punto (0, K 2 ) es
Y de forma similar que para el punto (K 1, 0) se tiene por desparametrización,
Donde
Así, como en el punto crítico anterior, se puede observar por la relación inversamente proporcional entre las variables N 1d y N 2d una familia de hipérbolas cercanas al punto (0, K 2 ).
De este modo la figura 4 permite corroborar lo mencionado y observar el comportamiento de las poblaciones en la vecindad de este punto.
Dado que los valores propios de la matriz A tienen parte real positiva y parte real negativa, se concluye que el punto (0, K 2 ) es un punto silla e inestable del sistema (9), con relaciones mutualistas positivas en su escenario positivo.
4.4 Ejemplo del modelo mutualista
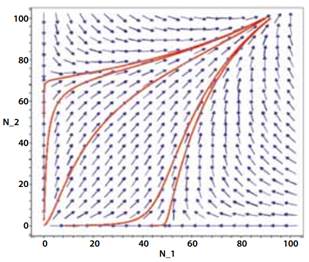
Para un análisis del punto crítico
se muestra su retrato de fase obtenido por métodos computacionales aplicando los siguientes parámetros:
donde se aprecia como dos especies que comparten una relación mutualista, tienden a estabilizar el crecimiento de ambas poblaciones, cerca del punto crítico (K 1, K 2) con cierta probabilidad a sobrepasar el límite impuesto por la capacidad de carga del ecosistema.
CONCLUSIONES
Los procedimientos matemáticos expuestos, demostraron que el modelo es inestable en los punto silla, es decir donde las relaciones entre las poblaciones no existen, pero a la vez, permitió establecer que dos especies pueden tener relaciones de cooperación que les permita desarrollarse, bajo unas condiciones preestablecidas de: tasas de crecimiento, capacidad de carga y competitividad (figura 5).
El modelo mutualista de Lotka-Volterra constituye un avance teóricomatemático importante para el desarrollo de esquemas de sostenibilidad y sustentabilidad ambiental enmarcados dentro de la bioeconomía y el biodesarrollo.
La bioeconomía se está constituyendo en una alternativa de búsqueda de bienestar social para las poblaciones desde la endogeneidad y la territorialidad. Ejemplo de ello son las prácticas Agroecológicas que en países como España, Estados Unidos, Australia, Ecuador, Bolivia y Colombia, se han iniciado.
La bioeconomía debe ser un elemento de trabajo en la planeación territorial del departamento de Nariño, pues el contemplar relaciones de equilibrio bioeconómico (Gordon, 1954) puede mejorar la sustentabilidad ambiental, la especialización productiva y la dinámica competitiva del departamento.
La bioeconomía sumada a procesos ciencia, tecnología e innovación (CTeI) puede dar soluciones a los problemas de energía, alimentos, salud y cambio climático, generando beneficios económicos, biológicos y sociales, para gran parte de la población mundial. Aquí, Latinoamérica puede generar un papel importante, pues su alto potencial en recursos, y su alta importancia como fuente de alimentos y biomasa, brinda a este continente una oportunidad para liderar procesos de sostenibilidad ambiental, sostenibilidad alimentaria, y bienestar social de la población mundial.
Por todo lo anterior, la planeación económica, social y política, tiene grandes posibilidades de cambiar los actuales entornos de crisis: ambiental, alimentaria, humanitaria y económica. Pero para ello la población debe concienciarse de la necesidad de mantener límites frente a la producción y el poder del mercado, sobre ello Absalón Machado (2011) establece que el desarrollo rural en Colombia dependerá de que exista “más Estado en el mercado y menos mercado en el Estado”, refiriéndose a la necesidad de que la planeación nacional debe replantearse y debe colocar limites a esa explotación irracional de los recursos, pues solo ello permitirá garantizar una sostenibilidad ambiental, alimentaria y económica en este país; sin embargo, esta debe considerarse una medida urgente frente a las actuales alarmas a las distintas crisis.
Finalmente, este artículo se convierte en una aproximación teórico - matemática al análisis de modelos de biodesarrollo, por ende, es necesario iniciar trabajos investigativos que posibiliten mejorar este análisis y permitan tener una mejor visión sobre los modelos bioeconómicos discretos y continuos.
