Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Caldasia
Print version ISSN 0366-5232On-line version ISSN 2357-3759
Caldasia vol.32 no.2 Bogotá July/Dec. 2010
Modelación de la distribución potencial de especies arbóreas a escala nacional en Colombia: una aplicación para Palicourea angustifolia Kunth y Palicourea guianensis Aubl
DOLORS ARMENTERAS
MARK MULLIGAN
Departamento de Biología, Universidad Nacional de Colombia, Apartado 7495, Bogotá D. C., Colombia. darmenterasp@unal.edu.co
Environmental Monitoring and Modelling Research Group, Department of Geography, King's College London, Strand, London WC2R 2LS (UK). mark.mulligan@kcl.ac.uk
ABSTRACT
The results in this study illustrate the methods of using the existing species' present records and environmental data to produce a niche-based model based on Mahalanobis distances, and also to predict the distribution of a number of tree species in order to apply it on a national scale to a tropical country such as Colombia. The technique applied is based on the Mahalanobis distance, a generalised squared distance statistic. We used environmental data integrated into a GIS, and a georeferenced collection of localities of Palicourea angustifolia and Palicourea guianensis to produce and test the predictive models. We used record data for Warszewiczia coccinea to validate the model. The two Palicourea species show largely complementary potential ranges. P. angustifolia shows a clear Andean distribution with a presence in lower and upper mountain areas but not in the highlands or in the inter-Andean valleys. P. guianensis was predicted throughout most of the lowland areas of Colombia including lowland Amazonian forests, and most of the tropical savannas of Orinoquia. The model predicted an overlapping distribution of the two species of 93.9 km2. The Mahalanobian approach contributes to the development of biogeographically oriented modelling that makes the best use of the available data in data-scarce regions (such as most of the tropics). The technique provides key information about the environmental niche of the species being modelled, and allows comparisons between the species. The prediction achieved for the two species was considered satisfactory.
Key words. Colombia, GIS, Mahalanobis distance, ecological niche, Palicourea, predictive distributions model.
RESUMEN
Este estudio presenta una metodología para usar datos existentes actuales ambientales y de presencia de especies para producir un modelo de nicho ecológico basado en las distancias de Mahalanobis -un estadístico de distancia generalizada ajustada- y también para predecir la distribución de especies arbóreas a escala nacional en un país neotropical como es Colombia. Se utilizan datos ambientales integrados en un Sistema de Información Geográfica, y una serie localidades georeferenciadas de registros biológicos de Palicourea angustifolia y de Palicourea guianensis para producir y probar los modelos predictivos desarrollados. Las dos especies de Palicourea demuestran una distribución complementaria. P. angustifolia tiene una distribución claramente andina con presencia en áreas de montaña bajas y medias, pero no en la alta montaña ni en los valles inter-Andinos. Los resultados de la predicción de distribución para P. guianensis indican presencia en tierras bajas, incluyendo bosques amazónicos, y algunas zonas de la Orinoquia. La predicción del modelo indicó que existe un sobrelapamiento en la distribución de las dos especies con una superficie de 93.9 km2. El uso de la prueba de Mahalanobian contribuye al desarrollo d ela ciencia de la biogeografía ya que permite modelar patrones de distribución en regiones con poca o escasa información. La técnica presentada aquí proporciona información importante sobre el nicho ambiental de la especie que es modelada, y permite comparaciones de patrones de distribución entre especies. Para concluir, los modelos de ambas especies aquí estudiadas pueden considerarse como satisfactorios.
Palabras clave. Colombia, SIG, distancia Mahalanobis, nicho ecologico, Palicourea sp., modelo predictivo de distribución.
Recibido: 31/03/2009
Aceptado:28/07/2010
INTRODUCTION
Predictive distribution models are an important tool for understanding factors that control species distributions, and have been broadly used in biogeography, ecology, conservation planning, and natural resources management (Busby, 1986, 1988; Box et al. 1993; Anderson et al. 2003; Farber & Kadmon, 2003). Such models have been developed for temperate areas (Carpenter et al. 1993; Franklin, 1995; Austin & Meyers, 1996; Bolliger et al. 2000; Felicisimo et al. 2002; Scott et al. 2002); however, tropical regions, where the areas harbouring the highest biodiversity remain, have rarely been the subject of such studies, specially South America. It is in the tropics, and specially in the sparsely inventoried neotropics, that these models can be of a major value, and have their greatest potential (Stockwell & Peters, 1999; Anderson et al. 2003, Hernández et al. 2006; Hijmans & Graham, 2006).
Rapid assessments of biological diversity and its geographical distribution are required to develop sound conservation policies, but particularly for a basis from which to start monitoring biodiversity change toward the 2010 biodiversity target of reduced rates of biodiversity loss agreed at COP 7 of the Convention on Biological Diversity (CBD, 2000). However, monitoring requires a baseline inventory, and a full inventory is practically impossible to achieve in biologically rich countries with significant wilderness areas, such as Colombia. Information is incomplete and tends to be biased toward accessible sites and specific taxa (Bojorquez et al., 1993). The great expense of new inventories requires the full utilisation of the limited physical and biological data that already exist in order to design the optimal strategy for further inventory.
Primary biological inventory data exist in the tropics, in the best of cases, as georeferenced coordinates from localities where scientists from museums, universities, or herbaria have collected specimens for their study. Most of this data are held in museums and herbaria around the world, and if repatriated and organised as a georeferenced record, it can provide a considerable database for better understanding of species distributions (see webs of INBIO in Costa Rica and CONABIO in Mexico). This information is usually in the form of a record of observation and rarely contains data indicating either absence or abundance at collection sites, specially in poorly sampled tropical regions (Peterson & Cohoon, 1999; Anderson et al. 2003). Most of the current modelling approaches require both presence and absence of data for their estimation. Moreover, many of these have been applied using mostly climatic data (Busby, 1988; Carpenter et al. 1993; Jones et al. 1997; Smith et al. 1997; Peterson & Cohoon, 1999; Robertson et al. 2001; Wilds et al. 2000;), despite the fact that spatially detailed landscape data (elevation, slope gradient, slope aspect, soils, geology, land cover) are now widely available at coarse spatial resolutions, and are clearly important in determining species distributions (Velázquez et al. 1996; Pérez.Vega et al. 2008).
Techniques which can be applied using only presence records are much less developed (Robertson et al. 2001; Carpenter et al. 1993; Gower, 1971; Anderson et al. 2003). In this study we present the application of a technique for mapping potential species distributions that utilises presence data for the prediction, and that is based on the Mahalanobis distance or generalised squared distance statistic (Clark et al. 1993; Knick & Dyer, 1997; Knick & Rotenberry, 1998). One of the most important advantages of this technique is undoubtedly the ability to cope with the presence of data only, thus making no a priori assumptions about the distribution of the species, and also avoiding the use of potential false negatives (Dunn & Duncann, 2000). In addition, the approach developed here allows the implementation of environmental variables' input from multiple sources of continuous, categorical, or Boolean data (Bar-Hen & Daudin, 1995). Further, the possible different scales of measurement of input variables do not have any effect since the Mahalanobis statistic is dimensionless, being a function of standardised variables (Clark, et al. 1993; Knick & Rotenberry, 1998). Neither does it assume a normal distribution of the data, a normality that for most of the species is not satisfied (Austin & Smith, 1989). Nevertheless, its properties are best known when the assumption of multinormality is correct (Knick & Dyer, 1997). Last, the model developed here is firmly grounded in the niche theory that suggests the existence of optimal environmental conditions for species (Hutchinson, 1959; MacArthur, 1968; Whitaker, 1975).
Facilitating a strategic, cost-effective, and rapid inventory of Colombian biodiversity requires tools that use existing data to help focus on those areas in which the greatest diversity can be observed (and conserved) for the least cost, and to identify regions in which high diversity and rapid environmental change are in conflict. Given the rate of land use change and other forms of development in the Colombian countryside, and the lack of human and economic resources for wholescale inventory, some rapid science-based techniques for prioritisation of inventory and management activities are essential. Modelling species distributions has the potential to provide a much more spatially comprehensive assessment at the national scale than traditional point, plot, and transect-based studies, but will never be as reliable as field measurement, only more practical over large areas, or when there are reduced funding and other resources constraints. The main assumptions behind the modelling undertaken here are that:
--- the principles of the species' fundamental niche theory (Hutchinson, 1957) are correct.
--- on the national scale, environmental factors such as climate and topography control the distribution of species, and are more important than more local ecological factors (such as competition). The heterogeneity and variability of Colombian climates and landscapes features can be described adequately for the purposes of species distribution modelling at a 1km grain and using globally available datasets.
--- tree species distributions (under natural land cover) are controlled by these climatic and landscape drivers over other ecological interactions.
THE STUDY AREA
Colombia has a continental area of approximately 114 million hectares, representing 0.7% of the world's land surface. Colombia is geographically a variable country. The western part is mostly mountainous (45% of the territory) with the Andes which comprises of three cordilleras. However, most of the country is lowland plains located below 500 m. Due to its altitudinal variability determined by the presence of the three longitudinal mountain ranges, there is a diversity of climates. A diversity of geological and soil units are also associated with these cordilleras and their variable climates.
Although its flora and fauna are only partially inventoried, Colombia is thought to contain 10% of the world's biodiversity (in terms of vertebrate & plant species) making it one of the most biologically diverse regions in the world (IAvH, 1998; IAvH, 1998a). Colombia hosts a great variety of ecosystems including forests, savannah, arid ecosystems, and wetlands, and 50% of the area is still under natural cover.
METHODOLOGY
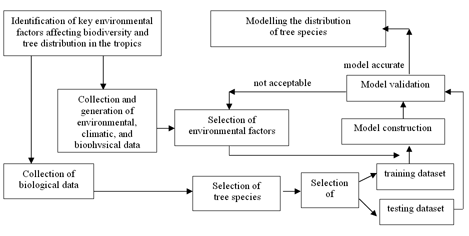
The objective of this research was to develop and apply in Colombia a methodology that successfully uses existing species' presence records and environmental data in a niche- based model to predict the distribution of the tree species. The general methodological approach of this research is summarised in Fig. 1, as a combination of environmental and biological species data collection, computer-based spatial modelling of environmental parameters, and a multivariate modelling procedure developed to predict species distributions.
Environmental data
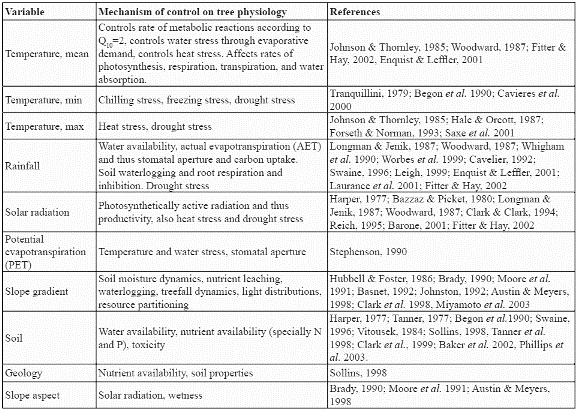
Ten environmental variables from a countrywide GIS dataset at the resolution of 1km2 (Armenteras, 2003) were analysed to construct the potential distribution model for the species. These consisted of seven continuous variables: mean, maximum, and minimum monthly temperatures (ºC), mean annual precipitation (mm), mean annual solar radiation (W m-2), annual potential evapotranspiration (mm), slope gradient (%), and three categorical variables: soil type, geology class, and slope aspect class. Climatic variables were modelled (Armenteras, 2003) by interpolating from point meteorological station datasets (Jones, 1991). SOLARFLUX (Rich et al. 1995) was used for modelling solar radiation receipt, and the Thornthwaite method provided the annual potential evapotranspiration (Armenteras, 2003). Slope gradient and slope aspect class were derived from the GTOPO30 DEM (USGS, 1996). Soil information was obtained from the Colombian Agustin Codazzi National Geographic Institute (IGAC). The soil map was constructed from regional and local studies all over Colombia and generalised at 1:1.500.000 into a national soil map by IGAC (1982). Geological information came from the South American Land Cover characteristics database of the EROS Data Center DAAC (USGS, 1996). All of the above factors have been shown to be indicators of potential physiological processes in trees such as growth and establishment (Table 1). Slope gradient is also an indicator of the variation of climatic properties within a cell since it is a measure of the within-cell range of elevation.
Species data
The available biological data on species distribution was compiled from national and international collections and museums including the collection at the Humboldt Institute Herbarium (CB); Missouri Botanical Garden (MO); Herbario Jardín Botánico "Joaquin Antonio Uribe" in Medellín (JAUM); Instituto de Investigación Científica del Valle del Cauca (INCIVA); New York Botanical Garden (NYBG); Herbario Amazonico Colombiano (COAH); the Herbario Nacional Colombiano (COL) at the Instituto de Ciencias Naturales (ICN) and Herbario Alfonso Fernandez Perez (HAFP). Many records were georeferenced by the original collector often using 1:500.000 topographic maps (IGAC, 1970-1085), while others were georeferenced according to the collection site name using cartography available for the site. All records were converted to the same coordinate system for this study: Geographic, decimal degrees, WGS 1984 Datum and integrated with the ARCVIEW GIS (ESRI Inc., 1998).
We focused on modelling the distribution of species of the family Rubiaceae because they are well-studied, are ecologically and taxonomically diverse with high species richness, and abundant in many ecosystems. Rubiaceae are amongst the families with the highest number of species in Andean and humid tropical forests in Latin America (Taylor, 1999; IAvH, 1999a). Rubiaceae are also well-understood taxonomically (Taylor, 1999; IAvH, 1999a) and are ecologically important: most of the species of Rubiaceae, specially of the genera Psychotria and Palicourea, are important sources of food for animals (IAvH, 1999a). This family has been relatively well-sampled geographically (Lozano, 1994; Anderson, 1995; IAvH, 1999a; Taylor, 1999, Rangel-Churrio, 1995, 2000: Rangel-Churrio et al. 1997). Finally, new data becomes available with almost every new field expedition being undertaken in Colombia.
To develop the predictive distribution model, we focused on two of the species that had more than 50 presence records: angustifolia Kunth 1818 (Rubiaceae) and Palicourea guianensis Aubl.1775. The first species belongs to the subgenus Montanae, and is generally found at higher elevations between 1,000-3,500 m (Taylor, 1997a, b). The second species belongs to the subgenus Palicourea, and is a widespread lowland species (Taylor, 1997a, b) generally found at lower elevations of 0-1,200 (1,500) m. We also used collection information for another lowland species of this family, Warszewiczia coccinea, to be used for validation purposes of the results.
Modelling approach
The approach used for the construction of potential distribution models is based on the Mahalanobis statistic (De Maesschalck et al. 2000), and has the following underlying assumption: given a set of environmental variables and a set of known species' locations, a training set can be built to define a multivariate space (m) that best describes the areas where a given species (j) is found and which may thus represent the "ideal conditions" for the species. The results can then be used to identify areas of the country where the environmental conditions are most similar to those of the "ideal" multivariate space for the species.
The Mahalanobis distance for mapping the potential habitat of species has been used successfully by Clark et al. (1993) and Knick & Dyer (1997). The Mahalanobis statistic can be used when there is only presence data, whereas other multivariate methods such as logistic regression or discriminant analysis require data on areas where the species is known to be present and also absent (Dunn & Duncan, 2000). In addition, Mahalanobis distances are the sum of the squares of uncorrelated standardised variables; this means that assumptions of multivariate normality do not have to be met (Clark et al. 1993). Indeed, the method corrects for correlation between the different variables which are compensated for by an estimated covariance matrix (C) used to create new uncorrelated variables (Hand, 1981; Duda, 1997). The Mahalanobis statistic is also dimensionless since it is a function of standardised variables (Hand, 1981; Duda, 1997). Mathematically, the Mahalanobis distance from a vector x to a mean vector m is defined as: r2 = (x-m)' C-1 (x-m), where C is the covariance matrix for a set of observed vectors and has been explained in earlier studies (Duda, 1997; Farber & Kadmon, 1993), and so we will not discuss it in detail here. For a given species, the vector m represents its "optimum environmental conditions". An index of similarity for a site can be obtained by calculating the distance from those sites which are characteristic to the vector m using the Mahalanobis statistic.
To estimate the Mahalanobis distances, C and m have to be calculated by performing a step-by-step matrix algebra amongst map layers containing environmental parameter information. We used an Avenue routine in ARCVIEW that automates this step and also assigns a Mahalanobis distance to every 1 x 1 km2 grid cell in the study area. Areas with higher similarity have a smaller distance than those that differ more from the environmental characteristics of the presence data locations.
To model tree species distribution using this approach, the available presence data for the species were split into training and testing datasets (Figure 2) using three different ratios of parameterisation to validation data chosen based on different percentages of total dataset to understand the effect of the parameterisation dataset size on the simulation quality better . Table 2 summarises the number of records used for running a predictive model, and also the records set aside for validation purposes for each species. The three ratios were used to construct ten random sets of presence records resulting in a total of thirty different model sets (ten for each ratio) per species. For validation purposes, absence for a species was inferred using the localities with no known record for it but where two other species of the same family had been collected: for example, absence data for Palicourea angustifolia equals those localities with recorded presence of Palicourea guianensis and Warszewiczia coccinea and no presence of P. angustifolia. The number of absence records used was fifty-one for P. angustifolia.
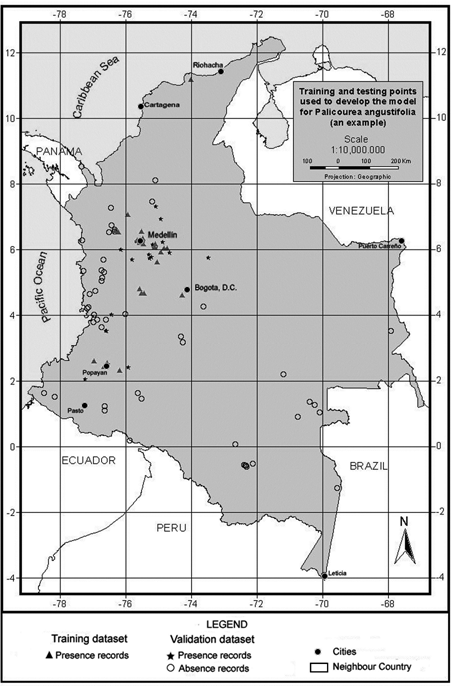
Figure 2. An example of the distribution of training and testing points to develop the model.
Table 2. Numbers of presence records used for training and testing for each species

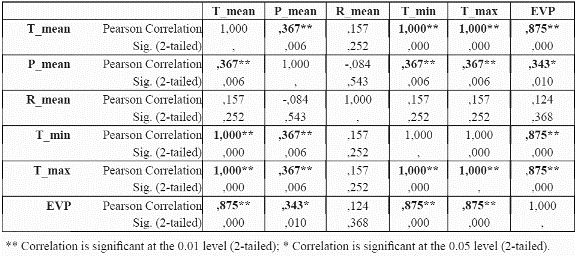
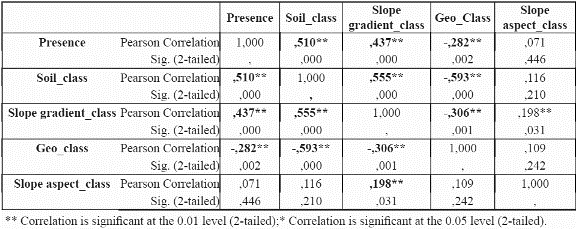
To reduce the dimensionality of the model, to minimise parameter redundancy and select the most meaningful variables, we performed bivariate correlation analyses for the species P. angustifolia (Table 3 and table 4) using significance levels of 0.05. For continuous variables (mean, maximum, minimum temperatures, mean precipitation and potential evapotranspiration), the correlations between these variables were analysed at localities with presence of the species. For continuous variables, a test of colinearity between each variable pair was performed. Only those variables which were not significantly collinear were incorporated into the model. If two variables were collinear, the controlling factor that has a more direct control on plant physiology and plant growth was chosen over the other variable, for example, temperature is collinear with elevation since elevation is a control of temperature. Temperature is a control of plant growth (see Table 1). Elevation is only a control on plant growth because of its impact on temperature (and other variables). Thus temperature is preferred to elevation (Velázquez 1994). The same process was undertaken for P. guianensis
Initially, preliminary testing was undertaken by producing predicted maps based on the Mahalanobis distance for P. angustifolia. We used ten different combinations of environmental parameters to identify the best fitted model for the species. The Mahalanobis distances were computed from the thirty different training datasets prepared earlier (3 parameterisation to validation ratios x 10 repetitions of randomly selected presence records). These resulted in a total of 300 predicted maps that represented a large dataset for further analysis.
For predictive distribution models, accuracy assessment is usually carried out through the construction of an error matrix (a cross tabulation of the number of correctly and incorrectly classified observations) from which several measures of model performance are derived (Stockwell & Noble, 1992; Fielding & Bell, 1997; Stockwell & Peterson, 2002b; Anderson et al. 2002a, 2003; Farber & Kadmon, 2003). Each one of the 300 predictive maps was independently validated with the testing datasets, and the results were summarised in an error matrix containing four measures of accuracy used commonly in this type of research: sensitivity, specificity, overall accuracy, and the Kappa statistic (Fielding & Bell, 1997; Farber & Kadmon, 2003).
Sensitivity is defined as the probability of correctly predicting a presence and specificity is of correctly predicting an absence. As aforementioned, we used records of the two other species for this study (P. guianensis and Warszewiczia coccinea) as absence sites to be included in the validation dataset. For the purpose of this study and for practical reasons we assumed that where there have been collection missions (focused on the same family) but no reports of the P. angustifolia, this species can be considered as absent from those localities.
We also undertook a preliminary survey of the Mahalanobis distance to be used as a threshold (d) beyond which a site is not considered as potentially suitable for the species. This threshold is used to determine the accuracy of the model. However it has to be taken into account that as the value of d increases, so does the the probability of including not only suitable sites but also potentially nonsuitable sites. We used the 90th percentile threshold after preliminary analyses (Armenteras, 2003). Table 6 summarises the results obtained for each of the environmental parameter combinations. The combination of variables that provided higher predictive success was selected for further analysis.
RESULTS
From the results in Table 3 and table 4, it can be observed that evapotranspiration and minimum and maximum temperature are highly correlated to mean temperature, and thus mean temperature was selected for further use in the distribution models and the other three variables were discarded. Although evapotranspiration was also a strong physiological control, the variable was not considered because it was a secondary data derived from the temperature dataset. For precipitation, although the results indicate a significant correlation of precipitation with mean temperature, the variable is sufficiently different from temperature in its physiological impact to make it worthy of inclusion. Regarding categorical variables, slope aspect does not seem to be an important variable for the species (i.e., no correlation at all with presence of the species was found), hence it was not used further. Slope aspect is usually only important for driving solar radiation loads at sites away from the equator where N-S radiation differences become very large. Slope aspect (like slope gradient) is also notoriously difficult to quantify from coarse resolution topographic data; hence it was removed from consideration.
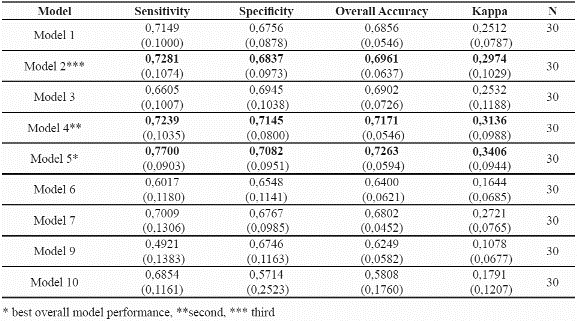
Accuracy measures were obtained for all the models and all model runs (Table 5). A threshold of the 90th percentile to the mean Mahalanobis distances of the training dataset was used for validation purposes, that is, areas within the 90th percentile to the mean mahalanobis distance were considered as suitable sites for the species. Table 5 summarises the results obtained for each one of the combinations of environmental parameters. Model 5 which uses: mean temperature, solar radiation, soil types, and slope gradient shows the highest predictive success for both species. Table 6 presents the corresponding accuracy assessments for the two species.
The standard deviation values are in parenthesis.
Predictive distribution models
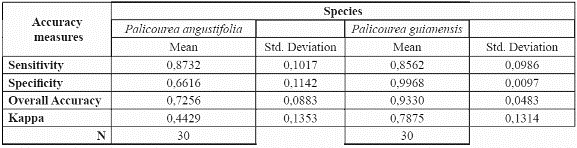
After demonstrating that the preliminary model validated well with an accuracy of over 0.8 for both species, we modelled the species' potential geographic distribution using the whole available dataset of presence records. The resulting map can be seen in Fig. 3 & fig. 4.
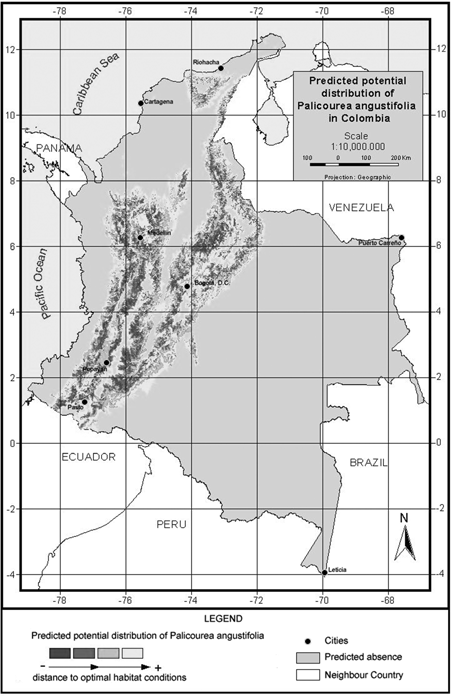
Figure 3. Model of predicted potential distribution for Palicourea angustifolia in Colombia.
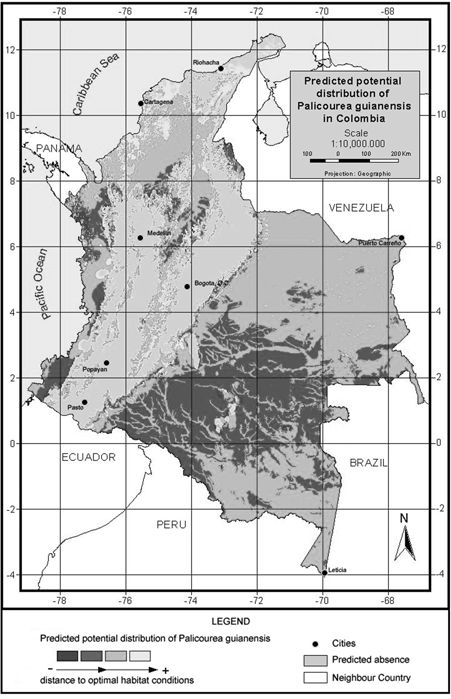
P. angustifolia and P. guianensis show largely complementary potential ranges (Fig. 3 & fig. 4). P. angustifolia shows a clear Andean distribution with presence in lower and upper mountain areas but neither in the highlands nor in the inter-Andean valleys. The model also predicts the potential distribution of the species in both the upper mountain areas of Sierra Nevada de Santa Marta and the Serrania de La Macarena. A total of 308,768 km2 are predicted as potentially suitable area for P. angustifolia. On the other hand, P. guianensis was predicted throughout most of the lowland areas of Colombia including lowland Amazonian forests, and most of the tropical savannas of Orinoquia. Predicted as unsuitable for the species are the few highland areas in the Amazon such as around the Araracuara formation and the hill complex of Mitu. In general terms, the species was not predicted in the wetter lowland areas of the Pacific region or in the most arid enclaves of la Guajira, although some lowland areas of the Sierra Nevada de Santa Marta are predicted as potentially suitable for the species. A large area of 1,004,777 km2 is predicted as potentially suitable for P. guianensis.
However, when analyzing the Mahalanobis distances observed from the 55 records used to construct the model for P. angustifolia, 5 of them (Table 7) have a Mahalanobis distance much higher than the 90% percentile used for model validation purposes. This means that they fall precisely in the predicted absence pixels. However, if we look in detail at each of these records, all of them are within 1-2 pixels (km) of larger areas predicted as presence areas (Fig. 5). A similar situation occurred with 5 out of 60 records of P. guianensis (Table 7, also occurring within 2 km ) pixels predicted by the model as sites of species presence for its model.
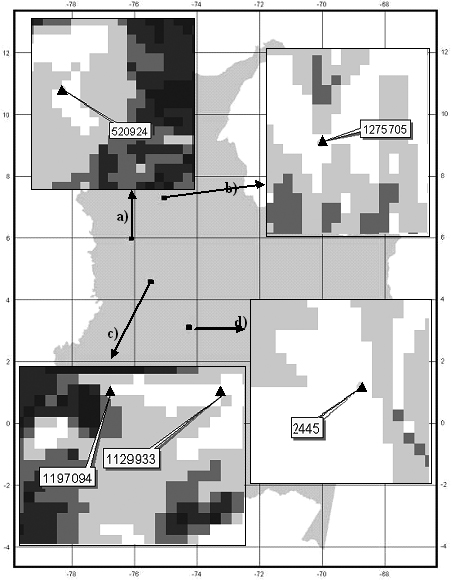
Figure 5. Location and specimen number of five presence records of P. angustifolia (a,b,c from Missouri Botanical Garden, d from HAFP database) predicted as absence. Pixel size is 1 km2.
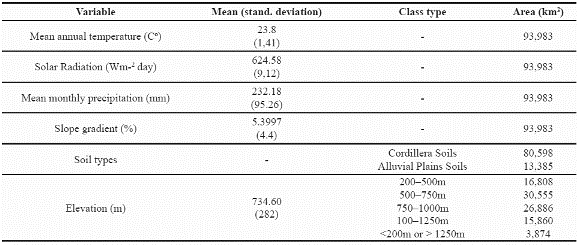
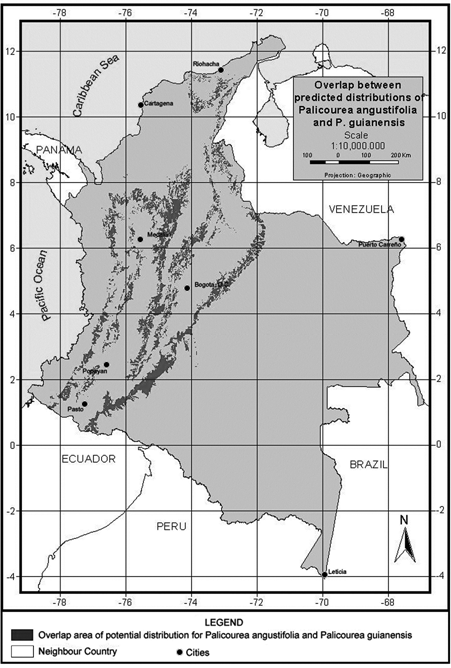
We undertook a final analysis of these two species, looking for areas in which the predicted distribution of the two species overlaps. Figure 6 illustrates the geographic extent (93.983 km2) of areas predicted suitable for species co-occurrence. This area of potential overlap between the two species represents 30.4% of the potential distribution of P. angustifolia and 9% of P. guianensis and the environmental characteristics of this are indicate a mean annual temperature around 23.8 degrees Celsius, 624.5Wm-2day of solar radiation and around 232 mm of mean monthly precipitation (see more details in Table 8).
DISCUSSION
This study focused on developing and testing an alternative methodology that may help optimising the use of the existing species' presence records and environmental data within the framework of a a niche-based model of species distribution to predict the range of tree species occurrence in a relatively simple and efficient manner in tropical countries
Species data for distribution modelling
A limited number of records were available for building the predictive distribution models. Out of the 3000 records collected, only 3 species of Rubiaceae had over 50 records available for modelling, and even these 3 species had to go through a database purge of their localities, having specimens repeated, localities incompletely, inaccurately reported or poorly georeferenced, and typing errors. Also, errors in the accuracy of the geographic coordinates of the species data were impossible to determine. Many samples were georeferenced from museum label descriptions, and these were often rather generally located, specially the older records, not to mention the known bias of collection sites, the lack of a sampling design, and the different origins of the data.
Another important source of error, particularly for those working in the tropics is the determination of the species. This was minimised by choosing the genera Palicourea, on which there is extensive systematic recent work (Taylor, 1996, 1997a, 1997b, 1999, & 2000).
Despite the deficiencies inherent in the use of primary inventory data, the model developed provides very useful information on the species distribution in relation to environmental controls.
Species distribution models
The technique developed here for mapping potential species distribution offers a number of advantages over other classical modelling techniques (Stockwell & Peters, 1999; Anderson et al. 2003). One of the most important is undoubtedly the ability to cope with presence-only data, thus not making any a priori assumption about the distribution of the species, and also avoiding the use of potential false negatives (Dunn & Duncann, 2000). However, we did use surrogate absence data in this case for validation purposes, but validation can be undertaken by other means (i.e., field inventories). The approach applied here allows the use of environmental variables from multiple sources and in continuous, categorical, or Boolean form (Bar-Hen & Daudin, 1995). Further, different measurement scales of input variables are not problematic since the Mahalanobis statistic is dimensionless, being a function of standardised variables (Clark et al. 1993; Knick & Rotenberry, 1998). Finally, the technique does not assume a normal distribution of the data, which, for most species, is not satisfied (Austin & Smith, 1989).
The model developed here is based on niche theory (Hutchinson, 1959; MacArthur, 1968; Whitaker, 1975), which has a strong background in ecological theory. However, it is important to clearly differentiate the fundamental versus the realised niche of species (Hutchinson, 1959) and to understand further that the predictions developed here represent neither of these, but rather a subset of the fundamental niche which is limited to the distribution of the species within the environments present (and studied) in Colombia. The approach is also limited due to the fact that only a few environmental variables are considered and others may be just as important but without readily available data such as for example historical or paleoclimatic data. No vegetation data, potential or current, has been incorporated in the model and neither has the current state of the ecosystems been considered, including deforestation, or other threats. Also no subgrid scale variability is taken into account which, at a spatial resolution of 1 km over heterogeneous mountain terrain means that the environmental properties distributed here and those experienced by individual trees on the ground may be quite different.
When many variables are involved, the Mahalanobis approach requires some kind of a priori manual data reduction to identify the most important input parameters for the model specially where there is significant correlation between the variables (Knick & Rotenberry, 1997; De Maesschalck et al. 2000; Wilds et al. 2000)
Data reduction
The most parsimonious model at a given level of prediction accuracy is always the best model (Mulligan & Wainwright, 2003). The data reduction results (Table 3 and table 4) lead to a considerable reduction of possible variables to be used in the model. Temperature variables were clearly collinear, since they are all modelled from linear regressions between station meteorological data and elevation. Similarly, potential evapotranspiration was derived from temperature using the Thornthwaite methodology (Section 3.3) in which temperature is a key variable. It turns out that no extra important information was provided through modelling these secondary variables since mean temperature remained as the best predictor. Temperature and precipitation were highly correlated at presence sites of P. angustifolia (probably because both are functions of elevation, though temperature is a nonlinear function). Due to the importance of precipitation in the physiology and distribution of species (Begon et al. 1990; Richerson & Lum, 1980; Brown & Gibson, 1983; Turner et al. 1988; Wright et al. 1993; Gaston, 2000), we did not rule out the incorporation of this data, alongside temperature, in the preliminary tests of the algorithm performance.
The predictive accuracy of the models in which we incorporated the precipitation data was substantially lower than more limited combinations of variables (Table 3 & table 4) such as mean temperature, solar radiation, soil type, and slope gradient. The Slope aspect was not incorporated into the modelling approach due to its tested irrelevance to the distribution of P. angustifolia. This is likely due to the fact that representation of the slope aspect experienced by trees in the field is rather difficult at a 1 km grain, and the same probably holds true for slope gradient.
Harrel et al. (1996) suggest that the number of final predictors in modelling should be m/10, where m is the total number of observations. In this analysis, and considering that the number of presence records is 55 for P. angustifolia and 60 for P. guianensis, 5 variables would be suggested, and 4 to 6 were tested with the best model resulting from 4 variables (Table 5).
Errors and accuracy
Several questions arise when looking at the issue of accuracy assessment. The first is that although the importance of understanding error in models is clear (Rykiel, 1996; Boone & Krohn, 2002; Elith et al. 2002; Guisan & Zimmermann 2000; Guisan et al. 2002), there is still some extent of subjectivity in the interpretation of model accuracy, specially for species' distribution models (Guisan & Zimmermann, 2000). Different measures of model performance have been proposed (Rykiel, 1996; Fielding & Bell, 1997; Guisan & Zimmermann, 2000; Anderson et al. 2003). For any given threshold, there are locations with values below it where the species is present (true positives) and absent (false positives). Similarly, there are sites that the model predicts as unsuitable (above the threshold) that are occupied (false negatives) and where the species is absent (true negatives). We chose to use error matrices and four measures of accuracy that required absence data (not required for the prediction, but useful in validation).
This leads to the question of how accurate it was to use other species' localities records as absence sites for the species that were modelled. In herbarium and collection datasets, "real" absence data does not exist, and this was partly the justification for undertaking a modelling approach which can use only presence data. However, wherever clearly related species are collected during the same collection missions by the same collectors, sites where P. angustifolia had not been collected but where P. guianensis had been, could be considered absence sites for P.angustifolia. Some 11 sites had collection records of both species at the same time suggesting that the species do overlap in distribution (7 out of 9 are located in overlapping distribution areas). This reaffirms the fact that the definition of absence sites for validation purposes was appropriate. One of the specimens collected for P. angustifolia ( NO. 1275705, MO) was not predicted by the model to be present in the locality collected (Table 7). This might suggest either the lack of inclusion of an important variable in the modelling exercise or some kind of interpolation error in the GIS databases, significant unmeasured subgrid variability in the environmental variables, or georeferencing error in the records. This record, which is less than 2 pixels away (2 km) from areas that were modelled as overlapping distribution areas for the species, seems to suggest the latter as a possibility. The other specimen of P. angustifolia (NO. 2469, HAFP) has a distance of over 15 km to the overlapping area. Both the localities which were incorrectly predicted in the model for P. angustifolia, were correctly predicted in the distribution model for P. guianensis. However, the localities where the P. angustifolia HAFP specimen is recorded has an elevation of 160 m, which is outside the natural range of the species. Arguably this might be probably a collection/measurement error, a typing error, or a species determination error. In general, observation or measurement errors lead to reduced predictability of models (Boone and Krohn, 2002)
Geographic distribution
Despite the propagation of measurement and systematic errors, effective prediction of test localities for both species could be achieved in all 3 significant models. Judgement by experts also gave a positive assessment of the resulting distribution patterns corresponding fairly well to the knowledge of the species and recorded records (C.M.Taylor, E. Calderon, pers. comm; Jimenez 2002, Rangel 1995, 2000). P. angustifolia shows a clear Andean distribution with presence in lower and upper montane areas but neither in the highlands nor in the inter-Andean valleys. The best fitted model also predicts the potential distribution of the species in both the upper mountain areas of Sierra Nevada de Santa Marta and the Serrania de La Macarena. Taylor (1997a, b) states that this species belongs to the subgenus Montanae, a notion that is in agreement with the modelling results obtained for this species.
On the other hand, P. guianensis was predicted throughout most lowland areas of Colombia including the lowland Amazon forests and most of the tropical savannas of Orinoquia. The few highland areas in the Amazon such as around the Araracuara formation and the hill complex of Mitu were unsuitable for the species. This species is a widespread lowland species (Taylor, 1997a,b). Taylor (1997a, b) classifies this species to the subgenus Palicourea and describes it as generally found at lower elevations, 0-1,200 (1,500) m, throughout the range of the genus. Again, this is consistent with the prediction of the obtained in this modelling effort.
CONCLUSIONS
Modelling of species' responses to static or changing environmental conditions has become an increasingly important part of modern ecology and biogeography. This kind of modelling can save time and money in the formulation and execution of biological inventories, a task which Colombia, along with other countries, is carrying out in fulfilment of its obligations to the Convention on Biological Diversity. Particularly in the tropics, modelling can provide a quicker and potentially more reliable approximation for identifying areas with high biological diversity when lack of resources or time constraints are in place, and complement small-area field inventory that might take longer to achieve. By limiting and approximate habitat niche of a species (with limitation since not all ecological or phylogenetic aspects are included), it is possible to predict its distribution-at least for environmentally determined, structural organisms like trees. However, the originality of the present approach lies in the fact that not only it is based on the concept of ecological niche, but in contrast to many statistical techniques, it needs only presence data sets. This property is very important because most currently available data for the tropical taxa are still of this kind. The focus on presence data is partly due to the fact that until recently the emphasis was to obtain site inventories instead of regional statistical analysis, so data were collected in a nonstratified or without concerns to sampling desing, in terms of spatial coverage.
The Mahanalobis technique provides key information about the niche of the species being modelled and allows comparisons on species distributions. Further, the methodology is well-suited for application in conservation biology i.e. the use of this kinf od models may have many applications such as the quick prediction of invasive species potential distribution or finding the best locations to reintroduce individuals of endangered species, the prioritisation of direct inventory efforts toward areas with high presence probability of a species, prediction of species' redistribution due to climate change. Further along the trophic chain, these models can help predict the distribution of animals that use these trees as a source of food, bearing in mind that are not indicative of healthy or viable populations at all, or perhaps most importantly in terms of Colombia's commitments to the CBD, to identify gaps for conservation priorities.
The approach adopted here, however, is rather simple. A more comprehensive model of the potential distribution of species would involve considering competitive interactions between species and the effects of disturbance or population dynamics. Also, the present approach assumes that the species have a unimodal response to environmental conditions. Further, this modelling approach relies on the assumption that the general form of species' response to environmental gradients is an optimum where the species is most likely to occur; the likelihood of occurrence decreases with distance from that optimum. However, also it has to be taken into account the factg taht this approach does not take into account interaction or changes in the interlinkages amongst factors, that is, parameter interaction would need to be incorporated in the future. In addition, the climatic fields used here are representative for canopy-level tree species only, whereas subcanopy species will experience a much altered microclimate. Nevertheless, the current need of tropical countries like Colombia is to have at least a basis from which to optimise available data to facilitate better geographical targeting of inventory and the spatially explicit prioritisation of conservation at the national scale. By building upon the techniques described here, we hope to provide a basis for the rapid identification of species-rich areas and areas in which particular species may be threatened or be best conserved,. This will contribute toward the national biodiversity conservation and management strategy.
ACKNOWLEDGMENTS
Many thanks go to all the different collections from which we obtained key information for this research: CB, Cesar Barbosa collection at Humboldt Institute Herbarium; MO, Missouri Botanical Garden; JAUM, Herbario Jardín Botánico "Joaquin Antonio Uribe" de Medellín; INCIVA, Instituto de Investigación Científica del Valle del Cauca; NYBG, New York Botanical Garden; COAH, Herbario Amazonico Colombiano; HAFP and Herbario de Alfonso Fernandez Perez, from Fundación Universitaria de Popayan, Herbarion Nacional Colombiano at the ICN Instituto de Ciencias Naturales. We wish to thank all of them and the people who made possible the access to these valuable records and specially to the HAFP director, Dairon Cardenas. We specially want to thank Dr. Charlotte Taylor, for not only allowing us access to the Missouri Botanical Garden database and herbarium, but also for her comments on all our inquiries regarding Rubiaceae. Our thanks to both the Humboldt Biological Resources Research Institute and the UK DfID British Council LINK programme for their financial contribution. We are thankful to Dr Fernando Gast for all his efforts, comments and supervision during the postgraduate work in past years that lead to this publication and finally many thanks to the three reviewers whose comments made possible the improvement of this paper and its final publication.
LITERATURE CITED
1. ANDERSON, L. 1995. Diversity and origins of andean Rubiaceae. In: S. Churchill, H. Baslev, E. Forero & J. Luteyn (eds). Biodiversity and conservation of neotropical montane forests: 441-450. The New York Botanical Garden, New York. [ Links ]
2. ANDERSON, R.P., M. GÓMEZ-LAVERDE & A.T. PETERSON. 2002a. Geographical distributions of spiny pocket mice in South America: insights from predictive models. Global Ecology and Biogeography 11: 131-141. [ Links ]
3. ANDERSON, R.P., A.T. PETERSON & M. GÓMEZ-LAVERDE. 2002b. Using niche-based GIS modeling to test geographic predictions of competitive exclusion and competitive release in South American pocket mice. Oikos 98: 3-16. [ Links ]
4. ANDERSON, R.P., D. LEW & A.T. PETERSON. 2003. Evaluating predictive models of species' distributions: criteria for selecting optimal models. Ecological Modelling 162 (3): 211-232. [ Links ]
5. ARMENTERAS, D. 2003. Modelling the potential distribution of tree species at the national scale using Geographic Information Systems. PhD Thesis. King's College London, University of London, UK. [ Links ]
6. ATKIN, M., D. ANDERSON, B. FRANCIS & J. HINDE. 1990. Statistical modelling in GLIM. Clarendon, Oxford, England. 374 pp. [ Links ]
7. AUSTIN, M.P., A.O. NICHOLLS & C.R. MARGULES. 1990. Measurement of the realized quantitative niche: environmental niches of five Eucalyptus species. Ecological monographs 60: 161-177. [ Links ]
8. AUSTIN, M.P. & T.M. SMITH. 1989. A new model for the continuum concept. Vegetation 83: 35-47. [ Links ]
9. AUSTIN, M.P. & J.A. MEYERS. 1996. Current approaches to modelling the environmental niche of eucalyptus: implication for management of forest biodiversity. Forest Ecology and Management 85: 95-106. [ Links ]
10. BAKER, T.R., D.F.R.P. BURSLEM & M.D. SWAINE. 2003. Associations between tree growth, soil fertility and water availability at local and regional scales in Ghanaian tropical rain forest. Journal of Tropical Ecology 19: 109-125. [ Links ]
11. BAR-HEN, A. & J. DAUDIN. 1995. Generalization of the Mahalanobis distance in the mixed case. Journal of Multivariate Analysis 53: 332-342. [ Links ]
12. BARONE, J.A. 1998. Effects of light availability and rainfall on leaf production in a moist tropical forest in central Panama. Journal of Tropical Ecology 14: 309-321. [ Links ]
13. BASNET, K. 1992. Effect of topography on the pattern of trees in Tabonuco (Dacryodes excelsa) dominated rain forest in Puerto Rico. Biotropica 3: 201-220. [ Links ]
14. BAZZAZ, F.A. & S.T.A. PICKETT. 1980. Physiological ecology of tropical succession: a comparative review. Annual Review of Ecology & Systematics 11: 287-310. [ Links ]
15. BEGON, M., J.L. HARPER, & C.R. TOWNSEND. 1990. Ecology, Individuals, populations and communities. 2nd ed. Blackwell, Oxford. [ Links ]
16. BOJÓRQUEZ-TAPIA, L.A., I. AZUARA, E. EZCURRA & O. FLORES-VILLELA. 1995. Identifying conservation priorities in México through geographic information-systems and modelling. Ecological Applications 5: 215-23 [ Links ]
17. BOLLIGER, J., F. KIENAST & H. BUGMANN. 2000. Comparing models for tree distributions: concept, structures, and behavior. Ecological Modelling 134: 89-102. [ Links ]
18. BOONE, R.B. & W.B. KROHN. 2002. Modelling tools and Accuracy assessment. In: Scott, J.M., Heglund, P.J., Morrison, M.L., Haufler, J.B., Raphael, M.G., Wall, W.A. & SAMSON, F.B. (eds). Predicting Species Occurrences: Issues of Accuracy and Scale: 265-270. Island Press, Washington, DC., USA [ Links ]
19. BOX, E.O., D.W. CRUMPACKER & D. HARDIN. 1993. A climatic model for location of plant species in Florida. U.S.A. Journal of Biogeography 20: 629-641. [ Links ]
20. BRADY, N.C. 1990. The nature and properties of soils (10th Edition). Macmillan, New York. 621 pp. [ Links ]
21. BROWN, J.H. & A.C. GIBSON. 1983. Biogeography. Mosby, St Louis, Missouri, USA. [ Links ]
22. BRZEZIECKI, B., F. KIENAST & O. WILDI. 1993. A simulated map of the potential natural forest vegetation of Switzerland. Journal of Vegetation Science 4: 499-508. [ Links ]
23. BRZEZIECKI, B., F. KIENAST & O. WILDI. 1994. Potential impacts of changing climate on the vegetation cover of Switzerland: a simulation experiment using GIS technology. In: Price, M.F. & D.I. Heywood (eds) Mountain environments and Geographic Information Systems: 263 - 279. Taylor & Francis Ltd., London, UK. [ Links ]
24. BUSBY, J.R. 1986. A biogeographical analysis of Nothofagus cunninghamii (Hook.) Oerst. in southeastern Australia. Australian Journal of Ecology 11: 1-7. [ Links ]
25. CARPENTER, G., A.N. GILLISON & J. WINTER 1993. DOMAIN a flexible modelling procedure for mapping potential distributions of plants and animals. Biodiversity and Conservation 2: 667-680. [ Links ]
26. CAVIERES, L.A., F. RADA, A. AZOCAR, C. GARCIA-NUÑEZ. & H.M. CABRERA. 2000. Gas exchange and low temperature resistance in two tropical high mountain tree species from the Venezuelan Andes. Acta Oecologica 21(3): 203-211. [ Links ]
27. CLARK, D.A. & D.B. CLARK. 1994. Climate-induced annual variation in canopy tree growth in a Costa Rican tropical rain forest. Journal of Ecology 82: 865-872. [ Links ]
28. CLARK, D.B., D.A. CLARK & J.M. REAR. 1998. Edaphic variation and the mesoscale distribution of tree species in a neotropical rain forest. Journal of Ecology 86: 101-112. [ Links ]
29. CLARK, D.B., M.W. PALMER & D.A. CLARK. 1999. Edaphic factors and the landscape-scale distributions of tropical rain forest. Ecology 80 (8): 2662-2671. [ Links ]
30. CLARK, J.D., J.E. DUNN & K.G. SMITH 1993. A multivariate model of female black bear habitat use for a geographic information system. Journal of Wildlife Management 57 (3): 519-527. [ Links ]
31. DE MAESSCHALCK, R., D. JOUAN-RIMBAUD & D.L. MASSART. 2000. Tutorial: The Mahalanobis distance. Chemometrics and Intelligent Laboratory Systems 50: 1-18. [ Links ]
32. DUDA, R.O. 1997. Pattern recognition for HCI. In: Human computer interface design course. Department of Electrical Engineering. San Jose State University. http://ww-engr.sjsu.edu. [ Links ]
33. DUNN, J.E & L. DUNCAN. 2000. Partitioning Mahalanobis D2 to Sharpen GIS Classification. In: Management Information Systems 2000: In: C.A. Brebbia & P. Pascolo (eds), GIS and Remote Sensing: 195-204. WIT Press, London. [ Links ]
34. ELITH, J., M.A. BURGMAN & H.M. REGAN. 2002. Mapping epistemic uncertainties and vague concepts in predictions of species distribution. Ecological Modelling 157(2-3): 313-329. [ Links ]
35. ENQUIST, B.J. & A.J. LEFFLER. 2001. Long-term tree ring chronologies from sympatric tropical dry-forest trees: individualistic responses to climatic variation. Journal of Tropical Ecology 17: 41-60. [ Links ]
36. ESRI INC. 1998. ARVIEW GIS VERSION 3.1. Environmental Systems Research Institute Inc, USA. [ Links ]
37. FARBER, O. & R. KADMON. 2003. Assessment of alternative approaches for bioclimatic modeling with special emphasis on the Mahalanobis distance. Ecological Modelling 160 (1-2): 115-130. [ Links ]
38. FELICISIMO, A.M., E. FRANCES, J.M. FERNÁNDEZ, A. GONZÁLEZ-DIEZ & J. VARAS. 2002. Modeling the potential distribution of forests with a GIS. Photogrammetric Engineering & Remote Sensing 68 (5): 455-461. [ Links ]
39. FIELDING, A.H. & J.F. BELL. 1997. A review of methods for the assessment of prediction errors in conservation presence/absence models. Environmental Conservation 24: 38-49. [ Links ]
40. FITTER, A.H & R.K.M. HAY. 2002. Environmental Physiology of Plants. Third Edition. Academic Press. [ Links ]
41. FORSETH, I.N. & J.M. NORMAN. 1991. Modelling of solar irradiance, leaf energy budget, and canopy photosynthesis. In: D.O. Hall, J.M.O. Scurlock, H.R. Bolhar-Nordenkampf, R.C. Leegood & S.P. Long (eds), Techniques in Photosynthesis and Productivity Research for a Changing Environment: Chapman & Hall, London. [ Links ]
42. FRANKLIN, J. 1995. Predictive vegetation mapping: geographic modelling of biospatial patterns in relation to environmental gradients. Progress in Physical Geography 19: 474-499. [ Links ]
43. GASTON, K.J. 2000. Global patterns in biodiversity. Nature 403: 220-226. [ Links ]
44. GOWER, J.C. 1971. A general coefficient of similarity and some of its properties. Biometrics 27: 857-71. [ Links ]
45. GUISAN, A. & N.E. ZIMMERMANN. 2000. Predictive habitat distribution models in ecology. Ecological Modelling 135: 147-186. [ Links ]
46. GUISAN, A., T.C. EDWARDS & T. HASTIE. 2002. Generalized linear and generalized additive models in studies of species distributions: setting the scene. Ecological Modelling 157(2-3): 89-100. [ Links ]
47. HALE, M.G. & D.M. ORCUTT. 1987. The Physiology of Plants Under Stress. John Wiley and Sons. New York. [ Links ]
48. HAND, D.J. 1981. Discriminant Classification. John Wiley and Sons, Chichester, UK. [ Links ]
49. HARPER, J.L. 1977. Population biology of Plants. Academic Press, 8th edition. [ Links ]
50. HERNANDEZ P.A., C.H. GRAHAM, L.L. MASTER & D.L. ALBERT. 2006. The effect of sample size and species characteristics on performance of different species distribution modeling methods. Ecography 29: 773-785. [ Links ]
51. HIJMANS R.J. & C.H. GRAHAM. 2006. The ability of climate envelope models to predict the effect of climate change on species distributions. Global Change Biology 12:1-10. [ Links ]
52. HUBBELL, S.P. & R.B. FOSTER. 1994. Commonness and rarity in a neotropical forest: implications for tropical tree conservation. In: M.E. Soule (ed.): Conservation biology: the science of scarcity and diversity: 205-231. Sinauer Associates, Sunderland, MA. [ Links ]
53. HUTCHINSON, G.E. 1957. Concluding remarks. Cold Springs Harbour Symposia on Quantitative Biology 22: 415-427. [ Links ]
54. HUTCHINSON, G.E 1959. Homage to Santa Rosalia, or why are there so many kinds of animals. American Naturalist 93: 145-159. [ Links ]
55. IAVH, 1998. Colombia biodiversidad siglo XXI: propuesta técnica para la formulación de un plan de acción nacional en biodiversidad. Instituto de Investigación de Recursos Biológicos Alexander von Humboldt, Ministerio del Medio Ambiente, Departamento Nacional de Planeación, Bogotá, 254 pp. [ Links ]
56. IAVH, 1998a. Informe Nacional sobre el Estado de la Biodiversidad 1997- Colombia. Instituto de Investigación de Recursos Biológicos Alexander von Humboldt, PNUMA, Ministerio del Medio Ambiente, Bogotá, 3 vol. [ Links ]
57. IAVH, 1999. Caracterización de la biodiversidad en áreas prioritarias de la vertiente oriental de la cordillera Oriental. Grupo de Exploración y Monitoreo Ambiental. Instituto de Investigación de Recursos Biológicos Alexander von Humboldt, Villa de Leyva, Colombia. Internal Report. [ Links ]
58. IAVH, 1999a. Manual de metodologías para el desarrollo de inventarios y monitoreo de la biodiversidad. Grupo de Exploración y Monitoreo Ambiental, Instituto de Investigación de Recursos Biológicos Alexander von Humboldt, Villa de Leyva, Colombia. [ Links ]
59. IGAC 1970-1985. Topographic maps. Scale 1:500.00. Instituto Geográfico Agustín Codazzi. Bogotá, Colombia. [ Links ]
60. IGAC, 1982. Mapa de suelos de Colombia. Escala 1:1.500.000. Instituto Geográfico Agustín Codazzi, Bogotá, Colombia. [ Links ]
61. JIMÉNEZ-B., L.C. 2002. Lista de las colecciones colombianas de Rubiaceae depositadas en el Herbario Nacional Colombiano (Col)/ Checklist of the Colombian collections of Rubiaceae deposited at the Colombian National Herbarium (COL). Caldasia 24(1): 41-64 [ Links ]
62. JOHNSON, I.R. & J.H.M. THORNLEY. 1985. Temperature dependence of plant and crop processes. Annals of Botany 55: 1-24. [ Links ]
63. JOHNSTON, M.H. 1992. Soil vegetation relationships in a tabonuco forest community in the Luquillo Mountains of Puerto Rico. Journal of Tropical Ecology 8: 253-263. [ Links ]
64. JONES, P.G. 1991. The CIAT climate database version 3.41. Centro Internacional de Agricultura Tropical (CIAT), Cali, Colombia [ Links ]
65. JONES, P.G., S.E. BEEBE, J. TOHME & N.W. GALWEY. 1997. The use of geographical information systems in biodiversity exploration and conservation. Biodiversity and Conservation 6: 947-958. [ Links ]
66. KNICK, S.T. & D.L. DYER. 1997. Distribution of black-tailed jackrabbit habitat determined by GIS in southwestern Idaho. Journal of Wildlife Management 61: 75-85. [ Links ]
67. KNICK, S.T. & J.T. ROTENBERRY. 1998. Limitations to mapping habitat use areas in changing landscapes using the Mahalanobis distance. Journal of Agricultural, Biological and Environmental Statistics 3: 311-322. [ Links ]
68. LAURANCE, W.F., G.B. WILLIAMSON, P. DELAMO-NICA, A. OLIVEIRA, T.E. LOVEJOY, C. GASCON & L. POHL. 2001. Effects of a strong drought on Amazonian forest fragments and edges. Journal of Tropical Ecology 17: 771-785. [ Links ]
69. LONGMAN, K.A. & J. JENIK 1987. Tropical forest and its environment. 2nd edition. Longman Scientific & Technical, England. [ Links ]
70. MACARTHUR, R. 1968. The theory of the niche. In: R.C. Lewontin (ed.), Population Biology and Evolution: 159-176. Syracuse University Press, Syracuse, New York. [ Links ]
71. MIYAMOTO, K., E. SUZUKI, T. KOHYAMA, T. SEINO, E. MIRMANTO & H. SIMBOLON. 2003. Habitat differentiation among tree species with small-scale variation of humus depth and topography in a tropical heath forest of Central Kalimantan, Indonesia. Journal of Tropical Ecology 19: 43-54. [ Links ]
72. MOORE, I.D., R.B. GRYSON & A.R. LADSON. 1991. Digital terrain modelling: a review of hydrological, geomorphological, and biological applications. Hydrological Processes 5: 3-30. [ Links ]
73. MONTAÑA, C. & P. GREIGH-SMITH. 1990. Correspondence analysis of species by environmental variable matrices. Journal of Vegetation Science 1: 453-460. [ Links ]
74. MULLIGAN, M. & J. WAINWRIGHT. 2003. Modelling and model building. In: J. Wainwright & M. Mulligan (eds) Environmental Modelling: finding the simplicity in complexity: 7-73. Wiley, London. [ Links ]
75. PÉREZ-VEGA, A., J.F. MAS, A. VELÁZQUEZ & L. VÁZQUEZ. 2008. Modelling vegetation diversity types in Mexico based upon topographic features. Interciencia 33(2): 88-95. [ Links ]
76. PETERSON, A.T. & K.P. COHOON. 1999. Sensitivity of distributional prediction algorithms to geographic data completeness. Ecological Modelling 117: 159-164. [ Links ]
77. PHILLIPS, O.L., P. NÚÑEZ VARGAS, A.L. MONTEAGUDO, A. PEÑA CRUZ, M.E. CHUSPE ZANS, W.G. SÁNCHEZ, M. YLI-HALLA & S. ROSE. 2003. Habitat association among Amazonian tree species: a landscape-scale approach. Journal of Ecology 91: 757-775 [ Links ]
78. RANGEL-CH., J.O. 1995. (ed.) Colombia Diversidad Biótica I. Clima, Centros de concentración de especies, fauna. Instituto de Ciencias Naturales-Universidad Nacional de Colombia-INDERENA. 442 pp. Santafé de Bogotá. [ Links ]
79. RANGEL-CH., J.O. 2000. (ed.). Colombia Diversidad Biótica III. La región de vida paramuna. Instituto de Ciencias Naturales - Instituto Alexander von Humboldt. 902 pp. Bogotá. [ Links ]
80. RANGEL, J.O., P. LOWY & M. AGUILAR. 1997. Colombia Diversidad Biótica II. Tipos de vegetación en Colombia. Instituto de Ciencias Naturales-Universidad Nacional de Colombia-IDEAM. 436 pp. Santafé de Bogotá. [ Links ]
81. REICH, P.B. 1995. Phenology of tropical forests: patterns, causes and consequences. Canadian Journal of Botany 73: 164-174. [ Links ]
82. RICH, P.M., W.A. HETRICK & S.C. SAVINGS. 1995. Modelling topographical influences on solar radiation: manual for the SOLARFLUX model. LA-12989-M, Los Alamos National Laboratories, Los Alamos, USA. [ Links ]
83. RICHERSON, P.J. & K. LUM. 1980. Patterns of plant species diversity in California: relation to weather and topography. American Naturalist 116: 504-536. [ Links ]
84. ROBERTSON, M.P., N. CAITHNESS & M.H. VILLET. 2001. A PCA-based modelling technique for predicting environmental suitability for organisms from presence records. Diversity and Distributions 7: 15-27. [ Links ]
85. RYKIEL, E.J. 1996. Testing ecological models: the meaning of validation. Ecological Modelling 90: 229-244. [ Links ]
86. SAXE, H., M.G.R. CANNELL, Ø. JOHNSEN, M.G. RYAN & G. VOURLITIS. 2001. Tree and forest functioning in response to global warming. New Phytologist 149 (3): 369-399. [ Links ]
87. SCOTT, J.M., P.J. HEGLUND, M.L. MORRISON, J.B. HAUFLER, M.G. RAPHAEL, W.A. WALL & F.B. SAMSON. (eds) 2002. Predicting Species Occurrences: Issues of Accuracy and Scale. Island Press, Washington, DC, 868 pp. [ Links ]
88. SMITH, A.P., N. HORNING & D. MOORE. 1997. Regional biodiversity planning and Lemur conservation with GIS in Western Madagascar. Conservation Biology 11 (2): 498-512. [ Links ]
89. SOLLINS, P. 1998. Factors influencing species composition in tropical lowland rain forest: does soil matter?. Ecology 79 (1): 23-30. [ Links ]
90. STEPHENSON, N.L. 1990. Climatic controls on vegetation distribution: the role of the water balance. American Naturalist 135: 649-670. [ Links ]
91. STOCKWELL, D.R.B. & I.R. NOBLE. 1992. Induction of sets of rules from animal distribution data: a robust and informative method of data analysis. Math. Comput. Simul. 33: 385-390. [ Links ]
92. STOCKWELL, D. & D. PETERS. 1999. The GARP modelling system: problems and solutions to automated spatial prediction. International Journal of Geographical Information Sciences 13: 143-158. [ Links ]
93. STOCKWELL, D.R.B. & A.T. PETERSON. 2002. Effects of sample size on accuracy of species distribution models. Ecological Modelling 148: 1-13. [ Links ]
94. SWAINE, M.D. 1996. Rainfall and soil fertility as factors limiting forest species distributions in Ghana. Journal of Ecology 84: 419-428. [ Links ]
95. TANNER, E.V.J. 1977. Four montane rain forests of Jamaica: a quantitative characterization of the floristics, the soils and the foliar mineral nutrient levels and a discussion of their inter-relations. Journal of Ecology 65: 883-918. [ Links ]
96. TANNER, E.V.J., P.M. VITOUSEK & E. CUEVAS. 1998. Experimental investigation of nutrient limitation of forest growth on wet tropical mountains. Ecology 79: 10-22. [ Links ]
97. TAYLOR, C.M. 1996. Overview of the Psychotrieae (Rubiaceae) in the Neotropics. Opera Botanica Belgium 7: 261-270. [ Links ]
98. TAYLOR, C.M. 1997a. Conspectus of the genus Palicourea (Rubiaceae: Psychotrieae) with the description of some new species from Ecuador and Colombia. Annals Missouri Botanical Garden 84 (2): 224-262. [ Links ]
99. TAYLOR, C.M. 1997b. New species of Palicourea and Psychotria (Rubiaceae: Psychotrieae) from northwestern Colombia. Novon 7: 191-200. [ Links ]
100. TAYLOR, C.M. 1999. Lista preliminar de las especies de Rubiaceae de Colombia. En: Memorias del primer congreso nacional de botánica. Santafé de Bogotá: Universidad Nacional, Instituto de Ciencias Naturales, 1999. [ Links ]
101. TAYLOR, C.M. 2000. New species and a new name in Palicourea (Rubiaceae: Psychotrieae) from northwestern South America. Novon 10: 78-87. [ Links ]
102. THOMAS, J.W. 1979. Wildlife habitats in managed forests: the Blue Mountains of Oregon and Washington. U.S.D.A. For. Serv. Agric. Handbook, 553. 512 pp. [ Links ]
103. TRANQUILLINI, W. 1979. Physiological Ecology of the Alpine Timberline. Springer-Verlag, New York. [ Links ]
104. TURNER, J.R.G., J.J. LENNON & J.A. LAWRENSON. 1988. British bird distributions and the energy theory. Nature 335: 539-541. [ Links ]
105. U.S. GEOLOGICAL SURVEY-EROS DATA CENTER. 1996. GTOPO 30. US Geological Survey, Sioux Falls, SD, USA. [ Links ]
106. U.S. FISH AND WILDLIFE SERVICE. 1981. Standards for the development of suitability index models. Ecological Services Manual 103. US Department of Interior, Fish and Wildlife Service. Division of Ecological Services. Government Printing Office, Washington D.C., USA. [ Links ]
107. VELÁZQUEZ, A. 1994. Multivariate analysis of the vegetation of the volcanoes Tláloc and Pelado, Mexico. Journal of Vegetation Science 5: 263-270. [ Links ]
108. VELÁZQUEZ, A. & G. W. HEIL. 1996. Habitat analysis of the volcano rabbit (Romerolagus diazi) by different statistical methods. Journal of Applied Ecology 33: 543-554. [ Links ]
109. VERNER, J. & BOSS, A.S. 1980. California Wildlife and their habitats: western Sierra Nevada. US Department of Agriculture, Forest Service. General Technical Report PSW 37. Pacific Southwest Forest and Range Experiment Station, Berkeley, California, USA. [ Links ]
110. VITOUSEK, P.M. 1984. Litterfall, nutrient cycling, and nutrient limitation in tropical forests. Ecology 65: 285-298. [ Links ]
111. WALKER, P.A. & K.D. COCKS. 1991. HABITAT: a procedure for modelling a disjoint environmental envelope for a plant or animal species. Global Ecology Biogeography Letters 1: 108-18. [ Links ]
112. WHITTAKER, R.H. 1975. Communities and Ecosystems. 2nd edition. Macmillan, New York. [ Links ]
113. WILDS, S., J.R. BOETSCH, F.T. VAN MANEN, J.D. CLARK & P.S. WHITE. 2000. Modeling the distributions of species and communities in Great Smoky Mountains National Park. Computers and Electronics in Agriculture 27 (1-3): 389-392. [ Links ]
114. WHIGHAM, D.F., P. ZUGASTY TOWLE, E. CABRERA CANO, J. O'NEILL & E. LEY. 1990. The effect of annual variation in precipitation on growth and litter production in a tropical dry forest in the Yucatan of Mexico. Tropical Ecology 31: 23-34. [ Links ]
115. WOODWARD, F.I. 1987. Climate and Plant Distribution. Cambridge University Press, Cambridge, UK, 174 pp. [ Links ]
116. WRIGHT, D.H., D.J. CURRIE & B.A. MAURER. 1993. Energy supply and patterns of species richness on local and regional scales. In: R.E. Ricklefs & D. Schluter (eds), Species Diversity: Historical and geographical perspectives: 66-74, University of Chicago Press, Chicago, USA. [ Links ]
117. WORBES, M. 1999. Annual growth rings, rainfall-dependent growth and long-term growth patterns of tropical trees form the Caparo Forest Reserve in Venezuela. Journal of Ecology 87: 391-403. [ Links ]