Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista de la Academia Colombiana de Ciencias Exactas, Físicas y Naturales
Print version ISSN 0370-3908
Rev. acad. colomb. cienc. exact. fis. nat. vol.36 no.141 Bogotá Oct./Dec. 2012
FÍSICA
1 Escuela de Física, Universidad Industrial de Santander, Ciudad Universitaria, Bucaramanga 680002, Colombia, Correo electrónico: joferoru@gmail.com
2 Centro de Investigaciones en Ciencias Básicas y Aplicadas, Universidad Antonio Nariño, Cra 3 Este # 47A - 15, Bogotá D.C. 110231, Colombia, Correo electrónico: yeinzon.rodriguez@uan.edu.co
3 Escuela de Física, Universidad Industrial de Santander, Ciudad Universitaria, Bucaramanga 680002, Colombia, Correo electrónico: yrodrig@uis.edu.co
Resumen
Los estudios experimentales de las supernovas tipo Ia y de la radiación cósmica de fondo han mostrado la reciente expansión acelerada del Universo. Para explicar este comportamiento, se introdujo una forma hipotética de energía llamada la energía oscura. Por otro lado, la presencia de una constante cosmológica en las ecuaciones de campo provoca una expansión acelerada del Universo; así, esta última se identifica con la energía oscura. Además, la energía del estado de vacío exhibe las mismas consecuencias de una constante cosmológica; por consiguiente, el valor experimental de la energía de vacío debe contribuir al valor experimental de la constante cosmológica, y ambos deben tener el mismo orden de magnitud. Sin embargo, al comparar los dos valores, hay una diferencia de más de 55 órdenes de magnitud. Con el fin de establecer concordancia, es necesario hacer un ajuste fino en el valor experimental de la constante cosmológica. La imposibilidad de evitar un ajuste fino se conoce como el viejo problema de la constante cosmológica. Se han planteado muchas soluciones, tales como la sustitución de la constante cosmológica por un campo escalar; sin embargo, estas soluciones no resuelven realmente el problema. Se presentará una solución alternativa, en la cual la constante cosmológica es complementada con un nuevo término originado a partir de modificaciones de la gravedad. La modificación se realiza mediante la introducción de una función f (R, G), donde R es el escalar de Ricci y G es el invariante de Gauss-Bonnet. El término nuevo, que se puede interpretar como un fluido cósmico con una forma particular para su ecuación de estado, evoluciona en el tiempo relajando de manera dinámica la enorme diferencia entre la energía de vacío y la constante cosmológica.
Palabras clave: Constante cosmológica, energía oscura, gravedad modificada.
Abstract
The experimental studies of the type Ia supernovae and of the cosmic microwave background radiation have shown the recent accelerated expansion of the Universe. To explain this behavior, a hypothetical form of energy called the dark energy was introduced. On the other hand, the presence of a cosmological constant in the field equations causes an accelerated expansion of the Universe; thus, the latter is identified with the dark energy. Moreover, the energy of the vacuum state exhibits the same consequences of a cosmological constant; therefore, the experimental value of the vacuum energy must contribute to the experimental value of the cosmological constant, and both values must have the same order of magnitude. However, when the two values are compared, there exists a difference of more than 55 orders of magnitude. In order to establish concordance, it is necessary to do a fine-tuning in the experimental value of the cosmological constant. The impossibility to avoid this fine-tuning is called the old cosmological constant problem. Many solutions have been raised, such as the replacement of the cosmological constant by a scalar field; however, these solutions do not actually solve the problem. We will present an alternative solution, in which the cosmological constant is complemented by a new term originated from modifications of gravity. The modification is performed by introducing a function f (R, G), where R is the Ricci scalar and G is the Gauss-Bonnet invariant. The new term, which can be interpreted as a cosmic fluid with a particular form for its equation of state, evolves in time dynamically relaxing the enormous difference between the vacuum energy and the cosmological constant.
Keywords: Cosmological constant, dark energy, modified gravity.
1.   Introducción
En la teoría general de la relatividad el tensor momentum-energía es la fuente del campo gravitatorio. Por lo tanto, es el valor mismo de la energía, y no la diferencia entre estados, la cantidad decisiva en el comportamiento de los fenómenos gravitacionales; es decir, cualquier tipo de energía, incluyendo la energía proveniente del estado de vacío, debe ser incluida en el análisis de la física gravitacional. La energía de vacío permea el Universo entero creando un campo gravitacional que produce una expansión acelerada; este resultado también puede ser obtenido al introducir una constante de naturaleza netamente geométrica en las ecuaciones de Einstein. Por consiguiente, la constante cosmológica (CC) "física", Λfis, debe comprender dos contribuciones: una relacionada con una constante Λdes, llamada la CC desnuda y, por otro lado, la contribución del estado de vacío de los campos que permean el Universo, denominada la CC inducida Λind . El valor teórico de la contribución de estos campos es del orden de 108 GeV4 (Kane, 1993)4.
Los resultados experimentales del estudio de las supernovas tipo Ia (Perlmutter et. al., 1999; Riess et. al., 1998) y los datos de la radiación cósmica de fondo (Komatsu et. al., 2011), implican la existencia de una forma hipotética de energía denominada la energía oscura (EO), cuyas características son similares a las de la CC. En consecuencia, es razonable tomar como medida de la CC la cantidad de EO presente en el Universo. La EO constituye un 73 % de la densidad de energía total del Universo (Jarosik et. al., 2011; Komatsu et. al., 2011; Larson et. al., 2011) siendo el valor experimental de su densidad del orden de 10-47  GeV4. Al comparar este valor con la contribución de los campos que permean el Universo, se obtiene la enorme diferencia de 55 órdenes de magnitud. Con el único fin de obtener concordancia entre los resultados teóricos y experimentales, se elige el valor de Λdes  de tal forma que se cancelan 55 cifras significativas de manera exacta; sin embargo, es evidente que esta elección no proporciona una explicación satisfactoria del porqué del pequeño valor observado de Λfis a pesar de la enorme contribución de los campos. La imposibilidad de evitar la contribución de los campos sin recurrir a un ajuste fino se denomina el primer o viejo problema de la CC (Weinberg, 1989).
Como solución al viejo problema de la CC se ha reemplazado Λdes por campos escalares (Abbot, 1985; Armendariz- Picon, Mukhanov & Steinhardt, 2000; Barr, 1987; Barr & Hochberg, 1988; Caldwell, Dave & Steinhardt, 1998; Ford, 1987; Peccei, Sola & Wetterich, 1987; Sola, 1989; Yoo & Watanabe, 2012); sin embargo, esta sustitución no resuelve realmente el problema (Weinberg, 1989). Para dar una verdadera solución al primer problema de la CC se deben garantizar dos hechos: primero, la cancelación libre de ajustes finos de la contribución de los campos, y, segun do, no se debe alterar la historia térmica del Universo. En las Refs. (Bauer, 2010; Bauer, Sola & Stefancic, 2010a; Bauer, Sola & Stefancic, 2010b) se presentóuna posible solución en donde estos dos hechos se satisfacen. En este tipo de solución, la CC desnuda no se sustituye por campos escalares sino que es complementada por un término prove niente de la modificación de la gravedad. La modificación se realiza a través de la introducción de una función de la forma f (R, G), que involucra el invariante de Gauss-Bonnet G (Chern, 1945). La construcción del nuevo funcional garantiza que en la nueva teoría de la gravedad, el principio de equivalencia y la conservación del cuadrimomentum se sigan cumpliendo. El resultado efectivo de la modificación es la aparición de un nuevo fluido cósmico llamado el "Cosmón". La presencia del Cosmón en las ecuaciones de campo provoca la cancelación dinámica de la contribución de los campos. Debido al origen gravitacional del Cosmón, la expansión del Universo pone en acción el mecanismo de cancelación y a su vez, la cancelación garantiza que la expansión del Universo sea la esperada. Adicionalmente, la ecuación de estado (EDE) de la combinación CC-Cosmón es no homogénea, lo cual implica que el presente modelo está relacionado con la posible solución al viejo problema de la CC presentada en la Ref. (Stefancic, 2009). En cuanto a la diferencia entre una EDE homogénea y una no homogénea, se deben observar las variables físicas presentes en la EDE: cuando están presen tes únicamente la densidad de energía ρ y la presión p del fluido en cuestión, i.e. cuando la EDE se puede escribir de la forma f (ρ, p) = 0, se dice que ésta es homogénea; por el contrario, cuando se involucra otras cantidades diferentes se dice que la EDE es no homogénea, i.e. ésta tiene la forma f (ρ, p) = g(x), en donde x representa una o más cantidades diferentes a ρ y p. En el presente modelo la EDE depende adicionalmente del parámetro de Hubble H y del parámetro de desaceleración q= -aä/ Â 2 siendo a el parámetro de expansión.
 2 siendo a el parámetro de expansión.
Es importante mencionar que al referirse a una EDE no homogénea, no se está haciendo referencia a un espacio no homogéneo: más aún, en el análisis del presente artículo se asume, siguiendo el principio cosmológico, un espacio homogéneo e isótropo y por lo tanto la métrica de fondo es la métrica de Friedmann-Robertson-Walker (FRW). Por último, la construcción de la función f (R, G) provee una correcta transición entre las etapas conocidas del Universo y, por ende, respeta su historia térmica.
Para ilustrar el problema se calculará en la sección 2 la energía de vacío a partir del mecanismo de ruptura espontánea de la simetría o mecanismo de Higgs; también se mostrará por qué la energía del estado base se comporta gravitacionalmente como una constante cosmológica. En la sección 3 se expondrá de forma clara y precisa el viejo problema de la constante cosmologica; en este punto se expondrá por qué las soluciones planteadas hasta el momento no han sido satisfactorias. Posteriormente, en la sección 4 se presentarán las motivaciones que llevaron al planteamiento de un modelo de gravedad modificada como la posible solución (Bauer, 2010; Bauer, Sola & Stefancic, 2010a; Bauer, Sola & Stefancic, 2010b), haciéndose un énfasis especial en la idea fundamental que éste propone; se describirá cómo obtener las ecuaciones de campo a partir del principio de acción estacionaria y cómo a partir de ellas se obtienen las respectivas ecuaciones que gobiernan la evolución cosmológica; además, se mencionarán las condiciones que se deben satisfacer para proporcionar una verdadera solución acorde con las observaciones. Con el propósito de comprender detalladamente la posible solución, se estudiará en la sección 5 un modelo de juguete que a su vez permitirá plantear conjeturas acerca de la forma explícita de las funciones que describen un modelo realista. Finalmente, en la sección 6 se discutirá teóricamente el comportamiento del modelo realista, analizando su comportamiento a lo largo de la historia térmica del Universo y mostrando que se exhibe una correcta transición entre las épocas conocidas.
La métrica a utilizar a lo largo del desarrollo del artículo tiene signatura (+,-, -, -). Los índices griegos representan cualquiera de los números {0, 1, 2, 3} y los índices latinos cualquiera de los números {1, 2, 3}. Los índices repetidos implican sumatoria, a menos de que se indique lo contrario. La derivada parcial ∂µÂ Av  se denotará por Av,µ y la derivada covariante ѵ Av por Av;µ. Los símbolos de Christoffel estándados por:
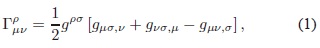
y las componentes del tensor de Riemann y Ricci por:
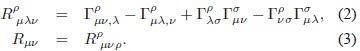
Aunque existen numerosas fuentes de energía de vacío dependiendo del modelo de partículas fundamentales que se trabaje, el problema será ilustrado en el contexto del vacío electrodébil (Kane, 1993; Weinberg, 1995). Este vacío proveniente del mecanismo de ruptura espontánea de la simetría o mecanismo de Higgs es el responsable de la masa de los bosones W± y Z (y de todos los fermiones con masa). El campo del Higgs formalmente se describe por un doblete de campos escalares; sin embargo, por razones prácticas, se utilizará un solo campo escalar f. La acción del sistema contiene la constante Λdes  (la CC desnuda) cuya naturaleza es netamente geométrica:
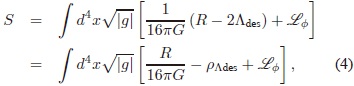
en donde G es la constante de gravitación universal, R el escalar de Ricci, Lf  es la densidad lagrangiana que describe los campos energía-materia, y g es el determinante de la métrica gµv  en consideración. De acuerdo con el principio de equivalencia (Weinberg, 1972), la densidad lagrangiana de un campo escalar f en cualquier sistema de referencia se obtiene al reemplazar hµv  por gµv  5:
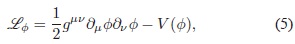
en donde el potencial V (f) esta dado por:
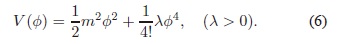
De esta manera, la acción en la Ec. (4) se puede expresar como:
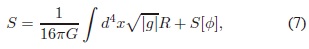
en donde
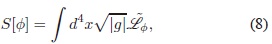
con
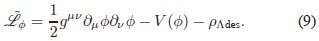
A partir de las expresiones (8) y (9) se calcula el tensor momentum-energía
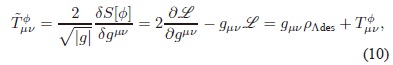
en donde
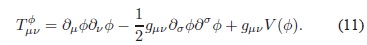
En el estado de vacío no existe energía cinética ni gradiente, por consiguiente sólo contribuyen la constante ρΛdes  y el valor esperado en el vacío del potencial V (f):
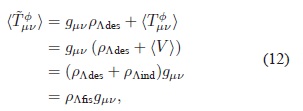
en donde ρΛind es el valor esperado en el vacío del potencial V (f). La expresión (12) tiene la misma forma del tensor momentum-energía asociado a la constante cosmológica introducida originalmente por Einstein (Einstein, 1917). Es decir, la "verdadera" densidad de energía asociada con la CC, que se denotará por ρΛfis , comprende dos contribuciones: una dada por la constante geométrica ρΛdes , y otra dada por el valor esperado en el vacío del potencial V (f).
Como se observa en la figura 1A, cuando m2 < 0 el potencial V (f) posee dos mínimos con f ≠ 0, a diferencia del caso cuando m2  > 0 en donde V (f) posee un solo mínimo con f = 0. Los mínimos corresponden a los valores esperados en el vacío para f (Cheng & Li, 1984). Para el caso descrito en la figura 1A, el escoger uno de los dos mínimos, por ejemplo el mínimo de la derecha, y construir una teoría de perturbaciones alrededor del valor de f en este punto, conduce a un rompimiento de la simetría6 que se tenía originalmente en el lagrangiano. De esta manera la partícula asociada al campo f (el bosón de Higgs) obtiene una masa física igual a M  = (-2m2)½ . Sin embargo, el teorema de Goldstone (Cheng & Li, 1984) implica la existencia de bosones sin masa cuando se rompe la simetría de esta manera, lo cual es contrario a lo observado experimentalmente, ya que los bosones W± y Z son masivos. No obstante, si se construye un lagrangiano invariante ante transformaciones de gauge locales (lo cual requiere introducir un doblete de campos), se puede evadir el teorema de Goldstone y obtener finalmente bosones masivos. Debido a que el objetivo de esta sección consiste en ilustrar sobre cómo se encuentra el valor del vacío electrodébil y no en proveer un cálculo riguroso de las masa de los bosones, es suficiente trabajar con el lagrangiano (5). El valor esperado en el vacío de f que corresponde al valor de uno de los mínimos de la figura 1A (el de la derecha por ejemplo) es:
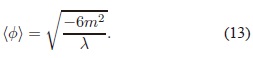
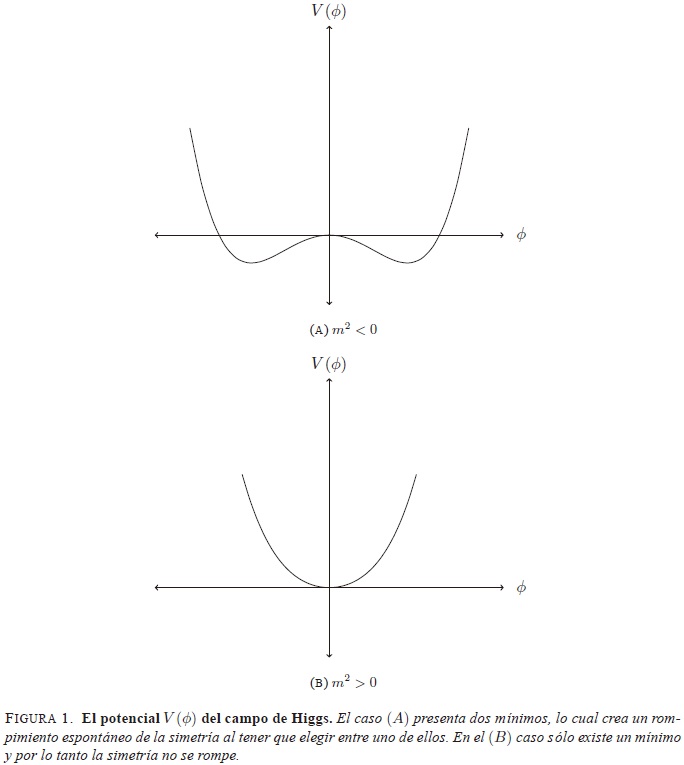
En conclusión, la transición de fase electrodébil requiere que 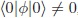 , lo cual induce una densidad de energía de vacío ρΛind  = (V). En un nivel clásico, la densidad de energía del vacío electrodébil tiene el valor (Kane, 1993; Weinberg, 1995):
, lo cual induce una densidad de energía de vacío ρΛind  = (V). En un nivel clásico, la densidad de energía del vacío electrodébil tiene el valor (Kane, 1993; Weinberg, 1995):
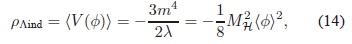
en donde 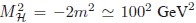 es la masa física al cuadrado del bosón de Higgs (Aad et. al., 2012; Chatrchyan et. al., 2012)7 El valor de experimental de
es la masa física al cuadrado del bosón de Higgs (Aad et. al., 2012; Chatrchyan et. al., 2012)7 El valor de experimental de 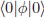 se obtiene a partir de la constante de Fermi GF Â (Beringer et. al., 2012):
se obtiene a partir de la constante de Fermi GF Â (Beringer et. al., 2012):
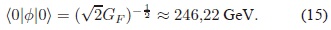
Reemplazando estos valores en (14), se obtiene que el valor esperado en el vacío para el potencial V (f) es aproximadamente igual a -108 GeV4.
Como se verá en la siguiente sección, al comparar el valor deducido en esta sección con el valor experimental obtenido a partir de datos cosmológicos, se encuentra una diferencia abismal de 55 órdenes de magnitud. Se mostrará en dicha sección los primeros intentos para dar una solución a este problema, así como también se argumentará por qué tales in tentos no lo solucionan realmente.
Los resultados experimentales (Perlmutter et al., 1999; Riess et al., 1998) muestran que el Universo no sólo se ex pande, sino que lo hace de una forma acelerada. Este hecho llevóa la hipótesis de la existencia de una nueva forma de energía llamada la EO, cuyas características deben ser similares a las de la CC con el fin de obtener el tipo de expansión observada. De esta manera, la EO se constituye en la medida experimental de la CC. Por otra parte, los resultados de las Refs. (Jarosik et. al., 2011; Komatsu et. al., 2011; Larson et. al., 2011) muestran que el Universo es prácticamen te plano, lo cual implica que, dado el monto de contenido material observado, existe un 73 % de energía faltante. La EO también proporciona una solución a este problema, constituyéndose en la cantidad de energía faltante. El orden de magnitud de la densidad de EO se puede calcular a partir del valor central de su parámetro de densidad WΛ (Komatsu et. al., 2011):
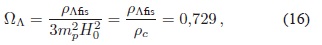
en donde 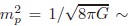 1018 GeV es la masa reducida de Planck y
1018 GeV es la masa reducida de Planck y 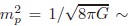 10-47  GeV4 es la densidad de energía crítica. A partir de la Ec. (16), se obtiene que ρΛfis  = ρc · 0,729 ∼ 10-47  GeV4, por lo tanto, este último valor se constituye en el orden de magnitud del valor experimental de la CC.
10-47  GeV4 es la densidad de energía crítica. A partir de la Ec. (16), se obtiene que ρΛfis  = ρc · 0,729 ∼ 10-47  GeV4, por lo tanto, este último valor se constituye en el orden de magnitud del valor experimental de la CC.
En la sección anterior se encontróque el valor de la con tribución del vacío electrodébil es del orden de 108 GeV4, y ya que los experimentos descritos en las Referencias (Bressi, Carugno, Onofrio & Ruoso, 2002; Casimir,1948; Mohideen & Roy, 1998) demuestran la realidad indiscutible de la energía de vacío, el vacío electrodébil se constituye en una fuente real del campo gravitatorio. Al comparar este valor teórico con el valor experimental mostrado anteriormente, se puede decir que la teoría predice una cantidad que es 55 órdenes de magnitud mayor que el valor observado. Esto ha sido llamado por algunos autores como "la peor predicción teórica en la historia de la física" (Efstathaiou, Hobson & Lasenby, 2006). Ahora, si se supone que los campos sólo contribuyen con el valor exacto de ρΛind  = -108 GeV4 y que el valor observado es exactamente 10-47  GeV4; la teoría por sí sola no consigue obtener concordancia entre los dos resultados, a menos que se escoja el valor ρΛdes  con una precisión de 55 cifras significativas. Por otro lado, debido a que en teoría cuántica de campos no es importante el valor de la energía sino la diferencia entre dos estados diferentes, se puede cambiar el valor de la energía de vacío añadiendo una constante arbitraria; sin embargo, lo anterior nos indica que siempre se debe escoger esta última constante con 55 cifras signifi cativas de precisión. Esto muestra realmente que las teorías actuales son incapaces de dar una explicación satisfactoria a la existencia del pequeño valor observado de ρ Λfis, a pesar del enorme valor de ρΛind.
Lo expuesto anteriormente se conoce como el primer o viejo problema de la CC. Quien quiera resolver este problema debe preguntarse: ¿Cómo cancelar, sin recurrir a ajustes finos, la enorme contribución de los campos? Como so lución a este cuestionamiento, se ha reemplazado ρΛdes  por campos escalares (Abbot, 1985; Barr, 1987; Barr & Hoch berg, 1988; Ford, 1987; Peccei, Sola & Wetterich, 1987; Sola, 1989) (también en modelos de quintaesencia (Caldwell, Dave & Steinhardt, 1998; Yoo & Watanabe, 2012) y k-esencia (Armendariz-Picon, Mukhanov & Steinhardt, 2000; Yoo & Watanabe, 2012)). Sin embargo, en la Ref. (Weinberg, 1989) se mostróque esto no es realmente la so lución al problema; la demostración consiste básicamente en que si se logra la cancelación dinámica del vacío cuántico, los campos no satisfacen las ecuaciones de movimiento que se derivan a partir de su densidad lagrangiana, y viceversa: si los campos satisfacen las ecuaciones de movimiento, éstos no logran solucionar el problema de ajuste fino (Weinberg, 1996).
La motivación principal que condujo al planteamiento de la presente solución se encuentra en la Referencia (Stefan cic, 2009) en donde se muestra un modelo cosmológico que contiene un fluido cósmico adicional con una EDE no homogénea de la forma p = wρ + bH -a, con a > 0. El modelo exhibe en épocas tardías una expansión acelerada producto de una CC efectiva de pequeño valor. Como se verá más detalladamente en la sección 5, cuando la CC es complementada por una función de la forma 1/H 2n, siendo n un número natural, es posible cancelar en épocas tardías y sin necesidad de recurrir a un ajuste fino, la contribución de los campos que permean el Universo. Esto se debe a que el nuevo término, al ser un cociente que involucra a H, es muy grande en épocas tardías cuando el parámetro de Hubble es muy pequeño. Para épocas dominadas por la radiación o la materia, el valor de ρΛfis se relaja mediante la introducción de términos de la forma 1/(q - 1) o 1/(q -  ½Â ), respectivamente (Bauer, Sola & Stefancic, 2010a). En resumen, se busca construir un modelo cosmológico en donde la CC es complementada por un nuevo fluido cósmico, llamado el "Cosmón", para provocar de esta manera la aparición de una EDE efectiva no homogénea. Este mecanismo, originado en la presencia del Cosmón, que reduce de manera significativa el gran valor de ρΛfis , se llamará de ahora en adelante el "mecanismo de relajacioón de la CC. No obstante, el origen y la naturaleza del "Cosmón" no son claros.
En la Referencia (Nojiri  &  Odintsov, 2005) se mostróque una EDE no homogénea es en realidad la descripción efectiva de una teoría modificada de la gravedad; es decir, el Cosmón no es una particula, sino la manifestaci ón de una teoría modificada de la gravedad. Gracias a la forma que poseen el escalar de Ricci y el invariante de Gauss-Bonnet en la métrica de Friedmann-Robertson-Walker, se pueden obtener algebraicamente los términos 1/(q - 1) y 1/(q -  ½) a partir de ellos. Todo lo anterior sugiere que una teoría modificada de la gravedad que involucre el escalar de Ricci y el invariante de Gauss-Bonnet conduce a una posible solución al viejo problema de la CC; la presentación de esta teoría de gravedad modificada se realizará en la siguiente subsección. Se debe mencionar que la solución al ser de origen gravitacional, en contraste con las soluciones en términos de campos escalares, goza de la gran ventaja de ser un mecanismo autointeractuante, i.e., aparte de conseguir la cancelación dinámica de ρΛfis , provoca simultáneamente que el Universo evolucione a través de la historia térmica estándar. Por último, se debe mencionar que el enorme valor de ρΛfis no es un problema sino que garantiza el mismo éxito de la solución (como se observará en la sección 5).
4.1.  Principio variacional. En  las  Referencias (Bauer, 2010; Bauer, Sola & Stefancic, 2010a; Bauer, Sola & Ste fancic, 2010b) se presenta la siguiente teoría modificada de la gravedad como la posible solución al problema:
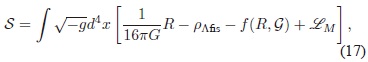
en donde G es el invariante de Gauss-Bonnet dado por:
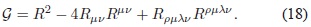
Puesto que el invariante de Gauss-Bonnet es un escalar que se construye a partir de sumas algebraicas de contracciones del tensor de Riemann, la presente teoría es coherente con el principio general de relatividad, el principio de equivalencia y la conservación del cuadrimomentum (Einstein, 1922).
La forma especifica de f (R, G) es:
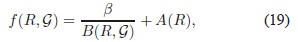
en donde A(R) Â es un polinomio de orden bajo (empezando desde el orden 2 debido a que los ordenes 0 y 1 ya están incluidos en la acción de Einstein-Hilbert con CC); las motiva ciones para la introducción de este término no son relevantes en la solución del problema de ajuste fino debido a que su im portancia se encuentra en épocas tempranas del universo. El invariante de Gauss-Bonnet no se incluyóen este polinomio ya que al ser un invariante topológico no tendrá ningún efecto en las ecuaciones de campo resultantes (Armsen, 1977). El primer término en la Ec. (19), conformado por la constante b y el polinomio B en R y G, es el responsable de la cancelación dinámica de la energía vacío. Con el propósito de obtener una densidad lagrangiana con una dimensión de masa correcta8, la constante b debe poseer una dimensión igual a:

en donde n es la dimensión de masa característica del poli nomio B (R, G).
Para comprender cómo se origina la cancelación dinámica a partir del funcional (17), primero se derivan las ecuaciones de campo utilizando el principio de acción estacionaria, i.e. la variación a primer orden de (17) es igual a cero:9
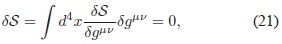
El término dS/dgµv  en (21) corresponde a la derivada funcional, la cual es igual a:
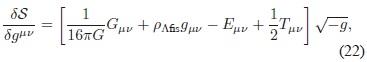
en donde Eµv es
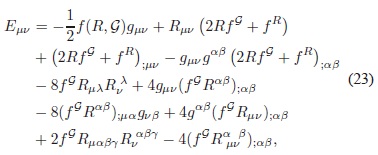
siendo f YÂ Â = ∂f /∂Y . Por el lema fundamental del cálculo variacional se obtiene que

y, por lo tanto, las ecuaciones de campo son:
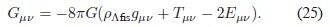
En el término ρΛfis , que corresponde a la densidad de energía de la CC "física", no se ha hecho un ajuste fino en ρ Λdes para cancelar ρΛind . Deteniéndose un instante en este punto, se puede intuir que el resultado efectivo de la modificación de la gravedad consiste en la introducción de un nuevo tensor Eµv , el cual puede ser interpretado como "tensor momentum-energía" inducido gravitacionalmente. Como se verá posteriormente, este nuevo término hace que el ajuste fino sea innecesario.
4.2.  Cosmología f (R, G).  Es obvio que la modificación de la gravedad ocasiona que la cosmología sea distinta a la estándar. Sin embargo, no es el propósito obtener una cosmología diferente, sino solucionar el viejo problema sin distorsionar la conocida historia térmica del Universo. Se verá que el resultado efectivo de la modificación es la introducción de un nuevo fluido cósmico, llamado el Cosmón, con una EDE no homogénea. Debido a que el tensor Eµv  (interpretado como el tensor momentum-energía asociado al Cosmón) es originado a partir de modificaciones de la gravedad, las expresiones para su densidad de energía y su presión en un universo de Friedmann-Robertson-Walker serán una función del parámetro de expansión a (véase el Apéndice B) . Por consiguiente, el Cosmón no será un ente estático sino un ente dinámico que evoluciona a medida que el Universo se expande.
4.2.1.  Ecuaciones  modificadas  de  Friedmann. Con  el propósito de comprender la naturaleza del tensor Eµv, se ha llan las componentes de las ecuaciones de campo con el primer índice contravariante y el segundo covariante. A partir de la componente 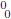 se obtiene que:
se obtiene que:
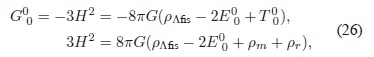
en donde
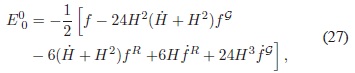
con ρm  y ρr siendo las densidades de energía de la materia y la radiación respectivamente. Esta ecuación corresponde a la primera ecuación de Friedmann modificada. Al comparar con la primera ecuación de Friedmann, se observa que la única diferencia es el término E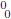 . Si la gravedad a escalas cosmológicas está descrita por la Ec. (17), desde la perspectiva de la ecuaciones de campo usuales el término E
. Si la gravedad a escalas cosmológicas está descrita por la Ec. (17), desde la perspectiva de la ecuaciones de campo usuales el término E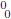 Â es una densidad de energía que evoluciona en el tiempo; es decir, el resultado efectivo de la modificación es la aparición de una densidad de energía variable en el tiempo:
 es una densidad de energía que evoluciona en el tiempo; es decir, el resultado efectivo de la modificación es la aparición de una densidad de energía variable en el tiempo:

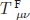 , de un nuevo fluido cósmico denominado el "Cosmón".
, de un nuevo fluido cósmico denominado el "Cosmón". De acuerdo con el principio cosmológico (Weinberg, 1972), el Cosmón debe comportarse como un fluido perfecto, Tµv  = (ρ + p)uµuv - pgµv. En un sistema de referencia donde el Cosmón está en reposo (uµ = 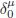 ), su densidad de energía y presión son:
), su densidad de energía y presión son:
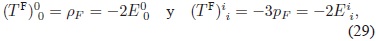
con:
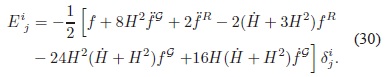
Gracias a la construcción de la función f (R, G) a partir de invariantes de curvatura, la integral 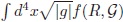 es un escalar; por lo tanto, el tensor Eµv cumple la identidad de Bianchi,
es un escalar; por lo tanto, el tensor Eµv cumple la identidad de Bianchi, 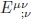 = 0, la cual implica que el Cosmón cumpla individualmente la ecuación de continuidad:
= 0, la cual implica que el Cosmón cumpla individualmente la ecuación de continuidad:
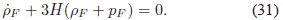
"La EDE para el Cosmon" es pF Â = wFÂ ρF. Se puede observar de las ecuaciones (27) y (30) que el parámetro de estado wFÂ Â es una función no trivial de H y q.
Para derivar la segunda ecuación modificada de Friedmann se halla la componente ii de las ecuaciones de campo:
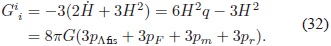
Reorganizando la ecuación (32), y teniendo en cuenta que la presión de la materia es cero, se obtiene una ecuación que involucra únicamente la radiación, la CC y el Cosmón:
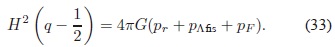
Si se ignoran los términos correspondientes a la CC y al Cosmón, se deduce que en una época dominada por la materia q debe ser igual a ½, es decir, cuando el Cosmón se cancela con la CC, se obtiene el resultado esperado. La ausencia del Cosmón en las ecuaciones no permitiría el desarrollo de una época dominada por la materia a menos que se realice un ajuste fino en la CC.
Al sumar la Ec. (26) con la Ec. (32) para eliminar H2 se llega a la segunda ecuación de Friedmann modificada:
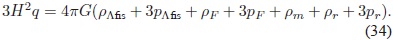
Por último, restando la segunda ecuación de Friedmann modificada de la primera, se obtiene una ecuación en donde se incluyen únicamente la materia, la CC y el Cosmón:
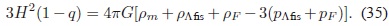
Nuevamente, haciendo un análisis similar, la presencia o ausencia del Cosmón en las ecuaciones permite o prohíbe la existencia de una época dominada por la radiación caracterizada por un parámetro de desaceleración igual a 1.
Sintetizando, el modelo de gravedad modificada permite definir una CC efectiva. La densidad de energía y la presión de la CC efectiva están dadas por:
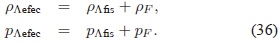
La EDE de la CC efectiva es pΛefec = wefecρΛefec, en donde
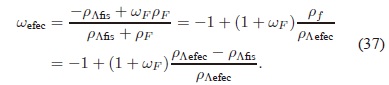
Debido a que ρΛfis es una constante y que wFÂ Â es una función de H y q, el parámetro de estado de la CC efectiva es una función de ρΛefec, H y q; por consiguiente su EDE es no homogénea. La EDE permite reescribir la segunda ecuación de Friedmann de la siguiente manera:
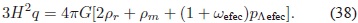
A partir de la EDE para cada fluido y de la ecuación (34), se obtiene una expresión para el parámetro de desaceleración q:
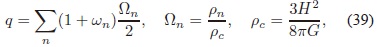
en donde n representa cada uno de los fluidos que componen el Universo. El parámetro de estado wΛefec, al depen der de H Â y q es una función del tiempo. En la sección 6 se mostrará cualitativamente cómo debe ser su evolución en las épocas dominadas por la materia y la radiación. La expresión para el parámetro de desaceleración q hoy en día no es simplemente 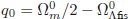 (según el modelo ΛCDM), sino:
(según el modelo ΛCDM), sino:
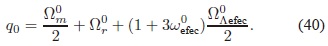
4.3.  Condiciones sobre f (R, G).  En virtud de que la presente solución no debe solamente cancelar dinámicamente el valor de la energía de vacío sino que también debe reproducir satisfactoriamente la cosmología estándar, f (R, G) debe cumplir ciertas condiciones que garantizan que se logre dicho objetivo. Las condiciones son (Bauer, Sola & Stefancic, 2010a):
1. Debido a la creación de las partículas del modelo estándar en la época de recalentamiento, justo des pués y en el inicio de la época dominada por la radiación, la densidad de energía ρΛefec debe coincidir prácticamente con el enorme valor de la densidad de energía de vacío. Para una época anterior, el mecanis mo de relajación no debe funcionar, puesto que oca sionaría daños al funcionamiento de los modelos inflacionarios. La primera condición se puede resumir en:
en donde
es el parámetro de Hubble característico de esta época.
La presencia de A(R) Â no provoca que el valor de ρΛfis se altere ya que a una escala de gran unificación, en donde
con
1016 GeV, se tiene que de H y q, el parámetro de estado de la CC efectiva es una
y por lo tanto
i.e. R2 es despreciable; la razón para introducir el polinomio A(R)Â radica en producir una inflación de tipo Starobinsky (Starobinsky, 1980) o una inflación de tipo anómala (Antoniadis & Mottola, 1992; Sola, 2008; Sola & Shapiro, 2002) y de esta manera crear una transición entre la época inflacionaria y el mecanismo de relajación. El polinomio A también provee una vía de escape a inestabilidades encontradas en el formalismo métrico (Sotiriou & Faroni, 2010) y posibilidades de renormalización a altas energías. No obstante, el polinomio no cumplirá ninguna función en el mecanismo de relajación y será ignorado en el análisis subsecuente.
2. La presencia del Cosmón no debe distorsionar la historia térmica del universo, por consiguiente, el valor ρΛefec hoy en día debe coincidir esencialmente con el valor medido experimentalmente de 10-47Â GeV4. En vista de que la diferencia entre el valor experimental y el valor arrojado por teoría cuántica de campos es abismal, se necesita básicamente que los dos valores se cancelen mutuamente, i.e. ρΛfis ∼ -ρF; para esto, B deber ser tan pequeño como para que el cociente crezca y se produzca la cancelación. La segunda condición se resume en:
Al tratar de satisfacer las condiciones anteriores en cada una de las etapas de la historia térmica, se podrá construir la forma explícita de la función B. Los detalles acerca de la cancelación dinámica y de la construcción de B se presentarán en las siguientes secciones.
Para entender de manera más precisa cómo el mecanismo garantiza que la relajación se realice mediante un proceso espontáneo y no mediante ajustes finos en la CC, se analizará un modelo de juguete en tres escenarios diferentes. Para solucionar el primer problema de la CC se debe dar razón acerca del pequeño valor medido de la CC a pesar del enorme valor del vacío cuántico. La razón consiste, según (Bauer, Sola & Stefancic, 2010a), en que se está ignorando el término Eµv en las ecuaciones de campo, el cual cancela de manera espontánea el vacío cuántico provocando que el valor observado sea muy pequeño:
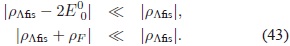
5.1. Época actual. La cancelación en épocas tardías del Universo se obtiene con ρFÂ Â = b/H2. Al reemplazar en la primera ecuación modificada de Friedmann (26) se obtiene:
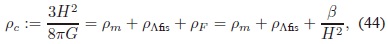
cuya solución es:
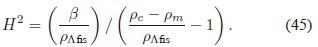
Actualmente 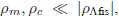 por consiguiente el primer término del denominador en la expresión (45) se puede despreciar y la solución es
por consiguiente el primer término del denominador en la expresión (45) se puede despreciar y la solución es 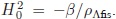 El enorme valor de ρΛfis no es un problema dentro de este modelo, sino que por el contrario, ocasiona que el parámetro de Hubble actual sea pequeño. Sin la presencia de ρF Â la ecuación estaría dominada por la enorme CC provocando que H sea grande en oposición a los resultados experimentales.
El enorme valor de ρΛfis no es un problema dentro de este modelo, sino que por el contrario, ocasiona que el parámetro de Hubble actual sea pequeño. Sin la presencia de ρF Â la ecuación estaría dominada por la enorme CC provocando que H sea grande en oposición a los resultados experimentales.
El mecanismo también puede ser analizado desde un punto de vista diferente. Debido a que el parámetro de Hubble al cuadrado hoy en día 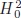 es muy pequeño comparado con
es muy pequeño comparado con 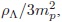 el término 1/H2 se hace muy grande y, escogiendo correctamente el signo de b se obtiene la cancelación de la CC. De ahora en adelante, relajar la CC es equivalente a hacer B → 0. La elección de la constante b no se constituye en un ajuste fino ya que pequeños cambios en b no producirán grandes cambios en H0; el pequeño valor de H0 Â es debido al gran valor de ρΛfis siendo únicamente necesario ajustar las unidades.
el término 1/H2 se hace muy grande y, escogiendo correctamente el signo de b se obtiene la cancelación de la CC. De ahora en adelante, relajar la CC es equivalente a hacer B → 0. La elección de la constante b no se constituye en un ajuste fino ya que pequeños cambios en b no producirán grandes cambios en H0; el pequeño valor de H0 Â es debido al gran valor de ρΛfis siendo únicamente necesario ajustar las unidades.
5.2. Época de radiación y de materia. Para analizar la época dominada por la radiación se toma como ejemplo el vacío electrodébil cuyo valor es negativo. El efecto de una CC negativa en esta época se deduce de la solución de la ecuación de Friedmann con densidades de energía ρr y ρΛfis  comparables en magnitud, y bajo la condición de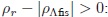
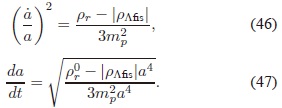
La solución viene dada por:

De la figura 2 se observa que la presencia de una energía de vacío negativa en la época de radiación provoca el recolapso del universo. Para evitar que esto suceda se introduce nuevamente un término que contrarresta el enorme valor de vacío electrodébil. Sin embargo, en este caso, el parámetro de Hubble es grande y no funciona el método utilizado para la época actual; así se debe complementar la función B con un término que tienda a cero en esta época:

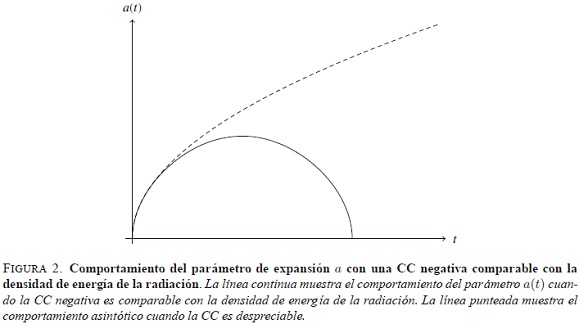
Justo al inicio de la época de radiación, la energía de vacío negativa provocará que el parámetro de desaceleración tienda a valores positivos (recolapso del Universo). A medida que q se acerca a 1, B → 0. Por consiguiente, el valor de la densidad de energía inducida gravitacionalmente tiende a ser muy grande y cancela de esta manera el valor de la CC. El valor de q será muy cercano a 1 pero nunca igual, puesto que el proceso se detendrá cuando la cancelación cause que la radiación sea dominante. Si q llegará a ser mayor que 1, ρ F Â dominaría sobre ρΛfis, lo cual es equivalente a la presencia de una CC positiva que nuevamente provocaría que q tendiera a 1. Por esta razón se concluye que el modelo, con q ≈ 1, es estable. En resumen, el mecanismo de relajación provoca que se presente un período de radiación, y a su vez, la misma existencia de la época de radiación permite que el mecanismo funcione. Para la época dominada por la materia la expresión (½ - q) relaja la CC debido a razones similares.
6.   Modelo realista
En la sección anterior se mostrócómo relajar la CC en las diferentes épocas del Universo; sin embargo, cada modelo descrito implica un período de existencia infinita sin una transición entre épocas. A partir de lo trabajado anteriormente, se infiere que para lograr el objetivo de una adecuada transición entre épocas, se requiere que la función B contenga cada uno de los términos H 2, (1 - q) y (q - ½); para ello, en los artículos (Bauer, 2010; Bauer, Sola & Stefancic, 2010a; Bauer, Sola & Stefancic, 2010b) se propone el siguiente ansatz:
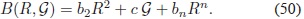
Del Apéndice B, se observa que cualquiera de los términos en la Ec. (50) aporta un término proporcional a H 2n. Si se elige b2  = 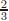 y c = 2 , se obtiene (q - 2 ). El último término proporciona (1 - q) sin necesidad de fijar la constante bn, la cual se denotará por y. De acuerdo con lo anterior, el ansatz mejorado es:
y c = 2 , se obtiene (q - 2 ). El último término proporciona (1 - q) sin necesidad de fijar la constante bn, la cual se denotará por y. De acuerdo con lo anterior, el ansatz mejorado es:
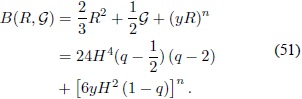
El término proporcional a (1 - q) será el responsable de relajar la CC en la época de radiación cuando H es grande; por consiguiente, éste debe dominar sobre el primero, para lo cual es necesario que n > 2. En la época de equivalencia entre la radiación y materia, los dos términos deben ser del mismo orden y por lo tanto:

Las ecuaciones de campo resultantes (véase el apéndice B.2) son no lineales y bastantes complejas, lo cual dificulta una solución analítica de ellas. Por consiguiente, para entender cualitativamente el modelo, se realizará a continuación un análisis teórico aproximado del comportamiento de la función (51) en cada época del Universo. Aunque es posible hacer un completo análisis numérico del modelo, esto se encuentra fuera del alcance del artículo; sin embargo, se presentará un análisis numérico asintótico del modelo en la época actual.
6.1. Época  de  radiación. Primeramente, es  importante mencionar que la forma en la que opera concretamente el mecanismo de relajación de la CC en las épocas de radiación y materia para este modelo realista es diferente a la presentada en el modelo de juguete. La época de radiación está caracterizada por q ≈ 1 y por H2a ρr a a-4. Para relajar la CC se requiere que B → 0. Debido al valor de q, los términos en B poseen signos contrarios y es posible la cancelación aproximada de ambos si [H2(1 - q)]n∼ H4. De aquí, se deduce que H2(1 - q)∼ H  ∝ a-4(
 ∝ a-4(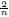 ). Reemplazando en la ecuación (35) se encuentra que
). Reemplazando en la ecuación (35) se encuentra que
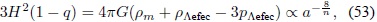
por lo tanto 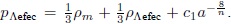 Cuando finaliza la época de radiación, q se hace diferente de 1; por lo tanto, para que se presente una transición suave a la época de materia, en donde H2a a-3, se requiere que n =
Cuando finaliza la época de radiación, q se hace diferente de 1; por lo tanto, para que se presente una transición suave a la época de materia, en donde H2a a-3, se requiere que n = 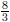 . Utilizando la ecuación de continuidad y la regla de la cadena,
. Utilizando la ecuación de continuidad y la regla de la cadena, 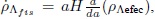 se llega a la siguiente ecuación diferencial ordinaria con coeficientes variables:
se llega a la siguiente ecuación diferencial ordinaria con coeficientes variables:
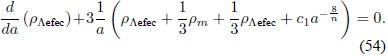
Al solucionar la Ec. (54) con la ayuda de un sistema de álgebra computacional, se obtiene una expresión para ρΛefec:
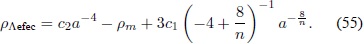
A partir de la expresión anterior se obtiene el parámetro de estado wefec válido en esta época:
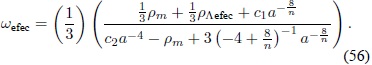
En el límite cuando a → 0, es decir, en la época temprana de radiación, wefec → Â 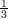 ; en la época tardía de radiación, cuando a → ∞, wefec → 0.
; en la época tardía de radiación, cuando a → ∞, wefec → 0.
6.2. Época de materia. La época dominada por la materia está caracterizada por q  ≈ ½, H2  a ρm a a-3. Realizando un análisis similar, la condición B → 0 implica que H4 (q -  ½)∼ H2n. A partir de la ecuación (33) se obtiene que:
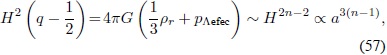
y por lo tanto 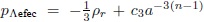 . Â Al escoger
.  Al escoger 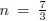 se obtiene una transición suave entre la época dominada por la radiación y la época dominada por la materia. Nuevamente, utilizando la ecuación de continuidad, se llega a una ecuación diferencial para ρ Λefec:
se obtiene una transición suave entre la época dominada por la radiación y la época dominada por la materia. Nuevamente, utilizando la ecuación de continuidad, se llega a una ecuación diferencial para ρ Λefec:
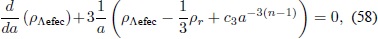
cuya solución es:
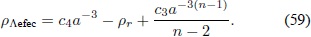
El parámetro de estado en esta época es:
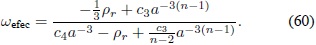
Para la época temprana (a → 0) el parámetro tiende a 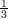 , y para la época tardía (a → ∞) tiende a 0.
, y para la época tardía (a → ∞) tiende a 0.
Anteriormente, se mostrócómo se debe escoger el valor de n para producir una correcta transición entre las etapas; sin embargo, el valor obtenido en los dos casos es diferente y por consiguiente se escogerá un valor cercano a las dos con diciones, n= 3. Esta selección también es congruente con la condición que se impuso al principio, n > 2. Finalmente, el ansatz completo es:
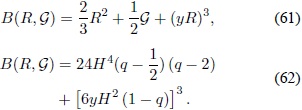
Se podría replicar en este punto que el análisis presentado no es valido, ya que la densidad de energía inducida no contiene únicamente la función 1/B. Sin embargo, al examinar los términos adicionales, se observa que están acompañados por la derivada de la función 1/B, lo cual implica que ρF Â sea una función de la forma:
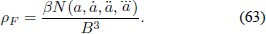
De esta manera, se mantiene la idea de hacer B → 0 para relajar el enorme valor de ρΛfis .
6.3. Época actual. Para la época actual el parámetro de Hubble H Â es muy pequeño y por lo tanto se desprecia el segundo término en la Ec. (62) (Bauer, Sola & Stefancic, 2010a), o en otras palabras se impone y = 0 en el modelo. En este caso, no se puede producir una cancelación aproximada entre dos términos, por lo cual la relajación de la CC está soportada en el pequeño valor de H (del mismo modo que se analizóen el modelo de juguete). Así, la densidad de energía inducida gravitacionalmente en la época actual es10:
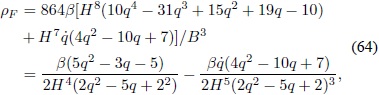
y la ecuación de Friedmann modificada es:

En un análisis asintótico, ρm → 0, y la densidad de energía crítica se hace todavía mas pequeña, ρc → 0; por lo tanto la ecuación (65) se reduce a:
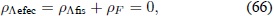
i.e.
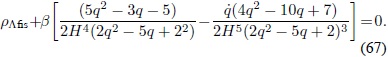
Si se plantean las siguientes variables adimensionales 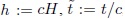 , en donde
, en donde 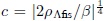 , se obtieneÂ
, se obtiene 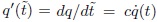 .  Lo anterior permite reescribir la ecuación (67) de la siguiente manera:
. Â Lo anterior permite reescribir la ecuación (67) de la siguiente manera:
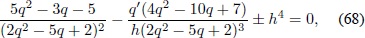
i.e.
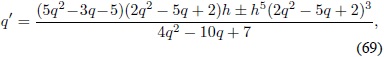
en donde el signo + corresponde al caso 2ρ Λfis /b  > 0 y el signo - al caso 2ρΛfis /b  < 0. La derivada del parámetro de Hubble adimensional con respecto al tiempo adimensional está relacionada con el parámetro de desaceleración mediante la siguiente expresión11:
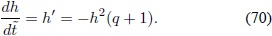
De las ecuaciones (69) y (70) se pueden construir ecuaciones diferenciales de primer orden para h(q) o q(h):
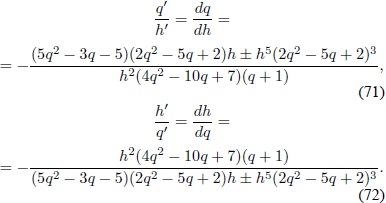
En la figura 3A se muestra una familia de soluciones numéricas de las ecuaciones anteriores. La línea continua gruesa y gris que divide las gráficas en dos regiones representa q' = 0, lo que es igual a la curva:
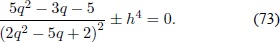
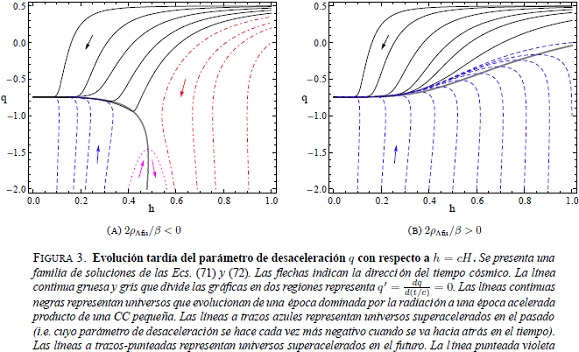
La soluciones interesantes son aquéllas que corresponden a universos provenientes de una época de radiación, i.e. las líneas negras en la figura 3B. Se puede observar que estas últimas, independientemente de las condiciones iniciales, evolucionan en el tiempo hacia el punto (h = 0, q ≈ -0,74), el cual describe un universo con expansión acelerada. Este comportamiento es similar al predicho en los modelos de quintaesencia (Caldwell, Dave & Steinhardt, 1998; Yoo & Watanabe, 2012). En contraste, para obtener un universo de Sitter, el cual corresponde al punto (h= 3-3/4, q  = -1), se necesita un juste fino en las condiciones iniciales. En el caso descrito en la figura 3A, que corresponde a la situación en la que la densidad de energía de la CC y la constante b poseen signo contrarios, el mecanismo de relajación actúa de la misma forma que fue descrita en el modelo de juguete. En el caso descrito en la figura 3B se muestra que aun cuando la densidad de energía de la CC y la constante b posean igual signo, las soluciones tienden al punto (h= 0, q ≈ -0,74).
7.   Conclusiones
Se estudió la posible solución al viejo problema de la constante cosmológica, originada en el modelo de gravedad modificada descrito por la acción en la Ec. (17), que involucra una función f (R, G) dependiente del escalar de Ricci y del invariante de Gauss-Bonnet. Las ecuaciones de campo, derivadas a partir del principio de acción estacionaria, muestran que el resultado efectivo de la modificación consiste en la introducción de un nuevo tensor momentum-energía Eµv. Al estudiar la cosmología inducida por las ecuaciones modificadas de Friedmann, se mostróque la idea esencial detrás de la modificación de la gravedad consiste en introducir un término variable que cancela dinámicamente el enorme valor de la densidad de energía de vacío. Con el fin de obtener la conocida historia térmica del Universo, se impusieron condiciones que permiten acotar la forma funcional de f (R, G).
A  partir  del  estudio  de  un modelo de juguete  se mostró cómo el mecanismo, sin necesidad de realizar un ajuste fino, relaja de manera dinámica el enorme valor del vacío cuántico en diferentes épocas del Universo, y genera un proceso de retroalimentación. También, bajo el estudio de este modelo de juguete, se construyó la forma de f (R, G) de tal modo que el modelo corresponde a uno real:
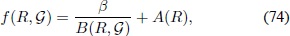
con
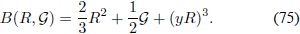
Apéndice A. Obtención de las ecuaciones de campo
A continuación se mostrarán los detalles del cálculo de las ecuaciones de campo para una gravedad modificada del tipo FÂ (R, S, T ), y a partir de esta expresión general se obtendrán las respectivas ecuaciones para una gravedad de tipo FÂ (R, G).
El funcional que describe este primer tipo de gravedad es:
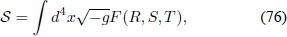
en donde 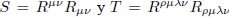 . Para obtener la ecuaciones de campo se realiza una variación a primer orden al funcional S. Primeramente, a partir de
. Para obtener la ecuaciones de campo se realiza una variación a primer orden al funcional S. Primeramente, a partir de 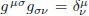 , las variaciones del tensor métrico doblemente covariante y doblemente contravariante son:
, las variaciones del tensor métrico doblemente covariante y doblemente contravariante son:
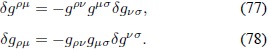
La variación de los símbolos de Christoffel es:
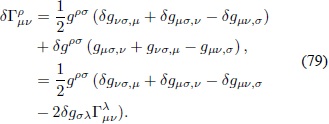
Por conveniencia, se hallan las derivadas covariantes de las variaciones de la métrica calculadas con respecto a la métrica gµv:
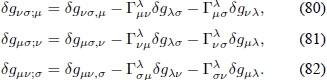
Utilizando la propiedad de simetría de los símbolos de Christoffel 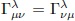 y restando la ecuación (82) de la suma de las ecuaciones (80) y (81), se obtiene
y restando la ecuación (82) de la suma de las ecuaciones (80) y (81), se obtiene
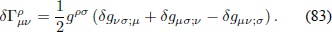
Debido a que las variaciones son con respecto a gµv , se debe introducir la Ec. (78) en la Ec. (83):
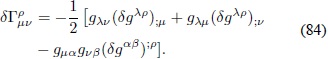
La variación del tensor de Riemann es:
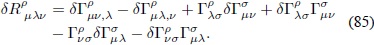
Puesto que la diferencia de dos símbolos de Christoffel es un tensor (Carroll, 2004), se puede hallar su derivada covariante:
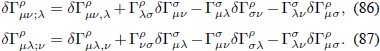
Así, al restar la Ec.(87) de la Ec. (86) se obtiene una expresión más adecuada (Carroll, 2004):
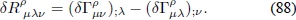
Con las expresiones anteriores se mostrará la variación del funcional (76). Debido a que la operación variación d cumple la regla de Leibniz, se divide la variación en dos partes:
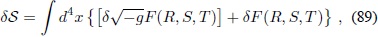
en donde dF (R, S, T) es:
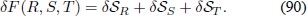
La variación del primer término de la integral, 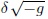 es:
es:
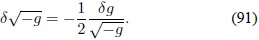
Para hallar dg se utiliza el hecho que ln(det A) = Tr(ln A):
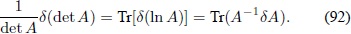
Realizando la sustitución A = gµv , A-1= gµv se obtiene:
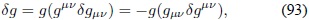
y reemplazando en la Ec. (91) se llega a la expresión:
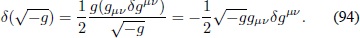
A partir de este punto, el superíndice que acompañe la letra F denotará derivación parcial con respecto a éste, F X= ∂FÂ /∂XÂ . La variación dSRÂ Â es:
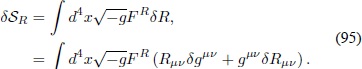
Para hallar la variación del tensor de Ricci se utiliza la expresión (88)
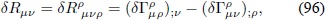
y a partir de la Ec. (84) se obtiene:
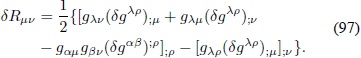
Reemplazando la expresión anterior en la Ec. (95) se obtiene
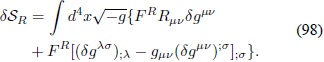
Ahora se integra por partes dos veces12 para obtener una expresión en donde la variación de la métrica no sea operada por una derivada covariante. Debido a las condiciones de frontera 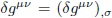 , cada vez que se realiza este proceso se ignoran los términos de superficie:
, cada vez que se realiza este proceso se ignoran los términos de superficie:
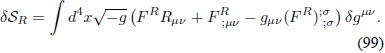
La variación dSSes:
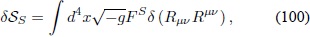
en donde
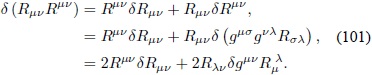
Utilizando la expresión (97) se obtiene:
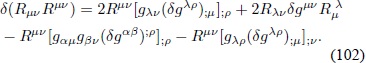
Reemplazando en la Ec. (100):
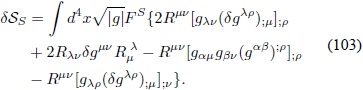
Integrando por partes dos veces y eliminando los términos de superficie se obtiene:
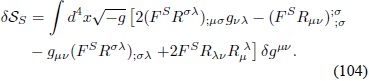
Por último, la variación dST Â es:
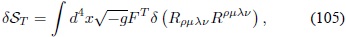
con
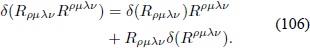
Utilizando las propiedades de simetría del tensor de Riemann se llega a:
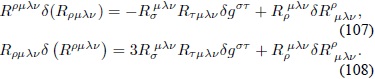
Por lo tanto, la Ec. (106) queda expresada como:
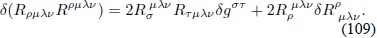
A partir de la Ec. (88) se llega a:
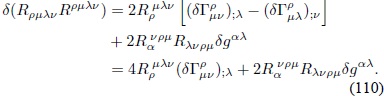
Al reemplazar la expresión (84) y emplear la primera identidad de Bianchi 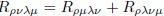 se obtiene:
se obtiene:
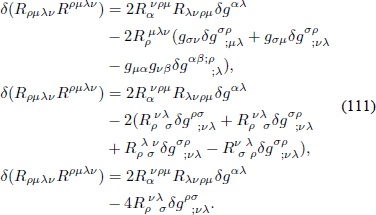
Si se reemplaza lo anterior en la Ec. (105) y se eliminan nuevamente los términos de superficie al integrar por partes, la Ec. (105) resulta en:
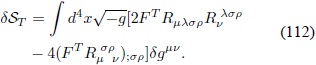
Finalmente, se obtiene la expresión completa para la va riación a primer orden de la Ec. (76) (Bauer, Sola & Stefancic, 2010a):
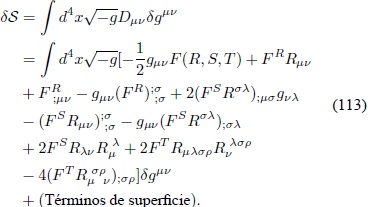
De acuerdo con el principio de acción estacionaria, las ecua ciones de campo en el vacío para una gravedad del tipo FÂ (R, S, T ) son:
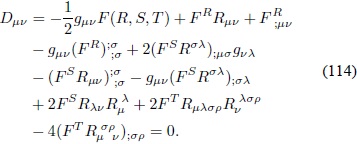
Las  ecuaciones de  campo para una gravedad de  tipo F (R, G) se obtienen utilizando la regla de la cadena en las derivadas parciales de F de la siguiente manera:
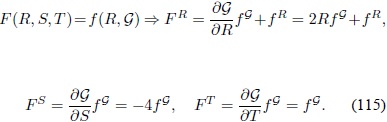
Por consiguiente las respectivas ecuaciones de campo en el vacío son:
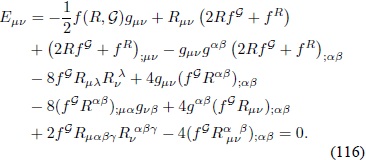
Terminando, la expresión (114) con F RÂ Â Â = Â 1, F SÂ Â = 0, FT = 0 corresponde a las ecuaciones de campo de Einstein en el vacío:
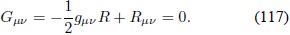
Apéndice B. Obtención de las ecuaciones de campo para una gravedad tipo f (R, G) en un universo de FRW
Se presentarán los cálculos para obtener las ecuaciones que describen el comportamiento del Universo cuando la gravedad está descrita por la acción (17). Los símbolos de Christoffel en FRW son (Weinberg, 2008):
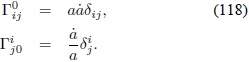
Las componentes que no se mencionen son cero. Con las ex presiones anteriores se hallan las componentes del tensor de Riemann:
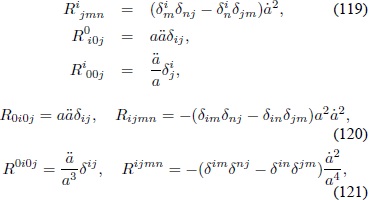
y las componentes del tensor de Ricci:
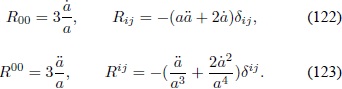
El escalar de Ricci, los escalares S, T Â y el invariante de Gauss-Bonnet G se obtienen a partir de las expresiones anteriores:
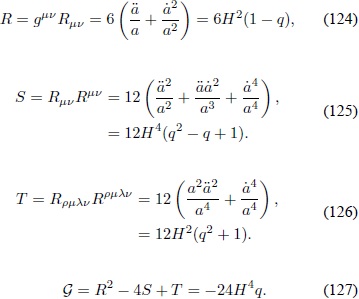
Tensor de Einstein y Eµv . Las componentes del tensor de Einstein 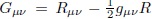 se obtienen a partir de las expresiones (122) y (124). La componente
se obtienen a partir de las expresiones (122) y (124). La componente 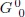 :
:
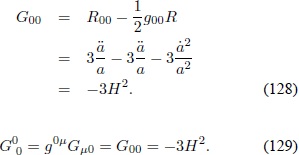
La componente 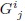 :
:
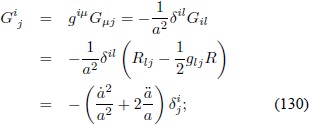
dado que 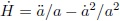 , la Ec. (130) se reduce a
, la Ec. (130) se reduce a
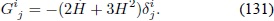
Con el objeto de hallar la expresión específica de Eµv  en la Ec. (116) en la métrica de FRW, primeramente se expande
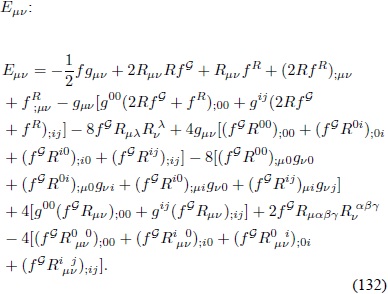
La componente 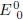 Â esta dada por:
 esta dada por:
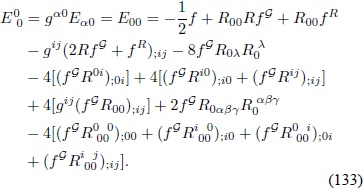
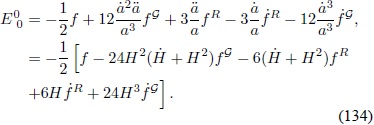
Se obtiene la componente 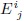 al contraer Eaj  con la métrica:
al contraer Eaj  con la métrica:
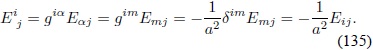
Según la Ec. (132), la componente Eij tiene la forma:
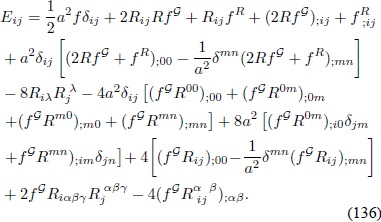
Nuevamente utilizando las expresiones (119) a (124) se obtiene que:
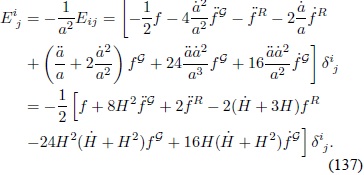
Ecuación modificada de Friedmann. Se mostrará a continuación la forma explícita de la primera ecuación de Friedmann modificada:
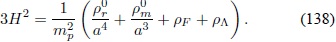
Para esto es necesario conocer la forma explicita de ρ F . De la subsección anterior se conoce que ρ F Â está dada por:
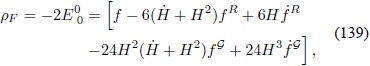
en donde

y
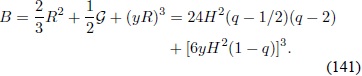
Se procede a calcular las diferentes derivadas de la función
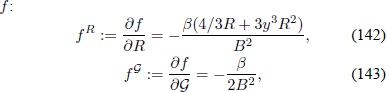
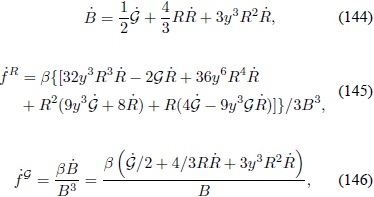
y las derivadas con respecto al tiempo de los invariantes de curvatura en la métrica de FRW:
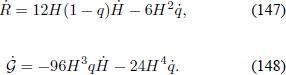
Al reemplazar las expresiones anteriores en la ecuación (139) se obtiene:
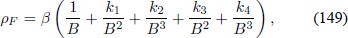
en donde
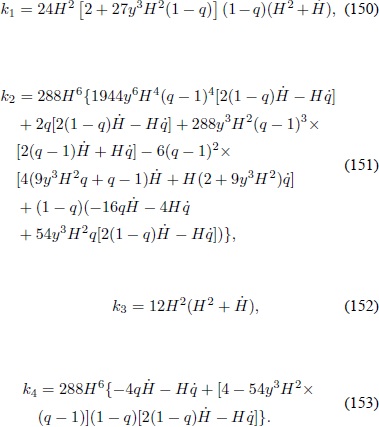
Por lo tanto
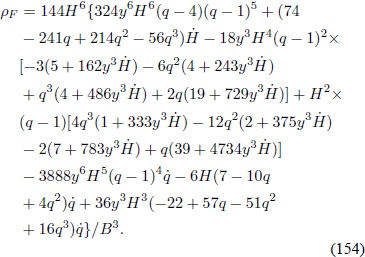
Se puede observar que los términos k 2 y k4 incluyen la derivada del parámetro de desaceleración con respecto al tiempo, por lo tanto la ecuación diferencial es de tercer grado en a(t). Con el fin de disminuir el orden de la ecuación, se expresan todas la funciones como una función del parámetro a:
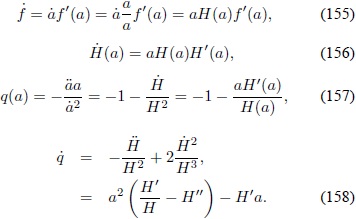
Al hacer este cambio de variable, se obtiene una expresión para la densidad de energía en donde el parámetro de Hubble es una función explicita de a:
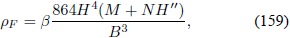
con
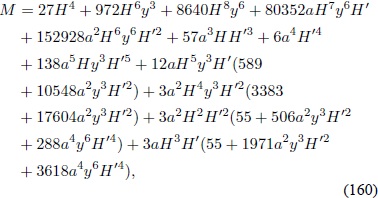
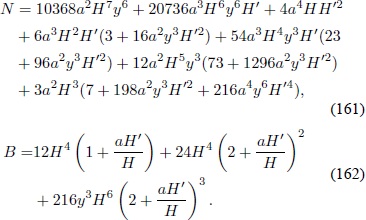
Si se reemplaza (159) en (138) se obtiene la forma explícita de la ecuación de Friedmann modificada:
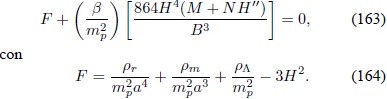
4 Este valor se obtiene teniendo en cuenta únicamente el vacío electrodébil; a una escala de gran unificación el valor es del orden de 1064Â GeV4Â .
5 En realidad, el principio de covariancia establece que se debe reemplazar h µv por g µv  y las derivadas parciales por derivadas covariantes; sin embargo, en el caso de un campo escalar las derivadas parciales y covariantes son iguales. En el caso de un campo vectorial, donde el término es de la forma F µv  = A µ;v  - Av;v , se cancelan los símbolos de Christoffel y de nuevo no es necesario reemplazar las derivadas parciales por derivadas coraviantes, F µv  = A µ,v  - Av,v .
6 El lagrangiano (5) no es invariante de gauge local pero sí posee simetría de Lorentz, hermiticidad y simetría bajo la transformación f → -f.
7 Hasta el momento, las observaciones realizadas en el LHC acerca de la nueva partícula descubierta y candidata a ser el bosón de Higgs son consistentes con las características predichas por el Modelo Estándar; sin embargo, es necesario confirmar otras características como sus números cuánticos.
8 La acción S posee dimensiones de energía integrada en el tiempo; por lo tanto, en unidades naturales, su dimensión de masa es 0. En consecuencia, la dimensión de la densidad lagrangiana debe ser M4.
9 Si se desea conocer los detalles de este cálculo, véase el Apéndice A.
10 Para obtener este resultado, se debe reemplazar 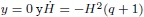 en la Ec. (154) del Apéndice B.
en la Ec. (154) del Apéndice B.
11 Esto se obtiene reemplazando las variables adimensionales 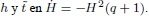
12 Este procedimiento es válido gracias a que el operador derivada covariante cumple la regla de Leibnitz. Así, integrar por partes en este caso conduce a:
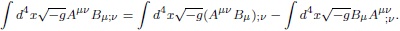
Cada vez que se integra por partes, la operación derivada covariante pasa de un término al otro en el producto. En virtud del teorema de Stokes, se observa que el primer término, a la derecha de la igualdad, es igual a la integral de superficie del vector Aµv Bµ en la frontera; de aquí, proviene el nombre de términos de superficie.
Agradecimientos
Y.R. cuenta con el apoyo financiero de la Fundación para la Promoción de la Investigación y la Tecnología del Banco de la República mediante proyecto de investigación número 3025 CT-2012-02, y de la VCTI (UAN) mediante proyecto de investigación número 2011254.
Referencias [ Links ]
Abbot L., 1985. A mechanism for reducing the value of the cosmological constant, Phys. Lett. B 150, 427. [ Links ]
Antoniadis I. & Mottola E., 1992. 4-D quantum gravity in the conformal sector, Phys. Rev. D 45, 2013. [ Links ]
Armendariz-Picon C., Mukhanov V. & Steinhardt P. J., 2000. A dynamical solution to the problem of a small cosmological constant and late-time cosmic acceleration, Phys. Rev. Lett. 85, 4438. [ Links ]
Armsen M., 1977. A variational proof of the Gauss-Bonnet formula, Manuscripta. Math. 20, 245. [ Links ]
Barr S., 1987. An attempt at a classical cancellation of the cosmological constant, Phys. Rev. D 36, 1691. [ Links ]
Barr S. & Hochberg D., 1988. Dynamical adjustment of the cosmological constant, Phys. Lett. B 211, 49. [ Links ]
Bauer F., 2010. The cosmological constant and the relaxed universe, J. Phys. Conf. Ser. 259, 012083. [ Links ]
Bauer F., Sola J. & Stefancic H., 2010a. Dynamically avoiding fine-tuning the cosmological constant: the "relaxed universe", JCAP 1012, 029. [ Links ]
Bauer F., Sola J. & Stefancic H., 2010b. The relaxed universe: towards solving the cosmological constant problem dynamically from an effective action functional of gravity, Phys. Lett. B 688, 269. [ Links ]
Bauer F., Sola J. & Stefancic H., 2011. Relaxing a large cosmolo gical constant in the astrophysical domain, Mod, Phys. Lett. A 26, 2556. [ Links ]
Beringer J. et. al. 2012. Review of Particle Physics (RPP), Phys. Rev. D 86, 010001. [ Links ]
Bressi G., Carugno G., Onofrio R. & Ruoso G., 2002. Measurement of the Cassimir force between parallel metallic surfaces, Phys. Rev. Lett. 88, 041804. [ Links ]
Bruneton J.-P. et. al., 2012. Fab Four: when John and George play gravitation and cosmology, Adv. Astron. 2012, 430694. [ Links ]
Caldwell R. R., Dave R. & Steinhardt P. J., 1998. Cosmological imprint of an energy component with general equation of state, Phys. Rev. Lett. 80, 1582. [ Links ]
Carroll S., 2004. Spacetime and geometry: an introduction to general relativity, Addison Wesley, San Francisco, USA. [ Links ]
Casimir H. B. G., 1948. On the attraction between two perfectly conducting plates, Indag. Math. 10, 261. [ Links ]
Charmousis C., Copeland E. J., Padilla A. & Saffin P. M., 2012a. General second order scalar-tensor theory, self tuning, and the Fab Four, Phys. Rev. Lett. 108, 051101. [ Links ]
Charmousis C., Copeland E. J., Padilla A. & Saffin P. M., 2012b. Self-tuning and the derivation of the Fab Four, Phys. Rev. D 85, 104040. [ Links ]
Chatrchyan S. et. al., [CMS Collaboration], 2012. Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC, Phys. Lett. B 716, 30. [ Links ]
Cheng T.-P. & Li L.-F., 1984. Gauge theory of elementary particle physics, Clarendon Press, Oxford, UK. [ Links ]
Chern S.-S., 1945. On the curvatura integra in Riemannian manifold, Ann. of Math. 46, 674. [ Links ]
Copeland E. J., Padilla A. & Saffin P. M., 2012. The cosmology of the Fab-Four, JCAP 1212, 026. [ Links ]
Efstathiou G., Hobson M. P. & Lasenby A. N., 2006. General relativity: an introduction for physicists, Cambridge University Press, Cambridge, UK. [ Links ]
Einstein A., 1917. Cosmological consideration in the general theory of relativity, Sitz. Preuss. Akad. Wiss. Berlin (Math.Phys.) 1917, 142. [ Links ]
Einstein A., 1922. The meaning of relativity, Taylor & Francis, London, UK. [ Links ]
Ford L. H., 1987. Cosmological damping by unstable scalar fields, Phys. Rev. D 35, 2339. [ Links ]
Jarosik N. et. al., 2011. Seven-year Wilkinson Microwave Anisotropy (WMAP) observations: sky maps, systematic errors and basic results, Astrophy. J. Suppl. Ser. 192, 14. [ Links ]
Kane G., 1993. Modern elementary particle physics, Addison-Wesley, Massachussets, USA. [ Links ]
Komatsu E. et. al., 2011. Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: cosmological interpretation, Astrophys. J. Suppl. Ser. 192, 18. [ Links ]
Larson D. et. al., 2011. Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: power spectra and WMAP derived parameters, Astrophys. J. Suppl. Ser. 192, 16. [ Links ]
Mohideen U. & Roy A., 1998. Precision measurement of the Casimir force from 0.1 to 0.9 µm, Phys. Rev. Lett. 81, 4549. [ Links ]
Nojiri S. & Odintsov S. D., 2005. Inhomegeneous equation of state of the universe: phantom era, future singularity and crossing the phantom barrier, Phys. Rev. D 72, 023003. [ Links ]
Padilla A., Saffin P. M. & Zhou S.-Y., 2010. Bi-galileon theory I: motivation and formulation, JHEP 1012, 031. [ Links ]
Padilla A., Saffin P. M. & Zhou S.-Y., 2011. Bi-galileon theory II: phenomenology, JHEP 1101, 099. [ Links ]
Peccei R. D., Sola J. & Wetterich C., 1987. Adjusting the cosmo logical constant dynamically: cosmons and new force weaker than gravity, Phys. Lett. B 195, 183. [ Links ]
Perlmutter S. et. al., 1999. Measurements of and from 42 high-redshift supernovae, Astrophys. J. 517, 565. [ Links ]
Riess A. G. et. al., 1998. Observational evidence from supernovae for an accelerating universe and a cosmological constant, Astron. J. 116, 1009. [ Links ]
Sola J., 1989. The cosmological constant and the fate of the cosmon in Weyl conformal gravity, Phys. Lett. B 228, 317. [ Links ]
Sola J., 2008. Dark energy: a quantum fossil from the inflationary universe?, J. Phys. A 41, 164066. [ Links ]
Sola J. & Shapiro I. L., 2002. Massive fields temper anomaly induced inflation, Phys. Lett. B 530, 10. [ Links ]
Sotiriou T. P. & Faroni V., 2010. f (R) theories of the gravity, Rev. Mod. Phys. 82, 451. [ Links ]
Starobinsky A. A., 1980. A new type of isotropic cosmological models without singularity, Phys. Lett. B 91, 99. [ Links ]
Stefancic H, 2009. The solution of the cosmological constant problem from the inhomogeneous equation of state a hint from modified gravity?, Phys. Lett. B 670, 246. [ Links ]
Weinberg S., 1972. Gravitation and cosmology: principles and applications of the general theory of relativity, John Wiley & Sons, New York, USA. [ Links ]
Weinberg S., 1989. The cosmological constant problem, Rev. Mod. Phys. 61, 1. [ Links ]
Weinberg S., 1995. The quantum theory of fields, Volume 2: modern applications, Cambridge University Press, Cambridge, UK. [ Links ] Weinberg  S.,  1996.  Theories  of  the  cosmological  constant, arXiv:astro-ph/9610044. [ Links ]
Weinberg S., 2008. Cosmology, Oxford University Press, Oxford, UK. [ Links ]
Yoo J. & Watanabe Y., 2012. Theoretical models of dark energy, Int. J. Mod. Phys. D 21, 1230002. [ Links ]
Recibido: 6 de septiembre de 2012
Aceptado para su publicación: 30 de enero de 2013