Departamento de Matemáticas, Universidad del Valle, Cali, Colombia. *Correspondencia: J. R. Quintero: jose.quintero@correounivalle.edu.co.

Recibido marzo 2014; aceptado diciembre 2014.

Abstract

In this paper we establish the existence of periodic travelling waves for a 2D Boussinesq type system in threedimensional water-wave dynamics in the weakly nonlinear long-wave regime. For wave speed |c| > 1 and large surface tension, we are able to characterize these solutions through spatial dynamics by reducing a linearly ill-posed mixed type initial value problem to a center manifold of finite dimension and infinite codimension. We will see that this center manifold contains all globally defined small-amplitude solutions of the travelling wave equation for the Boussinesq system that are periodic in the direction of propagation.

Key words: periodic travelling waves, center manifold approach, stability

Resumen

En este artículo establecemos un resultado de existencia de ondas periódicas para un sistema 2D del tipo Boussinesq que describe la evolución de ondas de agua de gran elongación y pequeña ampitud que son débilmente lineales. Para velocidad de onda |c| > 1 y tensión superficial suficientemente grande, estas soluciones son caracterizadas a través de dinámica espacial al reducir el problema de valor inicial (mal puesto a nivel lineal) a una variedad central de dimensión finita y codimensión infinita. Se mostrará que dicha variedad central contiene todas las soluciones de onda viajera de pequenã amplitud para el sistema tipo Boussinesq que son periódicas en la dirección de propagación de la onda.

Palabras clave: ondas viajeras periódicas, método de variedad central, estabilidad.

1. Introduction

This paper presents an existence result of nonlinear travelling water waves which are periodic in their direction of propagation and have a pulse structure in the unbounded transverse spatial direction. As done for a wide range of applications, we use spatial dynamics and center manifold reduction to obtain such a result in a model related with the water-wave problem. Here the expression "spatial dynamics" means to perform a method in which a system of partial differential equations governing a physical problem is formulated as a evolutionary equation (in general ill-posed)

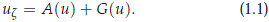
in which an unbounded spatial coordinate plays the role of the timelike variable z (see Kirchgässner (1982)). In this paper the method is applied to studying the existence of non trivial periodic travelling wave for the Boussinesq type system related with the water wave problem

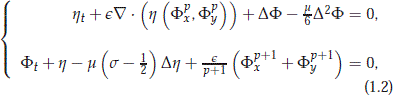
where √m = h₀/L is the ratio of undisturbed fluid depth to typical wave length (long-wave parameter or dispersion coefficient), and ∈ is the ratio of typical wave amplitude to fluid depth (amplitude parameter or nonlinearity coefficient), s^-1 is the Bond number (associated with the surface tension), F is the rescale nondimensional velocity potential on the bottom z = 0, and h is the rescaled free surface elevation. We consider waves which are periodic in a moving frame of reference, so that they are periodic in the variable x - ct, where t denotes the temporal variable. For this physical problem, we have a bounded spacelike coordinates (the vertical direction), which is bounded because the fluid has finite depth, and the coordinate x - ct which is considered bounded because we are looking for periodic wave in this variable. So, since there is not any restriction upon the behavior of the waves in the spatial direction y transverse to their direction of propagation, we are allowed to use it as timelike variable. We apply spatial dynamics to the problem by formulating this as an evolutionary system of the form (1.1) with z = y in an infinite-dimensional phase space consisting of periodic functions of x-ct (see Grover & Schneider (2001), Sandstede & Scheel(1999), Sandstede & Scheel(2004), and Haragus-Courcelle & Schneider (1999) for applications to respectively nonlinear wave equations, reaction-diffusion equations, and Taylor-Couette problems, and Quintero & Pego(2002) for periodic nonlinear travelling for the Benney-Luke model).

In the case of wave speed |c| > 1 and bond number s > ½, the Boussinesq system (1.2) under consideration in this paper has a very close relationship with the Benney-Luke model derived in Quintero & Pego(1999) when a > b and also with the KP-II model (s > 1/3), in the sense that travelling waves for the Boussinesq system (1.2) can generate travelling waves for the Benney-Luke model and the KP-II model, up to some order. Event tough this fact, in the regime of wave speed |c| > 1 and bond number s > ½, the Boussinesq system (1.2) seems to be closer to the linearized system of the exact water wave problem with surface tension (see Grover (2001), Grover & Mielke(2001)) since both models share ill-posed spatial evolution equations with finite-dimensional center manifolds, while for the Benney-Luke model in the same regime and also for the KP-II model there are ill-posed spatial evolution equations with infinite-dimensional center manifolds.

It is well known that a finite-dimensional dynamical system whose linear part has purely imaginary eigenvalues admits an invariant manifold called the center manifold which contains all its small, bounded solutions. The dimension of the center manifold is determined by the number of purely imaginary eigenvalues (e.g., see Vanderbauwhede (1989)). This type of results under special hypotheses has been extended for infinite-dimensional evolutionary systems whose linear part has either finite or even infinite number of purely imaginary eigenvalues, showing in particular that the original problem is locally equivalent to a system of ordinary differential equations whose solutions can be expressed in terms of the solution on the center space (tangent to the center manifold). A generalization regarding invariant manifolds of infinite dimension and codimension in nonautonomous systems was obtained by Scarpellini (1990), but his hypotheses require that the operator A₁ (A restricted to the hyperbolic space) be bounded from H to H. We also have some works by Mielke (1991) and Vanderbauwhede & Iooss(1982), Quintero & Pego(2002), among others. The general strategy of our proof will follow closely the lines of Vanderbauwhede (1989) (also see Quintero & Pego(2002), Kirchgässner (1982), Mielke (1988), Mielke (1992) for the case of a finite-dimensional center manifold in an ill-posed system for which the spectrum of A₁ is unbounded on both sides of the imaginary axis. In order to accomplish this, we need to transform the travelling wave system into an integral equation that must contain all small bounded solutions. By modifying the nonlinearity f outside a neighborhood of 0 using a cutoff function, we are able to obtain an invariant local manifold as a consequence of the contraction mapping argument.

The main differences between our results and those in Vanderbauwhede & Iooss(1982) are that our cutoff occurs in a space with less regularity than the space regularity and also that the nonlinear part has a smoothing property. This facts are clever to control the norm of solutions in the right space using an indefinite energy which turns out to be "definite" on the center manifold. The stronger assumption on the nonlinear term f imposed in the present work is completely natural for the present application to the Boussinesq system.

In this paper we describe all small travelling waves that translate steadily for s > ½ with supercritical speed |c| > 1, which are periodic in the direction of translation (or orthogonal to it). In this regime, after rescaling ∈ and m, the traveling-wave system for (1.2) takes the form

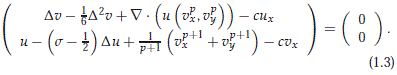
Existence of periodic travelling waves follows by considering the system (1.3) as an evolution equation where y acts as the "time" variable. In this case when we seek for x-periodic travelling wave solutions, the initial-value problem for the system (1.3) considered as an evolution equation in the variable y has mixed type due to the fact that the Cauchy problem turns out to be linearly ill-posed for wave speed |c| large enough and large bond number (s > ½ ). To be more precise, at the linear level there are finite many central modes (pure imaginary eigenvalues) and infinitely many hyperbolic modes. As a consequence of this fact, the existence result of x-periodic travelling wave solutions involves using an invariant center manifold of finite dimension and infinite codimension. This center manifold contains all globally defined smallamplitude solutions of the travelling wave equation for the Boussinesq system that are x-periodic in the direction of propagation.

2. Periodic travelling waves for |c| > 1 and s > ½

Recall that x-periodic travelling-wave profile (u, u) should satisfy the system (1.3). In order to look for the existence of x-periodic travelling waves of period 2p, we set the new variables

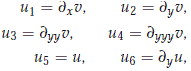
then we have for g ( s - ½) = 1 that

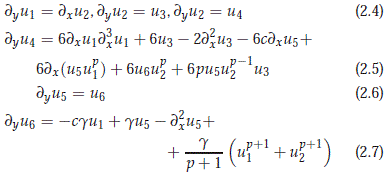
In terms of the new variable U^t = (u₁, u₂, u₃, u₄, u₅, u₆), we see that this system can be rewritten as an evolution in which y is considered as the time variable

where we have that

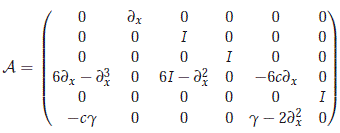
and also

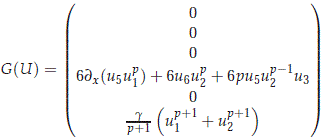
Now, for a given integer r ≥ 0, let 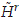denote the Sobolev space of 2p-periodic functions on R whose weak derivatives up to order k are square-integrable. Then 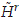is a Hilbert space with norm given by

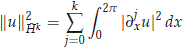
We will study the existence of x-periodic solutions for (2.8) in the Hilbert spaces H and X defined by

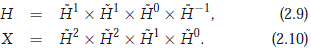
Note that X is densely embedded in H. If we assume that 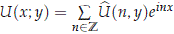, then we see that

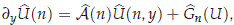
where the matrix ∈ 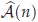has the form

It is straightforward to see that the characteristic polynomial P(n, b) of is given by

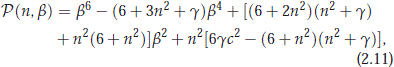
where g > 0, |c| > 0 and n ∈ Z. We note that the eigenvalues for are roots of the cubic polynomial p_n in the variable l = b² given by

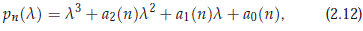
where a₀(n), a₁(n) and a₂(n) are defined as

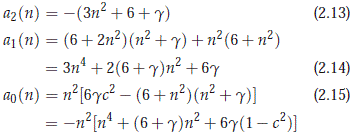
Eigenvalues of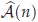

We want to compute the eigenvalues of 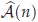. For n = 0, we have that a₀(0) = 0, a₁(0) = 6g > 0, a₂(0) = – (6 + g) < 0 and the cubic equation (2.12) can be easily solve since

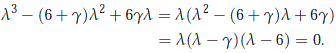
In other words, we have the existence of six eigenvalues for 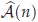given by,

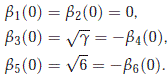
Assume now that n ≠ 0. We will see that for g > 0 and c² > 1 large enough, the polynomial p_n has a real root l₁(n) which is negative for a finite number of n's and positive for infinitely many n's. To do this we need somehow to localize the roots of the polynomial p'n for n ≠ 0. Note that

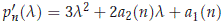
has real roots given by

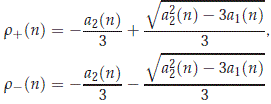
since

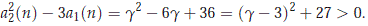
Moreover, a direct computation shows that

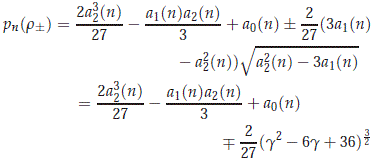
From this, we conclude for any n ≠ 0 that

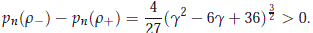
On the other hand, we have that

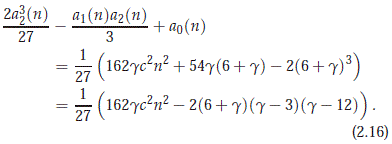
Using this we have that

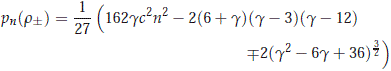
We set f (g) = (g² - 6g + 36)³ - ((6+ g)(g - 3)(g -12))². We see that f (0) = f (6) = 0 and that f '(0) = f '(6) = 0, so we have that

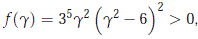
which implies that

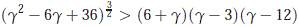
and so, we have for g > 0 that

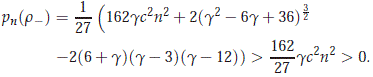
Now we note that

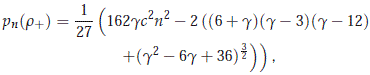
so, we have that p_n(r₊) is positive for |n| large and could be negative for a finite number of n's. As a consequence of this, for n ≠ 0 the polynomial p_n has a real root l₁(n), whose sign depends on the sign of a₀(n). In the case pn(r+) > 0, there are two conjugate complex roots l₂(n) and l₃(n) = l₂(n), and in the case pn(r+) < 0 there are two positive real root l₂(n) ≥ l₃(n) > 0. Finally, we want to determine the sign of l₁(n) for g > 0. We first observe for c² > 1 large enough and g > 0 that there is n₀ ≠ 0 such that

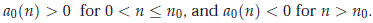
From this fact, we conclude for c² > 1 large enough and g > 0 that

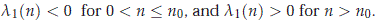
Right and left eigenvectors of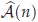

As we established above, b₁(0) = b₂(0) = 0 is an eigenvalue. We see directly that the eigenvectors are

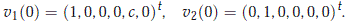
and left eigenvectors

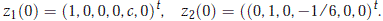
The eigenvalue b₃(0) = √g = -b₄(0) are single eigenvalues with right eigenvectors

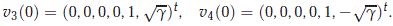
and left eigenvectors

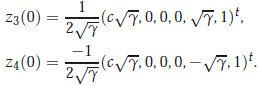
On the other hand, the eigenvalue b₅(0) = √6 = -b₆(0) are single eigenvalues with right eigenvectors

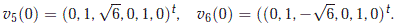
and left eigenvectors

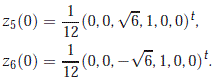
Now, we will describe the form of the eigenvalues for 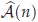for n ≠ 0. In this case, we have that

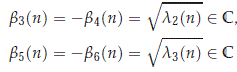
and for g > 0 we have that

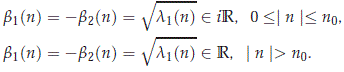
A direct computation shows for 1 ≤ m ≤ 6 that b_m(n) is a single eigenvalue with right eigenvector

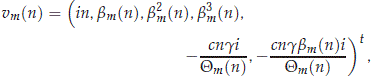
where Q_m(n) = b²_m(n) - (g + n²). It is also straightforward to show that left eigenvector z_m(n) is given by

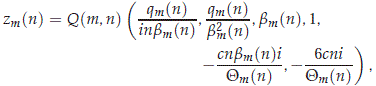
where q_m(n) = b²_m(n)(b²_m(n) - (6 + n²)) and Q(m, n) is taken such that

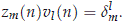
If we introduce the matrices Z(n) and V(n) given by

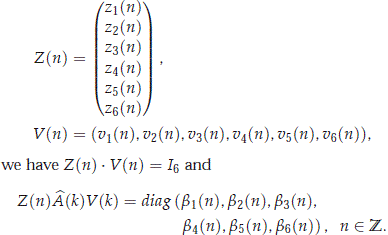
Now, we observe that given any vector 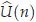∈ R⁶, we may write

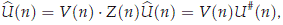
Where

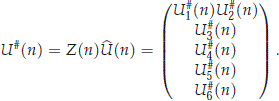
Using this representation, we have for 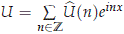that

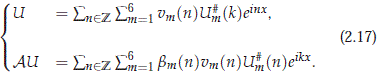
We define the projections p₀ and p₁ for g > 0 by

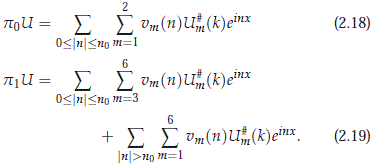
We see directly from the explicit form of the roots of the polynomial p_n that |b_m(n)| grows asymptotically linearly in |n|. In fact, we must recall that the roots l_m(n) of ∈ 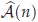for 1 ≤ m ≤ 3 depend on the discriminant D(n) of p_n defined as

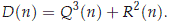
where Q and R are defined by

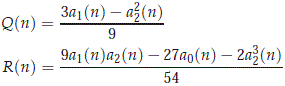
More concretely, we have the following known result that characterizes the roots for a cubic polynomial

1. if D(n) is positive, then p_n has one real root (l₁(n)) and two are complex conjugates (l₂(n) and l₃(n) = l₂(n)).

2. if D(n) is negative, then p_n has three different real roots, and

3. if D(n) = 0, then p_n has three real roots, with two of them are equal (l₂(n) = l₃(n)).

Moreover, the roots of the polynomial p_n defined in (2.12) are explicitly given by

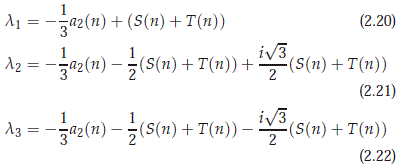
where S(n) and R(n) are numbers defined as

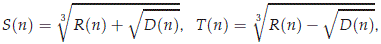
such that S(n) + T(n) ∈ R and that S(n) - T(n) ∈ R for D(n) ≥ 0, and S(n) + T(n) ∈ R and that S(n) - T(n) iR for D(n) < 0. In this particular case, we have for n ≠ 0 that

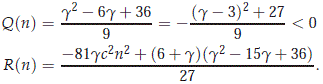
Using this we see that Q(n) = O(1) and R(n) = O(n²) for |n| large enough, meaning that D(n) = O(n⁴) for |n| large enough, and that |S(n)| = |T(n)| = O(n²) for |n| large enough. Using previous facts and formulas (2.20)- (2.22) for |n| large enough, we conclude for 1 ≤ m ≤ 3 and |n| large enough

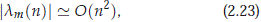
and so, for |n| large enough and 1 ≤ m ≤ 6, we have that

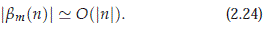
Using this fact it is not difficult to verify that in terms of the coefficient vectors U^#(n) we have the following equivalence of norms:

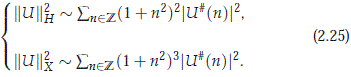
From the equivalences in (2.25) it is evident that p₀ and p₁ are bounded on H and on X with p₀ + p₁ = I, and it is clear that AX_j ⊂ H_j where X_j = p_jX and H_j = p_jH for j = 0, 1. This yields the spectral decompositions H = H₀ ⊕ H₁ and X = X₀ ⊕ X₁.

2.1. Center manifolds of finite dimension and infinite codimension

Here we consider an abstract differential equations of the form

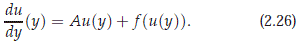
where X and Hare Banach spaces with X densely embedded in H, A ∈ L (X, H), the space of bounded linear operators from X to H, and f is continuously differentiable from H into H with f(0) = 0 and Df(0) = 0. We will assume that the nonlinear part f has the regularizing effect: f (H) ⊂ X. This hypothesis on f is a stronger condition than those imposed in many works related with the existence center manifolds, but this completely natural for the Boussinesq type system considered in this paper. Existence of a local finite dimensional center manifold can be established in the same fashion as the approach used in Quintero & Pego(2002) in the case of having a center space with infinite dimension and infinite codimension for the Benney-Luke model. As in the later model, we must observe that the cutoff will be performed in the H norm, and not in the X norm as in Quintero & Pego(2002). This is important since we need to use an energy functional which is defined on H, which is conserved in time for classical solutions (taking values in X), but is indefinite in general. Fortunately for us, this energy controls the H norm for solutions on the center manifold. So, we require obtaining a center manifold that contains solutions with large X norm but small H norm. This is a consequence that the nonlinearity f has a smoothing property, mapping H into X.

We will state the result for the existence of a locally invariant center manifold of classical solutions for the system (2.26) under certain conditions which allow the center subspace (that associated with the purely imaginary spectrum of A) to have finite dimension and infinite codimension. We start with some basic definitions and some hypotheses:

Definition 2.1. Let J ⊂ R be an open interval and u: R → H be a function. We say that u is a classical solution of (2.26) on J if the mapping y → u(y) is continuous from J into X, is differentiable from J into H and (2.26) holds for all y ∈ J.

Let b > 0, let Y and Z be Banach spaces and U be an open set in Y. We define the Banach spaces Cb(U, Z), Lip(U, Z) and Y^b by

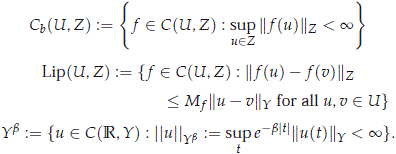
Throughout this section we assume that there are bounded projections p₀ and p₁ on H such that

(i) (i) H = H₀ ⊕ H₁ with H_i : = p_i(H),

(ii) p_i|X is bounded from X to X, and

(iii) AX_i ⊆ H_i where Xi := p_i(X), for i= 0, 1.

We see that equation (2.26) can be rewritten as the first order system

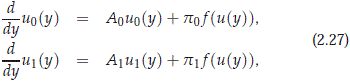
where A_i ∈ L (X_i, H_i) with A_iy = p_iAy for y ∈ X_i.
We assume the following splitting properties for the operator A₁, associated with the linear evolution equation du/dy = Au.

(H1) There exists a > 0 and a positive function M1 on [0, a) such that for any b ∈ [0, a) and for any g1 ∈ C (R, X1) ∩ H^b₁ the equation

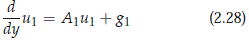
has a unique solution in H^b₁ given by u₁ = K₁g₁, where K₁∈ L(H^b₁ ) with ||K₁|| _L(H^b1) ≤ M₁(b). Furthermore ||K₁|| L(X^b₁) ≤ M₁(b).

As done by J. Quintero and R. Pegoin the case of the Benney-Luke model (see Quintero & Pego(2002)), we easily have that

Theorem 2.1 (Local Center Manifold Theorem). Let H, X, A, p₀, p₁ and f be as above, and let

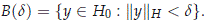
Then for all sufficiently small d > 0 there exists j_d : H₀ → X₁ such that

(i) j_d(0) = 0 and Dj_d(0) = 0.

(ii) j_d ∈ C_b(H₀, X₁) ∩ Lip(H₀, X₁), and on any ball B(d '), j_d has Lipschitz constant L(d ') satisfying L(d ') < ½ and L(d ') → 0 as d ' → 0⁺.

(iii) The manifoldMd ⊂ X given by

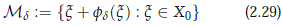
is a local integral manifold for (2.26) over B(d) ∩ X₀. That is, given any y ∈ M_d there is a continuous map u: R → M_d with u(0) = y, such that for any open interval J containing 0 with p₀u(J) ⊂ B(d) it follows that u is a classical solution of (2.26) on J. Moreover, u0 := p0u is the unique classical solution on J with u₀(0) = p₀y to the reduced equation

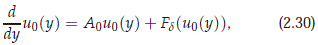
where Fd : H₀ → X₀ is locally Lipschitz and is given by Fd(w):= p₀ f ( w + j_d(w)).

(iv) For any open interval J ⊂ R, every classical solution u₀ ∈ C¹(J, H₀) ∩ C(J, X₀) of the reduced equation (2.30) such that u₀(y) ∈ B(d) for all y ∈ J yields, via u= u₀ + j_d(u₀), a classical solution u of the full equation (2.26) on J.

(v) The manifold M_d contains all classical solutions on R that satisfy ||u(y)||_H ≤ d for all y.

2.2. Linear dynamics analysis.

Now we are interested in establishing the solvability conditions to the linear level. First we consider the center subspace H₀. We define the bounded C₀-group {S₀(y)}_y∈R on H₀ with infinitesimal generator A₀ = A |_X0 by

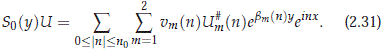
Now, we want to determine the Green function to solve the problem in the hyperbolic subspace H₁. Let us consider the inhomogeneous linear equation

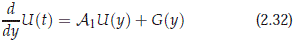
where A₁ = A|_X1 . We need to observe that |ℜ(l_m(n)| ≥ a > 0 for all n ∈ Z, except for m = 1, 2 when n ≠ 0. Let 0 ≤ 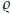< a and let G ∈ C(R, X₁) ∩ H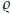₁, where for any Banach space Y,

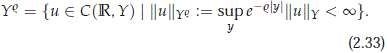
Hereafter we will assume m and n are such that 1 ≤ m ≤ 6 and n ∈ Z \ {0}, or m = 5, 6 for n= 0. Suppose U ∈ C¹(R, H₁) ∩ C(R, X₁) is a solution belonging to H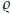₁. Then using the Fourier series expansion in x and multiplying by the matrix Z(n) yields the differential equation

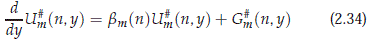
The functions G^#_m(n, ·) and U^#_m(n, ·) belong to R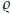 (Y = R in (2.33)). From the fact that |b_m(n)| ≥ a > , we conclude necessarily that

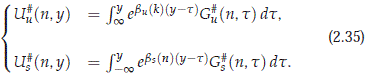
where for 0 <| n |≤ n₀ we have u = 3, 5 and s= 4, 6, and for | n |> n₀ we have u= 1, 3, 5 and s= 2, 4, 6. As a direct consequence any solution of (2.32) in H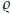₁ is unique. We will see that the formulas (2.35) together with the representation for U= p₁U in (2.19) allow us to establish the existence of a solution in H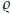₁. To see this, we decompose equation (2.32) using projections into the "unstable" and "stable" subspaces. The projections for U ∈ H are

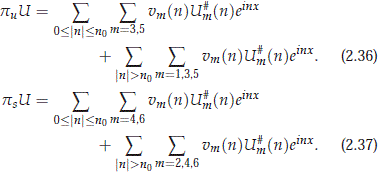
Clearly p_u and p_s are bounded on H and X and p_u + p_s= p₁. Now, we introduce a Green's function operator S(y) defined for nonzero y ∈ R by

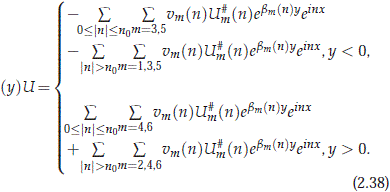
By the definition of the norm in H and X (see (2.25)), we have that

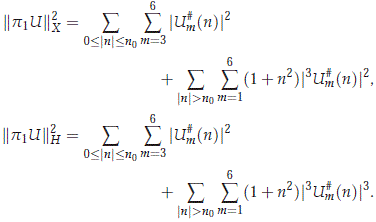
On the other hand, for 1 ≤ m ≤ 6 and y ≠ 0 and n ≠ 0, we have that

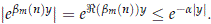
Using this fact, we see directly for Y = H or X that,

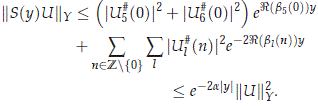
We also have for y > 0 that

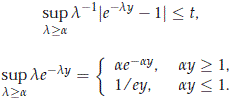
Following the same type of calculation and using previous facts, one can easily verify that for some constant C (independent of y) we have the following norm bounds:

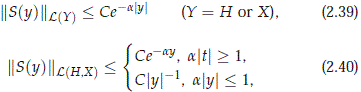
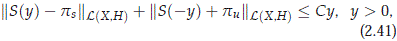
where L(Y) and L(H, X) respectively denote the space of bounded operators on Y, and from H to X. Clearly, we have that S(y) → p_s(resp. -p_u) strongly as y → 0⁺ (resp. 0^-). Therefore the families {S(y)}_y>0 and {-S(-y)}_y>0 are analytic semigroups in p_sH and p_uH respectively (?, p.62). Moreover, we also have that S is C¹ from R \ {0} to L(H) with dS(y)/dy = A₁S(y). Therefore, we conclude that equation (2.35) yield the formula

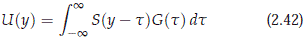
for the solution of (2.32). Finally, we need to establish that U ∈ C(R, X), U ∈ H₁, and dU/dy exists in H and satisfies (2.32). The computations in this case follows as those done for the Benney-Luke equation in ?, but for completeness we include the details. First observe that

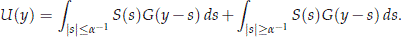
The first term is in C(R, X) since G ∈ C(R, X) and we have the estimate (2.39). Now, since G ∈ H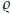, the we may use (2.40) to see that the second integral converges in X uniformly on compact sets in y. Then we have that U ∈ C(R, X).
On the other hand, using (2.39) we have for Y = H or X that U ∈ Y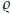. In fact, if G ∈ Y 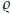then

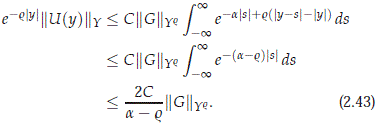
Moreover, we have that

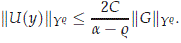
It remains to show U = p_sU +p_uU is differentiable in H and satisfies (2.32). We check in a standard fashion that p_sU is differentiable. For h > 0 we compute

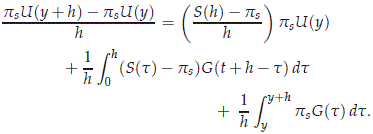
Using (2.41) and G ∈ C(R, X), as h → 0⁺ we deduce that

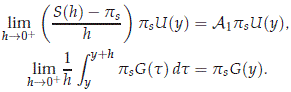
Since we have that S(y) → p_s strongly as y → 0⁺, the we have that

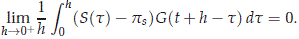
Hence the right derivative exists and satisfies D₊p_sU(t) = A₁p_sU(t) + p_sG(t), so is continuous into H. It follows that p_sU is differentiable. We may treat p_uU in a similar way, and conclude that U is differentiable and satisfies (2.32). So, from the Theorem 2.1, we have established that system (2.8) admits a local center manifold having the properties stated in the Theorem.

2.3. Global existence and stability for g > 0 and |c| > 1 (large enough)

We are now interested in proving global existence of classical solutions on the local center manifold, for initial data that is small in H-norm, which follows from the fact that the zero solution is stable on the center manifold characterized by the graph of a function j_d : H₀ → X₁. We use strongly the existence an energy functional that  is conserved in time for classical solutions. We define the energy functional e : H → R by e(U) = e₀(U)+e₁(U), where the quadratic part is

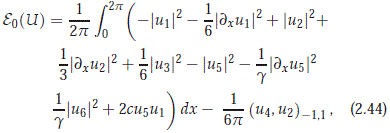
where (·, ·)_-1,1 represents the pairing between 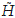^-1 and 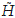¹, and the remaining part is

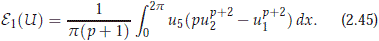
From the definition, e is a smooth function from H to R. After multiplying appropriately the equation (2.6) by u₂ and equation (2.7) by u₆, one can easily verify that if U ∈ C¹(R, H) is a classical solution of the first order equation (2.8), then for all y ∈ R

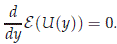
Even though previous property, this energy can not be used to obtain a solution throughout the variational method since neither e nor e₀ is not positive define in the space H. We will see that energy e₀ is positive on the center space H₀, and also that this controls the norm of U in H, via the center manifold result. We note that from the definition of the variable U = (u₁, u₂, u₃, u₄, u₅, u₆), we have a priori that u₁ = ∂_xv has mean zero on [0, 2p], meaning that ₁(0) = 0.

Lemma 2.1. Let |c| > 1 large enough and g > 0. Then there is a positive constant M₀ > 1 such that for any U ∈ H₀ with ₁(0) = 0,

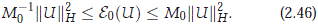
Proof. From the Fourier series representation of U ∈ H₀ given with 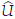₁(0) = 0, we have that

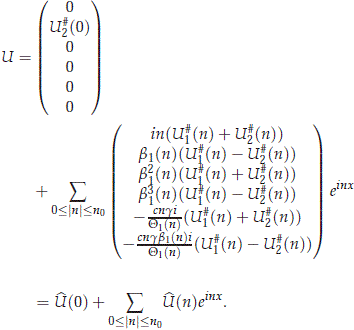
We also have that 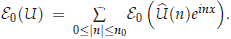We note that

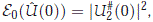
On the other hand, for b₁(n) = b we have that

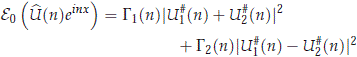
where

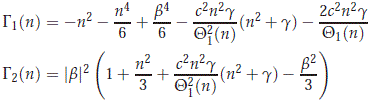
Since for |c| > 1 (large enough) we have that b²₁(n) = l₁(n) < 0 for 0 < n ≤ n₀, then we have the right side of the second term is positive. Now, for the first term, we use the polynomial equation for b₁(n) given in (2.11). First note that

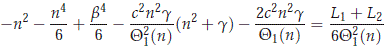
where L₁ and L₂ are given by

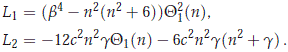
But we have that

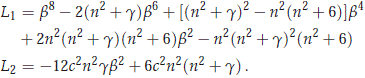
Using this, we get that

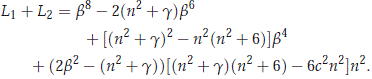
But from (2.11), we have that

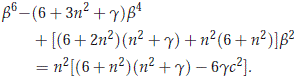
Then using that b²₁(n) < 0 for 0 < n ≤ n₀, we finally get that

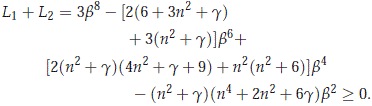
This fact implies that

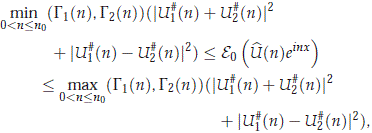
which implies that

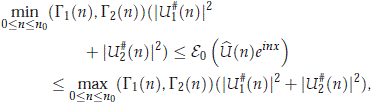
In other words, we have shown that

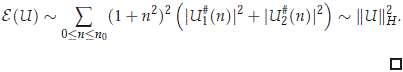
The first consequence of this fact is the following result:

Corollary 2.1. Let |c| > 1 large enough and g > 0. Then there are d₁ > 0 and M₁ > 1 such that for any U ∈ H₀ with 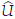₁(0) = 0 and ||U||_H < d₁,

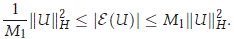
Proof. First note that from the Hölder inequality with q = p + 2, there is some positive constant C = C(p) (independent of U) such that

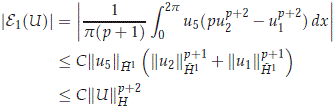
Moreover for some constants C₀ and C₁ = C₁(p) (independent of U), we conclude that

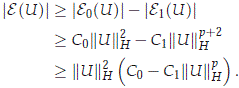
Let d₁ > 0 be such that C₀ - d ^p₁C₁ > 0. Then for ||U||_H ≤ d₁ with U ∈ H₀ \ {0} we have that

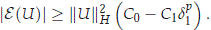
The second claim of this lemma follows directly. In fact, for U ∈ H we have that

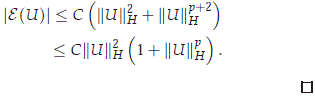
Now, we are interested in estimating the energy e on the center manifold. In other words, we want to obtain a similar estimates for the lift of e to the center manifold M_d.

Lemma 2.2. sl Let j_d as in Theorem 2.1. Then there exist constants d₂ > 0 and C₂ > 1 such that for all x ∈ H₀ with ||x||_H < d₂ we have

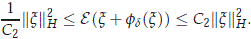
Proof. Let us define the functional 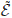: H₀ → R by

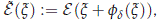
where the function j_d is defined in Theorem (2.1). First note that ||j_d(x)||_H = 0(||x||_H). Since e is smooth and e(0) = 0, then e'(x) = O(||x||_H). As a consequence of this fact and that e₁(U) = 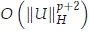, we have for x ∈ H₀ that

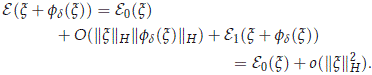
as ||x||_H → 0. Then by the previous result, we get the conclusion.

We first establish that solutions starting in the center manifold are appropriately bounded.

Lemma 2.3. Let x ∈ X₀ be such that 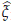₁(0) = 0 and that ||x||_X ≤ d₂. There exists a unique classical solution U(x, ·) for the full problem (without cutoff) (2.8) on R with initial condition p₀ ° U(x, 0) = x such that on any open interval J containing 0,

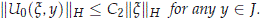
Proof. We may assume that d₂ small enough such that d₂ << d. Let x ∈ X₀ be such that ||x||_X ≤ d₂. Now, from Theorem 2.1, there exists a unique continuous function U form R to the local center manifold M_d such that p₀(U(0)) = x, which turns out to be a classical solution of the equation (2.8) on any open interval J ⊂ R containing 0 such that ||p₀(U(y))||_H ≤ d for any y ∈ J. On the other hand, since U is a classical solution and the energy E is conserved, then we have for any y ∈ J that

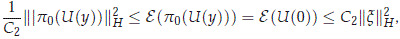
meaning ||p₀(U(y))||_H ≤ C₂||x||_H, for any y ∈ J as desired. A continuation argument shows that U is a classical solution for the full problem (without cutoff) (2.8) on R.

Now we are in position to state the main result on the existence and the stability on the center manifold. The proof of this result follows in the same fashion as the Benney-Luke equation done by Quintero and Pego in ?.

Theorem 2.2. (Global Existence and stability on the center manifold) Let j_d be given by applying Theorem 2.1 to (2.8). There exist positive constants d₃ and C₃ such that, for any x ∈ X₀ with 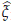₁(0) = 0 and ||x||_H ≤ d₃, there is a unique classical solution U on R to (2.8) such that p₀U(0) = x and ||U(y)||_H ≤ 2C₂||x||_H for all y ∈ R. Moreover, for any T > 0 the map taking x to U is Lipschitz continuous from H₀ to C([–T, T], H).

Acknowledgments. J. R. Quintero was supported by the Mathematics Department at Universidad del Valle (Colombia) under the project C.I. 7910.

References

Grover, M. (2001). An existence theory for three-dimensional periodic travelling gravity-capillary water waves with bounded transverse profiles. Physica D 152(1): 295-415.         [ Links ]

Grover, M., Mielke, A. (2001). A spatial dynamics approach to three-dimensional gravity-capillary steady water waves. Proc. Royal Soc. Edin. A131(1): 83-136.         [ Links ]

Grover, M., Schneider, A. (2001). Modulating pulse solutions for a class of nonlinear wave equations. Commun. Math. Phys. 219: 489-522.         [ Links ]

Haragus-Courcelle M., Schneider G. (1999). Bifurcating fronts for the Taylor-Couette problem in infinite cylinders. Z. Angew. Math. Phys. 50: 120-151.         [ Links ]

Kirchgässner, A. (1982). Wave solutions of reversible systems and applications. J. Diff. Eqns. 45: 113-127.         [ Links ]

Mielke, A. (1988). Reduction of quasilinear elliptic equations in cylindrical domains with applications. Math. Meth. Appli. Sci. 101: 51-56.         [ Links ]

Mielke, A. (1991). Hamiltonian and Lagrangian Flows on Center Manifolds. Berlin: Springer-Verlag.         [ Links ]

Mielke, A. (1992). On nonlinear problems of mixed type: a qualitative theory using infinite-dimensional center manifolds. J. Dyn. Diff. Eqns. 4 (1): 419-443.         [ Links ]

Pazy, A. (1983). Semigroups of Linear Operators and Applications to Partial Differential Equations. Springer-Verlag, New York.         [ Links ]

Quintero J., Pego R. (1999). Two-dimensional solitary waves for a Benney-Luke equation. Physica D 132: 476-496.         [ Links ]

Quintero J., Pego R. (2002). A host of Travelling Waves in a Model of Three-Dimensional Water-Wave Dynamics. Nonlinear Science 12: 59-83.         [ Links ]

Sandstede B., Scheel A. (1999). An Essential instability of pulses and bifurcations to modulated travelling waves. Proc. Roy. Soc. Edin. A 129: 1263-1290.         [ Links ]

Sandstede B., Scheel A. (2004). Defects in oscillatory media: Toward a classification. SIAM J. Appl. Dynam. Syst. 3: 1-68.         [ Links ]

Scarpellini, B. (1990). On nonlinear problems of mixed type: a qualitative theory using infinite-dimensional center manifold.I and II. J. Appl. Math. Phys. (ZAMP). 42: 289-314.         [ Links ]

Vanderbauwhede, A., and Iooss, G. (1982). On nonlinear problems of mixed type: a qualitative theory using infinitedimensional center manifold. I and II. Dynamics Reported,New Series 1: 125-163.         [ Links ]

Vanderbauwhede A. (1989). Centre manifolds, normal forms and elementary bifurcations. Dynamics Reported, New Series 2: 89-169.         [ Links ]