doi: http://dx.doi.org/10.18257/raccefyn.339

Universidad Nacional de Colombia, Facultad de Minas, Grupo TAYEA, Medellín, Colombia. Correspondencia: Farid Chejne J., fchejne@unal.edu.co
Artículo de posesión para el ingreso como miembro correspondiente a la Academia Colombiana de Ciencias Exactas, Físicas y Naturales el 6 de abril de 2016

Recibido: 12 de febrero de 2016. Aceptado: 2 de junio de 2016

Resumen

Se presenta una descripción de la forma como se afronta el problema de la abstracción mental, necesaria para el desarrollo de un modelo matemático, capaz de describir los fenómenos que rigen el comportamiento de la dinámica de procesos naturales, ante perturbaciones externas al sistema. El objetivo de este trabajo es encontrar la ecuación de balance, partiendo desde la ecuación de Liouville clásica en la escala microscópica hasta las ecuaciones de balance a escala macroscópica o ecuaciones de Navier-Stokes. Dividiendo magnitudes físicas como la velocidad en dos partes, una de ellas relacionada con el valor promedio y la otra con el fluctuante, genera la posibilidad de saltar de un escala a otra y así reducir la complejidad. En el artículo también se menciona de manera resumida el hecho que la complejidad se construye a partir de unidades simples; de esta manera, los modelos se consideran una abstracción de la realidad en la que se le asigna una ecuación matemática en diferentes escalas, tanto temporal como espacial, para explicar cómo la naturaleza se comporta y cómo ella se moldea para lograr sus determinadas formas.

Palabras clave: modelamiento, multi-escala, ecuaciones de balance.

Abtract

A description of how everyone does abstractions to develop a mathematical model is presented; as well as the ability to describe the behaviour of nature processes dynamic when there are external perturbations. The aim of this work is to find the balance equation, starting from the classical Liouville equation on the microscopic scale until the balance equations on a macroscopic scale or Navier-Stokes equations. By dividing physical quantities such as velocity in two parts, one of which related to the average value and the other one with the fluctuation; it is possible to jump from one scale to another and reduces complexity. At this point, the complexity is constructed from simple units; therefore, the models are considered reality abstractions based on a mathematical equation formulated at different levels, both on time and space; as consequence, nature takes its shape due to the external influence, without forget the nature laws, by modifying the shape, adapting and looking for the less energy demand.

Key words: Modelling, mult-scale, balance equations.

Introducción

La importancia de desarrollar modelos se relaciona con la dificultad de entender y explicar fenómenos desde el punto de vista experimental, con la imposibilidad de operar el sistema real en regiones de riesgo, y con tiempos de ensayo demasiado largos en los sistemas reales (días o meses); versus el corto tiempo de solución del modelo (segundos o minutos) en el computador que permite replicar la experimentación de fenómenos traslapados, predecir nuevos comportamientos, comprender la física del problema y reducir los costos de la experimentación. Los modelos matemáticos se usan como herramientas científicas para aproximarse a la determinación de estructuras y reactividad química, de condiciones óptimas de diseño de una etapa o proceso, para la delimitación de la región de operación óptima de un sistema, para el diseño de sistemas de monitoreo, automatización, control y diagnóstico de fallas. También, se usa para caracterización y creación de conocimiento sobre el comportamiento de un proceso; en fin, los modelos se utilizan para explicar y controlar diversos fenómenos en nuestro entorno y para pronosticar los acontecimientos venideros (Myung, I. J. 2000, Moore, J. 2015).

Los modelos permiten darle explicación a las observaciones y por ende, facilitan el conocimiento de las características de la naturaleza. Un modelo teórico es la formulación en términos de expresiones matemáticas de las suposiciones y sus consecuencias, bajo el supuesto que dichas relaciones identifican el proceso en particular del mundo real.

Cualquiera que sea el proceso se pueden desarrollar modelos determinísticos y estocásticos, dependiendo de la incertidumbre en las variables que identifican el proceso. Los modelos determinísticos permiten una predicción exacta con base en ecuaciones cuya solución es precisa y sin lugar a incertidumbre; contrario a lo estocásticos, en los cuales el nivel de incertidumbre es alto y lo que se predice es la probabilidad de ocurrencia de eventos.

La naturaleza toma forma. La naturaleza toma forma, respetando leyes que rigen su comportamiento ante la influencia externa y hacen que los eventos naturales se orienten a través de la repetición de una unidad oculta, modificando la forma para adaptarse, actuando con el menor gasto energético posible. La dinámica del movimiento de los objetos se rige por la ley de Newton y sus diversas modificaciones; la relación entre un sistema y sus alrededores se rige por las leyes de la termodinámica. Los científicos siempre buscan clasificar y darle explicación a las formas básicas que se presentan en la naturaleza. Se conoce que la complejidad de las formas que se presentan en la naturaleza es generada por la gran variedad de la ruptura espontánea de la simetría y es representada por un gran número de ecuaciones simétricas como los balances de energía, momento y materia; de otro lado, ecuaciones no simétricas como la segunda ley de la termodinámica.

Con la postulación de las leyes fundamentales de la termo-dinámica (la primera ley predice la conservación de la energía y la segunda, la no conservación de la distribución de los estados energéticos), nuestro entendimiento de la naturaleza toma forma, modificando su entorno, adaptándose y repitiendo una unidad básica oculta un sin número de veces. La naturaleza siempre busca lograr lo máximo con el mínimo ajuste posible, el camino más corto con el menor gasto energético, respetando siempre las leyes fundamentales.

Existe un patrón de conjunto, el cual se repite: mucha información en un extremo, conducción entre un extremo y el otro, luego distribución nuevamente de la información. Esto se observa en los árboles, en los ríos desde su nacimiento en las montañas hasta su desembocadura en el mar, en el sistema circulatorio y nervioso de los seres vivos, entre otros (ver Figura 1).

La forma irregular de los límites del sistema en la naturaleza mantiene activa su interacción entre ésta y su entorno, facilita el intercambio de materia, energía e información y de esta manera la auto-organización en los sistemas. Para clasificar las formas, existe por ejemplo, la propuesta de los sistemas de ramificación (Bell, A.D. 1986), que distingue tres categorías: ciegos, deficientes visuales y los patrones de auto-organización; donde hay un enfoque en propiedades algorítmicas de la formación de patrones.

Stevens (Bell, A. D. 1986), propone cuatro tipos de patrones: meandros, espirales, explosiones y ramificación; algo similar a esto se puede encontrar en la clasificación de los tipos de interfaces en la naturaleza de acuerdo con Stevens, P. S. (1974): Interfaz de movimiento en un medio desordenado (flujo en materiales porosos, la propagación de frentes de llama, etc.), procesos de deposición (deposición de átomos, formación de gotas de agua, procesos de cristalización, etc.) y los sistemas biológicos (crecimiento bacteriano, plegables y torsiones de proteínas en el espacio, etc.) (Prusinkiewicz, P. 1998).

Hay varias teorías para explicar las formas básicas de la naturaleza, pero el modelado de la forma sigue siendo un campo abierto para la investigación científica. Thompson (1917), describe que las formas de los seres vivos se debe a las fuerzas y las propiedades físicas que intervienen en los procesos biológicos. De otro lado, los mecanismos de Turing (1952) dan una explicación simple para un gran número de formas en la naturaleza basado en que existen zonas fluctuantes que logran desestabilizar el sistema y lo hacen evolucionar hacia otras estructuras coherentes (líneas de cebras y leopardos de dibujos sobre la piel de los peces tropicales).

Según Sharon, et al. (2005), el teorema central de la geometría diferencial, demostrado por Gauss, señala que la métrica de una superficie (curvatura de Gauss) depende de la forma en que esta se adopta en el espacio. Se encuentra que la forma de las fronteras de hojas y flores no pueden ser planas, sino onduladas, y que siempre que existan discrepancias entre la tasa de crecimiento de las hojas de las fronteras y sus centros, aparecerán ondas como las que se aprecia en las membranas biológicas, líquenes, babosas marinas, coles y orquídeas (Eran, S.; Michael M. and Harry, L. S. 1986). En la clasificación de las semillas de girasol, en la formación en espiral de una concha o de un cono de pino y en el patrón de crecimiento de las ramas de un árbol, por ejemplo, se encontró que la secuencia de la serie de Fibonacci es común en estos casos. Debe haber presentado las mismas leyes básicas y, por tanto, una representación matemática similar.

Los sistemas naturales y los hechos por el hombre tienen un propósito y un tamaño finito, sujeto a restricciones de flujo y de tamaño (Bejan, A. 2000), de ahí la importancia de los procesos de optimización que se llevan a cabo de forma natural o guiada por el ser humano. En la medida que los flujos de materia y energía son restringidos, y que adicionalmente existen restricciones de tamaño, los sistemas tienen formas irregulares que facilitan el uso de los recursos. Se puede decir que la segunda ley de la termodinámica rige principalmente este proceso de optimización restringida; todo lo ajusta a un principio de economía que es lo que se establece en definitiva el curso de la evolución.

Podría hablarse sobre los puntos críticos en los que un sistema se vuelve inestable y donde da lugar a la bifurcación (Prigogine, I. Nicolis, G. 1987), a la auto-organización o a los puntos restrictivos que hacen que la naturaleza aumente su complejidad para aprovechar el máximo posible los diferentes flujos de materia y energía (Bejan, A. 1997; 2005; Kurchan J. 2005); por ejemplo, cálculos de bifurcaciones, basados en la teoría de la dinámica de los sistemas no lineales, muestran que hexágonos son una de las primeras formas en que aparece, en el borde de la incertidumbre, y que esta estructura de simetría se ve favorecida en relación con otros.

Sin embargo, estos casos que acaban de ser citados son diferentes interpretaciones del mismo principio, que es la segunda ley de la termodinámica. Los sistemas naturales y las acciones de los seres humanos tienen un propósito, con sujeción a las limitaciones de flujo y tamaño. Como los flujos de materia y energía están restringidos y existen otras restricciones geométricas, los sistemas tienen formas irregulares que facilitan el uso de los recursos.

Se cree que este proceso de optimización sujeto a restricciones se rige principalmente por la ley principal del universo, según Einstein, ajustado a un principio de economía que es lo que se establece en definitiva el curso de la evolución. En este documento se discute la hipótesis de que la naturaleza evoluciona para modificar sus diferentes formas como consecuencia de las limitaciones impuestas por la "segunda ley de la termodinámica" y que permite ramificar los estados del sistema cuando hay suficiente flujo de cualquier bien conservador.

El problema de la escala espacial y temporal. Un sistema natural está constituido por partículas elementales, las cuales puede agruparse para conformar una unidad básica (v.g. el núcleo de un átomo), esta a su vez puede ligarse entre sí para construir una estructura molecular, definiéndose así un especie o grupo funcional con características de conjunto definidas y diferentes a las de la unidad básica (ver Figura 2a). Estas estructuras moleculares pueden agruparse para construir una zona definida de materia, constituyéndose en clúster, los cuales se unen y forman los granos, para luego construir a partir de un grupo de granos las partículas (ver Figura 2a y 2b).

Los grupos de partículas forman zonas sólidas dentro de un material poroso, dando lugar a otra escala superior del orden de nanómetro con distribución no uniforme de tamaño y forma de poros. Se hacen las siguientes preguntas: ¿ Si se tiene un gas con 1023 partículas en permanente movimiento aleatorio y sin dirección definida, ¿qué es lo que se mueve cuando un elemento mecánico como un ventilador pone movimiento el fluido y lo hace desplazar de un punto a otro?; ¿Cómo actúa la gravedad u cualquier fuerza externa sobre las partículas individuales de tamaño pequeño y masa pequeña?; ¿Será que las fuerzas externas actúan sobre el conjunto y no sobre partículas individuales? y ¿Cómo se forman las interacciones dentro de un conjunto de partículas?. Al igual que la escala espacial, se presenta la escala temporal, en la que variaciones en el tiempo son solo perceptibles si se registran dichos cambios en tiempos muy pequeños. Por ejemplo, las colisiones a escala molecular solo son detectables si se miden los efectos en tiempos en la misma escala; de lo contrario, éstas se perciben en escalas temporales mayores mediante el promedio de las fluctuaciones, que dan origen a las leyes constitutivas como la Ley de Fourier, Fick, Ohm y Newton.

En el caso de las escalas temporales se trae a colación el problema de la turbulencia, como el chorro de agua que se ilustra en la Figura 3. La escala temporal se puede percibir al tratar de medir el tiempo de colisión entre las partículas fundamentales de agua, el cual es diferente del tiempo de colisión en un grupo de partículas o clúster.

Entre otro orden de ideas y relacionado con el mismo ejemplo de la turbulencia, la escala temporal también se percibe al medir la velocidad de un punto o conjuntos de partículas fundamentales en el tiempo. Se observa en la Figura 3, que la velocidad promedio medible a escala macroscópica varía en el tiempo y se puede deducir una función de distribución de velocidades en esa escala, tomando el número de repeticiones de un valor dado de la velocidad; la cual permite definir una función de densidad de probabilidades (Probability Density Function-PDF). Estas fluctuaciones en el tiempo de la velocidad del conjunto de partículas es consecuencia de las variaciones de la velocidad de cada partícula en una escala de tiempo mucho menor.

Construyendo el modelo matemático

Aproximarse a modelar la naturaleza es describirla mediante una ecuación, normalmente es una tarea que se desarrolla construyendo desde lo simple hasta lo complejo, teniendo en cuenta que la naturaleza se describe por un sistemas de N partículas interactuantes entre ellas y cada partícula posee una dinámica regida por las leyes de la mecánica. Para este fin, se requiere la posición y la velocidad de cada partícula para su descripción completa, la cual es tarea difícil de realizar, puesto que habrá que resolver un sistema de ecuaciones de un enorme tamaño del orden de 6,023x10²³ ecuaciones simultáneas.

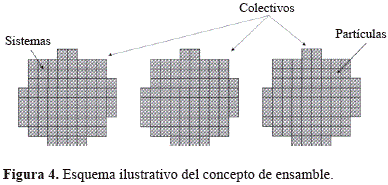
Por lo tanto, se recurre al concepto del colectivo (ensemble), ideada por Josiah Williard Gibbs a finales del siglo XIX y necesario para describir el mundo (Reichl, L.E. 1998; Gibb, M. 1960; Landau L.D. and Lifshitz, E. M. 1969; Tolman, R. 1979; Hoyos, B. A. and Chejne F. 2015; Chejne F. et.al. 2013; Bird, R. B. et. al. 2002). Un colectivo es un número infinito de sistemas caracterizado por dinámicas y variables de estado idénticas (N, V, T, ó E), pero con condiciones iniciales diferentes (ver Figura 4), un ejemplo de aplicación de estos colectivos se puede ver en (Reichl, L.E. 1998).

La descripción estadística completa de un sistema de N partículas está dada en término de una función de distribución:

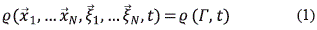
Cuya dinámica se rige por la ecuación de Liouville clásica:

Donde el operador de Liouville se define con base en el Hamiltoniano (H) y en las coordenadas generalizadas (q_i, p_i) de la siguiente manera:

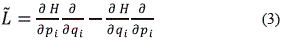
La solución de la ecuación (2) solo es formal y útil para fines teóricos; por lo tanto, se debe tener una ecuación de evolución reducida, la cual se haya integrando sobre todas las posiciones y velocidades con excepción de una:

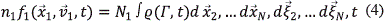
Donde f₁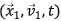 representa el número de partículas con posición, velocidad y tiempo igual a 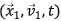por unidad de volumen en el espacio físico, por unidad de volumen en el espacio de las velocidades en un tiempo t; N₁ es el número de partículas de la especie 1 y n₁ es el número de partículas N₁ dividido por el volumen del sistema. De esta manera se tiene una visión de la naturaleza con base en la dinámica de una partícula, afirmando que lo que le pasa a ella, es lo que le pasa a las demás. La dinámica del grupo de partículas está regida por la ecuación cinética y una de ellas, es la ecuación de Boltzmann, la cual se puede expresar de la siguiente manera:

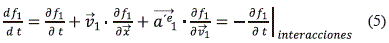
Donde, el lado izquierdo de la ecuación (5) representa el cambio en el tiempo del número se partículas por unidad del volumen del espacio físico y el de velocidad; por su parte, el lado derecho corresponde al efecto de las interacciones del grupo de partículas N₁ con el resto. La ecuación (5) contiene toda la información de la dinámica del número de partícula del mismo tipo 1, en donde la influencia del resto de partículas (2…N) se resumen en el último término de la ecuación (5) y representa el término de interacciones. 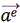corresponde a la aceleración o a la fuerza externa dividida por la masa que actúa sobre el sistema.

Sin embargo, no es fácil obtener una solución ni analítica, ni numérica y muchas veces se recurre a realizar un nuevo promedio para un grupo de partículas constituyéndose una nueva escala mesoscópica superior a la microscópica denominada "Coarse Graining". Este nuevo promedio permite definir una nueva ecuación en la escala mesoscópica con :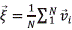

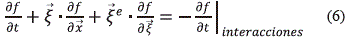
donde es la velocidad instantánea de un conjunto de partículas en un punto del espacio, es una variable independiente de las variables espacial y temporal; f es la nueva función de la variable espacial, de la velocidad y del tiempo, en un nivel de escala superior al que se tendría con la ecuación (5). De otro lado, se puede tener un nuevo promedio de los diferentes momentos (n=0 corresponde a la masa; n=1, al momentum y n=2, a la energía) con base en la función de distribución:

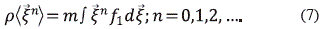
La ecuación de evolución para el promedio de áⁿñ o también llamada ecuación de transporte o de balance es obtenida al multiplicar la ecuación de Boltzmann o ecuación cinética (Eq. 6) por ⁿ e integrando sobre todo el dominio del campo de velocidades para llegar a:

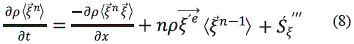
El primer término del lado derecho de la ecuación (8) corresponde al flux del promedio de la correlación del momento ⁿ con la velocidad del conjunto de partículas; el siguiente, es el efecto de las fuerzas externas, en el que r^'e corresponden al campo de fuerza externa y 'S_z"' es el término fuente debido a las interacciones entre las partículas. La ecuación (8) es el modelo matemático que permite simular cualquier fenómeno natural en la escala hidrodinámica (De Groot, S. R. 1968; Haase, R. 1990; Hines, A. and Maddox, R. 1987; Velásuqez, J. E. and Chejne, F. 2003). No obstante, se requiere conoce la correlación entre la velocidad y los diferentes momentos, el cual se hace difícil y se recurre a un nuevo promedio para la velocidad áñ, el cual es el valor promedio de la velocidad que constituye la escala superior, la macroscópica; La velocidad instantánea del conjunto de partículas y la velocidad media están relacionadas mediante la expansión en serie de Taylor:

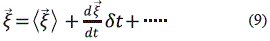
La expansión en serie de Taylor se propone que puede expresarse así:

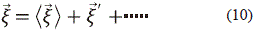
Este conjunto de partículas se mantiene unidas por fuerzas intermoleculares o en equilibrio local, en el nivel microscópico y se mueven como un todo; no obstante, cada conjunto de partículas tiene su propia dinámica identificada por una velocidad individual, cuya diferencia con la velocidad promedio da lugar a las fluctuaciones de la velocidad ^' la escala macroscópica.

Algo interesante es que el conjunto de partículas ayuda a interpretar las diferentes escalas, desde la microscópica, mesoscópica hasta la macroscópica; en la cual, ese conjunto de partículas actúa como una nueva partícula o punto en la nueva escala, interactuando con otros puntos del mismo sistema y generando interacciones de conjunto o fenómenos de transporte. Así que los fenómenos de transporte que se conocen como el transporte de especies, momentum, energía y de carga son interacciones de conjunto; aún más, el conjunto de partículas actúan como un todo y sienten el efecto de fuerzas externas (v.g. la gravedad), dando lugar al concepto del medio continuo (ver Figura 5).

De esta manera, la velocidad promedio se puede interpretar como la velocidad que posee una partícula individual ubicada en el marco de referencia del conjunto de partículas que se mueve como un todo. Si el sistema conformado por el medio continuo está estático, la velocidad de conjunto es cero; sin embargo, el movimiento aleatorio de las partículas individuales persiste y da lugar al entendimiento de las fluctuaciones.

De esta manera, teniendo en cuenta la división de la velocidad en su parte promedio y su parte fluctuante se puede construir las diferentes ecuaciones de balance. En el caso de n=0 para un sistema conformado por varias especies (j=1,2…), en la que , la ecuación (8) se convierte en la ecuación de balance por especies, en la que el término fuente corresponde a las reacciones que permiten la generación o destrucción de especies:

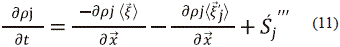
El tensor rjá^jñ es la expresión microscópica del flujo dispersivo o difusivo de una especie respecto del conjunto; el cual puede ser modelado mediante una ley constitutiva, que en el caso lineal corresponde a La ley de Fick. El primer término de la ec. (11) es la tasa de acumulación de la especie j en el tiempo, el primer término del lado derecho de la ec. (11) corresponde a la expresión convectiva; el segundo, a la difusiva y el tercero a la tasa de generación o destrucción de la especie j por reacciones químicas.

Con base en la ecuación (11) se puede lograr la ecuación de continuidad tomando la sumatoria sobre todas las especies y teniendo en cuenta que :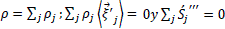

En el caso de n=1 la ecuación (8) se convierte en la ecuación de balance de momentum, en el que el término fuente es cero como consecuencia de la conservación del momentum y recordando que = áñ + ^'

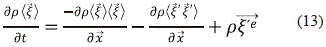
El tensor rá^{' '}ñ es la expresión microscópica del tensor de esfuerzo, el cual incluye el tensor debido a las fuerzas viscosas y el correspondiente a la presión. Este término puede ser modelado mediante una ley constitutiva, que en el caso lineal corresponde a La ley de Newton.

En el caso de n=2, la ecuación (8) se convierte en la ecuación de balance de energía, en el que el término fuente correspondería a una absorción o liberación de radiación y nuevamente recordando que = áñ + ^':

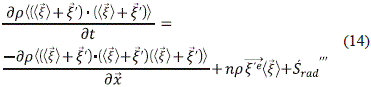
La ecuación (14) puede expresarse de la siguiente manera, luego de una manipulación algebraica:

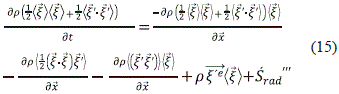
El término ½rá^' · ^'ñ es la representación microscópica de la energía interna, rá½(^' · ^')^'ñ corresponde al flux de calor transportado, el cual debe ser modelado y una de las propuestas es la Ley de Fourier.

Hasta este punto, se ha mostrado como de la ec. (5) se deriva las ecuaciones de Navier-Stokes; así mismo, esta se puede extender al caso de problemas que requieren el balance de población en una escala inferior a las de Navier-Stokes. En el caso del balance de población, el término de interacción corresponde a los términos de muerte y nacimiento de partículas o entes de la población que se estudia, la variable puede ser tomada como la variable interna del sistema (volumen, longitud, radio de partículas, etc.) y ^'e con la tasa de cambio de la variable externa. Adicionalmente, la ecuación de balance (ec 8) se pueden expresar de una forma compacta así:

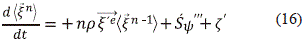
Donde 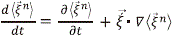es la derivada substancial, z' representa un término aleatorio para dar cuenta de los efectos fluctuantes del mundo micro y que son desconocidos. Por lo tanto, se ha convertido una ecuación determinista en otra estocástica al estilo de Langevin, la cual requerirá de un tratamiento especial basado en una dinámica en la que se determina una función de distribución de estados posibles mediante ecuaciones estocásticas, como la ecuación Maestra, Fokker-Plank o la de Kolmogorov (Einstein, A. 1905; Gardiner, C. W. 2004; Stachel, J. 1998; Öttinger, H. C, 1996; Serra, R. et al. 1986; Kubo, R. 1966; Callen, H. B. and Welton T.A. 1951).

Casos particulares

Como casos particulares de aplicación de las ecuaciones de balances a diferentes escalas se pueden analizar en diferentes referencias del autor. Modelos aplicados a la combustión y gasificación en lecho fluidizado y fijo en dos fases, se pueden apreciar en la referencias (Chejne, F., Lopera E. and Londoño, C. 2011; Chejne F. and Hernández J. P. 2002; Chejne, F, Hernández J. P. and Florez W. F. 2000); modelos de procesos químicos en hornos rotatorios se puede observar en las referencias (Granados D. A., Chejne F. and Mejía J. M. 2015; Granados D. A., Chejne F., Mejía J. M., Gómez C. A., Berrio A. and Jurado W. J. 2013); casos en los que se modelan sistemas que usan energía alternativa se ven en las referencias (Chejne F. et al., 2011; Mejía J.M. et al., 2005); problemas relacionados con la inestabilidad de las ecuaciones de balance (Navier-Stokes) se describe en la referencia (Rivera A. and Chejne F. 2004) y problemas relacionados con efectos de la transferencia de calor y masa se encuentran en las referencias (Chejne F. et al., 2002 and Chejne F. et al., 2015). En esta sección se presenta la descripción de dos modelos en el que se tocan diferentes escalas espacio temporal. Uno relacionado con la escala termodinámica o global (Maya J. C. and Chejne F. 2016), el otro en el que se combina dos escalas espaciales que permite simular problemas fluidodinámicos (Mejía J. M. et al., 2015).

Modelo matemático para reacciones sólido-gas con sinterización simultánea.

La distribución del tamaño de grano y la sinterización afectan el desarrollo de la microestructura durante las reacciones sólido-gas, problema de interés en los modelos clásicos de grano (Georgakis C. et al., 1979). Para estudiar este efecto se desarrolló un modelo basado en balances de población para tener en cuenta la distribución de tamaño de grano en el interior del pellet y al mismo tiempo considerar la sinterización mediante los términos de muerte y nacimiento en el balance de población.

A medida que la reacción química procede, el radio de grano aumenta o disminuye (r_p) dependiendo del volumen molar del producto sólido y del proceso de sinterización, mientras que el radio del núcleo sin reaccionar (r_c) disminuye (Ver Figura 6).

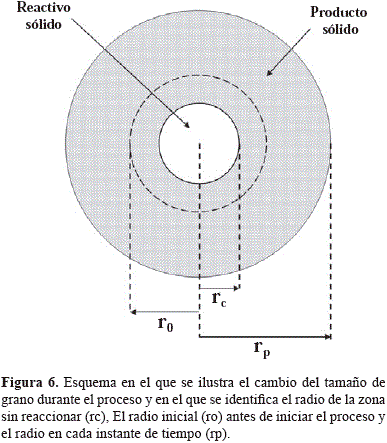
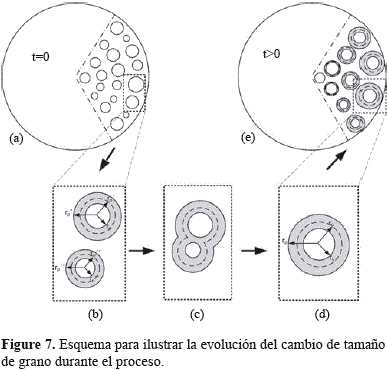
En el nuevo modelo llamado "modelo de distribución de tamaño de grano cambiante" se considera que la partícula está compuesta de un gran número de granos con una distribución inicial de radio (ver Figura 7) r_o no uniforme, luego cada grano cambia de tamaño debido a la Reacción química y a la sinterización.

La reacción considerada en este modelo es:

El balance de material para el gas se describe con base en la ecuación (11) sin el término convectivo, solo el difusivo 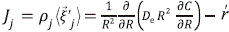, donde C es la densidad molar de la especie j, D_e es coeficiente de difusión efectiva, R es la variable espacial y el término de generación se relaciona con la reacción química 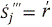así:

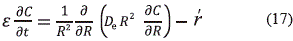
Sujeto a las siguientes condiciones de frontera 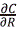= 0 en R=0 y C = C_b en R=R_p, con una expresión para la tasa de reacción en la fase gaseosa tipo núcleo sin reaccionar de la siguiente forma (Bhattacharya and P. Purohit P. 2004; Szekely J. and Propster M. 1975):

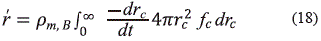
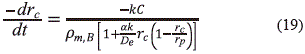
k es la constante cinética para la reacción tipo Arrhenius, y De = Dg∈² es la difusividad de la especie A en un medio libre afectada por la porosidad e de acuerdo con (García- Liabano F. et al., 2002). La conversión local se define de la siguiente manera:

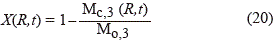
En consecuencia se puede hallar la conversión promedio en todo el pellet:

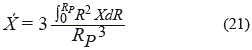
La evolución de la función de distribución se puede predecir con base en la ec. (6) en el que término de aceleración corresponde a la variación 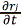, los términos de generación o destrucción corresponde a los de nacimiento y muerte (B y D) (Falola A. et al., 2013):

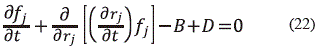
Donde f_j es la función de densidad de distribución de radio de grano y representa el número de granos de radio r_j por unidad de volumen, B es la tasa de nacimiento de nuevos granos, mientras que D es la tasa de desaparición de granos por sinterización. La ecuación de balance de población se puede transformar en ecuaciones de momento, que son más fáciles de resolver. Multiplicando la ecuación (9) por r_jⁿ e integrando entre 0 y ∞ para obtener una nueva ecuación:

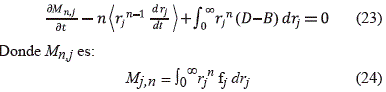
Con n= 0,1,2,3…y j=o, c, p; en consecuencia se presenta tres ecuaciones para tener en cuenta la evolución de los tres radios de granos según Figura 6. El resultado clave del modelo es la predicción correcta de la conversión en el tiempo tal como se ilustra en la Figura 8.

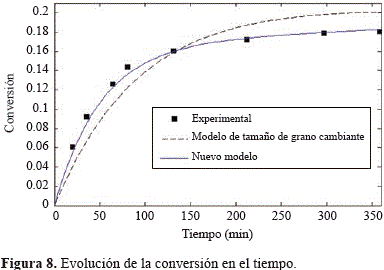
El nuevo modelo propuesto por Maya y Chejne predice el comportamiento de la conversión con mayor exactitud que el modelo clásico llamado "Modelo de tamaño de grano cambiante" (Georgakis C. et al. 1979).

Modelo de un sistema fluido dinámico

Un sistema fluido dinámico está conformado por una o varias especies en movimiento en espacios abiertos o confinados, dando sentido al flujo de fluidos en sistemas de combustión, mezclado de especies, separación de sustancias en equipos como ciclones, etc. Un ejemplo que es de interés para la ingeniería es la predicción del mezclado de una especie que entra como un chorro de un fluido a una cámara donde existe otro fluido en movimiento o estático.

La dinámica de fluidos se puede simular mediante las ecuaciones de balances (ec. 11-13, 15) presentadas en su forma apropiada y en la escala macroscópica. Para el caso del balance por especies y considerando la densidad por especies, rj = rYj; la velocidad promedio o de bulto, 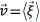; el flux de la especie j modelado mediante la Ley de Fick, Jj = rj á_j ñ= 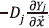, en el que Dj es la difusividad de la especie j en el medio y el término de generación representado por la generación o destrucción de especies mediante reacción química 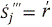j^"'; la ecuación (11) se transforma en:

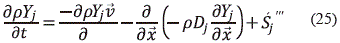
Realizando la suma para todas las especies, la ec. (25) se transforma en la ecuación de continuidad,

En el caso del balance de momento y teniendo en cuenta que el tensor de esfuerzo viscoso más la presión es el correspondiente al término de fluctuaciones 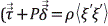, la cual se modela mediante la Ley de Newton, la ec. (13) y se convierte en:

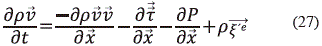
En el caso del balance de entalpía, se construye primero la ecuación para la energía cinética con base en la ec. (27). El balance de energía cinética se halla al multiplicar la ecuación de momento (ec. 27) por el campo de velocidad obteniéndose la ecuación de balance para la energía cinética:

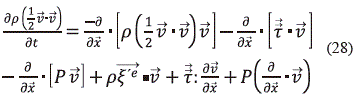
Una vez obtenida la expresión para la energía cinética, se toma la ecuación para la energía, ec. (15) con h = ½á^' · ^'ñ + P · (1/r), el término fluctuante se modela mediante la Ley de Fourier, 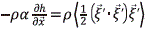, en el que a es la difusividad térmica y se le resta la ec. (28) para lograr una expresión del balance de entalpía (h):

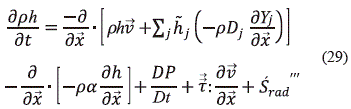
Cuando se tiene el fluido en régimen turbulento, tanto la fracción de la especie j (Y_A) y el campo de velocidad (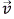) es una cantidad fluctuante en la escala macroscópica y puede descomponerse en el tiempo, de la misma manera como se descompuso el campo de velocidad de la escala mesoscópica (ec. 9):

En la ec. (30) los valores promedios son en el tiempo: 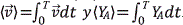. De esta manera las ec. (25-27 y 29) se convierten en el modelo Reynolds Averaged Navier-Stokes Equations (RANS):

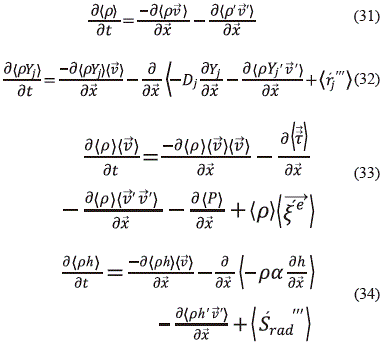
Nuevamente aparece un término adicional ár' 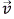' ñ en la ec. (31), árY_j' 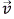' ñ en la ec. (32), árñ á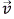' '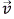ñ en la ec. (33) y árh' 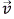' ñ en la ec. (34), los cuales deben ser modelados para tener un sistema cerrado. Para ello existe diversas propuestas como el modelo k - e para el caso de la ecuación de momento (ec. 30).

También, se puede hacer la descomposición del campo de velocidades en el espacio:

Donde 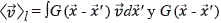es una función de filtrado que significa realizar un promedio entre dos puntos del espacio, suavizando el comportamiento aleatorio y permitiendo reducir tiempo de cómputo. Luego se utiliza el concepto de promedio de Favre:

Con lo cual, las ec. (26 y 27) se convierten en el modelo Large Eddy Simulation- LES se obtiene la nueva ecuación del momento (aberi F. A. et al. 1999; Pope S.B. 1990):

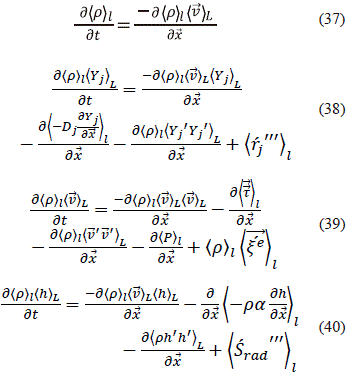
Aquí también, los términos adicionales árñ_l á Y_j' Y_j' ñ_L, (árñ_l á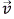' ' 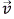ñ_L) y árh' h' ñ_L deben ser modelado para lograr un sistema de ecuaciones cerrado que para la fluctuación en el esfuerzo existen varias propuestas como Smagorinsky model (Mejía J. M. 2012).

Esquema probabilístico. Situaciones como el caso turbulento en que las cantidades fluctúan debido a las condiciones, tanto iniciales, como de fronteras; o que el medio por donde fluye la materia hace que las cantidades físicas no sean uniformes en el tiempo ni en el espacio, sino que varían y lo hacen de manera rápida; obligando al modelador tener que solucionar las ecuaciones de balance en una escala de tiempo y del espacio muy pequeña, demandando un enorme costo computacional. En consecuencia, en este caso se puede utilizar un método estocástico que permite hallar una función de distribución de ocurrencia de fluctuaciones mediante una ecuación diferencial estocástica (DSE), para luego encontrar el promedio de la correlación entre las variables fluctuantes o aleatorias y su promedio.

Se trata ahora de lograr un modelo escala para las funciones escalares como la fracción de cada especie o la entalpía. Para ello, se discute el método de la Función de densidad de Masa Filtrada (FMDF), denotada por F_L(y; 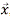, t); donde, y es un vector que incluye el dominio de las fracciones de cada especie y otras cantidades escalares como la entalpía:

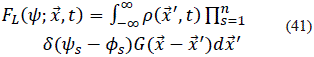
Es importante ver que la integral de F_L(y; 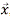, t) sobre todo el dominio del campo escalar es el promedio de la densidad filtrada:

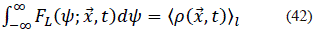
Con base en las propiedades de F_L(y; 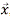, t), la ecuación de Kolmogorov, el teorema de Bayes se logra una ecuación de transporte para FL(y; 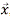, t):

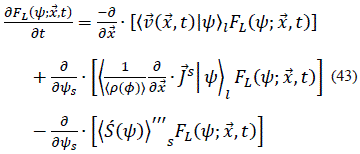
La cual es la ecuación exacta de transporte de FMDF; sin embargo, existen términos que deben ser modelados como lo son el primer y segundo término del lado derecho de la ec. (43). Dada la alta dimensionalidad de la ec. (43), su solución numérica suele realizarse mediante métodos de partículas. Se define un sistema de partículas sin masa que evolucionan en los dominios temporal, espacial y composicional, basado en un conjunto de ecuaciones estadísticamente equivalente a la Ec. (43). Así, un ensemble de partículas estocásticas da cuenta de la evolución de FMDF discreta.

De acuerdo con el número de partículas empleadas, la aproximación LES-FMDF permite obtener una mayor resolución espacial, reduciendo así la incertidumbre existente en la subescala. Es por esto que se ha reportado que la dependencia de los modelos de subescala se relaja cuando se emplean métodos de partículas para la solución de la FMDF. La discusión anterior puede también interpretarse como un proceso de escalado "natural" en donde el comportamiento de la física del transporte y mezclado de escalas espaciales menores a la de LES se transmite hacia las superiores a través del promedio de ensemble de partículas que, individualmente, evolucionaban de acuerdo con las leyes naturales de la evolución.

Como aplicación del método estocástico combinado con el método de LES para el caso del campo de velocidades se describe con detalle en la tesis de doctorado de Juan Manuel Mejía Cárdenas y dirigida por el autor de la presente revisión (Mejía J. M. 2012). El caso tratado en la tesis se refiere al chorro de fluido que se observa al descargar un fluido a través de un orificio. La predicción del contorno turbulento se puede observar en la Figura 9.

Nuevamente, la combinación de métodos, en esta caso el método Large Eddy Simulation-LES y otro de corte estocástico como FMDF ha permitido simular con eficacia el chorro de un fluido entrando a un espacio confinado.

Apuntes finales

Se ha mostrado en este artículo de manera sucinta que para predecir la dinámica de los sistemas naturales se debe conocer la velocidad y la posición de un número enorme de partículas. Una vez conocidas estas dos magnitudes en cada instante de tiempo, se tiene definido los diferentes estados; los cuales, muchos de ellos son repetidos. En consecuencia, se tiene la posibilidad de tener una función que da cuenta de la probabilidad de construir una distribución de estados y por ende, se tendrá una función de densidad de probabilidades (PDF), la cual es una función que depende de 3N variables espaciales, 3N variables de velocidad y una del tiempo; por lo tanto, es una tarea difícil de resolver y se requiere reducir la complejidad.

La reducción exige integrar la PDF sobre 6N-1 variables de espacio y de velocidad, para obtener una función reducida que identifica un grupo de estados asumidos por grupos de una partícula de un mismo tipo, que solo depende de una variable de espacio y otra de velocidad en el espacio fase y por supuesto del tiempo. De esta manera se pasa a una nueva escala mayor, en la que existe una función de distribución de probabilidades de un conjunto de estados generados por la dinámica de una sola partícula y que recibe información del resto de partículas, como una información adicional fluctuante.

Las múltiples escalas de los sistemas naturales son modelados con base en la descomposición de cantidades físicas entre un valor promedio y un término fluctuante. El término que agrupa el valor puntual de una cantidad física constituye un valor promedio y permite el nacimiento de una nueva escala mayor. De otro lado, el término fluctuante rescata la información de la escala menor, el cual genera términos adicionales en las ecuaciones de balance que deben ser modelados.

Los esfuerzos encaminados a obtener información de la escala menor han permitido la definición de leyes constitutivas como aquellas que se utilizan para modelar los fenómenos de transporte (la Ley de Fick, Fourier, Newton y de Ohm). También existen esfuerzos para modelar la escala microscópica y otra que corresponde a una escala mayor, la mesoscópica, en conexión con el mundo micro a través de la ecuaciones de la mecánica clásica y términos aleatorios que permiten encontrar expresiones teóricas de los términos abiertos y sin definir en las ecuaciones de balance (Schindler M. 2010; Español P. 2013; Tyagi M. 2010).

Finalmente, se deben tener estrategias de solución numérica y para ello se proponen métodos novedosos como los elementos de fronteras y multi-dominio (Flórez W. F., Power H. and Chejne F., 2002; 2002; 2000; 2000), los cuales generan soluciones de las ecuaciones de balance y en algunos casos superan los métodos de diferencias finitas, volúmenes finitos y elementos finitos.

Agradecimientos

El autor agradece al profesor Fanor Mondragón de la U. de A., a Juan Manuel Mejía, Carlos Gómez, Diego Alejandro Camargo, Juan Carlos Maya y Jessi Osorio, que enriquecieron este manuscrito con sus aportes. Adicionalmente, un especial agradecimiento a mis estudiantes de Maestría y de doctorado del grupo TAYEA que aportaron de manera indirecta a la elaboración del presente artículo, entre ellos, Jorge Montoya, Carlos Valdés, Víctor Borda, David Granados, Jader Alean, Esteban Largo, Alejandro Jaramillo, Liliana López, Adriana Blanco, Gloria Marrugo, Robert Macías, Javier Ordoñez, Alejandro Ricalde, Raiza, Gabriel y Daniela; a los profesores del grupo TAYEA, Bibian Hoyos, Carlos Londoño, Javier de la Cruz, Daniel Barrága y Farid B. Cortés; a los profesores, y primeros estudiantes de doctorado Whady Felipe Flórez, Alejandro Rivera, Oscar Ochoa, Vladimir Martínez y Erika Arenas y mi amigo Alana Hill del Grupo Energía y Termodinámica de la UPB; finalmente, al profesor Germán Poveda por su confianza y apoyo incondicional, así como a la Universidad Nacional de Colombia.

Conflicto de intereses

El autor declara no tener conflicto de intereses.

Bibliografía

Bell, A. D. (1986). The simulation of branching patterns in modular organisms. Philos. Trans. Royal Society London, Ser. B, 313: 143-169.         [ Links ]

Bejan, A. (2000). Shape and Structure, from Engineering to Nature. Cambridge University Press.         [ Links ]

Bejan, A. (1997). Advanced Engineering Thermodynamics. John Wiley and Sons.         [ Links ]

Bejan, A. (2005). The Constructal Law of Organization in Nature: Tree - Shaped Flow and Body Size. The Journal of Experimental Biology, 208: 1677-1686.         [ Links ]

Bhattacharya, A., Purohit, P. (2004). Predicting reaction rates for non-catalytic fluid-solid reactions in presence of structural changes in the solid phase. Chemical Engineering Journal, 102 (2): 141-149         [ Links ]

Byron Bird R., Warren E. Stewart, E. N. Lightfoot, (2002). Fenómenos de Transporte. United State: John Wiley & Sons.         [ Links ]

Callen H. B., Welton, T. A. (1951), Irrevarsibility and Genralized Noise. Physical Review 83: 1.         [ Links ]

Chejne, F., Hernández, J. P. W., Florez W.F. and Hill, A.F.J. (2000). Modelling and simulation of time-dependent coal combustion processes in stacks. Fuel 79: 987-997.         [ Links ]

Chejne, F., Hernández, J. P. (2002). Modelling and Simulation of Coal Gasification Process in Fludized Bed. Fuel, v. 81 p.1687-1702.         [ Links ]

Chejne, F., Ragimova, T., Florez, W.F., Hernández, J.P. (2002). Theoretical Model for heat transfer in the single crystal making. Revista de La Facultad de Ingeniería Universidad de Antioquia. ISSN: 01202064 v. Junio, (26) p.79-89.         [ Links ]

Chejne, F., Lopera, E., Londoño, C.A. (2011). Modelling and simulation of a coal gasification process in pressurized fluidized bed. Fuel; 90: 399-411.         [ Links ]

Chejne, F., Macías, A., Estrada, D., Velasquez, H. I., Londoño, C. A. (2011), Radiation model for predicting temperature evolution in solar cooker, DYNA ISSN 0012-7353,Nro 166, pp 68-74, Medellin, Abril.         [ Links ]

Chejne F., F. Moukalled, C. A. Gómez (2013). A Simple Derivation of Crooks Relation; International Journal of Thermodynamics (IJoT), ISSN 1301-9724/e-ISSN 2146- 1511, Vol. 16 (No 3), pp 97-101.         [ Links ]

Chejne, F., Camargo. D.A., Pabón E., CarrascoMarín, F. (2015). Effect on mass transference phenomena by textural change inside monolithic carbon aerogels. Editor and place of publication: 14321181, 09477411 Heat Mass Transfer, Germany, January.         [ Links ]

De Groot S. R. (1968). Termodinámica de los Procesos Irreversibles. Madrid: Alhambra, p 268.         [ Links ]

Einstein, A. (1905). On the movement of small particles suspended in a stationary liquid demanded by the molecular kinetic theory of heat; Annalen der Physik 17: 549-560.         [ Links ]

Eran, S., M. Michael and L. S. Harry, (1986). Philosophical Transactions of the Royal Society of London, Series B, 313, pp. 143-169.         [ Links ]

Español, P. (2013). The Micro-Meso connection also known as Non-equilibrium Statistical Mechanics also known as The Theory of Coarse-Graining. Lecture notes at UAM, Madrid, España, Noviembre.         [ Links ]

Falola, A., Borissova, A., Wang, X. Z. (2013). Extended method of moment for general population balance models including size dependent growth rate, aggregation and breakage kernels. Computers & Chemical Engineering, 56: 1-11.         [ Links ]

Flórez, W., H. Power, H., F. Chejne, F. (2000). Multi-domain dual reciprocity BEM approach for the Navier-Stokes system of equations Communications in Numerical Methods in Engineering ISSN: 1069-8299 Wiley v.16 fasc. p.671-681.         [ Links ]

Flórez Escobar, W., H. Power, H., F. Chejne, F. (2000). Conservative interpolation for the boundary integral solution of the Navier-Stoker equations. Computational v.26 fasc. p.507-513         [ Links ]

Flórez, W., H. Power, H., F. Chejne, F. (2002). Método de elementos de frontera multi-dominio para problemas no newtonianos y no isotérmicos. In Matemáticas Enseñanza Universitaria,         [ Links ]

Flórez, W., H. Pawer, H. F. Chejne, F. (2002). Numerical Solution of Thermal Convection Problems Using the Multi-domain Boundary Element Method. Numerical Methods For Partial Differential Equations, ISSN: 0749-159X Wiley v.18 fasc.3 p.469-482.         [ Links ]

García-Labiano, F., Abad, F. A., de Diego, I. F., Gayán, P., Adánez, J. (2002). Calcination of calcium-based sorbents at pressure in a broad range of CO2 concentrations. Chemical Engineering Science, 57 (13): 2381-2393.         [ Links ]

Gardiner, C.W. (2004). Handbook of Stochastic Methods; Springer, Germany, 3rd Edition.         [ Links ]

Georgakis, C., Chang, C.W., Szekely, J. (1979). A changing grain size model for gas-solid reactions. Chemical Engineering Science, 34 (8): 1072-1075.         [ Links ]

Gibb, M. (1960). Elementary principles in Statically Mechanics, Dover, New York.         [ Links ]

Granados, D. A., Chejne, F., Mejía, J.M. (2015). Oxy-fuel combustion as an alternative for increasing lime production in rotary kilns: 03062619 Applied Energy, Amsterdam - Holland November.         [ Links ]

Granados, D. A., Chejne, F., Mejía, J. M., Gómez, C.A. Berrío, A., Jurado, W.J. (2013). Effect of flue gas recirculation during oxy-fuel combustion in a rotary cement kiln; Energy 1-11.         [ Links ]

Hoyos, B.A., Chejne, F. (2015). Comparison of molecular models of carbon monoxide for calculation of vapor-liquid equilibrium. Rev. Fac. Ing. Univ. Antioquia, Medellín - Colombia, Junio.         [ Links ]

Haase, R. (1990). Thermodynamics of Irreversible Processes. New York: Dover, p 513.         [ Links ]

Hines, A., Maddox, R. (1987). Transferencia de Masa: Funda-mentos y Aplicaciones. México: Prentice Hall, p 568.         [ Links ]

Jaberi, F. A., Colucci, P. J., James, S., Givi P., Pope, S. B. (1999). Filtered mass density function for large-eddy simulation of turbulent reacting flow. J. Fluid Mech. vol 401, pp 85-121.         [ Links ]

Kurchan, J. (2005). In and Out Equilibrium. Nature, Vol. 433, 20.         [ Links ]

Landau, L. D. E. M. Lifshitz. (1969). Física Estadística, Reverté, Barcelona.         [ Links ]

Maya, J.C., Chejne, F. (2016). Novel Model For Non Catalytic Solid-Gas Reactions With Structural Changes By Chemical Reaction And Sintering. Chemical Engineering Science, pp. 258-268.         [ Links ]

Mejía, J. M., Chejne, F., Smith, R., Rodríguez, L.F., Fernández, O., Dyner, I. (2005). Propuestas Metodológicas para el diseño de aspas de turbinas de viento de Eje horizontal. Rev. Energética Universidad Nacional de Colombia, 33, Julio. ISSN 0120-9833.         [ Links ]

Mejía, J. M. (2012). Scalar transport and mixing using large eddy simulation. Tesis doctorado, Facultad de Minas, Universidad Nacional de Colombia.         [ Links ]

Mejía, J.M., Sadiki, A., Molina, A., Chejne, F., Pantangi, P. (2015). Large Eddy Simulation of the mixing of a passive scalar in a high-Schmidt turbulent jet. Editor and place of publication: 0098-2202 Journal Of Fluids Engineering- Transactions Of The ASME, Washington - United States, January.         [ Links ]

Mejía, J. M., Chejne, F., Molina, A., Sadiki, A. (2015). Scalar Mixing Study at High-Schmidt Regime in a Turbulent Jet Flow Using Large-Eddy Simulation/Filtered Density Function Approach, Editor and place of publication: 0098- 2202 Journal Of Fluids Engineering-Transactions Of The ASME, Washington - United States, October.         [ Links ]

Myung, I.J. (2000). The Importance of Complexity in Model Selection. Journal of Mathematical Psychology 44: 190-204.         [ Links ]

Moore, J. (2015). Pragmatism, mathematical models and the scientific ideal of prediction and control. Behavioural Processes 114: 2-13.         [ Links ]

Öttinger, H.C. (1996). Stochastic Process in Polymeric Fluid. Springer, Germany.         [ Links ]

Kubo, R. (1966). The Fluctuation-Dissipation theorem, Rep. Prog. Phys. 29: 255.         [ Links ]

Pope, S. B. (1990). Computations of turbulent combustion: Progress and challenges. Proceeding of the Combustion Institute; 23: 591-612.         [ Links ]

Prigogine, I. G. Nicolis. (1987). La Estructura de lo Complejo. Editorial Alianza.         [ Links ]

Prusinkiewicz, P. (1998). Modeling of spatial structure and development of plants: a review. Scientia Horticulturae, Volume 74, Issues 1-2, 30 April, Pages 113-149         [ Links ]

Reichl, L.E. (1998). A Modern Course in Statistical Physics", John Wiley and sons, Inc., "2nd edition         [ Links ]

Rivera, A., Chejne, F. (2004). Non-linear phenomena in thermo-acoustic engines. Revista Journal of Non-Equilibrium Thermodynamics, ISSN 0340-0204, Vol. 29, No 3, p. 209-220.         [ Links ]

Serra, R., Andretta, M., Company M., and Zanarini, G. (1986). Introduction To The Physics of Complex Systems. Pergamon press, Headington Hill Hall, Oxford, England.         [ Links ]

Sharon, E. M. Marden M and H. L. Swinney, H.L. (2005). Flores y Hojas Onduladas. Investigación y Ciencia, 344, pp.70-77, Mayo.         [ Links ]

Stachel, J. (1998). Einstein's Miraculous Year; edited and introduced by Princeton University Press, USA.         [ Links ]

Stevens, P.S. (1974). Patterns in Nature," Little, Brown and Co., Boston. P 256.         [ Links ]

Schindler, M. (2010). A numerical test of stress correlation in fluctuating hydrodynamics. Chemical Physics 375: 327-336.         [ Links ]

Szekely, J., Propster, M. (1975). A structural model for gas solid reactions with a moving boundary-VI: The effect of grain size distribution on the conversion of porous solids. Chemical Engineering Science, 30 (9): 1049-1055.         [ Links ]

Thompson, D. W. (1917). On growth and form. Cambridge [Eng.] University press.         [ Links ]

Tolman, R. (1979). The Principles of Statistical Mechanics. Dover, New York.         [ Links ]

Turing, A. (1952). On the Chemical Basis of Morphogenesis. Philosophical Transactions of the Royal Society of London, Series B, 327, pp. 37-52.         [ Links ]

Tyagi, M. (2010). Probability Density Function approach for modeling multi-phase flow in porous media. Dissertation ETH Zurich No. 18997.         [ Links ]

Velásquez J.E., Chejne F. (2003). Estudio de los fenómenos acoplados en transporte y transferencia: Aprovechamiento por la Ingeniería Química. Ingeniería Química, No. 398.         [ Links ]

Ye, R., C. Xiang, J. Lin, Z. Peng, K., Yan, H.Z., Tour, J. M. (2013). Coal as an abundant source of graphene quantum dots. Nature Communications, 4: 2943.         [ Links ]