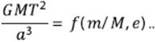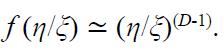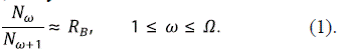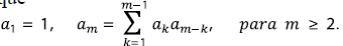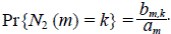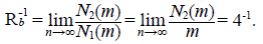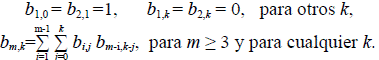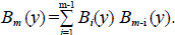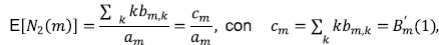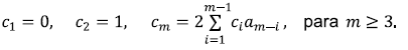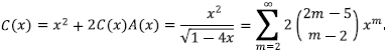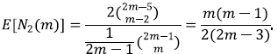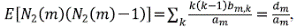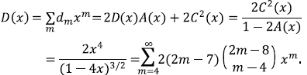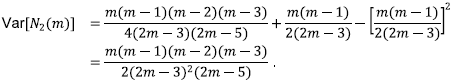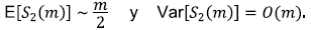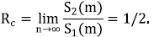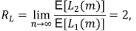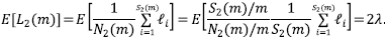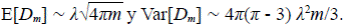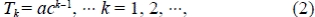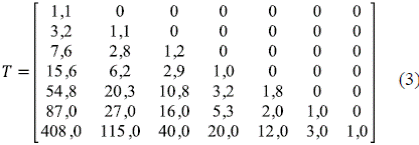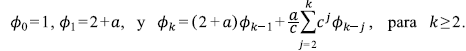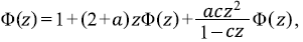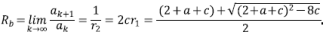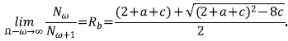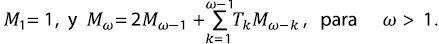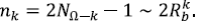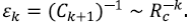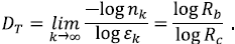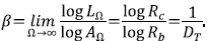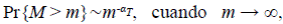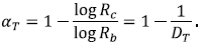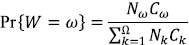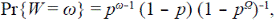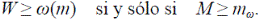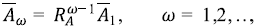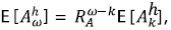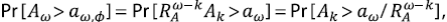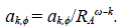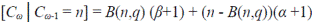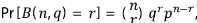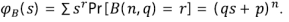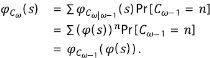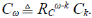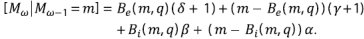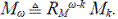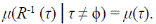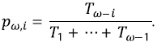Introducción

En el prefacio de su libro, ^{Leopold (1994)} anota que no existe una teoría sobre la acción y el comportamiento de los ríos y que tal falta ha contribuido a su degradación. Se atreve a proponer una hipótesis para fundar esa teoría, y no parte de cero, hay aportes anteriores importantes, algunos de los cuales él mismo ha contribuido a construir durante una vida entera de trabajo práctico y teórico. El concepto principal de su propuesta es la aleatoriedad, pues las leyes físicas que controlan la formación y la evolución de los ríos no los determinan unívocamente. En la medida en que hay variabilidad y múltiples orígenes, por ejemplo el clima, hay lugar a diferentes respuestas de los ríos. Aunque elemental, y probablemente fácil de aceptar por lo general, este principio tiene profundas consecuencias que no necesariamente se incorporan en la teoría y la práctica. A partir de este primer principio el autor procede a proponer otros dos derivados.

El primero se refiere a que las estructuras y las formas de los ríos, así como los ajustes ante eventuales cambios, responden a lo más probable, principio que sigue la línea de los fundamentos de la mecánica estadística. El segundo principio derivado, que también se nutre con ideas de la termodinámica, se refiere a la tendencia a minimizar el trabajo total y la uniformidad en la disipación de la energía. Claramente, el principio básico de la aleatoriedad es necesario. El primer principio derivado, en el que se observa lo más probable, es lógico. El segundo, en cambio, no se requiere de forma directa en este trabajo.

Las redes de drenaje son auto formadas y auto mantenidas. Las regularidades que se observan son, por lo tanto, el resultado de procesos de realimentación complejos. La función de las redes es el transporte de agua y de sedimentos. En este sentido, el ambiente externo, la hidrología, el clima y la litología controlan su desarrollo y mantenimiento. En la medida en que estos controles permanezcan estables, hay lugar al equilibrio en las redes de drenaje. La red es una entidad orgánica, un sistema, así que lo que sucede en una de sus partes afecta las otras, estabilidad que se refleja en las numerosas regularidades observadas empíricamente. Es claro que la estabilidad es estadística y se observa a una escala de tiempo geomorfológica, del orden de entre varios años y varias décadas.

La red, sus características topológicas, planares, altitudinales y su geometría hidráulica, son el resultado de los eventos formadores. En general, los flujos de agua y de sedimento más frecuentes no son los que forman la red, sino los eventos de frecuencia intermedia, lo suficientemente grandes como para tener capacidad geomorfológica y lo suficientemente frecuentes para que su efecto acumulado deje la huella. Los eventos muy frecuentes son de menor magnitud y no tienen capacidad de trabajo, en tanto que los eventos extraordinarios son muy infrecuentes. En general, la frecuencia efectiva de los eventos formadores disminuye aguas arriba, es decir que en las cabeceras el principal trabajo geomorfológico lo hacen los eventos mayores y más infrecuentes. La pregunta importante desde esta perspectiva se refiere a la interpretación de las marcas del origen en la geomorfología: ¿cómo leer en las propiedades geomorfológicas las claves para la hidrología? (^{Leopold, et al., 1964}).

En escalas menores de tiempo, la forma de la tierra, así como las características de la red y su geometría hidráulica, determinan el movimiento del agua y los sedimentos. El estudio de las crecientes, especialmente, debe incorporar la geomorfología. Se carece de datos sobre la gran mayoría de cuencas, tanto en los países menos desarrollados como en los avanzados. Entre los hidrólogos ha habido un esfuerzo en este sentido, cuya historia se remonta 100 años (^{Dawdy, et al., 2012}), e incluye los estudios de regionalización, el concepto de predicción en cuencas sin medición (Prediction in Ungauged Basins, PUB) (^{Dawdy, 2007}; ^{Sivapalan, et al., 2003}), y el concepto de semejanza y homogeneidad hidrológicas. En los últimos 30 años, se ha desarrollado una teoría no lineal con base geofísica (^{Gupta & Waymire, 1998}; ^{Gupta, et al., 2007}; ^{Gupta, 2016}). Dado un campo de precipitación, la teoría requiere la predicción a partir de hidrógrafas de escorrentía en cada nudo de la red, para lo cual es necesario un modelo que transforme la lluvia en escorrentía (^{Furey, et al., 2013}), e incorpore la dinámica espacio-temporal del flujo en la red de drenaje (^{Mantilla, 2007}). Para modelar está dinámica debe recurrirse a la topología, la geometría planar de la red y a su geometría hidráulica.

El concepto de semejanza juega un papel fundamental.

¿Qué simetrías se mantienen ante los cambios de escala?

¿Es posible usar las observaciones de una o varias cuencas para extrapolarlas a otras de una misma región homogénea, con el correspondiente factor de escalamiento? ¿Cuál es el factor de escalamiento?

Semejanza

Aunque el tema de la semejanza en física es muy amplio, se intenta aquí un muy breve resumen (^{Gupta & Mesa, 2014}; ^{Barenblatt, 1996}, 2003). La idea fundamental es que las leyes de la naturaleza son independientes del sistema de unidades que se escoja para las mediciones. Como consecuencia, estas leyes son invariantes ante los cambios de escala. Matemáticamente, esto se expresa mediante funciones homogéneas, lo que implica leyes potenciales. De allí se desprende el teorema Pi de Buckingham, que permite simplificar la matemática, por ejemplo, reduciendo el número de argumentos necesarios de las funciones que expresan una ley física, o cambiando una ecuación de derivadas parciales por una ecuación diferencial ordinaria. La mayoría de los ejemplos exitosos de aplicación del análisis dimensional comparten una propiedad importante, que no siempre se enfatiza, pero que es muy necesaria. Hay una manera clara de separar entre variables importantes y aquellas que no son significativas, bien por muy grandes o muy pequeñas.

Por ejemplo, es posible derivar la tercera ley de Kepler usando solo el análisis dimensional (^{Gibbings, 2011}). La variable de interés es T, el período orbital del planeta que depende de su masa m, la masa del Sol M, las dimensiones de la órbita representadas por los semiejes de las elipses a y b, y la constante universal de gravedad G, lo cual da origen a tres productos, uno que involucra el período y otros dos independientes, que pueden ser a/b o, en términos de la excentricidad, e ² = 1 - (b/a)², y el otro, la relación entre las masas, m/M. Es decir,

Aunque esta aplicación del teorema Pi es un avance importante, es posible ir mucho más allá si se considera que los dos números adimensionales, argumentos de la función a la derecha, son pequeños y, por lo tanto, no deben tener un papel significativo. Esta consideración, importante desde el punto de vista físico, se traduce en términos matemáticos en que la función f tiende a un límite no trivial cuando sus dos argumentos tienden a cero. En este contexto, no trivial significa que el límite es un número diferente a cero o a infinito. Con base en otros argumentos, se sabe que en este caso el límite es 4π ². En general, se dice que un problema es “autosemejante de primer orden” si existe el límite de la función f y este límite no es trivial cuando alguno de los productos adimensionales va a cero (o a infinito, si se toma el recíproco) (^{Barenblatt, 2003}).

Sin embargo, hay muchos casos en los cuales un producto adimensional no se puede despreciar a pesar de ser o muy grande o muy pequeño. Matemáticamente, esto significa que el límite de f no existe o es trivial (cero o infinito). En estos casos, se pierde la capacidad de simplificación de la autosemejanza de primer orden. No se pueden despreciar las variables correspondientes que, aunque pequeñas, siguen teniendo un papel. No obstante, existe una generalización del concepto de autosemejanza que se puede aplicar a aquellos casos para los cuales existe el límite trivial. Dicha generalización consiste en suponer que el límite (a cero o a infinito) es potencial. Esto se conoce como “autosemejanza asintótica de segunda clase”. ^{Barenblatt (1996)} desarrolla el concepto con mayor profundidad. Para determinar los exponentes, los cuales son anómalos, es decir no son los que indica el análisis dimensional, se requiere de otras herramientas, como los ‘grupos de renormalización’ en mecánica estadística, por ejemplo. En general no es posible su determinación mediante el análisis dimensional.

Un ejemplo simple es la determinación de la longitud de una curva fractal, en contraste con la de una curva suave (^{Barenblatt, 2003}). Sea Lη la longitud de la poligonal de segmentos de longitud ξ que aproxima una curva continua y va entre dos puntos separados por la distancia 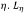depende de los dos parámetros dimensionales η y ξ. La aplicación del análisis dimensional da que 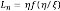. Para una curva suave, por ejemplo un semicírculo, a medida que ξ → 0 el argumento η/ξ → ∞, la función f va a un límite no trivial, en este caso π/2, en tanto que para una curva fractal, el límite de f cuando η/ξ → ∞ es infinito. De hecho, a partir de la geometría fractal se sabe que

El exponente anómalo D > 1, es decir, la dimensión fractal, no se puede determinar a partir del análisis dimensional. ^{Barenblatt (1996)} presentó un método para proceder en estos casos, y numerosos ejemplos de turbulencia, relaciones alométricas en biología y aguas subterráneas, entre otros.

Las propiedades empíricas observadas en las redes de drenaje y la geometría hidráulica sugieren que ocurren el escalamiento y la autosemejanza, no de primer orden, sino de segunda clase.

Las leyes de Horton

^{Horton (1945)} descubrió las leyes que llevan su nombre en el análisis cuantitativo de redes de drenaje extraídas de mapas. La motivación original era la definición del tamaño de un río a partir de la jerarquía de sus tributarios. El método más usado para definir la jerarquía en un patrón de ramificación es el método de ordenamiento de Horton-Strahler, también conocido como el método de Strahler (^{Strahler, 1952}; ¹⁹⁵⁷), el cual modifica ligeramente el ordenamiento original de Horton. El ordenamiento de Strahler asigna el orden ω = 1 a todos los nacimientos, es decir, las corrientes que no se bifurcan cuando se recorren hacia aguas arriba. Estas corrientes corresponden al mayor nivel de resolución para la red y, por lo tanto, definen la escala espacial. Al avanzar aguas abajo, cuando dos corrientes de igual orden ω se juntan, forman una corriente de orden ω + 1. Cuando dos corrientes de orden diferente se encuentran, el canal aguas abajo preserva el orden del mayor de los dos. Esto se aplica a lo largo de toda la red, y ordena todos los segmentos (tramo de río entre dos confluencias consecutivas, o entre un nacimiento y la siguiente confluencia, o entre la última confluencia y la salida de la cuenca). El orden a la salida se denota como Ω. Según esta definición, cualquier red tiene únicamente una corriente (sucesión consecutiva de segmentos del mismo orden) de orden Ω, que también se le asigna a la cuenca. En un mapa este ordenamiento de Strahler es equivalente uno a uno al procedimiento de poda (como si fuera un árbol, de hecho las redes son árboles de acuerdo a la teoría matemática de grafos). Es decir, si todos los segmentos de orden 1 se podan y se reordena la red, los segmentos originales de orden 2 son ahora de orden 1, los de orden 3 pasan a ser ahora de orden 2, y así sucesivamente. El orden de la cuenca decrece hacia una unidad y el procedimiento de ordenación pone de presente la estructura de ramificación y autosemejanza. Toda subcuenca es una cuenca.

Este ordenamiento sirvió para encontrar las leyes de composición de Horton, también conocidas simplemente como leyes de Horton. La más conocida es la ley del número de corrientes Nω de orden ω en una cuenca de orden Ω. Tradicionalmente, le ley se escribe como

El número RB se denomina la relación de bifurcación. Las observaciones en redes reales indican que hay un rango estrecho de posibles valores de RB, típicamente entre 3 y 5. Estas leyes no son formales, no se han demostrado con base a primeros principios, son de carácter estadístico, es decir hay lugar a la variabilidad. Sin embargo, se reportan ampliamente para redes de drenaje en diversidad de ambientes. Se han observado relaciones semejantes para la longitud, la pendiente, el área y otras variables de la geometría hidráulica. Como se verá, se puede demostrar la existencia de las leyes de Horton en varios de los modelos propuestos, como el modelo de Shreve o el modelo de ramificación geométrico.

El modelo de Shreve

^{Shreve (1966}, 1967, 1969, 1974) desarrolló el llamado modelo aleatorio de las redes de drenaje, lo que aportó el primer intento de explicación teórica de las observaciones condensadas en la ecuación (1). El modelo tiene tres pro- piedades muy importantes. Como se verá, se fundamenta en muy pocas premisas que, además, son simples. Esta primera característica es clave en un modelo, que no es otra cosa que un instrumento para comprender la realidad. No tiene mucho sentido que el modelo sea tan complejo como la realidad. La segunda propiedad del modelo es que involucra la variabilidad, lo que coincide con el principio fundamental de Leopold del que se habló en la introducción. Consecuencia directa de esta propiedad es que se observa lo más probable. La tercera propiedad es que el modelo se puede verificar, o falsificar. Esta característica es esencial en la ciencia. Los modelos ajustables no permiten avanzar en la comprensión. En general, es fácil obtener un resultado determinado de varias maneras, algunas por razones equivocadas. La única manera de avanzar en el conocimiento es poniendo a prueba lo que hasta el momento se toma como verdad. El modelo aleatorio de Shreve cumple con esta propiedad y las otras dos señaladas antes. Como se verá, la evidencia con la que se cuenta apunta en contra del modelo, es decir el modelo no pasa la prueba. A continuación se ilustran estas ideas con predicciones contrastadas con observaciones. Otras fuentes que pueden consultarse en este sentido son los estudios de ^{Mesa (1986)}, ^{Mesa & Gupta (1987)}, ^{Mantilla, et al. (2000}) y ^{Troutman & Karlinger (1998)}.

Hipótesis del modelo aleatorio

En el modelo aleatorio tiene un papel importante el concepto de magnitud de un segmento, que cuenta el número de fuentes aguas arriba. La primera hipótesis del modelo es que todas las redes topológicamente diferentes (RTD) de igual magnitud m, son igualmente probables. La segunda es que las longitudes y las áreas de los segmentos de una red provienen de variables aleatorias independientes. Con estas pocas hipótesis es posible construir la teoría. El número de las RTD de magnitud m crece muy rápido con m, lo que da origen a una convergencia estadística en el mismo sentido de la ley de los grandes números y del teorema del límite central.

Número de las RTD de una magnitud dada

Sea am el número de las RTD de magnitud m. Toda red de magnitud m > 1 puede concebirse como compuesta por dos subredes: de magnitud k la de la izquierda y, por lo tanto, m - k, la de la derecha. El número de posibles RTD a la izquierda es ak y a la derecha es am-k. Con base en el principio multiplicativo, hay ak am-k maneras de que esto ocurra. Ahora k puede tomar cualquier valor entre 1 y m - 1. En resumen se tiene que

Al aplicar la fórmula recursivamente se tiene que {am} = {1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, ...}.

La función generatriz 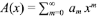permite obtener una fórmula explícita, pues si se aplica a la anterior ecuación de recurrencia se tiene A(x) = x + A2 (x). Las funciones generatrices son una poderosa herramienta para resolver múltiples problemas que, de otra manera, serían intratables, pero su potencial raramente se explota. En realidad, son un caso particular de la familia de transformadas, entre las que se encuentran la transformada de Laplace, la función carac- terística y la función generatriz de momentos. Se pueden encontrar mayores detalles en ^{Feller (1968)}. Recurriendo al algebra elemental se obtiene A(x) = 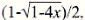que se expande en series usando el teorema binomial y, por lo tanto, es una fórmula explícita para los coeficientes

La última aproximación usa la fórmula de ^{Stirling (1730}): n!~n _n e- _n √2πn, que da excelentes aproximaciones incluso para valores moderados de n, por ejemplo, 1!≅0,9221; 2!≅1,919; 5!=120≅118,019; 10!=3 628 800≅3 598 600 (^{Feller, 1968}).

Se invita al lector a tomar papel y lápiz y hacer un esquema de las diferentes redes para una magnitud siquiera de 6. También es instructivo seguir el detalle de cada uno de los pasos de esta y las siguientes demostraciones.

Bifurcación: ley de los grandes números

Sea N _ω (m) el número de corrientes de orden ω en una red tomada al azar entre la población de las RTD de magnitud m. Según la hipótesis del modelo, Nω(m) es una variable aleatoria cuya distribución de probabilidades se puede calcular y, por lo tanto, también su media y su varianza.

Sea b _m,k el número de las RTD con magnitud m y con k corrientes de orden 2. Por lo tanto, al aplicar la hipótesis y la fórmula elemental de probabilidad como la fracción entre el número de casos favorables sobre el número de casos posibles,

Se va a demostrar que cuando m → ∞, E[N ₂ (m)] crece como m/4, mientras que Var[N ₂ (m)] crece como m/16, por lo tanto, Var[N ₂(m)/m] → 0 y se tiene la convergencia en una probabilidad de N ₂(m)/m y una constante de

Este resultado, aplicado repetidamente usando el argumento de la poda, explica la ley de bifurcación de Horton (ecuación (1)). Sin embargo, con la limitación de que asintóticamente R _b = 4.

Para proceder a la demostración se escribe una ecuación en recurrencia para b _m,k usando los mismos argumentos que en la sección anterior: descomposición en subredes y funciones generatrices,

Sea B _m (y) = ∑b _m,k yk, luego B _m (1) = a _m , B1 (y) = 1, B ₂ (y) = y, y para m ≥ 3

La tarea es calcular E[N ₂ (m)] y Var[N ₂ (m)],

que se obtiene de tomar la derivada en la ecuación para B _m (y), luego

Por lo tanto, C(x) = ∑c _m x ^m , la función generatriz de la secuencia c _m satisface

de donde se puede calcular

Ahora, usando la segunda derivada de B se procede al cálculo de Var[N ₂ (m)],

donde para m > 2 y d ₁ = d ₂ = 0. Luego la función generatriz cumple

Recordando la fórmula de la varianza, se tiene que

Esto completa la demostración.

La importancia del cálculo de la varianza y del límite (ley de grandes números) que se desprende reside en la posibilidad de contrastar la variabilidad natural con las pre- dicciones del modelo mediante pruebas estadísticas, como se ilustrará más adelante.

Ley del número de segmentos de Horton

Con base en el mismo tipo de argumentos, ^{Mesa (1986)} encuentra una ley de grandes números para Sω (m), el número de segmentos de orden ω en una red de magnitud m que explica la ley de Horton para el número de segmentos, con relación R _c . Para ω = 2 y m → ∞

Por lo tanto, como S ₁ = m, se tiene la siguiente convergencia en probabilidad cuando m → ∞

Ley de longitudes de Horton

De acuerdo a las hipótesis las longitudes de los segmentos son variables aleatorias independientes idénticamente distribuidas 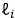con media λ. Luego, del anterior resultado se deduce que la relación entre L ₂ (m), la longitud de una corriente de orden 2 y L ₁ (m), la longitud de una corriente de orden 1, tiende a la siguiente relación de longitudes cuando m → ∞

entonces, claramente E[L ₁ (m)] = λ. Para calcular el valor esperado de L ₂ (m) se pueden sumar las longitudes de todos los segmentos de orden 2 y dividir por el número de corrientes,

Si la media de las longitudes de los segmentos externos y los internos no es la misma, R _L deberá afectarse por la relación entre estas. Además, usando el argumento del podado, la extensión a los órdenes subsiguientes no es directa, en vista de que en las corrientes de orden ω ≥ 3 habrá otros segmentos no contabilizados en este cálculo como resultado de los tributarios laterales de orden menor a ω - 1. Como en el caso de la relación de bifurcación, asintóticamente el modelo está limitado topológicamente a R _L = 2.

Ley de áreas de Horton

Con base en un argumento semejante al anterior y en la hipótesis sobre la independencia de las áreas de los segmentos, así como la ley de grandes números de la teoría de probabilidades para un número aleatorio de sumandos, se obtiene directamente la ley de Horton para las áreas, puesto que una red o subred de magnitud arbitraria k tiene exactamente 2k - 1 segmentos.

Relación entre el área y la longitud

Bajo la hipótesis adicional de que la longitud de los segmentos es exponencial, ^{Mesa (1986)} (ver también ^{Mesa & Gupta, 1987}) encontró lo siguientes resultados para D _m , el diámetro de una red de magnitud m cuando m → ∞,

No hay pues ley de grandes números para esta variable, sino convergencia en la distribución cuando D _m se escala con m ^0.5, es decir, es diferente de los casos anteriores, en los cuales la varianza tiende a cero (^{Mesa, 1986}; ^{Gupta, et al., 1990}). En la literatura se ha reportado la famosa Ley de ^{Hack (1957)} y pueden consultarse también otros estudios posteriores de ^{Mueller (1973}), ^{Eagleson (1970)} y ^{Shreve (1974)}, en los cuales se indica que el exponente del área para calcular la longitud del canal principal es del orden de 0,5533 para cuencas con un rango de siete órdenes de magnitud en todo el mundo. Se ha reportado que cuando se separan los datos por rango de áreas, el exponente es aproximadamente de 0,6 para cuencas menores de 20.000 km², de aproximadamente 0,5 para cuencas de hasta 250.000 km², y para cuencas mayores decae a 0,466. Los resultados del modelo permiten calcular el valor del exponente para cualquier valor de m; específicamente para 10, 100 y 500, los exponentes son 0,608; 0,530 y 0,513, respectivamente. Todo indica que las discrepancias son significativas (ver Figura 1).

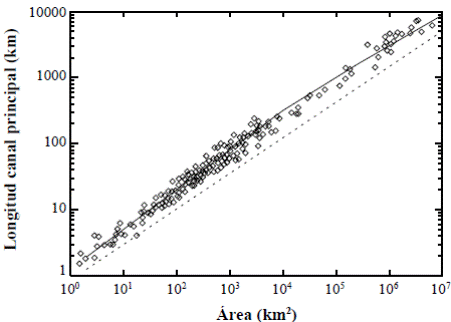
Figura 1 Diagrama de dispersión entre la longitud y el área para 461 cuencas en todo el mundo, incluidas las mayores (elaboración propia a partir de datos de ^{Hack (1957)}, ^{Langbein, et al. (1947)} y ^{Leopold, et al. (1964)}). La línea continua tiene tramos de pendientes de 0,6, 0,5 y 0,466, respectivamente. La línea punteada tiene una pendiente de 0,5533 y está desplazada verticalmente para mejorar la visibilidad. 

Relación entre magnitud y orden

Sea M _ω la magnitud de una red de orden ω; dado que intuitivamente se sabe que cuando la magnitud aumenta, también aumenta el orden, es posible calcular los momentos asintóticos de la distribución de M _ω cuando m → ∞,

No hay, pues, ley de grandes números para esta variable,sino la indicación de una convergencia en la distribución cuando se escala adecuadamente.

En un estudio de muchas cuencas de los Estados Unidos, ^{Peckham (1995b}) encontró desviaciones muy grandes entre las observaciones y las predicciones. Las observaciones para una de las cuencas consideradas fueron: {Mω} = {1,3,14,63,3 18,1643,5859,31764}; En tanto que las predicciones fueron: {1, 3, 11, 43, 171, 683, 2731, 10923}.

Evidencia empírica

Parece haber un patrón en las desviaciones entre las observaciones y las predicciones. En primer lugar, cuando se evalúa la varianza en el modelo, las desviaciones son muy significativas, varias desviaciones estándares por encima del valor esperado. En segundo lugar, las desviaciones parecen estar siempre en el mismo sentido. Las cuencas naturales tienden a ser mucho más esbeltas que las predicciones del modelo. Por ejemplo, para un orden dado, la magnitud observada es muy superior a la predicción, lo que quiere decir que el modelo subestima la tendencia a que haya más tributarios laterales de orden menor. Este punto quedará más claro al estudiar el modelo de Tokunaga

Modelo de Tokunaga

La propiedad fundamental de las redes de drenaje que captura el modelo determinístico de Tokunaga es la recursividad o autosemejanza; las redes resultantes se denominan árboles topológicamente autosemejantes (ATS). Las fuentes principales para esta sección son los estudios de ^{Tokunaga (1978}, ¹⁹⁶⁶), ^{LaBarbera & Rosso (1989)}, ^{de Vries, et al. (1994}), ^{Peckham (1995a}, ^1995b), ^{Peckham & Gupta (1999)}, ^{Rodríguez-Iturbe & Rinaldo (2001}), y ^{Mantilla, et al. (2000}).

Eiji Tokunaga introdujo el modelo que lleva su nombre (^{Tokunaga, 1966}, ¹⁹⁷⁸) basándose en el ordenamiento de Strahler y usando una construcción autosemejante. A diferencia del modelo de ^{Shreve (1967)}, este es determinístico, y no incorpora la variabilidad estadística observada. La topología es recursiva, como se explica a continuación, y la longitud de todos los segmentos se asume constante, igual a λ.

^{Peckham (1995a)} mostró que, a pesar de que geométricamente es muy simple y su única estructura es la recursividad topológica, el modelo de Tokunaga tiene capacidad de describir varias de las propiedades observadas en las redes de drenaje naturales. Por ejemplo, la relación de la bifurcación en las redes naturales está en el rango de 3 < R _B < 5, lo que el modelo de Tokunaga puede representar, en tanto que el modelo aleatorio predice R _B = 4.

Construcción

El concepto clave para la construcción de los árboles es el generador de tributarios laterales T _ω,ω-k , que es el número de corrientes de orden ω - k que lateralmente se unen a las corrientes de orden ω. Como las redes naturales exhiben variabilidad, T _ω,ω-k se puede interpretar como el número medio. Es decir, se considera la clase de redes determi- nísticas en la cual toda corriente de orden ω tiene dos tri- butarios aguas arriba y T _ω,ω-k tributarios laterales de orden ω - k donde ω varía entre dos y el orden de la cuenca Ω, y k varía entre 1 y ω - 1.

Los árboles topológicamente autosemejantes (ATS) son un subconjunto de esta clase para los cuales los generadores cumplen con T _ω,ω-k = T _k , k = 2, 3, .... Es decir, los generadores solo dependen de la diferencia de órdenes, no del orden mismo. Si los generadores se organizan en forma matricial, resulta una matriz de Toeplitz para los árboles auto-semejantes, pero Tokunaga impuso más restricciones en los generadores, considerando que T _k /T _k-1 = c, k = 2, 3, ..., y T ₁ = a, donde c y a son parámetros constantes asociados a la topología de una red particular. Esto lleva a la siguiente expresión para los generadores,

lo cual representa los ATS promedio (^{Dodds & Rothman, 1999}). Estos parámetros se pueden estimar a partir de las observaciones en una red natural. La Figura 2 muestra ejemplos de orden 4. La Tabla 1 presenta los valores promedio con los parámetros a = 1 y c = 2.

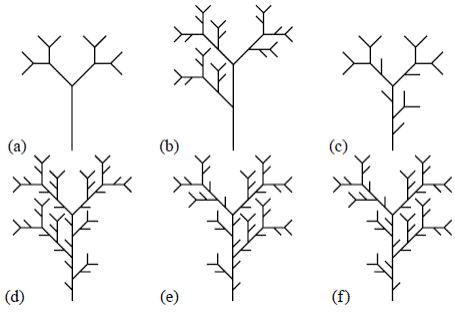
Figura 2 Árboles autosemejantes de orden 4. (a) Tk = 0 para todo k; (b) T1 = 1, Tk = 0 para k > 1; (c) T1 = 0, Tk = 2k-2 para k > 1; (d-f) Tk = 2k-1 para todo k. Los grados de libertad se ilustran de izquierda a derecha (tomado de ^{Peckham, 1995b}). 

Tabla 1 Valores para el modelo autosemejante con los parámetros a = 1 y c = 2, los cuales corresponden a R _B = 4, R _M = 4, y R _C = 2, lo que equivale al modelo promedio de Shreve (tomado de ^{Peckham, 1995b}). C _ω y T _ω se definen en las secciones sobre “Construcción” y “Ley del número de segmentos”, respectivamente. 

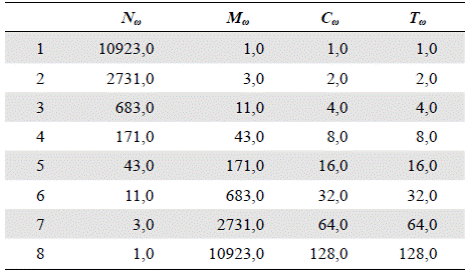
Sea N _ω el número de corrientes de orden ω. De la definición de los ATS se desprende la siguiente ecuación de recurrencia para N _ω , es decir, el número total de corrientes de orden ω en la red:

La ecuación está expresada para proceder recursivamente con el cálculo desde el orden mayor Ω hasta el orden menor 1. El primer término de la derecha expresa el hecho de que por cada corriente de orden ω + 1 se requieren dos corrientes de orden ω que la preceden aguas arriba, más las demás tributarias laterales de orden ω que caen en canales de orden mayor a ω, las cuales están contabilizadas en el segundo término.

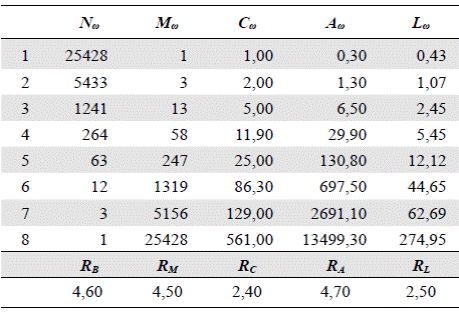
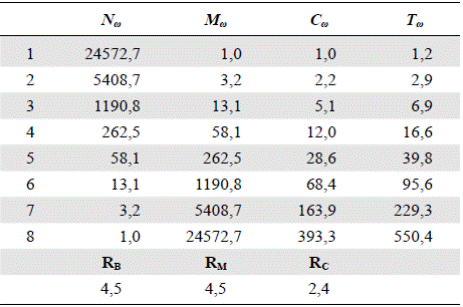
^{Peckham (1995b)} analizó varias cuencas. La Tabla 2 presenta los valores promedio observados para la cuenca del río Kentucky y la Tabla 3, las predicciones del modelo de Tokunaga. La ecuación (3) muestra la matriz de tributarios laterales ((T _ω,ω-k )), ω = 2, 3,…, Ω, k = 1, 2, …, Ω - 1 para esta cuenca:

Tabla 2 Mediciones para la red de drenaje del río Kentucky (tomado de ^{Peckham, 1995b}) 

Tabla 3 Valores correspondientes al río Kentucky en el modelo autosemejante con los parámetros a = 1,2 y c = 2,4 (tomado de ^{Peckham, 1995b}) 

Ley de bifurcación de Horton

MacConnell & Gupta (2008) demostraron la ley de Horton para los ATS usando funciones generatrices para la secuencia N _ω y los generadores de Tokunaga. Es decir, demostraron que N _ω /N _ω+1 converge en R _B en el límite cuando Ω - ω → ∞. El límite aplica para corrientes de orden pequeño, ω = 1, 2, ..., a medida que el orden Ω → ∞. La interpretación de este límite de MacConnell & Gupta (2008) es la siguiente: “Note que si el orden de la red Ω puede incrementarse, es de esperar que haya más corrientes. Sin embargo, cuando todas las corrientes de los órdenes menores ω y ω +1 en una cuenca de orden muy grande Ω se cuentan, es de esperar que se ha contado una porción significativa de los tributarios laterales, y que por tanto la relación de bifurcación observada se acerca a la relación teórica. Este argumento clarifica el uso del límite, Ω - ω → ∞”.

El primer paso es la sustitución ϕ _k = N _Ω-k con la que se reescribe la ecuación de recurrencia como

Si Φ(z) = ∑Φ _k z ^k , es fácil ver que lo que se resuelve en

con 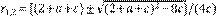, y las raíces del denominador 1 - (2 + a + c) z + 2cz2. Para la expansión en series se procede mediante el método tradicional de fracciones parciales con coeficientes indeterminados para obtener ak = (αr1 -(k+1) + βr2 -(k+1))/(2c). Por lo tanto, el resultado de interés para la relación de bifurcación es

En otras palabras,

Nótese que los árboles del modelo aleatorio son también autosemejantes en la media con a = 1 y c = 2. En este caso, la predicción del modelo de Tokunaga RB = 4 concuerda con las del modelo aleatorio (^{Shreve, 1967}) (Tabla 1).

Ley de magnitudes

A partir del anterior resultado, MacConnell & Gupta (2008) también dedujeron una ley de Horton para la magnitud Mω de una corriente de orden ω, y para ω = 1,2,.... Nótese que todos los árboles de orden ω en cualquier ATS tienen la misma Mω. La siguiente ecuación evidencia claramente la construcción:

Nótese el parecido de esta expresión con la correspondiente para Nω y el cambio subsiguiente en los subíndices. La identidad Mj = NΩ-j+1 se demuestra fácilmente por inducción: claramente M1 = NΩ = 1, ahora se asume para j - 1 y se demuestra para j usando la expresión de recurrencia para Mj. No es sorprendente, entonces, que exista una ley de magnitudes de Horton con una relación RM igual a la relación de bifurcación,

donde RM = RB es la relación de magnitudes de Horton. Las observaciones soportan esta ley (^{Peckham, 1995b}).

Ley del número de segmentos

Sea Cω el número de segmentos en una corriente de orden ω en un ATS. Como en el caso anterior, todas las corrientes del mismo orden tienen igual número de segmentos, que es 1 más la suma del número de sus tributarios laterales, es decir, 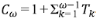. Existe una ley de Horton para el número de segmentos, con la correspondiente relación de segmentos 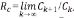. Para los generadores de Tokunaga es fácil mostrar que RC = c.

Leyes geométricas de Horton

Las anteriores leyes topológicas se generalizan en leyes geo- métricas si se asume la segunda hipótesis de Shreve. Es decir, se tendrían una ley de longitudes (proporcional al número de segmentos) y una ley de áreas (proporcional a la magnitud).

Fractalidad

Es apenas natural que un árbol autosemejante sea fractal (ver, por ejemplo, en ^{Feder, 1988}, detalles sobre los fractales). Para investigar esta propiedad se requiere asumir una estructura geométrica. La más simple es la que asume que todos los segmentos tienen igual longitud.

Una manera cómoda de estudiar este tema es proceder a una construcción iterativa semejante a la empleada para otros fractales, construcción que es equivalente a la definición. Se inicia con la corriente de orden mayor Ω, que se asume de longitud unitaria. En cada etapa sucesiva k se incorporan las corrientes de orden Ω - k, para k = 1,2, ..., Ω - 1. En la etapa k se tiene un pre-árbol binario con nk pre-segmentos. Lo equivalente a la magnitud en esta etapa es el número de segmentos externos en el pre-árbol, que es NΩ - k. Luego,

Como factor de escala εk para las longitudes en esta etapa se toma el inverso del número de pre-segmentos en la corriente principal (que tiene longitud unitaria):

Luego, la dimensión fractal se calcula por la fórmula usual como

Como RB = RA y la longitud de los segmentos son constantes, la relación de longitudes de Horton es RC = RL, y se sigue que RL = RA 1/DT. Para las redes naturales se ha observado que 1,7 < DT < 1,8. La clase de árboles ATS predice valores de DT menores o iguales a 2.

Ley de Hack

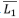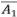Debe recordarse que se ha reportado que L = aAβ, con β mayor que 0,5. La autosemejanza de un ATS tiene algo que decir sobre este exponente. Supóngase, como en el caso anterior, que el área de una subcuenca es proporcional a su magnitud y que la longitud de una sucesión de corrientes es proporcional al número total de segmentos en la sucesión. Sean y la longitud y el área promedio de los segmentos de orden 1, luego 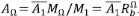. Para los ATS, el canal principal está formado por una cadena de corrientes de órdenes sucesivos desde 1 hasta Ω, luego LΩ = ∑Lω = 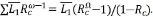. Por lo tanto, el exponente β se puede calcular a partir de

Nótese que según el modelo de Tokunaga, el exponente de Hack es β = 1/DT ≥ 1/2, en concordancia con las observaciones.

Cola de la distribución de magnitud

Un resultado importante observado en redes de drenaje naturales (^{de Vries, 1994}) tiene que ver con la distribución de la magnitud M de un segmento tomado al azar entre todos los segmentos que conforman una red de orden Ω suficientemente grande:

Donde

Es decir que αT + β = 1. La demostración de este resultado se apoya en la relación existente entre la magnitud y el orden en los árboles topológicamente semejantes. Sea W el orden de un segmento tomado al azar entre todos los segmentos de un ATS de orden Ω. La siguiente expresión de la probabilidad de que esta variable aleatoria tome un valor particular es simplemente el cociente entre el número de segmentos de tal orden y el número total de segmentos:

Asumiendo que Ω es grande y haciendo uso de la ley de Horton, 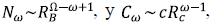se puede aproximar la anterior probabilidad como

donde p = R _c /R _B ≤ 1, que tiende a una distribución geométrica cuando Ω → ∞ por lo tanto,

Ahora, para un ATS, todos los pre-árboles completos de orden ω tienen la misma magnitud m _ω ∼ 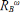que para un Ω grande y todos los segmentos de tal pre-árbol tienen una magnitud menor o igual a m _ω , o sea que la magnitud del segmento de la raíz del pre-árbol es exactamente igual y el resto es menor. Por lo tanto, la magnitud de un segmento solo puede ser mayor que m _ω si su orden es mayor que ω. Asimismo, el orden de un segmento solo puede ser mayor que ω si su magnitud es mayor que m _ω . Es decir, los siguientes eventos son equivalentes:

Por lo tanto, como ω(m) = log m/log RB, se tiene

con α _T = 1 - log R _c /log R _b Claramente, α _T ≤ 1/2, lo que concuerda con las observaciones hechas (^{Peckham, 1995b}).

Modelo de Gupta-Veitzer

Aunque el modelo aleatorio tiene en cuenta la variabilidad, tradicionalmente el análisis de las redes de drenaje en geomorfología se hace en términos de promedios. El modelo de Tokunaga describe mejor las observaciones que el modelo aleatorio, pero es determinístico. ^{Peckham & Gupta (1999)} presentaron una reformulación de las leyes de Horton en términos de distribuciones de probabilidad que denominaron “leyes de Horton generalizadas”. Por ejemplo, las distribuciones de probabilidad de las áreas de drenaje sometidas a nuevas escalas por sus medias 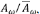colapsan en una única distribución común a todas (ver la Figura 3) para la cuenca de Whitewater en Kansas).

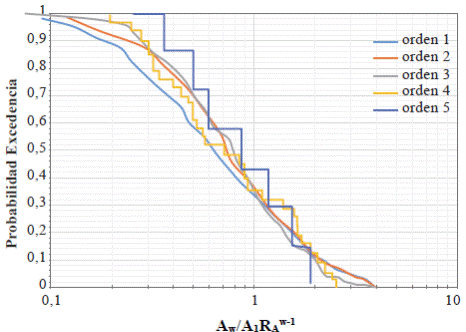
Figura 3 Escalamiento de la distribución de probabilidades del área con el orden (ley de Horton generalizada) para la red del río Whitewater en Kansas, Estados Unidos (modificada de ^{Mantilla & Gupta, 2005}). 

Hay dos componentes en este argumento. Para empezar, la ley de Horton para la media de las áreas de drenaje 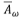de orden ω, que se puede escribir como,

con R _A , y la relación de Horton para las áreas. Esto se generaliza a

donde 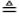significa igualdad en la distribución de las probabilidades. Como existe una ley de Horton para las medias, se sigue que

Nótese que esto implica que para los momentos de orden h,

Así como para el percentil

por lo tanto a _k,ϕ , el percentil de orden ϕ para A _k , escala de manera que

El modelo de ^{Veitzer & Gupta (2000)} apunta a incorporar los elementos de autosemejanza y recurrencia del modelo de Tokunaga en un marco aleatorio para formular una teoría de las leyes de Horton generalizadas. Otras fuentes para esta sección son ^{Mantilla & Gupta (2005)}, ^{Mantilla, et al. (2010)}, y ^{Mantilla, et al. (2012)}.

Construcción

Lo primero es reemplazar el proceso recursivo de generación de los ATS. En cada etapa, cada segmento externo se reemplaza por un generador tomado al azar de un conjunto de generadores externos con probabilidad p' _k de ocurrir. El generador externo k tiene un número de nodos adicionales (sin incluir las fuentes) igual a n _k . Asimismo, cada segmento interno se reemplaza por un generador de segmentos internos tomado al azar del conjunto de generadores internos, con una probabilidad de p _i y m _i nodos adicionales. Ambas selecciones son independientes e independientes entre sí. En la Figura 4 y en la Figura 5 se ilustra el esquema de un generador determinístico y de uno aleatorio, respectivamente.

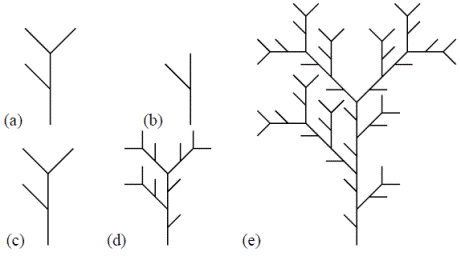
Figura 4 Esquema de construcción de una red determinística a partir de los generadores indicados: (a) para el segmento externo, (b) para el segmento interno, de orden 2 en (c), de orden 3 en (d) y de orden 4 en (e) 

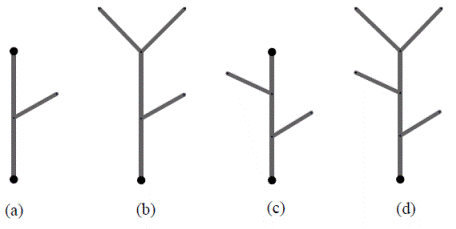
Figura 5 Esquema de la construcción de una red aleatoria a partir de los generadores indicados. Con probabilidad p cada segmento interno se reemplaza por el generador (a), y con probabilidad q = 1-p, se reemplaza por el generador (c). Cada segmento externo se reemplaza de manera independiente por el generador (b) o (d) con probabilidades p y q. 

Específicamente en la Figura 5 se trabaja con dos generadores externos (p = p'₁ = 0,7, γ = n ₁ = 2) y (q = p'₂ = 0,3, δ = n ₂ = 3) y dos internos (p = p ₁ = 0,7, α = m ₁ = 1) y (q = p ₂ = 0,3, β = m ₂ = 2). En la tercera etapa de construcción se tienen 51 posibles realizaciones, con sus respectivas probabilidades. En la Figura 6 se muestran 12 de ellas.

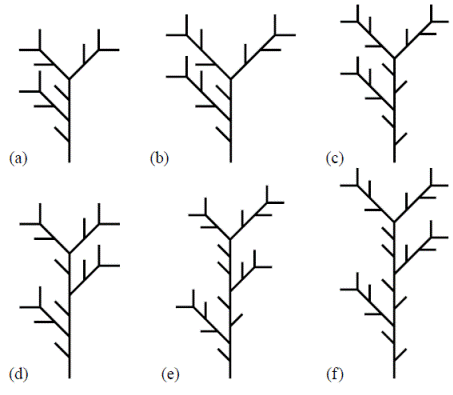
Figura 6 Seis de los 51 árboles topológicamente diferentes de orden 3 que se pueden obtener usando los generadores que se ilustran en la Figura 5. Las respectivas probabilidades son: (a) p⁶, (b) p³q³, (c) pq⁵, (d) p⁷q, (e) p³q⁵ y (f) q⁸. 

Para especificar completamente el proceso de construcción, es necesario definir los generadores externos e internos y sus respectivas probabilidades. Lo usual es que se trabaje con pocos generadores tanto externos como internos. En el ejemplo, solo se trabajó con dos en ambos casos.

De esta construcción resulta un conjunto de árboles cuyo número aumenta rápidamente a medida que crece el orden. Ajustándose a la filosofía del modelo aleatorio, lo que se observa es lo más probable. Para cualquiera de las variables de interés hay una distribución cuyo estudio debe permitir obtener las regularidades observadas como una predicción del modelo en el sentido de las leyes generalizadas.

Ley de Horton para el número de segmentos

Sea C _ω el número aleatorio de segmentos en una corriente de orden ω en la etapa k de la construcción. Se puede ver que la siguiente relación condicional es válida:

donde B (n,q) es una variable aleatoria con distribución binomial que puede tomar los posibles valores de 0, 1, ..., n con probabilidad

y función generatriz

Por tanto, 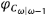, la función generatriz condicional de 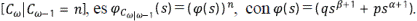Para calcular φω, la función generatriz no condicional de Cω, se procede así:

Esta expresión es semejante a la que de la teoría de procesos de ramificación del tipo de Galton-Watson y permite utilizar un resultado asintótico conocido para el caso, en el cual el valor esperado del número de descendientes μi es mayor que 1. En este caso, μ _i = αp + βq + 1. El resultado es que C _ω /μ ^ω converge con la probabilidad 1 en una variable aleatoria, lo cual se puede escribir como

Ley de la magnitud de Horton

Sea M _ω la magnitud de una red de orden ω en la etapa k de construcción. Se procede de manera semejante al caso anterior, teniendo en cuenta que cada segmento externo da origen a γ + 1 o a δ + 1 segmentos externos con probabilidad p y q respectivamente, y que cada segmento interior da origen a α o β nuevos segmentos exteriores con probabilidad p y q, respectivamente. Luego

Usando las funciones generatrices ϕ _Mω|ω-1 (s) = (ϕ(s)) ^m , con ϕ(s) = (qs ^β + ps ^α )(q' s ^δ+1 + p' s ^γ+1) y ϕ _Mω (s) = ϕ _Mω-1 (ϕ(s)), M _ω /η ^ω converge igualmente con la probabilidad 1 en una variable aleatoria, lo cual se puede escribir como

En este caso, η = μi + μ _e + 1 = αp + βq + γp' + δq' + 1.

Ley de la bifurcación de Horton

Sea el número de corrientes de orden k-j en la etapa k de construcción, con j = 0,1,..., k-1. La identidad 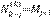, que se encontró por primera vez en el caso del modelo de Tokunaga, permite extender la ley de magnitudes a la ley de bifurcación, con R _m = R _B .

Leyes de longitud y de área de Horton

Las leyes topológicas anteriores dan lugar a leyes geométricas tal como en los modelos anteriores.

Modelo geométrico de ramificación

En un conjunto de artículos, ^{Kovchegov & Zaliapin (2016}, ²⁰¹⁷, ²⁰¹⁸) desarrollaron la estructura de un proceso estocástico geométrico de ramificación que genera árboles autosemejantes de acuerdo al modelo de Tokunaga y que pone sobre bases matemáticas más firmes los modelos de Tokunaga y de Gupta-Veitzer. Sin entrar en todos los detalles matemáticos, se presenta un recuento de las ideas principales.

Como la propuesta es estocástica, hay lugar a la variabilidad y lo que se observa es lo más probable. Por lo tanto, se sigue la filosofía discutida en la introducción (^{Shreve, 1966}, ^{Leopold, et al., 1964}). Para empezar, la matriz de tributarios laterales T _ω,ω-k , es decir, el número de corrientes de orden ω-k que lateralmente se unen a las corrientes de orden ω, se interpreta como el valor esperado.

El modelo desarrollado permite la justificación teórica de que (i), las observaciones empíricas de los árboles naturales son topológicamente autosemejantes (ATS), es decir, cumplen con T _ω,ω-k = T _k , k = 2, 3, ...,y (ii), la hipótesis de que la secuencia T _k = ac ^k-1 , k = 1, 2, ... (ecuación 2), es una secuencia geométrica.

Para este modelo, la operación de podado ya mencionada consiste en remover los segmentos de orden 1, es decir, dado un árbol τ de orden ω, el resultado es un árbol R (τ) de orden ω - 1. El concepto de invariancia bajo podado para un árbol aleatorio, que es una realización de un proceso estocástico, significa que la medida de probabilidad del árbol μ cumple con

Uno de los resultados importantes de ^{Kovchegov & Zaliapin (2017)} es que las realizaciones de procesos estocásticos con medida de probabilidad invariante bajo poda son árboles autosemejantes, es decir, se cumple T _ω,ω-k = T _k , k = 2, 3, .... Debe recordarse que T _ω,ω-k es el cociente entre el valor esperado del número de tributarios laterales de orden ω-k que le caen a una corriente de orden ω y el número de corrientes de orden ω.

La otra operación importante introducida por ^{Kovchegov & Zaliapin (2018)} es el desfase temporal que consiste en remover el segmento de la raíz. El resultado es que cada árbol de orden ω > 1 da lugar, en general, a un par de árboles, aunque si la operación actúa sobre un árbol de orden 1, este desaparece. La operación puede actuar sobre un conjunto plural de árboles. La invarianza ante el desfase temporal da lugar a árboles que cumplen con la ecuación (2).

Proceso de ramificación geométrico

Dada una secuencia T _k , k = 2, 3, y 0 < p < 1, se define S _k 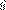= 1 + T1 + ... + T _k , para k ≥ 0. El proceso estocástico ς(s), indexado por el tiempo discreto s, describe el crecimiento de la población de acuerdo a las siguientes condiciones:

Conclusiones

Los modelos de Gupta-Veitzer o el de ramificación geométrica cumplen con incorporar la aleatoriedad y describir adecuadamente las observaciones, manteniendo hipótesis simples. Entre sus características más interesantes está la posibilidad de generalizar las leyes de Horton a equivalencia de distribuciones debidamente escaladas.

Todavía deben someterse a prueba estos modelos contrastándolos con una base de datos representativa de las observaciones, y con resultados teóricos que cuantifiquen la probabilidad de fluctuaciones con respecto a los valores esperados.

También hay otras líneas de trabajo que no se discutieron aquí por motivos de espacio y que se relacionan con la autosemejanza de la geometría hidráulica (^{Gupta & Mesa, 2014}). Es decir, debe trascenderse el análisis de las propiedades planimétricas para incorporar variables de interés dinámico como la pendiente, la velocidad, el ancho y la profundidad de la corriente, así como la rugosidad. Las observaciones empíricas indican que hay una dependencia potencial de estas variables con el caudal. La hidrología entra a jugar un papel en la medida en que el caudal, como variable aleatoria, se relaciona con el área de la cuenca, la cual, a su vez, está relacionada con la magnitud sobre la cual se estableció la ley de Horton generalizada. La relación entre el caudal y el área de la cuenca es aproximadamente lineal para caudales medios o mínimos, pero es potencial para los caudales máximos con exponente menor de uno. Esta cadena de relaciones implica la autosemejanza estadística (leyes de Horton generalizadas) para las variables de la geometría hidráulica y la hidrología en el sentido de semejanza incompleta o asintótica de segunda clase. Al parecer, el exponente anómalo proviene del hecho de que no toda la cuenca contribuye al pico de la creciente. La explicación completa de estas observaciones mediante una adecuada construcción teórica sigue siendo un problema fundamental de la hidrología. De todas maneras, una consecuencia es la interpretación de estas relaciones potenciales como leyes generalizadas de Horton para cada una de las variables.

La autosemejanza de las cuencas y su geometría hidráulica tienen, a su vez, implicaciones profundas para la construcción de una teoría hidrológica de las crecientes y de la semejanza hidrológica (^{Gupta, 2016}), aspecto que también está en desarrollo.