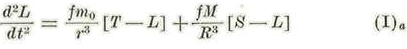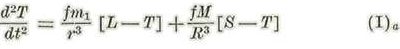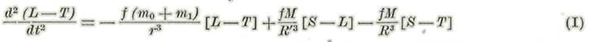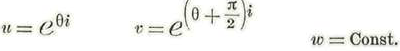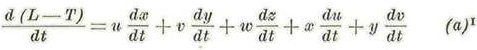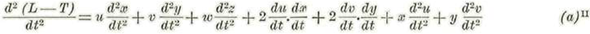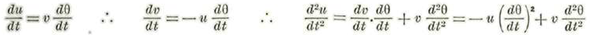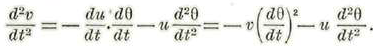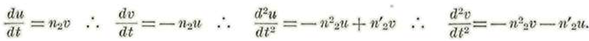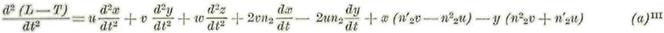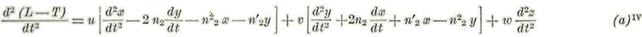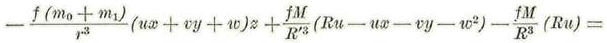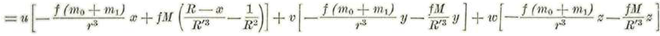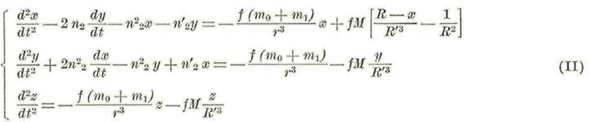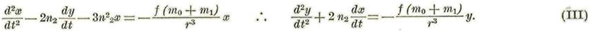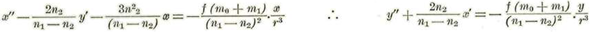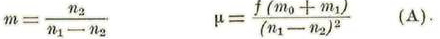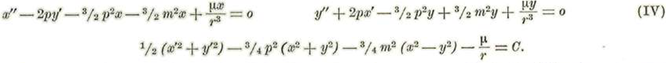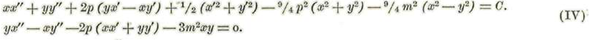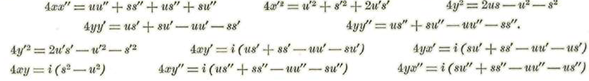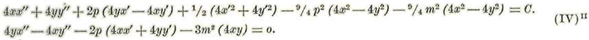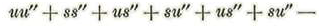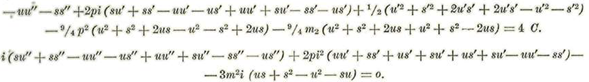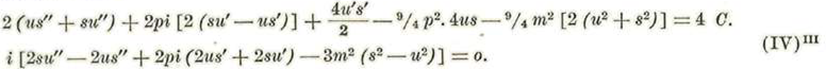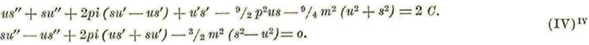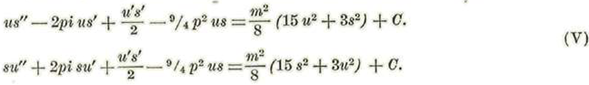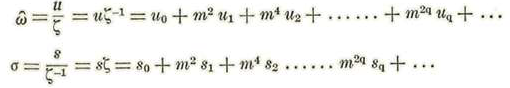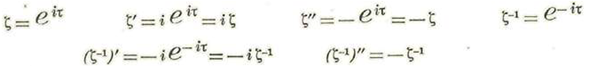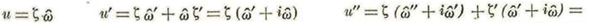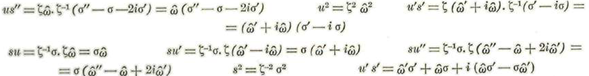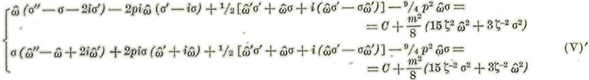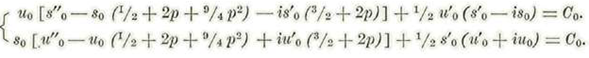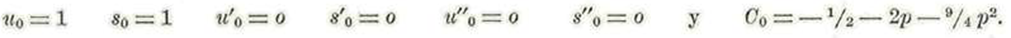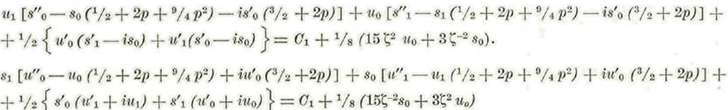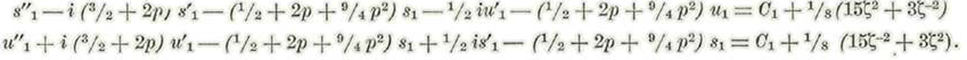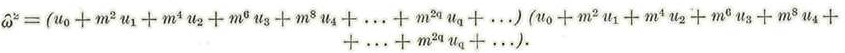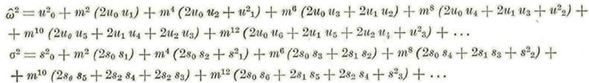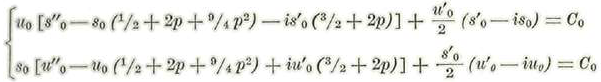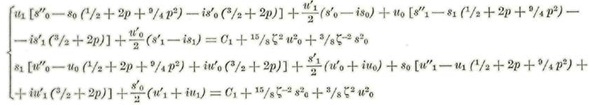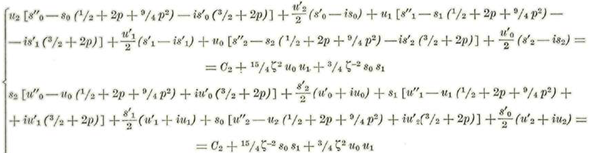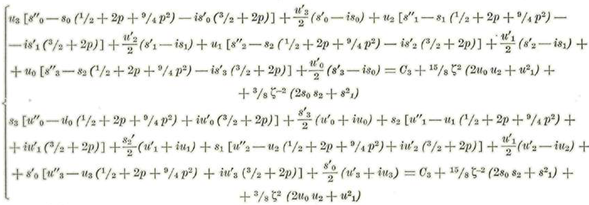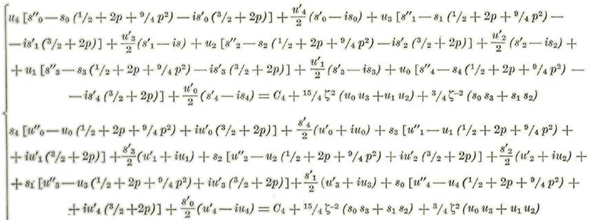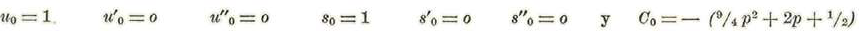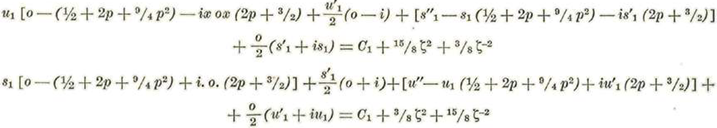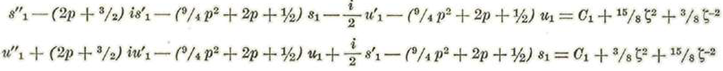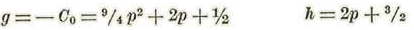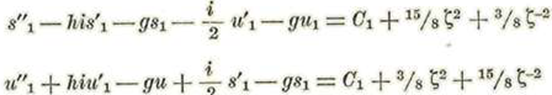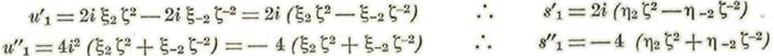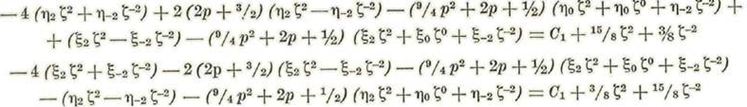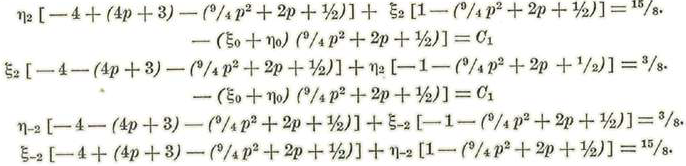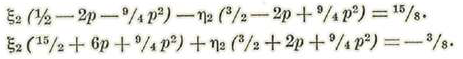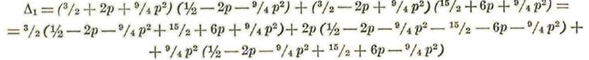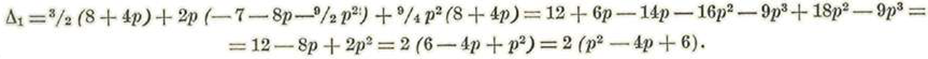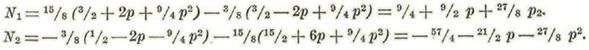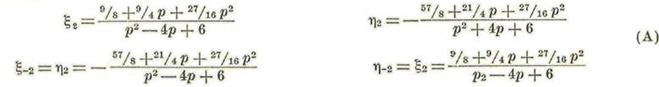ECUACION VECTORIAL

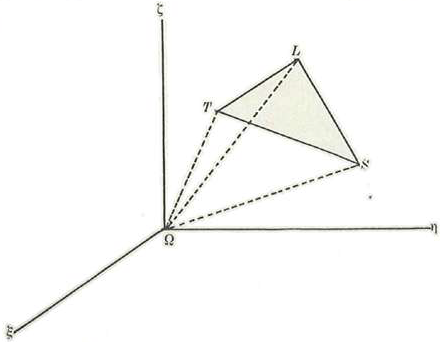
Representemos por T L y S respectivamente los vectores: Ω T Ω L Ω S que definen las posiciones absolutas de la tierra, luna y el sol con relación a un sistema de coordenadas fijo en el espacio: Ω ξ η ζ (fig. 1); por m₀ m₁ y M las masas de la tierra, la luna y el sol, y por f la atracción de la unidad de masa sobre la unidad de distancia.

Las ecuaciones de movimiento de la luna y de la tierra, después de divididas por las respectivas masas son:

Restando la primera ecuación de la segunda, se halla:

Tal es la ecuación vectorial que representa el movimiento relativo de la luna con relación a la tierra.

2-ECUACIONES DE MOVIMIENO DE LA LUNA CON RELACIÓN A EJES GIRATORIOS

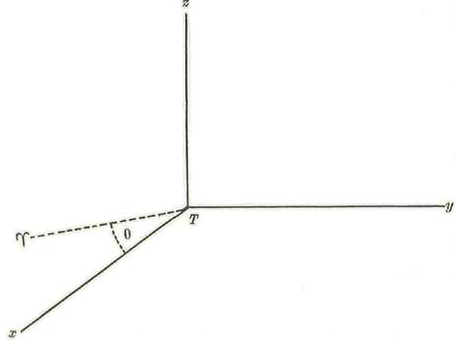
Tomemos (fig. 2.) un sistema coordenado con origen en la tierra, por plano x t y el plano de la eclíptica y por eje Tx la línea que va de la tierra al sol. Llamemos u v y w los versores de los ejes Tx Ty Tz respectivamente. Si representamos por θ la longitud del sol ♈TS. Tenemos:

Además, representando por x y z las coordenadas cartesianas de la luna, tendremos: L - T = ux + vy + wz (a)

Derivando dos veces sucesivas a (L-T) con relación a t tendremos:

Puesto que w=constante y

Ahora bien, puesto que u=Ҽ^θi y 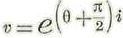tendremos:

Así:

Pongamos para simplificar

Así tendremos:

Así se tendrá para la ecuación vectorial de la posición de la luna:

O bien

Además se tiene para las cantidades que figuranen el 2° miembro de (1):

Sustituyendo en (1) e igualando los coeficientes de los mismo versores se tendrán las ecuaciones buceadas, así:

4-ECUACIONES DE HILL

Si se desprecian la paralaja solar, la excentricidad de la órbita terrestre y la inclinación de la órbita se hasta en (II).

R=R’ n’₂=0 n₂=constante, y en fin: z=z’=z’’=0. Entonces tendremos dos ecuaciones en lugar de tres, a saber:

Puesto que 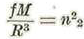ya que la órbita terrestre se haría circular.

Tales son las llamadas ecuaciones de Hill.

Llamaremos r y θ el radio vector de la luna y su longitud con relación a un equinoxio fijo. Llamemos n₁ el valor medio de 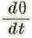y pongamos para nueva variable τ=(n₁-n₂)t. Si pues, llamamos p=f(t) a una función de t, tendremos, derivando con relación a т y llamandolo p’ y p’’ a las derivadas con relación a 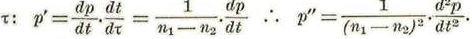. Dividiendo, pues las ecuaciones de Hill por (n₁-n₂)² y representando por x’ x’’ e y’ y’’ las derivadas primeras y segundas de las coordenadas con relación a т tendremos:

Pongamos para simplificar:

Así tendremos:

Si multiplicamos la primera por dx=x’dx y la segunda por dy=y’dx y las sumamos, se tendrá, después de integrar: 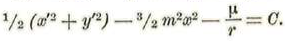Que es la integral de Jacobi.

5-ECUACIONES DE POINCARE

En lugar de considerar el sistema (III) o (III)' consideremos un sistema más general, de acuerdo con Poncairé, a saber:

Estas ecuaciones se reducen a las de Hill cuando se hace p=m. Siendo la última la que corresponde a la integral de Jacobi.

Multipliquemos primeramente la primera ecuación por x, la segunda por y y la tercera por uno y sumémoslas. Luégo multipliquemos la primera por y la segunda por (-ω) y la tercera por cero y sumémoslas también. Tendremos:

Hagamos el siguiente cambio de variables: u=x+yi s=x-yi Así tendremos: 2x = u + s 2¡y = u - s 2x’ = u' + s' 2iy’ = u' - s' 2x" = u" + 8" 2iy'’ = u" - s".

De donde se deduce:

Multiplicando las ecuaciones (IV)' por 4 se tendrá:

Substituyendo en éstos los valores hallados obtendremos:

Reduciendo se halla:

O bien:

Restando de la primera la segunda y luégo sumándolas, se hallará, después de dividir por 2:

Después de desarrollada la solución de las ecuaciones (V) según las potencias crecientes de m² se hará p = m para que las ecuaciones (V) se hagan idénticas a las de Hill.

Emplearemos la notación de H. Poincaré (Mécanique celéste-Tom. III. Nos. 327. etc.). Las ecuaciones en cuestión admiten un solución periódica, que no es la solución general, pero la que contiene los términos del grado cero, y con ellos la desigualdad conocida desde la Edad Media con el nombre de Variación, y la cual nos proponemos desarrollar.

Pongamos:

Tenemos:

Además tenemos:

Sustituyendo en (V) se obtiene:

Sustituyendo los valores de ώ ώ' ώ" σ σ’ σ" y C en función de m e igualando en ambos miembros los coeficientes de las mismas potencias de esta cantidad se obtiene sucesivamente:

Coeficientes de m°

Las cuales se satisfacen para

Las ecuaciones que nos dan los coeficientes de m² son:

Coeficintes de m²

Notando que u₀=s₀=1 u’=s’₀=s’’₀=0 Se tendrá:

Coeficientes de m²

Estas ecuaciones son lineales, de coeficientes constantes y con segundo miembro, y se integran fácilmente como lo veremos más adelante. Por lo pronto formaremos las parejas de ecuaciones correspondientes a los coeficientes de m ⁴ m ⁶ , m⁸ etc. Pero antes de continuar desarrollaremos los segundos miembros de las ecuaciones (v)' según las diversas potencias de m² para lo cual principiaremos por los desarrollos de ώ² y o². Tendremos:

Así:

Los segundos miembros de la ecuación en cuestión serán

Sustituyendo los desarrollos en las ecuaciones (V)' e igualando los coeficientes de las mismas potencias de m se halla:

Coeficientes m⁰

Coeficientes m²

Coeficientes de m ⁴

Coeficientes m⁶

Coeficientes de m⁸

Coeficientes de m¹⁰

Coeficientes de m¹²

Las ecuaciones correspondientes a los coeficientes de m ⁰ se satisfacen para los siguientes valores:

Sustituyendo en las ecuaciones correspondientes a los coeficientes de m ² los valores de índice cero, se halla:

O también:

Pongamos, para simplificar:

Así tendremos:

Busquemos los coeficientes de ζ² ζ⁰ y ζ^-2 en u₁ y 8₁ Para lo cual pondremos:

Hemos impuesto la condición en u₀=1 s₀=1. En general, hemos impuesto la de que los coeficientes de ζ en uζ^-1 y en sζ sean iguales a la unidad y fijando de esta manera el valor de la constante C. Pero como dicha constante aparece de la integral de Jacobi y depende del valor µ y de los valores iniciales de las coordenadas de la luna y de sus velocidades, debemos introducir una constante a ₀ como factor de C con el fin de satisfacer a la condición expresada. Esta corrección la hacemos al final de estos cálculos

Sustituyendo los valores de. u₁, u’₁ u''₁ s’₁ y s’’₁ en las ecuaciones anteriores, tendremos:

Igualando en cada ecuación los coeficientes de ζ² ζ^o y ζ^-2 obtendremos:

O bien, tendremos

O también:

Llamemos N₁ y N'₁ los coeficientes ξ₂ y n₂ respectivamente. Tendremos:

Se tendrá, pues:

La constante C = C ₀ + m² C₁,+ m ⁴ C ₂ + ... siendo una constante arbitraria de integración, podemos considerarla independiente de m. Es decir: C = C ₀ y C₁= C ₂ =….= o. Se tendrá pues:

ξo = o ηo = o. Por tanto: u ₁ = ξ₂ ζ² + η₂ ζ^-2 s₁ = η₂ ζ² + ξ₂ ζ^-2 (B)

El factor a₀ proveniente de C₀, está implícito en ξ₂ y η₂. Además nos falta dar el valor p=m

Nota-Debe introducirse un factor constante a₀ en la constante C pues se ha hecho arbitrariamente u₀ = s₀ = 1, debiendo estas cantidades tener un valor numérico distinto. Esto se hará más adelante.

(Concluirá).

NOTA_ DE LA DIRECCION-Por tratarse de un trabajo de Garavito tan importante como éste, conviene acompañarlo con notas explicativas dedicadas a la mayoría de nuestros lectores, quienes, sin ellas, tal vez carecieran de los elementos indispensables para juzgarte. Estas notas, claro está, no son necesarias para quienes estén familiarizados con los problemas referentes a la Astronomía de posición.

a). Los antiguos se dieron cuenta del movimiento mensual de la luna, según el cual este astro describe un circulo máximo entre las estrellas en un intervalo de 27^d 7^h 43^m. Notaron, además, que el plano de ese círculo no es fijo, pero que conservo, con respecto al descrito por el sol en un año (la eclíptica), una inclinación fija. También vieron que la línea de intersección de los dos planos dichos (línea de los nodos) se desaloja gradualmente con el tiempo de manera de dar la vuelta completa a la eclíptica en 18 años 8 meses, y que la dirección del movimiento de esa línea es de oriente a occidente, contraria a la del desalojamiento de la luna entre las estrellas. Esos astrónomos antiguos sabían que de acuerdo con este movimiento de la línea de los nodos, sucede que al cabo de 223 revoluciones de la luna con relación al sol, éste, la luna y la línea citada, vuelven a ocupar sensiblemente sus posicionei, relativas, de donde resulta que los eclipses vuelven a reproducirse de nuevo. Tal es el llamado periodo de los raros, conocido desde tiempos de los caldeos.

Como ese número de revoluciones lunares no corresponde a un número completo de dias la reproducción de los eclipses, tanto de sol como de tuna, no se verifica tan sencillamente. Además, y lo habían observado los antiguos, el movimiento de la luna sobre su órbita no es uniforme.

La complejidad de los movimientos lunares fue, pues, objeto de la observación de los astrónomos desde un principio. Así en la época de Galileo, ya casi se conocían la mayor parte de las desigualdades que daban lugar a divergencias notables entre el cálculo y la observación, verificada especialmente en los eclipses totales de sol que permiten gran precisión en la determinación de los instantes de los contactos, aun con instrumentos rudimentarios.

Así, pues, puede decirse que el estudio de la mecánica de la luna, al aparecer Newton, se elevó por sí solo a la categoría de problema fundamental para la comprobación de la ley de la gravitación, lo que ha justificado que muchos matemáticos hayan consagrado especial atención a las causas perturbatrices a que se deben las divergencias anotadas.

b). Para el cálculo de la posición de la luna en un instante dado, se debe tener en cuenta que los valores de los elementos de su movimiento deberán ser deducidos de un gran número de observaciones que se extienden a largos intervalos de tiempo. Entonces es necesario determinar las influencias perturbatrices de los otros planetas además de la influencia solar.

Generalmente, al tratar de calcular la posición de un cuerpo celeste, tales perturbaciones se pueden considerar desde dos puntos de vista distintos. En uno de ellos se parte de una época dada; esto es de la posición del cuerpo en dicha época. Para esa posición se podrán calcular las acciones de los otros planetas y sus efectos se integrarán sucesivamente por el método llamado de cuadraturas mecánicas, o de Encke. Considerando las derivadas de los elementos también se pueden integrar dejando el tiempo indeterminado. Luego se compararían los resultados de la observación con los del cálculo, partiendo de elementos osculadores aproximados e incrementos de sus errores, y estableciendo un gran número de ecuaciones de condición que se tratarían por el método de los menores cuadrados, a fin de determinar los valores exactos para otra época dada.

c). En Mecánica celeste se estudia la manera de formar los desarrollos de los elementos y de las coordenadas de modo satisfacer a las ecuaciones de movimiento. Estos desarrollos son series cuyo término general es de la forma:

A µ ^a M t^m cos (vt + h), en los cuales A y h son constantes, μ un pequeño factor dependiente de la relación de las masas perturbadoras a la masa central, o de cualquiera otro parámetro especial, M un monomio que contiene potencias enteras de cantidades pequeñas del orden de las excentricidades y de las inclinaciones, y, finalmente v un número de la forma k₁, n₁, + k₂ n ₂ +.....en donde k ₁ , k₂, etc. son números enteros positivos o negativos y n, n¡ etc. ¡os movimientos medios de los planetas.

Estos términos contienen cuatro caracteres que sirven para definir su importancia, a saber: 1⁹ El orden, definido por el exponente a del pequeño factor µ; 2° El grado del monomio M respecto de las cantidades que figuran en él; 3° La clase que depende de los pequeños divisores en el denominador, debidos a las integraciones sucesivas, y 4° El rango, o sea la diferencia entre el exponente a y el m del tiempo (a - m). Resulta de esto que cuando (a - m) es pequeño para términos de orden elevado, la potencia m del tiempo es muy grande y el término crece rápidamente con el tiempo, haciendo al fin divergente la serie.

Finalmente, los términos del desarrollo pueden clasificarse en términos periódicos, que son aquellos en donde el exponente m del tiempo es cero, esto es en donde el tiempo no figura fuera de los signos seno o coseno; términos mixtos en donde el tiempo figura tanto fuera como dentro de las funciones circulares seno o coseno, y los términos seculares, en donde v = o, y el tiempo no figura sino en el factor externo.

Los términos de pequeño rango son los que producen desigualdades que van creciendo con el tiempo.

d). Las tablas astronómicas fundadas sobre los elementos osculadores a una fecha dada, y en cuya conformación no se han tenido en cuenta sino los términos hasta de cierto orden, principiaron, al fin de cierto tiempo, a dar divergencias tales que se hace necesario cambiarlas fundándolas sobre elementos osculadores correspondientes a otra fecha posterior,

Poincaré ha demostrado que los desarrollos de las coordenadas y de los elementos pueden, por procedimientos especiales, ser transformados de manera de hacer desaparecer en ellos los términos seculares.

e). En el caso en que se trata del movimiento de la luna con relación a la tierra, esta última hace las veces de esto central, mientras que el sol, de masa enorme, desempeña el simple papel de cuerpo perturbador.

El coeficiente µ de la función perturbatriz está constituido por la relación de la masa del sol a la masa del sistema de la tierra y la luna multiplicado por el cubo de la relación de las distancias de la tierra a la luna y al sol.

Este factor tiene un valor muy superior al que corresponde a las perturbaciones planetarias. Si se aplicara al movimiento de la luna el método de Lagrange los desarrollos a que se llegaría serían tan poco convergentes que no podrían prestar servicio alguno. Tal es la dificultad que ha presentado desde un principio el movimiento de la luna.

f). Newton explicó varias de las desigualdades del movimiento de la luna tales como la variación, la ecuación anual y el movimiento del nodo, y descubrió por la teoría muchas otras que la observación no había aun puesto de manifiesto; pero no logró explicar satisfactoriamente el movimiento del perigeo ni la evección, por causa de la deficiencia del análisis matemático de su época.

Claireaut y d’Alambert plantearon, muy posteriormente, las ecuaciones de movimiento de los tres cuerpos y aplicaron su método a la luna atraída por la tierra según la ley de Newton y bajo la acción perturbatriz del sol.

Las desigualdades que Newton no había logrado vencer resistieron también tenazmente a los nuevos investigadores, hasta el punto de que Claireaut creyó ver en la imperfección de la ley de Newton la causa de tales dificultades. Sin embargo, los últimos estudios, que culminaron en los trabajos de Hill, Brown y Poincaré, han dado bastante éxito a la investigación en este campo.

g). En el campo gravitatorio el trabajo que habría que desarrollar para vencer la gravitación y llevar el astro considerado hasta el infinito, se llama energía potencial. La suma de la energía cinética y de la potencial es constante en todo el movimiento, según el principio de la conservación de la energía.

Suponiendo trazado por el planeta, según la dirección del movimiento, un segmento de recta de longitud igual al producto de la masa del planeta por la velocidad de que está animado en un instante, producto que se denomina cantidad de movimiento del planeta, resulta que el área del triángulo cuyo vértice es el centro del sol y cuya base es la cantidad de movimiento del planeta es una constante. La ley de Newton, considerando un planeta y el sol conduce, pues, a las leyes de Kepler generalizadas. Estas leyes se verifican muy aproximadamente a causa de que las masas de los planetas son muy pequeñas respecto de la masa solar; pero no son rigurosas.

Para prever con exactitud la posición de un planeta a largo plazo, es necesario estudiar su movimiento no sólo bajo la influencia del sol sino bajo la de otros planetas. La aceleración de que está animado cada planeta es la suma geométrica de las aceleraciones debidas no sólo a la acción solar sino también a las atracciones de los otros planetas. El sol, a su vez, está solicitado por todos los planetas y tendrá a cada instante, una aceleración que es la resultante de todas las aceleraciones debidas a las acciones planetarias.

Para referir los movimientos planetarios a tres planos que pasen por el centro del sol, es necesario aplicar a todos los cuerpos del sistema solar una aceleración igual y opuesta a la del sol. Se debe, pues, agregar a la aceleración resultante de todas las acciones atractivas que actúan sobre cada uno de los planetas, una aceleración ficticia igual y opuesta a la que anima al sol, para definir el movimiento relativo del planeta.

Planteado así el problema, se expresa la aceleración total de cada planeta mediante una suma geométrica de muchos términos, el primero de los cuales se refiere a la acción solar y los otros a las acciones planetarias y a la resultante de las acciones planetarias sobre el sol multiplicada por la relación de la masa del planeta a la del sol, estimada en sentido contrario.

h). Se pueden hacer tantas teorías de la luna fundadas en la ley newtoniana, como sistemas coordenados fijos o movibles se puedan idear; pero no todas conducen a resultados utilizables en el cálculo de las tablas lunares debido a la mayor o menor convergencia que se obtenga con unas o con otras en las aproximaciones sucesivas.

Las primeras tablas que se hicieron de la luna tomaban de la teoría la forma matemática de las desigualdades y de la observación el valor de los coeficientes. La primera teoría completa de los movimientos de la luna, fundada sobre la ley de gravitación, se debió a Demoisseau, Laplace expuso una teoría fundada sobre ecuaciones deducidas de las del movimiento mediante una transformación en la cual el radio vector está reemplazado por el inverso de su proyección sobre la eclíptica y la latitud por su tangente, y en donde la longitud de la luna ha sido tomada como variable independiente y el tiempo como función de esta variable. Estas fórmulas, en las que sólo se tiene en cuenta la acción perturbadora del sol, han servido de base a muchas teorías de la luna en que algunos investigadores han cambiado la variable independiente: longitud, por la anomalía excéntrica.

Las dificultades que ha presentado el problema en lo que respecta a la poca convergencia de las series ha sido el motivo por el cual los más ilustres matemáticos de todas las épocas y países, se han ocupado del movimiento de la luna, más complejo, desde algunos puntos de vista, que los de los planetas, según se ha visto atrás.

i). Cierto caso ideal referente a una solución periódica puede presentar una desigualdad considerable, y, además, aproximarse al caso del movimiento de la luna. Esta desigualdad tendría un coeficiente también muy próximo de la desigualdad correspondiente al movimiento de la luna. Así será fácil pasar del caso ideal al caso real.

Tal fue la manera como Hill llegó a determinar el coeficiente de la variación de la luna. Las ecuaciones de movimiento, así planteadas por Hill, forman un sistema de cuarto orden y admiten una integral que había sido hallada antes por Jacobi.

j). Las ecuaciones de segundo orden del movimiento relativo de la luna, supuesta nula la inclinación de la órbita y considerando los ejes animados de un movimiento de rotación uniforme, fueron transformadas por Hill por medio de dos variables imaginarías conjugadas. Hill desarrolló las nuevas variables, o, mejor dicho, sus relaciones a cierta exponencial, y las integró por desarrollo en serie siguiendo las potencias crecientes de la relación de la velocidad angular media del sol a la velocidad angular media de la luna con relación al sol. Estos desarrollos resultan referentes a la cuarta potencia de la relación indicada, lo cual los hace muy convergentes. Así fue como Hill halló la desigualdad conocida con el nombre de variación.

El movimiento del nodo y del perigeo, la evección, las desigualdades de orden superior y las que provienen de las acciones planetarias se refieren a artificios de cálculo tan complejos que no pueden ser indicados aquí, ni someramente siquiera.

De todos modos se llega en la teoría de la luna a series cuyos términos son de la forma indicada, y cuyos senos y cosenos se refieren a ángulos dependientes de la distancia angular de la luna al sol, de la luna al nodo, de la luna al perigeo, etc., términos que representan las llamadas desigualdades del movimiento.

El coeficiente µ de la función perturbatriz está constituido por la relación de la masa del sol a la masa del sistema de la tierra y la luna multiplicado por el cubo de la relación de las distancias de la tierra a la luna y al sol.

Este factor tiene un valor muy superior al que corresponde a las perturbaciones planetarias. Si se aplicara al movimiento de la luna el método de Lagrange los desarrollos a que se llegaría serían tan poco convergentes que no podrían prestar servicio alguno. Tal es la dificultad que ha presentado desde un principio el movimiento de la luna.

f). Newton explicó varías de las desigualdades del movimiento de la luna tales como la variación, la ecuación anual y el movimiento del nodo, y descubrió por la teoría muchas otras que la observación no había aún puesto de manifiesto; pero no logró explicar satisfactoriamente el movimiento del perigeo ni la evección, por causa de la deficiencia del análisis matemático de su época.

Claireaut y d'Alambert plantearon, muy posteriormente, las ecuaciones de movimiento de los tres cuerpos y aplicaron su método a la luna atraída por la tierra según la ley de Newton y bajo la acción perturbatriz del sol.

Las desigualdades que Newton no había logrado vencer resistieron también tenazmente a los nuevos investigadores, hasta el punto de que Claireaut creyó ver en la imperfección de la ley de Newton la causa de tales dificultades. Sin embargo, los últimos estudios, que culminaron en los trabajos de Hill, Brown y Poincaré, han dado bastante éxito a la investigación en este campo.

g). En el campo gravitatorio el trabajo que habría que desarrollar para vencer la gravitación y llevar el astro considerado hasta el infinito, se llama energía potencial. La suma de la energía cinética y de la potencial es constante en todo el movimiento, según el principio de la conservación de la energía.

Suponiendo trazado por el planeta, según la dirección del movimiento, un segmento de recta de longitud igual al producto de la masa del planeta por la velocidad de que está animado en un instante, producto que se denomina cantidad de movimiento del planeta, resulta que el área del triángulo cuyo vértice es el centro del sol y cuya base es la cantidad de movimiento del planeta es una constante. La ley de Newton, considerando un planeta y el sol conduce, pues, a las leyes de Kepler generalizadas. Estas leyes se verifican muy aproximadamente a causa de que las masas de los planetas son muy pequeñas respecto de la masa solar; pero no son rigurosas.

Para prever con exactitud la posición de un planeta a largo plazo, es necesario estudiar su movimiento no sólo bajo la influencia del sol sino bajo la de otros planetas. La aceleración de que está animado cada planeta es la suma geométrica de las aceleraciones debidas no sólo a la acción solar sino también a las atracciones de los otros planetas. El sol, a su vez, está solicitado por todos los planetas y tendrá a cada instante, una aceleración que es la resultante de todas las aceleraciones debidas a las acciones planetarias.

Para referir los movimientos planetarios a tres planos que pasen por el centro del sol, es necesario aplicar a todos los cuerpos del sistema solar una aceleración igual y opuesta a la del sol. Se debe, pues, agregar a la aceleración resultante de todas las acciones atractivas que actúan sobre cada uno de los planetas, una aceleración ficticia igual y opuesta a la que anima al sol, para definir el movimiento relativo del planeta.

Planteado así el problema, se expresa la aceleración total de cada planeta mediante una suma geométrica de muchos términos, el primero de los cuales se refiere a la acción solar y los otros a las acciones planetarias y a la resultante de les acciones planetarias sobre el sol multiplicada por la relación de la masa del planeta a le del sol, estimada en sentido contrario.

h). Se pueden hacer tantas teorías de la luna fundadas en la ley newtoniana, como sistemas coordenados fijos o movibles se puedan idear; pero no todas conducen a resultados utilizables en el cálculo de las tablas lunares debido a la mayor o menor convergencia que se obtenga con unas o con otras en las aproximaciones sucesivas.

Las primeras tablas que se hicieron de la luna tomaban de la teoría la forma matemática de las desigualdades y de la observación el valor de los coeficientes. La primera teoría completa de los movimientos de la luna, fundada sobre la ley de gravitación, se debió a Demoisseau. Laplace expuso una teoría fundada sobre ecuaciones deducidas de las del movimiento mediante una transformación en la cual el radio vector está reemplazado por el inverso do su proyección sobre la eclíptica y la latitud por su tangente, y en donde la longitud de la luna ha sido tomada como variable independiente y el tiempo como función de esta variable. Estas fórmulas, en las que sólo se tiene en cuenta la acción perturbadora del sol, han servido de base a muchas teorías de la luna en que algunos investigadores han cambiado la variable independiente: longitud, por la anomalía excéntrica.

Las dificultades que ha presentado el problema en lo que respecta a la poca convergencia de las series ha sido el motivo por el cual los más ilustres matemáticos de todas las épocas y países, se han ocupado del movimiento de la luna, más complejo, desde algunos puntos de vista, que los de los planetas, según se ha visto atrás.

i). Cierto caso ideal referente a una solución periódica puede presentar una desigualdad considerable, y, además, aproximarse al caso del movimiento de la luna. Esta desigualdad tendría un coeficiente también muy próximo de la desigualdad correspondiente al movimiento de la luna. Así será fácil pasar del caso ideal al caso real.

Tal fue la manera como Hill llegó a determinar el coeficiente de la variación de la luna. Las ecuaciones de movimiento, así planteadas por Hill, forman un sistema de cuarto orden y admiten una integral que había sido hallada antes por Jacobi.

j). Las ecuaciones de segundo orden del movimiento relativo de la luna, supuesta nula la inclinación de la órbita y considerando los ejes animados de un movimiento de rotación uniforme, fueron transformadas por Hill por medio de dos variables imaginarias conjugadas. Hill desarrolló las nuevas variables, o, mejor dicho, sus relaciones a cierta exponencial, y las integró por desarrollo en serie siguiendo las potencias crecientes de la relación de la velocidad angular media del sol a la velocidad angular media de la luna con relación al sol. Estos desarrollos resultan referentes a la cuarta potencia de la relación indicada, lo cual los hace muy convergentes. Así fue como Hill halló la desigualdad conocida con el nombre de variación.

El movimiento del nodo y del perigeo, la evección, las desigualdades de orden superior y las que provienen de las acciones planetarias se refieren a artificios de cálculo tan complejos que no pueden ser indicados aquí, ni someramente siquiera. ''

De todos modos se llega en la teoría de la luna a series cuyos términos son de la forma indicada, y cuyos senos y cosenos se refieren a ángulos dependientes de la distancia angular de la luna al sol, de la luna al nodo, de la luna al perigeo, etc., términos que representan las llamadas desigualdades del movimiento.

En los eclipses las distancias angulares de la luna al sol y al nodo afectan sensiblemente los mismos valores, y las desigualdades periódicas que dependen de dichos ángulos, tienen iguales valores y se eliminan, no quedando, en cambio, sino las que provienen de otros argumentos. Además, comparando las observaciones de eclipses convenientemente escogidos se pueden eliminar también las que dependen del perigeo, de la anomalía del sol, etc.

Se comprende por esto, sin dificultad, cuán importante es la observación de los eclipses en lo que respecta a la teoría del movimiento de la luna, para determinar uno de los elementos más importante, como es la longitud media, a fin de lograr, tarde o temprano, fijar el límite de precisión en las determinaciones basadas sobre la ley de la gravitación.

k). De todo lo anterior resulta que la teoría de la luna debe exponerse en dos partes; en la primera debe buscarse cuál sería el movimiento de este astro si no existiesen sino el sol, la tierra y la luna reducidos a puntos materiales; en la segunda se investiga cómo este movimiento puede turbarse por la atracción de los planetas y por influencia del aplastamiento terrestre. El estudio de Garavito, a que nos referimos, trata de la primera parte del problema que ha preocupado a los mayores matemáticos. La segunda era objeto de sus meditaciones cuando le sorprendió la muerte.

La primera parte no es sino un caso particular del problema de los tres cuerpos, cuya dificultad no proviene sino de la magnitud relativamente considerable, de las perturbaciones producidas. La relación de la fuerza perturbatriz a la atracción del cuerpo central es del orden de 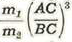siendo m₁, la masa del cuerpo perturbador m₂. ¿ la del cuerpo central y AC y BC las distancias mutuas de los tres cuerpos. Esta relación es producto de dos factores: uno, la relación de las masas, otro, el cubo de la relación de las distancias. En el caso de los planetas el primer factor es muy pequeño y el segundo finito. En el caso de la luna, por el contrario, el primer factor es grande y el segundo es muy pequeño. De esto resulta que el producto de los dos factores es pequeño, sin lo cual el problema no podría resolverse sino por aproximaciones sucesivas, pero mucho menos pequeño que en el caso de los planetas; de suerte que la aproximación es menos lenta. (Poincaré. Mécanique Céleste. Généralités sur la théorie de la lune).

En las dispersas y confusas notículas anteriores hemos tratado de dar una idea al lector de la importancia del problema a que dedicó Garavito largas vigilias y que ha sido objeto de la preocupación de calculistas de primera fuerza. La sola relación histórica de los trabajos dirigidos a la solución del complejo movimiento de la luna constituye parte interesantísima de la Mecánica Celeste de Tisserand. Su reproducción en estas páginas sería suficiente para demostrar la gran importancia que concedemos a los últimos escritos del sabio matemático colombiano, encaminados a complementar la obra de Hansen, de Delaunay, de Hill, de Brown y de Poincaré.

Antes de ahora no había sino tres métodos para construir tablas de la luna: el de Hansen, el de Delaunay y el de Hill-Brown. El de Hansen es el que ha servido para calcular las tablas usuales de exactitud notable. Según Poincaré, si ellas se apartan de las observaciones, las divergencias anotadas no se deben a un detecto del método sino a la omisión de algún término proveniente de la acción de los planetas, o a alguna otra causa desconocida. El éxito de Hansen se ha debido a que buscó directamente los valores numéricos de los coeficientes sin pasar por una expresión algebraica. Su método tiene más de práctico que de solución matemática.

Delaunay hizo todo lo contrario, según Poincaré; todos sus coeficientes se expresan por series en donde figuran las diferentes constantes del movimiento de la luna y cuyos coeficientes son números racionales determinados exactamente.

Brown adoptó una posición intermedie. Sus coeficientes no son ni puramente numéricos, como los de Hansen, ni puramente analíticos como los de Delaunay. Se presentan bajo la forma de series según las potencias de los diversos elementos, excepto la relación de los movimientos medios.

Los coeficientes de estas series están calculados numéricamente, pero estos coeficientes no son ya números racionales: son funciones de la relación de los movimientos medios, que podrían igualmente desarrollarse en series, pero para los cuales se limita el cálculo a determinar el valor numérico. Como el método de Brown, según Poincaré, es mucho más directo que los otros, con él se ha podido avanzar la aproximación mucho más lejos.

El método de Hill, al cual nos hemos referido en las notas i) y j), en combinación con el método de Brown, dio lugar al llamado método de Hill-Brown, que ha servido a Garavito, como a modo de derrotero, para establecer sus ecuaciones según artificios que le son propios.

Como programa de observación para los observatorios de posición, está aún vigente el que indica la determinación de los contactos, tanto internos como externos, en los eclipses de sol, con el rigor con que lo permiten el moderno instrumental y la conservación del tiempo, que ha llegado a ser casi perfecta por medio de péndulos de extraordinaria precisión y con el concurso de señales horarias por radio.

Uno de los elementos canónicos que ha presentado mayores dificultades en su determinación ha sido la longitud media de la luna. La observación de los eclipses de sol desde la más remota antigüedad ha servido, como dijimos, para definir por la observación ese elemento, considerando que cuanto mayor sea el número de datos más perfecta será su determinación.

Grandes han sido los progresos que se han hecho en la observación de los eclipses de sol, y la teoría del movimiento de la luna se ha perfeccionado cada día más. De modo que para la Ciencia continúa siendo de altísimo interés un programa de estudio que confiere igual importancia a la Mecánica celeste a la que se ha dado a los sistemas y elementos de observación.

De la comparación del valor teórico de la longitud medio de la luna con el valor observado de este elemento se podré deducir, tarde o temprano, si hay o no otra causa, distinta de la ley de la gravitación, que puede influir en los movimientos celestes. Esto hablando en los términos de la Mecánica clásica.

Brevemente hemos tratado de exponer en estas notículas, las razones que tenemos para creer que las ecuaciones finales de Garavito para construir unas nuevas tablas de la luna, tienen una importancia capital, y constituyen su mayor contribución a la Ciencia astronómica.