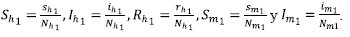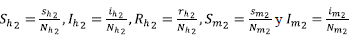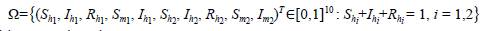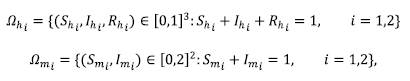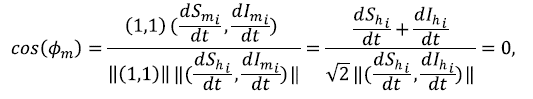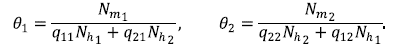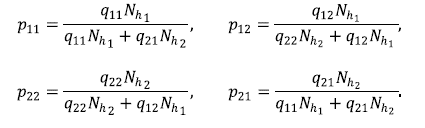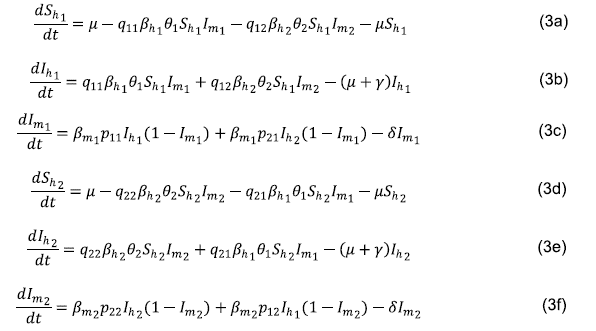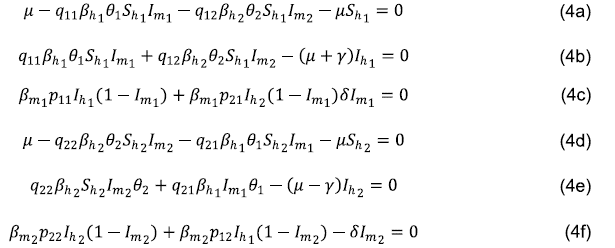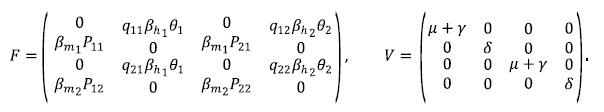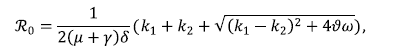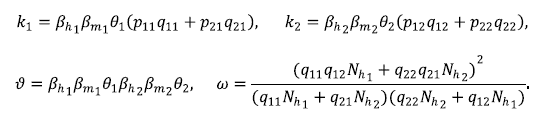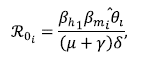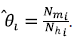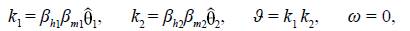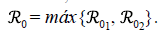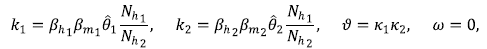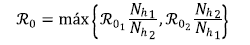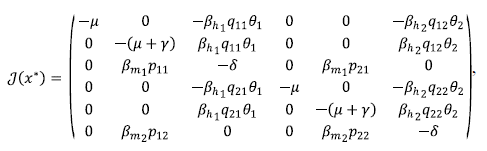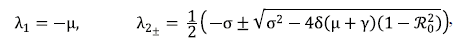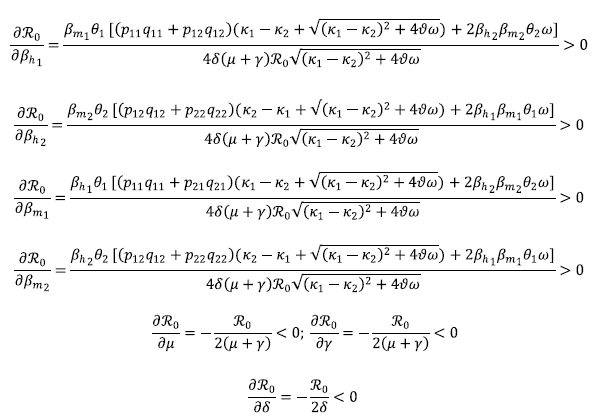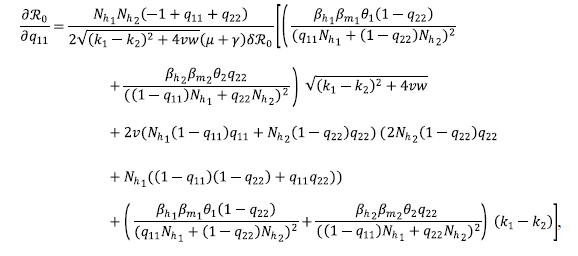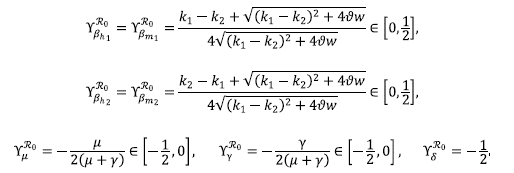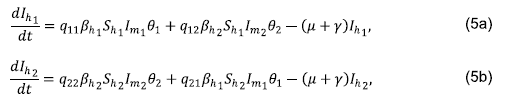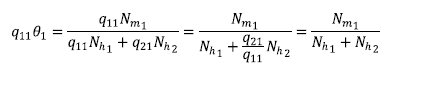Espanhol (pdf)
Artigo em XML
Referências do artigo
Tradução automática
Enviar este artigo por email
Citado por SciELO 
Citado por Google 
Similares em
SciELO 
Similares em Google 
Permalink
Introducción
El dengue, una de las enfermedades transmitidas por vectores más importantes, constituye uno de los mayores problemas de salud pública a nivel mundial. Sus características biológicas implican un alto poder endémico en territorios por debajo de los 1.800 m s.n.m. (Travi & Montoya, 1994). Por su geografía, todo el territorio colombiano es propicio para la aparición del virus causante de la enfermedad y el Valle del Cauca es uno de los departamentos que reporta más casos (Padilla et al., 2012), siendo su capital, ubicada aproximadamente a 1.000 m s.n.m., la que mayor número de casos reporta. Por ello es de vital importancia estudiar la propagación de la enfermedad y, en este sentido, la modelación matemática resulta ser una herramienta útil, ya que permite describir en forma simplificada el comportamiento del fenómeno (Jacquez & Simon, 1993).
El acelerado aumento de las poblaciones urbanas, especialmente en zonas de bajos recursos, ha agudizado las conductas que promueven los problemas de salubridad, entre ellos, el mal almacenamiento del agua (Velandia & Castellanos, 2011). Esta situación puede favorecer el crecimiento de la población de mosquitos y, por ende, la propagación de enfermedades de transmisión indirecta como el dengue, el Zika y el chikungunya (MinSalud, 2017). Ahora bien, las personas prefieren vivir en lugares cercanos a las ciudades para garantizar una cierta distancia de las grandes concentraciones de personas propias del área urbana y evitar, entre otras cosas, el contagio de enfermedades. En consecuencia, deben desplazarse para llegar a sus sitios de estudio, trabajo y atención médica. Es lo que sucede con los municipios aledaños a la ciudad de Santiago de Cali, cuyos habitantes se desplazan frecuentemente hacia la capital, donde permanecen un tiempo (que aquí denominamos tiempo de permanencia, entendido como la fracción de tiempo promedio que una persona pasa en una zona), para luego volver a su lugar de residencia. Estos desplazamientos son factores importantes en la propagación de enfermedades, ya que facilitan que una infección pueda extenderse de una zona a otra.
Lasluisa et al. (2019) presentan un análisis de un modelo metapoblacional en el que consideran que la población de humanos se divide en susceptible de infectarse e infectada, lo cual supone que no se adquiere inmunidad contra la enfermedad. En el caso del dengue se considera la circulación de varias cepas del virus, por lo que las personas pueden infectarse cada que tienen contacto con un mosquito infectado. La simplicidad de este modelo permite un análisis clásico de la situación de manera sencilla. Por otra parte, Barrios et al. (2018) consideran que la población de humanos está dividida en susceptible, expuesta, infectada y recuperada, lo que permite modelar la transmisión del dengue considerando un solo serotipo en circulación; este modelo es más complejo y su análisis resulta más complicado. Nuestro interés se centró únicamente en la circulación de un solo serotipo de dengue porque es un modelo más próximo a la realidad que el de Lasluisa et al. (2019) y más sencillo que el de Barrios et al. (2018), lo que permite que matemáticamente sea más tratable y los resultados sean igual de importantes.
Nuestro objetivo fue diseñar y analizar un modelo metapoblacional de tipo SIR-SI para estudiar la dinámica del dengue en dos zonas independientes con interacción entre sus individuos y hacer un análisis cualitativo clásico bajo los siguientes supuestos: se consideraron dos zonas y se tuvo en cuenta el tiempo de permanencia de las personas en cada una de ellas; las tasas de natalidad, mortalidad y recuperación de los humanos se consideraron las mismas en las dos zonas, así como las tasas de natalidad y mortalidad de los mosquitos; no se consideró el desplazamiento de los mosquitos entre las zonas y se contempló un único serotipo de dengue. Por último, se presentaron y analizaron las simulaciones numéricas de posibles desplazamientos.
Materiales y métodos
Descripción del modelo
El dengue es una infección vírica transmitida por la picadura de mosquitos, principalmente Aedes aegypti. Para la transmisión del dengue, el mosquito debe entrar en contacto con un humano infectado durante la fase de viremia de la enfermedad, lo que lo deja infectado por el resto de su vida. El mosquito infectado entra en contacto con un humano susceptible de infectarse con el virus, quien pasa a ser un humano infectado. La enfermedad no se transmite de persona a persona y sus síntomas más comunes son la fiebre, el dolor de cabeza y de articulaciones y la erupción rojiza en la piel (MinSalud, 2017). Con esto presente, se describió la interacción de humanos y mosquitos infectados con dengue considerando los siguientes supuestos:
Dos zonas en las que las poblaciones de humanos y mosquitos permanecen constantes en el tiempo, las cuales se expresaron como N hi . y N mi , respectivamente, con i tomando el valor 1 para la zona 1 y 2 para la zona 2.
En nuestro modelo se consideró una clasificación de tipo SIR (Castillo & Brauer, 2001) para la población de humanos infectados; los humanos susceptibles de infectarse se representaron como shi, los humanos infectados como i hi . y los recuperados por r hi . en cada zona, planteándose la ecuación N hi . = s hi . + i hi . + r hi .
Para la población de mosquitos se empleó una clasificación de tipo SI, es decir, mosquitos susceptibles, denotados como s mi , e infectados como i mi . para la ecuación N hi . = s mi +i mi .
En cuanto a los desplazamientos de los humanos, se tuvo en cuenta el tiempo de su permanencia en cada zona representado como q ij donde i y j tomaron el valor de 1 o 2. Además, este parámetro de movilidad cumplió con q11 + q12 = 1 y q22 + q21 = 1, considerando que q ij correspondía a la fracción de tiempo promedio que un humano de la zona i pasa en la zona j. Por el contrario, no se consideró el desplazamiento de la población de mosquitos entre las zonas. Debe anotarse que debido a los desplazamientos de los humanos, las poblaciones en las zonas cambiaron según su tiempo de permanencia en ellas, por lo que Σ j 2 = 1 qjiNhj -, donde i = 1, 2 es la población efectiva de humanos en la zona i.
Se supuso que la tasa de natalidad y mortalidad de la población de humanos, µ, y la tasa de recuperación, y, eran iguales en ambas zonas.
Asimismo, se asumió que las tasas de natalidad y mortalidad de los mosquitos, δ, eran iguales en ambas zonas.
Además de y se planteó βi h . como la tasa de contactos efectivos entre un humano susceptible y un mosquito infectado de la zona i y βi m . como la tasa de contactos efectivos entre un mosquito susceptible y un humano infectado en la zona i.
Así, se estableció que las dinámicas de infección en humanos y mosquitos de la zona i tenía dos formas de llevarse a cabo:
Dinámica de infección en humanos
1. Cuando permanecen en su zona y allí tienen contacto con un mosquito infectado, lo cual se representó con la expresión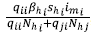 
, donde el numerador representa el número de contactos efectivos de infección y el denominador, la población efectiva de la zona i.
2. Cuando pasan un tiempo en la otra zona y tienen contacto con un mosquito infectado de dicha zona, lo cual se representó con la expresión
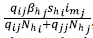, donde el numerador nuevamente corresponde al número de contactos efectivos de infección y el denominador, a la población efectiva de la zona j.
Dinámica de infección en los mosquitos
1. Cuando tienen contacto con los humanos infectados que no se desplazaron de la zona i, lo cual se representó con la expresión
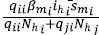, donde el numerador corresponde al número de contactos efectivos de infección y el denominador, a la población efectiva de la zona i.
2. Cuando tienen contacto con los humanos infectados de la zona j que se desplazaron a la zona i, lo cual se representó con la expresión
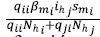, donde el numerador corresponde al número de contactos efectivos de infección y el denominador, a la población efectiva de la zona i.
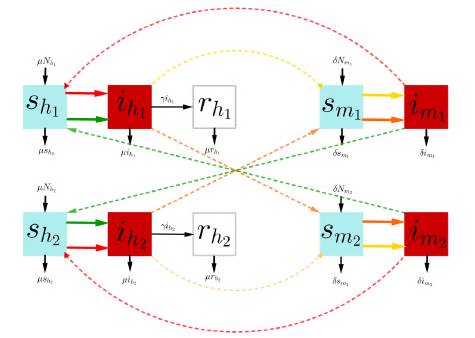
En la figura 1 se presenta esquemáticamente la dinámica de transmisión del dengue aquí expuesta. Las flechas verticales indican la entrada por nacimientos y la salida por muerte de la población en cada etapa, en tanto que las flechas punteadas de color rojo y verde representan cómo se contagia el humano susceptible de las zonas 1 y 2 con un mosquito de las correspondientes zonas 1 y 2. Las flechas punteadas de color amarillo y naranja representan cómo se contagia el mosquito susceptible de las zonas 1 y 2. Por último, las flechas horizontales verdes, rojas y negras indican el cambio de etapa de un humano susceptible a infectado y de infectado a recuperado. Análogamente, las flechas horizontales amarillas y naranjas indican el cambio de etapa de un mosquito susceptible a infectado.
El sistema de ecuaciones que describe el modelo metapoblacional SIR-SI es el siguiente:
Las ecuaciones (1b) y (1g) indican la variación de la población de humanos infectados en el tiempo en las zonas 1 y 2, respectivamente. Los dos primeros términos corresponden al número de nuevas infecciones y el tercer y cuarto términos, a la desaparición por muerte y recuperación de los humanos infectados. Las ecuaciones (1e) y (1j) indican la variación de la población de mosquitos infectados en el tiempo en las zonas 1 y 2, respectivamente. Los dos primeros términos representan el número de nuevas infecciones y el tercer término, la desaparición por muerte de los mosquitos infectados.
Tomando en cuenta la definición del parámetro qij, se tiene que cuando q11 = 1 y q22 = 1, no hay movilidad entre las zonas, es decir, hay dinámicas aisladas. Por el otro lado, si q11 = 0 y q22 = 0, hay intercambio de poblaciones entre las zonas. En los casos en que q11 = 1 y q22 = 0 o q11 = 0 y q22 = 1, se tiene que solo hay movilidad hacia la zona 1 o la zona 2, respectivamente, situación a la que se denominó movilidad completa en una zona.
Para efectos de facilitar los cálculos, se normalizó el modelo mediante la introducción de las siguientes variables que representan la proporción de humanos y mosquitos existentes en cada zona:
Zona 1:
Zona 2:
En consecuencia, el sistema (1) de ecuaciones se convierte en
Para comenzar, es importante saber si el sistema (2) tiene sentido biológico, para lo cual se adoptó el siguiente teorema.
Teorema 1. La región de interés biológico
es positivamente invariante.
Demostración 1. Al considerar la población constante, bastaría demostrar que el cambio del sistema de ecuaciones apunta hacia el interior de la región cuando se toma algún punto de los hiperplanos que limitan la región.
Sean
considerando Ω = Ωh1× Ωm1× Ωh2× Ωm2
Se pasó a demostrar que Ωhi. era positivamente invariante. En efecto Ωhi está limitado por los siguientes hiperplanos:
donde i = 1,2.
Luego se analizó el cambio del sistema de ecuaciones (2) al tomar un punto arbitrario de los hiperplanos que limitan Ωhi.
• Si Shi. = 0, entonces
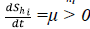. Es decir, Shi.es creciente, lo que indica que, al tomar un punto arbitrario del hiperplano, el cambio es hacia el interior de Ωhi.
• Si Ihi. = 0, entonces
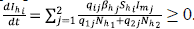. Es decir, Ihi.es creciente, lo que indica que, al tomar un punto arbitrario del hiperplano, el cambio es hacia el interior de Ωhi.
• Si Rhi. = 0, entonces
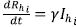. Es decir, Rhi.es creciente, lo que indica que, al tomar un punto arbitrario del hiperplano, el cambio es hacia el interior de Ωhi.
• Si Shi+Ihi.+Rhi. = 1, sea ϕh el ángulo formado entre el vector normal del hiperplano y el vector de cambio del sistema, el cual está dado por la ecuación, indicando que
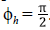. Es decir, que el vector de cambio del sistema está sobre el hiperplano.
Análogamente, se continuó para demostrar que Ωmi era positivamente invariante. Se analizó el cambio del sistema de ecuaciones (2) al tomar un punto arbitrario de los hiperplanos que limitan Ωmi.
• Si Smi. = 0, entonces
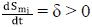. Es decir, Smi. es creciente, lo que indica que, al tomar un punto arbitrario del hiperplano, el cambio apunta hacia el interior de Ωmi.
• Si Imi. = 0, entonces
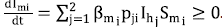. Luego, Imi. es creciente, lo que indica que, al tomar un punto arbitrario del hiperplano, el cambio es hacia el interior de Ωmi.
• Si Imi. + Imi. = 1, sea ϕm el ángulo formado entre el vector normal del hiperplano y el vector de cambio del sistema, el cual está dado por la ecuación:
indicándonos que
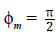, es decir, que el vector de cambio del sistema está sobre el hiperplano.
Además, se denotó el número de mosquitos en la zona i por humanos efectivos en la zona i como θ¡, lo que está dado por:
Asimismo, se denotó como pjj la proporción de humanos efectivos de la zona i en la zona j, lo que está dado por:
Además, el modelo (2) se pudo reducir a seis ecuaciones, ya que se que se consideraron poblaciones constantes, es decir, Rhi = 1 - Shi. y Smi = 1 - Imi para i = 1,2.
Con lo anterior, el modelo metapoblacional (2) se reescribió como:
Puntos de equilibrio
Para analizar el comportamiento cualitativo del sistema se calcularon los puntos de equilibrio, los cuales correspondían a las soluciones del sistema de ecuaciones
Por un lado, mediante inspección se pudo verificar que x* = (1,0,0,1,0,0) era una solución del sistema (4), lo que se denomina punto de equilibrio libre de enfermedad, por el otro, debido a la complejidad del sistema (4) no es posible hallar una forma explícita de otro punto de equilibrio. Más adelante se muestra la existencia y unicidad de este.
Número reproductivo básico (ℛ0)
En los modelos epidemiológicos uno de los principales objetivos es hallar qué condiciones determinan la aparición de una epidemia. Estas condiciones se pueden determinar mediante el ℛ0, número reproductivo básico, que representa el número de nuevas infecciones producidas por un individuo infeccioso introducido en una población libre de enfermedad (Van den Driessche & Watmough, 2002), por lo que es importante determinarlo.
Siguiendo los lineamientos planteados en Van den Driessche & Watmough (2002) y Martcheva (2015) para calcular el ℛ0, es necesario determinar el cuadrado del radio espectral de la matriz de la próxima generación, la cual está dada por FV-1 (Material suplementario 1, https://www.raccefyn.co/index.php/raccefyn/article/view/1604/3231).
Por consiguiente, el ℛ0 del modelo (3) queda dado por
Donde
Se utilizó la misma técnica de Van den Driessche & Watmough (2002) para hallar el número reproductivo básico de la zona i, ℛ0, y se encontró que
donde
Ahora bien, al analizar los casos en que no hay movilidad y se intercambian las poblaciones de las zonas, se obtuvieron los siguientes resultados:
1. Sin movilidad entre las zonas, es decir cuando q11 = 1 y q22 = 1, se obtuvieron las siguientes igualdades:
lo que implica que cuando no hay movilidad, se obtiene
2. Al intercambiar las poblaciones entre las zonas, es decir, q11 = 0 y q22 = 0, se obtuvieron las siguientes igualdades:
lo que implica que al hacer intercambio de poblaciones entre las zonas,
Así, el ℛ0 es dependiente del número de humanos en la zona i por el número de humanos en la zona j.
Estabilidad del equilibrio libre de enfermedad
Se presenta un resultado que establece bajo qué condición la enfermedad tiende a desaparecer, es decir, el punto de equilibrio libre de enfermedad del modelo (3) asintótica-mente estable.
Teorema 2. Si ℛ0 < 1, entonces el punto de equilibrio libre de enfermedad es asintóticamente estable.
Demostración 2. Al calcular el jacobiano del sistema (3) y evaluarlo en x*, se obtiene:
cuyos valores propios están dados por:
donde σ = μ + γ + δ y λ1 y λ2± son de multiplicidad dos, cada uno. Claramente, λ 1 siempre es negativo, ya que μ > 0. Para estudiar λ2± se tomaron dos casos:
1. Si ℛ0 > 1, se tiene que 1 - ℛ20 > 0, por lo tanto,
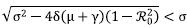, es decir que
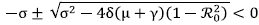. Luego, λ2± < 0.
2. Si ℛ0 > 1, se tiene que 1 - ℛ20 < 0, por lo tanto,
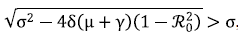, es decir que
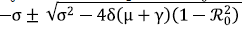no siempre es menor que cero. Luego, λ2+ > 0 y λ2- < 0.
En conclusión, se tiene que cuando ℛ0 < 1, el punto de equilibrio libre de enfermedad es asintóticamente estable.
Dado que el equilibrio libre de enfermedad, x*, es estable cuando ℛ0 < 1, interesa saber cómo se comporta cualitativamente el sistema cuando ℛ0 > 1.
Teorema 3. Suponga que la red de contacto (la red de movilidad entre las zonas) está fuertemente conectada, entonces el sistema (3) tiene un equilibrio endémico único si 1 < ℛ0. Además, este equilibrio es localmente asintóticamente estable.
Como nuestro interés se centró en ver el efecto de la propagación del dengue cuando hay movilidad de las personas entre las zonas, se supuso que siempre había flujo de población humana entre ellas, excluyendo los casos de intercambio de poblaciones entre las zonas o de movilidad hacia una sola zona. Por lo tanto, con base en el teorema (3.1) de Iggidr et al. (2016), y considerando una red de contacto fuertemente conectada, se obtuvo el resultado del teorema 3 (Jacquez & Simon,1993; Smith, 1995) (Material suplementario 2, https://www.raccefyn.co/index.php/raccefyn/article/view/1604/3231).
Análisis de sensibilidad del ℛ0
Al calcular el ℛ0, se observó que estaba en función de nueve parámetros, por lo que se procedió a estudiar la sensibilidad de ℛ0 frente a cada uno de ellos para así analizar cuál era el efecto de los parámetros sobre el 320, determinar cuáles parámetros deberían ser afectados para intentar controlar la dinámica del sistema y lograr cambios cualitativos en el sistema.
Primero, se analizó la derivada parcial de ℛ0 con respecto a cada uno de los parámetros:
Estos cálculos evidenciaron que ℛ0 era una función creciente con respecto a βh1, βh2, βm1, βm2 y decreciente con respecto a μ, γ, δ. Así, para que ℛ0 fuera pequeño debían disminuirse una o varias de las tasas de infección, βh1, βh2, βm1, βm2 o aumentar las tasas de natalidad, mortalidad o recuperación en humanos y mosquitos dada por μ, δ, γ.
Por otra parte,
donde A sería el conjunto con la siguiente propiedad: A = {q11, q22 ∈ (0,1) : q11 + q22-1 = = 0}, es decir, que los puntos que pertenecen a A son un cero de
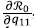, y hay un punto crítico de ℛ0en dirección de q . Sin embargo, no se logró establecer la naturaleza de los puntos que pertenecen a A, por ende, no se pudo ver el efecto que causa el parámetro q11 en ℛ0. Es decir, q no afecta monótonamente a ℛ0.
Procediendo análogamente para
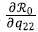se obtuvo el mismo resultado (Material suplementario 1,https://www.raccefyn.co/index.php/raccefyn/article/view/1604/3231).
Segundo, para tener un mejor análisis de la sensibilidad de ℛ0 con respecto a los parámetros del modelo, se utilizó el índice de sensibilidad normalizado presentado en Chitnis et al.
(2008). Este índice de ℛ0 con respecto al parámetro p, se definió como
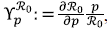, el cual fue útil para medir la sensibilidad o la capacidad de respuesta del ℛ0 a un cambio en su parámetro.
Por ejemplo, para el caso de
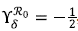, este índice de sensibilidad permite obtener la siguiente relación: cuando la tasa de natalidad de los mosquitos aumenta un 10 %, el ℛ0 disminuye en un
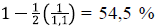(Smith, 1995). Cabe anotar que los índices de sensibilidad en valor absoluto no son mayores que 0,5.
Resultados y discusión
Se presentan las simulaciones numéricas del modelo (3) para estudiar qué tanta influencia tienen los tiempos de permanencia de los humanos en las diferentes zonas en la variación de la población de humanos infectados.
Las gráficas de las simulaciones se obtuvieron mediante la herramienta tecnológica Wolfram Mathematica utilizando los valores estimados de los parámetros del modelo SIR-SI (Sepulveda, 2015) obtenidos al ajustar los casos de dengue reportados a la Secretaría Municipal de Salud de Cali en el 2010, dado que este modelo SIR-SI describe una situación similar a esta (Tabla 1).
Para las simulaciones numéricas se tomaron iguales valores estimados de los parámetros, así como iguales condiciones iniciales en ambas zonas (se tomó una zona con población más alta que la otra para simular un escenario más común, en el que una zona es una ciudad grande y la otra una ciudad cercana, pero más pequeña) (Tablas 1y2). Se consideraron dos situaciones en cada zona para el ℛ0 es decir, ℛ0< 1 o ℛ0> 1, i ∈ {1,2}, para lo cual se varió la probabilidad de infección en los humanos tomando dos valores para βhi, correspondientes a β hi . = 3,52 x 102, 10,58 x 102, y haciendo que ℛ0 tomara valores de 0,5866 y 1,1734, respectivamente.
Dinámica aislada
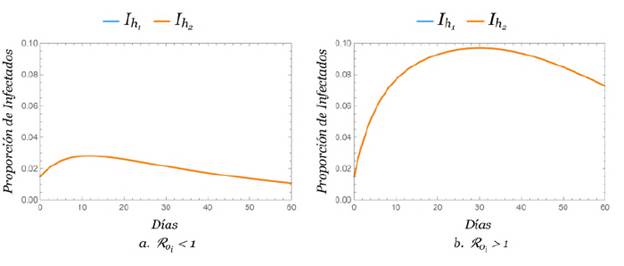
Mostramos cómo se comporta la dinámica del dengue sin incluir la movilidad, es decir, que q 11 = q 22 = 1. La dinámica aislada permitió saber el porcentaje de infectados en cada zona y observar el impacto de la movilidad en cada una de ellas.
Las gráficas en la figura 2 muestran el porcentaje de humanos infectados cuando ℛ0i . < 1 y 1 < ℛ0i . respectivamente. Puede observarse que las gráficas se superponen, lo que se debe a que se trabajó en proporciones con condiciones iniciales iguales; debe aclararse que en poblaciones absolutas estas difieren completamente, cuando está dado ℛ0i para hacer las simulaciones.
En los casos en que ℛ01 < 1, 1 < ℛ02 y 1 < ℛ01, ℛ02 < 1, se obtuvo una combinación de las gráficas presentadas en la figura 2.
Intercambio de poblaciones entre las zonas
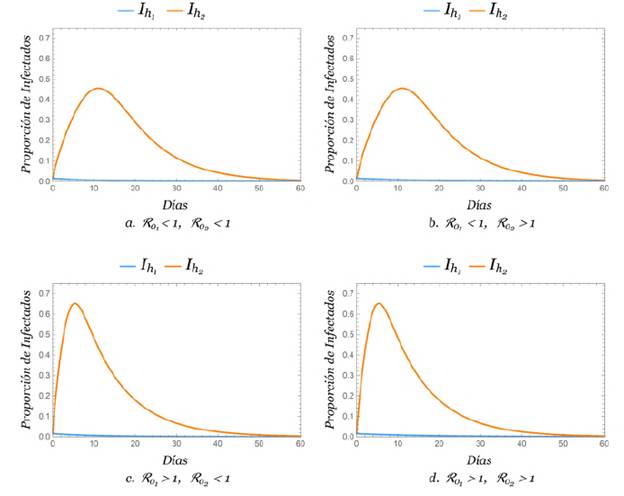
Se evidenció el efecto del cambio de zona de la población completa de humanos, es decir que q11 = q22 = 0. Los resultados fueron dos parejas de gráficas equivalentes, es decir, que cualitativamente se comportan de igual manera (Figura 3), con la proporción de humanos infectados de las zonas 1 y 2 en las zonas 2 y 1, respectivamente.
En este escenario se pudo empezar a notar que la movilidad afectó fuertemente a la población de humanos de la zona 2, ya que al hacer el intercambio de población de humanos, la densidad de mosquitos, es decir, el número de mosquitos por humano en la zona 1, fue mucho mayor, con el consecuente aumento de la probabilidad de infección en esa zona y un mayor riesgo para la población de humanos de la zona 2. Además, la infección de humanos de la zona 2 fue más alta en la situación en que ℛ01 > 1.
Movilidad entre las zonas
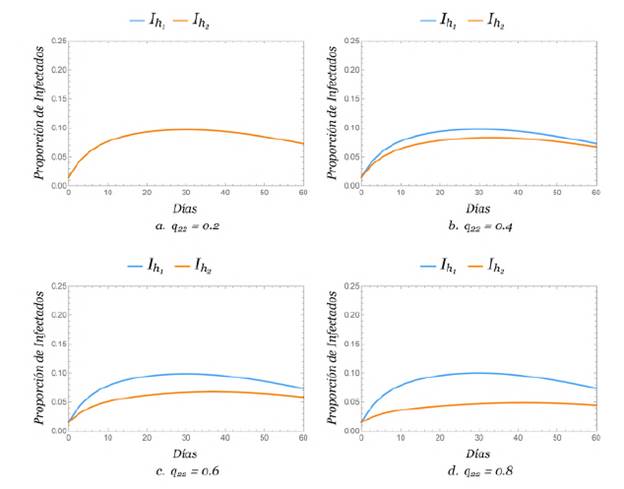
Se evidenció el efecto de la movilidad en la propagación del dengue tomando un valor para q y viendo el efecto que causaba la variación de q22, es decir, tomando la proporción de tiempo de permanencia de los humanos de la zona 1 como q = 0,8,0,6,0,4 y 0,2, y considerando la proporción de tiempo de permanencia de los humanos en la zona 2 como q22 = 0,8,0,6,0,4 y 0,2. Además, se consideró que ℛ0 > 1.
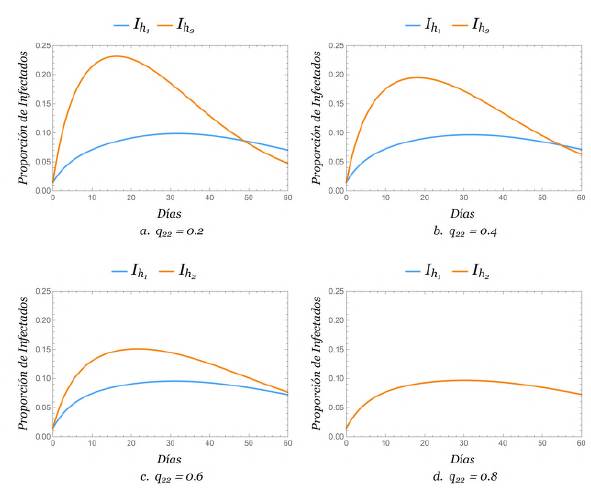
En todos los escenarios se encontró que al aumentar la movilidad de la zona 2 hacia la zona 1, el porcentaje de humanos infectados de la zona 2 aumentaba, en tanto que el porcentaje de infectados de la zona 1 relativamente seguía siendo el mismo. Se plantearon los casos en los que q 11 = 0,8 y q 11 = 0,2, respectivamente, los cuales se observan en las gráficas de las figuras 4y5.
Esto nos lleva a concluir que la movilidad afectó fuertemente a la población de la zona pequeña, es decir, la zona 2. Además, cuando q11 + q22 = 1, las figuras 4a y5d se superpusieron debido a las condiciones iniciales consideradas, lo que sugiere que las ecuaciones de humanos infectados de la zona 1 y la zona 2 fueron proporcionalmente iguales.
En efecto,
como se tiene que
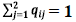con i = 1,2, para el primer término de la ecuación (5a) se puede notar que
Procediendo análogamente para los factores q
12
θ
2, q
22
θ
2 y q
21
θ
1, se obtuvo que q
11
θ
1 = q
21
θ
1 y q
22
θ
2 =
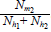
Por último, en las simulaciones numéricas se observó que cuando ℛ01 < 1 y ℛ02 > 1 se obtuvo que ℛ0 < 1, y cuando ℛ01 > 1 y ℛ02 < 1, se obtuvo > 1. Luego 320 estuvo directamente relacionado con el valor de ℛ0.
Conclusiones
En este estudio se propone un modelo metapoblacional de tipo SIR-SI que representa la dinámica de transmisión del dengue en dos zonas conectadas por el tiempo de permanencia de los humanos en ellas.
Se hizo el análisis cualitativo al modelo mediante el cálculo de los puntos de equilibrio y se estudiaron las condiciones en que se logró su estabilidad. El primero, es decir, el libre de enfermedad, se encontró trivial en la inspección, en tanto que, para el segundo, el endémico, no fue posible establecer una expresión analítica, por lo que se procedió a demostrar mediante los lineamientos expuestos en Iggidr et al. (2016) que este punto existía y era único.
También se calculó el número reproductivo básico asociado a nuestro modelo para concluir que si ℛ0< 1, el punto de equilibrio libre de enfermedad era asintóticamente estable, es decir, la enfermedad tendía a desaparecer. Además, se comprobó que si ℛ0 > 1, el punto de equilibrio endémico era asintóticamente estable, es decir, la enfermedad persistía en el tiempo. A continuación se procedió a analizar la sensibilidad de ℛ0 con respecto a los parámetros del modelo. Así, primero, mediante las derivadas parciales de ℛ0 con respecto a cada uno de los parámetros, se obtuvo ℛ0 en función de un solo parámetro y se concluyó que esta era una función que crecía a medida que β
h1
, β
h2
, β
m1
, β
m2
aumentaban y decrecía al aumentar μ, γ, δ. Luego, utilizando el índice de sensibilidad normalizado se tomó como ejemplo
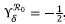, con lo cual se evidenció que cuando δ aumentaba en un 10 %, el ℛ0 disminuía en un 54,5 %. Además, se evidenció que los valores de los índices de sensibilidad en valor absoluto no eran mayores que 0,5.
En las simulaciones numéricas, después de analizar varios escenarios, se pudo concluir que la movilidad afectó fuertemente la zona más pequeña, la zona 2, debido a que con la movilidad, la proporción de mosquitos en la zona 1 resultaba ser mucho más alta, aumentando la probabilidad de infección en los humanos de la zona 2 cuando pasaban tiempo en la zona 1. Por último, con los valores de los parámetros y las condiciones iniciales consideradas en las simulaciones se observó una relación directa de ℛ0 con ℛ01.
Debe enfatizarse que, con base en el modelamiento y los resultados de este estudio, se pueden diseñar estrategias para la reducción de infectados por el virus del dengue mediante la introducción de controles que tengan en cuenta que la movilidad y el tiempo de permanencia de los humanos en las zonas es una característica fundamental en la propagación de la enfermedad. Debe hacerse, además, un análisis de costo-beneficio de las estrategias para la ejecución efectiva de una política de control que logre disminuir el número de infectados por el virus del dengue y reducir sus costos.
