Factor de pérdida global en estructuras de acero con amortiguadores viscoelásticos mediante ecuaciones de estado

Global loss factor in steel structures with viscoelastic dampers through state equations

Jhon Jairo Gil-Peláez¹, Luis Suarez²

¹Ph.D. Civil Engineering Universidad Santo Tomás. Bucaramanga, Colombia jhon_gil@hotmail.com
²Ph.D. Engineering Mechanics University of Puerto Rico. Mayaguez, Puerto Rico luis.suarez3@upr.edu

RESUMEN

En este trabajo se presenta un método basado en el uso de valores propios complejos para determinar los factores de pérdida globales y las frecuencias naturales equivalentes en un pórtico de acero con amortiguadores viscoelásticos en las barras de arrastramiento. Los valores propios complejos se obtienen de resolver el problema de valor propio asociado con las ecuaciones de movimiento escritas como ecuaciones de estado de primer orden. Un estudio utilizando modelos tridimensionales de elementos finitos desarrollados en el programa ABAQUS incluyendo variaciones con la frecuencia de los materiales también se hizo. Las estimaciones de los factores de pérdidas globales se lograron a partir de un análisis de los pórticos sometidos a una carga armónica en régimen mediante el método de la potencia media. El estudio permite comprobar la eficacia de la técnica sobre el nivel de amortiguación adicional que puede ser logrado.

PALABRAS CLAVE: Amortiguadores viscoelásticos, materiales viscoelásticos, disipación de energía, factor de pérdida.

ABSTRACT

In this work, is presented a method based on use complex eigenvalues to determine factors of overall loss and equivalent natural frequencies in a steel frame with viscoelastic dampers in the bracing bars. The complex eigenvalues are obtained to solve the eigenvalue problem associated with the equations of motion written as state equations of first order. A study using three-dimensional finite element models developed in ABAQUS program including variations with frequency of materials was also made. The estimations at the global loss factors was achieved from an analysis of the frames subjected to a harmonic load in regime using the half power method. The study allows to check the effectiveness of the technique on the level of additional damping can be achieved.

KEYWORDS: Viscoelastic dampers, viscoelastic materials, energy dissipation, loss factor.

1. INTRODUCCIÓN

Los materiales viscoelásticos, debido a sus características de amortiguamiento, son muy usados en ingeniería aeroespacial y mecánica para controlar las vibraciones en estructuras y máquinas. Los materiales viscoelásticos son aquellos, que cuando son sometidos a una deformación, una parte de este trabajo se almacena y puede ser recuperado como energía elástica de deformación mientras que la otra parte se disipa sin deformaciones inelásticas [1]. El amortiguamiento viscoelástico se observa en muchos polímeros como la goma. El comportamiento dinámico de un material viscoelástico se puede determinar mediante dos módulos de cortante, el módulo de almacenamiento G' y el módulo de pérdida G''. Estos módulos son funciones de la frecuencia, la temperatura y algunas veces de la deformación por cortante. Algunos modelos utilizados para representar este comportamiento se pueden consultar en Flugge [2] y Lewandowski & Chorazyc-zewski [3], Una medida del amortiguamiento que es capaz de proveer un material se puede obtener considerando su capacidad de disipar energía bajo cargas cíclicas. La razón entre la energía disipada a la energía almacenada en un ciclo multiplicada por 1/2n se conoce como "factor de pérdida" n y es un índice de la efectividad de un tratamiento de amortiguamiento. Este factor n puede ser expresado en términos de los módulos de almacenamiento y de pérdida como n = G''/G' [4] y se puede obtener experimentalmente, o de gráficas provistas por el fabricante del material, o de gráficas disponibles en la literatura especializada, como Nashif, et al. [5] y Sun & Lu [6] . Luca Ghiringhellia & Terraneob, [7] desarrollaron una metodología experimental / predictiva para determinar el comportamiento en frecuencia del módulo complejo de materiales viscoelásticos. Modelos de elementos finitos y una aplicación inversa de la técnica de energía de deformación modal se utilizaron para obtener las curvas del módulo de almacenamiento y factor de pérdida de material viscoelástico.

Los materiales viscoelásticos se han usado en ingeniería civil en amortiguadores viscoelásticos para reducir las oscilaciones inducidas por viento. En las últimas décadas también se han aplicado para mitigar la respuesta a cargas sísmicas Kara-vasilis et al. [8], Kim et al. [9] , Chang & Lin [10] , Chang, et al. [11], Aiken, et al. [12] y Lobo, et al. [13]. Algunas aplicaciones en ingeniería civil de amortiguadores viscoelásticos se presentan en Constantin, et al., [14]. Cuando se usan materiales viscoelásticos en edificios, se instalan en forma de láminas pequeñas que se colocan entre dos placas de acero unidas a los elementos estructurales por medio de barras de arrastramiento. La primera aplicación de este tipo de disipador aparece en las torres gemelas del World Trade Center en 1969, donde se emplearon alrededor de 10 000 amortiguadores [15] .

Mahmoodi y Keel [16] presentaron expresiones para calcular las propiedades de los amortiguadores viscoelásticos y los resultados obtenidos al estudiar 10 amortiguadores. Xu et al. [17] presentaron un método de análisis de optimización sintética de estructuras con amortiguadores viscoelásticos, para determinar los parámetros óptimos y la localización de los amortiguadores. Bilbao et al. [18] describieron y validaron dos métodos eficientes para modelar el amortiguamiento en estructuras con amortiguadores viscoelásticos: el método de la energía modal y el método basado en energías disipadas. Una metodología para modelar sistemas y estructuras con amortiguadores viscoelásticos se propone en [19]. Saidi et al. [20] utilizaron amortiguadores viscoelás-ticos para reducir las excesivas vibraciones en pisos. Moliner et al. [21] expusieron un estudio sobre la capacidad de absorción de energía de amortiguadores viscoelásticos para reducir las vibraciones de las vigas simplemente apoyadas

de un puente de ferrocarril de alta velocidad. Ri-jnen et al. [22] estudiaron diferentes formas de introducir amortiguamiento pasivo a través de materiales viscoelásticos en una caja de aluminio. Gil y Suárez [23] , [24] trabajaron el amortiguamiento de estructuras en acero mediante amortiguadores viscoelásticos y mostraron la variación del factor de pérdida con respecto al parámetro de cortante. Otros autores como Lu et al. [25] y Chang et al. [26] mostraron que la respuesta de edificios a terremotos puede ser reducida significativamente por el gran incremento en el amortiguamiento estructural que proveen los amortiguadores viscoelásticos. Min et al. [27] estudiaron un pórtico de 5 pisos construido a escala completa con amortiguadores viscoelásticos y sometido a cargas armónicas. Lewandowski & Pawlak [28] realizaron el análisis dinámico de un pórtico con amortiguadores viscoelásticos, para lo cual utilizaron modelos reológicos fraccionales. Pawlak & Lewandowski [29] hicieron el análisis dinámico de una estructura con amortiguadores viscoelás-ticos y presentaron un método para determinar las características dinámicas de las estructuras. Bergman y Hanson [30] presentaron un método para diseñar amortiguadores viscoelásticos.

En este trabajo se propone modelar con elementos finitos y con el programa ABAQUS una estructura de acero con un amortiguador viscoelástico. El objetivo es proponer un método relativamente sencillo que se pueda usar para obtener estimaciones precisas de los factores de pérdida globales para distintos modos, como también las frecuencias naturales que se obtienen al colocar amortiguadores viscoelásticos en pórticos de edificios. Esta técnica no es novedosa y ha sido implementada en numerosos edificios reales. Sin embargo, el estudio que se hizo en esta investigación usando modelos de elementos finitos tridimensionales que incluyen las variaciones con la frecuencia de los materiales y el cálculo de los factores de pérdida globales a partir de un análisis de los pórticos sometidos a una carga armónica en régimen no ha sido reportado en la literatura. Este estudio permite comprobar la efectividad de esta técnica en cuanto al nivel de amortiguamiento adicional que se puede lograr. Más importante aún, permite comprobar la precisión del método simple propuesto para obtener los factores de pérdida globales. El método se basa en usar los autovalores complejos que se obtienen al resolver el problema de autovalores asociado a las ecuaciones de movimiento escritas como ecuaciones de estado de primer orden.

2. DETERMINACIÓN DE LOS FACTORES DE PÉRDIDA GLOBALES DE ESTRUCTURAS CON AMORTIGUADORES VISCOELÁSTICOS

Para hallar los factores de pérdida modales se podría generar una matriz de amortiguamiento para toda la estructura, escribir las ecuaciones de movimiento tradicionales de segundo orden como ecuaciones de estado (de primer orden), resolver el problema de autovalores asociado a estas últimas ecuaciones, calcular los autovalores complejos y con ellos definir razones de amortiguamiento equivalentes. Este procedimiento se explica y se implementa en un programa de MATLAB en una sección posterior, pero limitado a estructuras modeladas como edificios de corte. Desafortunadamente, hasta el presente y hasta donde los autores conocen, ninguno de los programas comerciales disponibles en el mercado tiene implementado el método antes descrito. Aquellos programas que sí permiten definir una matriz de amortiguamiento global [C] (por ej., ABAQUS, SAP2000), usan integración en el tiempo para resolver las ecuaciones de movimiento que tienen una matriz de amortiguamiento arbitraria, o sea no desacoplan el sistema de ecuaciones diferenciales. Esto es todo lo que necesita si lo que se busca es obtener la respuesta en el tiempo a cargas dinámicas. Sin embargo, para esta investigación lo que se busca es establecer la efectividad de un amortiguador viscoelástico, no comparando respuestas sino hallando los factores de pérdida globales que el amortiguador introduce en los modos más bajos.

Por lo tanto, dado que se va a usar el programa ABAQUS para modelar estructuras con amortiguadores viscoelásticos, los factores de pérdida globales se deben obtener usando un procedimiento indirecto. Hay básicamente dos métodos simples que permiten cuantificar el amortiguamiento en una estructura mediante un ensayo experimental: ellos son: el "método de la media potencia" y el "método del decremento logarítmico". Si bien, como se mencionó, estos métodos se basan en datos obtenidos de experimentos físicos, mediante ABAQUS se van a simular numéricamente los ensayos.

3. DETERMINACIÓN DE LAS FRECUENCIAS NATURALES Y DEL FACTOR DE PÉRDIDA

Un método muy usado para obtener las frecuencias naturales y el factor de pérdida de una viga, consiste en realizar un análisis de vibración forzada para una excitación armónica, en un rango de frecuencias que capture los modos de vibración de interés del sistema, con el fin de poder obtener la amplitud del desplazamiento vertical versus la frecuencia de la fuerza aplicada para un punto de la viga. La frecuencia natural amortiguada roj y el factor de pérdida modal del sistema n para un determinado modo "j" se deducen aproximadamente de la curva de respuesta. La curva presenta una amplitud máxima en cada frecuencia natural. Las frecuencias roa y rob por debajo y por arriba de una frecuencia natural en la cual la amplitud de la respuesta es √2/2 veces la amplitud de la frecuencia de resonancia se conocen como "puntos de media potencia". Estas frecuencias se muestran en la Fig. 1. El factor de pérdida modal η_j. (1) se puede calcular aproximadamente usando el método de la media potencia, como la razón de la diferencia de las frecuencias ω_b y ω_a a la frecuencia natural amortiguada:

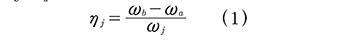
Debe tenerse presente que para sistemas de múltiples grados de libertad el método de la media potencia es aproximado, debido a que se supone que a la amplitud en resonancia solo contribuye el modo resonante. Esta es una suposición bastante precisa para los modos más bajos y para estructuras de edificios regulares. Para los modos más altos o para estructuras especiales, la suposición puede no producir buenos resultados.

4. ANÁLISIS DE UN PÓRTICO PLANO CON EXCITACIÓN ARMÓNICA Y UN AMORTIGUADOR VISCOELÁSTICO

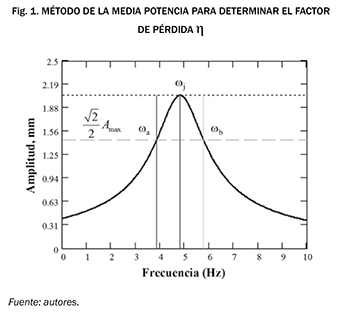
Una manera de utilizar un material viscoelástico para disipar energía en una estructura consiste en colocar el material viscoelástico entre dos placas elásticas como se muestra en la Fig. 2 . Cuando las dos placas elásticas experimentan un desplazamiento relativo longitudinal entre ellas se produce una deformación por cortante en el material viscoelástico. Esta deformación se puede aprovechar como un mecanismo de disipación de energía colocando el dispositivo en la estructura.

4.1 Fuerza provista por un amortiguador viscoelástico

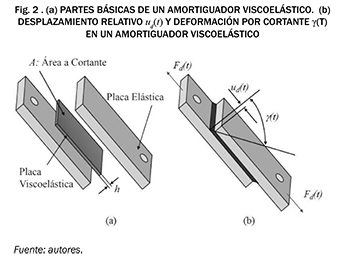
Cuando un amortiguador viscoelástico se somete a una carga sinusoidal con una frecuencia ω, la deformación por cortante γ(t) y el esfuerzo cortante τ(t) en el material viscoelástico lineal varían con la misma frecuencia ω, pero en general fuera de fase [4], De este modo, para su formulación se pueden utilizar las siguientes expresiones (2) y (3):

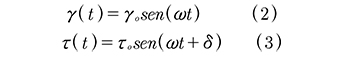
donde γ_o y τ_o representan los máximos valores de la deformación y el esfuerzo por cortante respectivamente. El parámetro δ es un ángulo de fase asociado al amortiguamiento. Para una de formación γ o dada, τ_o y δ son funciones de ω, muy especialmente en los materiales viscoelásticos. Desarrollando el seno de (3), utilizando (2) y la derivada de γ(t) respecto al tiempo se puede escribir el esfuerzo cortante τ(t) de la forma (4):

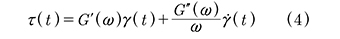
donde los parámetros: 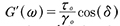y 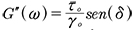se definen como el módulo de almacenamiento a cortante y el módulo de pérdida a cortante del material viscoelástico respectivamente.

Si para un amortiguador como el que se muestra en la Fig. 2 se expresa la deformación por cortante γ(t) del material viscoelástico en términos del desplazamiento longitudinal u_d(t), la fuerza F_d(t) en el amortiguador se puede escribir como (5):

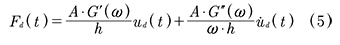
donde A es el área a cortante y h el espesor del material viscoelástico.

Por conveniencia (5) puede escribirse de la forma (6):

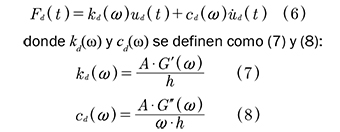
Debe destacarse que (6) es estrictamente válida para un movimiento armónico a una frecuencia ω.

4.2 Ecuación de movimiento de un pórtico plano con un amortiguador viscoelástico

A continuación se deriva la ecuación de movimiento para un pórtico plano modelado como un sistema de un grado de libertad y con un amortiguador viscoelástico en su diagonal. Se considera que el pórtico se comporta como un edificio de corte. La Fig. 3 (a) muestra el modelo usado. En este modelo k representa la rigidez lateral de las columnas, m la masa, c_d y k_d son las propiedades del amortiguador definidas por las ecuaciones (7) y (8), respectivamente, 0 es el ángulo que forma el amortiguador con una línea horizontal, F(t) la fuerza armónica actuando sobre la masa, F(t) la fuerza en el amortiguador y V(t) la fuerza cortante en cada columna.

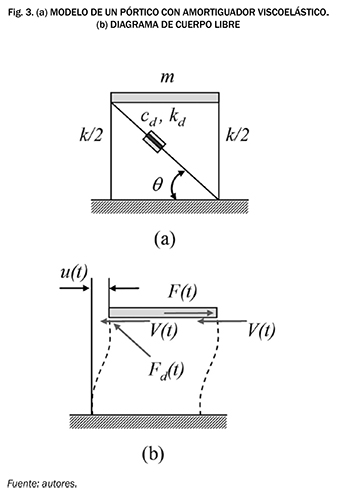
Aplicando la segunda ley de Newton al diagrama de cuerpo libre que se muestra en la Fig. 3 (b), teniendo en cuenta que la fuerza cortante en cada columna es v( t) = 1/2 ku(t), donde 1/2k y u(t) son la rigidez y el desplazamiento lateral de una columna respectivamente, se obtiene (9):

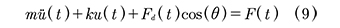
La fuerza F_d(t) se puede expresar en términos del desplazamiento axial u(t) y de la velocidad del amortiguador utilizando (6). A su vez, es sencillo demostrar que el desplazamiento u(t) se puede relacionar con u(t) como U_d (t) = u(t)cos(θ). Teniendo en cuenta lo anterior, (9) se puede escribir (10):

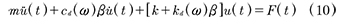
Donde β = cos²(θ). Esta ecuación tiene la misma forma que la de un sistema de un grado de libertad con amortiguamiento viscoso si se fija el valor de ω.

El análisis anterior se puede extender a un pórtico de varios pisos para generar las ecuaciones de movimiento, las cuales se suelen representar en forma matricial (11):

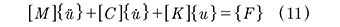
Donde [M], [C] y [K] son las matrices de masa, de amortiguamiento y de rigidez de la estructura respectivamente y {F} se conoce como el vector de fuerzas externas. A manera de ejemplo se muestra la representación matricial para un pórtico de dos pisos de la Fig. 4;

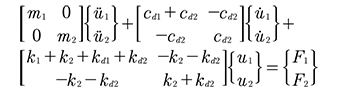
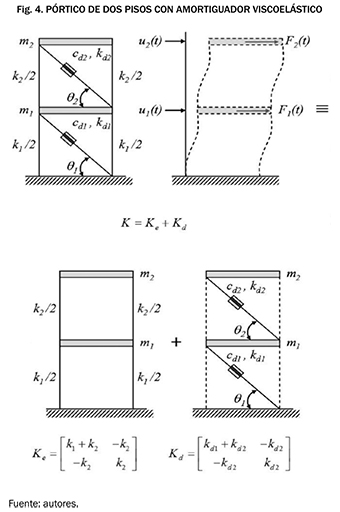
Obsérvese que la matriz de rigidez [K] obtenida en este modelo es la suma de dos matrices, [K]= [K_e]+ [K_d], donde [K_e] es la matriz asociada a la rigidez del pórtico sin los amortiguadores y [K_d] representa la contribución a la rigidez lateral de los amortiguadores viscoelásticos.

5. ECUACIONES DE MOVIMIENTO EN EL ESPACIO DE ESTADO

La respuesta del modelo presentado en la sección anterior se puede calcular resolviendo ecuaciones diferenciales desacopladas y combinando las soluciones a través de modos de vibración mediante el uso de las llamadas "ecuaciones de estado" [31]. Usando este concepto es posible encontrar unas razones de amortiguamiento modal y frecuencias naturales equivalentes. A continuación se presenta un resumen de los conceptos teóricos involucrados.

5.1 Vibraciones libres de sistemas dinámicos generales

La ecuación de movimiento de un sistema dinámico en vibraciones libres tiene la forma (12):

[M]{q } + [C]{ q } + [K]{ q } = {0 } (12)

donde {q} es el vector con n desplazamientos en función del tiempo, [M] es la matriz de masa, [C] y [K] son las matrices de amortiguamiento y de rigidez respectivamente.

Para resolver el problema sin integrar paso a paso el sistema completo de ecuaciones se puede transformar (12) al llamado "espacio de estado". Para esto se despeja de (12) el vector de aceleraciones y se agrega una identidad de la forma (13) y (14):

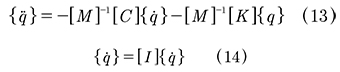
Con los dos vectores en el lado derecho de (13) se puede definir un vector {z} de dimensión N=2n, llamado "vector de estado". Este vector {z} tiene la forma (15):

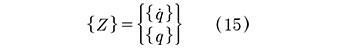
Si además se define una matriz [A] como (16):

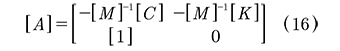
se pueden escribir las ecuaciones (13) y (14) como un conjunto de ecuaciones diferenciales de primer orden, (17) llamadas "ecuaciones de estado":

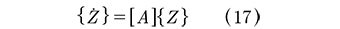
Para resolver (17) se supone una solución de la forma (18):

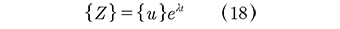
donde {u} y X son un vector de coeficientes y una constante respectivamente, ambos desconocidos. Después de reemplazar esta solución en (17) y simplificar e^λt se obtiene el siguiente problema de autovalores (19):

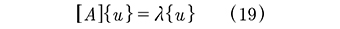
a partir del cual es posible obtener {u} y X. Los N autovalores y autovectores son, en general, cantidades complejas, aunque en algunos casos pueden ser reales. Cuando son cantidades complejas aparecen en pares complejos conjugados. Los autovectores {u}_j con su correspondiente autovalor m permiten formar un conjunto de soluciones de (18) de la forma:

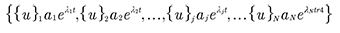
La solución general de (18) se puede obtener como una combinación lineal de cada una de estas soluciones, de la la forma (20):

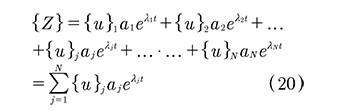
Si se define una matriz [U] cuyas columnas son los autovectores, (20) se puede escribir como (21):

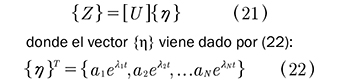
Para hallar las constantes a. se evalúa la expresión (21) en t=0:

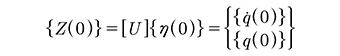
de la cual se puede obtener {h(0)} (o sea las constantes a_j) con la expresión (23):

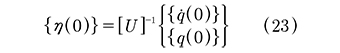
Con este resultado se completa la solución de las ecuaciones de movimiento (12).

5.2 Razones de amortiguamiento modal y frecuencias naturales equivalentes

Puede demostrarse que es posible obtener razones de amortiguamiento modal y frecuencias naturales equivalentes para sistemas estructurales generales a partir de las partes real e imaginaria de λ_j=λ_Rj+iλ_Ij, La frecuencia natural equivalente ω_j (24) es el módulo del autovalor complejo λ_j:

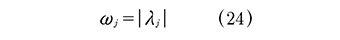
La razón de amortiguamiento modal equivalente ξ_J se obtiene como (25):

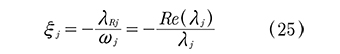
Con el valor encontrado para la razón de amortiguamiento equivalente ξ_J se puede calcular un factor de pérdida equivalente η utilizando la relación η_j =2ξ_j.

6. IMPLEMENTACIÓN DEL MODELO EN MATLAB

Para encontrar los amortiguamientos modales y las frecuencias naturales equivalentes de un pórtico de varios pisos con amortiguadores viscoelásticos en su diagonal se implementó un programa en MATLAB utilizando las ecuaciones de estado. El objetivo era comparar estos valores obtenidos con un modelo simple con los calculados mediante un modelo sofisticado generado con el programa ABAQUS. En primera instancia, el programa encuentra las frecuencias naturales de la estructura sin amortiguamiento. Estas frecuencias naturales se obtienen resolviendo el problema de autovalores de la estructura sin amortiguamiento (26):

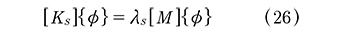
Una vez se obtiene los autovalores λ_sj, las frecuencias naturales ω_sj se obtienen como (27):

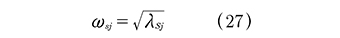
El resultado anterior se utiliza para definir las propiedades del amortiguador viscoelástico, k_d(ω) y C(ω) , reemplazando ra por la frecuencia natural ω_Sj del modo en consideración. Esta aproximaciónes aceptable debido a que la presencia de los amortiguadores no cambia significativamente los valores de las frecuencias naturales de la estructura no amortiguada. Una vez se han definido las propiedades de los amortiguadores, se pueden encontrar las matrices de rigidez [K] y de amortiguamiento [C] de la estructura amortiguada. Para calcular la razón de amortiguamiento modal y la frecuencia natural equivalente el programa utiliza los autovalores complejos del problema de autovalores asociado a las ecuaciones de estado. Para esto se define la matriz [A] de acuerdo con (16), se resuelve (19) y después se utilizan las ecuaciones (24) y (25).

7. MODELAMIENTO DE PÓRTICOS CON AMORTIGUADORES VISCOELÁSTICOS

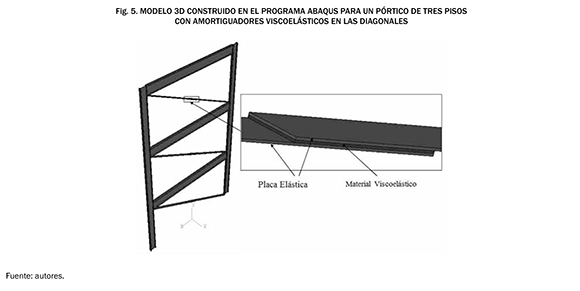
Tres pórticos de uno, dos y tres pisos se modelaron utilizando elementos finitos con el programa ABAQUS. Las columnas son perfiles de acero W 14X22 con una longitud de 2743 m (9 pies). Se consideró un área aferente en planta de 3 m por 6 m y las cargas muertas y vivas actuando en los pisos de 5 kPa y 2 kPa, respectivamente. En el cómputo de la masa propia del pórtico también se consideró la masa asociada a las cargas muertas y a un 25% de las cargas vivas. Esta masa se distribuyó de manera uniforme en el volumen de la viga. Para las vigas se utilizó un perfil W 18X35. El amortiguador considerado tenía un material viscoelástico con una longitud de 508 mm, un ancho de 154.2 mm y un espesor de 6.35 mm. La forma del amortiguador que se utilizó se muestra en la Fig. 2. Las propiedades del material viscoelástico se obtuvieron de un Nomograma de un polímero viscoelástico 3M TM 110. Las diagonales y las vigas se consideraron como cuerpos rígidos, para lo cual se utilizó un módulo de elasticidad mucho mayor que el del acero. En los modelos elaborados se representaron tanto las capas elásticas como las viscoelásticas con elementos finitos tridimensionales tipo C3D20, siendo estos elementos sólidos (tipo "ladrillo") de orden cuadrático con 20 nodos. El modelo desarrollado en ABAQUS para el pórtico de tres pisos se muestra en la Fig. 5.

Se hizo un análisis de vibración forzada en el programa ABAQUS para una excitación armónica, en un rango de frecuencias que capturó los primeros tres modos de vibración del pórtico. De este análisis se obtuvo la amplitud del desplazamiento horizontal de un punto de la columna como función de la frecuencia de la fuerza aplicada para posteriormente aplicar el método de la media potencia explicado en la Sección 3 y determinar así la frecuencia natural amortiguada y el factor de pérdida asociado a cada modo. Los resultados para el primer modo de los tres pórticos se muestran en la Tabla I. Los tres pórticos también fueron analizados usando el programa desarrollado en MATLAB. Los resultados obtenidos para el primer modo de vibración de los tres pórticos se resumen en la Tabla I.

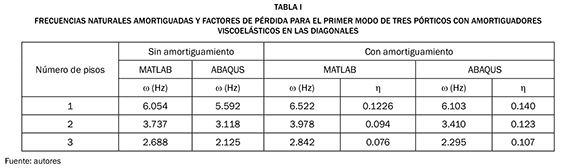
Para propósitos de comparación se incluyen en la Tabla I los resultados obtenidos con ABAQUS. En esta tabla se puede notar que la frecuencia natural del pórtico sin amortiguadores no cambia significativamente con respecto a la del pórtico con amortiguadores, en promedio, la frecuencia natural del pórtico con amortiguador es un 6.6% mayor con respecto al pórtico sin amortiguadores, lo cual valida el hecho de utilizar la frecuencia natural de la estructura sin amortiguamiento para definir las propiedades del material viscoelástico. El factor de pérdida calculado con un modelo de elementos finitos tridimensional para los pórticos de uno, dos y tres pisos difieren en 14.2%, 30.9% y 40.8%, respectivamente, con respecto al valor obtenido con el modelo simple implementado en Matlab. También se puede notar cómo disminuye el valor del factor de pérdida a medida que aumenta el número de pisos. Esta disminución se puede comprender si se analizan los autovectores asociados al primer modo de cada uno de los tres pórticos. Si se normaliza el máximo desplazamiento modal a 1, se puede notar que el desplazamiento relativo del pórtico de un piso es mayor que aquellos entre los pisos de los pórticos de 2 y 3 pisos. Puesto que la deformación por cortante en el amortiguador depende del desplazamiento relativo entre pisos, se tiene una menor deformación por cortante cuando el número de pisos aumenta, y por consiguiente una menor disipación de energía. Los valores en la Tabla I muestran que el modelo simple de MATLAB se puede usar para determinar el factor de amortiguamiento sin tener que recurrir a un programa sofisticado como ABAQUS. El modelo simple descrito en la Sección 4.2 junto con el procedimiento de la Sección 5 permite ahorrar el tiempo asociado a la generación del modelo de elementos finitos en ABAQUS, hacer el análisis en frecuencia y aplicar el método de la media potencia.

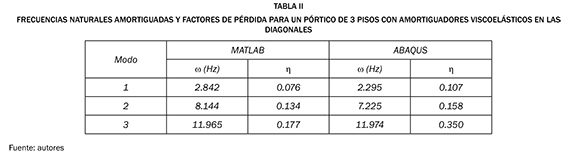
Ahora, si se examinan los tres modos de vibración para el pórtico de 3 pisos, se puede notar que los desplazamientos relativos entre pisos son menores para el primer modo y por lo tanto se espera un menor factor de pérdida en este modo, siendo mayor en el tercer modo. Como verificación de la afirmación anterior se muestran en la Tabla II los resultados que se encontraron para los factores de pérdida del pórtico de 3 pisos.

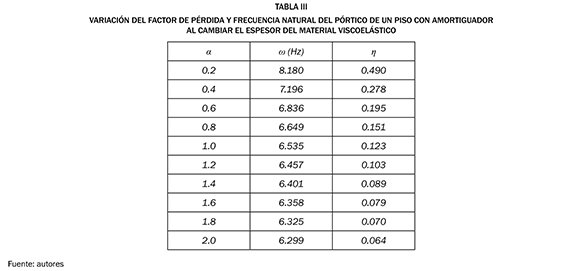
Revisando (5) se puede observar que una manera de incrementar la contribución del amortiguador viscoelástico a la disipación de energía consiste en aumentar el coeficiente C_d(ω) = A.G''(ω)/(ω.h), lo cual se puede conseguir aumentando el área a cortante A o disminuyendo el espesor h del material viscoelástico. Sin embargo, es necesario tener en cuenta que disminuir el espesor h conlleva una mayor deformación por cortante y si esta no se controla se podría superar un valor límite que cause la falla del material viscoelástico. La Tabla III muestra los resultados que se obtienen al variar el espesor del material viscoelástico en el pórtico de un piso. Para especificar el espesor del material viscoelástico se define un factor α entre 0.2 y 2, tal que h=αh₀, donde h₀=6.35 mm. Se observa que la frecuencia natural y el factor de pérdida disminuyen cuando se aumenta el espesor del material viscoelástico.

CONCLUSIONES

Un procedimiento simple que utiliza las ecuaciones de estado asociadas a las ecuaciones de movimiento de un edificio de corte con amortiguadores viscoelásticos en las diagonales de arriostramiento se puede usar para encontrar los factores de pérdida modales y las frecuencias naturales amortiguadas. La frecuencia natural del pórtico con amortiguador es en promedio un 6.6% mayor con respecto a la frecuencia del pórtico sin amortiguadores, lo cual valida el hecho de utilizar la frecuencia natural de la estructura sin amortiguamiento para definir las propiedades del material viscoelástico. Los resultados muestran que el factor de pérdida calculado con un modelo de elementos finitos tridimensional para los pórticos de uno, dos y tres pisos difieren en 14.2%, 30.9% y 40.8%, respectivamente, con respecto al valor obtenido con el modelo simple implementado en Matlab.

REFERENCIAS

[1] R. M. Christensen, "Theory of Viscoelasticity: an Introduction," New York: Academic Press, 1971.         [ Links ]

[2] W. Flugge, "Viscoelasticity," Waltham, Massachusetts: Blaisdell Publishing Company, 1967.         [ Links ]

[3] R. Lewandowski y B. Chorazyczewski, "Identification of the parameters of the Kelvin-Voigt and the Maxwell fractional models, used to modeling of viscoelastic dampers," Computers & Structures , vol. 88, pp. 1-17, 2010.         [ Links ]

[4] T. T. Soong y G. F. Dargush, "Passive Energy Dissipation Systems in Structural Engineering," Chichester: John Wiley & Sons, 1997.         [ Links ]

[5] A. D. Nashif, D. I. G. Jones y J. Henderson, "Vibration Damping," New York: John Wiley & Sons, 1985.         [ Links ]

[6] C. T. Sun y Y P Lu, "Vibration Damping of Structural Elements," Englewood Cliffs, New Jersey: Prentice Hall PRT, 1995.         [ Links ]

[7] G. Luca Ghiringhellia y M. Terraneob, "Analytically driven experimental characterisation of damping inviscoelastic materials," Aerospace Science and Technology, vol. 40, pp. 75-85, 2015.         [ Links ]

[8] T. Karavasilis, T. Blakeborough y M. Williams, "Development of nonlinear analytical model and seismic analyses of a steel frame with self-centering devices and viscoelastic dampers," Computers and Structures, vol. 89, p. 1232-1240, 2011.         [ Links ]

[9] J. Kim, J. Ryu and L. Chung, "Seismic performance of structures connected by viscoelastic dampers," Engineering Structures, vol. 28, pp. 183-195, 2006.         [ Links ]

[10] K. C. Chang y Y. Y. Lin, "Seismic Response of Full-Scale Structure with Added Viscoelastic Dampers," vol. 130, n° 4, pp. 600-608, 2004.         [ Links ]

[11] K. C. Chang, T. T. Soong, S.-T. Oh y M. Lai, "Seismic Behavior of Steel Frame with Added Viscoelastic Dampers," vol. 121, n° 10, pp. 1418-1426, 1995.         [ Links ]

[12] I. D. Aiken, J. M. Kelly y P Mahmoodi, "The Application of Viscoelastic Dampers to Seismically Resistant Stru-ture," vol. 3, pp. 459-468, 1990.         [ Links ]

[13] R. F Lobo, J. M. Bracci, K. L. Shen, A. M. Reinhorn y T. T. Soong, "Inelastic Response of R/C Structures with Viscoelastic Braces," vol. 9, n° 3, pp. 419-446, 1993.         [ Links ]

[14] C. Constantin, A. Filiatrault y V. Bertero, "Principles of passive supplemental damping and seismic isolation," Pavia: IUSS Press, 2006.         [ Links ]

[15] P. Mahmoodi, L. E. Robertson, M. Yontar, C. Moy y L. Feld, "Performance of Viscoelastic Dampers in World Trade-Center Towers. Dynamics of Structures," pp. 632-644, August 1987        [ Links ]

[16] P. Mahmoodi y C. J. Keel, "Performance of Viscoelastic Structural Dampers for the Columbia Center Building, Building motion in wind," pp. 83-106, 1986.         [ Links ]

[17] Z.-D. Xu, H.-T. Zhao y A.-Q. Li, "Optimal analysis and experimental study on structures with viscoelastic dampers," Journal of Sound and Vibration, vol. 273, pp. 607-618, 2004.         [ Links ]

[18] A. Bilbao, R. Aviles, J. Agirrebeitia y G. Ajuria, "Proportional damping approximation for structures with added viscoelastic dampers," Finite Elements in Analysis and Design, vol. 42, pp. 492-502, 2006.         [ Links ]

[19] A. de Lima, D. Rade and F Le'poreNeto, "An efficient modeling methodology of structural systems containing viscoelastic dampers based on frequency response function substructuring," Mechanical Systems and Signal Processing, vol. 23, p. 1272-1281, 2009.         [ Links ]

[20] I. Saidi, E. F Gad, J. L. Wilson y N. Haritos, "Development of passive viscoelastic damper to attenuate excessive floor vibrations," Engineering Structures, vol. 33, pp. 3317-3328, 2011.         [ Links ]

[21] E. Moliner, P Museros y M. Martinez-Rodrigo, "Retrofit of existing railway bridges of short to medium spans for high-speed traffic using viscoelastic dampers," Engineering Structures, vol. 40, pp. 519-528, 2012.         [ Links ]

[22] M. Rijnen, F Pasteuning, R. Fey, G. vanSchothorst y H. Nijmeijer, "A numerical and experimental study on viscoelastic damping of a 3D structure," Journal of Sound and Vibration, vol. 349, pp. 80-98, 2015.         [ Links ]

[23] J. J. Gil Peláez, "Disertación. Amortiguamiento en estructuras de acero utilizando materiales viscoelás-ticos," Mayaguez: Departamento de Ingeniería Civil y Agrimensura, UPRM, 2008.         [ Links ]

[24] J. J. Gil Peláez y L. E. Suarez, "Amortiguamiento de estructuras de acero mediente tratamiento a cortante," Iteckne, vol. 7, n° 1, pp. 34-45, 2010.         [ Links ]

[25] L.-Y Lu, G.-L. Lin y M.-H. Shih, "An experimental study on a generalized Maxwell model for nonlinear viscoelastic dampers used in seismic isolation," Engineering Structures, vol. 34, p. 111-123, 2012.         [ Links ]

[26] K. C. Chang, S. J. Chen y M. L. Lai, "Inelastic Behavior of Steel Frames with Added Viscoelastic Dampers," vol. 122, n° 10, pp. 1178-1186, 1996.         [ Links ]

[27] K.-W. Min, J. Kim y S.-H. Lee, "Vibration Test of 5-Storey Steel Frame with Viscoelastic Dampers," vol. 26, pp. 831-839, 2004.         [ Links ]

[28] R. Lewandowski and Z. Pawlak, "Dynamic analysis of frames with viscoelastic dampers modelled by rheological models with fractional derivatives," Journal of Soundand Vibration, vol. 330, pp. 923-936, 2011.         [ Links ]

[29] Z. Pawlak y R. Lewandowski, "The continuation method for the eigenvalue problem of structures with viscoelastic dampers," Computers and Structures, vol. 125, p. 53-61, 2013.         [ Links ]

[30] D. M. Bergman y R. D. Hanson, "Viscoelastic Mechanical Damping Devices Tested at Real Eathquake Displacements," vol. 9, n° 3, pp. 389-417, 1993.         [ Links ]

[31] L. Meirovitch, "Elements of Vibration Analysis," New York: McGraw-Hill, 1986.         [ Links ]

[32] F. Hejazi, A. Zabihi y M. Jaafar, "Development of elas-to-plastic viscous damper finite element model for reinforced concrete frames," Soil Dynamics and Earthquake Engineering, vol. 65, pp. 284-293, 2014.         [ Links ]