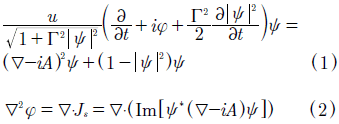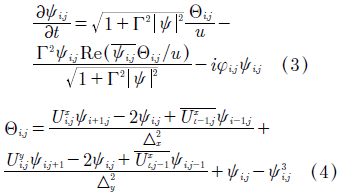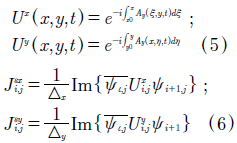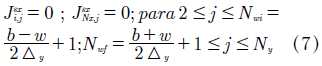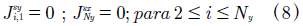Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Iteckne
versão impressa ISSN 1692-1798
Iteckne vol.14 no.1 Bucaramanga jan./jun. 2017
Transport phenomena in superconductors: kinematic vortex
Fenómeno de transporte en superconductores: vórtices cinemáticos
José José Barba-Ortega1, Ely Dannier Valbuena-Niño2, Miryam Rincón-Joya3
1 Ph.D. Física. Universidad Nacional de Colombia, Bogotá D.C., Colombia. Foundation of Researchers in Science and Technology of Materials, Colombia. jjbarbao@unal.edu.co.
2 Ph.D.(c) Ingeniería Mecánica. Universidad Politécnica de Madrid, Madrid, España. Universidad Industrial de Santander, Bucaramanga, Colombia. Foundation of Researchers in Science and Technology of Materials, Colombia. deydannv@gmail.com.
3 Ph.D. Física. Universidad Nacional de Colombia. Bogotá D.C., Colombia. mrinconj@unal.edu.co.
ABSTRACT
The phenomenological Ginzburg-Landau theory (FGLT) is a strong tool in understanding the physics of the superconductors at low critical temperature in the presence of applied fields and currents. The FGLT is derived from the second order transition theory of Landau based on critical phenomena, leading to a set of two coupled nonlinear Ginzburg-Landau equations (GLE). In this paper, we solve the GLE to a superconducting slab of Al in presence of applied current j at zero magnetic fields. We have analysed the appearance and subsequent annihilation of vortex-anti-vortex pairs in the middle of the sample at an external applied current j1. A small resistivity is found in Meissner range in the current-voltage curve at j ≤ j1.
KEYWORDS: Ginzburg-Landau, Superconductors, Vortex.
RESUMEN
La teoría fenomenológica Ginzburg-Landau (FGLT) es una fuerte herramienta para entender la física de los materiales superconductores a temperaturas críticas en presencia de campos magnéticos y corrientes aplicadas. El FGLT se deriva de la teoría del segundo orden de transición de Landau basada en un fenómeno crítico, llevada a un conjunto de dos ecuaciones no lineales Ginzburg-Landau (GLE). En el presente trabajo, resolvimos las ecuaciones de GLE en una placa superconductora en presencia de una corriente aplicada a campo magnético cero. Analizamos la aparición y aniquilación de pares vórtice y anti-vórtice en la mitad de la placa con una corriente externa aplicada. Una pequeña resistividad es encontrada en el rango Meissner en la curva de corriente-voltaje.
PALABRAS CLAVE: Ginzburg-Landau, Superconductor, Vórtice.
1. INTRODUCTION
The dynamics of vortices in low critical temperature superconductors have many technological, scientific and industrial applications from the point of view of electrical current transport. The magnetic flux penetrates in a superconductor type II in the form of quantized fluxoids called vortices Abrikosov-Shubnikov, these vortices locally destroy the superconducting state and it is only possible when the Lorentz force, due to applied currents, exceed the anchoring forces of the structural defects, magnetic or topological of the material, leading to Joule heat appearance. The control and/ or manipulation of vortex state is very important to limit the loss of heat in the electronic elements and lead to the manufacture of new devices such as rectifiers of currents, logic elements, photon detectors, fabrication of SQUIDs, etc. [1]-[10].
In the absence of magnetic field is possible the existence of pairs vortex-anti-vortex, known as kinematic vortices, they appear as a result of the magnetic field originated by the applied currents (Ampere's law). The theory most commonly used to analyse the physical of the conventional superconductivity or superconductivity at low critical temperature Tc, is the phenomenological theory Ginzburg-Landau (FGLT). The FGLT is based on the second order phase transition of Landau and describes the superconducting state through the pseudo-function of complex wave ψ(r,t), whose magnitude squared represents the density of superconducting electrons and of the vector potential A(r,t), related to the magnetic induction as B =  ×A . A large amount of experimental y theoretical work has been done since the discovery of this state of matter in 1911.
×A . A large amount of experimental y theoretical work has been done since the discovery of this state of matter in 1911.
One of the first applications in engineering was in nano-structures superconductor-magneto in centres production of anchoring in superconducting films, in these structures a critical current superconductor increases due to periodicity of anchor centres [11]-[12].
M. V. Milosevic, et al., studied the effect of electric current in superconductor-magneto hybrid microstructures, he found that a critical current increases with the inclusion of such defects and superconductivity persists to larger currents applied [13]. Berdiyorov G., et al., analysed the temperature dependency of an applied current to zero field on the vortex dynamics in a thin plate of Nb, in this study the state of flux-flow is dynamically stable at low temperatures, their results are in good qualitative agreement with experiments. The effect of the functionality of surface about the electronic transport properties in Ti3C2-MXene was analysed, finding that the design of materials based on MXene may be useful in energy storage where the electronic transport can be maximized. Using three-dimensional simulations the authors showed that vortices Abrikosov captured in a Josephson cavity in the presence of external current generate vortices-anti-vortex pairs, the frequency of tunnelling of these pairs increase in a band of determinate frequencies [14]-[15].
The study of vortex-anti-vortex pair generation in the absence of applied magnetic field has been extensively studied by Berdiyorov, et al., he showed that an external current can produce these pairs in a thin plate, commonly called vortices kinematic [16]. P. Sanchez-Lotero, et al., analysed the flux-flow resistivity in superconducting films of different widths, found an anchoring vortices induced by the superficial superconductivity, this anchoring prevents a movement of the vortices and the appearance of voltage leading to a transition of the mesoscopic to macroscopic regimen [17]. J. Barba-Ortega et al., studied theoretically the dependence of the boundary conditions and the dimensionality on the magnetic response of a low Tc superconductor, he found that a superconducting/ superconducting interface at higher critical temperature Tc increases the superconductor/ normal transition field and enhanced the superficial superconductivity, also he show that the upper and lower fields are independent of the dimensionality of the sample [18]-[19].Golod T., et al., provided a proof of concept of the Abrikosov vortex as a random access memory cell, wherein a vortex is used as an informatics bit, the cells are characterized by an infinity magnetoresistance between states 0 and 1 in a time short of access and an energy extremely low recording. The nonvolatility and the perfect repeatability are inherent to such device, due to the quantized nature of the vortex [20]. In this work we resolved the time dependent Ginzburg-Landau equations in an isotropic type II superconducting slab in presence of an applied electric current at zero magnetic field. For low values of the applied current a small resistivity is found due to metallic contacts where a current is applied. For a certain value of current J1 a pair vortex-anti-vortex is created in the half of the slab and the resistivity increases abruptly. Consequential creations and annihilations of vortices-antivortex pairs are appreciated.
2. THEORETICAL FORMALISM
The Ginzburg-Landau model take account of the superconducting electronic density and of the magnetic response of the material through of the functions ψ and A in the presence of external currents related with the electrostatic potential φ at temperature T = 0 through (1) e (2):
Js is the supercurrent density in units of J0 = CΦ0/8π2λ2ξ, where λ is the penetration length and ξ the coherence length, ψ in units of ψ0 = (α /β)1/2, and β are two phenomenological parameters characteristic of the material, length in units of ξ, time t in units of, potential vector A in units of Hc2ξ, where Hc2 is the second critical field, scalar potential φ in  /2et units. Γ = 2τEψ0/
/2et units. Γ = 2τEψ0/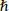 , (τE is the collision inelastic electronic. For τE
, (τE is the collision inelastic electronic. For τE  10ns , so Γ
10ns , so Γ  1000), we choose U = 5.79 [21]-[24].The external electric current is applied in points where ψ = 0 e
1000), we choose U = 5.79 [21]-[24].The external electric current is applied in points where ψ = 0 e 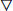 φ = -J (Metallic contacts), in another points, the Neumann boundary conditions were used and J
φ = -J (Metallic contacts), in another points, the Neumann boundary conditions were used and J =
= 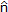 ·(-i
·(-i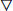 + A)ψ|n = 0 [23]. The studied sample is a superconducting Al slab ((ξ0) = 100nm) [25], of cross section transversal axb in the (x,y) plane. The equations (1) and (2) were numerically solved using the link variable method (Uψ) in a rectangle with Nx × Ny cells, grid size Δx × Δy'Nx = a/Δx e Ny = b/Δy [22].
+ A)ψ|n = 0 [23]. The studied sample is a superconducting Al slab ((ξ0) = 100nm) [25], of cross section transversal axb in the (x,y) plane. The equations (1) and (2) were numerically solved using the link variable method (Uψ) in a rectangle with Nx × Ny cells, grid size Δx × Δy'Nx = a/Δx e Ny = b/Δy [22].
If ψ(xi,yj) = ψij, φ(xi,yj)= φi,j for i = 1, Nx + 1, j = 1, Ny + 1, The GLE can be written as:
Where the new variables of the method (Uψ) and the superconductor currents formed 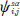 In the axes a = x,y are given by:
In the axes a = x,y are given by:
The conditions of contour out of the metallic contact of width W where the external current is applied for Jsx and ψ are:
Within of metallic contact we have ψi,j = ψNx+1j = 0 for Nwi ≤ j ≤ Nwf.
3. RESULTS AND DISCUSION
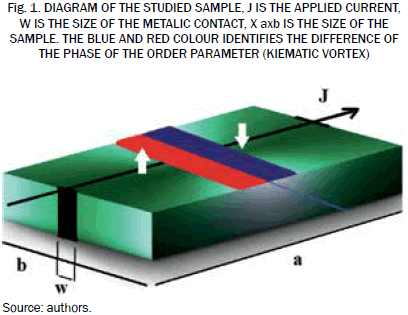
The parameters used in our simulation were: sample size a × b = 12ξ × 8ξ, Δx = Δy = 0.1, ΔJ = 10-3, Δt = 0.001, W = 0.2 parameter Ginzburg-Landau typical for the aluminium is k = 1.0. The initial conditions for the simulation are: Meissner state ψ(x,y,0,t = 0) = 1 and Ji(t = 0) = 0.0 to jf(t) = 6.0 . A very interesting fact in this type of systems is the appearance of vortices in the absence of magnetic field, called kinematic vortices. Physically, these vortices, like Abrikosov vortices, are points in space-time where the psedo-function of superconductor wave or order parameter has a degree equal to zero, and its phase changes a value 2πN around these points, N indicates the vorticity. We showed that these pairs of vortices nucleating in the sides perpendicular to the direction of application of the current at a half point of the slab; subsequently enter annihilating in the centre. In the absence of field, both vortices appear at the same time and annihilate crossing the border simultaneously in the line x = a/2 (Fig. 1). If you apply a magnetic field in the sample the dynamic of kinematic vortexanti-vortex pair change considerably, the points of creation-annihilation of these pairs are determined by distribution of currents in the system [16].
Fig. 2(A) shows the voltage curve V/V0 and the resistivity obtained by the derivative t = 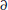 V/
V/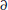 J as a function of applied current J/J0 (window), for mesoscopic regime this resistivity shows that the presence of the superficial barrier allow a little resistivity at low applied currents. Fig. 2(B) shows the voltage as a function of the time and frequency ντ a function of applied current (window). As can be seen, for low values of the applied current, the superconducting material experiences a slight resistance, this can be explained by the resistivity of the metallic contacts where the current is applied (ψ = 0), in these points is zero superconductivity (ohmic material). Increasing the current at a determinate value J1 = 1.76 appears a discontinuity in the resistivity curve (window, Fig. 2(A)) representing the entry of a pair of vortices kinematic in the plate, likewise can to observe the abrupt leap of the voltage as function of time (Fig. 2(B)). In Fig. 3 we have graphically the phase of order parameter Δ
J as a function of applied current J/J0 (window), for mesoscopic regime this resistivity shows that the presence of the superficial barrier allow a little resistivity at low applied currents. Fig. 2(B) shows the voltage as a function of the time and frequency ντ a function of applied current (window). As can be seen, for low values of the applied current, the superconducting material experiences a slight resistance, this can be explained by the resistivity of the metallic contacts where the current is applied (ψ = 0), in these points is zero superconductivity (ohmic material). Increasing the current at a determinate value J1 = 1.76 appears a discontinuity in the resistivity curve (window, Fig. 2(A)) representing the entry of a pair of vortices kinematic in the plate, likewise can to observe the abrupt leap of the voltage as function of time (Fig. 2(B)). In Fig. 3 we have graphically the phase of order parameter Δ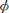 for several applied currents. A circulation of the phase of the order parameter through an enclosed path that has N vortices will be equal to 2πN . In this figure we appreciated that the entry of vortex occurs in the middle part of sample x = a/2 and phase variation goes from red to blue Δ
for several applied currents. A circulation of the phase of the order parameter through an enclosed path that has N vortices will be equal to 2πN . In this figure we appreciated that the entry of vortex occurs in the middle part of sample x = a/2 and phase variation goes from red to blue Δ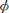 = r and from blue to red Δ
= r and from blue to red Δ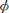 = -π, that is total vorticity Δ
= -π, that is total vorticity Δ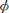 = 0 and N = 0 , then we have a pair vortex-anti-vortex that nucleates by the half of the sample. The pairs of kinematic vortices enter in the sample overcoming the Beam-Livington barrier energy and annihilating in the centre of the material. Of Up to bottom and from left to right the settings of phase are given for currents J = 1.76, 1.82, 1.86, 1.90, 2.18, 2.68, 2.70, 2.76, 3.10, 3.36, in all of them we have pairs vortex-anti-vortex and Δ
= 0 and N = 0 , then we have a pair vortex-anti-vortex that nucleates by the half of the sample. The pairs of kinematic vortices enter in the sample overcoming the Beam-Livington barrier energy and annihilating in the centre of the material. Of Up to bottom and from left to right the settings of phase are given for currents J = 1.76, 1.82, 1.86, 1.90, 2.18, 2.68, 2.70, 2.76, 3.10, 3.36, in all of them we have pairs vortex-anti-vortex and Δ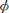 = 0 . Superconductivity is completely destroyed at the points where the electric current is applied, so we cannot have accurate information of the phase changes present.
= 0 . Superconductivity is completely destroyed at the points where the electric current is applied, so we cannot have accurate information of the phase changes present.
4. CONCLUSION
We solved the time dependent Ginzburg-Landau equations to study the appearance and subsequence annihilation of vortices-anti-vortex kinematics pairs in a superconducting slab at zero magnetic field and with a applied external current J. We note that for J < J1 a small resistivity appears due to the presence of metallic contacts, but at J = J1 at a time t1, abrupt jumps in the resistivity of the slab occur due to entrance of pairs vortex-antivortex. Increasing the applied current the superconductivity is destroyed and an ohmic behaviour is observed in the voltage-current curve.
ACKNOWLEDGEMENT
We thank Professor Edson Sardella of the Physics Department of the Universidade Estadual Paulista, Bauru, Brazil, for the helpful discussions.
REFERENCES
[1] J. Van de Vondel, C. C. de Souza, B. Y. Zhu, M. Morelle and V. V. Moshchalkov, "Vortex-Rectification Effects in Films with Periodic Asymmetric Pinning", Phys. Rev. Lett., vol. 94, p. 057003, 2005. [ Links ]
[2] K. Yu, T. W. Heitmann, C. Song, M. P. DeFeo, B. L. T. Plourde, M. B. S. Hesselberth and P. H. Kes, "Asymmetric weak-pinning superconducting channels: Vortex ratchets", Phys. Rev. B, vol. 76, p. 220507, 2007. [ Links ]
[3] K. Yu, M. B. S. Hesselberth, P. H. Kes and B. L. T. Plourde, "Vortex dynamics in superconducting channels with periodic constrictions", Phys. Rev. B, vol 81, p. 184503, 2010. [ Links ]
[4] M. B. Hastings, C. J. O. Reichhardt and C. Reichhardt, "Ratchet Cellular Automata", Phys. Rev. Lett., vol 90, p. 247004, 2003. [ Links ]
[5] T. Puig, E. Rosseel, M. Baert, M. J. V. Bael, V. V. Moshchalkov and Y. Bruynseraede, "Stable vortex configurations in superconducting 2x2 antidot clusters", Appl. Phys. Lett., vol 70, p. 3155, 1997. [ Links ]
[6] G. Karapetrov, V. Yefremenko, G. Mihajlovic, J. E. Pearson, M. Lavarone, V. Novosad and S. D. Bader, "Evidence of vortex jamming in Abrikosov vortex flux flow regime", Phys. Rev. B, vol. 86, p. 054524, 2012. [ Links ]
[7] G. Berdiyorov, K. Harrabi, F. Oktasendra, K. Gasmi, A. I. Mansour, J. P. Maneval and F. M. Peeters, "Dynamics of current-driven phase-slip centers in superconducting strips", Phys. Rev. B, vol. 90, 054506, 2014. [ Links ]
[8] F. Rogeri, R. Zadorosny, P. N. Lisboa-Filho, E. Sardella and W. A. Ortiz, "Magnetic field profile of a mesoscopic SQUID-shaped superconducting film", Supercond. Sci. Technol., vol. 26, p. 075005, 2013. [ Links ]
[9] R. I. Rey, A. R. Álvarez, C. Carballeira, J. Mosqueira, F. Vidal, S. Salem, A. D. Alvarenga, R. Zhang and H. Luo, "Measurements of the superconducting fluctuations in optimally doped BaFe2-xNixAs2 under high magnetic fields: probing the 3D-anisotropic Ginzburg-Landau approach", Supercond. Sci. Technol., vol. 27, p. 07500, 2014. [ Links ]
[10] P. J. Pereira, V. V. Moshchalkov and L. F. Chibotaru, "Efficient solution of 3D Ginzburg-Landau problem for mesoscopic superconductors", J. Phys. Conf. Ser., vol. 490, p. 012220, 2014. [ Links ]
[11] J. I. Martin, "Flux Pinning in a Superconductor by an Array of Submicrometer Magnetic Dots", Phys. Rev. Lett., vol. 79, p. 1929, 1997. [ Links ]
[12] D. J. Morgan and J. B. Ketterson, "Asymmetric Flux Pinning in a Regular Array of Magnetic Dipoles", Phys. Rev. Lett., vol. 80, p. 3614, 1998. [ Links ]
[13] M. V. Milosevic, G. R. Berdiyorov and F. M. Peeters, "Mesoscopic Field and Current Compensator Based on a Hybrid Superconductor-Ferromagnet Structure", Phys. Rev. Lett., vol. 95, p. 147004, 2005. [ Links ]
[14] G. R. Berdiyorov, "Effect of surface functionalization on the electronic transport properties of Ti3C2 MXene", Eurp. Phys. Lett., vol. 111, p. 67002, 2015. [ Links ]
[15] G. R. Berdiyorov, K. Harrabi, J. P. Maneval and F. M. Peeters, "Effect of pinning on the response of superconducting strips to an external pulsed current", Supercond. Sci. Technol, vol. 28, p. 25004, 2015. [ Links ]
[16] G. R. Berdiyorov, M. V. Milosevic, F. M. Peeters and D. Y. Vodolazov, "Kinematic vortex-antivortex lines in strongly driven superconducting stripes", Phys. Rev. B, 79 184506, 2009. [ Links ]
[17] P. Sánchez, J. Albino Aguiar, D. Domínguez, "Behavior of the flux-flow resistivity in mesoscopic superconductors", Physica C, vol. 503, p. 15, 2014. [ Links ]
[18] J. Barba-Ortega, E. Sardella, J. A. Aguiar, "Superconducting boundary conditions for mesoscopic circular samples", Sci. Technol., vol. 24, p. 015001, 2011. [ Links ]
[19] J. Barba-Ortega, E. Sardella, J. A. Aguiar, "Superconducting properties of a parallelepiped mesoscopic superconductor: A comparative study between the 2D and 3D Ginzburg-Landau models", Phys. Lett. A. vol. 379, no. 7, p. 732, 2015. [ Links ]
[20] T. Golod, A. Iovan V. M. Krasnov, "Single Abrikosov vortices as quantized information bits", Nature Communications, vol. 6, p. 8628, 2015. [ Links ]
[21] A. C. Bolech, G. C. Buscaglia, A. López, Connectivity and Superconductivity, in: J. Berger, J. Rubinstein, Ed. Heidelberg, New York: Springer, 2000. [ Links ]
[22] D. Gropp, H. G. Kaper, G. K. Leaf, D. M. Levine, M. Palumbo, V. M. Vinokur, "Numerical simulation of vortex dynamics in type-II superconductors", J. Comput. Phys., Vol. 123, p. 254, 1996. [ Links ]
[23] P. G. de Gennes, "Superconductivity of Metals and Alloys", Ed. New York: Addison-Wesley, 1994, p. 274. [ Links ]
[24] L. Kramer and R. J. Watts-Tobin, "Theory of Dissipative Current-Carrying States in Superconducting Filaments", Phys. Rev. Lett., vol. 40, p. 1041, 1978. [ Links ]
[25] D. S. Golubovic, W. V. Pogosov, M. Morelle and V. V. Moshchalkov, "Influence of the stray field of a magnetic dot on the nucleation of superconductivity in a disk", Europhys. Lett., vol. 65, p. 4, 2004. [ Links ]