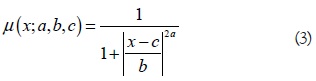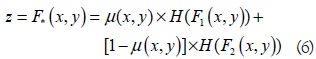Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ingenierías Universidad de Medellín
Print version ISSN 1692-3324On-line version ISSN 2248-4094
Rev. ing. univ. Medellín vol.10 no.19 Medellín July/Dec. 2011
ARTÍCULOS
GENERATION OF COMPLEX NONLINEAR BENCHMARK FUNCTIONS FOR OPTIMIZATION USING FUZZY SETS AND CLASSICAL TEST FUNCTIONS
GENERACIÓN DE FUNCIONES BENCHMARK COMPLEJAS NO LINEALES PARA OPTIMIZACIÓN USANDO CONJUNTOS DIFUSOS Y FUNCIONES DE PRUEBA CLÁSICAS
Eddy Mesa**; Juan David Velásquez***; Patricia Jaramillo****
** Ingeniera Mecánica, Universidad de Antioquia, Colombia, 2006; Miembro del grupo de Optimización Heurística y Algoritmos Bio-Inspirados, Facultad de Minas, Universidad Nacional de Colombia. Dirección de correspondencia: Cra 80 65-223, Bloque M8A, Of. 201. Medellín, Colombia. Tel. +57 +4 425 5350. Correo electrónico: ejmesad@unal.edu.co
*** Autor para correspondencia. Doctor en Ingeniería-Área Sistemas Energéticos, Universidad Nacional de Colombia, sede Medellín, Colombia, 2009; Magíster en Ingeniería de Sistemas, Ingeniero Civil, Profesor Asociado de la Escuela de Sistemas, Facultad de Minas, Universidad Nacional de Colombia, sede Medellín. Miembro del grupo de Optimización Heurística y Algoritmos Bio-Inspirados, Facultad de Minas, Universidad Nacional de Colombia. Dirección de correspondencia: Cra 80 65-223, Bloque M8A, Of. 206. Medellín, Colombia. Tel. +57 +4 425 5370. Correo electrónico: jdvelasq@unal.edu.co
**** Doctora en Planificación y Gestión de Recursos Hidráulicos, Universidad Politécnica de Valencia, Valencia, España. Profesora Asociado de la Escuela de Sistemas, Facultad de Minas, Universidad Nacional de Colombia, sede Medellín. Directora del grupo de Optimización Heurística y Algoritmos Bio-inspirado, Facultad de Minas, Universidad Nacional de Colombia. Dirección de correspondencia: Cra 80 65-223, Bloque M8A, Of. 213. Medellín, Colombia. Tel. +57 +4 425 5343. Correo electrónico: gpjarami@unal.edu.co
Recibido: 28/01/2010
Aceptado: 03/08/2011
ABSTRACT
In this paper, we present a novel methodology to generate complex functions using two-dimensional fuzzy sets as weights for combining classical benchmark functions. These new functions have different characteristics from original ones, but the minimum, borders and geometry characteristics of the functions are still known. Three different combinations of two functions (Rosenbrock and Bukin's F4) are used to exemplify the method and its potential to generate specific test functions to study and improve optimization methods.
Key words: minimization, maximization, fuzzy operators, global optimization, test problems.
RESUMEN
En este artículo se presenta una metodología novedosa para generar funciones complejas usando conjuntos borrosos bidimensionales como pesos para combinar funciones clásicas de prueba. Estas nuevas funciones tienen características diferentes pero el mínimo, los bordes y la geometría de las nuevas funciones se conoce. Tres combinaciones diferentes de dos funciones (Rosenbrock y F4 de Bukin) se utilizan para ejemplificar el método y su potencial como generador de funciones de prueba para estudiar y mejorar métodos de optimización.
Palabras clave: minimización, maximización, operadores difusos, optimización global, problemas de prueba.
INTRODUCTION
Optimization (maximization or minimization) of continuous nonlinear functions is an important problem in sciences, mathematics, engineering and economics, due to many real-world problems would be solved in these terms [1]. However, nonlinear optimization is usually a hard problem; their difficulties are related to the complexity of goal function, constrains, topology of the search region and limitations of the optimization methodology.
Optimization field has several types of problems, e.g. combinatorial optimization, integer optimization, quadratic optimization, and other; and a universal optimizer does not exist. Talking about optimizers, Wolpert and Macready emphasize two points: First, when an optimizer is designed for a specific problem, it works better for the problem than other generic optimizer. Second, there are not harder problems, but there are different types of problems. It means that each type of problem has specific characteristics and it agrees to them an optimizer could have better performance that another one [2]. I.e. For developing and comparing new methods, and for solving real world problems efficiently, we will want benchmark functions with the highest number of characteristics available or the most closed characteristic to the real problem. Moreover, scientific community provides special test to compare methods [3].
There are some well-known test functions [4-7]. They are characterized by their behavior, which is manifested by the features of the generated surface, but regularly these functions are limited to specific characteristics. For example, the Rosenbrock function has its global optimum inside of a narrow valley, while in the Bukin's F4 function the minimum is located inside a canon. The aim of this paper is to present a new methodology for generating or specifying complex test functions to prove and tune heuristic optimization algorithms. To do that, we use fuzzy sets theory to combining well-known to generate new functions.
The paper is organized as follows. In Section 2, we review some aspects of classical test functions. Following, fuzzy set theory is introduced in Section 3. In Section 4, we state the description of the proposed methodology. Next, some examples are presented in Section 5. Finally, we conclude in Section 6.
1. CLASSICAL TEST FUNCTIONS
The use of well-known test functions is a common procedure for testing global optimization algorithms, such that, these functions are standard literature benchmarks [4-7]. Thus, researchers are able to compare their results against other methodologies whose results are validated and accepted by the scientific community. Usually, a set of functions is used to evaluate the behavior of a specific algorithm in different conditions and to determine their robustness.
A classical benchmark is the Rosenbrock's function (Figure 1):
It has a global minimum in f(1,1) = 0. A standard initial point is x0 = 1 and y0 = –1.2. DeJong bounded the function to the interval defined as –2.048 ≤ x ≤ 2.048 to use it in heuristic optimization [8]. And Yao et al. [9] report and extend this function to n dimension using the borders in [–30,30]n, which increase the complexity because it is a bigger search region. Other classical benchmark is the Bukin's F4 function (Figure 2):
Proposed by Bukin [10] with a global minimum in f (0,0) = 0. The standard initial point x0 = 1 and y0 = 1, and there are not borders available.
Test functions are classified in terms of surface's features and the primitive functions used for its construction (or setting-up). Several features are described as following:
• The dimensionality of the functions definition: for a fixed number of dimensions or in a general way.
• The modality or ruggedness: quantity of local optimal (maximum and minimum) points. They are classified in unimodal functions with a global minimum and multimodal with several minimums.
• The homogeneity: the characteristic of the relationship between variables (separable or no separable).
The above features would have a great impact in the behavior of a specific optimization algorithm. For example, it is well known that gradient based methods have poor behavior optimizing functions with a huge number of local optimal points, because they are trapped in a local optimum and they are not able to escape out.
2. FUZZY SETS AND FUZZY OPERATIONS
In classical sets theory, the membership of an element to a set is a binary function returning zero when the element not belongs to the set and one in otherwise. In fuzzy set theory, the discrete set {0, 1} for the range of membership function is changed by the interval [0, 1]. Zero and one still represents the absolute certainty of that element belongs or not belongs to the set. The intermediate values between zero and one represent uncertainty, such that, partial membership is allowed [11].
The generalized bell function is a typical method for specifying the membership function of a fuzzy set [11]:
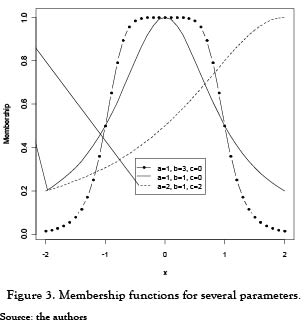
Examples of the generalized bell function with different values for the parameters a, b and c are shown in Figure 3.
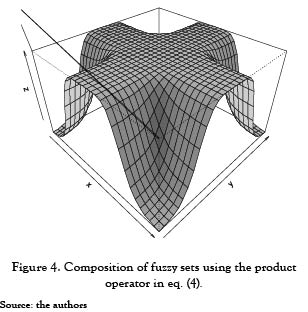
One-dimensional fuzzy sets, as in equation (3), can be extended to the X×Y plane, using a fuzzy set for each axis, and then applying any fuzzy operator. This process is the so-called composition of fuzzy sets e.g. several bi-dimensional fuzzy sets would be obtained using the one-dimensional fuzzy membership functions µ(x; 1, 3, 0) and µ(y; 1, 3, 0) for representing a fuzzy set for each axis, and composite it by means of any fuzzy operator; In Figure 4, we present the fuzzy set obtained using the product operator defined as:
while the two-dimensional fuzzy set presented in Figure 5 is obtained using the minimum operator:
An extensive recompilation of fuzzy operators is presented in [11] and [12].
3. PROPOSED METHODOLOGY
We propose the generation of new test functions by means of a weighted sum of two functions defined by the modeler. Two-dimensional fuzzy membership is restricted to the interval [0, 1], then the operator are used as the weights in the sum of functions. Thus, if F1(x,y) and F2(x,y) are classical benchmark test functions, a new test function would be generated as:
In the previous equation, H(•) is the function F(x,y) scaled to the interval [0, 1]. The main idea of this methodology is to obtain new functions with similar characteristics to a certain problem, with the advantage, over real problem, of knowing function's characteristics like minimums, topology, etc. Also, this methodology provides a large number of functions with different characteristics. So, we can obtain a nearer simulation of the method's performance for a specific sort of problems.
4. EXAMPLES
To demonstrate the proposed methodology, we create three new test function combining Rosenbrock's (see Equation (1)) and Bukin's F4 (see Equation (2)) test functions using the operators described. In the sake of a clear vision of the functions' details, we limited the plots in a range in [–3,3]2.
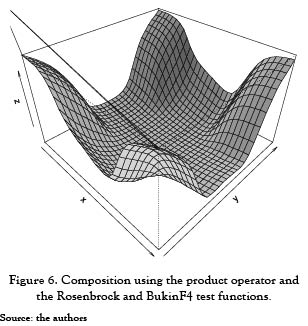
In Figure 6, we present the surface obtained when µ(x,y) is defined as in equation (4); the obtained function shows that the function BukinF4's canon is extended with the features of the Rosenbrock's function, while the edges retain the regularity of the function Bukin F4, but with the softness of the Rosenbrock's function. It would be the first function.
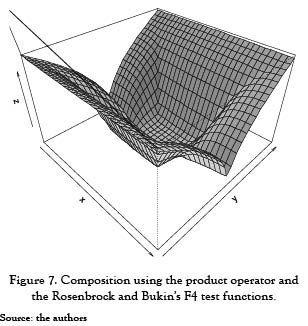
The generated second function is shown in Figure 7. For this, µ(x,y) is defined as in equation (5), as in the previous figure. It still has a combination of both functions that produce a different surface, but reminds the same minimum value: min f (1,1) = f (0,0) = 0.
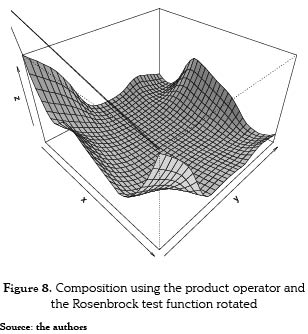
Moreover, complex surfaces may be generated using only one function too. For example, we use a rotated version of the original Rosenbrock's function as F2(x,y) in Eq. (6). Figure 8 presents the obtained surface using only the Rosenbrock function and the product operator. The gradient 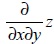 of the generated function is plot in Figure 9. One of the criteria of complexity for optimization problems is the existence of planar regions on the gradient plot, which is evident in the figure.
of the generated function is plot in Figure 9. One of the criteria of complexity for optimization problems is the existence of planar regions on the gradient plot, which is evident in the figure.
5. CONCLUSIONS
In this paper, we present a novel methodology to generate new complex test functions for testing, comparing and tuning global optimization algorithms. Our methodology is based in the combination of two two-dimensional classical test functions using a weighted sum. These weights are generated by means of a two-dimensional fuzzy set. Thus, using only two initial test functions, many complex surfaces can be generated changing the parameters and composition operators used for generating the two-dimensional fuzzy sets. Although several topologies could be generated, the characteristics of the function are still known, so the new function remains a good benchmark.
REFERENCES
[1] P. M. Pardalos, y M. G. C. Resende, ed, ''Handbook of Applied Optimization,'' New York: Oxford University Press, 2002 [ Links ]
[2] W. G. Macready, y D. H. Wolpert, ''What makes an optimization problem hard?,'' Complexity, vol. 5, pp. 40-46, 1996. [ Links ]
[3] S. Das y P. N. Suganthan. ''Problem Definitions and Evaluation Criteria for CEC 2011 Competition on Testing Evolutionary Algorithms on Real World Optimization Problems''. Singapore, 2010. Available: http://web.mysites.ntu.edu.sg/epnsugan/PublicSite/Shared%20Documents/CEC%202011-%20RWP/Tech-Rep.pdf [ Links ]
[4] W. Hock y K. Schittkowski. ''Test Examples for Nonlinear Programming Codes'', Lecture Notes in Economics and Mathematical Systems, vol. 187, Springer 1981. [ Links ]
[5] J.J. Moré, et al. ''Testing Unconstrained Optimization Software'', ACM Transactions on Mathematical Software, vol. 7, no. 1, pp. 17-41, 1981. [ Links ]
[6] I. Bongartz, et al. ''CUTE: Constrained and Unconstrained Testing Environment'', ACM Transactions on Mathematical Software, vol. 21, no. 1, pp. 123-160, 1995. [ Links ]
[7] N. I. M. Gould, et al. ''CUTEr (and SifDec): a Constrained and Unconstrained Testing Environment, revisited'', ACM Transactions on Mathematical Software, vol. 29, no. 4, pp. 373-394, 2003. [ Links ]
[8] K. A. De Jong. ''Analysis Of The Behavior Of A Class Of Genetic Adaptive System''. University of Michigan. Michigan, Technical Report No. 185, 1975 [ Links ]
[9] X. Yao, Y. Liu, y G. Lin. ''Evolutionary programming made faster'', IEEE Transactions on Evolutionary Computation. Vol. 3, no. 2, pp. 82-102,1999 [ Links ]
[10] A. D. Bukin. ''New Minimization Strategy For Non-Smooth Functions'', Budker Institute of Nuclear Physics preprint Novosibirsk, BUDKER-INP-1997-79, 1997 [ Links ]
[11] J.-S.R, Jang, et al., Neuro-Fuzzy and Soft Computing: A computational approach to learning and machine intelligence. Prentice Hall, 1996. [ Links ]
[12] N. Kasabov. Foundations of Neural Networks, Fuzzy Systems, and Knowledge Engineering, 2nd edn, Massachusetts Institute of Technology, 1998. [ Links ]
* Artículo de investigación científica y tecnológica. Es producto de la investigación realizada por el grupo de Optimización Heurística y Algoritmos Bio-Inspirados. Patrocinado por la Facultad de Minas, Universidad Nacional de Colombia, Medellín, Colombia.